add exam column
Browse filesThis view is limited to 50 files because it contains too many changes.
See raw diff
- APMO/segment_script/segment.py +1 -0
- APMO/segment_script/segment_02_03.py +1 -0
- APMO/segmented/en-apmo1989_sol.jsonl +6 -6
- APMO/segmented/en-apmo1990_sol.jsonl +9 -9
- APMO/segmented/en-apmo1991_sol.jsonl +7 -7
- APMO/segmented/en-apmo1992_sol.jsonl +5 -5
- APMO/segmented/en-apmo1993_sol.jsonl +5 -5
- APMO/segmented/en-apmo1994_sol.jsonl +7 -7
- APMO/segmented/en-apmo1999_sol.jsonl +6 -6
- APMO/segmented/en-apmo2000_sol.jsonl +6 -6
- APMO/segmented/en-apmo2002_sol.jsonl +10 -10
- APMO/segmented/en-apmo2003_sol.jsonl +7 -7
- APMO/segmented/en-apmo2004_sol.jsonl +8 -8
- APMO/segmented/en-apmo2005_sol.jsonl +5 -5
- APMO/segmented/en-apmo2006_sol.jsonl +5 -5
- APMO/segmented/en-apmo2007_sol.jsonl +8 -8
- APMO/segmented/en-apmo2008_sol.jsonl +5 -5
- APMO/segmented/en-apmo2009_sol.jsonl +5 -5
- APMO/segmented/en-apmo2010_sol.jsonl +5 -5
- APMO/segmented/en-apmo2013_sol.jsonl +5 -5
- APMO/segmented/en-apmo2014_sol.jsonl +5 -5
- APMO/segmented/en-apmo2015_sol.jsonl +5 -5
- APMO/segmented/en-apmo2016_sol.jsonl +8 -8
- APMO/segmented/en-apmo2017_sol.jsonl +7 -7
- APMO/segmented/en-apmo2018_sol.jsonl +9 -9
- APMO/segmented/en-apmo2019_sol.jsonl +10 -10
- APMO/segmented/en-apmo2020_sol.jsonl +8 -8
- APMO/segmented/en-apmo2021_sol.jsonl +8 -8
- APMO/segmented/en-apmo2022_sol.jsonl +10 -10
- APMO/segmented/en-apmo2023_sol.jsonl +8 -8
- APMO/segmented/en-apmo2024_sol.jsonl +8 -8
- Balkan_MO/segment_script/segment_type1 .py +1 -0
- Balkan_MO/segment_script/segment_type2.py +1 -0
- Balkan_MO/segment_script/segment_type3.py +1 -0
- Balkan_MO/segmented/en-2008-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2009-BMO-type2.jsonl +4 -4
- Balkan_MO/segmented/en-2010-BMO-type2.jsonl +4 -4
- Balkan_MO/segmented/en-2011-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2012-BMO-type3.jsonl +7 -7
- Balkan_MO/segmented/en-2013-BMO-type2.jsonl +4 -4
- Balkan_MO/segmented/en-2014-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2015-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2016-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2017-BMO-type3.jsonl +4 -4
- Balkan_MO/segmented/en-2018-BMO-type3.jsonl +5 -5
- Balkan_MO/segmented/en-2019-BMO-type1.jsonl +4 -4
- Balkan_MO/segmented/en-2020-BMO-type1.jsonl +8 -8
- Balkan_MO/segmented/en-2021-BMO-type1.jsonl +7 -7
- Balkan_MO/segmented/en-2022-BMO-type1.jsonl +9 -9
- Balkan_MO/segmented/en-2023-BMO-type1.jsonl +5 -5
APMO/segment_script/segment.py
CHANGED
|
@@ -80,6 +80,7 @@ def write_pairs(output_file: Path, pairs):
|
|
| 80 |
'tier': "T1",
|
| 81 |
'problem_label': problem_label,
|
| 82 |
'problem_type': None,
|
|
|
|
| 83 |
'problem': problem,
|
| 84 |
'solution': solution,
|
| 85 |
'metadata': {
|
|
|
|
| 80 |
'tier': "T1",
|
| 81 |
'problem_label': problem_label,
|
| 82 |
'problem_type': None,
|
| 83 |
+
'exam': 'APMO',
|
| 84 |
'problem': problem,
|
| 85 |
'solution': solution,
|
| 86 |
'metadata': {
|
APMO/segment_script/segment_02_03.py
CHANGED
|
@@ -80,6 +80,7 @@ def write_pairs(output_file: Path, pairs):
|
|
| 80 |
'tier': "T1",
|
| 81 |
'problem_label': problem_label,
|
| 82 |
'problem_type': None,
|
|
|
|
| 83 |
'problem': problem,
|
| 84 |
'solution': solution,
|
| 85 |
'metadata': {
|
|
|
|
| 80 |
'tier': "T1",
|
| 81 |
'problem_label': problem_label,
|
| 82 |
'problem_type': None,
|
| 83 |
+
'exam': 'APMO',
|
| 84 |
'problem': problem,
|
| 85 |
'solution': solution,
|
| 86 |
'metadata': {
|
APMO/segmented/en-apmo1989_sol.jsonl
CHANGED
|
@@ -1,6 +1,6 @@
|
|
| 1 |
-
{"year": "1989", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $x_{1}, x_{2}, \\ldots, x_{n}$ be positive real numbers, and let\n\n$$\nS=x_{1}+x_{2}+\\cdots+x_{n}\n$$\n\nProve that\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq 1+S+\\frac{S^{2}}{2!}+\\frac{S^{3}}{3!}+\\cdots+\\frac{S^{n}}{n!}\n$$", "solution": "Let $\\sigma_{k}$ be the $k$ th symmetric polynomial, namely\n\n$$\n\\sigma_{k}=\\sum_{\\substack{|S|=k \\\\ S \\subseteq\\{1,2, \\ldots, n\\}}} \\prod_{i \\in S} x_{i},\n$$\n\nand more explicitly\n\n$$\n\\sigma_{1}=S, \\quad \\sigma_{2}=x_{1} x_{2}+x_{1} x_{3}+\\cdots+x_{n-1} x_{n}, \\quad \\text { and so on. }\n$$\n\nThen\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right)=1+\\sigma_{1}+\\sigma_{2}+\\cdots+\\sigma_{n}\n$$\n\nThe expansion of\n\n$$\nS^{k}=\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)^{k}=\\underbrace{\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right) \\cdots\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)}_{k \\text { times }}\n$$\n\nhas at least $k$ ! occurrences of $\\prod_{i \\in S} x_{i}$ for each subset $S$ with $k$ indices from $\\{1,2, \\ldots, n\\}$. In fact, if $\\pi$ is a permutation of $S$, we can choose each $x_{\\pi(i)}$ from the $i$ th factor of $\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)^{k}$. Then each term appears at least $k$ ! times, and\n\n$$\nS^{k} \\geq k!\\sigma_{k} \\Longleftrightarrow \\sigma_{k} \\leq \\frac{S^{k}}{k!}\n$$\n\nSumming the obtained inequalities for $k=1,2, \\ldots, n$ yields the result.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
-
{"year": "1989", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $x_{1}, x_{2}, \\ldots, x_{n}$ be positive real numbers, and let\n\n$$\nS=x_{1}+x_{2}+\\cdots+x_{n}\n$$\n\nProve that\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq 1+S+\\frac{S^{2}}{2!}+\\frac{S^{3}}{3!}+\\cdots+\\frac{S^{n}}{n!}\n$$", "solution": "By AM-GM,\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq\\left(\\frac{\\left(1+x_{1}\\right)+\\left(1+x_{2}\\right)+\\cdots+\\left(1+x_{n}\\right)}{n}\\right)^{n}=\\left(1+\\frac{S}{n}\\right)^{n}\n$$\n\nBy the binomial theorem,\n\n$$\n\\left(1+\\frac{S}{n}\\right)^{n}=\\sum_{k=0}^{n}\\binom{n}{k}\\left(\\frac{S}{n}\\right)^{k}=\\sum_{k=0}^{n} \\frac{1}{k!} \\frac{n(n-1) \\ldots(n-k+1)}{n^{k}} S^{k} \\leq \\sum_{k=0}^{n} \\frac{S^{k}}{k!}\n$$\n\nand the result follows.\nComment: Maclaurin's inequality states that\n\n$$\n\\frac{\\sigma_{1}}{n} \\geq \\sqrt{\\frac{\\sigma_{2}}{\\binom{n}{2}}} \\geq \\cdots \\geq \\sqrt[k]{\\frac{\\sigma_{k}}{\\binom{n}{k}}} \\geq \\cdots \\geq \\sqrt[n]{\\frac{\\sigma_{n}}{\\binom{n}{n}}}\n$$\n\nThen $\\sigma_{k} \\leq\\binom{ n}{k} \\frac{S^{k}}{n^{k}}=\\frac{1}{k!} \\frac{n(n-1) \\ldots(n-k+1)}{n^{k}} S^{k} \\leq \\frac{S^{k}}{k!}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
-
{"year": "1989", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Prove that the equation\n\n$$\n6\\left(6 a^{2}+3 b^{2}+c^{2}\\right)=5 n^{2}\n$$\n\nhas no solutions in integers except $a=b=c=n=0$.", "solution": "We can suppose without loss of generality that $a, b, c, n \\geq 0$. Let $(a, b, c, n)$ be a solution with minimum sum $a+b+c+n$. Suppose, for the sake of contradiction, that $a+b+c+n>0$. Since 6 divides $5 n^{2}, n$ is a multiple of 6 . Let $n=6 n_{0}$. Then the equation reduces to\n\n$$\n6 a^{2}+3 b^{2}+c^{2}=30 n_{0}^{2}\n$$\n\nThe number $c$ is a multiple of 3 , so let $c=3 c_{0}$. The equation now reduces to\n\n$$\n2 a^{2}+b^{2}+3 c_{0}^{2}=10 n_{0}^{2}\n$$\n\nNow look at the equation modulo 8:\n\n$$\nb^{2}+3 c_{0}^{2} \\equiv 2\\left(n_{0}^{2}-a^{2}\\right) \\quad(\\bmod 8)\n$$\n\nIntegers $b$ and $c_{0}$ have the same parity. Either way, since $x^{2}$ is congruent to 0 or 1 modulo 4 , $b^{2}+3 c_{0}^{2}$ is a multiple of 4 , so $n_{0}^{2}-a^{2}=\\left(n_{0}-a\\right)\\left(n_{0}+a\\right)$ is even, and therefore also a multiple of 4 , since $n_{0}-a$ and $n_{0}+a$ have the same parity. Hence $2\\left(n_{0}^{2}-a^{2}\\right)$ is a multiple of 8 , and\n\n$$\nb^{2}+3 c_{0}^{2} \\equiv 0 \\quad(\\bmod 8)\n$$\n\nIf $b$ and $c_{0}$ are both odd, $b^{2}+3 c_{0}^{2} \\equiv 4(\\bmod 8)$, which is impossible. Then $b$ and $c_{0}$ are both even. Let $b=2 b_{0}$ and $c_{0}=2 c_{1}$, and we find\n\n$$\na^{2}+2 b_{0}^{2}+6 c_{1}^{2}=5 n_{0}^{2}\n$$\n\nLook at the last equation modulo 8:\n\n$$\na^{2}+3 n_{0}^{2} \\equiv 2\\left(c_{1}^{2}-b_{0}^{2}\\right) \\quad(\\bmod 8)\n$$\n\nA similar argument shows that $a$ and $n_{0}$ are both even.\nWe have proven that $a, b, c, n$ are all even. Then, dividing the original equation by 4 we find\n\n$$\n6\\left(6(a / 2)^{2}+3(b / 2)^{2}+(c / 2)^{2}\\right)=5(n / 2)^{2}\n$$\n\nand we find that $(a / 2, b / 2, c / 2, n / 2)$ is a new solution with smaller sum. This is a contradiction, and the only solution is $(a, b, c, n)=(0,0,0,0)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
-
{"year": "1989", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.\nAnswer: $\\frac{25}{49}$.", "solution": "Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。\n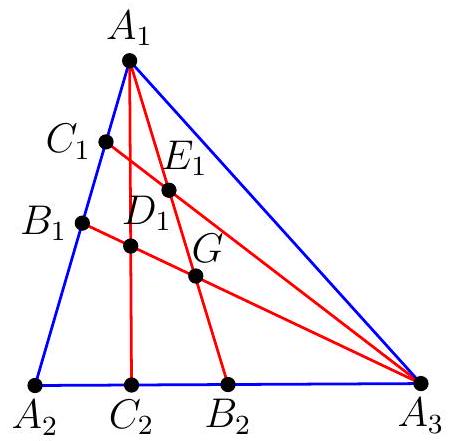\n\nBy Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,\n\n$$\n\\frac{A_{1} B_{1}}{A_{1} A_{2}} \\cdot \\frac{D_{1} A_{3}}{D_{1} B_{1}} \\cdot \\frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \\Longleftrightarrow \\frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \\cdot 3=6 \\Longleftrightarrow \\frac{D_{1} B_{1}}{A_{3} B_{1}}=\\frac{1}{7}\n$$\n\nSince $A_{3} G=\\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and\n\n$$\n\\frac{G D_{1}}{G A_{3}}=\\frac{4}{14}=\\frac{2}{7}\n$$\n\nSimilar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\\frac{2}{7}$.\nBy Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,\n\n$$\n\\frac{C_{1} A_{1}}{C_{1} A_{2}} \\cdot \\frac{E_{1} B_{2}}{E_{1} A_{1}} \\cdot \\frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \\Longleftrightarrow \\frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \\cdot \\frac{1}{2}=\\frac{3}{2} \\Longleftrightarrow \\frac{A_{1} E_{1}}{A_{1} B_{2}}=\\frac{2}{5}\n$$\n\nIf $A_{1} B_{2}=15 u$, then $A_{1} G=\\frac{2}{3} \\cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\\frac{2}{5} \\cdot 15 u=4 u$, and\n\n$$\n\\frac{G E_{1}}{G A_{1}}=\\frac{4}{10}=\\frac{2}{5}\n$$\n\nSimilar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\\frac{2}{5}$.\nThen $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\\frac{2}{7}: \\frac{2}{5}=-\\frac{5}{7}$, and the ratio of their area is $\\left(\\frac{5}{7}\\right)^{2}=\\frac{25}{49}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution\n"}}
|
| 5 |
-
{"year": "1989", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $S$ be a set consisting of $m$ pairs $(a, b)$ of positive integers with the property that $1 \\leq a<$ $b \\leq n$. Show that there are at least\n\n$$\n4 m \\frac{\\left(m-\\frac{n^{2}}{4}\\right)}{3 n}\n$$\n\ntriples $(a, b, c)$ such that $(a, b),(a, c)$, and $(b, c)$ belong to $S$.", "solution": "Call a triple $(a, b, c)$ good if and only if $(a, b),(a, c)$, and $(b, c)$ all belong to $S$. For $i$ in $\\{1,2, \\ldots, n\\}$, let $d_{i}$ be the number of pairs in $S$ that contain $i$, and let $D_{i}$ be the set of numbers paired with $i$ in $S$ (so $\\left|D_{i}\\right|=d_{i}$ ). Consider a pair $(i, j) \\in S$. Our goal is to estimate the number of integers $k$ such that any permutation of $\\{i, j, k\\}$ is good, that is, $\\left|D_{i} \\cap D_{j}\\right|$. Note that $i \\notin D_{i}$ and $j \\notin D_{j}$, so $i, j \\notin D_{i} \\cap D_{j}$; thus any $k \\in D_{i} \\cap D_{j}$ is different from both $i$ and $j$, and $\\{i, j, k\\}$ has three elements as required. Now, since $D_{i} \\cup D_{j} \\subseteq\\{1,2, \\ldots, n\\}$,\n\n$$\n\\left|D_{i} \\cap D_{j}\\right|=\\left|D_{i}\\right|+\\left|D_{j}\\right|-\\left|D_{i} \\cup D_{j}\\right| \\leq d_{i}+d_{j}-n\n$$\n\nSumming all the results, and having in mind that each good triple is counted three times (one for each two of the three numbers), the number of good triples $T$ is at least\n\n$$\nT \\geq \\frac{1}{3} \\sum_{(i, j) \\in S}\\left(d_{i}+d_{j}-n\\right)\n$$\n\nEach term $d_{i}$ appears each time $i$ is in a pair from $S$, that is, $d_{i}$ times; there are $m$ pairs in $S$, so $n$ is subtracted $m$ times. By the Cauchy-Schwartz inequality\n\n$$\nT \\geq \\frac{1}{3}\\left(\\sum_{i=1}^{n} d_{i}^{2}-m n\\right) \\geq \\frac{1}{3}\\left(\\frac{\\left(\\sum_{i=1}^{n} d_{i}\\right)^{2}}{n}-m n\\right) .\n$$\n\nFinally, the sum $\\sum_{i=1}^{n} d_{i}$ is $2 m$, since $d_{i}$ counts the number of pairs containing $i$, and each pair $(i, j)$ is counted twice: once in $d_{i}$ and once in $d_{j}$. Therefore\n\n$$\nT \\geq \\frac{1}{3}\\left(\\frac{(2 m)^{2}}{n}-m n\\right)=4 m \\frac{\\left(m-\\frac{n^{2}}{4}\\right)}{3 n} .\n$$\n\nComment: This is a celebrated graph theory fact named Goodman's bound, after A. M. Goodman's method published in 1959. The generalized version of the problem is still studied to this day.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
-
{"year": "1989", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Determine all functions $f$ from the reals to the reals for which\n(1) $f(x)$ is strictly increasing,\n(2) $f(x)+g(x)=2 x$ for all real $x$, where $g(x)$ is the composition inverse function to $f(x)$.\n(Note: $f$ and $g$ are said to be composition inverses if $f(g(x))=x$ and $g(f(x))=x$ for all real x.)\n\nAnswer: $f(x)=x+c, c \\in \\mathbb{R}$ constant.", "solution": "Denote by $f_{n}$ the $n$th iterate of $f$, that is, $f_{n}(x)=\\underbrace{f(f(\\ldots f}_{n \\text { times }}(x)))$.\nPlug $x \\rightarrow f_{n+1}(x)$ in (2): since $g\\left(f_{n+1}(x)\\right)=g\\left(f\\left(f_{n}(x)\\right)\\right)=f_{n}(x)$,\n\n$$\nf_{n+2}(x)+f_{n}(x)=2 f_{n+1}(x)\n$$\n\nthat is,\n\n$$\nf_{n+2}(x)-f_{n+1}(x)=f_{n+1}(x)-f_{n}(x)\n$$\n\nTherefore $f_{n}(x)-f_{n-1}(x)$ does not depend on $n$, and is equal to $f(x)-x$. Summing the corresponding results for smaller values of $n$ we find\n\n$$\nf_{n}(x)-x=n(f(x)-x) .\n$$\n\nSince $g$ has the same properties as $f$,\n\n$$\ng_{n}(x)-x=n(g(x)-x)=-n(f(x)-x) .\n$$\n\nFinally, $g$ is also increasing, because since $f$ is increasing $g(x)>g(y) \\Longrightarrow f(g(x))>$ $f(g(y)) \\Longrightarrow x>y$. An induction proves that $f_{n}$ and $g_{n}$ are also increasing functions.\nLet $x>y$ be real numbers. Since $f_{n}$ and $g_{n}$ are increasing,\n\n$$\nx+n(f(x)-x)>y+n(f(y)-y) \\Longleftrightarrow n[(f(x)-x)-(f(y)-y)]>y-x\n$$\n\nand\n\n$$\nx-n(f(x)-x)>y-n(f(y)-y) \\Longleftrightarrow n[(f(x)-x)-(f(y)-y)]<x-y\n$$\n\nSumming it up,\n\n$$\n|n[(f(x)-x)-(f(y)-y)]|<x-y \\quad \\text { for all } n \\in \\mathbb{Z}_{>0}\n$$\n\nSuppose that $a=f(x)-x$ and $b=f(y)-y$ are distinct. Then, for all positive integers $n$,\n\n$$\n|n(a-b)|<x-y\n$$\n\nwhich is false for a sufficiently large $n$. Hence $a=b$, and $f(x)-x$ is a constant $c$ for all $x \\in \\mathbb{R}$, that is, $f(x)=x+c$.\nIt is immediate that $f(x)=x+c$ satisfies the problem, as $g(x)=x-c$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "1989", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $x_{1}, x_{2}, \\ldots, x_{n}$ be positive real numbers, and let\n\n$$\nS=x_{1}+x_{2}+\\cdots+x_{n}\n$$\n\nProve that\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq 1+S+\\frac{S^{2}}{2!}+\\frac{S^{3}}{3!}+\\cdots+\\frac{S^{n}}{n!}\n$$", "solution": "Let $\\sigma_{k}$ be the $k$ th symmetric polynomial, namely\n\n$$\n\\sigma_{k}=\\sum_{\\substack{|S|=k \\\\ S \\subseteq\\{1,2, \\ldots, n\\}}} \\prod_{i \\in S} x_{i},\n$$\n\nand more explicitly\n\n$$\n\\sigma_{1}=S, \\quad \\sigma_{2}=x_{1} x_{2}+x_{1} x_{3}+\\cdots+x_{n-1} x_{n}, \\quad \\text { and so on. }\n$$\n\nThen\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right)=1+\\sigma_{1}+\\sigma_{2}+\\cdots+\\sigma_{n}\n$$\n\nThe expansion of\n\n$$\nS^{k}=\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)^{k}=\\underbrace{\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right) \\cdots\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)}_{k \\text { times }}\n$$\n\nhas at least $k$ ! occurrences of $\\prod_{i \\in S} x_{i}$ for each subset $S$ with $k$ indices from $\\{1,2, \\ldots, n\\}$. In fact, if $\\pi$ is a permutation of $S$, we can choose each $x_{\\pi(i)}$ from the $i$ th factor of $\\left(x_{1}+x_{2}+\\cdots+x_{n}\\right)^{k}$. Then each term appears at least $k$ ! times, and\n\n$$\nS^{k} \\geq k!\\sigma_{k} \\Longleftrightarrow \\sigma_{k} \\leq \\frac{S^{k}}{k!}\n$$\n\nSumming the obtained inequalities for $k=1,2, \\ldots, n$ yields the result.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
+
{"year": "1989", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $x_{1}, x_{2}, \\ldots, x_{n}$ be positive real numbers, and let\n\n$$\nS=x_{1}+x_{2}+\\cdots+x_{n}\n$$\n\nProve that\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq 1+S+\\frac{S^{2}}{2!}+\\frac{S^{3}}{3!}+\\cdots+\\frac{S^{n}}{n!}\n$$", "solution": "By AM-GM,\n\n$$\n\\left(1+x_{1}\\right)\\left(1+x_{2}\\right) \\cdots\\left(1+x_{n}\\right) \\leq\\left(\\frac{\\left(1+x_{1}\\right)+\\left(1+x_{2}\\right)+\\cdots+\\left(1+x_{n}\\right)}{n}\\right)^{n}=\\left(1+\\frac{S}{n}\\right)^{n}\n$$\n\nBy the binomial theorem,\n\n$$\n\\left(1+\\frac{S}{n}\\right)^{n}=\\sum_{k=0}^{n}\\binom{n}{k}\\left(\\frac{S}{n}\\right)^{k}=\\sum_{k=0}^{n} \\frac{1}{k!} \\frac{n(n-1) \\ldots(n-k+1)}{n^{k}} S^{k} \\leq \\sum_{k=0}^{n} \\frac{S^{k}}{k!}\n$$\n\nand the result follows.\nComment: Maclaurin's inequality states that\n\n$$\n\\frac{\\sigma_{1}}{n} \\geq \\sqrt{\\frac{\\sigma_{2}}{\\binom{n}{2}}} \\geq \\cdots \\geq \\sqrt[k]{\\frac{\\sigma_{k}}{\\binom{n}{k}}} \\geq \\cdots \\geq \\sqrt[n]{\\frac{\\sigma_{n}}{\\binom{n}{n}}}\n$$\n\nThen $\\sigma_{k} \\leq\\binom{ n}{k} \\frac{S^{k}}{n^{k}}=\\frac{1}{k!} \\frac{n(n-1) \\ldots(n-k+1)}{n^{k}} S^{k} \\leq \\frac{S^{k}}{k!}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
+
{"year": "1989", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Prove that the equation\n\n$$\n6\\left(6 a^{2}+3 b^{2}+c^{2}\\right)=5 n^{2}\n$$\n\nhas no solutions in integers except $a=b=c=n=0$.", "solution": "We can suppose without loss of generality that $a, b, c, n \\geq 0$. Let $(a, b, c, n)$ be a solution with minimum sum $a+b+c+n$. Suppose, for the sake of contradiction, that $a+b+c+n>0$. Since 6 divides $5 n^{2}, n$ is a multiple of 6 . Let $n=6 n_{0}$. Then the equation reduces to\n\n$$\n6 a^{2}+3 b^{2}+c^{2}=30 n_{0}^{2}\n$$\n\nThe number $c$ is a multiple of 3 , so let $c=3 c_{0}$. The equation now reduces to\n\n$$\n2 a^{2}+b^{2}+3 c_{0}^{2}=10 n_{0}^{2}\n$$\n\nNow look at the equation modulo 8:\n\n$$\nb^{2}+3 c_{0}^{2} \\equiv 2\\left(n_{0}^{2}-a^{2}\\right) \\quad(\\bmod 8)\n$$\n\nIntegers $b$ and $c_{0}$ have the same parity. Either way, since $x^{2}$ is congruent to 0 or 1 modulo 4 , $b^{2}+3 c_{0}^{2}$ is a multiple of 4 , so $n_{0}^{2}-a^{2}=\\left(n_{0}-a\\right)\\left(n_{0}+a\\right)$ is even, and therefore also a multiple of 4 , since $n_{0}-a$ and $n_{0}+a$ have the same parity. Hence $2\\left(n_{0}^{2}-a^{2}\\right)$ is a multiple of 8 , and\n\n$$\nb^{2}+3 c_{0}^{2} \\equiv 0 \\quad(\\bmod 8)\n$$\n\nIf $b$ and $c_{0}$ are both odd, $b^{2}+3 c_{0}^{2} \\equiv 4(\\bmod 8)$, which is impossible. Then $b$ and $c_{0}$ are both even. Let $b=2 b_{0}$ and $c_{0}=2 c_{1}$, and we find\n\n$$\na^{2}+2 b_{0}^{2}+6 c_{1}^{2}=5 n_{0}^{2}\n$$\n\nLook at the last equation modulo 8:\n\n$$\na^{2}+3 n_{0}^{2} \\equiv 2\\left(c_{1}^{2}-b_{0}^{2}\\right) \\quad(\\bmod 8)\n$$\n\nA similar argument shows that $a$ and $n_{0}$ are both even.\nWe have proven that $a, b, c, n$ are all even. Then, dividing the original equation by 4 we find\n\n$$\n6\\left(6(a / 2)^{2}+3(b / 2)^{2}+(c / 2)^{2}\\right)=5(n / 2)^{2}\n$$\n\nand we find that $(a / 2, b / 2, c / 2, n / 2)$ is a new solution with smaller sum. This is a contradiction, and the only solution is $(a, b, c, n)=(0,0,0,0)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
+
{"year": "1989", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.\nAnswer: $\\frac{25}{49}$.", "solution": "Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。\n\n\nBy Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,\n\n$$\n\\frac{A_{1} B_{1}}{A_{1} A_{2}} \\cdot \\frac{D_{1} A_{3}}{D_{1} B_{1}} \\cdot \\frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \\Longleftrightarrow \\frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \\cdot 3=6 \\Longleftrightarrow \\frac{D_{1} B_{1}}{A_{3} B_{1}}=\\frac{1}{7}\n$$\n\nSince $A_{3} G=\\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and\n\n$$\n\\frac{G D_{1}}{G A_{3}}=\\frac{4}{14}=\\frac{2}{7}\n$$\n\nSimilar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\\frac{2}{7}$.\nBy Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,\n\n$$\n\\frac{C_{1} A_{1}}{C_{1} A_{2}} \\cdot \\frac{E_{1} B_{2}}{E_{1} A_{1}} \\cdot \\frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \\Longleftrightarrow \\frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \\cdot \\frac{1}{2}=\\frac{3}{2} \\Longleftrightarrow \\frac{A_{1} E_{1}}{A_{1} B_{2}}=\\frac{2}{5}\n$$\n\nIf $A_{1} B_{2}=15 u$, then $A_{1} G=\\frac{2}{3} \\cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\\frac{2}{5} \\cdot 15 u=4 u$, and\n\n$$\n\\frac{G E_{1}}{G A_{1}}=\\frac{4}{10}=\\frac{2}{5}\n$$\n\nSimilar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\\frac{2}{5}$.\nThen $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\\frac{2}{7}: \\frac{2}{5}=-\\frac{5}{7}$, and the ratio of their area is $\\left(\\frac{5}{7}\\right)^{2}=\\frac{25}{49}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution\n"}}
|
| 5 |
+
{"year": "1989", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $S$ be a set consisting of $m$ pairs $(a, b)$ of positive integers with the property that $1 \\leq a<$ $b \\leq n$. Show that there are at least\n\n$$\n4 m \\frac{\\left(m-\\frac{n^{2}}{4}\\right)}{3 n}\n$$\n\ntriples $(a, b, c)$ such that $(a, b),(a, c)$, and $(b, c)$ belong to $S$.", "solution": "Call a triple $(a, b, c)$ good if and only if $(a, b),(a, c)$, and $(b, c)$ all belong to $S$. For $i$ in $\\{1,2, \\ldots, n\\}$, let $d_{i}$ be the number of pairs in $S$ that contain $i$, and let $D_{i}$ be the set of numbers paired with $i$ in $S$ (so $\\left|D_{i}\\right|=d_{i}$ ). Consider a pair $(i, j) \\in S$. Our goal is to estimate the number of integers $k$ such that any permutation of $\\{i, j, k\\}$ is good, that is, $\\left|D_{i} \\cap D_{j}\\right|$. Note that $i \\notin D_{i}$ and $j \\notin D_{j}$, so $i, j \\notin D_{i} \\cap D_{j}$; thus any $k \\in D_{i} \\cap D_{j}$ is different from both $i$ and $j$, and $\\{i, j, k\\}$ has three elements as required. Now, since $D_{i} \\cup D_{j} \\subseteq\\{1,2, \\ldots, n\\}$,\n\n$$\n\\left|D_{i} \\cap D_{j}\\right|=\\left|D_{i}\\right|+\\left|D_{j}\\right|-\\left|D_{i} \\cup D_{j}\\right| \\leq d_{i}+d_{j}-n\n$$\n\nSumming all the results, and having in mind that each good triple is counted three times (one for each two of the three numbers), the number of good triples $T$ is at least\n\n$$\nT \\geq \\frac{1}{3} \\sum_{(i, j) \\in S}\\left(d_{i}+d_{j}-n\\right)\n$$\n\nEach term $d_{i}$ appears each time $i$ is in a pair from $S$, that is, $d_{i}$ times; there are $m$ pairs in $S$, so $n$ is subtracted $m$ times. By the Cauchy-Schwartz inequality\n\n$$\nT \\geq \\frac{1}{3}\\left(\\sum_{i=1}^{n} d_{i}^{2}-m n\\right) \\geq \\frac{1}{3}\\left(\\frac{\\left(\\sum_{i=1}^{n} d_{i}\\right)^{2}}{n}-m n\\right) .\n$$\n\nFinally, the sum $\\sum_{i=1}^{n} d_{i}$ is $2 m$, since $d_{i}$ counts the number of pairs containing $i$, and each pair $(i, j)$ is counted twice: once in $d_{i}$ and once in $d_{j}$. Therefore\n\n$$\nT \\geq \\frac{1}{3}\\left(\\frac{(2 m)^{2}}{n}-m n\\right)=4 m \\frac{\\left(m-\\frac{n^{2}}{4}\\right)}{3 n} .\n$$\n\nComment: This is a celebrated graph theory fact named Goodman's bound, after A. M. Goodman's method published in 1959. The generalized version of the problem is still studied to this day.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
+
{"year": "1989", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Determine all functions $f$ from the reals to the reals for which\n(1) $f(x)$ is strictly increasing,\n(2) $f(x)+g(x)=2 x$ for all real $x$, where $g(x)$ is the composition inverse function to $f(x)$.\n(Note: $f$ and $g$ are said to be composition inverses if $f(g(x))=x$ and $g(f(x))=x$ for all real x.)\n\nAnswer: $f(x)=x+c, c \\in \\mathbb{R}$ constant.", "solution": "Denote by $f_{n}$ the $n$th iterate of $f$, that is, $f_{n}(x)=\\underbrace{f(f(\\ldots f}_{n \\text { times }}(x)))$.\nPlug $x \\rightarrow f_{n+1}(x)$ in (2): since $g\\left(f_{n+1}(x)\\right)=g\\left(f\\left(f_{n}(x)\\right)\\right)=f_{n}(x)$,\n\n$$\nf_{n+2}(x)+f_{n}(x)=2 f_{n+1}(x)\n$$\n\nthat is,\n\n$$\nf_{n+2}(x)-f_{n+1}(x)=f_{n+1}(x)-f_{n}(x)\n$$\n\nTherefore $f_{n}(x)-f_{n-1}(x)$ does not depend on $n$, and is equal to $f(x)-x$. Summing the corresponding results for smaller values of $n$ we find\n\n$$\nf_{n}(x)-x=n(f(x)-x) .\n$$\n\nSince $g$ has the same properties as $f$,\n\n$$\ng_{n}(x)-x=n(g(x)-x)=-n(f(x)-x) .\n$$\n\nFinally, $g$ is also increasing, because since $f$ is increasing $g(x)>g(y) \\Longrightarrow f(g(x))>$ $f(g(y)) \\Longrightarrow x>y$. An induction proves that $f_{n}$ and $g_{n}$ are also increasing functions.\nLet $x>y$ be real numbers. Since $f_{n}$ and $g_{n}$ are increasing,\n\n$$\nx+n(f(x)-x)>y+n(f(y)-y) \\Longleftrightarrow n[(f(x)-x)-(f(y)-y)]>y-x\n$$\n\nand\n\n$$\nx-n(f(x)-x)>y-n(f(y)-y) \\Longleftrightarrow n[(f(x)-x)-(f(y)-y)]<x-y\n$$\n\nSumming it up,\n\n$$\n|n[(f(x)-x)-(f(y)-y)]|<x-y \\quad \\text { for all } n \\in \\mathbb{Z}_{>0}\n$$\n\nSuppose that $a=f(x)-x$ and $b=f(y)-y$ are distinct. Then, for all positive integers $n$,\n\n$$\n|n(a-b)|<x-y\n$$\n\nwhich is false for a sufficiently large $n$. Hence $a=b$, and $f(x)-x$ is a constant $c$ for all $x \\in \\mathbb{R}$, that is, $f(x)=x+c$.\nIt is immediate that $f(x)=x+c$ satisfies the problem, as $g(x)=x-c$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo1990_sol.jsonl
CHANGED
|
@@ -1,9 +1,9 @@
|
|
| 1 |
-
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "Let $I$ be the intersection of $A G$ and $E F$.\nLet $\\delta=A I . I G-F I$ IE. Then\n\n$$\nA I=A D / 2, \\quad I G=A D / 6, \\quad F I=B C / 4=I E\n$$\n\nFurther, applying the cosine rule to triangles $A B D, A C D$ we get\n\n$$\n\\begin{aligned}\nA B^{2} & =B C^{2} / 4+A D^{2}-A D \\cdot B C \\cdot \\cos \\angle B D A, \\\\\nA C^{2} & =B C^{2} / 4+A D^{2}+A D \\cdot B C \\cdot \\cos \\angle B D A, \\\\\n\\text { so } \\quad A D^{2} & =\\left(A B^{2}+A C^{2}-B C^{2} / 2\\right) / 2\n\\end{aligned}\n$$\n\nHence\n\n$$\n\\begin{aligned}\n\\delta & =\\left(A B^{2}+A C^{2}-2 B C^{2}\\right) / 24 \\\\\n& =\\left(4 A B \\cdot A C \\cdot \\cos \\angle B A C-A B^{2}-A C^{2}\\right)\n\\end{aligned}\n$$\n\nNow $A E F G$ is a cyclic quadrilateral if and only if $\\delta=0$, i.e. if and only if\n\n$$\n\\begin{aligned}\n\\cos \\angle B A C & =\\left(A B^{2}+A B^{2}\\right) /(4 \\cdot A B \\cdot A C) \\\\\n& =(A B / A C+A C / A B) / 4\n\\end{aligned}\n$$\n\n5\nNow $A B / A C+A C / A B \\geq 2$. Hence $\\cos \\angle B A C \\geq 1 / 2$ and so $\\angle B A C \\leq 60^{\\circ}$.\nFor $\\angle B A C>60^{\\circ}$ there is no triangle with the required property.\nFor $\\angle B A C=60^{\\circ}$ there exists, within similarity, precisely one triangle (which is equilateral) having the required property.\nFor $\\angle B A C<60^{\\circ}$ there exists, within similarity, again precisely one triangle having the required property (even though for fixed median $A E$ there are two, but one arises from the other by interchanging point $B$ with point $C$, thus proving them to be similar).", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "# FIRST SOLUTION\n\n"}}
|
| 2 |
-
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "(Mr Marcus Brazil, La Trobe University, Bundoora, Melbourne, Australia):\nWe require, as above,\n\n$$\nA I \\cdot I G=E I \\cdot I F\n$$\n\n(which by (1) is equivalent to $A D^{2} / 3=C D^{2}$, i.e. $A D=C D \\cdot \\sqrt{3}$ ).\nLet, without loss of generality, $C D=1$. Then $A$ lies on the circle of radius $\\sqrt{3}$ with centre $D$. If $C D$ and $D A$ are perpendicular, the angle $B A C$ is $60^{\\circ}$, otherwise it must be less.\nIn this case, for each angle $B A C$ there are two solutions, which are congruent.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "\nSECOND SOLUTION "}}
|
| 3 |
-
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "in the figure as shown below, we first show that it is necessary that $\\angle A$ is less than $90^{\\circ}$ if the quadrilateral $A E G F$ ; cyclic.\n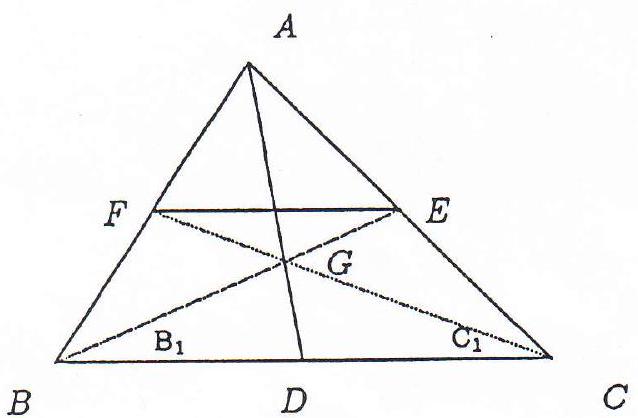\n\nNow, since $E F \\| B C$, we get\n\n$$\n\\begin{aligned}\n\\angle E G F & =180^{\\circ}-\\left(B_{1}+C_{1}\\right) \\\\\n& \\geq 180^{\\circ}-(B+C) \\\\\n& =A .\n\\end{aligned}\n$$\n\n(1)\n\nThus, if $A E G F$ is cyclic, we would have $\\angle E G F+\\angle A=180^{\\circ}$. Therefore it is necessary that $0<\\angle A \\leq 90^{\\circ}$.\n\n## Continuation \"A\"\n\nLet $O$ be the circumcentre of $\\triangle A F E$. Without loss of generality, let the radius of this circle be 1.\nWe then let $A=1, F=z=e^{i \\theta}$ and $E=z e^{2 i \\alpha}=e^{i(\\theta+2 \\alpha)}$.\nThen $\\angle A=\\alpha, 0<\\alpha \\leq 90^{\\circ}$, and $0<\\theta<360^{\\circ}-2 \\alpha$.\nThus,\n\n$$\nB=2 z-1\n$$\n\nand\n\n$$\n\\begin{aligned}\nG & =\\frac{1}{3}(2 z-1)+\\frac{2}{3}\\left(z e^{2 i \\alpha}\\right) \\\\\n& =\\frac{1}{3}\\left(2 e^{i \\theta}+2 e^{i(\\theta+2 \\alpha)}-1\\right)\n\\end{aligned}\n$$\n\nFor quadrilateral $A F G E$ to be cyclic, it is now necessary that\n\n$$\n|G|=1 .\n$$\n\n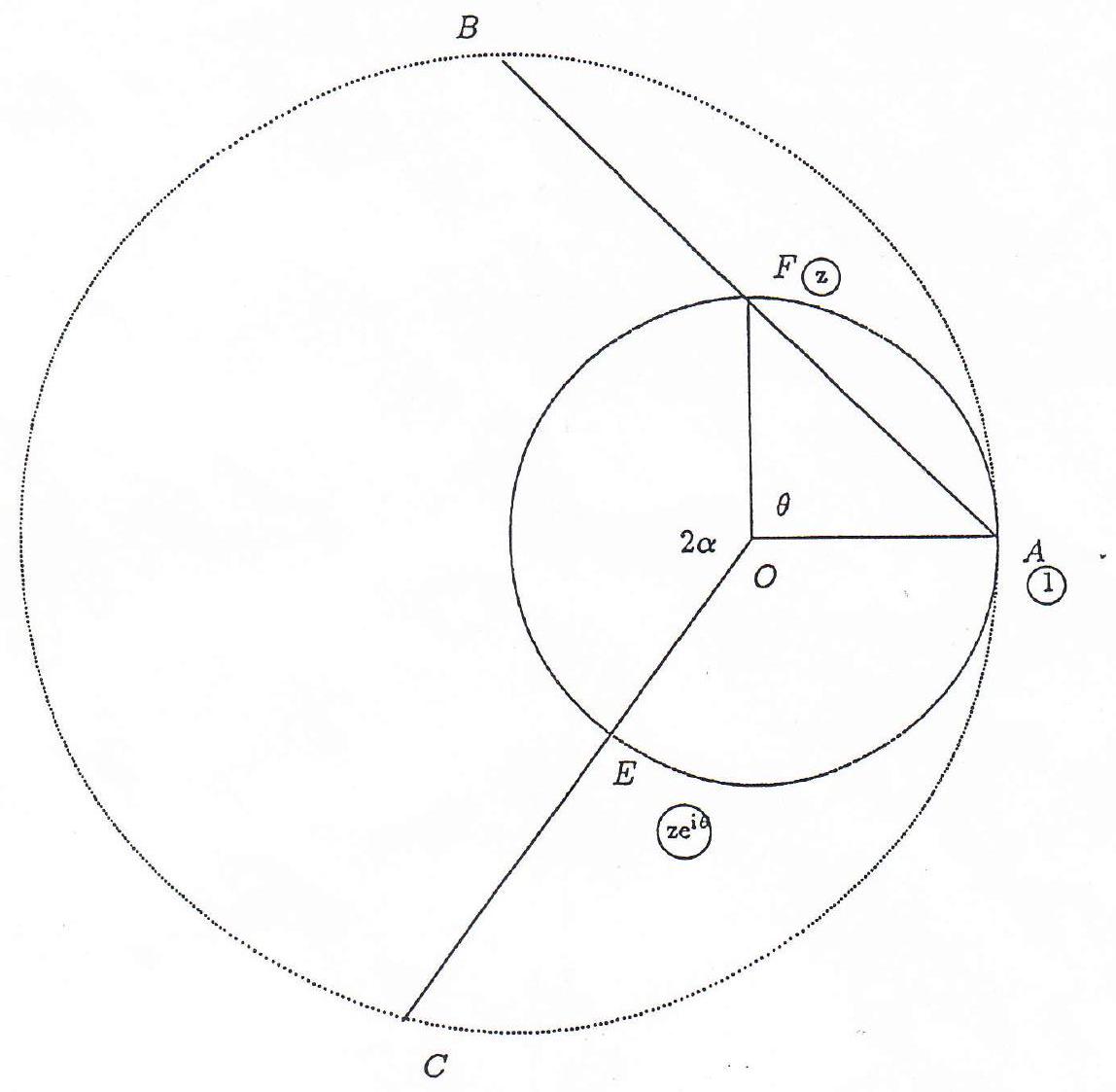\n\nFor $|G|=1$, we must have\n\n$$\n\\begin{aligned}\n9= & (2 \\cos (\\theta)+2 \\cos (\\theta+2 \\alpha)-1)^{2}+(2 \\sin (\\theta)+2 \\sin (\\theta+2 \\alpha))^{2} \\\\\n= & 4\\left(\\cos ^{2}(\\theta)+\\sin ^{2}(\\theta)\\right)+4\\left(\\cos ^{2}(\\theta+2 \\alpha)+\\sin ^{2}(\\theta+2 \\alpha)\\right)+1 \\\\\n& +8(\\cos (\\theta) \\cos (\\theta+2 \\alpha)+\\sin (\\theta) \\sin (\\theta+2 \\alpha))-4 \\cos (\\theta)-4 \\cos (\\theta+2 \\alpha) \\\\\n= & 9+8 \\cos (2 \\alpha)-8 \\cos (\\alpha) \\cos (\\theta+\\alpha)\n\\end{aligned}\n$$\n\nso that\n\n$$\n\\cos (\\theta+\\alpha)=\\frac{\\cos (2 \\alpha)}{\\cos (\\alpha)}\n$$\n\n] Now, $\\left|\\frac{\\cos (2 \\alpha)}{\\cos (\\alpha)}\\right| \\leq 1$ if and only if $\\alpha \\in\\left(0,60^{\\circ}\\right]$ in the range of $\\alpha$ under consideration, that is $\\alpha \\in\\left(0,00^{\\circ}\\right]$. There is equality if and only if $\\alpha=60^{\\circ}$.\n\n$\\square$ Note there is only one solution. The apparent other solution is the mirror image of the first. We are solving for $\\alpha+\\theta$. The other solution is $360^{\\circ}-\\alpha-\\theta$.\n\n## Continuation \"B\"\n\nLet $O$ be the circumcentre of triangle $A E F$. Let $A P$ be a diameter of this circle. Construct the circle with centre $P$ and radius $A P$. Then $B$ and $C$ lie on this circle.\n\nIt is clear that the problem is solved if we allow the angle $\\angle B A C=\\alpha$ to vary and restrict $B$ and $C$ to the constructed circle.\n\nLet $\\theta$ be the angle from the drawn axis. Then $\\theta$ lies in the range $\\left(0,180^{\\circ}-\\alpha\\right)$. We must not forget the necessary restriction of $\\alpha$, that is $\\alpha \\in\\left(0,90^{\\circ}\\right.$.\n\n\nNow, $D$ lies on an arc of a circle, centre $P$, radius $P D$ exterior to the circle, centre $O$, radius $A O$.\nBy similarity, $G$, lies on an arc of a circle, centre $Q$, radius $Q G$ where $A Q=\\frac{2}{3} A P$ and $Q G=\\frac{2}{3} P D$.\nFor the quadrilateral $A F G E$ to be cyclic, we must have that the radius $Q G$ is greater than or equal to $Q P$.\nThe easiest way to calulate these radii is to consider the case in which the diameter $A P$ bisects the angle $\\angle B A C$.\nThus we re-draw the diagram as below. Let $A H$ be a diameter of the larger circle.\n\n\nThus we have $A H=4$ and by similar triangles,\n\n$$\n\\frac{A D}{A B}=\\frac{A B}{A H}=\\cos \\left(\\frac{\\alpha}{2}\\right)\n$$\n\nso that\n\n$$\n\\begin{aligned}\nA D & =4 \\cos ^{2}\\left(\\frac{\\alpha}{2}\\right) \\\\\n& =2+2 \\cos (\\alpha) .\n\\end{aligned}\n$$\n\nThus $P D=2 \\cos (\\alpha)$ and $Q G=\\frac{2}{3} 2 \\cos (\\alpha)=\\frac{4}{3} \\cos (\\alpha)$.\nThe necessary condition for a cyclic quadrilateral is then\n\n$$\n\\frac{4}{3}(1+\\cos (\\alpha)) \\geq 2\n$$\n\n[5\n\n$$\n\\cos (\\alpha) \\geq \\frac{1}{2}\n$$\n\n:7\nThus it is clear that there is precisely one (up to similarity) solution for $0<\\alpha \\leq 60^{\\circ}$ and no solutions otherwise.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "\nTHIRD SOLUTION\n"}}
|
| 4 |
-
{"year": "1990", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \\ldots, a_{n}$ taken $k$ at a time.\nShow that\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}^{2} a_{1} a_{2} \\ldots a_{n}, \\quad \\text { for } \\quad k=1,2, \\ldots, n-1\n$$", "solution": "$$\n\\binom{n}{k} a_{1} a_{2} \\ldots a_{n}\n$$\n\n$2=\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}} \\cdot a_{1} a_{2} \\ldots a_{n} / a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}$\n(and using the Cauchy-Schwarz inequality)\n\n$$\n\\begin{aligned}\n& \\leq\\left(\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}\\right)^{\\frac{1}{2}} \\cdot\\left(\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{1} a_{2} \\ldots a_{n} / a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}\\right)^{\\frac{1}{2}} \\\\\n& =S_{k}^{\\frac{1}{2}} \\cdot S_{n-k}^{\\frac{1}{2}}\n\\end{aligned}\n$$\n\nTherefore\n\n$$\n\\binom{n}{k}^{2} a_{1} a_{2} \\ldots a_{n} \\leq S_{k} S_{n-k}\n$$\n\nq.e.d.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 2", "solution_match": "# FIRST SOLUTION\n\n"}}
|
| 5 |
-
{"year": "1990", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \\ldots, a_{n}$ taken $k$ at a time.\nShow that\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}^{2} a_{1} a_{2} \\ldots a_{n}, \\quad \\text { for } \\quad k=1,2, \\ldots, n-1\n$$", "solution": "(provided by the Canadian Problems Committee).\nWrite $S_{k}$ as $\\sum_{i=1}^{\\binom{n}{k}} t_{i}$. Then\n주\n\n$$\nS_{n-k}=\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left(\\sum_{i=1}^{\\binom{n}{k}} \\frac{1}{t_{i}}\\right)\n$$\n\n$$\n\\text { so that } \\left.\\begin{array}{rl}\nS_{k} S_{n-k} & =\\left(\\prod_{m=1}^{n} a_{m}\\right) \\cdot\\left(\\begin{array}{l}\n\\binom{n}{k} \\\\\ni=1\n\\end{array} t_{i}\\right)\\left(\\begin{array}{l}\n\\binom{n}{k} \\\\\n\\sum_{j=1}^{2}\n\\end{array} \\frac{1}{t_{j}}\\right) \\\\\n& =\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left[\\sum_{i=1}^{\\binom{n}{k}} 1+\\sum_{i=1}^{\\binom{n}{k}} \\sum_{j=1}^{n} \\begin{array}{l}\nn \\\\\nk\n\\end{array}\\right) \\\\\n\\frac{t_{i}}{} \\\\\nt_{j}\n\\end{array}\\right] .\n$$\n\nAs there are\n\n$$\n\\frac{\\binom{n}{k}^{2}-\\binom{n}{k}}{2}\n$$\n\nterms in the sum\n\n\n$$\n\\begin{aligned}\nS_{k} S_{n-k} & \\geq\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left[\\binom{n}{k}+2 \\cdot \\frac{\\binom{n}{k}^{2}-\\binom{n}{k}}{2}\\right] \\\\\n& =\\binom{n}{k}^{2}\\left(\\prod_{m=1}^{n} a_{m}\\right)\n\\end{aligned}\n$$\n\nsince $\\frac{t_{i}}{t_{j}}+\\frac{t_{j}}{t_{i}} \\geq 2$ for $t_{i}, t_{j}>0$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 2", "solution_match": "\nSECOND SOLUTION "}}
|
| 6 |
-
{"year": "1990", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Consider all the triangles $A B C$ which have a fixed base $A B$ and whose altitude from $C$ is a constant $h$. For which of these triangles is the product of its altitudes a maximum?", "solution": "Let $h_{a}$ and $h_{b}$ be the altitudes from $A$ and $B$, respectively. Then\n\n$$\n\\begin{aligned}\nA B \\cdot h \\cdot A C \\cdot h_{b} \\cdot B C \\cdot h_{a} & =8 . \\text { area of } \\triangle A B C)^{3} \\\\\n& =(A B \\cdot h)^{3},\n\\end{aligned}\n$$\n\n园\nwhich is a constant. So the product $h . h_{a} \\cdot h_{b}$ attains its maximum when the product $A C . B C$ attains its minimum.\nSince\n\n$$\n\\begin{aligned}\n(\\sin C) \\cdot A C \\cdot B C & =B C \\cdot h_{a} \\\\\n& =2 \\cdot \\text { area of } \\triangle A B C\n\\end{aligned}\n$$\n\n(3)\nwhich is a constant, $A C \\cdot B C$ attains its minimum when $\\sin C$ reaches its maximum. There are two cases:\n(a) $h \\leq A B / 2$. Then there exists a triangle $A B C$ which has a right angle at $C$, and for precisely such a triangle $\\sin C$ attains its maximum, namely 1 .\n(b) $h>A B / 2$. In this case the angle at $C$ is acute and assumes its maximum when the triangle is isosceles.\n\nNote that a solution using calculus obviously exists.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 3", "solution_match": "# SOLUTION:"}}
|
| 7 |
-
{"year": "1990", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "A set of 1990 persons is divided into non-intersecting subsets in such a way that\n(a) no one in a subset knows all the others in the subset;\n(b) among any three persons in a subset, there are always at least two who do not know each other; and\n(c) for any two persons in a subset who do not know each other, there is exactly one person in the same subset knowing both of them.\n(i) Prove that within each subset, every person has the same number of acquaintances.\n(ii) Determine the maximum possible number of subsets.\n\nNote: it is understood that if a person $A$ knows person $B$, then person $B$ will know person $A$; an acquaintance is someone who is known. Every person is assumed to know one's self.", "solution": "(i) Let $S$ be a subset of persons satisfying conditions (a), (b) and (c). Let $x \\in S$ be one who knows the maximum number of persons in $S$.\nAssume that $x$ knows $x_{1}, x_{2}, \\ldots, x_{n}$. By (b), $x_{i}$ and $x_{j}$ are strangers if $i \\neq j$. For each $x_{i}$, let $N_{i}$ be the set of persons in $S$ who know $x_{i}$ but not $x$. Note that, for $i \\neq j, N_{i}$ has no person in common with $N_{j}$, otherwise there would be more than one person knowing $x_{i}$ and $x_{j}$, contradicting (c).\nBy (a) we may assume that $N_{1}$ is not empty.) Let $y_{1} \\in N_{1}$. By (c), for each $k>1$, there is exactly one person $y_{k}$ in $N_{k}$ who knows $y_{1}$. This means that $y_{1}$ knows $n$ persons, namely $x_{1}, y_{2}, \\ldots, y_{n}$.\nBecause $n$ is the maximal number of persons in $S$ a person in $S$ can know, $y_{1}$ knows exactly $n$ persons in $S$. By precisely the same reasoning we find that each person in $N_{i}$, $i=1,2, \\ldots, n$, knows exactly $n$ persons in $S$.\nLetting $y_{1}$ take the role of $x$ in our argument, we see that also each $x_{i}$ knows exactly $n$ persons. Note that, by (c), every person in $S$ other than $x, x_{1}, \\ldots, x_{n}$, must be in some $N_{j}$. Therefore every person in $S$ knows exactly $n$ persons in $S$ and thus has the same number of acquaintances in $S$.\n(ii) To maximize the number of subsets, we have to minimize the size of each group. The smallest possible subset is one in which every person knows exactly two persons, and hence there must be exactly five persons in the subset, forming a cycle where two persons stand side by side only if they know each other. Therefore the maximum possible number of subsets is 1990/5 $=398$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 4", "solution_match": "# SOLUTION:"}}
|
| 8 |
-
{"year": "1990", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Show that for every integer $n \\geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.", "solution": "(provided by the Canadian Problems Committee).\nThe basic building blocks will be right angled triangles with sides $p, q$ (which are positive integers) adjacent to the right angle.\n\n\nIn the first instance, we take $p=q=1$ and construct five basic building blocks: $L_{1}, L_{2}, M, R_{1}$ and $R_{2}$ 。\n\n## [3)\n\n\n$L_{1}$\n\n$L_{2}$\n\nM\n\n$R_{1}$\n\n$R_{2}$\n\nWe shall now build convex hexagons by taking, on the left, one of the blocks $L_{i}$, attaching $n$ copies of the block $M$, and finally attaching one of the blocks $R_{j}$. We must therefore exclude the case when $(i, j)=(2,1)$ for this does not generate a hexagon. Further, for $(i, j)=(1,1)$ or $(i, j)=(1,2)$, we require that $n \\geq 1$, whereas for $(i, j)=$ $(2,2)$, we only need require that $n \\geq 0$.\n\nThus, with the obvious interpretation:\n$L_{1}+n M+R_{1}$ gives a convex hexagon containing $2+4 n+2=4 n+4 \\quad(n \\geq 1)$ congruent triangles;\n$L_{1}+n M+R_{2}$ gives a convex hexagon containing $2+4 n+3=4 n+5(n \\geq 1)$ congruent triangles; and\n$L_{2}+n M+R_{2}$ gives a convex hexagon containing $3+4 n+3=4 n+6 \\quad(n \\geq 0)$ congruent triangles, or $4 n+2(n \\geq 1)$ congruent triangles.\n\nWe shall now modify the lengths of the sides of the right triangle to obtain the case of $4 n+3 \\quad(n \\geq 1)$ congruent triangles.\n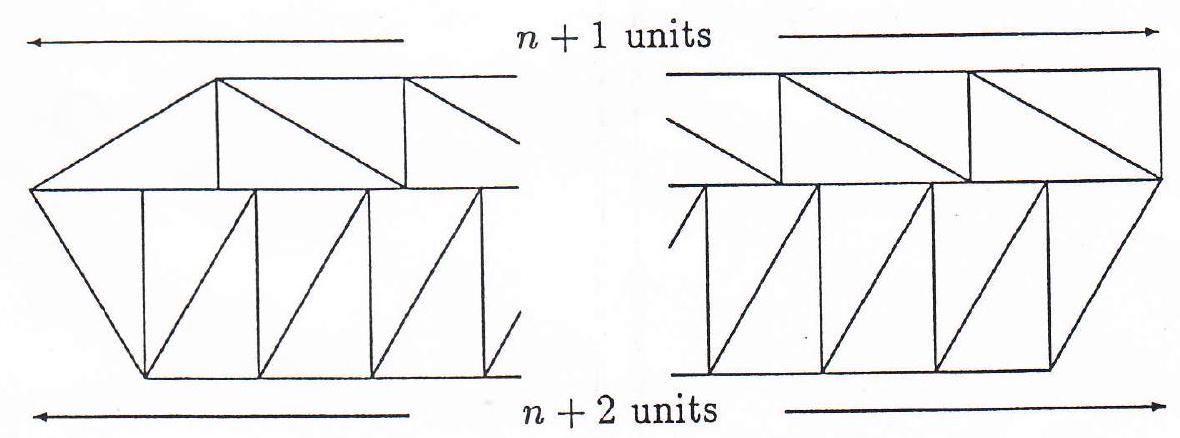\n\nSo we have $2 n+1$ triangles in the top part and $2 n+2$ triangles in the bottom part. In order to match, we need\n\n$$\n(n+1) p=(n+2) q\n$$\n\nso we take\n\n$$\nq=n+1 \\quad \\text { and } \\quad p=n+2\n$$\n\nThis completes the solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 5", "solution_match": "\nFIRST SOLUTION "}}
|
| 9 |
-
{"year": "1990", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Show that for every integer $n \\geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.", "solution": "(provided by the Canadian Problems Committee):\nThe basic building blocks will be right angled triangles with sides $m, n$ (which are positive integers) adjacent to the right angle.\n\n\nWe construct an \"UPPER CONFIGURATION\", being a rectangle consisting of $m$ building block units of pairs of triangles with the side of length $n$ as base. This gives a base length of $n m$ across the configuration.\n\nWe further construct a \"LOWER CONFIGURATION\", being a triangle with base up, consisting along the base of $n$ building block units. Again, we have a base length of $m n$ across the configuration.\n\nTwo triangles in the upper configuration are shaded horizontally. One triangle in the lower configuration is also shaded horizontally. Another triangle in the lower configuration is shaded vertically.\n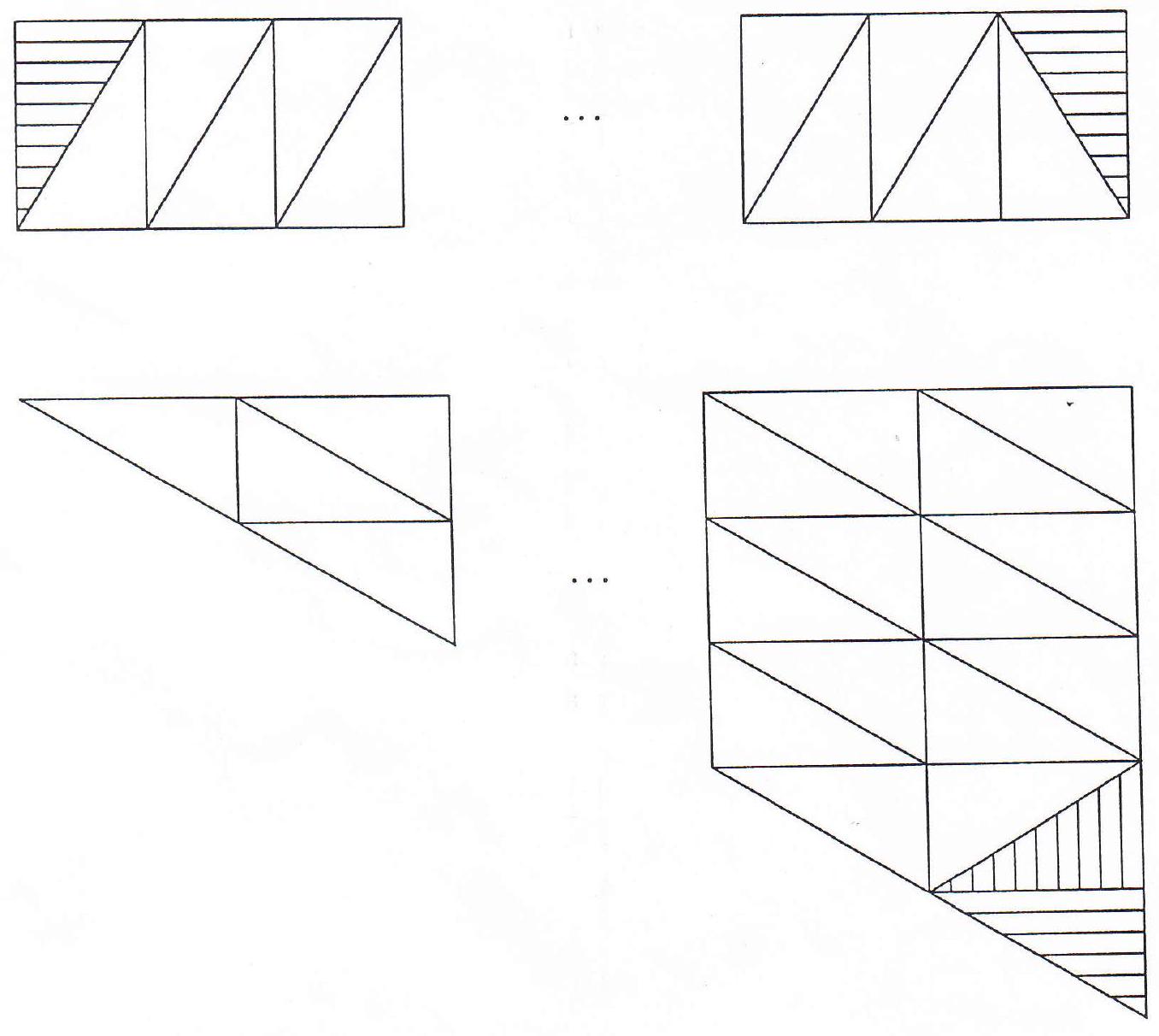\n\nNow consider the figure obtained by joining the two configurations along the base line of common length nm. To create the classes of hexagons defined below, it is necessary that both $n \\geq 3$ and $m \\geq 3$.\n\nWe create a class of convex hexagons (class 1 ) by omitting the three triangles that are shaded horizontally. The other class of convex hexagons (class 2) is obtained by omitting all shaded triangles.\n\nNow count the total number of triangles in the full configuration.\nThe upper configuration gives $2 m$ triangles. The lower configuration gives\n\n$$\n\\sum_{k=1}^{n}(2 k-1)=n^{2} \\quad \\text { triangles. }\n$$\n\nThus the total number of triangles in a hexagon in class 1 is\n\n$$\n2 m-2+n^{2}-1\n$$\n\nand the total number of triangle in a hexagon in class 2 is\n\n$$\n2 m-2+n^{2}-2\n$$\n\nThese, together with the restrictions on $n$ and $m$, generate all positive integers greater than or equal to 11.\n\nFor the integers $6,7,8,9$ and 10 , we give specific examples:\n\n\n6\n\n\n7\n\n\n8\n\n\n9\n\n\n10\n\nThis completes the solution.\n\nThere are $\\binom{n}{k}$ products of the $a_{i}$ taken $k$ at a time. Amongst these products any given $a_{i}$ will appear $\\binom{n-1}{k-1}$ times, since $\\binom{n-1}{k-1}$ is the number of ways of choosing the other factors of the product. So the $\\mathrm{AM} / \\mathrm{GM}$ inequality gives\n\n## ④\n\n$$\n\\frac{S_{k}}{\\binom{n}{k}} \\geq\\left[\\prod_{i=1}^{n} a_{i}^{\\binom{n-1}{k-1}}\\right]^{\\frac{1}{n}\\binom{n}{n}}\n$$\n\nBut $\\binom{n}{k}=\\frac{n}{k}\\binom{n-1}{k-1}$, leading to\n6 S $\\quad S_{k} \\geq\\binom{ n}{k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{k}{n}}$.\nHence\n田\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{k}{n}}\\binom{n}{n-k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{n-k}{n}}=\\binom{n}{k}^{2}\\left(\\prod_{1}^{n} a_{i}\\right) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 5", "solution_match": "\nSECOND SOLUTION "}}
|
|
|
|
| 1 |
+
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "Let $I$ be the intersection of $A G$ and $E F$.\nLet $\\delta=A I . I G-F I$ IE. Then\n\n$$\nA I=A D / 2, \\quad I G=A D / 6, \\quad F I=B C / 4=I E\n$$\n\nFurther, applying the cosine rule to triangles $A B D, A C D$ we get\n\n$$\n\\begin{aligned}\nA B^{2} & =B C^{2} / 4+A D^{2}-A D \\cdot B C \\cdot \\cos \\angle B D A, \\\\\nA C^{2} & =B C^{2} / 4+A D^{2}+A D \\cdot B C \\cdot \\cos \\angle B D A, \\\\\n\\text { so } \\quad A D^{2} & =\\left(A B^{2}+A C^{2}-B C^{2} / 2\\right) / 2\n\\end{aligned}\n$$\n\nHence\n\n$$\n\\begin{aligned}\n\\delta & =\\left(A B^{2}+A C^{2}-2 B C^{2}\\right) / 24 \\\\\n& =\\left(4 A B \\cdot A C \\cdot \\cos \\angle B A C-A B^{2}-A C^{2}\\right)\n\\end{aligned}\n$$\n\nNow $A E F G$ is a cyclic quadrilateral if and only if $\\delta=0$, i.e. if and only if\n\n$$\n\\begin{aligned}\n\\cos \\angle B A C & =\\left(A B^{2}+A B^{2}\\right) /(4 \\cdot A B \\cdot A C) \\\\\n& =(A B / A C+A C / A B) / 4\n\\end{aligned}\n$$\n\n5\nNow $A B / A C+A C / A B \\geq 2$. Hence $\\cos \\angle B A C \\geq 1 / 2$ and so $\\angle B A C \\leq 60^{\\circ}$.\nFor $\\angle B A C>60^{\\circ}$ there is no triangle with the required property.\nFor $\\angle B A C=60^{\\circ}$ there exists, within similarity, precisely one triangle (which is equilateral) having the required property.\nFor $\\angle B A C<60^{\\circ}$ there exists, within similarity, again precisely one triangle having the required property (even though for fixed median $A E$ there are two, but one arises from the other by interchanging point $B$ with point $C$, thus proving them to be similar).", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "# FIRST SOLUTION\n\n"}}
|
| 2 |
+
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "(Mr Marcus Brazil, La Trobe University, Bundoora, Melbourne, Australia):\nWe require, as above,\n\n$$\nA I \\cdot I G=E I \\cdot I F\n$$\n\n(which by (1) is equivalent to $A D^{2} / 3=C D^{2}$, i.e. $A D=C D \\cdot \\sqrt{3}$ ).\nLet, without loss of generality, $C D=1$. Then $A$ lies on the circle of radius $\\sqrt{3}$ with centre $D$. If $C D$ and $D A$ are perpendicular, the angle $B A C$ is $60^{\\circ}$, otherwise it must be less.\nIn this case, for each angle $B A C$ there are two solutions, which are congruent.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "\nSECOND SOLUTION "}}
|
| 3 |
+
{"year": "1990", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "In $\\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.\nFor each value of $\\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?", "solution": "in the figure as shown below, we first show that it is necessary that $\\angle A$ is less than $90^{\\circ}$ if the quadrilateral $A E G F$ ; cyclic.\n\n\nNow, since $E F \\| B C$, we get\n\n$$\n\\begin{aligned}\n\\angle E G F & =180^{\\circ}-\\left(B_{1}+C_{1}\\right) \\\\\n& \\geq 180^{\\circ}-(B+C) \\\\\n& =A .\n\\end{aligned}\n$$\n\n(1)\n\nThus, if $A E G F$ is cyclic, we would have $\\angle E G F+\\angle A=180^{\\circ}$. Therefore it is necessary that $0<\\angle A \\leq 90^{\\circ}$.\n\n## Continuation \"A\"\n\nLet $O$ be the circumcentre of $\\triangle A F E$. Without loss of generality, let the radius of this circle be 1.\nWe then let $A=1, F=z=e^{i \\theta}$ and $E=z e^{2 i \\alpha}=e^{i(\\theta+2 \\alpha)}$.\nThen $\\angle A=\\alpha, 0<\\alpha \\leq 90^{\\circ}$, and $0<\\theta<360^{\\circ}-2 \\alpha$.\nThus,\n\n$$\nB=2 z-1\n$$\n\nand\n\n$$\n\\begin{aligned}\nG & =\\frac{1}{3}(2 z-1)+\\frac{2}{3}\\left(z e^{2 i \\alpha}\\right) \\\\\n& =\\frac{1}{3}\\left(2 e^{i \\theta}+2 e^{i(\\theta+2 \\alpha)}-1\\right)\n\\end{aligned}\n$$\n\nFor quadrilateral $A F G E$ to be cyclic, it is now necessary that\n\n$$\n|G|=1 .\n$$\n\n\n\nFor $|G|=1$, we must have\n\n$$\n\\begin{aligned}\n9= & (2 \\cos (\\theta)+2 \\cos (\\theta+2 \\alpha)-1)^{2}+(2 \\sin (\\theta)+2 \\sin (\\theta+2 \\alpha))^{2} \\\\\n= & 4\\left(\\cos ^{2}(\\theta)+\\sin ^{2}(\\theta)\\right)+4\\left(\\cos ^{2}(\\theta+2 \\alpha)+\\sin ^{2}(\\theta+2 \\alpha)\\right)+1 \\\\\n& +8(\\cos (\\theta) \\cos (\\theta+2 \\alpha)+\\sin (\\theta) \\sin (\\theta+2 \\alpha))-4 \\cos (\\theta)-4 \\cos (\\theta+2 \\alpha) \\\\\n= & 9+8 \\cos (2 \\alpha)-8 \\cos (\\alpha) \\cos (\\theta+\\alpha)\n\\end{aligned}\n$$\n\nso that\n\n$$\n\\cos (\\theta+\\alpha)=\\frac{\\cos (2 \\alpha)}{\\cos (\\alpha)}\n$$\n\n] Now, $\\left|\\frac{\\cos (2 \\alpha)}{\\cos (\\alpha)}\\right| \\leq 1$ if and only if $\\alpha \\in\\left(0,60^{\\circ}\\right]$ in the range of $\\alpha$ under consideration, that is $\\alpha \\in\\left(0,00^{\\circ}\\right]$. There is equality if and only if $\\alpha=60^{\\circ}$.\n\n$\\square$ Note there is only one solution. The apparent other solution is the mirror image of the first. We are solving for $\\alpha+\\theta$. The other solution is $360^{\\circ}-\\alpha-\\theta$.\n\n## Continuation \"B\"\n\nLet $O$ be the circumcentre of triangle $A E F$. Let $A P$ be a diameter of this circle. Construct the circle with centre $P$ and radius $A P$. Then $B$ and $C$ lie on this circle.\n\nIt is clear that the problem is solved if we allow the angle $\\angle B A C=\\alpha$ to vary and restrict $B$ and $C$ to the constructed circle.\n\nLet $\\theta$ be the angle from the drawn axis. Then $\\theta$ lies in the range $\\left(0,180^{\\circ}-\\alpha\\right)$. We must not forget the necessary restriction of $\\alpha$, that is $\\alpha \\in\\left(0,90^{\\circ}\\right.$.\n\n\nNow, $D$ lies on an arc of a circle, centre $P$, radius $P D$ exterior to the circle, centre $O$, radius $A O$.\nBy similarity, $G$, lies on an arc of a circle, centre $Q$, radius $Q G$ where $A Q=\\frac{2}{3} A P$ and $Q G=\\frac{2}{3} P D$.\nFor the quadrilateral $A F G E$ to be cyclic, we must have that the radius $Q G$ is greater than or equal to $Q P$.\nThe easiest way to calulate these radii is to consider the case in which the diameter $A P$ bisects the angle $\\angle B A C$.\nThus we re-draw the diagram as below. Let $A H$ be a diameter of the larger circle.\n\n\nThus we have $A H=4$ and by similar triangles,\n\n$$\n\\frac{A D}{A B}=\\frac{A B}{A H}=\\cos \\left(\\frac{\\alpha}{2}\\right)\n$$\n\nso that\n\n$$\n\\begin{aligned}\nA D & =4 \\cos ^{2}\\left(\\frac{\\alpha}{2}\\right) \\\\\n& =2+2 \\cos (\\alpha) .\n\\end{aligned}\n$$\n\nThus $P D=2 \\cos (\\alpha)$ and $Q G=\\frac{2}{3} 2 \\cos (\\alpha)=\\frac{4}{3} \\cos (\\alpha)$.\nThe necessary condition for a cyclic quadrilateral is then\n\n$$\n\\frac{4}{3}(1+\\cos (\\alpha)) \\geq 2\n$$\n\n[5\n\n$$\n\\cos (\\alpha) \\geq \\frac{1}{2}\n$$\n\n:7\nThus it is clear that there is precisely one (up to similarity) solution for $0<\\alpha \\leq 60^{\\circ}$ and no solutions otherwise.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 1 ", "solution_match": "\nTHIRD SOLUTION\n"}}
|
| 4 |
+
{"year": "1990", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \\ldots, a_{n}$ taken $k$ at a time.\nShow that\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}^{2} a_{1} a_{2} \\ldots a_{n}, \\quad \\text { for } \\quad k=1,2, \\ldots, n-1\n$$", "solution": "$$\n\\binom{n}{k} a_{1} a_{2} \\ldots a_{n}\n$$\n\n$2=\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}} \\cdot a_{1} a_{2} \\ldots a_{n} / a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}$\n(and using the Cauchy-Schwarz inequality)\n\n$$\n\\begin{aligned}\n& \\leq\\left(\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}\\right)^{\\frac{1}{2}} \\cdot\\left(\\sum_{1 \\leq i_{1}<i_{2}<\\ldots<i_{k} \\leq n} a_{1} a_{2} \\ldots a_{n} / a_{i_{1}} a_{i_{2}} \\ldots a_{i_{k}}\\right)^{\\frac{1}{2}} \\\\\n& =S_{k}^{\\frac{1}{2}} \\cdot S_{n-k}^{\\frac{1}{2}}\n\\end{aligned}\n$$\n\nTherefore\n\n$$\n\\binom{n}{k}^{2} a_{1} a_{2} \\ldots a_{n} \\leq S_{k} S_{n-k}\n$$\n\nq.e.d.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 2", "solution_match": "# FIRST SOLUTION\n\n"}}
|
| 5 |
+
{"year": "1990", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \\ldots, a_{n}$ taken $k$ at a time.\nShow that\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}^{2} a_{1} a_{2} \\ldots a_{n}, \\quad \\text { for } \\quad k=1,2, \\ldots, n-1\n$$", "solution": "(provided by the Canadian Problems Committee).\nWrite $S_{k}$ as $\\sum_{i=1}^{\\binom{n}{k}} t_{i}$. Then\n주\n\n$$\nS_{n-k}=\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left(\\sum_{i=1}^{\\binom{n}{k}} \\frac{1}{t_{i}}\\right)\n$$\n\n$$\n\\text { so that } \\left.\\begin{array}{rl}\nS_{k} S_{n-k} & =\\left(\\prod_{m=1}^{n} a_{m}\\right) \\cdot\\left(\\begin{array}{l}\n\\binom{n}{k} \\\\\ni=1\n\\end{array} t_{i}\\right)\\left(\\begin{array}{l}\n\\binom{n}{k} \\\\\n\\sum_{j=1}^{2}\n\\end{array} \\frac{1}{t_{j}}\\right) \\\\\n& =\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left[\\sum_{i=1}^{\\binom{n}{k}} 1+\\sum_{i=1}^{\\binom{n}{k}} \\sum_{j=1}^{n} \\begin{array}{l}\nn \\\\\nk\n\\end{array}\\right) \\\\\n\\frac{t_{i}}{} \\\\\nt_{j}\n\\end{array}\\right] .\n$$\n\nAs there are\n\n$$\n\\frac{\\binom{n}{k}^{2}-\\binom{n}{k}}{2}\n$$\n\nterms in the sum\n\n\n$$\n\\begin{aligned}\nS_{k} S_{n-k} & \\geq\\left(\\prod_{m=1}^{n} a_{m}\\right)\\left[\\binom{n}{k}+2 \\cdot \\frac{\\binom{n}{k}^{2}-\\binom{n}{k}}{2}\\right] \\\\\n& =\\binom{n}{k}^{2}\\left(\\prod_{m=1}^{n} a_{m}\\right)\n\\end{aligned}\n$$\n\nsince $\\frac{t_{i}}{t_{j}}+\\frac{t_{j}}{t_{i}} \\geq 2$ for $t_{i}, t_{j}>0$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 2", "solution_match": "\nSECOND SOLUTION "}}
|
| 6 |
+
{"year": "1990", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Consider all the triangles $A B C$ which have a fixed base $A B$ and whose altitude from $C$ is a constant $h$. For which of these triangles is the product of its altitudes a maximum?", "solution": "Let $h_{a}$ and $h_{b}$ be the altitudes from $A$ and $B$, respectively. Then\n\n$$\n\\begin{aligned}\nA B \\cdot h \\cdot A C \\cdot h_{b} \\cdot B C \\cdot h_{a} & =8 . \\text { area of } \\triangle A B C)^{3} \\\\\n& =(A B \\cdot h)^{3},\n\\end{aligned}\n$$\n\n园\nwhich is a constant. So the product $h . h_{a} \\cdot h_{b}$ attains its maximum when the product $A C . B C$ attains its minimum.\nSince\n\n$$\n\\begin{aligned}\n(\\sin C) \\cdot A C \\cdot B C & =B C \\cdot h_{a} \\\\\n& =2 \\cdot \\text { area of } \\triangle A B C\n\\end{aligned}\n$$\n\n(3)\nwhich is a constant, $A C \\cdot B C$ attains its minimum when $\\sin C$ reaches its maximum. There are two cases:\n(a) $h \\leq A B / 2$. Then there exists a triangle $A B C$ which has a right angle at $C$, and for precisely such a triangle $\\sin C$ attains its maximum, namely 1 .\n(b) $h>A B / 2$. In this case the angle at $C$ is acute and assumes its maximum when the triangle is isosceles.\n\nNote that a solution using calculus obviously exists.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 3", "solution_match": "# SOLUTION:"}}
|
| 7 |
+
{"year": "1990", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "A set of 1990 persons is divided into non-intersecting subsets in such a way that\n(a) no one in a subset knows all the others in the subset;\n(b) among any three persons in a subset, there are always at least two who do not know each other; and\n(c) for any two persons in a subset who do not know each other, there is exactly one person in the same subset knowing both of them.\n(i) Prove that within each subset, every person has the same number of acquaintances.\n(ii) Determine the maximum possible number of subsets.\n\nNote: it is understood that if a person $A$ knows person $B$, then person $B$ will know person $A$; an acquaintance is someone who is known. Every person is assumed to know one's self.", "solution": "(i) Let $S$ be a subset of persons satisfying conditions (a), (b) and (c). Let $x \\in S$ be one who knows the maximum number of persons in $S$.\nAssume that $x$ knows $x_{1}, x_{2}, \\ldots, x_{n}$. By (b), $x_{i}$ and $x_{j}$ are strangers if $i \\neq j$. For each $x_{i}$, let $N_{i}$ be the set of persons in $S$ who know $x_{i}$ but not $x$. Note that, for $i \\neq j, N_{i}$ has no person in common with $N_{j}$, otherwise there would be more than one person knowing $x_{i}$ and $x_{j}$, contradicting (c).\nBy (a) we may assume that $N_{1}$ is not empty.) Let $y_{1} \\in N_{1}$. By (c), for each $k>1$, there is exactly one person $y_{k}$ in $N_{k}$ who knows $y_{1}$. This means that $y_{1}$ knows $n$ persons, namely $x_{1}, y_{2}, \\ldots, y_{n}$.\nBecause $n$ is the maximal number of persons in $S$ a person in $S$ can know, $y_{1}$ knows exactly $n$ persons in $S$. By precisely the same reasoning we find that each person in $N_{i}$, $i=1,2, \\ldots, n$, knows exactly $n$ persons in $S$.\nLetting $y_{1}$ take the role of $x$ in our argument, we see that also each $x_{i}$ knows exactly $n$ persons. Note that, by (c), every person in $S$ other than $x, x_{1}, \\ldots, x_{n}$, must be in some $N_{j}$. Therefore every person in $S$ knows exactly $n$ persons in $S$ and thus has the same number of acquaintances in $S$.\n(ii) To maximize the number of subsets, we have to minimize the size of each group. The smallest possible subset is one in which every person knows exactly two persons, and hence there must be exactly five persons in the subset, forming a cycle where two persons stand side by side only if they know each other. Therefore the maximum possible number of subsets is 1990/5 $=398$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 4", "solution_match": "# SOLUTION:"}}
|
| 8 |
+
{"year": "1990", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Show that for every integer $n \\geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.", "solution": "(provided by the Canadian Problems Committee).\nThe basic building blocks will be right angled triangles with sides $p, q$ (which are positive integers) adjacent to the right angle.\n\n\nIn the first instance, we take $p=q=1$ and construct five basic building blocks: $L_{1}, L_{2}, M, R_{1}$ and $R_{2}$ 。\n\n## [3)\n\n\n$L_{1}$\n\n$L_{2}$\n\nM\n\n$R_{1}$\n\n$R_{2}$\n\nWe shall now build convex hexagons by taking, on the left, one of the blocks $L_{i}$, attaching $n$ copies of the block $M$, and finally attaching one of the blocks $R_{j}$. We must therefore exclude the case when $(i, j)=(2,1)$ for this does not generate a hexagon. Further, for $(i, j)=(1,1)$ or $(i, j)=(1,2)$, we require that $n \\geq 1$, whereas for $(i, j)=$ $(2,2)$, we only need require that $n \\geq 0$.\n\nThus, with the obvious interpretation:\n$L_{1}+n M+R_{1}$ gives a convex hexagon containing $2+4 n+2=4 n+4 \\quad(n \\geq 1)$ congruent triangles;\n$L_{1}+n M+R_{2}$ gives a convex hexagon containing $2+4 n+3=4 n+5(n \\geq 1)$ congruent triangles; and\n$L_{2}+n M+R_{2}$ gives a convex hexagon containing $3+4 n+3=4 n+6 \\quad(n \\geq 0)$ congruent triangles, or $4 n+2(n \\geq 1)$ congruent triangles.\n\nWe shall now modify the lengths of the sides of the right triangle to obtain the case of $4 n+3 \\quad(n \\geq 1)$ congruent triangles.\n\n\nSo we have $2 n+1$ triangles in the top part and $2 n+2$ triangles in the bottom part. In order to match, we need\n\n$$\n(n+1) p=(n+2) q\n$$\n\nso we take\n\n$$\nq=n+1 \\quad \\text { and } \\quad p=n+2\n$$\n\nThis completes the solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 5", "solution_match": "\nFIRST SOLUTION "}}
|
| 9 |
+
{"year": "1990", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Show that for every integer $n \\geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.", "solution": "(provided by the Canadian Problems Committee):\nThe basic building blocks will be right angled triangles with sides $m, n$ (which are positive integers) adjacent to the right angle.\n\n\nWe construct an \"UPPER CONFIGURATION\", being a rectangle consisting of $m$ building block units of pairs of triangles with the side of length $n$ as base. This gives a base length of $n m$ across the configuration.\n\nWe further construct a \"LOWER CONFIGURATION\", being a triangle with base up, consisting along the base of $n$ building block units. Again, we have a base length of $m n$ across the configuration.\n\nTwo triangles in the upper configuration are shaded horizontally. One triangle in the lower configuration is also shaded horizontally. Another triangle in the lower configuration is shaded vertically.\n\n\nNow consider the figure obtained by joining the two configurations along the base line of common length nm. To create the classes of hexagons defined below, it is necessary that both $n \\geq 3$ and $m \\geq 3$.\n\nWe create a class of convex hexagons (class 1 ) by omitting the three triangles that are shaded horizontally. The other class of convex hexagons (class 2) is obtained by omitting all shaded triangles.\n\nNow count the total number of triangles in the full configuration.\nThe upper configuration gives $2 m$ triangles. The lower configuration gives\n\n$$\n\\sum_{k=1}^{n}(2 k-1)=n^{2} \\quad \\text { triangles. }\n$$\n\nThus the total number of triangles in a hexagon in class 1 is\n\n$$\n2 m-2+n^{2}-1\n$$\n\nand the total number of triangle in a hexagon in class 2 is\n\n$$\n2 m-2+n^{2}-2\n$$\n\nThese, together with the restrictions on $n$ and $m$, generate all positive integers greater than or equal to 11.\n\nFor the integers $6,7,8,9$ and 10 , we give specific examples:\n\n\n6\n\n\n7\n\n\n8\n\n\n9\n\n\n10\n\nThis completes the solution.\n\nThere are $\\binom{n}{k}$ products of the $a_{i}$ taken $k$ at a time. Amongst these products any given $a_{i}$ will appear $\\binom{n-1}{k-1}$ times, since $\\binom{n-1}{k-1}$ is the number of ways of choosing the other factors of the product. So the $\\mathrm{AM} / \\mathrm{GM}$ inequality gives\n\n## ④\n\n$$\n\\frac{S_{k}}{\\binom{n}{k}} \\geq\\left[\\prod_{i=1}^{n} a_{i}^{\\binom{n-1}{k-1}}\\right]^{\\frac{1}{n}\\binom{n}{n}}\n$$\n\nBut $\\binom{n}{k}=\\frac{n}{k}\\binom{n-1}{k-1}$, leading to\n6 S $\\quad S_{k} \\geq\\binom{ n}{k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{k}{n}}$.\nHence\n田\n\n$$\nS_{k} S_{n-k} \\geq\\binom{ n}{k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{k}{n}}\\binom{n}{n-k}\\left(\\prod_{i=1}^{n} a_{i}\\right)^{\\frac{n-k}{n}}=\\binom{n}{k}^{2}\\left(\\prod_{1}^{n} a_{i}\\right) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl", "problem_match": "# Question 5", "solution_match": "\nSECOND SOLUTION "}}
|
APMO/segmented/en-apmo1991_sol.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "1991", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.", "solution": "Let $R$ be the midpoint of $A C$; so $B R$ is a median and contains the centroid $G$.\n\n\nIt is well known that $\\frac{A G}{A M}=\\frac{2}{3}$; thus the ratio of the similarity between $A X Y$ and $A B C$ is $\\frac{2}{3}$. Hence $G X=\\frac{1}{2} X Y=\\frac{1}{3} B C$.\nNow look at the similarity between triangles $Q B C$ and $Q G X$ :\n\n$$\n\\frac{Q G}{Q B}=\\frac{G X}{B C}=\\frac{1}{3} \\Longrightarrow Q B=3 Q G \\Longrightarrow Q B=\\frac{3}{4} B G=\\frac{3}{4} \\cdot \\frac{2}{3} B R=\\frac{1}{2} B R .\n$$\n\nFinally, since $\\frac{B M}{B C}=\\frac{B Q}{B R}, M Q$ is a midline in $B C R$. Therefore $M Q=\\frac{1}{2} C R=\\frac{1}{4} A C$ and $M Q \\| A C$. Similarly, $M P=\\frac{1}{4} A B$ and $M P \\| A B$. This is sufficient to establish that $M P Q$ and $A B C$ are similar (with similarity ratio $\\frac{1}{4}$ ).", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
-
{"year": "1991", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.", "solution": "Let $S$ and $R$ be the midpoints of $A B$ and $A C$, respectively. Since $G$ is the centroid, it lies in the medians $B R$ and $C S$.\n\n\nDue to the similarity between triangles $Q B C$ and $Q G X$ (which is true because $G X \\| B C$ ), there is an inverse homothety with center $Q$ and ratio $-\\frac{X G}{B C}=\\frac{X Y}{2 B C}$ that takes $B$ to $G$ and $C$ to $X$. This homothety takes the midpoint $M$ of $B C$ to the midpoint $K$ of $G X$.\n\nNow consider the homothety that takes $B$ to $X$ and $C$ to $G$. This new homothety, with ratio $\\frac{X Y}{2 B C}$, also takes $M$ to $K$. Hence lines $B X$ (which contains side $A B$ ), $C G$ (which contains the median $C S$ ), and $M K$ have a common point, which is $S$. Thus $Q$ lies on midline $M S$.\nThe same reasoning proves that $P$ lies on midline $M R$. Since all homothety ratios are the same, $\\frac{M Q}{M S}=\\frac{M P}{M R}$, which shows that $M P Q$ is similar to $M R S$, which in turn is similar to $A B C$, and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
-
{"year": "1991", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Suppose there are 997 points given in a plane. If every two points are joined by a line segment with its midpoint coloured in red, show that there are at least 1991 red points in the plane. Can you find a special case with exactly 1991 red points?", "solution": "Embed the points in the cartesian plane such that no two points have the same $y$-coordinate. Let $P_{1}, P_{2}, \\ldots, P_{997}$ be the points and $y_{1}<y_{2}<\\ldots<y_{997}$ be their respective $y$-coordinates. Then the $y$-coordinate of the midpoint of $P_{i} P_{i+1}, i=1,2, \\ldots, 996$ is $\\frac{y_{i}+y_{i+1}}{2}$ and the $y$-coordinate of the midpoint of $P_{i} P_{i+2}, i=1,2, \\ldots, 995$ is $\\frac{y_{i}+y_{i+2}}{2}$. Since\n\n$$\n\\frac{y_{1}+y_{2}}{2}<\\frac{y_{1}+y_{3}}{2}<\\frac{y_{2}+y_{3}}{2}<\\frac{y_{2}+y_{4}}{2}<\\cdots<\\frac{y_{995}+y_{997}}{2}<\\frac{y_{996}+y_{997}}{2}\n$$\n\nthere are at least $996+995=1991$ distinct midpoints, and therefore at least 1991 red points. The equality case happens if we take $P_{i}=(0,2 i), i=1,2, \\ldots, 997$. The midpoints are $(0, i+j)$, $1 \\leq i<j \\leq 997$, which are the points $(0, k)$ with $1+2=3 \\leq k \\leq 996+997=1993$, a total of $1993-3+1=1991$ red points.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
-
{"year": "1991", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}, b_{1}, b_{2}, \\ldots, b_{n}$ be positive real numbers such that $a_{1}+a_{2}+\\cdots+a_{n}=b_{1}+b_{2}+$ $\\cdots+b_{n}$. Show that\n\n$$\n\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}} \\geq \\frac{a_{1}+a_{2}+\\cdots+a_{n}}{2}\n$$", "solution": "By the Cauchy-Schwartz inequality,\n\n$$\n\\left(\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}}\\right)\\left(\\left(a_{1}+b_{1}\\right)+\\left(a_{2}+b_{2}\\right)+\\cdots+\\left(a_{n}+b_{n}\\right)\\right) \\geq\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)^{2} .\n$$\n\nSince $\\left(\\left(a_{1}+b_{1}\\right)+\\left(a_{2}+b_{2}\\right)+\\cdots+\\left(a_{n}+b_{n}\\right)\\right)=2\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)$,\n\n$$\n\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}} \\geq \\frac{\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)^{2}}{2\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{2}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "1991", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.\n\nAnswer: All powers of 2 .", "solution": "Number the children from 0 to $n-1$. Then the teacher hands candy to children in positions $f(x)=1+2+\\cdots+x \\bmod n=\\frac{x(x+1)}{2} \\bmod n$. Our task is to find the range of $f: \\mathbb{Z}_{n} \\rightarrow \\mathbb{Z}_{n}$, and to verify whether the range is $\\mathbb{Z}_{n}$, that is, whether $f$ is a bijection.\nIf $n=2^{a} m, m>1$ odd, look at $f(x)$ modulo $m$. Since $m$ is odd, $m|f(x) \\Longleftrightarrow m| x(x+1)$. Then, for instance, $f(x) \\equiv 0(\\bmod m)$ for $x=0$ and $x=m-1$. This means that $f(x)$ is not a bijection modulo $m$, and there exists $t$ such that $f(x) \\not \\equiv t(\\bmod m)$ for all $x$. By the Chinese Remainder Theorem,\n\n$$\nf(x) \\equiv t \\quad(\\bmod n) \\Longleftrightarrow \\begin{cases}f(x) \\equiv t & \\left(\\bmod 2^{a}\\right) \\\\ f(x) \\equiv t & (\\bmod m)\\end{cases}\n$$\n\nTherefore, $f$ is not a bijection modulo $n$.\nIf $n=2^{a}$, then\n\n$$\nf(x)-f(y)=\\frac{1}{2}(x(x+1)-y(y+1))=\\frac{1}{2}\\left(x^{2}-y^{2}+x-y\\right)=\\frac{(x-y)(x+y+1)}{2} .\n$$\n\nand\n\n$$\nf(x) \\equiv f(y) \\quad\\left(\\bmod 2^{a}\\right) \\Longleftrightarrow(x-y)(x+y+1) \\equiv 0 \\quad\\left(\\bmod 2^{a+1}\\right)\n$$\n\nIf $x$ and $y$ have the same parity, $x+y+1$ is odd and $(*)$ is equivalent to $x \\equiv y\\left(\\bmod 2^{a+1}\\right)$. If $x$ and $y$ have different parity,\n\n$$\n(*) \\Longleftrightarrow x+y+1 \\equiv 0 \\quad\\left(\\bmod 2^{a+1}\\right)\n$$\n\nHowever, $1 \\leq x+y+1 \\leq 2\\left(2^{a}-1\\right)+1=2^{a+1}-1$, so $x+y+1$ is not a multiple of $2^{a+1}$. Therefore $f$ is a bijection if $n$ is a power of 2 .", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
-
{"year": "1991", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.\n\nAnswer: All powers of 2 .", "solution": "We give a full description of $a_{n}$, the size of the range of $f$.\nSince congruences modulo $n$ are defined, via Chinese Remainder Theorem, by congruences modulo $p^{\\alpha}$ for all prime divisors $p$ of $n$ and $\\alpha$ being the number of factors $p$ in the factorization of $n, a_{n}=\\prod_{p^{\\alpha} \\| n} a_{p^{\\alpha}}$.\nRefer to the first solution to check the case $p=2: a_{2^{\\alpha}}=2^{\\alpha}$.\nFor an odd prime $p$,\n\n$$\nf(x)=\\frac{x(x+1)}{2}=\\frac{(2 x+1)^{2}-1}{8}\n$$\n\nand since $p$ is odd, there is a bijection between the range of $f$ and the quadratic residues modulo $p^{\\alpha}$, namely $t \\mapsto 8 t+1$. So $a_{p^{\\alpha}}$ is the number of quadratic residues modulo $p^{\\alpha}$.\nLet $g$ be a primitive root of $p^{\\alpha}$. Then there are $\\frac{1}{2} \\phi\\left(p^{\\alpha}\\right)=\\frac{p-1}{2} \\cdot p^{\\alpha-1}$ quadratic residues that are coprime with $p: 1, g^{2}, g^{4}, \\ldots, g^{\\phi\\left(p^{n}\\right)-2}$. If $p$ divides a quadratic residue $k p$, that is, $x^{2} \\equiv k p$ $\\left(\\bmod p^{\\alpha}\\right), \\alpha \\geq 2$, then $p$ divides $x$ and, therefore, also $k$. Hence $p^{2}$ divides this quadratic residue, and these quadratic residues are $p^{2}$ times each quadratic residue of $p^{\\alpha-2}$. Thus\n\n$$\na_{p^{\\alpha}}=\\frac{p-1}{2} \\cdot p^{\\alpha-1}+a_{p^{\\alpha}-2} .\n$$\n\nSince $a_{p}=\\frac{p-1}{2}+1$ and $a_{p^{2}}=\\frac{p-1}{2} \\cdot p+1$, telescoping yields\n\n$$\na_{p^{2 t}}=\\frac{p-1}{2}\\left(p^{2 t-1}+p^{2 t-3}+\\cdots+p\\right)+1=\\frac{p\\left(p^{2 t}-1\\right)}{2(p+1)}+1\n$$\n\nand\n\n$$\na_{p^{2 t-1}}=\\frac{p-1}{2}\\left(p^{2 t-2}+p^{2 t-4}+\\cdots+1\\right)+1=\\frac{p^{2 t}-1}{2(p+1)}+1\n$$\n\nNow the problem is immediate: if $n$ is divisible by an odd prime $p, a_{p^{\\alpha}}<p^{\\alpha}$ for all $\\alpha$, and since $a_{t} \\leq t$ for all $t, a_{n}<n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "1991", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Given are two tangent circles and a point $P$ on their common tangent perpendicular to the lines joining their centres. Construct with ruler and compass all the circles that are tangent to these two circles and pass through the point $P$.", "solution": "Throughout this problem, we will assume that the given circles are externally tangent, since the problem does not have a solution otherwise.\nLet $\\Gamma_{1}$ and $\\Gamma_{2}$ be the given circles and $T$ be their tangency point. Suppose $\\omega$ is a circle that is tangent to $\\Gamma_{1}$ and $\\Gamma_{2}$ and passes through $P$.\nNow invert about point $P$, with radius $P T$. Let any line through $P$ that cuts $\\Gamma_{1}$ do so at points $X$ and $Y$. The power of $P$ with respect to $\\Gamma_{1}$ is $P T^{2}=P X \\cdot P Y$, so $X$ and $Y$ are swapped by this inversion. Therefore $\\Gamma_{1}$ is mapped to itself in this inversion. The same applies to $\\Gamma_{2}$. Since circle $\\omega$ passes through $P$, it is mapped to a line tangent to the images of $\\Gamma_{1}$ (itself) and $\\Gamma_{2}$ (also itself), that is, a common tangent line. This common tangent cannot be $P T$, as $P T$ is also mapped to itself. Since $\\Gamma_{1}$ and $\\Gamma_{2}$ have exactly other two common tangent lines, there are two solutions: the inverses of the tangent lines.\n\n\nWe proceed with the construction with the aid of some macro constructions that will be detailed later.\n\nStep 1. Draw the common tangents to $\\Gamma_{1}$ and $\\Gamma_{2}$.\nStep 2. For each common tangent $t$, draw the projection $P_{t}$ of $P$ onto $t$.\nStep 3. Find the inverse $P_{1}$ of $P_{t}$ with respect to the circle with center $P$ and radius $P T$.\nStep 4. $\\omega_{t}$ is the circle with diameter $P P_{1}$.\nLet's work out the details for steps 1 and 3 . Steps 2 and 4 are immediate.\nStep 1. In this particular case in which $\\Gamma_{1}$ and $\\Gamma_{2}$ are externally tangent, there is a small shortcut:\n\n- Draw the circle with diameter on the two centers $O_{1}$ of $\\Gamma_{1}$ and $O_{2}$ of $\\Gamma_{2}$, and find its center $O$.\n- Let this circle meet common tangent line $O P$ at points $Q, R$. The required lines are the perpendicular to $O Q$ at $Q$ and the perpendicular to $O R$ at $R$.\n\n\nLet's show why this construction works. Let $R_{i}$ be the radius of circle $\\Gamma_{i}$ and suppose without loss of generality that $R_{1} \\leq R_{2}$. Note that $O Q=\\frac{1}{2} O_{1} O_{2}=\\frac{R_{1}+R_{2}}{2}, O T=O O_{1}-R_{1}=\\frac{R_{2}-R_{1}}{2}$, so\n\n$$\n\\sin \\angle T Q O=\\frac{O T}{O Q}=\\frac{R_{2}-R_{1}}{R_{1}+R_{2}}\n$$\n\nwhich is also the sine of the angle between $O_{1} O_{2}$ and the common tangent lines.\nLet $t$ be the perpendicular to $O Q$ through $Q$. Then $\\angle\\left(t, O_{1} O_{2}\\right)=\\angle(O Q, Q T)=\\angle T Q O$, and $t$ is parallel to a common tangent line. Since\n\n$$\nd(O, t)=O Q=\\frac{R_{1}+R_{2}}{2}=\\frac{d\\left(O_{1}, t\\right)+d\\left(O_{2}, t\\right)}{2}\n$$\n\nand $O$ is the midpoint of $O_{1} O_{2}, O$ is also at the same distance from $t$ and the common tangent line, so these two lines coincide.\nStep 3. Finding the inverse of a point $X$ given the inversion circle $\\Omega$ with center $O$ is a well known procedure, but we describe it here for the sake of completeness.\n\n- If $X$ lies in $\\Omega$, then its inverse is $X$.\n- If $X$ lies in the interior of $\\Omega$, draw ray $O X$, then the perpendicular line $\\ell$ to $O X$ at $X$. Let $\\ell$ meet $\\Omega$ at a point $Y$. The inverse of $X$ is the intersection $X^{\\prime}$ of $O X$ and the line perpendicular to $O Y$ at $Y$. This is because $O Y X^{\\prime}$ is a right triangle with altitude $Y X$, and therefore $O X \\cdot O X^{\\prime}=O Y^{2}$.\n- If $X$ is in the exterior of $\\Omega$, draw ray $O X$ and one of the tangent lines $\\ell$ from $X$ to $\\Omega$ (just connect $X$ to one of the intersections of $\\Omega$ and the circle with diameter $O X$ ). Let $\\ell$ touch $\\Omega$ at a point $Y$. The inverse of $X$ is the projection $X^{\\prime}$ of $Y$ onto $O X$. This is because $O Y X^{\\prime}$ is a right triangle with altitude $Y X^{\\prime}$, and therefore $O X \\cdot O X^{\\prime}=O Y^{2}$.\n\n$X$ is inside $\\Omega$\n", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "1991", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.", "solution": "Let $R$ be the midpoint of $A C$; so $B R$ is a median and contains the centroid $G$.\n\n\nIt is well known that $\\frac{A G}{A M}=\\frac{2}{3}$; thus the ratio of the similarity between $A X Y$ and $A B C$ is $\\frac{2}{3}$. Hence $G X=\\frac{1}{2} X Y=\\frac{1}{3} B C$.\nNow look at the similarity between triangles $Q B C$ and $Q G X$ :\n\n$$\n\\frac{Q G}{Q B}=\\frac{G X}{B C}=\\frac{1}{3} \\Longrightarrow Q B=3 Q G \\Longrightarrow Q B=\\frac{3}{4} B G=\\frac{3}{4} \\cdot \\frac{2}{3} B R=\\frac{1}{2} B R .\n$$\n\nFinally, since $\\frac{B M}{B C}=\\frac{B Q}{B R}, M Q$ is a midline in $B C R$. Therefore $M Q=\\frac{1}{2} C R=\\frac{1}{4} A C$ and $M Q \\| A C$. Similarly, $M P=\\frac{1}{4} A B$ and $M P \\| A B$. This is sufficient to establish that $M P Q$ and $A B C$ are similar (with similarity ratio $\\frac{1}{4}$ ).", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
+
{"year": "1991", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.", "solution": "Let $S$ and $R$ be the midpoints of $A B$ and $A C$, respectively. Since $G$ is the centroid, it lies in the medians $B R$ and $C S$.\n\n\nDue to the similarity between triangles $Q B C$ and $Q G X$ (which is true because $G X \\| B C$ ), there is an inverse homothety with center $Q$ and ratio $-\\frac{X G}{B C}=\\frac{X Y}{2 B C}$ that takes $B$ to $G$ and $C$ to $X$. This homothety takes the midpoint $M$ of $B C$ to the midpoint $K$ of $G X$.\n\nNow consider the homothety that takes $B$ to $X$ and $C$ to $G$. This new homothety, with ratio $\\frac{X Y}{2 B C}$, also takes $M$ to $K$. Hence lines $B X$ (which contains side $A B$ ), $C G$ (which contains the median $C S$ ), and $M K$ have a common point, which is $S$. Thus $Q$ lies on midline $M S$.\nThe same reasoning proves that $P$ lies on midline $M R$. Since all homothety ratios are the same, $\\frac{M Q}{M S}=\\frac{M P}{M R}$, which shows that $M P Q$ is similar to $M R S$, which in turn is similar to $A B C$, and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
+
{"year": "1991", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Suppose there are 997 points given in a plane. If every two points are joined by a line segment with its midpoint coloured in red, show that there are at least 1991 red points in the plane. Can you find a special case with exactly 1991 red points?", "solution": "Embed the points in the cartesian plane such that no two points have the same $y$-coordinate. Let $P_{1}, P_{2}, \\ldots, P_{997}$ be the points and $y_{1}<y_{2}<\\ldots<y_{997}$ be their respective $y$-coordinates. Then the $y$-coordinate of the midpoint of $P_{i} P_{i+1}, i=1,2, \\ldots, 996$ is $\\frac{y_{i}+y_{i+1}}{2}$ and the $y$-coordinate of the midpoint of $P_{i} P_{i+2}, i=1,2, \\ldots, 995$ is $\\frac{y_{i}+y_{i+2}}{2}$. Since\n\n$$\n\\frac{y_{1}+y_{2}}{2}<\\frac{y_{1}+y_{3}}{2}<\\frac{y_{2}+y_{3}}{2}<\\frac{y_{2}+y_{4}}{2}<\\cdots<\\frac{y_{995}+y_{997}}{2}<\\frac{y_{996}+y_{997}}{2}\n$$\n\nthere are at least $996+995=1991$ distinct midpoints, and therefore at least 1991 red points. The equality case happens if we take $P_{i}=(0,2 i), i=1,2, \\ldots, 997$. The midpoints are $(0, i+j)$, $1 \\leq i<j \\leq 997$, which are the points $(0, k)$ with $1+2=3 \\leq k \\leq 996+997=1993$, a total of $1993-3+1=1991$ red points.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
+
{"year": "1991", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}, b_{1}, b_{2}, \\ldots, b_{n}$ be positive real numbers such that $a_{1}+a_{2}+\\cdots+a_{n}=b_{1}+b_{2}+$ $\\cdots+b_{n}$. Show that\n\n$$\n\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}} \\geq \\frac{a_{1}+a_{2}+\\cdots+a_{n}}{2}\n$$", "solution": "By the Cauchy-Schwartz inequality,\n\n$$\n\\left(\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}}\\right)\\left(\\left(a_{1}+b_{1}\\right)+\\left(a_{2}+b_{2}\\right)+\\cdots+\\left(a_{n}+b_{n}\\right)\\right) \\geq\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)^{2} .\n$$\n\nSince $\\left(\\left(a_{1}+b_{1}\\right)+\\left(a_{2}+b_{2}\\right)+\\cdots+\\left(a_{n}+b_{n}\\right)\\right)=2\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)$,\n\n$$\n\\frac{a_{1}^{2}}{a_{1}+b_{1}}+\\frac{a_{2}^{2}}{a_{2}+b_{2}}+\\cdots+\\frac{a_{n}^{2}}{a_{n}+b_{n}} \\geq \\frac{\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)^{2}}{2\\left(a_{1}+a_{2}+\\cdots+a_{n}\\right)}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{2}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "1991", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.\n\nAnswer: All powers of 2 .", "solution": "Number the children from 0 to $n-1$. Then the teacher hands candy to children in positions $f(x)=1+2+\\cdots+x \\bmod n=\\frac{x(x+1)}{2} \\bmod n$. Our task is to find the range of $f: \\mathbb{Z}_{n} \\rightarrow \\mathbb{Z}_{n}$, and to verify whether the range is $\\mathbb{Z}_{n}$, that is, whether $f$ is a bijection.\nIf $n=2^{a} m, m>1$ odd, look at $f(x)$ modulo $m$. Since $m$ is odd, $m|f(x) \\Longleftrightarrow m| x(x+1)$. Then, for instance, $f(x) \\equiv 0(\\bmod m)$ for $x=0$ and $x=m-1$. This means that $f(x)$ is not a bijection modulo $m$, and there exists $t$ such that $f(x) \\not \\equiv t(\\bmod m)$ for all $x$. By the Chinese Remainder Theorem,\n\n$$\nf(x) \\equiv t \\quad(\\bmod n) \\Longleftrightarrow \\begin{cases}f(x) \\equiv t & \\left(\\bmod 2^{a}\\right) \\\\ f(x) \\equiv t & (\\bmod m)\\end{cases}\n$$\n\nTherefore, $f$ is not a bijection modulo $n$.\nIf $n=2^{a}$, then\n\n$$\nf(x)-f(y)=\\frac{1}{2}(x(x+1)-y(y+1))=\\frac{1}{2}\\left(x^{2}-y^{2}+x-y\\right)=\\frac{(x-y)(x+y+1)}{2} .\n$$\n\nand\n\n$$\nf(x) \\equiv f(y) \\quad\\left(\\bmod 2^{a}\\right) \\Longleftrightarrow(x-y)(x+y+1) \\equiv 0 \\quad\\left(\\bmod 2^{a+1}\\right)\n$$\n\nIf $x$ and $y$ have the same parity, $x+y+1$ is odd and $(*)$ is equivalent to $x \\equiv y\\left(\\bmod 2^{a+1}\\right)$. If $x$ and $y$ have different parity,\n\n$$\n(*) \\Longleftrightarrow x+y+1 \\equiv 0 \\quad\\left(\\bmod 2^{a+1}\\right)\n$$\n\nHowever, $1 \\leq x+y+1 \\leq 2\\left(2^{a}-1\\right)+1=2^{a+1}-1$, so $x+y+1$ is not a multiple of $2^{a+1}$. Therefore $f$ is a bijection if $n$ is a power of 2 .", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
+
{"year": "1991", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.\n\nAnswer: All powers of 2 .", "solution": "We give a full description of $a_{n}$, the size of the range of $f$.\nSince congruences modulo $n$ are defined, via Chinese Remainder Theorem, by congruences modulo $p^{\\alpha}$ for all prime divisors $p$ of $n$ and $\\alpha$ being the number of factors $p$ in the factorization of $n, a_{n}=\\prod_{p^{\\alpha} \\| n} a_{p^{\\alpha}}$.\nRefer to the first solution to check the case $p=2: a_{2^{\\alpha}}=2^{\\alpha}$.\nFor an odd prime $p$,\n\n$$\nf(x)=\\frac{x(x+1)}{2}=\\frac{(2 x+1)^{2}-1}{8}\n$$\n\nand since $p$ is odd, there is a bijection between the range of $f$ and the quadratic residues modulo $p^{\\alpha}$, namely $t \\mapsto 8 t+1$. So $a_{p^{\\alpha}}$ is the number of quadratic residues modulo $p^{\\alpha}$.\nLet $g$ be a primitive root of $p^{\\alpha}$. Then there are $\\frac{1}{2} \\phi\\left(p^{\\alpha}\\right)=\\frac{p-1}{2} \\cdot p^{\\alpha-1}$ quadratic residues that are coprime with $p: 1, g^{2}, g^{4}, \\ldots, g^{\\phi\\left(p^{n}\\right)-2}$. If $p$ divides a quadratic residue $k p$, that is, $x^{2} \\equiv k p$ $\\left(\\bmod p^{\\alpha}\\right), \\alpha \\geq 2$, then $p$ divides $x$ and, therefore, also $k$. Hence $p^{2}$ divides this quadratic residue, and these quadratic residues are $p^{2}$ times each quadratic residue of $p^{\\alpha-2}$. Thus\n\n$$\na_{p^{\\alpha}}=\\frac{p-1}{2} \\cdot p^{\\alpha-1}+a_{p^{\\alpha}-2} .\n$$\n\nSince $a_{p}=\\frac{p-1}{2}+1$ and $a_{p^{2}}=\\frac{p-1}{2} \\cdot p+1$, telescoping yields\n\n$$\na_{p^{2 t}}=\\frac{p-1}{2}\\left(p^{2 t-1}+p^{2 t-3}+\\cdots+p\\right)+1=\\frac{p\\left(p^{2 t}-1\\right)}{2(p+1)}+1\n$$\n\nand\n\n$$\na_{p^{2 t-1}}=\\frac{p-1}{2}\\left(p^{2 t-2}+p^{2 t-4}+\\cdots+1\\right)+1=\\frac{p^{2 t}-1}{2(p+1)}+1\n$$\n\nNow the problem is immediate: if $n$ is divisible by an odd prime $p, a_{p^{\\alpha}}<p^{\\alpha}$ for all $\\alpha$, and since $a_{t} \\leq t$ for all $t, a_{n}<n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "1991", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Given are two tangent circles and a point $P$ on their common tangent perpendicular to the lines joining their centres. Construct with ruler and compass all the circles that are tangent to these two circles and pass through the point $P$.", "solution": "Throughout this problem, we will assume that the given circles are externally tangent, since the problem does not have a solution otherwise.\nLet $\\Gamma_{1}$ and $\\Gamma_{2}$ be the given circles and $T$ be their tangency point. Suppose $\\omega$ is a circle that is tangent to $\\Gamma_{1}$ and $\\Gamma_{2}$ and passes through $P$.\nNow invert about point $P$, with radius $P T$. Let any line through $P$ that cuts $\\Gamma_{1}$ do so at points $X$ and $Y$. The power of $P$ with respect to $\\Gamma_{1}$ is $P T^{2}=P X \\cdot P Y$, so $X$ and $Y$ are swapped by this inversion. Therefore $\\Gamma_{1}$ is mapped to itself in this inversion. The same applies to $\\Gamma_{2}$. Since circle $\\omega$ passes through $P$, it is mapped to a line tangent to the images of $\\Gamma_{1}$ (itself) and $\\Gamma_{2}$ (also itself), that is, a common tangent line. This common tangent cannot be $P T$, as $P T$ is also mapped to itself. Since $\\Gamma_{1}$ and $\\Gamma_{2}$ have exactly other two common tangent lines, there are two solutions: the inverses of the tangent lines.\n\n\nWe proceed with the construction with the aid of some macro constructions that will be detailed later.\n\nStep 1. Draw the common tangents to $\\Gamma_{1}$ and $\\Gamma_{2}$.\nStep 2. For each common tangent $t$, draw the projection $P_{t}$ of $P$ onto $t$.\nStep 3. Find the inverse $P_{1}$ of $P_{t}$ with respect to the circle with center $P$ and radius $P T$.\nStep 4. $\\omega_{t}$ is the circle with diameter $P P_{1}$.\nLet's work out the details for steps 1 and 3 . Steps 2 and 4 are immediate.\nStep 1. In this particular case in which $\\Gamma_{1}$ and $\\Gamma_{2}$ are externally tangent, there is a small shortcut:\n\n- Draw the circle with diameter on the two centers $O_{1}$ of $\\Gamma_{1}$ and $O_{2}$ of $\\Gamma_{2}$, and find its center $O$.\n- Let this circle meet common tangent line $O P$ at points $Q, R$. The required lines are the perpendicular to $O Q$ at $Q$ and the perpendicular to $O R$ at $R$.\n\n\nLet's show why this construction works. Let $R_{i}$ be the radius of circle $\\Gamma_{i}$ and suppose without loss of generality that $R_{1} \\leq R_{2}$. Note that $O Q=\\frac{1}{2} O_{1} O_{2}=\\frac{R_{1}+R_{2}}{2}, O T=O O_{1}-R_{1}=\\frac{R_{2}-R_{1}}{2}$, so\n\n$$\n\\sin \\angle T Q O=\\frac{O T}{O Q}=\\frac{R_{2}-R_{1}}{R_{1}+R_{2}}\n$$\n\nwhich is also the sine of the angle between $O_{1} O_{2}$ and the common tangent lines.\nLet $t$ be the perpendicular to $O Q$ through $Q$. Then $\\angle\\left(t, O_{1} O_{2}\\right)=\\angle(O Q, Q T)=\\angle T Q O$, and $t$ is parallel to a common tangent line. Since\n\n$$\nd(O, t)=O Q=\\frac{R_{1}+R_{2}}{2}=\\frac{d\\left(O_{1}, t\\right)+d\\left(O_{2}, t\\right)}{2}\n$$\n\nand $O$ is the midpoint of $O_{1} O_{2}, O$ is also at the same distance from $t$ and the common tangent line, so these two lines coincide.\nStep 3. Finding the inverse of a point $X$ given the inversion circle $\\Omega$ with center $O$ is a well known procedure, but we describe it here for the sake of completeness.\n\n- If $X$ lies in $\\Omega$, then its inverse is $X$.\n- If $X$ lies in the interior of $\\Omega$, draw ray $O X$, then the perpendicular line $\\ell$ to $O X$ at $X$. Let $\\ell$ meet $\\Omega$ at a point $Y$. The inverse of $X$ is the intersection $X^{\\prime}$ of $O X$ and the line perpendicular to $O Y$ at $Y$. This is because $O Y X^{\\prime}$ is a right triangle with altitude $Y X$, and therefore $O X \\cdot O X^{\\prime}=O Y^{2}$.\n- If $X$ is in the exterior of $\\Omega$, draw ray $O X$ and one of the tangent lines $\\ell$ from $X$ to $\\Omega$ (just connect $X$ to one of the intersections of $\\Omega$ and the circle with diameter $O X$ ). Let $\\ell$ touch $\\Omega$ at a point $Y$. The inverse of $X$ is the projection $X^{\\prime}$ of $Y$ onto $O X$. This is because $O Y X^{\\prime}$ is a right triangle with altitude $Y X^{\\prime}$, and therefore $O X \\cdot O X^{\\prime}=O Y^{2}$.\n\n$X$ is inside $\\Omega$\n", "metadata": {"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo1992_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "1992", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "A triangle with sides $a, b$, and $c$ is given. Denote by $s$ the semiperimeter, that is $s=(a+b+c) / 2$. Construct a triangle with sides $s-a, s-b$, and $s-c$. This process is repeated until a triangle can no longer be constructed with the sidelengths given.\nFor which original triangles can this process be repeated indefinitely?\nAnswer: Only equilateral triangles.", "solution": "The perimeter of each new triangle constructed by the process is $(s-a)+(s-b)+(s-c)=$ $3 s-(a+b+c)=3 s-2 s=s$, that is, it is halved. Consider a new equivalent process in which a similar triangle with sidelengths $2(s-a), 2(s-b), 2(s-c)$ is constructed, so the perimeter is kept invariant.\nSuppose without loss of generality that $a \\leq b \\leq c$. Then $2(s-c) \\leq 2(s-b) \\leq 2(s-a)$, and the difference between the largest side and the smallest side changes from $c-a$ to $2(s-a)-2(s-c)=$ $2(c-a)$, that is, it doubles. Therefore, if $c-a>0$ then eventually this difference becomes larger than $a+b+c$, and it's immediate that a triangle cannot be constructed with the sidelengths. Hence the only possibility is $c-a=0 \\Longrightarrow a=b=c$, and it is clear that equilateral triangles can yield an infinite process, because all generated triangles are equilateral.", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
-
{"year": "1992", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "In a circle $C$ with centre $O$ and radius $r$, let $C_{1}, C_{2}$ be two circles with centres $O_{1}, O_{2}$ and radii $r_{1}, r_{2}$ respectively, so that each circle $C_{i}$ is internally tangent to $C$ at $A_{i}$ and so that $C_{1}, C_{2}$ are externally tangent to each other at $A$.\nProve that the three lines $O A, O_{1} A_{2}$, and $O_{2} A_{1}$ are concurrent.", "solution": "Because of the tangencies, the following triples of points (two centers and a tangency point) are collinear:\n\n$$\nO_{1} ; O_{2} ; A, \\quad O ; O_{1} ; A_{1}, \\quad O ; O_{2} ; A_{2}\n$$\n\nBecause of that we can ignore the circles and only draw their centers and tangency points.\n\n\nNow the problem is immediate from Ceva's theorem in triangle $O O_{1} O_{2}$, because\n\n$$\n\\frac{O A_{1}}{A_{1} O_{1}} \\cdot \\frac{O_{1} A}{A O_{2}} \\cdot \\frac{O_{2} A_{2}}{A_{2} O}=\\frac{r}{r_{1}} \\cdot \\frac{r_{1}}{r_{2}} \\cdot \\frac{r_{2}}{r}=1\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
-
{"year": "1992", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be an integer such that $n>3$. Suppose that we choose three numbers from the set $\\{1,2, \\ldots, n\\}$. Using each of these three numbers only once and using addition, multiplication, and parenthesis, let us form all possible combinations.\n(a) Show that if we choose all three numbers greater than $n / 2$, then the values of these combinations are all distinct.\n(b) Let $p$ be a prime number such that $p \\leq \\sqrt{n}$. Show that the number of ways of choosing three numbers so that the smallest one is $p$ and the values of the combinations are not all distinct is precisely the number of positive divisors of $p-1$.", "solution": "In both items, the smallest chosen number is at least 2: in part (a), $n / 2>1$ and in part (b), $p$ is a prime. So let $1<x<y<z$ be the chosen numbers. Then all possible combinations are\n\n$$\nx+y+z, \\quad x+y z, \\quad x y+z, \\quad y+z x, \\quad(x+y) z, \\quad(z+x) y, \\quad(x+y) z, \\quad x y z\n$$\n\nSince, for $1<m<n$ and $t>1,(m-1)(n-1) \\geq 1 \\cdot 2 \\Longrightarrow m n>m+n, t n+m-(t m+n)=$ $(t-1)(n-m)>0 \\Longrightarrow t n+m>t m+n$, and $(t+m) n-(t+n) m=t(n-m)>0$,\n\n$$\nx+y+z<z+x y<y+z x<x+y z\n$$\n\nand\n\n$$\n(y+z) x<(x+z) y<(x+y) z<x y z .\n$$\n\nAlso, $(y+z) x-(y+z x)=(x-1) y>0 \\Longrightarrow(y+z) x>y+z x$ and $(x+z) y-(x+y z)=$ $(y-1) x>0 \\Longrightarrow(x+z) y>x+y z$. Therefore the only numbers that can be equal are $x+y z$ and $(y+z) x$. In this case,\n\n$$\nx+y z=(y+z) x \\Longleftrightarrow(y-x)(z-x)=x(x-1)\n$$\n\nNow we can solve the items.\n(a) if $n / 2<x<y<z$ then $z-x<n / 2$, and since $y-x<z-x, y-x<n / 2-1$; then\n\n$$\n(y-x)(z-x)<\\frac{n}{2}\\left(\\frac{n}{2}-1\\right)<x(x-1)\n$$\n\nand therefore $x+y z<(y+z) x$.\n(b) if $x=p$, then $(y-p)(z-p)=p(p-1)$. Since $y-p<z-p,(y-p)^{2}<(y-p)(z-p)=$ $p(p-1) \\Longrightarrow y-p<p$, that is, $p$ does not divide $y-p$. Then $y-p$ is a divisor $d$ of $p-1$ and $z-p=\\frac{p(p-1)}{d}$. Therefore,\n\n$$\nx=p, \\quad, y=p+d, \\quad z=p+\\frac{p(p-1)}{d}\n$$\n\nwhich is a solution for every divisor $d$ of $p-1$ because\n\n$$\nx=p<y=p+d<2 p \\leq p+p \\cdot \\frac{p-1}{d}=z .\n$$\n\nComment: If $x=1$ was allowed, then any choice $1, y, z$ would have repeated numbers in the combination, as $1 \\cdot y+z=y+1 \\cdot z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 4 |
-
{"year": "1992", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Determine all pairs $(h, s)$ of positive integers with the following property: If one draws $h$ horizontal lines and another $s$ lines which satisfy\n(i) they are not horizontal,\n(ii) no two of them are parallel,\n(iii) no three of the $h+s$ lines are concurrent,\nthen the number of regions formed by these $h+s$ lines is 1992 .\nAnswer: $(995,1),(176,10)$, and $(80,21)$.", "solution": "Let $a_{h, s}$ the number of regions formed by $h$ horizontal lines and $s$ another lines as described in the problem. Let $\\mathcal{F}_{h, s}$ be the union of the $h+s$ lines and pick any line $\\ell$. If it intersects the other lines in $n$ (distinct!) points then $\\ell$ is partitioned into $n-1$ line segments and 2 rays, which delimit regions. Therefore if we remove $\\ell$ the number of regions decreases by exactly $n-1+2=n+1$.\nThen $a_{0,0}=1$ (no lines means there is only one region), and since every one of $s$ lines intersects the other $s-1$ lines, $a_{0, s}=a_{0, s-1}+s$ for $s \\geq 0$. Summing yields\n\n$$\na_{0, s}=s+(s-1)+\\cdots+1+a_{0,0}=\\frac{s^{2}+s+2}{2} .\n$$\n\nEach horizontal line only intersects the $s$ non-horizontal lines, so $a_{h, s}=a_{h-1, s}+s+1$, which implies\n\n$$\na_{h, s}=a_{0, s}+h(s+1)=\\frac{s^{2}+s+2}{2}+h(s+1) .\n$$\n\nOur final task is solving\n\n$$\na_{h, s}=1992 \\Longleftrightarrow \\frac{s^{2}+s+2}{2}+h(s+1)=1992 \\Longleftrightarrow(s+1)(s+2 h)=2 \\cdot 1991=2 \\cdot 11 \\cdot 181\n$$\n\nThe divisors of $2 \\cdot 1991$ are $1,2,11,22,181,362,1991,3982$. Since $s, h>0,2 \\leq s+1<s+2 h$, so the possibilities for $s+1$ can only be 2,11 and 22 , yielding the following possibilities for $(h, s)$ :\n\n$$\n(995,1), \\quad(176,10), \\quad \\text { and }(80,21) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "1992", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Find a sequence of maximal length consisting of non-zero integers in which the sum of any seven consecutive terms is positive and that of any eleven consecutive terms is negative.\n\nAnswer: The maximum length is 16 . There are several possible sequences with this length; one such sequence is $(-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7)$.", "solution": "Suppose it is possible to have more than 16 terms in the sequence. Let $a_{1}, a_{2}, \\ldots, a_{17}$ be the first 17 terms of the sequence. Consider the following array of terms in the sequence:\n\n| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |\n| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |\n| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |\n| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |\n| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |\n| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |\n\nLet $S$ the sum of the numbers in the array. If we sum by rows we obtain negative sums in each row, so $S<0$; however, it we sum by columns we obtain positive sums in each column, so $S>0$, a contradiction. This implies that the sequence cannot have more than 16 terms. One idea to find a suitable sequence with 16 terms is considering cycles of 7 numbers. For instance, one can try\n\n$$\n-a,-a, b,-a,-a,-a, b,-a,-a, b,-a,-a,-a, b,-a,-a .\n$$\n\nThe sum of every seven consecutive numbers is $-5 a+2 b$ and the sum of every eleven consecutive numbers is $-8 a+3 b$, so $-5 a+2 b>0$ and $-8 a+3 b<0$, that is,\n\n$$\n\\frac{5 a}{2}<b<\\frac{8 a}{3} \\Longleftrightarrow 15 a<6 b<16 a\n$$\n\nThen we can choose, say, $a=7$ and $105<6 b<112 \\Longleftrightarrow b=18$. A valid sequence is then\n\n$$\n-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "1992", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "A triangle with sides $a, b$, and $c$ is given. Denote by $s$ the semiperimeter, that is $s=(a+b+c) / 2$. Construct a triangle with sides $s-a, s-b$, and $s-c$. This process is repeated until a triangle can no longer be constructed with the sidelengths given.\nFor which original triangles can this process be repeated indefinitely?\nAnswer: Only equilateral triangles.", "solution": "The perimeter of each new triangle constructed by the process is $(s-a)+(s-b)+(s-c)=$ $3 s-(a+b+c)=3 s-2 s=s$, that is, it is halved. Consider a new equivalent process in which a similar triangle with sidelengths $2(s-a), 2(s-b), 2(s-c)$ is constructed, so the perimeter is kept invariant.\nSuppose without loss of generality that $a \\leq b \\leq c$. Then $2(s-c) \\leq 2(s-b) \\leq 2(s-a)$, and the difference between the largest side and the smallest side changes from $c-a$ to $2(s-a)-2(s-c)=$ $2(c-a)$, that is, it doubles. Therefore, if $c-a>0$ then eventually this difference becomes larger than $a+b+c$, and it's immediate that a triangle cannot be constructed with the sidelengths. Hence the only possibility is $c-a=0 \\Longrightarrow a=b=c$, and it is clear that equilateral triangles can yield an infinite process, because all generated triangles are equilateral.", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
+
{"year": "1992", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "In a circle $C$ with centre $O$ and radius $r$, let $C_{1}, C_{2}$ be two circles with centres $O_{1}, O_{2}$ and radii $r_{1}, r_{2}$ respectively, so that each circle $C_{i}$ is internally tangent to $C$ at $A_{i}$ and so that $C_{1}, C_{2}$ are externally tangent to each other at $A$.\nProve that the three lines $O A, O_{1} A_{2}$, and $O_{2} A_{1}$ are concurrent.", "solution": "Because of the tangencies, the following triples of points (two centers and a tangency point) are collinear:\n\n$$\nO_{1} ; O_{2} ; A, \\quad O ; O_{1} ; A_{1}, \\quad O ; O_{2} ; A_{2}\n$$\n\nBecause of that we can ignore the circles and only draw their centers and tangency points.\n\n\nNow the problem is immediate from Ceva's theorem in triangle $O O_{1} O_{2}$, because\n\n$$\n\\frac{O A_{1}}{A_{1} O_{1}} \\cdot \\frac{O_{1} A}{A O_{2}} \\cdot \\frac{O_{2} A_{2}}{A_{2} O}=\\frac{r}{r_{1}} \\cdot \\frac{r_{1}}{r_{2}} \\cdot \\frac{r_{2}}{r}=1\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
+
{"year": "1992", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be an integer such that $n>3$. Suppose that we choose three numbers from the set $\\{1,2, \\ldots, n\\}$. Using each of these three numbers only once and using addition, multiplication, and parenthesis, let us form all possible combinations.\n(a) Show that if we choose all three numbers greater than $n / 2$, then the values of these combinations are all distinct.\n(b) Let $p$ be a prime number such that $p \\leq \\sqrt{n}$. Show that the number of ways of choosing three numbers so that the smallest one is $p$ and the values of the combinations are not all distinct is precisely the number of positive divisors of $p-1$.", "solution": "In both items, the smallest chosen number is at least 2: in part (a), $n / 2>1$ and in part (b), $p$ is a prime. So let $1<x<y<z$ be the chosen numbers. Then all possible combinations are\n\n$$\nx+y+z, \\quad x+y z, \\quad x y+z, \\quad y+z x, \\quad(x+y) z, \\quad(z+x) y, \\quad(x+y) z, \\quad x y z\n$$\n\nSince, for $1<m<n$ and $t>1,(m-1)(n-1) \\geq 1 \\cdot 2 \\Longrightarrow m n>m+n, t n+m-(t m+n)=$ $(t-1)(n-m)>0 \\Longrightarrow t n+m>t m+n$, and $(t+m) n-(t+n) m=t(n-m)>0$,\n\n$$\nx+y+z<z+x y<y+z x<x+y z\n$$\n\nand\n\n$$\n(y+z) x<(x+z) y<(x+y) z<x y z .\n$$\n\nAlso, $(y+z) x-(y+z x)=(x-1) y>0 \\Longrightarrow(y+z) x>y+z x$ and $(x+z) y-(x+y z)=$ $(y-1) x>0 \\Longrightarrow(x+z) y>x+y z$. Therefore the only numbers that can be equal are $x+y z$ and $(y+z) x$. In this case,\n\n$$\nx+y z=(y+z) x \\Longleftrightarrow(y-x)(z-x)=x(x-1)\n$$\n\nNow we can solve the items.\n(a) if $n / 2<x<y<z$ then $z-x<n / 2$, and since $y-x<z-x, y-x<n / 2-1$; then\n\n$$\n(y-x)(z-x)<\\frac{n}{2}\\left(\\frac{n}{2}-1\\right)<x(x-1)\n$$\n\nand therefore $x+y z<(y+z) x$.\n(b) if $x=p$, then $(y-p)(z-p)=p(p-1)$. Since $y-p<z-p,(y-p)^{2}<(y-p)(z-p)=$ $p(p-1) \\Longrightarrow y-p<p$, that is, $p$ does not divide $y-p$. Then $y-p$ is a divisor $d$ of $p-1$ and $z-p=\\frac{p(p-1)}{d}$. Therefore,\n\n$$\nx=p, \\quad, y=p+d, \\quad z=p+\\frac{p(p-1)}{d}\n$$\n\nwhich is a solution for every divisor $d$ of $p-1$ because\n\n$$\nx=p<y=p+d<2 p \\leq p+p \\cdot \\frac{p-1}{d}=z .\n$$\n\nComment: If $x=1$ was allowed, then any choice $1, y, z$ would have repeated numbers in the combination, as $1 \\cdot y+z=y+1 \\cdot z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 4 |
+
{"year": "1992", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Determine all pairs $(h, s)$ of positive integers with the following property: If one draws $h$ horizontal lines and another $s$ lines which satisfy\n(i) they are not horizontal,\n(ii) no two of them are parallel,\n(iii) no three of the $h+s$ lines are concurrent,\nthen the number of regions formed by these $h+s$ lines is 1992 .\nAnswer: $(995,1),(176,10)$, and $(80,21)$.", "solution": "Let $a_{h, s}$ the number of regions formed by $h$ horizontal lines and $s$ another lines as described in the problem. Let $\\mathcal{F}_{h, s}$ be the union of the $h+s$ lines and pick any line $\\ell$. If it intersects the other lines in $n$ (distinct!) points then $\\ell$ is partitioned into $n-1$ line segments and 2 rays, which delimit regions. Therefore if we remove $\\ell$ the number of regions decreases by exactly $n-1+2=n+1$.\nThen $a_{0,0}=1$ (no lines means there is only one region), and since every one of $s$ lines intersects the other $s-1$ lines, $a_{0, s}=a_{0, s-1}+s$ for $s \\geq 0$. Summing yields\n\n$$\na_{0, s}=s+(s-1)+\\cdots+1+a_{0,0}=\\frac{s^{2}+s+2}{2} .\n$$\n\nEach horizontal line only intersects the $s$ non-horizontal lines, so $a_{h, s}=a_{h-1, s}+s+1$, which implies\n\n$$\na_{h, s}=a_{0, s}+h(s+1)=\\frac{s^{2}+s+2}{2}+h(s+1) .\n$$\n\nOur final task is solving\n\n$$\na_{h, s}=1992 \\Longleftrightarrow \\frac{s^{2}+s+2}{2}+h(s+1)=1992 \\Longleftrightarrow(s+1)(s+2 h)=2 \\cdot 1991=2 \\cdot 11 \\cdot 181\n$$\n\nThe divisors of $2 \\cdot 1991$ are $1,2,11,22,181,362,1991,3982$. Since $s, h>0,2 \\leq s+1<s+2 h$, so the possibilities for $s+1$ can only be 2,11 and 22 , yielding the following possibilities for $(h, s)$ :\n\n$$\n(995,1), \\quad(176,10), \\quad \\text { and }(80,21) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "1992", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Find a sequence of maximal length consisting of non-zero integers in which the sum of any seven consecutive terms is positive and that of any eleven consecutive terms is negative.\n\nAnswer: The maximum length is 16 . There are several possible sequences with this length; one such sequence is $(-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7)$.", "solution": "Suppose it is possible to have more than 16 terms in the sequence. Let $a_{1}, a_{2}, \\ldots, a_{17}$ be the first 17 terms of the sequence. Consider the following array of terms in the sequence:\n\n| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |\n| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |\n| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |\n| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |\n| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |\n| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |\n\nLet $S$ the sum of the numbers in the array. If we sum by rows we obtain negative sums in each row, so $S<0$; however, it we sum by columns we obtain positive sums in each column, so $S>0$, a contradiction. This implies that the sequence cannot have more than 16 terms. One idea to find a suitable sequence with 16 terms is considering cycles of 7 numbers. For instance, one can try\n\n$$\n-a,-a, b,-a,-a,-a, b,-a,-a, b,-a,-a,-a, b,-a,-a .\n$$\n\nThe sum of every seven consecutive numbers is $-5 a+2 b$ and the sum of every eleven consecutive numbers is $-8 a+3 b$, so $-5 a+2 b>0$ and $-8 a+3 b<0$, that is,\n\n$$\n\\frac{5 a}{2}<b<\\frac{8 a}{3} \\Longleftrightarrow 15 a<6 b<16 a\n$$\n\nThen we can choose, say, $a=7$ and $105<6 b<112 \\Longleftrightarrow b=18$. A valid sequence is then\n\n$$\n-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo1993_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "1993", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral such that all sides have equal length and angle $\\angle A B C$ is 60 degrees. Let $\\ell$ be a line passing through $D$ and not intersecting the quadrilateral (except at $D)$. Let $E$ and $F$ be the points of intersection of $\\ell$ with $A B$ and $B C$ respectively. Let $M$ be the point of intersection of $C E$ and $A F$.\nProve that $C A^{2}=C M \\times C E$.", "solution": "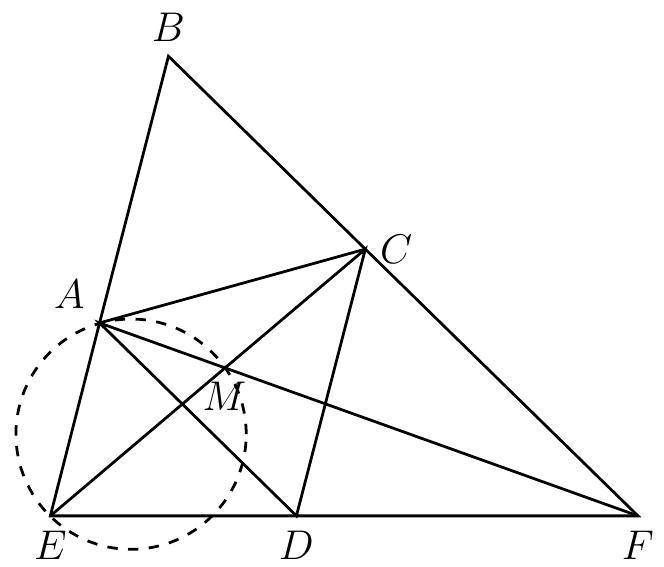\n\nTriangles $A E D$ and $C D F$ are similar, because $A D \\| C F$ and $A E \\| C D$. Thus, since $A B C$ and $A C D$ are equilateral triangles,\n\n$$\n\\frac{A E}{C D}=\\frac{A D}{C F} \\Longleftrightarrow \\frac{A E}{A C}=\\frac{A C}{C F}\n$$\n\nThe last equality combined with\n\n$$\n\\angle E A C=180^{\\circ}-\\angle B A C=120^{\\circ}=\\angle A C F\n$$\n\nshows that triangles $E A C$ and $A C F$ are also similar. Therefore $\\angle C A M=\\angle C A F=\\angle A E C$, which implies that line $A C$ is tangent to the circumcircle of $A M E$. By the power of a point, $C A^{2}=C M \\cdot C E$, and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
-
{"year": "1993", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Find the total number of different integer values the function\n\n$$\nf(x)=[x]+[2 x]+\\left[\\frac{5 x}{3}\\right]+[3 x]+[4 x]\n$$\n\ntakes for real numbers $x$ with $0 \\leq x \\leq 100$.\nNote: $[t]$ is the largest integer that does not exceed $t$.\nAnswer: 734.", "solution": "Note that, since $[x+n]=[x]+n$ for any integer $n$,\n\n$$\nf(x+3)=[x+3]+[2(x+3)]+\\left[\\frac{5(x+3)}{3}\\right]+[3(x+3)]+[4(x+3)]=f(x)+35,\n$$\n\none only needs to investigate the interval $[0,3)$.\nThe numbers in this interval at which at least one of the real numbers $x, 2 x, \\frac{5 x}{3}, 3 x, 4 x$ is an integer are\n\n- $0,1,2$ for $x$;\n- $\\frac{n}{2}, 0 \\leq n \\leq 5$ for $2 x$;\n- $\\frac{3 n}{5}, 0 \\leq n \\leq 4$ for $\\frac{5 x}{3}$;\n- $\\frac{n}{3}, 0 \\leq n \\leq 8$ for $3 x$;\n- $\\frac{n}{4}, 0 \\leq n \\leq 11$ for $4 x$.\n\nOf these numbers there are\n\n- 3 integers $(0,1,2)$;\n- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );\n- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );\n- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );\n- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).\n\nTherefore $f(x)$ increases 22 times per interval. Since $100=33 \\cdot 3+1$, there are $33 \\cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \\frac{1}{2}, 99 \\frac{1}{3}, 99 \\frac{2}{3}, 99 \\frac{1}{4}$, $99 \\frac{3}{4}, 99 \\frac{3}{5}$.\nThe total is then $33 \\cdot 22+8=734$.\nComment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of\n\n$$\n0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30\n$$\n\nin the interval $[0, f(100)]=[0,1166]$. Since $1166 \\equiv 11(\\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
-
{"year": "1993", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let\n\n$$\nf(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\\cdots+a_{0} \\quad \\text { and } \\quad g(x)=c_{n+1} x^{n+1}+c_{n} x^{n}+\\cdots+c_{0}\n$$\n\nbe non-zero polynomials with real coefficients such that $g(x)=(x+r) f(x)$ for some real number $r$. If $a=\\max \\left(\\left|a_{n}\\right|, \\ldots,\\left|a_{0}\\right|\\right)$ and $c=\\max \\left(\\left|c_{n+1}\\right|, \\ldots,\\left|c_{0}\\right|\\right)$, prove that $\\frac{a}{c} \\leq n+1$.", "solution": "Expanding $(x+r) f(x)$, we find that $c_{n+1}=a_{n}, c_{k}=a_{k-1}+r a_{k}$ for $k=1,2, \\ldots, n$, and $c_{0}=r a_{0}$. Consider three cases:\n\n- $r=0$. Then $c_{0}=0$ and $c_{k}=a_{k-1}$ for $k=1,2, \\ldots, n$, and $a=c \\Longrightarrow \\frac{a}{c}=1 \\leq n+1$.\n- $|r| \\geq 1$. Then\n\n$$\n\\begin{gathered}\n\\left|a_{0}\\right|=\\left|\\frac{c_{0}}{r}\\right| \\leq c \\\\\n\\left|a_{1}\\right|=\\left|\\frac{c_{1}-a_{0}}{r}\\right| \\leq\\left|c_{1}\\right|+\\left|a_{0}\\right| \\leq 2 c\n\\end{gathered}\n$$\n\nand inductively if $\\left|a_{k}\\right| \\leq(k+1) c$\n\n$$\n\\left|a_{k+1}\\right|=\\left|\\frac{c_{k+1}-a_{k}}{r}\\right| \\leq\\left|c_{k+1}\\right|+\\left|a_{k}\\right| \\leq c+(k+1) c=(k+2) c\n$$\n\nTherefore, $\\left|a_{k}\\right| \\leq(k+1) c \\leq(n+1) c$ for all $k$, and $a \\leq(n+1) c \\Longleftrightarrow \\frac{a}{c} \\leq n+1$.\n\n- $0<|r|<1$. Now work backwards: $\\left|a_{n}\\right|=\\left|c_{n+1}\\right| \\leq c$,\n\n$$\n\\left|a_{n-1}\\right|=\\left|c_{n}-r a_{n}\\right| \\leq\\left|c_{n}\\right|+\\left|r a_{n}\\right|<c+c=2 c,\n$$\n\nand inductively if $\\left|a_{n-k}\\right| \\leq(k+1) c$\n\n$$\n\\left|a_{n-k-1}\\right|=\\left|c_{n-k}-r a_{n-k}\\right| \\leq\\left|c_{n-k}\\right|+\\left|r a_{n-k}\\right|<c+(k+1) c=(k+2) c .\n$$\n\nTherefore, $\\left|a_{n-k}\\right| \\leq(k+1) c \\leq(n+1) c$ for all $k$, and $a \\leq(n+1) c$ again.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 4 |
-
{"year": "1993", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Determine all positive integers $n$ for which the equation\n\n$$\nx^{n}+(2+x)^{n}+(2-x)^{n}=0\n$$\n\nhas an integer as a solution.\n\n## Answer: $n=1$.", "solution": "If $n$ is even, $x^{n}+(2+x)^{n}+(2-x)^{n}>0$, so $n$ is odd.\nFor $n=1$, the equation reduces to $x+(2+x)+(2-x)=0$, which has the unique solution $x=-4$.\nFor $n>1$, notice that $x$ is even, because $x, 2-x$, and $2+x$ have all the same parity. Let $x=2 y$, so the equation reduces to\n\n$$\ny^{n}+(1+y)^{n}+(1-y)^{n}=0 .\n$$\n\nLooking at this equation modulo 2 yields that $y+(1+y)+(1-y)=y+2$ is even, so $y$ is even. Using the factorization\n\n$$\na^{n}+b^{n}=(a+b)\\left(a^{n-1}-a^{n-2} b+\\cdots+b^{n-1}\\right) \\quad \\text { for } n \\text { odd, }\n$$\n\nwhich has a sum of $n$ terms as the second factor, the equation is now equivalent to\n\n$$\ny^{n}+(1+y+1-y)\\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\\cdots+(1-y)^{n-1}\\right)=0\n$$\n\nor\n\n$$\ny^{n}=-2\\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\\cdots+(1-y)^{n-1}\\right) .\n$$\n\nEach of the $n$ terms in the second factor is odd, and $n$ is odd, so the second factor is odd. Therefore, $y^{n}$ has only one factor 2 , which is a contradiction to the fact that, $y$ being even, $y^{n}$ has at least $n>1$ factors 2 . Hence there are no solutions if $n>1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "1993", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $P_{1}, P_{2}, \\ldots, P_{1993}=P_{0}$ be distinct points in the $x y$-plane with the following properties:\n(i) both coordinates of $P_{i}$ are integers, for $i=1,2, \\ldots, 1993$;\n(ii) there is no point other than $P_{i}$ and $P_{i+1}$ on the line segment joining $P_{i}$ with $P_{i+1}$ whose coordinates are both integers, for $i=0,1, \\ldots, 1992$.\n\nProve that for some $i, 0 \\leq i \\leq 1992$, there exists a point $Q$ with coordinates $\\left(q_{x}, q_{y}\\right)$ on the line segment joining $P_{i}$ with $P_{i+1}$ such that both $2 q_{x}$ and $2 q_{y}$ are odd integers.", "solution": "Call a point $(x, y) \\in \\mathbb{Z}^{2}$ even or odd according to the parity of $x+y$. Since there are an odd number of points, there are two points $P_{i}=(a, b)$ and $P_{i+1}=(c, d), 0 \\leq i \\leq 1992$ with the same parity. This implies that $a+b+c+d$ is even. We claim that the midpoint of $P_{i} P_{i+1}$ is the desired point $Q$.\nIn fact, since $a+b+c+d=(a+c)+(b+d)$ is even, $a$ and $c$ have the same parity if and only if $b$ and $d$ also have the same parity. If both happen then the midpoint of $P_{i} P_{i+1}, Q=\\left(\\frac{a+c}{2}, \\frac{b+d}{2}\\right)$, has integer coordinates, which violates condition (ii). Then $a$ and $c$, as well as $b$ and $d$, have different parities, and $2 q_{x}=a+c$ and $2 q_{y}=b+d$ are both odd integers.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "1993", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C D$ be a quadrilateral such that all sides have equal length and angle $\\angle A B C$ is 60 degrees. Let $\\ell$ be a line passing through $D$ and not intersecting the quadrilateral (except at $D)$. Let $E$ and $F$ be the points of intersection of $\\ell$ with $A B$ and $B C$ respectively. Let $M$ be the point of intersection of $C E$ and $A F$.\nProve that $C A^{2}=C M \\times C E$.", "solution": "\n\nTriangles $A E D$ and $C D F$ are similar, because $A D \\| C F$ and $A E \\| C D$. Thus, since $A B C$ and $A C D$ are equilateral triangles,\n\n$$\n\\frac{A E}{C D}=\\frac{A D}{C F} \\Longleftrightarrow \\frac{A E}{A C}=\\frac{A C}{C F}\n$$\n\nThe last equality combined with\n\n$$\n\\angle E A C=180^{\\circ}-\\angle B A C=120^{\\circ}=\\angle A C F\n$$\n\nshows that triangles $E A C$ and $A C F$ are also similar. Therefore $\\angle C A M=\\angle C A F=\\angle A E C$, which implies that line $A C$ is tangent to the circumcircle of $A M E$. By the power of a point, $C A^{2}=C M \\cdot C E$, and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
+
{"year": "1993", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Find the total number of different integer values the function\n\n$$\nf(x)=[x]+[2 x]+\\left[\\frac{5 x}{3}\\right]+[3 x]+[4 x]\n$$\n\ntakes for real numbers $x$ with $0 \\leq x \\leq 100$.\nNote: $[t]$ is the largest integer that does not exceed $t$.\nAnswer: 734.", "solution": "Note that, since $[x+n]=[x]+n$ for any integer $n$,\n\n$$\nf(x+3)=[x+3]+[2(x+3)]+\\left[\\frac{5(x+3)}{3}\\right]+[3(x+3)]+[4(x+3)]=f(x)+35,\n$$\n\none only needs to investigate the interval $[0,3)$.\nThe numbers in this interval at which at least one of the real numbers $x, 2 x, \\frac{5 x}{3}, 3 x, 4 x$ is an integer are\n\n- $0,1,2$ for $x$;\n- $\\frac{n}{2}, 0 \\leq n \\leq 5$ for $2 x$;\n- $\\frac{3 n}{5}, 0 \\leq n \\leq 4$ for $\\frac{5 x}{3}$;\n- $\\frac{n}{3}, 0 \\leq n \\leq 8$ for $3 x$;\n- $\\frac{n}{4}, 0 \\leq n \\leq 11$ for $4 x$.\n\nOf these numbers there are\n\n- 3 integers $(0,1,2)$;\n- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );\n- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );\n- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );\n- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).\n\nTherefore $f(x)$ increases 22 times per interval. Since $100=33 \\cdot 3+1$, there are $33 \\cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \\frac{1}{2}, 99 \\frac{1}{3}, 99 \\frac{2}{3}, 99 \\frac{1}{4}$, $99 \\frac{3}{4}, 99 \\frac{3}{5}$.\nThe total is then $33 \\cdot 22+8=734$.\nComment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of\n\n$$\n0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30\n$$\n\nin the interval $[0, f(100)]=[0,1166]$. Since $1166 \\equiv 11(\\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
+
{"year": "1993", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let\n\n$$\nf(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\\cdots+a_{0} \\quad \\text { and } \\quad g(x)=c_{n+1} x^{n+1}+c_{n} x^{n}+\\cdots+c_{0}\n$$\n\nbe non-zero polynomials with real coefficients such that $g(x)=(x+r) f(x)$ for some real number $r$. If $a=\\max \\left(\\left|a_{n}\\right|, \\ldots,\\left|a_{0}\\right|\\right)$ and $c=\\max \\left(\\left|c_{n+1}\\right|, \\ldots,\\left|c_{0}\\right|\\right)$, prove that $\\frac{a}{c} \\leq n+1$.", "solution": "Expanding $(x+r) f(x)$, we find that $c_{n+1}=a_{n}, c_{k}=a_{k-1}+r a_{k}$ for $k=1,2, \\ldots, n$, and $c_{0}=r a_{0}$. Consider three cases:\n\n- $r=0$. Then $c_{0}=0$ and $c_{k}=a_{k-1}$ for $k=1,2, \\ldots, n$, and $a=c \\Longrightarrow \\frac{a}{c}=1 \\leq n+1$.\n- $|r| \\geq 1$. Then\n\n$$\n\\begin{gathered}\n\\left|a_{0}\\right|=\\left|\\frac{c_{0}}{r}\\right| \\leq c \\\\\n\\left|a_{1}\\right|=\\left|\\frac{c_{1}-a_{0}}{r}\\right| \\leq\\left|c_{1}\\right|+\\left|a_{0}\\right| \\leq 2 c\n\\end{gathered}\n$$\n\nand inductively if $\\left|a_{k}\\right| \\leq(k+1) c$\n\n$$\n\\left|a_{k+1}\\right|=\\left|\\frac{c_{k+1}-a_{k}}{r}\\right| \\leq\\left|c_{k+1}\\right|+\\left|a_{k}\\right| \\leq c+(k+1) c=(k+2) c\n$$\n\nTherefore, $\\left|a_{k}\\right| \\leq(k+1) c \\leq(n+1) c$ for all $k$, and $a \\leq(n+1) c \\Longleftrightarrow \\frac{a}{c} \\leq n+1$.\n\n- $0<|r|<1$. Now work backwards: $\\left|a_{n}\\right|=\\left|c_{n+1}\\right| \\leq c$,\n\n$$\n\\left|a_{n-1}\\right|=\\left|c_{n}-r a_{n}\\right| \\leq\\left|c_{n}\\right|+\\left|r a_{n}\\right|<c+c=2 c,\n$$\n\nand inductively if $\\left|a_{n-k}\\right| \\leq(k+1) c$\n\n$$\n\\left|a_{n-k-1}\\right|=\\left|c_{n-k}-r a_{n-k}\\right| \\leq\\left|c_{n-k}\\right|+\\left|r a_{n-k}\\right|<c+(k+1) c=(k+2) c .\n$$\n\nTherefore, $\\left|a_{n-k}\\right| \\leq(k+1) c \\leq(n+1) c$ for all $k$, and $a \\leq(n+1) c$ again.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 4 |
+
{"year": "1993", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Determine all positive integers $n$ for which the equation\n\n$$\nx^{n}+(2+x)^{n}+(2-x)^{n}=0\n$$\n\nhas an integer as a solution.\n\n## Answer: $n=1$.", "solution": "If $n$ is even, $x^{n}+(2+x)^{n}+(2-x)^{n}>0$, so $n$ is odd.\nFor $n=1$, the equation reduces to $x+(2+x)+(2-x)=0$, which has the unique solution $x=-4$.\nFor $n>1$, notice that $x$ is even, because $x, 2-x$, and $2+x$ have all the same parity. Let $x=2 y$, so the equation reduces to\n\n$$\ny^{n}+(1+y)^{n}+(1-y)^{n}=0 .\n$$\n\nLooking at this equation modulo 2 yields that $y+(1+y)+(1-y)=y+2$ is even, so $y$ is even. Using the factorization\n\n$$\na^{n}+b^{n}=(a+b)\\left(a^{n-1}-a^{n-2} b+\\cdots+b^{n-1}\\right) \\quad \\text { for } n \\text { odd, }\n$$\n\nwhich has a sum of $n$ terms as the second factor, the equation is now equivalent to\n\n$$\ny^{n}+(1+y+1-y)\\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\\cdots+(1-y)^{n-1}\\right)=0\n$$\n\nor\n\n$$\ny^{n}=-2\\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\\cdots+(1-y)^{n-1}\\right) .\n$$\n\nEach of the $n$ terms in the second factor is odd, and $n$ is odd, so the second factor is odd. Therefore, $y^{n}$ has only one factor 2 , which is a contradiction to the fact that, $y$ being even, $y^{n}$ has at least $n>1$ factors 2 . Hence there are no solutions if $n>1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "1993", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $P_{1}, P_{2}, \\ldots, P_{1993}=P_{0}$ be distinct points in the $x y$-plane with the following properties:\n(i) both coordinates of $P_{i}$ are integers, for $i=1,2, \\ldots, 1993$;\n(ii) there is no point other than $P_{i}$ and $P_{i+1}$ on the line segment joining $P_{i}$ with $P_{i+1}$ whose coordinates are both integers, for $i=0,1, \\ldots, 1992$.\n\nProve that for some $i, 0 \\leq i \\leq 1992$, there exists a point $Q$ with coordinates $\\left(q_{x}, q_{y}\\right)$ on the line segment joining $P_{i}$ with $P_{i+1}$ such that both $2 q_{x}$ and $2 q_{y}$ are odd integers.", "solution": "Call a point $(x, y) \\in \\mathbb{Z}^{2}$ even or odd according to the parity of $x+y$. Since there are an odd number of points, there are two points $P_{i}=(a, b)$ and $P_{i+1}=(c, d), 0 \\leq i \\leq 1992$ with the same parity. This implies that $a+b+c+d$ is even. We claim that the midpoint of $P_{i} P_{i+1}$ is the desired point $Q$.\nIn fact, since $a+b+c+d=(a+c)+(b+d)$ is even, $a$ and $c$ have the same parity if and only if $b$ and $d$ also have the same parity. If both happen then the midpoint of $P_{i} P_{i+1}, Q=\\left(\\frac{a+c}{2}, \\frac{b+d}{2}\\right)$, has integer coordinates, which violates condition (ii). Then $a$ and $c$, as well as $b$ and $d$, have different parities, and $2 q_{x}=a+c$ and $2 q_{y}=b+d$ are both odd integers.", "metadata": {"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo1994_sol.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "1994", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ be a function such that\n(i) For all $x, y \\in \\mathbb{R}$,\n\n$$\nf(x)+f(y)+1 \\geq f(x+y) \\geq f(x)+f(y)\n$$\n\n(ii) For all $x \\in[0,1), f(0) \\geq f(x)$,\n(iii) $-f(-1)=f(1)=1$.\n\nFind all such functions $f$.\nAnswer: $f(x)=\\lfloor x\\rfloor$, the largest integer that does not exceed $x$, is the only function.", "solution": "Plug $y \\rightarrow 1$ in (i):\n\n$$\nf(x)+f(1)+1 \\geq f(x+1) \\geq f(x)+f(1) \\Longleftrightarrow f(x)+1 \\leq f(x+1) \\leq f(x)+2\n$$\n\nNow plug $y \\rightarrow-1$ and $x \\rightarrow x+1$ in (i):\n\n$$\nf(x+1)+f(-1)+1 \\geq f(x) \\geq f(x+1)+f(-1) \\Longleftrightarrow f(x) \\leq f(x+1) \\leq f(x)+1\n$$\n\nHence $f(x+1)=f(x)+1$ and we only need to define $f(x)$ on $[0,1)$. Note that $f(1)=$ $f(0)+1 \\Longrightarrow f(0)=0$.\nCondition (ii) states that $f(x) \\leq 0$ in $[0,1)$.\nNow plug $y \\rightarrow 1-x$ in (i):\n\n$$\nf(x)+f(1-x)+1 \\leq f(x+(1-x)) \\leq f(x)+f(1-x) \\Longrightarrow f(x)+f(1-x) \\geq 0\n$$\n\nIf $x \\in(0,1)$ then $1-x \\in(0,1)$ as well, so $f(x) \\leq 0$ and $f(1-x) \\leq 0$, which implies $f(x)+f(1-x) \\leq 0$. Thus, $f(x)=f(1-x)=0$ for $x \\in(0,1)$. This combined with $f(0)=0$ and $f(x+1)=f(x)+1$ proves that $f(x)=\\lfloor x\\rfloor$, which satisfies the problem conditions, as since\n$x+y=\\lfloor x\\rfloor+\\lfloor y\\rfloor+\\{x\\}+\\{y\\}$ and $0 \\leq\\{x\\}+\\{y\\}<2 \\Longrightarrow\\lfloor x\\rfloor+\\lfloor y\\rfloor \\leq x+y<\\lfloor x\\rfloor+\\lfloor y\\rfloor+2$ implies\n\n$$\n\\lfloor x\\rfloor+\\lfloor y\\rfloor+1 \\geq\\lfloor x+y\\rfloor \\geq\\lfloor x\\rfloor+\\lfloor y\\rfloor .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
-
{"year": "1994", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.", "solution": "Embed $A B C$ in the complex plane, with $A, B$ and $C$ in the circle $|z|=R$, so $O$ is the origin. Represent each point by its lowercase letter. It is well known that $h=a+b+c$, so\n\n$$\nO H=|a+b+c| \\leq|a|+|b|+|c|=3 R .\n$$\n\nThe equality cannot occur because $a, b$, and $c$ are not collinear, so $O H<3 R$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 1"}}
|
| 3 |
-
{"year": "1994", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.", "solution": "Suppose with loss of generality that $\\angle A<90^{\\circ}$. Let $B D$ be an altitude. Then\n\n$$\nA H=\\frac{A D}{\\cos \\left(90^{\\circ}-C\\right)}=\\frac{A B \\cos A}{\\sin C}=2 R \\cos A\n$$\n\nBy the triangle inequality,\n\n$$\nO H<A O+A H=R+2 R \\cos A<3 R\n$$\n\nComment: With a bit more work, if $a, b, c$ are the sidelengths of $A B C$, one can show that\n\n$$\nO H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2} .\n$$\n\nIn fact, using vectors in a coordinate system with $O$ as origin, by the Euler line\n\n$$\n\\overrightarrow{O H}=3 \\overrightarrow{O G}=3 \\cdot \\frac{\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}}{3}=\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}\n$$\n\nso\n\n$$\nO H^{2}=\\overrightarrow{O H} \\cdot \\overrightarrow{O H}=(\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}) \\cdot(\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C})\n$$\n\nExpanding and using the fact that $\\overrightarrow{O X} \\cdot \\overrightarrow{O X}=O X^{2}=R^{2}$ for $X \\in\\{A, B, C\\}$, as well as\n$\\overrightarrow{O A} \\cdot \\overrightarrow{O B}=O A \\cdot O B \\cdot \\cos \\angle A O B=R^{2} \\cos 2 C=R^{2}\\left(1-2 \\sin ^{2} C\\right)=R^{2}\\left(1-2\\left(\\frac{c}{2 R}\\right)^{2}\\right)=R^{2}-\\frac{c^{2}}{2}$, we find that\n\n$$\n\\begin{aligned}\nO H^{2} & =\\overrightarrow{O A} \\cdot \\overrightarrow{O A}+\\overrightarrow{O B} \\cdot \\overrightarrow{O B}+\\overrightarrow{O C} \\cdot \\overrightarrow{O C}+2 \\overrightarrow{O A} \\cdot \\overrightarrow{O B}+2 \\overrightarrow{O A} \\cdot \\overrightarrow{O C}+2 \\overrightarrow{O B} \\cdot \\overrightarrow{O C} \\\\\n& =3 R^{2}+\\left(2 R^{2}-c^{2}\\right)+\\left(2 R^{2}-b^{2}\\right)+\\left(2 R^{2}-a^{2}\\right) \\\\\n& =9 R^{2}-a^{2}-b^{2}-c^{2}\n\\end{aligned}\n$$\n\nas required.\nThis proves that $O H^{2}<9 R^{2} \\Longrightarrow O H<3 R$, and since $a, b, c$ can be arbitrarily small (fix the circumcircle and choose $A, B, C$ arbitrarily close in this circle), the bound is sharp.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 2"}}
|
| 4 |
-
{"year": "1994", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be an integer of the form $a^{2}+b^{2}$, where $a$ and $b$ are relatively prime integers and such that if $p$ is a prime, $p \\leq \\sqrt{n}$, then $p$ divides $a b$. Determine all such $n$.\n\nAnswer: $n=2,5,13$.", "solution": "A prime $p$ divides $a b$ if and only if divides either $a$ or $b$. If $n=a^{2}+b^{2}$ is a composite then it has a prime divisor $p \\leq \\sqrt{n}$, and if $p$ divides $a$ it divides $b$ and vice-versa, which is not possible because $a$ and $b$ are coprime. Therefore $n$ is a prime.\nSuppose without loss of generality that $a \\geq b$ and consider $a-b$. Note that $a^{2}+b^{2}=(a-b)^{2}+2 a b$.\n\n- If $a=b$ then $a=b=1$ because $a$ and $b$ are coprime. $n=2$ is a solution.\n- If $a-b=1$ then $a$ and $b$ are coprime and $a^{2}+b^{2}=(a-b)^{2}+2 a b=2 a b+1=2 b(b+1)+1=$ $2 b^{2}+2 b+1$. So any prime factor of any number smaller than $\\sqrt{2 b^{2}+2 b+1}$ is a divisor of $a b=b(b+1)$.\nOne can check that $b=1$ and $b=2$ yields the solutions $n=1^{2}+2^{2}=5$ (the only prime $p$ is 2 ) and $n=2^{2}+3^{2}=13$ (the only primes $p$ are 2 and 3 ). Suppose that $b>2$.\nConsider, for instance, the prime factors of $b-1 \\leq \\sqrt{2 b^{2}+2 b+1}$, which is coprime with $b$. Any prime must then divide $a=b+1$. Then it divides $(b+1)-(b-1)=2$, that is, $b-1$ can only have 2 as a prime factor, that is, $b-1$ is a power of 2 , and since $b-1 \\geq 2$, $b$ is odd.\nSince $2 b^{2}+2 b+1-(b+2)^{2}=b^{2}-2 b-3=(b-3)(b+1) \\geq 0$, we can also consider any prime divisor of $b+2$. Since $b$ is odd, $b$ and $b+2$ are also coprime, so any prime divisor of $b+2$ must divide $a=b+1$. But $b+1$ and $b+2$ are also coprime, so there can be no such primes. This is a contradiction, and $b \\geq 3$ does not yield any solutions.\n- If $a-b>1$, consider a prime divisor $p$ of $a-b=\\sqrt{a^{2}-2 a b+b^{2}}<\\sqrt{a^{2}+b^{2}}$. Since $p$ divides one of $a$ and $b, p$ divides both numbers (just add or subtract $a-b$ accordingly.) This is a contradiction.\n\nHence the only solutions are $n=2,5,13$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "1994", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?\nAnswer: Yes.", "solution": "The answer is yes and we present the following construction: the idea is considering points in the unit circle of the form $P_{n}=(\\cos (2 n \\theta), \\sin (2 n \\theta))$ for an appropriate $\\theta$. Then the distance $P_{m} P_{n}$ is the length of the chord with central angle $(2 m-2 n) \\theta \\bmod \\pi$, that is, $2|\\sin ((m-n) \\theta)|$. Our task is then finding $\\theta$ such that (i) $\\sin (k \\theta)$ is rational for all $k \\in \\mathbb{Z}$; (ii) points $P_{n}$ are all distinct. We claim that $\\theta \\in(0, \\pi / 2)$ such that $\\cos \\theta=\\frac{3}{5}$ and therefore $\\sin \\theta=\\frac{4}{5}$ does the job. Proof of (i): We know that $\\sin ((n+1) \\theta)+\\sin ((n-1) \\theta)=2 \\sin (n \\theta) \\cos \\theta$, so if $\\sin ((n-1) \\theta$ and $\\sin (n \\theta)$ are both rational then $\\sin ((n+1) \\theta)$ also is. Since $\\sin (0 \\theta)=0$ and $\\sin \\theta$ are rational, an induction shows that $\\sin (n \\theta)$ is rational for $n \\in \\mathbb{Z}_{>0}$; the result is also true if $n$ is negative because $\\sin$ is an odd function.\nProof of (ii): $P_{m}=P_{n} \\Longleftrightarrow 2 n \\theta=2 m \\theta+2 k \\pi$ for some $k \\in \\mathbb{Z}$, which implies $\\sin ((n-m) \\theta)=$ $\\sin (k \\pi)=0$. We show that $\\sin (k \\theta) \\neq 0$ for all $k \\neq 0$.\nWe prove a stronger result: let $\\sin (k \\theta)=\\frac{a_{k}}{5^{k}}$. Then\n\n$$\n\\begin{aligned}\n\\sin ((k+1) \\theta)+\\sin ((k-1) \\theta)=2 \\sin (k \\theta) \\cos \\theta & \\Longleftrightarrow \\frac{a_{k+1}}{5^{k+1}}+\\frac{a_{k-1}}{5^{k-1}}=2 \\cdot \\frac{a_{k}}{5^{k}} \\cdot \\frac{3}{5} \\\\\n& \\Longleftrightarrow a_{k+1}=6 a_{k}-25 a_{k-1}\n\\end{aligned}\n$$\n\nSince $a_{0}=0$ and $a_{1}=4, a_{k}$ is an integer for $k \\geq 0$, and $a_{k+1} \\equiv a_{k}(\\bmod 5)$ for $k \\geq 1$ (note that $a_{-1}=-\\frac{4}{25}$ is not an integer!). Thus $a_{k} \\equiv 4(\\bmod 5)$ for all $k \\geq 1$, and $\\sin (k \\theta)=\\frac{a_{k}}{5^{k}}$ is an irreducible fraction with $5^{k}$ as denominator and $a_{k} \\equiv 4(\\bmod 5)$. This proves (ii) and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
-
{"year": "1994", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?\nAnswer: Yes.", "solution": "We present a different construction. Consider the (collinear) points\n\n$$\nP_{k}=\\left(1, \\frac{x_{k}}{y_{k}}\\right),\n$$\n\nsuch that the distance $O P_{k}$ from the origin $O$,\n\n$$\nO P_{k}=\\frac{\\sqrt{x_{k}^{2}+y_{k}^{2}}}{y_{k}}\n$$\n\nis rational, and $x_{k}$ and $y_{k}$ are integers. Clearly, $P_{i} P_{j}=\\left|\\frac{x_{i}}{y_{i}}-\\frac{x_{j}}{y_{j}}\\right|$ is rational.\nPerform an inversion with center $O$ and unit radius. It maps the line $x=1$, which contains all points $P_{k}$, to a circle (minus the origin). Let $Q_{k}$ be the image of $P_{k}$ under this inversion. Then\n\n$$\nQ_{i} Q_{j}=\\frac{1^{2} P_{i} P_{j}}{O P_{i} \\cdot O P_{j}}\n$$\n\nis rational and we are done if we choose $x_{k}$ and $y_{k}$ accordingly. But this is not hard, as we can choose the legs of a Pythagorean triple, say\n\n$$\nx_{k}=k^{2}-1, \\quad y_{k}=2 k\n$$\n\nThis implies $O P_{k}=\\frac{k^{2}+1}{2 k}$, and then\n\n$$\nQ_{i} Q_{j}=\\frac{\\left|\\frac{i^{2}-1}{i}-\\frac{j^{2}-1}{j}\\right|}{\\frac{i^{2}+1}{2 i} \\cdot \\frac{j^{2}+1}{2 j}}=\\frac{|4(i-j)(i j+1)|}{\\left(i^{2}+1\\right)\\left(j^{2}+1\\right)}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "1994", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "You are given three lists $A, B$, and $C$. List $A$ contains the numbers of the form $10^{k}$ in base 10, with $k$ any integer greater than or equal to 1 . Lists $B$ and $C$ contain the same numbers translated into base 2 and 5 respectively:\n\n| $A$ | $B$ | $C$ |\n| :--- | :--- | :--- |\n| 10 | 1010 | 20 |\n| 100 | 1100100 | 400 |\n| 1000 | 1111101000 | 13000 |\n| $\\vdots$ | $\\vdots$ | $\\vdots$ |\n\nProve that for every integer $n>1$, there is exactly one number in exactly one of the lists $B$ or $C$ that has exactly $n$ digits.", "solution": "Let $b_{k}$ and $c_{k}$ be the number of digits in the $k$ th term in lists $B$ and $C$, respectively. Then\n\n$$\n2^{b_{k}-1} \\leq 10^{k}<2^{b_{k}} \\Longleftrightarrow \\log _{2} 10^{k}<b_{k} \\leq \\log _{2} 10^{k}+1 \\Longleftrightarrow b_{k}=\\left\\lfloor k \\cdot \\log _{2} 10\\right\\rfloor+1\n$$\n\nand, similarly\n\n$$\nc_{k}=\\left\\lfloor k \\cdot \\log _{5} 10\\right\\rfloor+1\n$$\n\nBeatty's theorem states that if $\\alpha$ and $\\beta$ are irrational positive numbers such that\n\n$$\n\\frac{1}{\\alpha}+\\frac{1}{\\beta}=1\n$$\n\nthen the sequences $\\lfloor k \\alpha\\rfloor$ and $\\lfloor k \\beta\\rfloor, k=1,2, \\ldots$, partition the positive integers.\nThen, since\n\n$$\n\\frac{1}{\\log _{2} 10}+\\frac{1}{\\log _{5} 10}=\\log _{10} 2+\\log _{10} 5=\\log _{10}(2 \\cdot 5)=1\n$$\n\nthe sequences $b_{k}-1$ and $c_{k}-1$ partition the positive integers, and therefore each integer greater than 1 appears in $b_{k}$ or $c_{k}$ exactly once. We are done.\nComment: For the sake of completeness, a proof of Beatty's theorem follows.\nLet $x_{n}=\\alpha n$ and $y_{n}=\\beta n, n \\geq 1$ integer. Note that, since $\\alpha m=\\beta n$ implies that $\\frac{\\alpha}{\\beta}$ is rational but\n\n$$\n\\frac{\\alpha}{\\beta}=\\alpha \\cdot \\frac{1}{\\beta}=\\alpha\\left(1-\\frac{1}{\\alpha}\\right)=\\alpha-1\n$$\n\nis irrational, the sequences have no common terms, and all terms in both sequences are irrational.\nThe theorem is equivalent to proving that exactly one term of either $x_{n}$ of $y_{n}$ lies in the interval $(N, N+1)$ for each $N$ positive integer. For that purpose we count the number of terms of the union of the two sequences in the interval $(0, N)$ : since $n \\alpha<N \\Longleftrightarrow n<\\frac{N}{\\alpha}$, there are $\\left\\lfloor\\frac{N}{\\alpha}\\right\\rfloor$ terms of $x_{n}$ in the interval and, similarly, $\\left\\lfloor\\frac{N}{\\beta}\\right\\rfloor$ terms of $y_{n}$ in the same interval. Since the sequences are disjoint, the total of numbers is\n\n$$\nT(N)=\\left\\lfloor\\frac{N}{\\alpha}\\right\\rfloor+\\left\\lfloor\\frac{N}{\\beta}\\right\\rfloor\n$$\n\nHowever, $x-1<\\lfloor x\\rfloor<x$ for nonintegers $x$, so\n\n$$\n\\begin{aligned}\n\\frac{N}{\\alpha}-1+\\frac{N}{\\beta}-1<T(N)<\\frac{N}{\\alpha}+\\frac{N}{\\beta} & \\Longleftrightarrow N\\left(\\frac{1}{\\alpha}+\\frac{1}{\\beta}\\right)-2<T(N)<N\\left(\\frac{1}{\\alpha}+\\frac{1}{\\beta}\\right) \\\\\n& \\Longleftrightarrow N-2<T(N)<N,\n\\end{aligned}\n$$\n\nthat is, $T(N)=N-1$.\nTherefore the number of terms in $(N, N+1)$ is $T(N+1)-T(N)=N-(N-1)=1$, and the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "1994", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ be a function such that\n(i) For all $x, y \\in \\mathbb{R}$,\n\n$$\nf(x)+f(y)+1 \\geq f(x+y) \\geq f(x)+f(y)\n$$\n\n(ii) For all $x \\in[0,1), f(0) \\geq f(x)$,\n(iii) $-f(-1)=f(1)=1$.\n\nFind all such functions $f$.\nAnswer: $f(x)=\\lfloor x\\rfloor$, the largest integer that does not exceed $x$, is the only function.", "solution": "Plug $y \\rightarrow 1$ in (i):\n\n$$\nf(x)+f(1)+1 \\geq f(x+1) \\geq f(x)+f(1) \\Longleftrightarrow f(x)+1 \\leq f(x+1) \\leq f(x)+2\n$$\n\nNow plug $y \\rightarrow-1$ and $x \\rightarrow x+1$ in (i):\n\n$$\nf(x+1)+f(-1)+1 \\geq f(x) \\geq f(x+1)+f(-1) \\Longleftrightarrow f(x) \\leq f(x+1) \\leq f(x)+1\n$$\n\nHence $f(x+1)=f(x)+1$ and we only need to define $f(x)$ on $[0,1)$. Note that $f(1)=$ $f(0)+1 \\Longrightarrow f(0)=0$.\nCondition (ii) states that $f(x) \\leq 0$ in $[0,1)$.\nNow plug $y \\rightarrow 1-x$ in (i):\n\n$$\nf(x)+f(1-x)+1 \\leq f(x+(1-x)) \\leq f(x)+f(1-x) \\Longrightarrow f(x)+f(1-x) \\geq 0\n$$\n\nIf $x \\in(0,1)$ then $1-x \\in(0,1)$ as well, so $f(x) \\leq 0$ and $f(1-x) \\leq 0$, which implies $f(x)+f(1-x) \\leq 0$. Thus, $f(x)=f(1-x)=0$ for $x \\in(0,1)$. This combined with $f(0)=0$ and $f(x+1)=f(x)+1$ proves that $f(x)=\\lfloor x\\rfloor$, which satisfies the problem conditions, as since\n$x+y=\\lfloor x\\rfloor+\\lfloor y\\rfloor+\\{x\\}+\\{y\\}$ and $0 \\leq\\{x\\}+\\{y\\}<2 \\Longrightarrow\\lfloor x\\rfloor+\\lfloor y\\rfloor \\leq x+y<\\lfloor x\\rfloor+\\lfloor y\\rfloor+2$ implies\n\n$$\n\\lfloor x\\rfloor+\\lfloor y\\rfloor+1 \\geq\\lfloor x+y\\rfloor \\geq\\lfloor x\\rfloor+\\lfloor y\\rfloor .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
+
{"year": "1994", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.", "solution": "Embed $A B C$ in the complex plane, with $A, B$ and $C$ in the circle $|z|=R$, so $O$ is the origin. Represent each point by its lowercase letter. It is well known that $h=a+b+c$, so\n\n$$\nO H=|a+b+c| \\leq|a|+|b|+|c|=3 R .\n$$\n\nThe equality cannot occur because $a, b$, and $c$ are not collinear, so $O H<3 R$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 1"}}
|
| 3 |
+
{"year": "1994", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.", "solution": "Suppose with loss of generality that $\\angle A<90^{\\circ}$. Let $B D$ be an altitude. Then\n\n$$\nA H=\\frac{A D}{\\cos \\left(90^{\\circ}-C\\right)}=\\frac{A B \\cos A}{\\sin C}=2 R \\cos A\n$$\n\nBy the triangle inequality,\n\n$$\nO H<A O+A H=R+2 R \\cos A<3 R\n$$\n\nComment: With a bit more work, if $a, b, c$ are the sidelengths of $A B C$, one can show that\n\n$$\nO H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2} .\n$$\n\nIn fact, using vectors in a coordinate system with $O$ as origin, by the Euler line\n\n$$\n\\overrightarrow{O H}=3 \\overrightarrow{O G}=3 \\cdot \\frac{\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}}{3}=\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}\n$$\n\nso\n\n$$\nO H^{2}=\\overrightarrow{O H} \\cdot \\overrightarrow{O H}=(\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C}) \\cdot(\\overrightarrow{O A}+\\overrightarrow{O B}+\\overrightarrow{O C})\n$$\n\nExpanding and using the fact that $\\overrightarrow{O X} \\cdot \\overrightarrow{O X}=O X^{2}=R^{2}$ for $X \\in\\{A, B, C\\}$, as well as\n$\\overrightarrow{O A} \\cdot \\overrightarrow{O B}=O A \\cdot O B \\cdot \\cos \\angle A O B=R^{2} \\cos 2 C=R^{2}\\left(1-2 \\sin ^{2} C\\right)=R^{2}\\left(1-2\\left(\\frac{c}{2 R}\\right)^{2}\\right)=R^{2}-\\frac{c^{2}}{2}$, we find that\n\n$$\n\\begin{aligned}\nO H^{2} & =\\overrightarrow{O A} \\cdot \\overrightarrow{O A}+\\overrightarrow{O B} \\cdot \\overrightarrow{O B}+\\overrightarrow{O C} \\cdot \\overrightarrow{O C}+2 \\overrightarrow{O A} \\cdot \\overrightarrow{O B}+2 \\overrightarrow{O A} \\cdot \\overrightarrow{O C}+2 \\overrightarrow{O B} \\cdot \\overrightarrow{O C} \\\\\n& =3 R^{2}+\\left(2 R^{2}-c^{2}\\right)+\\left(2 R^{2}-b^{2}\\right)+\\left(2 R^{2}-a^{2}\\right) \\\\\n& =9 R^{2}-a^{2}-b^{2}-c^{2}\n\\end{aligned}\n$$\n\nas required.\nThis proves that $O H^{2}<9 R^{2} \\Longrightarrow O H<3 R$, and since $a, b, c$ can be arbitrarily small (fix the circumcircle and choose $A, B, C$ arbitrarily close in this circle), the bound is sharp.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 2"}}
|
| 4 |
+
{"year": "1994", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be an integer of the form $a^{2}+b^{2}$, where $a$ and $b$ are relatively prime integers and such that if $p$ is a prime, $p \\leq \\sqrt{n}$, then $p$ divides $a b$. Determine all such $n$.\n\nAnswer: $n=2,5,13$.", "solution": "A prime $p$ divides $a b$ if and only if divides either $a$ or $b$. If $n=a^{2}+b^{2}$ is a composite then it has a prime divisor $p \\leq \\sqrt{n}$, and if $p$ divides $a$ it divides $b$ and vice-versa, which is not possible because $a$ and $b$ are coprime. Therefore $n$ is a prime.\nSuppose without loss of generality that $a \\geq b$ and consider $a-b$. Note that $a^{2}+b^{2}=(a-b)^{2}+2 a b$.\n\n- If $a=b$ then $a=b=1$ because $a$ and $b$ are coprime. $n=2$ is a solution.\n- If $a-b=1$ then $a$ and $b$ are coprime and $a^{2}+b^{2}=(a-b)^{2}+2 a b=2 a b+1=2 b(b+1)+1=$ $2 b^{2}+2 b+1$. So any prime factor of any number smaller than $\\sqrt{2 b^{2}+2 b+1}$ is a divisor of $a b=b(b+1)$.\nOne can check that $b=1$ and $b=2$ yields the solutions $n=1^{2}+2^{2}=5$ (the only prime $p$ is 2 ) and $n=2^{2}+3^{2}=13$ (the only primes $p$ are 2 and 3 ). Suppose that $b>2$.\nConsider, for instance, the prime factors of $b-1 \\leq \\sqrt{2 b^{2}+2 b+1}$, which is coprime with $b$. Any prime must then divide $a=b+1$. Then it divides $(b+1)-(b-1)=2$, that is, $b-1$ can only have 2 as a prime factor, that is, $b-1$ is a power of 2 , and since $b-1 \\geq 2$, $b$ is odd.\nSince $2 b^{2}+2 b+1-(b+2)^{2}=b^{2}-2 b-3=(b-3)(b+1) \\geq 0$, we can also consider any prime divisor of $b+2$. Since $b$ is odd, $b$ and $b+2$ are also coprime, so any prime divisor of $b+2$ must divide $a=b+1$. But $b+1$ and $b+2$ are also coprime, so there can be no such primes. This is a contradiction, and $b \\geq 3$ does not yield any solutions.\n- If $a-b>1$, consider a prime divisor $p$ of $a-b=\\sqrt{a^{2}-2 a b+b^{2}}<\\sqrt{a^{2}+b^{2}}$. Since $p$ divides one of $a$ and $b, p$ divides both numbers (just add or subtract $a-b$ accordingly.) This is a contradiction.\n\nHence the only solutions are $n=2,5,13$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "1994", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?\nAnswer: Yes.", "solution": "The answer is yes and we present the following construction: the idea is considering points in the unit circle of the form $P_{n}=(\\cos (2 n \\theta), \\sin (2 n \\theta))$ for an appropriate $\\theta$. Then the distance $P_{m} P_{n}$ is the length of the chord with central angle $(2 m-2 n) \\theta \\bmod \\pi$, that is, $2|\\sin ((m-n) \\theta)|$. Our task is then finding $\\theta$ such that (i) $\\sin (k \\theta)$ is rational for all $k \\in \\mathbb{Z}$; (ii) points $P_{n}$ are all distinct. We claim that $\\theta \\in(0, \\pi / 2)$ such that $\\cos \\theta=\\frac{3}{5}$ and therefore $\\sin \\theta=\\frac{4}{5}$ does the job. Proof of (i): We know that $\\sin ((n+1) \\theta)+\\sin ((n-1) \\theta)=2 \\sin (n \\theta) \\cos \\theta$, so if $\\sin ((n-1) \\theta$ and $\\sin (n \\theta)$ are both rational then $\\sin ((n+1) \\theta)$ also is. Since $\\sin (0 \\theta)=0$ and $\\sin \\theta$ are rational, an induction shows that $\\sin (n \\theta)$ is rational for $n \\in \\mathbb{Z}_{>0}$; the result is also true if $n$ is negative because $\\sin$ is an odd function.\nProof of (ii): $P_{m}=P_{n} \\Longleftrightarrow 2 n \\theta=2 m \\theta+2 k \\pi$ for some $k \\in \\mathbb{Z}$, which implies $\\sin ((n-m) \\theta)=$ $\\sin (k \\pi)=0$. We show that $\\sin (k \\theta) \\neq 0$ for all $k \\neq 0$.\nWe prove a stronger result: let $\\sin (k \\theta)=\\frac{a_{k}}{5^{k}}$. Then\n\n$$\n\\begin{aligned}\n\\sin ((k+1) \\theta)+\\sin ((k-1) \\theta)=2 \\sin (k \\theta) \\cos \\theta & \\Longleftrightarrow \\frac{a_{k+1}}{5^{k+1}}+\\frac{a_{k-1}}{5^{k-1}}=2 \\cdot \\frac{a_{k}}{5^{k}} \\cdot \\frac{3}{5} \\\\\n& \\Longleftrightarrow a_{k+1}=6 a_{k}-25 a_{k-1}\n\\end{aligned}\n$$\n\nSince $a_{0}=0$ and $a_{1}=4, a_{k}$ is an integer for $k \\geq 0$, and $a_{k+1} \\equiv a_{k}(\\bmod 5)$ for $k \\geq 1$ (note that $a_{-1}=-\\frac{4}{25}$ is not an integer!). Thus $a_{k} \\equiv 4(\\bmod 5)$ for all $k \\geq 1$, and $\\sin (k \\theta)=\\frac{a_{k}}{5^{k}}$ is an irreducible fraction with $5^{k}$ as denominator and $a_{k} \\equiv 4(\\bmod 5)$. This proves (ii) and we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
+
{"year": "1994", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?\nAnswer: Yes.", "solution": "We present a different construction. Consider the (collinear) points\n\n$$\nP_{k}=\\left(1, \\frac{x_{k}}{y_{k}}\\right),\n$$\n\nsuch that the distance $O P_{k}$ from the origin $O$,\n\n$$\nO P_{k}=\\frac{\\sqrt{x_{k}^{2}+y_{k}^{2}}}{y_{k}}\n$$\n\nis rational, and $x_{k}$ and $y_{k}$ are integers. Clearly, $P_{i} P_{j}=\\left|\\frac{x_{i}}{y_{i}}-\\frac{x_{j}}{y_{j}}\\right|$ is rational.\nPerform an inversion with center $O$ and unit radius. It maps the line $x=1$, which contains all points $P_{k}$, to a circle (minus the origin). Let $Q_{k}$ be the image of $P_{k}$ under this inversion. Then\n\n$$\nQ_{i} Q_{j}=\\frac{1^{2} P_{i} P_{j}}{O P_{i} \\cdot O P_{j}}\n$$\n\nis rational and we are done if we choose $x_{k}$ and $y_{k}$ accordingly. But this is not hard, as we can choose the legs of a Pythagorean triple, say\n\n$$\nx_{k}=k^{2}-1, \\quad y_{k}=2 k\n$$\n\nThis implies $O P_{k}=\\frac{k^{2}+1}{2 k}$, and then\n\n$$\nQ_{i} Q_{j}=\\frac{\\left|\\frac{i^{2}-1}{i}-\\frac{j^{2}-1}{j}\\right|}{\\frac{i^{2}+1}{2 i} \\cdot \\frac{j^{2}+1}{2 j}}=\\frac{|4(i-j)(i j+1)|}{\\left(i^{2}+1\\right)\\left(j^{2}+1\\right)}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "1994", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "You are given three lists $A, B$, and $C$. List $A$ contains the numbers of the form $10^{k}$ in base 10, with $k$ any integer greater than or equal to 1 . Lists $B$ and $C$ contain the same numbers translated into base 2 and 5 respectively:\n\n| $A$ | $B$ | $C$ |\n| :--- | :--- | :--- |\n| 10 | 1010 | 20 |\n| 100 | 1100100 | 400 |\n| 1000 | 1111101000 | 13000 |\n| $\\vdots$ | $\\vdots$ | $\\vdots$ |\n\nProve that for every integer $n>1$, there is exactly one number in exactly one of the lists $B$ or $C$ that has exactly $n$ digits.", "solution": "Let $b_{k}$ and $c_{k}$ be the number of digits in the $k$ th term in lists $B$ and $C$, respectively. Then\n\n$$\n2^{b_{k}-1} \\leq 10^{k}<2^{b_{k}} \\Longleftrightarrow \\log _{2} 10^{k}<b_{k} \\leq \\log _{2} 10^{k}+1 \\Longleftrightarrow b_{k}=\\left\\lfloor k \\cdot \\log _{2} 10\\right\\rfloor+1\n$$\n\nand, similarly\n\n$$\nc_{k}=\\left\\lfloor k \\cdot \\log _{5} 10\\right\\rfloor+1\n$$\n\nBeatty's theorem states that if $\\alpha$ and $\\beta$ are irrational positive numbers such that\n\n$$\n\\frac{1}{\\alpha}+\\frac{1}{\\beta}=1\n$$\n\nthen the sequences $\\lfloor k \\alpha\\rfloor$ and $\\lfloor k \\beta\\rfloor, k=1,2, \\ldots$, partition the positive integers.\nThen, since\n\n$$\n\\frac{1}{\\log _{2} 10}+\\frac{1}{\\log _{5} 10}=\\log _{10} 2+\\log _{10} 5=\\log _{10}(2 \\cdot 5)=1\n$$\n\nthe sequences $b_{k}-1$ and $c_{k}-1$ partition the positive integers, and therefore each integer greater than 1 appears in $b_{k}$ or $c_{k}$ exactly once. We are done.\nComment: For the sake of completeness, a proof of Beatty's theorem follows.\nLet $x_{n}=\\alpha n$ and $y_{n}=\\beta n, n \\geq 1$ integer. Note that, since $\\alpha m=\\beta n$ implies that $\\frac{\\alpha}{\\beta}$ is rational but\n\n$$\n\\frac{\\alpha}{\\beta}=\\alpha \\cdot \\frac{1}{\\beta}=\\alpha\\left(1-\\frac{1}{\\alpha}\\right)=\\alpha-1\n$$\n\nis irrational, the sequences have no common terms, and all terms in both sequences are irrational.\nThe theorem is equivalent to proving that exactly one term of either $x_{n}$ of $y_{n}$ lies in the interval $(N, N+1)$ for each $N$ positive integer. For that purpose we count the number of terms of the union of the two sequences in the interval $(0, N)$ : since $n \\alpha<N \\Longleftrightarrow n<\\frac{N}{\\alpha}$, there are $\\left\\lfloor\\frac{N}{\\alpha}\\right\\rfloor$ terms of $x_{n}$ in the interval and, similarly, $\\left\\lfloor\\frac{N}{\\beta}\\right\\rfloor$ terms of $y_{n}$ in the same interval. Since the sequences are disjoint, the total of numbers is\n\n$$\nT(N)=\\left\\lfloor\\frac{N}{\\alpha}\\right\\rfloor+\\left\\lfloor\\frac{N}{\\beta}\\right\\rfloor\n$$\n\nHowever, $x-1<\\lfloor x\\rfloor<x$ for nonintegers $x$, so\n\n$$\n\\begin{aligned}\n\\frac{N}{\\alpha}-1+\\frac{N}{\\beta}-1<T(N)<\\frac{N}{\\alpha}+\\frac{N}{\\beta} & \\Longleftrightarrow N\\left(\\frac{1}{\\alpha}+\\frac{1}{\\beta}\\right)-2<T(N)<N\\left(\\frac{1}{\\alpha}+\\frac{1}{\\beta}\\right) \\\\\n& \\Longleftrightarrow N-2<T(N)<N,\n\\end{aligned}\n$$\n\nthat is, $T(N)=N-1$.\nTherefore the number of terms in $(N, N+1)$ is $T(N+1)-T(N)=N-(N-1)=1$, and the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo1999_sol.jsonl
CHANGED
|
@@ -1,6 +1,6 @@
|
|
| 1 |
-
{"year": "1999", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.", "solution": "and Marking Scheme:\nWe first note that the integer terms of any arithmetic progression are \"equally spaced\", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\\left(a_{i+j}-a_{i}\\right)$.\n\n1 POINT for realizing that the integers must be \"equally spaced\".\nThus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \\cdots, n$ and we need only to consider arithmetic progression of the form\n\n$$\n1,1+\\frac{1}{k}, 1+\\frac{2}{k}, \\cdots, 1+\\frac{k-1}{k}, 2,2+\\frac{1}{k}, \\cdots, n-1, \\cdots, n-1+\\frac{k-1}{k}, n\n$$\n\nThis has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.\n\n2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.\n\nThus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \\leq 1998$, then $(k+1) n-(k+1)+1 \\geq 2000$.\n\n4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).\n\nThat is, putting $k=\\lfloor 1999 /(n+1)\\rfloor$, we want the smallest integer $n$ so that\n\n$$\n\\left\\lfloor\\frac{1999}{n+1}\\right\\rfloor(n-1)+n \\geq 2000\n$$\n\nThis inequality does not hold if\n\n$$\n\\frac{1999}{n+1} \\cdot(n-1)+n<2000\n$$\n\n2 POINTS for setting up an inequality for $n$.\nThis simplifies to $n^{2}<3999$, that is, $n \\leq 63$. Now we check integers from $n=64$ on:\n\n$$\n\\begin{aligned}\n& \\text { for } n=64,\\left\\lfloor\\frac{1999}{65}\\right\\rfloor \\cdot 63+64=30 \\cdot 63+64=1954<2000 ; \\\\\n& \\text { for } n=65,\\left\\lfloor\\frac{1999}{66}\\right\\rfloor \\cdot 64+65=30 \\cdot 64+65=1985<2000 ; \\\\\n& \\text { for } n=66,\\left\\lfloor\\frac{1999}{67}\\right\\rfloor \\cdot 65+66=29 \\cdot 65+66=1951<2000 ; \\\\\n& \\text { for } n=67,\\left\\lfloor\\left\\lfloor\\frac{1999}{68}\\right\\rfloor \\cdot 66+67=29 \\cdot 66+67=1981<2000 ;\\right. \\\\\n& \\text { for } n=68,\\left\\lfloor\\frac{1999}{69}\\right\\rfloor \\cdot 67+68=28 \\cdot 67+68=1944<2000 ; \\\\\n& \\text { for } n=69,\\left\\lfloor\\frac{1999}{70}\\right\\rfloor \\cdot 68+69=28 \\cdot 68+69=1973<2000 ; \\\\\n& \\text { for } n=70,\\left\\lfloor\\frac{1999}{71}\\right\\rfloor \\cdot 69+70=28 \\cdot 69+70=2002 \\geq 2000 .\n\\end{aligned}\n$$\n\nThus the answer is $n=70$.\n1.POINT for checking these rumbers and finding that $n=70$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution "}}
|
| 2 |
-
{"year": "1999", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}, a_{2}, \\cdots$ be a sequence of real numbers satisfying $a_{i+j} \\leq a_{i}+a_{j}$ for all $i, j=1,2, \\cdots$. Prove that\n\n$$\na_{1}+\\frac{a_{2}}{2}+\\frac{a_{3}}{3}+\\cdots+\\frac{a_{n}}{n} \\geq a_{n}\n$$\n\nfor each positive integer $n$.", "solution": "and Marking Scheme:\n\nLetting $b_{i}=a_{i} / i,(i=1,2, \\cdots)$, we prove that\n\n$$\nb_{1}+\\cdots+b_{n} \\geq a_{n} \\quad(n=1,2, \\cdots)\n$$\n\nby induction on $n$. For $n=1, b_{1}=a_{1} \\geq a_{1}$, and the induction starts. Assume that\n\n$$\nb_{1}+\\cdots+b_{k} \\geq a_{k}\n$$\n\nfor all $k=1,2, \\cdots, n-1$. It suffices to prove that $b_{1}+\\cdots+b_{n} \\geq a_{n}$ or equivalently that\n\n$$\n\\begin{aligned}\n& n b_{1}+\\cdots+n b_{n-1} \\geq(n-1) a_{n} . \\\\\n& 3 \\text { POINTS for separating } a_{n} \\text { from } b_{1}, \\cdots, b_{n-1} \\text {. } \\\\\n& n b_{1}+\\cdots+n b_{n-1}=(n-1) b_{1}+(n-2) b_{2}+\\cdots+b_{n-1}+b_{1}+2 b_{2}+\\cdots+(n-1) b_{n-1} \\\\\n& =b_{1}+\\left(b_{1}+b_{2}\\right)+\\cdots+\\left(b_{1}+b_{2}+\\cdots+b_{n-1}\\right)+\\left(a_{1}+a_{2}+\\cdots+a_{n-1}\\right) \\\\\n& \\geq 2\\left(a_{1}+a_{2}+\\cdots+a_{n-1}\\right)=\\sum_{i=1}^{n-1}\\left(a_{i}+a_{n-i}\\right) \\geq(n-1) a_{n} .\n\\end{aligned}\n$$\n\n3 POINTS for the first inequaliny and 1 POINT for the rest.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution "}}
|
| 3 |
-
{"year": "1999", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $\\Gamma_{1}$ and $\\Gamma_{2}$ be two circles intersecting at $P$ and $Q$. The common tangent, closer to $P$, of $\\Gamma_{1}$ and $\\Gamma_{2}$ touches $\\Gamma_{1}$ at $A$ and $\\Gamma_{2}$ at $B$. The tangent of $\\Gamma_{1}$ at $P$ meets $\\Gamma_{2}$ at $C$, which is different from $P$ and the extension of $A P$ meets $B C$ at $R$. Prove that the circumcircle of triangle $P Q R$ is tangent to $B P$ and $B R$.", "solution": "and Marking Scheme:\n\nLet $\\alpha=\\angle P A B, \\beta=\\angle A B P$ y $\\gamma=\\angle Q A P$. Then, since $P C$ is tangent to $\\Gamma_{1}$, we have $\\angle Q P C=$ $\\angle Q B C=\\gamma$. Thus $A, B, R, Q$ are concyclic.\n\n3 POINTS for proving that $A, B, R, Q$ are concyclic.\nSince $A B$ is a common tangent to $\\Gamma_{1}$ and $\\Gamma_{2}$ then $\\angle A Q P=\\alpha$ and $\\angle P Q B=\\angle P C B=\\beta$. Therefore, since $A, B, R, Q$ are concyclic, $\\angle A R B=\\angle A Q B=\\alpha+\\beta$ and $\\angle B Q R=\\alpha$. Thus $\\angle P Q R=\\angle P Q B+$ $\\angle B Q R=\\alpha+\\beta$.\n\n$$\n2 \\text { POINTS for proving that } \\angle P Q R=\\angle P R B=\\alpha+\\beta\n$$\n\nSince $\\angle B P R$ is an exterior angle of triangle $A B P, \\angle B P R=\\alpha+\\beta$. We have\n\n$$\n\\angle P Q R=\\angle B P R=\\angle B R P\n$$\n\n1 POINT for proving $\\angle B P R=\\alpha+\\beta$.\nSo circumcircle of $P Q R$ is tangent to $B P$ and $B R$.\n1 POINT for concluding.\nRemark. 2POINTS can be given for proving that $\\angle P R B=\\angle R P B$ and 1 more POINT for attempting to prove (unsuccessfully) that $\\angle P R B=\\angle R P B=\\angle P Q R$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution "}}
|
| 4 |
-
{"year": "1999", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.", "solution": "and Marking Scheme:\n\nWithout loss of gencrality, assume that $|b| \\leq|a|$. If $b=0$, then $a$ must be a perfect square. So ( $a=k^{2}, b=0$ ) for each $k \\in Z$ is a solution.\nNow we consider the case $b \\neq 0$. Because $a^{2}+4 b$ is a perfect square, the quadratic equation\n\n$$\nx^{2}+a x-b=0\n$$\n\nhas two non-zero integral roots $x_{1}, x_{2}$.\n2 POINTS for noticing that this equation has integral roots.\nThen $x_{1}+x_{2}=-a$ and $x_{1} x_{2}=-b$, and from this it follows that\n\n$$\n\\frac{1}{\\left|x_{1}\\right|}+\\frac{1}{\\left|x_{2}\\right|} \\geq\\left|\\frac{1}{x_{1}}+\\frac{1}{x_{2}}\\right|=\\frac{|a|}{|b|} \\geq 1\n$$\n\nHence there is at least one root, say $x_{1}$, such that $\\left|x_{1}\\right| \\leq 2$.\n3 POINTS for finding that $\\left|x_{1}\\right| \\leq 2$.\n\nThere are the following possibilities.\n(1) $x_{1}=2$. Substituting $x_{1}=2$ into ( $*$ ) we get $b=2 a+4$. So we have $b^{2}+4 a=(2 a+4)^{2}+4 a=$ $4 a^{2}+20 a+16=(2 a+5)^{2}-9$. It is casy to see that the solution in non-negative integers of the equation $x^{2}-9=y^{2}$ is $(3,0)$. Hence $2 a+5= \\pm 3$. From this we obtain $a=-4, b=-4$ and $a=-1, b=2$. The latter should be rejected because of the assumption $|a| \\geq|b|$.\n(2) $x_{1}=-2$. Substituting $x_{1}=-2$ into (*) we get $b=4-2 a$. Hence $b^{2}+4 a=4 a^{2}-12 a+16=$ $(2 a-3)^{2}+7$. It is easy to show that the solution in non-negative integers of the equation $x^{2}+7=y^{2}$ is $(3,4)$. Hence $2 a-3= \\pm 3$. From this we obtain $a=3, b=-2$.\n(3) $x_{1}=1$. Substituting $x_{1}=1$ into $(*)$ we get $b=a+1$. Hence $b^{2}+4 a=a^{2}+6 a+1=(a+3)^{2}-8$. It is easy to show that the solution in non-negative integers of the equation $x^{2}-8=y^{2}$ is $(3,1)$. Hence $a+3= \\pm 3$. From this we obtain $a=-6, b=-5$.\n(4) $x_{1}=-1$. Substituting $x_{1}=-1$ into (*) we get $b=1-a$. Then $a^{2}+4 b=(a-2)^{2}, b^{2}+4 a=(a+1)^{2}$. Consequently, $a=k, b=1-k(k \\in Z)$ is a solution.\n\nTesting these solutions and by symmetry we obtain the following solutions\n\n$$\n(-4,-4),(-5,-6),(-6,-5),\\left(0, k^{2}\\right),\\left(k^{2}, 0\\right),(k, 1-k)\n$$\n\nwhere $k$ is an arbitrary integer. (Observe that the solution $(3,-2)$ obtained in the second possibility is included in the last solution as a special case.)\n\n1 POINT for writing up the correct answer.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# First Solution "}}
|
| 5 |
-
{"year": "1999", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.", "solution": "and Marking Scheme:\n\nWithout loss of generality assume that $|b| \\leq|a|$. Then $a^{2}+4 b \\leq a^{2}+4|a|<a^{2}+4|a|+4=(|a|+2)^{2}$. Given that $a^{2}+4 b$ is a perfect square and since $a^{2}+4 b$ y $a^{2}$ have same parity then $a^{2}+4 b \\neq(|a|+1)^{2}$, so\n\n$$\na^{2}+4 b \\leq a^{2}\n$$\n\n2 POINTS for proving (1).\nLet us consider three cases.\nCase 1. $a^{2}+4 b=a^{2}$. Then $b=0$ and $a$ must be a perfect square. So $a=k^{2}, b=0(k \\in Z)$ is a solution.\nCase 2. $a^{2}+4 b=(|a|-2)^{2}$. Then $b=1-|a|$, therefore $b^{2}+4 a=a^{2}-2|a|+4 a+1$ must be a perfect square.\nIf $a>0$ then $b^{2}+4 a=(a+1)^{2}$ is a perfect square for each $a \\in Z$. Consequently $a=k$ and $b=1-k$ ( $k \\in Z^{+}$) is a solution.\nIf $a=0$ then $b=1$, but from (1) $b$ must be non-positive.\nIf $a<0$ then $b^{2}+4 a=m^{2}-6 m+1$ must be a perfect square, where $m=-a>0$. For $m \\geq 8$\n\n$$\n(m-3)^{2}>m^{2}-6 m+1>(m-4)^{2}\n$$\n\ntherefore $m<8$. If $m=1,2,3,4,5$ then $m^{2}-6 m+1<0$. If $m=6, m^{2}-6 m+1=1$ is a perfect square thus $a=-6$ and $b=-5$ is a solution. If $m=7, m^{2}-6 m+1=8$ is not a perfect square.\n\n2 POINTS for case 1 and case 2.\nCase 3. $a^{2}+4 b \\leq(|a|-4)^{2}$. Since $|b| \\leq|a|$ then $b \\geq-|a|$, thus $a^{2}-4|a| \\leq a^{2}+4 b \\leq(|a|-4)^{2}$. It follows that $|a| \\leq 4$. We have following posibilities:\n\n## 1 POINT for finding that $|a| \\leq 4$ in this case.\n\n(a) $|a|=4$. Then $16+4 b=0$ or $b=-4$. Thus $b^{2}+4 a=16 \\pm 16$ must be a perfect square. So $a=-4$ y $b=-4$.\n(b) $|a|=3$. In this case $a^{2}+4 b=9+4 b \\leq 1$, then $9+4 b=0$ or $9+4 b=1$. The equation $9+4 b=0$ does not have integer solutions. The solution of the second equation is $b=-2$. Then $b^{2}+4 a=4 \\pm 12$ must be a perfect square, thus $a=3$.\n(c) $|a|=2 \\cdot a^{2}+4 b=4+4 b \\leq 4$. Since $4+4 b$ is cven and must be a perfect square then $4+4 b=4$ or $4+4 b=0$. Therefore $b=0$ or $b=-1$. If $b=0, b^{2}+4 a= \\pm 8$ is not a perfect square. If $b=-1$ then $b^{2}+4 a=1 \\pm 8$ is a perfect square if $a=2$. Thus $a=2$ and $b=-1$ is a solution.\n(d) $|a|=1$. Then $a^{2}+4 b=4 b+1 \\leq 9$. Since $4 b+1$ must be an odd perfect square then $4 b+1=1$ or $4 b+1=9$. So $b=0$ or $b=2$. If $b=0, b^{2}+4 a= \\pm 4$, then $a=1$. If $b=2$ then $a=-1$, but this is not possible because $|b| \\leq|a|$. Thus $a=1$ y $b=0$ is a solution in this case.\n(c) $|a|=0$. Since $|b| \\leq|a|$ then $b=0$.\n\n1 POINT for concluding case 3.\n\nTesting these solutions and by symmetry we obtain the following solutions:\n\n$$\n\\left(k^{2}, 0\\right),\\left(0, k^{2}\\right),(k, 1-k),(-6,-5),(-5,-6),(-4,-4)\n$$\n\nwhere $k$ is an arbitrary integer. Note that if $(k, 1-k)$ is a solution with $k>0$, then taking $t=1-k$, $k=1-t$, so $(1-t, t)$ is solution. Thus by symetry $(k, 1-k)$ is a solution for any integer.\n\n1 POINT for writing up the correct answer.\nRemark: I POINT can be given for checking that $(k, 1-k)$ is a solution. However NO POINT is given for finding any other particular solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Second Solution "}}
|
| 6 |
-
{"year": "1999", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $S$ be a set of $2 n+1$ points in the plane such that no three are collinear and no four concyclic. A circle will be called good if it has 3 points of $S$ on its circumference, $n-1$ points in its interior and $n-1$ in its exterior. Prove that the number of good circles has the same parity as $n$.", "solution": "and Marking Scheme:\n\nLemma 1. Let $P$ and $Q$ be two points of $S$. The number of good circles that contain $P$ and $Q$ on their circumference is odd.\n\n## Proof of Lemma 1.\n\n\n\nLet $N$ be the number of good circles that pass through $P$ and $Q$. Number the points on one side of the line $P Q$ by $A_{1}, A_{2}, \\ldots, A_{k}$ and those on the other side by $B_{1}, B_{2}, \\ldots, B_{m}$ in such a way that if $\\angle P A_{i} Q=\\alpha_{i}, \\angle P B_{j} Q=180-\\beta_{j}$ then $\\alpha_{1}>\\alpha_{2}>\\ldots>\\alpha_{k}$ and $\\beta_{1}>\\beta_{2}>\\ldots>\\beta_{m}$.\nNote that the angles $\\alpha_{1}, \\alpha_{2}, \\ldots, \\alpha_{k}, \\beta_{1}, \\beta_{2}, \\ldots, \\beta_{m}$ are all distinct since there are no four points in $S$ that are concyclic.\nObserve that the circle that passes through $P, Q$ and $A_{i}$ has $A_{j}$ in its interior when $\\alpha_{j}>\\alpha_{i}$ that is, when $i>j$; and it contains $B_{j}$ in its interior when $\\alpha_{i}+180-\\beta_{j}>180$, that is, when $\\alpha_{i}>\\beta_{j}$. Similar conditions apply to the circle that contains $P, Q$ and $B_{j}$.\n\n1 POINT for characterizing the points that lie inside a given circle ins terms of these angles, or for similar considerations.\nOrder the angles $\\alpha_{1}, \\alpha_{2}, \\ldots, \\alpha_{k}, \\beta_{1}, \\beta_{2}, \\ldots, \\beta_{m}$ from the greatest to least. Now transform $S$ as follows. Consider a $\\beta_{j}$ that bas an $\\alpha_{i}$ immediately to its left in such an ordering ( $\\ldots>\\alpha_{i}>\\beta_{j} \\ldots$ ). Consider a new set $S^{\\prime}$ that contains the same points as $S$ except for $A_{i}$ and $B_{j}$. These two points will be replaced by $A_{i}^{\\prime}$ and $B_{j}^{\\prime}$ that satisfy $\\angle P A_{i}^{\\prime} Q=\\beta_{j}=\\alpha_{i}^{\\prime}$ and $\\angle P B_{j}^{\\prime} Q=180-\\alpha_{i}^{\\prime \\prime}=180-\\beta_{j}^{\\prime}$. Thus $\\beta_{j}$ and $\\alpha_{i}$ have been interchanged and the ordering of the $\\alpha$ 's and $\\beta$ 's has only changed with respect to the relative order of $\\alpha_{i}$ and $\\beta_{j}$; we continue to have\n\n$$\n\\alpha_{1}>\\alpha_{2}>\\ldots>\\alpha_{i-1}>\\alpha_{i}^{\\prime}>\\alpha_{i+1}>\\ldots>\\alpha_{k}\n$$\n\nand\n\n$$\n\\beta_{1}>\\beta_{2}>\\ldots>\\beta_{j-1}>\\beta_{j}^{\\prime}>\\beta_{j+1}>\\ldots>\\beta_{m}\n$$\n\n1 POINT for this or another useful transformation of the set $S$.\nAnalyze the good circles in this new set $S^{\\prime}$. Clearly, a circle through $P, Q, A_{r}(r \\neq i)$ or through $P, Q, B_{s}(s \\neq j)$ that was good in $S$ will also be good in $S^{\\prime}$, because the order of $A_{r}$ (or $B_{s}$ ) relative to the rest of the points has not changed, and therefore the number of points in the interior or exterior of this circle has not changed. The only changes that could have taken place are:\na) If the circle $P, Q, A_{i}$ was good in $S$, the circle $P, Q, A_{i}^{\\prime}$ may not be good in $S^{\\prime}$.\nb) If the circle $P, Q, B_{j}$ was good in $S$, the circle $P, Q, B_{j}^{\\prime}$ may not be good in $S^{\\prime}$.\nc) If the circle $P, Q, A_{i}$ was not good in $S$, the circle $P, Q, A_{i}^{\\prime}$ may be good in $S^{\\prime}$.\nd) If the circle $P, Q, B_{j}$ was not good in $S$, the circle $P, Q, B_{j}^{\\prime}$ may be good in $S^{\\prime}$.\n\n1 POINT for realizing that the transformation can only change the \"goodness\" of these circles. But observe that the circle $P, Q, A_{i}$ contains the points $A_{1}, A_{2}, \\ldots, A_{i-1}, B_{j}, B_{j+1}, \\ldots, B_{m}$ and does not contain the points $A_{i+1}, A_{i+2}, \\ldots, A_{k}, B_{1}, B_{2}, \\ldots, B_{j-1}$ in its interior. Then this circle is good if and only if $i+m-j=k-i+j-1$, which we rewrite as $j-i=\\frac{1}{2}(m-k+1)$. On the other hand, the circle $P, Q, B_{j}$ contains the points $B_{j+1}, B_{j+2}, \\ldots, B_{m}, A_{1}, A_{2}, \\ldots, A_{i}$ and does not contain the points $B_{1}, B_{2}, \\ldots, B_{j-1}, A_{i+1}, A_{i+2}, \\ldots, A_{k}$ in its interior. Hence this circle is good if and only if $m-j+i=j-1+k-i$, which we rewrite as $j-i=\\frac{1}{2}(m-k+1)$.\nTherefore, the circle $P, Q, A_{i}$ is good if and only if the circle $P, Q, B_{j}$ is good. Similarly, the circle $P, Q, A_{i}^{\\prime}$ is good if and only if the circle $P, Q, B_{j}^{\\prime}$ is good. That is to say, transforming $S$ into $S^{\\prime}$ we lose either 0 or 2 good circles of $S$ and we gain either 0 or 2 good circles in $S^{\\prime}$.\n\n1 POINT for realizing that the \"goodness\" of these circles is changed in pairs.\nContinuing in this way, we may continue to transform $S$ until we obtain a new set $S_{0}$ such that the angles $\\alpha_{1}^{\\prime}, \\alpha_{2}^{\\prime}, \\ldots, \\alpha_{k}^{\\prime}, \\beta_{1}^{\\prime}, \\beta_{2}^{\\prime}, \\ldots, \\beta_{m}^{\\prime}$ satisfy\n\n$$\n\\beta_{1}^{\\prime}>\\beta_{2}^{\\prime}>\\ldots>\\beta_{n}^{\\prime}>\\alpha_{1}^{\\prime}>\\alpha_{2}^{\\prime}>\\ldots>\\alpha_{k}^{\\prime}\n$$\n\nand such that the number of good circles in $S_{0}$ has the same parity as $N$. We claim that $S_{0}$ has exactly one good circle. In this configuration, the circle $P, Q, A_{i}$ does not contain any $B_{j}$ and the circle $P, Q, B_{r}$ does not contain any $A_{s}$ (for all $\\left.i, j\\right)$, because $\\alpha_{a}+\\left(180-\\beta_{b}\\right)<180$ for all $a, b$. Hence, the only possible good circles are $P, Q, B_{m-n+1}$ (which contains the $n-1$ points $B_{m-n+2}, B_{m-n+3}, \\ldots, B_{m}$ ), if $m-n+1>0$, and the circle $P, Q, A_{n}$ (which contains the $n-1$ points $A_{1}, A_{2}, \\ldots, A_{n}$ ), if $n \\leq k$. But, since $m+k=2 n-1$, which we rewrite as $m-n+1=n-k$, exactly one of the inequalitites $m-n+1>0$ and $n \\leq k$ is satisfied. It follows that one of the points $B_{m-n+1}$ and $A_{n}$ corresponds to a good circle and the other does not. Hence, $S_{0}$ has exactly one good circle, and $N$ is odd.\n\n1 POINT for showing that this configuration has exactly one good circle.\n\nNow consider the $\\binom{2 n+1}{2}$ pairs of points in $S$. Let $a_{2 k+1}$ be the number of pairs of points through which exactly $2 k+1$ good circles pass. Then\n\n$$\na_{1}+a_{3}+a_{5}+\\ldots=\\binom{2 n+1}{2}\n$$\n\nBut then the number of good circles in $S$ is\n\n$$\n\\begin{aligned}\n\\frac{1}{3}\\left(a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\\ldots\\right) & \\equiv a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\\ldots \\\\\n& \\equiv a_{1}+a_{3}+a_{5}+a_{7}+\\ldots \\\\\n& \\equiv\\binom{2 n+1}{2} \\\\\n& \\equiv n(2 n+1) \\\\\n& \\equiv n(\\bmod 2) .\n\\end{aligned}\n$$\n\nHere we have taken into account that each good circle is counted 3 times in the expression $a_{1}+3 a_{3}+$ $5 a_{5}+7 a_{7}+\\ldots$ The desired result follows.\n\n2 POINTS for this computation.\n\n## Alteraative Proof of Lemma 1.\n\nLet, $A_{1}, A_{2}, \\ldots, A_{2 n-1}$ be the $2 n-1$ given points other than $P$ and $Q$.\nInvert the plane with respect to point $P$. Let $O, B_{1}, B_{2}, \\ldots, B_{2 n-1}$ be the images of points $Q, A_{1}, A_{2}, \\ldots, A_{2 n-1}$, respectively, under this inversion. Call point $B_{i}$ \"good\" if the line $O B_{i}$ splits the points $B_{1}, B_{2} \\ldots, B_{i-1}, B_{i+1}, \\ldots, B_{2 n-1}$ evenly, leaving $n-1$ of them to each side of it. (Notice that no other $B_{j}$ can lie on the line $O B_{i}$, or else the points $P, Q, A_{i}$ and $A_{j}$ would be concyclic.) Then it is clear that the circle through $P, Q$ and $A_{i}$ is good if and only if point $B_{i}$ is good. Therefore, it suffices to prove that the number of good points is odd.\n\n1 POINT for inverting and realizing the equivalence between good circles and good points. Notice that the good points depend only on the relative positions of rays $O B_{1}, O B_{2}, \\ldots, O B_{2 n-1}$, and not on the exact positions of points $B_{1}, B_{2}, \\ldots, B_{2 n-1}$. Therefore we may assume, for simplicity, that $B_{1}, B_{2}, \\ldots, B_{2 n-1}$ lie on the unit circle $\\Gamma$ with center $O$.\n\n1 POINT for this or a similar simplification.\nLet $C_{1}, C_{2}, \\ldots, C_{2 n-1}$ be the points diametrically opposite to $B_{1}, B_{2}, \\ldots, B_{2 n-1}$ in $\\Gamma$. As remarked earlier, no $C_{i}$ can coincide with one of the $B_{j}$ 's. We will call the $B_{i}$ 's \"white points\", and the $C_{i}$ 's \"black points\". We will refer to these $4 n-2$ points as the \"colored points\".\nNow we prove that the number of good points is odd, which will complete the proof of the lemma. We proceed by induction on $n$. If $n=1$, the result is trivial. Now assume that the result is true for $n=k$, and consider $2 k+1$ white points $B_{1}, B_{2}, \\ldots, B_{2 k+1}$ on the circle $\\Gamma$ (no two of which are diametrically opposite), and their diametrically opposite black points $C_{1}, C_{2}, \\ldots, C_{2 k+1}$. Call this configuration of points \"configuration 1 \". It is clear that we must have two consecutive colored points on $\\Gamma$ which have different colors, say $B_{i}$ and $C_{j}$. Now remove points $B_{i}, B_{j}, C_{i}$ and $C_{j}$ from $\\Gamma$, to obtain \"configuration 2 \", a configuration with $2 k-1$ points of each color.\n\n1 POINT for this or a similar transformation of the set.\nIt is easy to verify the following two claims:\n\n1. Point $B_{i}$ is good in configuration 1 if and only if point $B_{j}$ is good in configuration 1.\n2. Let $k \\neq i, j$. Then point $B_{k}$ is good in configuration 1 if and only if it is good in configuration 2.\n\nIt follows that, by removing points $B_{i}, B_{j}, C_{i}$ and $C_{j}$, the number of good points can either stay the same, or decreases by two. In any case, its parity remains unchanged. Since we know, by the induction hypothesis, that the number of good points in configuration 2 is odd, it follows that the number of good points in configuration 1 is also odd. This completes the proof.\n\n## Another Approach to Lemma 1.\n\nOne can give another inductive proof of lemma. 1, which combines the ideas of the two proofs that we have given. The idea is to start as in the first proof, with the characterization of the points inside a given circle.\n\n1 POINT\nThen we transform the set $S$ by removing the points $A_{i}$ and $B_{j}$ instead of replacing then by $A_{i}^{p}$ and $B_{j}^{\\prime}$.\n\n1 POINT\nIt can be shown that every one of the romaining circles going through $P$ and $Q$, contained exactly one of $A_{i}$ and $B_{j}$. Therefore, the only good circles we could have gained or lost are $P, Q, A_{i}$ and $P, Q, B_{j}$.\n\n2 POINTS\nFinally, we show that either both or none of these circles were good, so the parity of the number of good circles isn't changed by this transformation.\n\n1 POINT\n\nRemark: 2 POINTS can be given if the result has been fully proved for a particular case with $n>1$. (If more than one particular case has been analyzed completly, only 2 POINTS.) These points are awarded only if no progress has been made in the general solution of the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution "}}
|
|
|
|
| 1 |
+
{"year": "1999", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.", "solution": "and Marking Scheme:\nWe first note that the integer terms of any arithmetic progression are \"equally spaced\", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\\left(a_{i+j}-a_{i}\\right)$.\n\n1 POINT for realizing that the integers must be \"equally spaced\".\nThus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \\cdots, n$ and we need only to consider arithmetic progression of the form\n\n$$\n1,1+\\frac{1}{k}, 1+\\frac{2}{k}, \\cdots, 1+\\frac{k-1}{k}, 2,2+\\frac{1}{k}, \\cdots, n-1, \\cdots, n-1+\\frac{k-1}{k}, n\n$$\n\nThis has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.\n\n2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.\n\nThus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \\leq 1998$, then $(k+1) n-(k+1)+1 \\geq 2000$.\n\n4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).\n\nThat is, putting $k=\\lfloor 1999 /(n+1)\\rfloor$, we want the smallest integer $n$ so that\n\n$$\n\\left\\lfloor\\frac{1999}{n+1}\\right\\rfloor(n-1)+n \\geq 2000\n$$\n\nThis inequality does not hold if\n\n$$\n\\frac{1999}{n+1} \\cdot(n-1)+n<2000\n$$\n\n2 POINTS for setting up an inequality for $n$.\nThis simplifies to $n^{2}<3999$, that is, $n \\leq 63$. Now we check integers from $n=64$ on:\n\n$$\n\\begin{aligned}\n& \\text { for } n=64,\\left\\lfloor\\frac{1999}{65}\\right\\rfloor \\cdot 63+64=30 \\cdot 63+64=1954<2000 ; \\\\\n& \\text { for } n=65,\\left\\lfloor\\frac{1999}{66}\\right\\rfloor \\cdot 64+65=30 \\cdot 64+65=1985<2000 ; \\\\\n& \\text { for } n=66,\\left\\lfloor\\frac{1999}{67}\\right\\rfloor \\cdot 65+66=29 \\cdot 65+66=1951<2000 ; \\\\\n& \\text { for } n=67,\\left\\lfloor\\left\\lfloor\\frac{1999}{68}\\right\\rfloor \\cdot 66+67=29 \\cdot 66+67=1981<2000 ;\\right. \\\\\n& \\text { for } n=68,\\left\\lfloor\\frac{1999}{69}\\right\\rfloor \\cdot 67+68=28 \\cdot 67+68=1944<2000 ; \\\\\n& \\text { for } n=69,\\left\\lfloor\\frac{1999}{70}\\right\\rfloor \\cdot 68+69=28 \\cdot 68+69=1973<2000 ; \\\\\n& \\text { for } n=70,\\left\\lfloor\\frac{1999}{71}\\right\\rfloor \\cdot 69+70=28 \\cdot 69+70=2002 \\geq 2000 .\n\\end{aligned}\n$$\n\nThus the answer is $n=70$.\n1.POINT for checking these rumbers and finding that $n=70$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution "}}
|
| 2 |
+
{"year": "1999", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, \\cdots$ be a sequence of real numbers satisfying $a_{i+j} \\leq a_{i}+a_{j}$ for all $i, j=1,2, \\cdots$. Prove that\n\n$$\na_{1}+\\frac{a_{2}}{2}+\\frac{a_{3}}{3}+\\cdots+\\frac{a_{n}}{n} \\geq a_{n}\n$$\n\nfor each positive integer $n$.", "solution": "and Marking Scheme:\n\nLetting $b_{i}=a_{i} / i,(i=1,2, \\cdots)$, we prove that\n\n$$\nb_{1}+\\cdots+b_{n} \\geq a_{n} \\quad(n=1,2, \\cdots)\n$$\n\nby induction on $n$. For $n=1, b_{1}=a_{1} \\geq a_{1}$, and the induction starts. Assume that\n\n$$\nb_{1}+\\cdots+b_{k} \\geq a_{k}\n$$\n\nfor all $k=1,2, \\cdots, n-1$. It suffices to prove that $b_{1}+\\cdots+b_{n} \\geq a_{n}$ or equivalently that\n\n$$\n\\begin{aligned}\n& n b_{1}+\\cdots+n b_{n-1} \\geq(n-1) a_{n} . \\\\\n& 3 \\text { POINTS for separating } a_{n} \\text { from } b_{1}, \\cdots, b_{n-1} \\text {. } \\\\\n& n b_{1}+\\cdots+n b_{n-1}=(n-1) b_{1}+(n-2) b_{2}+\\cdots+b_{n-1}+b_{1}+2 b_{2}+\\cdots+(n-1) b_{n-1} \\\\\n& =b_{1}+\\left(b_{1}+b_{2}\\right)+\\cdots+\\left(b_{1}+b_{2}+\\cdots+b_{n-1}\\right)+\\left(a_{1}+a_{2}+\\cdots+a_{n-1}\\right) \\\\\n& \\geq 2\\left(a_{1}+a_{2}+\\cdots+a_{n-1}\\right)=\\sum_{i=1}^{n-1}\\left(a_{i}+a_{n-i}\\right) \\geq(n-1) a_{n} .\n\\end{aligned}\n$$\n\n3 POINTS for the first inequaliny and 1 POINT for the rest.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution "}}
|
| 3 |
+
{"year": "1999", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $\\Gamma_{1}$ and $\\Gamma_{2}$ be two circles intersecting at $P$ and $Q$. The common tangent, closer to $P$, of $\\Gamma_{1}$ and $\\Gamma_{2}$ touches $\\Gamma_{1}$ at $A$ and $\\Gamma_{2}$ at $B$. The tangent of $\\Gamma_{1}$ at $P$ meets $\\Gamma_{2}$ at $C$, which is different from $P$ and the extension of $A P$ meets $B C$ at $R$. Prove that the circumcircle of triangle $P Q R$ is tangent to $B P$ and $B R$.", "solution": "and Marking Scheme:\n\nLet $\\alpha=\\angle P A B, \\beta=\\angle A B P$ y $\\gamma=\\angle Q A P$. Then, since $P C$ is tangent to $\\Gamma_{1}$, we have $\\angle Q P C=$ $\\angle Q B C=\\gamma$. Thus $A, B, R, Q$ are concyclic.\n\n3 POINTS for proving that $A, B, R, Q$ are concyclic.\nSince $A B$ is a common tangent to $\\Gamma_{1}$ and $\\Gamma_{2}$ then $\\angle A Q P=\\alpha$ and $\\angle P Q B=\\angle P C B=\\beta$. Therefore, since $A, B, R, Q$ are concyclic, $\\angle A R B=\\angle A Q B=\\alpha+\\beta$ and $\\angle B Q R=\\alpha$. Thus $\\angle P Q R=\\angle P Q B+$ $\\angle B Q R=\\alpha+\\beta$.\n\n$$\n2 \\text { POINTS for proving that } \\angle P Q R=\\angle P R B=\\alpha+\\beta\n$$\n\nSince $\\angle B P R$ is an exterior angle of triangle $A B P, \\angle B P R=\\alpha+\\beta$. We have\n\n$$\n\\angle P Q R=\\angle B P R=\\angle B R P\n$$\n\n1 POINT for proving $\\angle B P R=\\alpha+\\beta$.\nSo circumcircle of $P Q R$ is tangent to $B P$ and $B R$.\n1 POINT for concluding.\nRemark. 2POINTS can be given for proving that $\\angle P R B=\\angle R P B$ and 1 more POINT for attempting to prove (unsuccessfully) that $\\angle P R B=\\angle R P B=\\angle P Q R$.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution "}}
|
| 4 |
+
{"year": "1999", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.", "solution": "and Marking Scheme:\n\nWithout loss of gencrality, assume that $|b| \\leq|a|$. If $b=0$, then $a$ must be a perfect square. So ( $a=k^{2}, b=0$ ) for each $k \\in Z$ is a solution.\nNow we consider the case $b \\neq 0$. Because $a^{2}+4 b$ is a perfect square, the quadratic equation\n\n$$\nx^{2}+a x-b=0\n$$\n\nhas two non-zero integral roots $x_{1}, x_{2}$.\n2 POINTS for noticing that this equation has integral roots.\nThen $x_{1}+x_{2}=-a$ and $x_{1} x_{2}=-b$, and from this it follows that\n\n$$\n\\frac{1}{\\left|x_{1}\\right|}+\\frac{1}{\\left|x_{2}\\right|} \\geq\\left|\\frac{1}{x_{1}}+\\frac{1}{x_{2}}\\right|=\\frac{|a|}{|b|} \\geq 1\n$$\n\nHence there is at least one root, say $x_{1}$, such that $\\left|x_{1}\\right| \\leq 2$.\n3 POINTS for finding that $\\left|x_{1}\\right| \\leq 2$.\n\nThere are the following possibilities.\n(1) $x_{1}=2$. Substituting $x_{1}=2$ into ( $*$ ) we get $b=2 a+4$. So we have $b^{2}+4 a=(2 a+4)^{2}+4 a=$ $4 a^{2}+20 a+16=(2 a+5)^{2}-9$. It is casy to see that the solution in non-negative integers of the equation $x^{2}-9=y^{2}$ is $(3,0)$. Hence $2 a+5= \\pm 3$. From this we obtain $a=-4, b=-4$ and $a=-1, b=2$. The latter should be rejected because of the assumption $|a| \\geq|b|$.\n(2) $x_{1}=-2$. Substituting $x_{1}=-2$ into (*) we get $b=4-2 a$. Hence $b^{2}+4 a=4 a^{2}-12 a+16=$ $(2 a-3)^{2}+7$. It is easy to show that the solution in non-negative integers of the equation $x^{2}+7=y^{2}$ is $(3,4)$. Hence $2 a-3= \\pm 3$. From this we obtain $a=3, b=-2$.\n(3) $x_{1}=1$. Substituting $x_{1}=1$ into $(*)$ we get $b=a+1$. Hence $b^{2}+4 a=a^{2}+6 a+1=(a+3)^{2}-8$. It is easy to show that the solution in non-negative integers of the equation $x^{2}-8=y^{2}$ is $(3,1)$. Hence $a+3= \\pm 3$. From this we obtain $a=-6, b=-5$.\n(4) $x_{1}=-1$. Substituting $x_{1}=-1$ into (*) we get $b=1-a$. Then $a^{2}+4 b=(a-2)^{2}, b^{2}+4 a=(a+1)^{2}$. Consequently, $a=k, b=1-k(k \\in Z)$ is a solution.\n\nTesting these solutions and by symmetry we obtain the following solutions\n\n$$\n(-4,-4),(-5,-6),(-6,-5),\\left(0, k^{2}\\right),\\left(k^{2}, 0\\right),(k, 1-k)\n$$\n\nwhere $k$ is an arbitrary integer. (Observe that the solution $(3,-2)$ obtained in the second possibility is included in the last solution as a special case.)\n\n1 POINT for writing up the correct answer.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# First Solution "}}
|
| 5 |
+
{"year": "1999", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.", "solution": "and Marking Scheme:\n\nWithout loss of generality assume that $|b| \\leq|a|$. Then $a^{2}+4 b \\leq a^{2}+4|a|<a^{2}+4|a|+4=(|a|+2)^{2}$. Given that $a^{2}+4 b$ is a perfect square and since $a^{2}+4 b$ y $a^{2}$ have same parity then $a^{2}+4 b \\neq(|a|+1)^{2}$, so\n\n$$\na^{2}+4 b \\leq a^{2}\n$$\n\n2 POINTS for proving (1).\nLet us consider three cases.\nCase 1. $a^{2}+4 b=a^{2}$. Then $b=0$ and $a$ must be a perfect square. So $a=k^{2}, b=0(k \\in Z)$ is a solution.\nCase 2. $a^{2}+4 b=(|a|-2)^{2}$. Then $b=1-|a|$, therefore $b^{2}+4 a=a^{2}-2|a|+4 a+1$ must be a perfect square.\nIf $a>0$ then $b^{2}+4 a=(a+1)^{2}$ is a perfect square for each $a \\in Z$. Consequently $a=k$ and $b=1-k$ ( $k \\in Z^{+}$) is a solution.\nIf $a=0$ then $b=1$, but from (1) $b$ must be non-positive.\nIf $a<0$ then $b^{2}+4 a=m^{2}-6 m+1$ must be a perfect square, where $m=-a>0$. For $m \\geq 8$\n\n$$\n(m-3)^{2}>m^{2}-6 m+1>(m-4)^{2}\n$$\n\ntherefore $m<8$. If $m=1,2,3,4,5$ then $m^{2}-6 m+1<0$. If $m=6, m^{2}-6 m+1=1$ is a perfect square thus $a=-6$ and $b=-5$ is a solution. If $m=7, m^{2}-6 m+1=8$ is not a perfect square.\n\n2 POINTS for case 1 and case 2.\nCase 3. $a^{2}+4 b \\leq(|a|-4)^{2}$. Since $|b| \\leq|a|$ then $b \\geq-|a|$, thus $a^{2}-4|a| \\leq a^{2}+4 b \\leq(|a|-4)^{2}$. It follows that $|a| \\leq 4$. We have following posibilities:\n\n## 1 POINT for finding that $|a| \\leq 4$ in this case.\n\n(a) $|a|=4$. Then $16+4 b=0$ or $b=-4$. Thus $b^{2}+4 a=16 \\pm 16$ must be a perfect square. So $a=-4$ y $b=-4$.\n(b) $|a|=3$. In this case $a^{2}+4 b=9+4 b \\leq 1$, then $9+4 b=0$ or $9+4 b=1$. The equation $9+4 b=0$ does not have integer solutions. The solution of the second equation is $b=-2$. Then $b^{2}+4 a=4 \\pm 12$ must be a perfect square, thus $a=3$.\n(c) $|a|=2 \\cdot a^{2}+4 b=4+4 b \\leq 4$. Since $4+4 b$ is cven and must be a perfect square then $4+4 b=4$ or $4+4 b=0$. Therefore $b=0$ or $b=-1$. If $b=0, b^{2}+4 a= \\pm 8$ is not a perfect square. If $b=-1$ then $b^{2}+4 a=1 \\pm 8$ is a perfect square if $a=2$. Thus $a=2$ and $b=-1$ is a solution.\n(d) $|a|=1$. Then $a^{2}+4 b=4 b+1 \\leq 9$. Since $4 b+1$ must be an odd perfect square then $4 b+1=1$ or $4 b+1=9$. So $b=0$ or $b=2$. If $b=0, b^{2}+4 a= \\pm 4$, then $a=1$. If $b=2$ then $a=-1$, but this is not possible because $|b| \\leq|a|$. Thus $a=1$ y $b=0$ is a solution in this case.\n(c) $|a|=0$. Since $|b| \\leq|a|$ then $b=0$.\n\n1 POINT for concluding case 3.\n\nTesting these solutions and by symmetry we obtain the following solutions:\n\n$$\n\\left(k^{2}, 0\\right),\\left(0, k^{2}\\right),(k, 1-k),(-6,-5),(-5,-6),(-4,-4)\n$$\n\nwhere $k$ is an arbitrary integer. Note that if $(k, 1-k)$ is a solution with $k>0$, then taking $t=1-k$, $k=1-t$, so $(1-t, t)$ is solution. Thus by symetry $(k, 1-k)$ is a solution for any integer.\n\n1 POINT for writing up the correct answer.\nRemark: I POINT can be given for checking that $(k, 1-k)$ is a solution. However NO POINT is given for finding any other particular solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Second Solution "}}
|
| 6 |
+
{"year": "1999", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $S$ be a set of $2 n+1$ points in the plane such that no three are collinear and no four concyclic. A circle will be called good if it has 3 points of $S$ on its circumference, $n-1$ points in its interior and $n-1$ in its exterior. Prove that the number of good circles has the same parity as $n$.", "solution": "and Marking Scheme:\n\nLemma 1. Let $P$ and $Q$ be two points of $S$. The number of good circles that contain $P$ and $Q$ on their circumference is odd.\n\n## Proof of Lemma 1.\n\n\n\nLet $N$ be the number of good circles that pass through $P$ and $Q$. Number the points on one side of the line $P Q$ by $A_{1}, A_{2}, \\ldots, A_{k}$ and those on the other side by $B_{1}, B_{2}, \\ldots, B_{m}$ in such a way that if $\\angle P A_{i} Q=\\alpha_{i}, \\angle P B_{j} Q=180-\\beta_{j}$ then $\\alpha_{1}>\\alpha_{2}>\\ldots>\\alpha_{k}$ and $\\beta_{1}>\\beta_{2}>\\ldots>\\beta_{m}$.\nNote that the angles $\\alpha_{1}, \\alpha_{2}, \\ldots, \\alpha_{k}, \\beta_{1}, \\beta_{2}, \\ldots, \\beta_{m}$ are all distinct since there are no four points in $S$ that are concyclic.\nObserve that the circle that passes through $P, Q$ and $A_{i}$ has $A_{j}$ in its interior when $\\alpha_{j}>\\alpha_{i}$ that is, when $i>j$; and it contains $B_{j}$ in its interior when $\\alpha_{i}+180-\\beta_{j}>180$, that is, when $\\alpha_{i}>\\beta_{j}$. Similar conditions apply to the circle that contains $P, Q$ and $B_{j}$.\n\n1 POINT for characterizing the points that lie inside a given circle ins terms of these angles, or for similar considerations.\nOrder the angles $\\alpha_{1}, \\alpha_{2}, \\ldots, \\alpha_{k}, \\beta_{1}, \\beta_{2}, \\ldots, \\beta_{m}$ from the greatest to least. Now transform $S$ as follows. Consider a $\\beta_{j}$ that bas an $\\alpha_{i}$ immediately to its left in such an ordering ( $\\ldots>\\alpha_{i}>\\beta_{j} \\ldots$ ). Consider a new set $S^{\\prime}$ that contains the same points as $S$ except for $A_{i}$ and $B_{j}$. These two points will be replaced by $A_{i}^{\\prime}$ and $B_{j}^{\\prime}$ that satisfy $\\angle P A_{i}^{\\prime} Q=\\beta_{j}=\\alpha_{i}^{\\prime}$ and $\\angle P B_{j}^{\\prime} Q=180-\\alpha_{i}^{\\prime \\prime}=180-\\beta_{j}^{\\prime}$. Thus $\\beta_{j}$ and $\\alpha_{i}$ have been interchanged and the ordering of the $\\alpha$ 's and $\\beta$ 's has only changed with respect to the relative order of $\\alpha_{i}$ and $\\beta_{j}$; we continue to have\n\n$$\n\\alpha_{1}>\\alpha_{2}>\\ldots>\\alpha_{i-1}>\\alpha_{i}^{\\prime}>\\alpha_{i+1}>\\ldots>\\alpha_{k}\n$$\n\nand\n\n$$\n\\beta_{1}>\\beta_{2}>\\ldots>\\beta_{j-1}>\\beta_{j}^{\\prime}>\\beta_{j+1}>\\ldots>\\beta_{m}\n$$\n\n1 POINT for this or another useful transformation of the set $S$.\nAnalyze the good circles in this new set $S^{\\prime}$. Clearly, a circle through $P, Q, A_{r}(r \\neq i)$ or through $P, Q, B_{s}(s \\neq j)$ that was good in $S$ will also be good in $S^{\\prime}$, because the order of $A_{r}$ (or $B_{s}$ ) relative to the rest of the points has not changed, and therefore the number of points in the interior or exterior of this circle has not changed. The only changes that could have taken place are:\na) If the circle $P, Q, A_{i}$ was good in $S$, the circle $P, Q, A_{i}^{\\prime}$ may not be good in $S^{\\prime}$.\nb) If the circle $P, Q, B_{j}$ was good in $S$, the circle $P, Q, B_{j}^{\\prime}$ may not be good in $S^{\\prime}$.\nc) If the circle $P, Q, A_{i}$ was not good in $S$, the circle $P, Q, A_{i}^{\\prime}$ may be good in $S^{\\prime}$.\nd) If the circle $P, Q, B_{j}$ was not good in $S$, the circle $P, Q, B_{j}^{\\prime}$ may be good in $S^{\\prime}$.\n\n1 POINT for realizing that the transformation can only change the \"goodness\" of these circles. But observe that the circle $P, Q, A_{i}$ contains the points $A_{1}, A_{2}, \\ldots, A_{i-1}, B_{j}, B_{j+1}, \\ldots, B_{m}$ and does not contain the points $A_{i+1}, A_{i+2}, \\ldots, A_{k}, B_{1}, B_{2}, \\ldots, B_{j-1}$ in its interior. Then this circle is good if and only if $i+m-j=k-i+j-1$, which we rewrite as $j-i=\\frac{1}{2}(m-k+1)$. On the other hand, the circle $P, Q, B_{j}$ contains the points $B_{j+1}, B_{j+2}, \\ldots, B_{m}, A_{1}, A_{2}, \\ldots, A_{i}$ and does not contain the points $B_{1}, B_{2}, \\ldots, B_{j-1}, A_{i+1}, A_{i+2}, \\ldots, A_{k}$ in its interior. Hence this circle is good if and only if $m-j+i=j-1+k-i$, which we rewrite as $j-i=\\frac{1}{2}(m-k+1)$.\nTherefore, the circle $P, Q, A_{i}$ is good if and only if the circle $P, Q, B_{j}$ is good. Similarly, the circle $P, Q, A_{i}^{\\prime}$ is good if and only if the circle $P, Q, B_{j}^{\\prime}$ is good. That is to say, transforming $S$ into $S^{\\prime}$ we lose either 0 or 2 good circles of $S$ and we gain either 0 or 2 good circles in $S^{\\prime}$.\n\n1 POINT for realizing that the \"goodness\" of these circles is changed in pairs.\nContinuing in this way, we may continue to transform $S$ until we obtain a new set $S_{0}$ such that the angles $\\alpha_{1}^{\\prime}, \\alpha_{2}^{\\prime}, \\ldots, \\alpha_{k}^{\\prime}, \\beta_{1}^{\\prime}, \\beta_{2}^{\\prime}, \\ldots, \\beta_{m}^{\\prime}$ satisfy\n\n$$\n\\beta_{1}^{\\prime}>\\beta_{2}^{\\prime}>\\ldots>\\beta_{n}^{\\prime}>\\alpha_{1}^{\\prime}>\\alpha_{2}^{\\prime}>\\ldots>\\alpha_{k}^{\\prime}\n$$\n\nand such that the number of good circles in $S_{0}$ has the same parity as $N$. We claim that $S_{0}$ has exactly one good circle. In this configuration, the circle $P, Q, A_{i}$ does not contain any $B_{j}$ and the circle $P, Q, B_{r}$ does not contain any $A_{s}$ (for all $\\left.i, j\\right)$, because $\\alpha_{a}+\\left(180-\\beta_{b}\\right)<180$ for all $a, b$. Hence, the only possible good circles are $P, Q, B_{m-n+1}$ (which contains the $n-1$ points $B_{m-n+2}, B_{m-n+3}, \\ldots, B_{m}$ ), if $m-n+1>0$, and the circle $P, Q, A_{n}$ (which contains the $n-1$ points $A_{1}, A_{2}, \\ldots, A_{n}$ ), if $n \\leq k$. But, since $m+k=2 n-1$, which we rewrite as $m-n+1=n-k$, exactly one of the inequalitites $m-n+1>0$ and $n \\leq k$ is satisfied. It follows that one of the points $B_{m-n+1}$ and $A_{n}$ corresponds to a good circle and the other does not. Hence, $S_{0}$ has exactly one good circle, and $N$ is odd.\n\n1 POINT for showing that this configuration has exactly one good circle.\n\nNow consider the $\\binom{2 n+1}{2}$ pairs of points in $S$. Let $a_{2 k+1}$ be the number of pairs of points through which exactly $2 k+1$ good circles pass. Then\n\n$$\na_{1}+a_{3}+a_{5}+\\ldots=\\binom{2 n+1}{2}\n$$\n\nBut then the number of good circles in $S$ is\n\n$$\n\\begin{aligned}\n\\frac{1}{3}\\left(a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\\ldots\\right) & \\equiv a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\\ldots \\\\\n& \\equiv a_{1}+a_{3}+a_{5}+a_{7}+\\ldots \\\\\n& \\equiv\\binom{2 n+1}{2} \\\\\n& \\equiv n(2 n+1) \\\\\n& \\equiv n(\\bmod 2) .\n\\end{aligned}\n$$\n\nHere we have taken into account that each good circle is counted 3 times in the expression $a_{1}+3 a_{3}+$ $5 a_{5}+7 a_{7}+\\ldots$ The desired result follows.\n\n2 POINTS for this computation.\n\n## Alteraative Proof of Lemma 1.\n\nLet, $A_{1}, A_{2}, \\ldots, A_{2 n-1}$ be the $2 n-1$ given points other than $P$ and $Q$.\nInvert the plane with respect to point $P$. Let $O, B_{1}, B_{2}, \\ldots, B_{2 n-1}$ be the images of points $Q, A_{1}, A_{2}, \\ldots, A_{2 n-1}$, respectively, under this inversion. Call point $B_{i}$ \"good\" if the line $O B_{i}$ splits the points $B_{1}, B_{2} \\ldots, B_{i-1}, B_{i+1}, \\ldots, B_{2 n-1}$ evenly, leaving $n-1$ of them to each side of it. (Notice that no other $B_{j}$ can lie on the line $O B_{i}$, or else the points $P, Q, A_{i}$ and $A_{j}$ would be concyclic.) Then it is clear that the circle through $P, Q$ and $A_{i}$ is good if and only if point $B_{i}$ is good. Therefore, it suffices to prove that the number of good points is odd.\n\n1 POINT for inverting and realizing the equivalence between good circles and good points. Notice that the good points depend only on the relative positions of rays $O B_{1}, O B_{2}, \\ldots, O B_{2 n-1}$, and not on the exact positions of points $B_{1}, B_{2}, \\ldots, B_{2 n-1}$. Therefore we may assume, for simplicity, that $B_{1}, B_{2}, \\ldots, B_{2 n-1}$ lie on the unit circle $\\Gamma$ with center $O$.\n\n1 POINT for this or a similar simplification.\nLet $C_{1}, C_{2}, \\ldots, C_{2 n-1}$ be the points diametrically opposite to $B_{1}, B_{2}, \\ldots, B_{2 n-1}$ in $\\Gamma$. As remarked earlier, no $C_{i}$ can coincide with one of the $B_{j}$ 's. We will call the $B_{i}$ 's \"white points\", and the $C_{i}$ 's \"black points\". We will refer to these $4 n-2$ points as the \"colored points\".\nNow we prove that the number of good points is odd, which will complete the proof of the lemma. We proceed by induction on $n$. If $n=1$, the result is trivial. Now assume that the result is true for $n=k$, and consider $2 k+1$ white points $B_{1}, B_{2}, \\ldots, B_{2 k+1}$ on the circle $\\Gamma$ (no two of which are diametrically opposite), and their diametrically opposite black points $C_{1}, C_{2}, \\ldots, C_{2 k+1}$. Call this configuration of points \"configuration 1 \". It is clear that we must have two consecutive colored points on $\\Gamma$ which have different colors, say $B_{i}$ and $C_{j}$. Now remove points $B_{i}, B_{j}, C_{i}$ and $C_{j}$ from $\\Gamma$, to obtain \"configuration 2 \", a configuration with $2 k-1$ points of each color.\n\n1 POINT for this or a similar transformation of the set.\nIt is easy to verify the following two claims:\n\n1. Point $B_{i}$ is good in configuration 1 if and only if point $B_{j}$ is good in configuration 1.\n2. Let $k \\neq i, j$. Then point $B_{k}$ is good in configuration 1 if and only if it is good in configuration 2.\n\nIt follows that, by removing points $B_{i}, B_{j}, C_{i}$ and $C_{j}$, the number of good points can either stay the same, or decreases by two. In any case, its parity remains unchanged. Since we know, by the induction hypothesis, that the number of good points in configuration 2 is odd, it follows that the number of good points in configuration 1 is also odd. This completes the proof.\n\n## Another Approach to Lemma 1.\n\nOne can give another inductive proof of lemma. 1, which combines the ideas of the two proofs that we have given. The idea is to start as in the first proof, with the characterization of the points inside a given circle.\n\n1 POINT\nThen we transform the set $S$ by removing the points $A_{i}$ and $B_{j}$ instead of replacing then by $A_{i}^{p}$ and $B_{j}^{\\prime}$.\n\n1 POINT\nIt can be shown that every one of the romaining circles going through $P$ and $Q$, contained exactly one of $A_{i}$ and $B_{j}$. Therefore, the only good circles we could have gained or lost are $P, Q, A_{i}$ and $P, Q, B_{j}$.\n\n2 POINTS\nFinally, we show that either both or none of these circles were good, so the parity of the number of good circles isn't changed by this transformation.\n\n1 POINT\n\nRemark: 2 POINTS can be given if the result has been fully proved for a particular case with $n>1$. (If more than one particular case has been analyzed completly, only 2 POINTS.) These points are awarded only if no progress has been made in the general solution of the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution "}}
|
APMO/segmented/en-apmo2000_sol.jsonl
CHANGED
|
@@ -1,6 +1,6 @@
|
|
| 1 |
-
{"year": "2000", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Compute the sum $S=\\sum_{i=0}^{101} \\frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\\frac{i}{101}$.\nAnswer: $S=51$.", "solution": "Since $x_{101-i}=\\frac{101-i}{101}=1-\\frac{i}{101}=1-x_{i}$ and\n\n$$\n1-3 x_{i}+3 x_{i}^{2}=\\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\\right)+x_{i}^{3}=\\left(1-x_{i}\\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},\n$$\n\nwe have, by replacing $i$ by $101-i$ in the second sum,\n\n$$\n2 S=S+S=\\sum_{i=0}^{101} \\frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\\sum_{i=0}^{101} \\frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\\sum_{i=0}^{101} \\frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,\n$$\n\nso $S=51$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
-
{"year": "2000", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Given the following arrangement of circles:\n\n\nEach of the numbers $1,2, \\ldots, 9$ is to be written into one of these circles, so that each circle contains exactly one of these numbers and\n(i) the sums of the four numbers on each side of the triangle are equal;\n(ii) the sums of squares of the four numbers on each side of the triangle are equal.\n\nFind all ways in which this can be done.\nAnswer: The only solutions are\n\nand the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side.", "solution": "Let $a, b$, and $c$ be the numbers in the vertices of the triangular arrangement. Let $s$ be the sum of the numbers on each side and $t$ be the sum of the squares of the numbers on each side. Summing the numbers (or their squares) on the three sides repeats each once the numbers on the vertices (or their squares):\n\n$$\n\\begin{gathered}\n3 s=a+b+c+(1+2+\\cdots+9)=a+b+c+45 \\\\\n3 t=a^{2}+b^{2}+c^{2}+\\left(1^{2}+2^{2}+\\cdots+9^{2}\\right)=a^{2}+b^{2}+c^{2}+285\n\\end{gathered}\n$$\n\nAt any rate, $a+b+c$ and $a^{2}+b^{2}+c^{2}$ are both multiples of 3 . Since $x^{2} \\equiv 0,1(\\bmod 3)$, either $a, b, c$ are all multiples of 3 or none is a multiple of 3 . If two of them are $1,2 \\bmod 3$ then $a+b+c \\equiv 0(\\bmod 3)$ implies that the other should be a multiple of 3 , which is not possible. Thus $a, b, c$ are all congruent modulo 3 , that is,\n\n$$\n\\{a, b, c\\}=\\{3,6,9\\}, \\quad\\{1,4,7\\}, \\quad \\text { or } \\quad\\{2,5,8\\}\n$$\n\nCase 1: $\\{a, b, c\\}=\\{3,6,9\\}$. Then $3 t=3^{2}+6^{2}+9^{2}+285 \\Longleftrightarrow t=137$.\n\n\nIn this case $x^{2}+y^{2}+3^{2}+9^{2}=137 \\Longleftrightarrow x^{2}+y^{2}=47$. However, 47 cannot be written as the sum of two squares. One can check manually, or realize that $47 \\equiv 3(\\bmod 4)$, and since $x^{2}, y^{2} \\equiv 0,1(\\bmod 4), x^{2}+y^{2} \\equiv 0,1,2(\\bmod 4)$ cannot be 47.\nHence there are no solutions in this case.\nCase 2: $\\{a, b, c\\}=\\{1,4,7\\}$. Then $3 t=1^{2}+4^{2}+7^{2}+285 \\Longleftrightarrow t=117$.\n\n\nIn this case $x^{2}+y^{2}+1^{2}+7^{2}=117 \\Longleftrightarrow x^{2}+y^{2}=67 \\equiv 3(\\bmod 4)$, and as in the previous case there are no solutions.\nCase 3: $\\{a, b, c\\}=\\{2,5,8\\}$. Then $3 t=2^{2}+5^{2}+8^{2}+285 \\Longleftrightarrow t=126$.\n\n\nThen\n\n$$\n\\left\\{\\begin{array} { c } \n{ x ^ { 2 } + y ^ { 2 } + 2 ^ { 2 } + 8 ^ { 2 } = 1 2 6 } \\\\\n{ t ^ { 2 } + u ^ { 2 } + 2 ^ { 2 } + 5 ^ { 2 } = 1 2 6 } \\\\\n{ m ^ { 2 } + n ^ { 2 } + 5 ^ { 2 } + 8 ^ { 2 } = 1 2 6 }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array}{c}\nx^{2}+y^{2}=58 \\\\\nt^{2}+u^{2}=97 \\\\\nm^{2}+n^{2}=37\n\\end{array}\\right.\\right.\n$$\n\nThe only solutions to $t^{2}+u^{2}=97$ and $m^{2}+n^{2}=37$ are $\\{t, u\\}=\\{4,9\\}$ and $\\{m, n\\}=\\{1,6\\}$, respectively (again, one can check manually.) Then $\\{x, y\\}=\\{3,7\\}$, and the solutions are\n\nand the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side. There are $3!\\cdot 2^{3}=48$ such solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
-
{"year": "2000", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.", "solution": "Let $A N$ meet the circumcircle of $A B C$ at point $K$, the midpoint of arc $B C$ that does not contain $A$.\n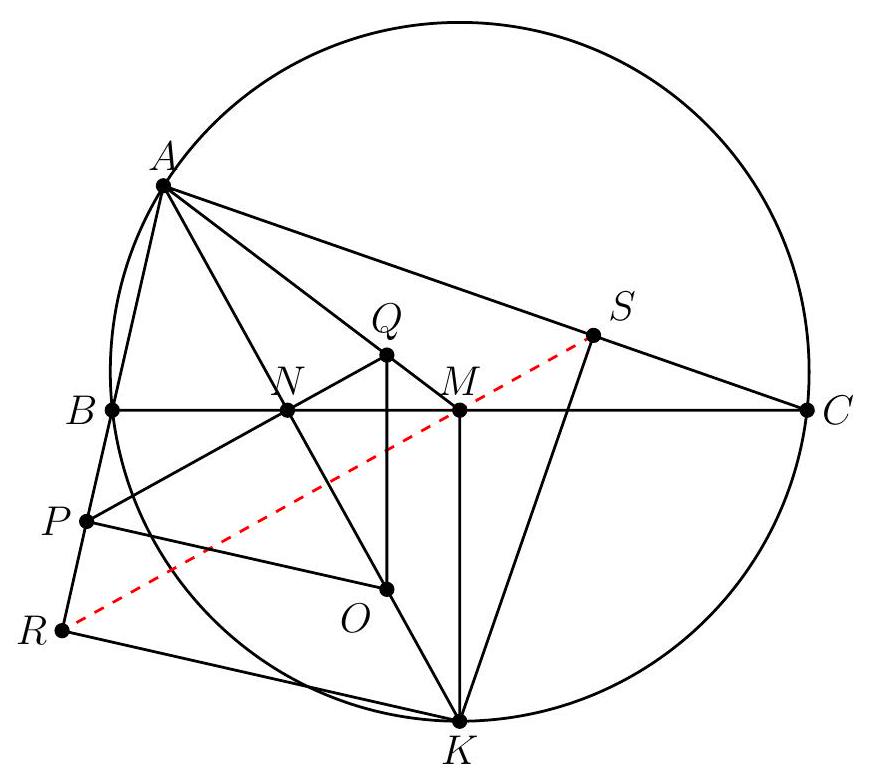\n\nThe orthogonal projection of $K$ onto side $B C$ is $M$. Let $R$ and $S$ be the orthogonal projections of $K$ onto lines $A B$ and $A C$, respectively. Points $R, M$, and $S$ lie in the Simson line of $K$ with respect to $A B C$. Since $K$ is in the bisector of $\\angle B A C, A R K S$ is a kite, and the Simson line $R M S$ is perpendicular to $A N$, and therefore parallel to $P Q$.\nNow consider the homothety with center $A$ that takes $O$ to $K$. Since $O P \\perp A B$ and $K R \\perp A B$, $O P$ and $K R$ are parallel, which means that $P$ is taken to $R$. Finally, line $P Q$ is parallel to line $R S$, so line $P Q$ is taken to line $R S$ by the homothety. Then $Q$ is taken to $M$, and since $O$ is taken to $K$, line $O Q$ is taken to line $M K$. We are done now: this means that $O Q$ is parallel to $M K$, which is perpendicular to $B C$ (it is its perpendicular bisector, as $M B=M C$ and $K B=K C$.)", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution 1"}}
|
| 4 |
-
{"year": "2000", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.", "solution": "Consider a cartesian plane with $A=(0,0)$ as the origin and the bisector $A N$ as $x$-axis. Thus $A B$ has equation $y=m x$ and $A C$ has equation $y=-m x$. Let $B=(b, m b)$ and $C=(c,-m c)$. By symmetry, the problem is immediate if $A B=A C$, that is, if $b=c$. Suppose that $b \\neq c$ from now on. Line $B C$ has slope $\\frac{m b-(-m c)}{b-c}=\\frac{m(b+c)}{b-c}$. Let $N=(n, 0)$.\nPoint $M$ is the midpoint $\\left(\\frac{b+c}{2}, \\frac{m b-m c}{2}\\right)$ of $B C$, so $A M$ has slope $\\frac{m(b-c)}{b+c}$.\nThe line through $N$ that is perpendicular to the $x$-axis $A N$ is $x=n$. Therefore\n\n$$\nP=(n, m n) \\quad \\text { and } \\quad Q=\\left(n, \\frac{m(b-c) n}{b+c}\\right) .\n$$\n\nIn the right triangle $A P O$, with altitude $A N, A N \\cdot A O=A P^{2}$. Thus\n\n$$\nn \\cdot A O=(0-n)^{2}+(0-m n)^{2} \\Longleftrightarrow A O=n\\left(m^{2}+1\\right) \\Longrightarrow O=\\left(n\\left(m^{2}+1\\right), 0\\right)\n$$\n\nFinally, the slope of $O Q$ is\n\n$$\n\\frac{\\frac{m(b-c) n}{b+c}-0}{n-n\\left(m^{2}+1\\right)}=-\\frac{b-c}{(b+c) m}\n$$\n\nSince the product of the slopes of $O Q$ and $B C$ is\n\n$$\n-\\frac{b-c}{(b+c) m} \\cdot \\frac{m(b+c)}{b-c}=-1\n$$\n\n$O Q$ and $B C$ are perpendicular, and we are done.\nComment: The second solution shows that $N$ can be any point in the bisector of $\\angle A$. In fact, if we move $N$ in the bisector and construct $O, P$ and $Q$ accordingly, then all lines $O Q$ obtained are parallel: just consider a homothety with center $A$ and variable ratios.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution 2"}}
|
| 5 |
-
{"year": "2000", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $n, k$ be given positive integers with $n>k$. Prove that\n\n$$\n\\frac{1}{n+1} \\cdot \\frac{n^{n}}{k^{k}(n-k)^{n-k}}<\\frac{n!}{k!(n-k)!}<\\frac{n^{n}}{k^{k}(n-k)^{n-k}} .\n$$", "solution": "The inequality is equivalent to\n\n$$\n\\frac{n^{n}}{n+1}<\\binom{n}{k} k^{k}(n-k)^{n-k}<n^{n}\n$$\n\nwhich suggests investigating the binomial expansion of\n\n$$\nn^{n}=((n-k)+k)^{n}=\\sum_{i=0}^{n}\\binom{n}{i}(n-k)^{n-i} k^{i}\n$$\n\nThe $(k+1)$ th term $T_{k+1}$ of the expansion is $\\binom{n}{k} k^{k}(n-k)^{n-k}$, and all terms in the expansion are positive, which implies the right inequality.\nNow, for $1 \\leq i \\leq n$,\n\n$$\n\\frac{T_{i+1}}{T_{i}}=\\frac{\\binom{n}{i}(n-k)^{n-i} k^{i}}{\\binom{n}{i-1}(n-k)^{n-i+1} k^{i-1}}=\\frac{(n-i+1) k}{i(n-k)}\n$$\n\nand\n\n$$\n\\frac{T_{i+1}}{T_{i}}>1 \\Longleftrightarrow(n-i+1) k>i(n-k) \\Longleftrightarrow i<k+\\frac{k}{n} \\Longleftrightarrow i \\leq k\n$$\n\nThis means that\n\n$$\nT_{1}<T_{2}<\\cdots<T_{k+1}>T_{k+2}>\\cdots>T_{n+1}\n$$\n\nthat is, $T_{k+1}=\\binom{n}{k} k^{k}(n-k)^{n-k}$ is the largest term in the expansion. The maximum term is greater that the average, which is the sum $n^{n}$ divided by the quantity $n+1$, therefore\n\n$$\n\\binom{n}{k} k^{k}(n-k)^{n-k}>\\frac{n^{n}}{n+1}\n$$\n\nas required.\nComment: If we divide further by $n^{n}$ one finds\n\n$$\n\\frac{1}{n+1}<\\binom{n}{k}\\left(\\frac{k}{n}\\right)^{k}\\left(1-\\frac{k}{n}\\right)^{n-k}<1\n$$\n\nThe middle term is the probability $P(X=k)$ of $k$ successes in a binomial distribution with $n$ trials and success probability $p=\\frac{k}{n}$. The right inequality is immediate from the fact that $P(X=k)$ is not the only possible event in this distribution, and the left inequality comes from the fact that the mode of the binomial distribution are given by $\\lfloor(n+1) p\\rfloor=\\left\\lfloor(n+1) \\frac{k}{n}\\right\\rfloor=k$ and $\\lceil(n+1) p-1\\rceil=k$. However, the proof of this fact is identical to the above solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
-
{"year": "2000", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Given a permutation $\\left(a_{0}, a_{1}, \\ldots, a_{n}\\right)$ of the sequence $0,1, \\ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\\left(a_{0}, a_{1}, \\ldots, a_{n}\\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \\ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \\ldots, 3,2,0)$ regular?\n\nAnswer: $n=2$ and $n=2^{k}-1, k$ positive integer.", "solution": "A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.\nIf $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.\nCall a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is\n\n$$\n\\begin{aligned}\n& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\\\\n& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\\\\n& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\\\\n& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\\\\n& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\\\\n& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\\\\n& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\\\\n& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 2, the second pass is\n\n$$\n\\begin{aligned}\n& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\\\\n& (1,2,14,15,12,13, \\mathbf{1 0}, 11,8,9,0,7,4,5,6,3) \\\\\n& (1,2, \\mathbf{1 4}, 15,12,13,0,11,8,9,10,7,4,5,6,3) \\\\\n& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 3 , the third pass is\n\n$$\n\\begin{aligned}\n& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\\\\n& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\\\\n& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\\\\n& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 4, the fourth pass is\n\n$$\n\\begin{aligned}\n& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\\\\n& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)\n\\end{aligned}\n$$\n\nAnd then one can successively perform the operations to eventually find\n\n$$\n(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)\n$$\n\nafter which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.\n\nCase 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \\ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.\nCase 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \\ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation\n\n$$\n[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \\ldots,[2 R: 3 R-1],[R: 2 R-1]\n$$\n\n$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.\nThen it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \\ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.\nStarting from $P_{r}, r>0$, 0 is successively transposed with $R, 3 R, \\ldots, N-R$. The numbers $0, N-R, N-3 R, \\ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become\n\n$$\n\\begin{gathered}\n{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \\ldots,} \\\\\n{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}\n\\end{gathered}\n$$\n\nNote that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.\nNow $0, N-R+1, N-3 R+1, \\ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become\n\n$$\n\\begin{gathered}\n{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \\ldots,} \\\\\n{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}\n\\end{gathered}\n$$\n\nThe same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \\ldots, R+u$ are shifted, $u=0,1,2, \\ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with\n\n$$\n[1: 2 R-1],(0),[N-2 R: N-1], \\ldots,[2 R: 4 R-1]\n$$\n\nwhich is precisely $P_{r+1}$.\nSince $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.\nCase 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \\geq 1$, and define $P_{0}, \\ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :\n\n$$\n\\left[1: 2^{a}-1\\right],(0),\\left[N-2^{a}: N-1\\right],\\left[N-2^{a+1}: N-2^{a}-1\\right], \\ldots,\\left[2^{a+1}: 3 \\cdot 2^{a}-1\\right],\\left[2^{a}: 2^{a+1}-1\\right]\n$$\n\nBut then 0 is transposed with $2^{a}, 3 \\cdot 2^{a}, \\ldots,(2 b-1) \\cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.\n\nComment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values\n\n$$\n1,2,5,14,47,189,891,4815,29547\n$$\n\nwhich is not catalogued at oeis.org.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
|
|
|
| 1 |
+
{"year": "2000", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Compute the sum $S=\\sum_{i=0}^{101} \\frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\\frac{i}{101}$.\nAnswer: $S=51$.", "solution": "Since $x_{101-i}=\\frac{101-i}{101}=1-\\frac{i}{101}=1-x_{i}$ and\n\n$$\n1-3 x_{i}+3 x_{i}^{2}=\\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\\right)+x_{i}^{3}=\\left(1-x_{i}\\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},\n$$\n\nwe have, by replacing $i$ by $101-i$ in the second sum,\n\n$$\n2 S=S+S=\\sum_{i=0}^{101} \\frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\\sum_{i=0}^{101} \\frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\\sum_{i=0}^{101} \\frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,\n$$\n\nso $S=51$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
+
{"year": "2000", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Given the following arrangement of circles:\n\n\nEach of the numbers $1,2, \\ldots, 9$ is to be written into one of these circles, so that each circle contains exactly one of these numbers and\n(i) the sums of the four numbers on each side of the triangle are equal;\n(ii) the sums of squares of the four numbers on each side of the triangle are equal.\n\nFind all ways in which this can be done.\nAnswer: The only solutions are\n\nand the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side.", "solution": "Let $a, b$, and $c$ be the numbers in the vertices of the triangular arrangement. Let $s$ be the sum of the numbers on each side and $t$ be the sum of the squares of the numbers on each side. Summing the numbers (or their squares) on the three sides repeats each once the numbers on the vertices (or their squares):\n\n$$\n\\begin{gathered}\n3 s=a+b+c+(1+2+\\cdots+9)=a+b+c+45 \\\\\n3 t=a^{2}+b^{2}+c^{2}+\\left(1^{2}+2^{2}+\\cdots+9^{2}\\right)=a^{2}+b^{2}+c^{2}+285\n\\end{gathered}\n$$\n\nAt any rate, $a+b+c$ and $a^{2}+b^{2}+c^{2}$ are both multiples of 3 . Since $x^{2} \\equiv 0,1(\\bmod 3)$, either $a, b, c$ are all multiples of 3 or none is a multiple of 3 . If two of them are $1,2 \\bmod 3$ then $a+b+c \\equiv 0(\\bmod 3)$ implies that the other should be a multiple of 3 , which is not possible. Thus $a, b, c$ are all congruent modulo 3 , that is,\n\n$$\n\\{a, b, c\\}=\\{3,6,9\\}, \\quad\\{1,4,7\\}, \\quad \\text { or } \\quad\\{2,5,8\\}\n$$\n\nCase 1: $\\{a, b, c\\}=\\{3,6,9\\}$. Then $3 t=3^{2}+6^{2}+9^{2}+285 \\Longleftrightarrow t=137$.\n\n\nIn this case $x^{2}+y^{2}+3^{2}+9^{2}=137 \\Longleftrightarrow x^{2}+y^{2}=47$. However, 47 cannot be written as the sum of two squares. One can check manually, or realize that $47 \\equiv 3(\\bmod 4)$, and since $x^{2}, y^{2} \\equiv 0,1(\\bmod 4), x^{2}+y^{2} \\equiv 0,1,2(\\bmod 4)$ cannot be 47.\nHence there are no solutions in this case.\nCase 2: $\\{a, b, c\\}=\\{1,4,7\\}$. Then $3 t=1^{2}+4^{2}+7^{2}+285 \\Longleftrightarrow t=117$.\n\n\nIn this case $x^{2}+y^{2}+1^{2}+7^{2}=117 \\Longleftrightarrow x^{2}+y^{2}=67 \\equiv 3(\\bmod 4)$, and as in the previous case there are no solutions.\nCase 3: $\\{a, b, c\\}=\\{2,5,8\\}$. Then $3 t=2^{2}+5^{2}+8^{2}+285 \\Longleftrightarrow t=126$.\n\n\nThen\n\n$$\n\\left\\{\\begin{array} { c } \n{ x ^ { 2 } + y ^ { 2 } + 2 ^ { 2 } + 8 ^ { 2 } = 1 2 6 } \\\\\n{ t ^ { 2 } + u ^ { 2 } + 2 ^ { 2 } + 5 ^ { 2 } = 1 2 6 } \\\\\n{ m ^ { 2 } + n ^ { 2 } + 5 ^ { 2 } + 8 ^ { 2 } = 1 2 6 }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array}{c}\nx^{2}+y^{2}=58 \\\\\nt^{2}+u^{2}=97 \\\\\nm^{2}+n^{2}=37\n\\end{array}\\right.\\right.\n$$\n\nThe only solutions to $t^{2}+u^{2}=97$ and $m^{2}+n^{2}=37$ are $\\{t, u\\}=\\{4,9\\}$ and $\\{m, n\\}=\\{1,6\\}$, respectively (again, one can check manually.) Then $\\{x, y\\}=\\{3,7\\}$, and the solutions are\n\nand the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side. There are $3!\\cdot 2^{3}=48$ such solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 3 |
+
{"year": "2000", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.", "solution": "Let $A N$ meet the circumcircle of $A B C$ at point $K$, the midpoint of arc $B C$ that does not contain $A$.\n\n\nThe orthogonal projection of $K$ onto side $B C$ is $M$. Let $R$ and $S$ be the orthogonal projections of $K$ onto lines $A B$ and $A C$, respectively. Points $R, M$, and $S$ lie in the Simson line of $K$ with respect to $A B C$. Since $K$ is in the bisector of $\\angle B A C, A R K S$ is a kite, and the Simson line $R M S$ is perpendicular to $A N$, and therefore parallel to $P Q$.\nNow consider the homothety with center $A$ that takes $O$ to $K$. Since $O P \\perp A B$ and $K R \\perp A B$, $O P$ and $K R$ are parallel, which means that $P$ is taken to $R$. Finally, line $P Q$ is parallel to line $R S$, so line $P Q$ is taken to line $R S$ by the homothety. Then $Q$ is taken to $M$, and since $O$ is taken to $K$, line $O Q$ is taken to line $M K$. We are done now: this means that $O Q$ is parallel to $M K$, which is perpendicular to $B C$ (it is its perpendicular bisector, as $M B=M C$ and $K B=K C$.)", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution 1"}}
|
| 4 |
+
{"year": "2000", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.", "solution": "Consider a cartesian plane with $A=(0,0)$ as the origin and the bisector $A N$ as $x$-axis. Thus $A B$ has equation $y=m x$ and $A C$ has equation $y=-m x$. Let $B=(b, m b)$ and $C=(c,-m c)$. By symmetry, the problem is immediate if $A B=A C$, that is, if $b=c$. Suppose that $b \\neq c$ from now on. Line $B C$ has slope $\\frac{m b-(-m c)}{b-c}=\\frac{m(b+c)}{b-c}$. Let $N=(n, 0)$.\nPoint $M$ is the midpoint $\\left(\\frac{b+c}{2}, \\frac{m b-m c}{2}\\right)$ of $B C$, so $A M$ has slope $\\frac{m(b-c)}{b+c}$.\nThe line through $N$ that is perpendicular to the $x$-axis $A N$ is $x=n$. Therefore\n\n$$\nP=(n, m n) \\quad \\text { and } \\quad Q=\\left(n, \\frac{m(b-c) n}{b+c}\\right) .\n$$\n\nIn the right triangle $A P O$, with altitude $A N, A N \\cdot A O=A P^{2}$. Thus\n\n$$\nn \\cdot A O=(0-n)^{2}+(0-m n)^{2} \\Longleftrightarrow A O=n\\left(m^{2}+1\\right) \\Longrightarrow O=\\left(n\\left(m^{2}+1\\right), 0\\right)\n$$\n\nFinally, the slope of $O Q$ is\n\n$$\n\\frac{\\frac{m(b-c) n}{b+c}-0}{n-n\\left(m^{2}+1\\right)}=-\\frac{b-c}{(b+c) m}\n$$\n\nSince the product of the slopes of $O Q$ and $B C$ is\n\n$$\n-\\frac{b-c}{(b+c) m} \\cdot \\frac{m(b+c)}{b-c}=-1\n$$\n\n$O Q$ and $B C$ are perpendicular, and we are done.\nComment: The second solution shows that $N$ can be any point in the bisector of $\\angle A$. In fact, if we move $N$ in the bisector and construct $O, P$ and $Q$ accordingly, then all lines $O Q$ obtained are parallel: just consider a homothety with center $A$ and variable ratios.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution 2"}}
|
| 5 |
+
{"year": "2000", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $n, k$ be given positive integers with $n>k$. Prove that\n\n$$\n\\frac{1}{n+1} \\cdot \\frac{n^{n}}{k^{k}(n-k)^{n-k}}<\\frac{n!}{k!(n-k)!}<\\frac{n^{n}}{k^{k}(n-k)^{n-k}} .\n$$", "solution": "The inequality is equivalent to\n\n$$\n\\frac{n^{n}}{n+1}<\\binom{n}{k} k^{k}(n-k)^{n-k}<n^{n}\n$$\n\nwhich suggests investigating the binomial expansion of\n\n$$\nn^{n}=((n-k)+k)^{n}=\\sum_{i=0}^{n}\\binom{n}{i}(n-k)^{n-i} k^{i}\n$$\n\nThe $(k+1)$ th term $T_{k+1}$ of the expansion is $\\binom{n}{k} k^{k}(n-k)^{n-k}$, and all terms in the expansion are positive, which implies the right inequality.\nNow, for $1 \\leq i \\leq n$,\n\n$$\n\\frac{T_{i+1}}{T_{i}}=\\frac{\\binom{n}{i}(n-k)^{n-i} k^{i}}{\\binom{n}{i-1}(n-k)^{n-i+1} k^{i-1}}=\\frac{(n-i+1) k}{i(n-k)}\n$$\n\nand\n\n$$\n\\frac{T_{i+1}}{T_{i}}>1 \\Longleftrightarrow(n-i+1) k>i(n-k) \\Longleftrightarrow i<k+\\frac{k}{n} \\Longleftrightarrow i \\leq k\n$$\n\nThis means that\n\n$$\nT_{1}<T_{2}<\\cdots<T_{k+1}>T_{k+2}>\\cdots>T_{n+1}\n$$\n\nthat is, $T_{k+1}=\\binom{n}{k} k^{k}(n-k)^{n-k}$ is the largest term in the expansion. The maximum term is greater that the average, which is the sum $n^{n}$ divided by the quantity $n+1$, therefore\n\n$$\n\\binom{n}{k} k^{k}(n-k)^{n-k}>\\frac{n^{n}}{n+1}\n$$\n\nas required.\nComment: If we divide further by $n^{n}$ one finds\n\n$$\n\\frac{1}{n+1}<\\binom{n}{k}\\left(\\frac{k}{n}\\right)^{k}\\left(1-\\frac{k}{n}\\right)^{n-k}<1\n$$\n\nThe middle term is the probability $P(X=k)$ of $k$ successes in a binomial distribution with $n$ trials and success probability $p=\\frac{k}{n}$. The right inequality is immediate from the fact that $P(X=k)$ is not the only possible event in this distribution, and the left inequality comes from the fact that the mode of the binomial distribution are given by $\\lfloor(n+1) p\\rfloor=\\left\\lfloor(n+1) \\frac{k}{n}\\right\\rfloor=k$ and $\\lceil(n+1) p-1\\rceil=k$. However, the proof of this fact is identical to the above solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
+
{"year": "2000", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Given a permutation $\\left(a_{0}, a_{1}, \\ldots, a_{n}\\right)$ of the sequence $0,1, \\ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\\left(a_{0}, a_{1}, \\ldots, a_{n}\\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \\ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \\ldots, 3,2,0)$ regular?\n\nAnswer: $n=2$ and $n=2^{k}-1, k$ positive integer.", "solution": "A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.\nIf $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.\nCall a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is\n\n$$\n\\begin{aligned}\n& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\\\\n& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\\\\n& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\\\\n& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\\\\n& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\\\\n& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\\\\n& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\\\\n& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 2, the second pass is\n\n$$\n\\begin{aligned}\n& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\\\\n& (1,2,14,15,12,13, \\mathbf{1 0}, 11,8,9,0,7,4,5,6,3) \\\\\n& (1,2, \\mathbf{1 4}, 15,12,13,0,11,8,9,10,7,4,5,6,3) \\\\\n& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 3 , the third pass is\n\n$$\n\\begin{aligned}\n& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\\\\n& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\\\\n& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\\\\n& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)\n\\end{aligned}\n$$\n\nAfter exchanging 0 and 4, the fourth pass is\n\n$$\n\\begin{aligned}\n& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\\\\n& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)\n\\end{aligned}\n$$\n\nAnd then one can successively perform the operations to eventually find\n\n$$\n(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)\n$$\n\nafter which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.\n\nCase 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \\ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.\nCase 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \\ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation\n\n$$\n[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \\ldots,[2 R: 3 R-1],[R: 2 R-1]\n$$\n\n$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.\nThen it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \\ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.\nStarting from $P_{r}, r>0$, 0 is successively transposed with $R, 3 R, \\ldots, N-R$. The numbers $0, N-R, N-3 R, \\ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become\n\n$$\n\\begin{gathered}\n{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \\ldots,} \\\\\n{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}\n\\end{gathered}\n$$\n\nNote that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.\nNow $0, N-R+1, N-3 R+1, \\ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become\n\n$$\n\\begin{gathered}\n{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \\ldots,} \\\\\n{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}\n\\end{gathered}\n$$\n\nThe same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \\ldots, R+u$ are shifted, $u=0,1,2, \\ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with\n\n$$\n[1: 2 R-1],(0),[N-2 R: N-1], \\ldots,[2 R: 4 R-1]\n$$\n\nwhich is precisely $P_{r+1}$.\nSince $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.\nCase 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \\geq 1$, and define $P_{0}, \\ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :\n\n$$\n\\left[1: 2^{a}-1\\right],(0),\\left[N-2^{a}: N-1\\right],\\left[N-2^{a+1}: N-2^{a}-1\\right], \\ldots,\\left[2^{a+1}: 3 \\cdot 2^{a}-1\\right],\\left[2^{a}: 2^{a+1}-1\\right]\n$$\n\nBut then 0 is transposed with $2^{a}, 3 \\cdot 2^{a}, \\ldots,(2 b-1) \\cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.\n\nComment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values\n\n$$\n1,2,5,14,47,189,891,4815,29547\n$$\n\nwhich is not catalogued at oeis.org.", "metadata": {"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution\n\n"}}
|
APMO/segmented/en-apmo2002_sol.jsonl
CHANGED
|
@@ -1,10 +1,10 @@
|
|
| 1 |
-
{"year": "2002", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $a_{1}, a_{2}, a_{3}, \\ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.\n\nLet\n\n$$\nA_{n}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{n}\n$$\n\nProve that\n\n$$\na_{1}!a_{2}!\\ldots a_{n}!\\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n$$\n\nwhere $\\left\\lfloor A_{n}\\right\\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \\times 2 \\times \\cdots \\times a$ for $a \\geq 1$ (and $0!=1$ ). When does equality hold?", "solution": "Assume without loss of generality that $a_{1} \\geq a_{2} \\geq \\cdots \\geq a_{n} \\geq 0$, and let $s=\\left\\lfloor A_{n}\\right\\rfloor$. Let $k$ be any (fixed) index for which $a_{k} \\geq s \\geq a_{k+1}$.\n\nOur inequality is equivalent to proving that\n\n$$\n\\frac{a_{1}!}{s!} \\cdot \\frac{a_{2}!}{s!} \\cdot \\ldots \\cdot \\frac{a_{k}!}{s!} \\geq \\frac{s!}{a_{k+1}!} \\cdot \\frac{s!}{a_{k+2}!} \\cdot \\ldots \\cdot \\frac{s!}{a_{n}!}\n$$\n\nNow for $i=1,2, \\ldots, k, a_{i}!/ s!$ is the product of $a_{i}-s$ factors. For example, 9!/5! $=9 \\cdot 8 \\cdot 7 \\cdot 6$. The left side of inequality (1) therefore is the product of $A=a_{1}+a_{2}+\\cdots+a_{k}-k s$ factors, all of which are greater than $s$. Similarly, the right side of (1) is the product of $B=(n-k) s-$ $\\left(a_{k+1}+a_{k+2}+\\cdots+a_{n}\\right)$ factors, all of which are at most $s$. Since $\\sum_{i=1}^{n} a_{i}=n A_{n} \\geq n s, A \\geq B$. This proves the inequality. [ 5 marks to here.]\n\nEquality in (1) holds if and only if either:\n(i) $A=B=0$, that is, both sides of (1) are the empty product, which occurs if and only if $a_{1}=a_{2}=\\cdots=a_{n}$; or\n(ii) $a_{1}=1$ and $s=0$, that is, the only factors on either side of (1) are 1 's, which occurs if and only if $a_{i} \\in\\{0,1\\}$ for all $i$. [2 marks for both (i) and (ii), no marks for (i) only.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n1. ", "solution_match": "# Solution 1."}}
|
| 2 |
-
{"year": "2002", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $a_{1}, a_{2}, a_{3}, \\ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.\n\nLet\n\n$$\nA_{n}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{n}\n$$\n\nProve that\n\n$$\na_{1}!a_{2}!\\ldots a_{n}!\\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n$$\n\nwhere $\\left\\lfloor A_{n}\\right\\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \\times 2 \\times \\cdots \\times a$ for $a \\geq 1$ (and $0!=1$ ). When does equality hold?", "solution": "Assume without loss of generality that $0 \\leq a_{1} \\leq a_{2} \\leq \\cdots \\leq a_{n}$. Let $d=a_{n}-a_{1}$ and $m=\\left|\\left\\{i: a_{i}=a_{1}\\right\\}\\right|$. Our proof is by induction on $d$.\n\nWe first do the case $d=a_{n}-a_{1}=0$ or 1 separately. Then $a_{1}=a_{2}=\\cdots=a_{m}=a$ and $a_{m+1}=\\cdots=a_{n}=a+1$ for some $1 \\leq m \\leq n$ and $a \\geq 0$. In this case we have $\\left\\lfloor A_{n}\\right\\rfloor=a$, so the inequality to be proven is just $a_{1}!a_{2}!\\ldots a_{n}!\\geq(a!)^{n}$, which is obvious. Equality holds if and only if either $m=n$, that is, $a_{1}=a_{2}=\\cdots=a_{n}=a$; or if $a=0$, that is, $a_{1}=\\cdots=a_{m}=0$ and $a_{m+1}=\\cdots=a_{n}=1$. [ 2 marks to here.]\n\nSo assume that $d=a_{n}-a_{1} \\geq 2$ and that the inequality holds for all sequences with smaller values of $d$, or with the same value of $d$ and smaller values of $m$. Then the sequence\n\n$$\na_{1}+1, a_{2}, a_{3}, \\ldots, a_{n-1}, a_{n}-1\n$$\n\nthough not necessarily in non-decreasing order any more, does have either a smaller value of $d$, or the same value of $d$ and a smaller value of $m$, but in any case has the same value of $A_{n}$. Thus, by induction and since $a_{n}>a_{1}+1$,\n\n$$\n\\begin{aligned}\na_{1}!a_{2}!\\ldots a_{n}! & =\\left(a_{1}+1\\right)!a_{2}!\\ldots a_{n-1}!\\left(a_{n}-1\\right)!\\cdot \\frac{a_{n}}{a_{1}+1} \\\\\n& \\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n} \\cdot \\frac{a_{n}}{a_{1}+1} \\\\\n& >\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n\\end{aligned}\n$$\n\nwhich completes the proof. Equality cannot hold in this case.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution 2."}}
|
| 3 |
-
{"year": "2002", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Find all positive integers $a$ and $b$ such that\n\n$$\n\\frac{a^{2}+b}{b^{2}-a} \\text { and } \\frac{b^{2}+a}{a^{2}-b}\n$$\n\nare both integers.", "solution": "By the symmetry of the problem, we may suppose that $a \\leq b$. Notice that $b^{2}-a \\geq 0$, so that if $\\frac{a^{2}+b}{b^{2}-a}$ is a positive integer, then $a^{2}+b \\geq b^{2}-a$. Rearranging this inequality and factorizing, we find that $(a+b)(a-b+1) \\geq 0$. Since $a, b>0$, we must have $a \\geq b-1$. [3 marks to here.] We therefore have two cases:\n\nCase 1: $a=b$. Substituting, we have\n\n$$\n\\frac{a^{2}+a}{a^{2}-a}=\\frac{a+1}{a-1}=1+\\frac{2}{a-1},\n$$\n\nwhich is an integer if and only if $(a-1) \\mid 2$. As $a>0$, the only possible values are $a-1=1$ or 2. Hence, $(a, b)=(2,2)$ or $(3,3)$. [1 mark.]\n\nCase 2: $a=b-1$. Substituting, we have\n\n$$\n\\frac{b^{2}+a}{a^{2}-b}=\\frac{(a+1)^{2}+a}{a^{2}-(a+1)}=\\frac{a^{2}+3 a+1}{a^{2}-a-1}=1+\\frac{4 a+2}{a^{2}-a-1} .\n$$\n\nOnce again, notice that $4 a+2>0$, and hence, for $\\frac{4 a+2}{a^{2}-a-1}$ to be an integer, we must have $4 a+2 \\geq a^{2}-a-1$, that is, $a^{2}-5 a-3 \\leq 0$. Hence, since $a$ is an integer, we can bound $a$ by $1 \\leq \\bar{a} \\leq 5$. Checking all the ordered pairs $(a, b)=(1,2),(2,3), \\ldots,(5,6)$, we find that only $(1,2)$ and $(2,3)$ satisfy the given conditions. [3 marks.]\n\nThus, the ordered pairs that work are\n\n$$\n(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)\n$$\n\nwhere the last two pairs follow by symmetry. [2 marks if these solutions are found without proof that there are no others.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2002", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be an equilateral triangle. Let $P$ be a point on the side $A C$ and $Q$ be a point on the side $A B$ so that both triangles $A B P$ and $A C Q$ are acute. Let $R$ be the orthocentre of triangle $A B P$ and $S$ be the orthocentre of triangle $A C Q$. Let $T$ be the point common to the segments $B P$ and $C Q$. Find all possible values of $\\angle C B P$ and $\\angle B C Q$ such that triangle $T R S$ is equilateral.", "solution": "We are going to show that this can only happen when\n\n$$\n\\angle C B P=\\angle B C Q=15^{\\circ} .\n$$\n\nLemma. If $\\angle C B P>\\angle B C Q$, then $R T>S T$.\nProof. Let $A D, B E$ and $C F$ be the altitudes of triangle $A B C$ concurrent at its centre $G$. Then $P$ lies on $C E, Q$ lies on $B F$, and thus $T$ lies in triangle $B D G$.\n\n\nNote that -\n\n$$\n\\angle F A S=\\angle F C Q=30^{\\circ}-\\angle B C Q>30^{\\circ}-\\angle C B P=\\angle E B P=\\angle E A R\n$$\n\nSince $A F=A E$, we have $F S>E R$ so that\n\n$$\nG S=G F-F S<G E-E R=G R .\n$$\n\nLet $T_{x}$ be the projection of $T$ onto $B C$ and $T_{y}$ be the projection of $T$ onto $A D$, and similarly for $R$ and $S$. We have\n\n$$\nR_{x} T_{x}=D R_{x}+D T_{x}>\\left|D S_{x}-D T_{x}\\right|=S_{x} T_{x}\n$$\n\nand\n\n$$\nR_{y} T_{y}=G R_{y}+G T_{y}>G S_{y}+G T_{y}=S_{y} T_{y}\n$$\n\nIt follows that $R T>S T$.\n[1 mark for stating the Lemma, 3 marks for proving it.]\nThus, if $\\triangle T R S$ is equilateral, we must have $\\angle C B P=\\angle B C Q$.\n\n\nIt is clear from the symmetry of the figure that $T R=T S$, so $\\triangle T R S$ is equilateral if and only if $\\angle R T A=30^{\\circ}$. Now, as $B R$ is an altitude of the triangle $A B C, \\angle R B A=30^{\\circ}$. So $\\triangle T R S$ is equilateral if and only if $R T B A$ is a cyclic quadrilateral. Therefore, $\\triangle T R S$ is equilateral if and only if $\\angle T B R=\\angle T A R$. But\n\n$$\n\\begin{aligned}\n90^{\\circ} & =\\angle T B A+\\angle B A R \\\\\n& =(\\angle T B R+\\angle R B A)+(\\angle B A T+\\angle T A R) \\\\\n& =\\left(\\angle T B R+30^{\\circ}\\right)+\\left(30^{\\circ}+\\angle T A R\\right)\n\\end{aligned}\n$$\n\nand so\n\n$$\n30^{\\circ}=\\angle T A R+\\angle T B R\n$$\n\nBut these angles must be equal, so $\\angle T A R=\\angle T B R=15^{\\circ}$. Therefore $\\angle C B P=\\angle B C Q=15^{\\circ}$. [3 marks for finishing the proof with the assumption that $\\angle C B P=\\angle B C Q$.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n3. ", "solution_match": "# Solution."}}
|
| 5 |
-
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "$$\n\\begin{aligned}\n\\sum_{\\text {cyclic }} \\sqrt{x+y z} & =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\frac{1}{x}+\\frac{1}{y z}} \\\\\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\frac{1}{x}\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)+\\frac{1}{y z}} \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\left(\\frac{1}{x}+\\frac{1}{y}\\right)\\left(\\frac{1}{x}+\\frac{1}{z}\\right)} \\quad[1 \\text { mark.] }\n\\end{aligned}\n$$\n\n$$\n\\begin{aligned}\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\left(\\frac{1}{x}+\\frac{1}{\\sqrt{y z}}\\right)^{2}+\\frac{(\\sqrt{y}-\\sqrt{z})^{2}}{x y z}} \\quad[2 \\text { marks. }] \\\\\n& \\geq \\sqrt{x y z} \\sum_{\\text {cyclic }}\\left(\\frac{1}{x}+\\frac{1}{\\sqrt{y z}}\\right) \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z}\\left(1+\\sum_{\\text {cyclic }} \\frac{1}{\\sqrt{y z}}\\right) \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z}+\\sum_{\\text {cyclic }} \\sqrt{x} \\quad[1 \\text { mark. }]\n\\end{aligned}\n$$\n\nNote. It is easy to check that equality holds if and only if $x=y=z=3$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 1."}}
|
| 6 |
-
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "Squaring both sides of the given inequality, we obtain\n\n$$\n\\begin{aligned}\n& \\sum_{\\text {cyclic }} x+\\sum_{\\text {cyclic }} y z+2 \\sum_{\\text {cyclic }} \\sqrt{x+y z} \\sqrt{y+z x} \\\\\n& \\quad \\geq x y z+2 \\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{x}+\\sum_{\\text {cyclic }} x+2 \\sum_{\\text {cyclic }} \\sqrt{x y} \\quad \\text { [1 mark.] }\n\\end{aligned}\n$$\n\nIt follows from the given condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ that $x y z=\\sum_{\\text {cyclic }} x y$. Therefore, the given inequality is equivalent to\n\n$$\n\\sum_{\\text {cyclic }} \\sqrt{x+y z} \\sqrt{y+z x} \\geq \\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{x}+\\sum_{\\text {cyclic }} \\sqrt{x y} . \\quad[2 \\text { marks.] }\n$$\n\nUsing the Cauchy-Schwarz inequality [or just $x^{2}+y^{2} \\geq 2 x y$ ], we see that\n\n$$\n(x+y z)(y+z x) \\geq\\left(\\sqrt{x y}+\\sqrt{x y z^{2}}\\right)^{2}, \\quad[1 \\text { mark. }]\n$$\n\nor\n\n$$\n\\sqrt{x+y z} \\sqrt{y+z x} \\geq \\sqrt{x y}+\\sqrt{z} \\sqrt{x y z} . \\quad[1 \\text { mark. }]\n$$\n\nTaking the cyclic sum of this inequality over $x, y$ and $z$, we get the desired inequality. [2 marks.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 2."}}
|
| 7 |
-
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "This is another way of presenting the idea in the first solution.\nUsing the condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ and the AM-GM inequality, we have\n\n$$\n\\begin{aligned}\nx+y z-\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{x}\\right)^{2} & =y z\\left(1-\\frac{1}{x}\\right)-2 \\sqrt{y z} \\\\\n& =y z\\left(\\frac{1}{y}+\\frac{1}{z}\\right)-2 \\sqrt{y z}=y+z-2 \\sqrt{y z} \\geq 0\n\\end{aligned}\n$$\n\nwhich gives\n\n$$\n\\sqrt{x+y z} \\geq \\sqrt{\\frac{y z}{x}}+\\sqrt{x} . \\quad[3 \\text { marks. }]\n$$\n\nSimilarly, we have\n\n$$\n\\sqrt{y+z x} \\geq \\sqrt{\\frac{z x}{y}}+\\sqrt{y} \\text { and } \\sqrt{z+x y} \\geq \\sqrt{\\frac{x y}{z}}+\\sqrt{z}\n$$\n\nAddition yields\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$\n\n[2 marks.] Using the condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ again, we have\n\n$$\n\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}=\\sqrt{x y z}\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)=\\sqrt{x y z}, \\quad[1 \\text { mark. }]\n$$\n\nand thus\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z} . \\quad[1 \\text { mark. }]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 3."}}
|
| 8 |
-
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "This is also another way of presenting the idea in the first solution.\nWe make the substitution $a=\\frac{1}{x}, b=\\frac{1}{y}, c=\\frac{1}{z}$. Then it is enough to show that\n\n$$\n\\sqrt{\\frac{1}{a}+\\frac{1}{b c}}+\\sqrt{\\frac{1}{b}+\\frac{1}{c a}}+\\sqrt{\\frac{1}{c}+\\frac{1}{a b}} \\geq \\sqrt{\\frac{1}{a b c}}+\\sqrt{\\frac{1}{a}}+\\sqrt{\\frac{1}{b}}+\\sqrt{\\frac{1}{c}},\n$$\n\nwhere $a+b+c=1$. Multiplying this inequality by $\\sqrt{a b c}$, we find that it can be written\n\n$$\n\\sqrt{a+b c}+\\sqrt{b+c a}+\\sqrt{c+a b} \\geq 1+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b} . \\quad[1 \\text { mark. }]\n$$\n\nThis is equivalent to\n\n$$\n\\begin{aligned}\n& \\sqrt{a(a+b+c)+b c}+\\sqrt{b(a+b+c)+c a}+\\sqrt{c(a+b+c)+a b} \\\\\n& \\geq a+b+c+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b}, \\quad[1 \\text { mark. }]\n\\end{aligned}\n$$\n\nwhich in turn is equivalent to\n\n$$\n\\sqrt{(a+b)(a+c)}+\\sqrt{(b+c)(b+a)}+\\sqrt{(c+a)(c+b)} \\geq a+b+c+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b}\n$$\n\n[1 mark.] (This is a homogeneous version of the original inequality.) By the Cauchy-Schwarz inequality (or since $b+c \\geq 2 \\sqrt{b c}$ ), we have\n\n$$\n\\left[(\\sqrt{a})^{2}+(\\sqrt{b})^{2}\\right]\\left[(\\sqrt{a})^{2}+(\\sqrt{c})^{2}\\right] \\geq(\\sqrt{a} \\sqrt{a}+\\sqrt{b} \\sqrt{c})^{2}\n$$\n\nor\n\n$$\n\\sqrt{(a+b)(a+c)} \\geq a+\\sqrt{b c} . \\quad[2 \\text { marks. }]\n$$\n\nTaking the cyclic sum of this inequality over $a, b, c$, we get the desired inequality. [2 marks.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "# Solution 4."}}
|
| 9 |
-
{"year": "2002", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:\n(i) there are only finitely many $s$ in R such that $f(s)=0$, and\n(ii) $f\\left(x^{4}+y\\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\\mathbf{R}$.", "solution": "The only such function is the identity function on $R$.\nSetting $(x, y)=(1,0)$ in the given functional equation (ii), we have $f(f(0))=0$. Setting $x=0$ in (ii), we find\n\n$$\nf(y)=f(f(y))\n$$\n\n[1 mark.] and thus $f(0)=f(f(0))=0$ [1 mark.]. It follows from (ii) that $f\\left(x^{4}+y\\right)=$ $x^{3} f(x)+f(y)$ for all $x, y \\in \\mathbf{R}$. Set $y=0$ to obtain\n\n$$\nf\\left(x^{4}\\right)=x^{3} f(x)\n$$\n\nfor all $x \\in \\mathrm{R}$, and so\n\n$$\nf\\left(x^{4}+y\\right)=f\\left(x^{4}\\right)+f(y)\n$$\n\nfor all $x, y \\in \\mathbf{R}$. The functional equation (3) suggests that $f$ is additive, that is, $f(a+b)=$ $f(a)+f(b)$ for all $a, b \\in \\mathbf{R}$. [1 mark.] We now show this.\n\nFirst assume that $a \\geq 0$ and $b \\in R$. It follows from (3) that\n\n$$\nf(a+b)=f\\left(\\left(a^{1 / 4}\\right)^{4}+b\\right)=f\\left(\\left(a^{1 / 4}\\right)^{4}\\right)+f(b)=f(a)+f(b)\n$$\n\nWe next note that $f$ is an odd function, since from (2)\n\n$$\nf(-x)=\\frac{f\\left(x^{4}\\right)}{(-x)^{3}}=\\frac{f\\left(x^{4}\\right)}{-x^{3}}=-f(x), \\quad x \\neq 0\n$$\n\nSince $f$ is odd, we have that, for $a<0$ and $b \\in R$,\n\n$$\n\\begin{aligned}\nf(a+b) & =-f((-a)+(-b))=-(f(-a)+f(-b)) \\\\\n& =-(-f(a)-f(b))=f(a)+f(b)\n\\end{aligned}\n$$\n\nTherefore, we conclude that $f(a+b)=f(a)+f(b)$ for all $a, b \\in R$. [2 mers.].]\nWe now show that $\\{s \\in \\mathrm{R} \\mid f(s)=0\\}=\\{0\\}$. Recall that $f(0)=0$. Assume that there is a nonzero $h \\in \\mathrm{R}$ such that $f(h)=0$. Then, using the fact that $f$ is additive, we inductively have $f(n h)=0$ or $n h \\in\\{s \\in R \\mid f(s)=0\\}$ for all $n \\in \\mathbf{N}$. However, this is a contradiction to the given condition (i). [1 mark.]\n\nIt's now easy to check that $f$ is one-to-one. Assume that $f(a)=f^{\\prime}(b)$ for some $a, b \\in \\mathbb{P}$. Then, we have $f(b)=f(a)=f(a-b)+f(b)$ or $f(a-b)=0$. This implies that $a-b \\in\\{s \\in$ $\\mathbf{R} \\mid f(s)=0\\}=\\{0\\}$ or $a=b$, as desired. From (1) and the fact that $f$ is one-to-one, we deduce that $f(x)=x$ for all $x \\in \\mathbf{R}$. [1 mark.] This completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution 1."}}
|
| 10 |
-
{"year": "2002", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:\n(i) there are only finitely many $s$ in R such that $f(s)=0$, and\n(ii) $f\\left(x^{4}+y\\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\\mathbf{R}$.", "solution": "Again, the only such function is the identity function on R .\nAs in Solution 1, we first show that $f(f(y))=f(y), f(0)=0$, and $f\\left(x^{4}\\right)=x^{3} f(x)$. [2 marks.] From the latter follows\n\n$$\nf(x)=0 \\Longrightarrow f\\left(x^{4}\\right)=0\n$$\n\nand from condition (i) we get that $f(x)=0$ only possibly for $x \\in\\{0,1,-1\\}$. [1 mark.]\nNext we prove\n\n$$\nf(a)=b \\Longrightarrow f(\\sqrt[4]{|a-b|})=0\n$$\n\nThis is clear if $a=b$. If $a>b$ then\n\n$$\n\\begin{aligned}\nf(a) & =f((a-b)+b)=(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(f(b)) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(b) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(f(a)) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(a),\n\\end{aligned}\n$$\n\nso $(a-b)^{3 / 4} f(\\sqrt[4]{a-b})=0$ which means $f(\\sqrt[4]{|a-b|})=0$. If $a<b$ we get similarly\n\n$$\n\\begin{aligned}\nf(b) & =f((b-a)+a)=(b-a)^{3 / 4} f(\\sqrt[4]{b-a})+f(f(a)) \\\\\n& =(b-a)^{3 / 4} f(\\sqrt[4]{b-a})+f(b)\n\\end{aligned}\n$$\n\nand again $f(\\sqrt[4]{|a-b|})=0$. [2 marks.]\nThus $f(a)=b \\Longrightarrow|a-b| \\in\\{0,1\\}$. Suppose that $f(x)=x+b$ for some $x$, where $|b|=1$. Then from $f\\left(x^{4}\\right)=x^{3} f(x)$ and $f\\left(x^{4}\\right)=x^{4}+a$ for some $|a| \\leq 1$ we get $x^{3}=a / b$, so $|x| \\leq 1$. Thus $f(x)=x$ for all $x$ except possibly $x= \\pm 1$. [ 1 mark.] But for example,\n\n$$\nf(1)=f\\left(2^{4}-15\\right)=2^{3} f(2)+f(f(-15))=2^{3} \\cdot 2-15=1\n$$\n\nand\n\n$$\nf(-1)=f\\left(2^{4}-17\\right)=2^{3} f(2)+f(f(-17))=2^{3} \\cdot 2-17=-1\n$$\n\n[1 mark.] This finishes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution 2."}}
|
|
|
|
| 1 |
+
{"year": "2002", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, a_{3}, \\ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.\n\nLet\n\n$$\nA_{n}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{n}\n$$\n\nProve that\n\n$$\na_{1}!a_{2}!\\ldots a_{n}!\\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n$$\n\nwhere $\\left\\lfloor A_{n}\\right\\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \\times 2 \\times \\cdots \\times a$ for $a \\geq 1$ (and $0!=1$ ). When does equality hold?", "solution": "Assume without loss of generality that $a_{1} \\geq a_{2} \\geq \\cdots \\geq a_{n} \\geq 0$, and let $s=\\left\\lfloor A_{n}\\right\\rfloor$. Let $k$ be any (fixed) index for which $a_{k} \\geq s \\geq a_{k+1}$.\n\nOur inequality is equivalent to proving that\n\n$$\n\\frac{a_{1}!}{s!} \\cdot \\frac{a_{2}!}{s!} \\cdot \\ldots \\cdot \\frac{a_{k}!}{s!} \\geq \\frac{s!}{a_{k+1}!} \\cdot \\frac{s!}{a_{k+2}!} \\cdot \\ldots \\cdot \\frac{s!}{a_{n}!}\n$$\n\nNow for $i=1,2, \\ldots, k, a_{i}!/ s!$ is the product of $a_{i}-s$ factors. For example, 9!/5! $=9 \\cdot 8 \\cdot 7 \\cdot 6$. The left side of inequality (1) therefore is the product of $A=a_{1}+a_{2}+\\cdots+a_{k}-k s$ factors, all of which are greater than $s$. Similarly, the right side of (1) is the product of $B=(n-k) s-$ $\\left(a_{k+1}+a_{k+2}+\\cdots+a_{n}\\right)$ factors, all of which are at most $s$. Since $\\sum_{i=1}^{n} a_{i}=n A_{n} \\geq n s, A \\geq B$. This proves the inequality. [ 5 marks to here.]\n\nEquality in (1) holds if and only if either:\n(i) $A=B=0$, that is, both sides of (1) are the empty product, which occurs if and only if $a_{1}=a_{2}=\\cdots=a_{n}$; or\n(ii) $a_{1}=1$ and $s=0$, that is, the only factors on either side of (1) are 1 's, which occurs if and only if $a_{i} \\in\\{0,1\\}$ for all $i$. [2 marks for both (i) and (ii), no marks for (i) only.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n1. ", "solution_match": "# Solution 1."}}
|
| 2 |
+
{"year": "2002", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, a_{3}, \\ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.\n\nLet\n\n$$\nA_{n}=\\frac{a_{1}+a_{2}+\\cdots+a_{n}}{n}\n$$\n\nProve that\n\n$$\na_{1}!a_{2}!\\ldots a_{n}!\\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n$$\n\nwhere $\\left\\lfloor A_{n}\\right\\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \\times 2 \\times \\cdots \\times a$ for $a \\geq 1$ (and $0!=1$ ). When does equality hold?", "solution": "Assume without loss of generality that $0 \\leq a_{1} \\leq a_{2} \\leq \\cdots \\leq a_{n}$. Let $d=a_{n}-a_{1}$ and $m=\\left|\\left\\{i: a_{i}=a_{1}\\right\\}\\right|$. Our proof is by induction on $d$.\n\nWe first do the case $d=a_{n}-a_{1}=0$ or 1 separately. Then $a_{1}=a_{2}=\\cdots=a_{m}=a$ and $a_{m+1}=\\cdots=a_{n}=a+1$ for some $1 \\leq m \\leq n$ and $a \\geq 0$. In this case we have $\\left\\lfloor A_{n}\\right\\rfloor=a$, so the inequality to be proven is just $a_{1}!a_{2}!\\ldots a_{n}!\\geq(a!)^{n}$, which is obvious. Equality holds if and only if either $m=n$, that is, $a_{1}=a_{2}=\\cdots=a_{n}=a$; or if $a=0$, that is, $a_{1}=\\cdots=a_{m}=0$ and $a_{m+1}=\\cdots=a_{n}=1$. [ 2 marks to here.]\n\nSo assume that $d=a_{n}-a_{1} \\geq 2$ and that the inequality holds for all sequences with smaller values of $d$, or with the same value of $d$ and smaller values of $m$. Then the sequence\n\n$$\na_{1}+1, a_{2}, a_{3}, \\ldots, a_{n-1}, a_{n}-1\n$$\n\nthough not necessarily in non-decreasing order any more, does have either a smaller value of $d$, or the same value of $d$ and a smaller value of $m$, but in any case has the same value of $A_{n}$. Thus, by induction and since $a_{n}>a_{1}+1$,\n\n$$\n\\begin{aligned}\na_{1}!a_{2}!\\ldots a_{n}! & =\\left(a_{1}+1\\right)!a_{2}!\\ldots a_{n-1}!\\left(a_{n}-1\\right)!\\cdot \\frac{a_{n}}{a_{1}+1} \\\\\n& \\geq\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n} \\cdot \\frac{a_{n}}{a_{1}+1} \\\\\n& >\\left(\\left\\lfloor A_{n}\\right\\rfloor!\\right)^{n}\n\\end{aligned}\n$$\n\nwhich completes the proof. Equality cannot hold in this case.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution 2."}}
|
| 3 |
+
{"year": "2002", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Find all positive integers $a$ and $b$ such that\n\n$$\n\\frac{a^{2}+b}{b^{2}-a} \\text { and } \\frac{b^{2}+a}{a^{2}-b}\n$$\n\nare both integers.", "solution": "By the symmetry of the problem, we may suppose that $a \\leq b$. Notice that $b^{2}-a \\geq 0$, so that if $\\frac{a^{2}+b}{b^{2}-a}$ is a positive integer, then $a^{2}+b \\geq b^{2}-a$. Rearranging this inequality and factorizing, we find that $(a+b)(a-b+1) \\geq 0$. Since $a, b>0$, we must have $a \\geq b-1$. [3 marks to here.] We therefore have two cases:\n\nCase 1: $a=b$. Substituting, we have\n\n$$\n\\frac{a^{2}+a}{a^{2}-a}=\\frac{a+1}{a-1}=1+\\frac{2}{a-1},\n$$\n\nwhich is an integer if and only if $(a-1) \\mid 2$. As $a>0$, the only possible values are $a-1=1$ or 2. Hence, $(a, b)=(2,2)$ or $(3,3)$. [1 mark.]\n\nCase 2: $a=b-1$. Substituting, we have\n\n$$\n\\frac{b^{2}+a}{a^{2}-b}=\\frac{(a+1)^{2}+a}{a^{2}-(a+1)}=\\frac{a^{2}+3 a+1}{a^{2}-a-1}=1+\\frac{4 a+2}{a^{2}-a-1} .\n$$\n\nOnce again, notice that $4 a+2>0$, and hence, for $\\frac{4 a+2}{a^{2}-a-1}$ to be an integer, we must have $4 a+2 \\geq a^{2}-a-1$, that is, $a^{2}-5 a-3 \\leq 0$. Hence, since $a$ is an integer, we can bound $a$ by $1 \\leq \\bar{a} \\leq 5$. Checking all the ordered pairs $(a, b)=(1,2),(2,3), \\ldots,(5,6)$, we find that only $(1,2)$ and $(2,3)$ satisfy the given conditions. [3 marks.]\n\nThus, the ordered pairs that work are\n\n$$\n(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)\n$$\n\nwhere the last two pairs follow by symmetry. [2 marks if these solutions are found without proof that there are no others.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2002", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an equilateral triangle. Let $P$ be a point on the side $A C$ and $Q$ be a point on the side $A B$ so that both triangles $A B P$ and $A C Q$ are acute. Let $R$ be the orthocentre of triangle $A B P$ and $S$ be the orthocentre of triangle $A C Q$. Let $T$ be the point common to the segments $B P$ and $C Q$. Find all possible values of $\\angle C B P$ and $\\angle B C Q$ such that triangle $T R S$ is equilateral.", "solution": "We are going to show that this can only happen when\n\n$$\n\\angle C B P=\\angle B C Q=15^{\\circ} .\n$$\n\nLemma. If $\\angle C B P>\\angle B C Q$, then $R T>S T$.\nProof. Let $A D, B E$ and $C F$ be the altitudes of triangle $A B C$ concurrent at its centre $G$. Then $P$ lies on $C E, Q$ lies on $B F$, and thus $T$ lies in triangle $B D G$.\n\n\nNote that -\n\n$$\n\\angle F A S=\\angle F C Q=30^{\\circ}-\\angle B C Q>30^{\\circ}-\\angle C B P=\\angle E B P=\\angle E A R\n$$\n\nSince $A F=A E$, we have $F S>E R$ so that\n\n$$\nG S=G F-F S<G E-E R=G R .\n$$\n\nLet $T_{x}$ be the projection of $T$ onto $B C$ and $T_{y}$ be the projection of $T$ onto $A D$, and similarly for $R$ and $S$. We have\n\n$$\nR_{x} T_{x}=D R_{x}+D T_{x}>\\left|D S_{x}-D T_{x}\\right|=S_{x} T_{x}\n$$\n\nand\n\n$$\nR_{y} T_{y}=G R_{y}+G T_{y}>G S_{y}+G T_{y}=S_{y} T_{y}\n$$\n\nIt follows that $R T>S T$.\n[1 mark for stating the Lemma, 3 marks for proving it.]\nThus, if $\\triangle T R S$ is equilateral, we must have $\\angle C B P=\\angle B C Q$.\n\n\nIt is clear from the symmetry of the figure that $T R=T S$, so $\\triangle T R S$ is equilateral if and only if $\\angle R T A=30^{\\circ}$. Now, as $B R$ is an altitude of the triangle $A B C, \\angle R B A=30^{\\circ}$. So $\\triangle T R S$ is equilateral if and only if $R T B A$ is a cyclic quadrilateral. Therefore, $\\triangle T R S$ is equilateral if and only if $\\angle T B R=\\angle T A R$. But\n\n$$\n\\begin{aligned}\n90^{\\circ} & =\\angle T B A+\\angle B A R \\\\\n& =(\\angle T B R+\\angle R B A)+(\\angle B A T+\\angle T A R) \\\\\n& =\\left(\\angle T B R+30^{\\circ}\\right)+\\left(30^{\\circ}+\\angle T A R\\right)\n\\end{aligned}\n$$\n\nand so\n\n$$\n30^{\\circ}=\\angle T A R+\\angle T B R\n$$\n\nBut these angles must be equal, so $\\angle T A R=\\angle T B R=15^{\\circ}$. Therefore $\\angle C B P=\\angle B C Q=15^{\\circ}$. [3 marks for finishing the proof with the assumption that $\\angle C B P=\\angle B C Q$.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n3. ", "solution_match": "# Solution."}}
|
| 5 |
+
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "$$\n\\begin{aligned}\n\\sum_{\\text {cyclic }} \\sqrt{x+y z} & =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\frac{1}{x}+\\frac{1}{y z}} \\\\\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\frac{1}{x}\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)+\\frac{1}{y z}} \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\left(\\frac{1}{x}+\\frac{1}{y}\\right)\\left(\\frac{1}{x}+\\frac{1}{z}\\right)} \\quad[1 \\text { mark.] }\n\\end{aligned}\n$$\n\n$$\n\\begin{aligned}\n& =\\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{\\left(\\frac{1}{x}+\\frac{1}{\\sqrt{y z}}\\right)^{2}+\\frac{(\\sqrt{y}-\\sqrt{z})^{2}}{x y z}} \\quad[2 \\text { marks. }] \\\\\n& \\geq \\sqrt{x y z} \\sum_{\\text {cyclic }}\\left(\\frac{1}{x}+\\frac{1}{\\sqrt{y z}}\\right) \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z}\\left(1+\\sum_{\\text {cyclic }} \\frac{1}{\\sqrt{y z}}\\right) \\quad[1 \\text { mark. }] \\\\\n& =\\sqrt{x y z}+\\sum_{\\text {cyclic }} \\sqrt{x} \\quad[1 \\text { mark. }]\n\\end{aligned}\n$$\n\nNote. It is easy to check that equality holds if and only if $x=y=z=3$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 1."}}
|
| 6 |
+
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "Squaring both sides of the given inequality, we obtain\n\n$$\n\\begin{aligned}\n& \\sum_{\\text {cyclic }} x+\\sum_{\\text {cyclic }} y z+2 \\sum_{\\text {cyclic }} \\sqrt{x+y z} \\sqrt{y+z x} \\\\\n& \\quad \\geq x y z+2 \\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{x}+\\sum_{\\text {cyclic }} x+2 \\sum_{\\text {cyclic }} \\sqrt{x y} \\quad \\text { [1 mark.] }\n\\end{aligned}\n$$\n\nIt follows from the given condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ that $x y z=\\sum_{\\text {cyclic }} x y$. Therefore, the given inequality is equivalent to\n\n$$\n\\sum_{\\text {cyclic }} \\sqrt{x+y z} \\sqrt{y+z x} \\geq \\sqrt{x y z} \\sum_{\\text {cyclic }} \\sqrt{x}+\\sum_{\\text {cyclic }} \\sqrt{x y} . \\quad[2 \\text { marks.] }\n$$\n\nUsing the Cauchy-Schwarz inequality [or just $x^{2}+y^{2} \\geq 2 x y$ ], we see that\n\n$$\n(x+y z)(y+z x) \\geq\\left(\\sqrt{x y}+\\sqrt{x y z^{2}}\\right)^{2}, \\quad[1 \\text { mark. }]\n$$\n\nor\n\n$$\n\\sqrt{x+y z} \\sqrt{y+z x} \\geq \\sqrt{x y}+\\sqrt{z} \\sqrt{x y z} . \\quad[1 \\text { mark. }]\n$$\n\nTaking the cyclic sum of this inequality over $x, y$ and $z$, we get the desired inequality. [2 marks.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 2."}}
|
| 7 |
+
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "This is another way of presenting the idea in the first solution.\nUsing the condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ and the AM-GM inequality, we have\n\n$$\n\\begin{aligned}\nx+y z-\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{x}\\right)^{2} & =y z\\left(1-\\frac{1}{x}\\right)-2 \\sqrt{y z} \\\\\n& =y z\\left(\\frac{1}{y}+\\frac{1}{z}\\right)-2 \\sqrt{y z}=y+z-2 \\sqrt{y z} \\geq 0\n\\end{aligned}\n$$\n\nwhich gives\n\n$$\n\\sqrt{x+y z} \\geq \\sqrt{\\frac{y z}{x}}+\\sqrt{x} . \\quad[3 \\text { marks. }]\n$$\n\nSimilarly, we have\n\n$$\n\\sqrt{y+z x} \\geq \\sqrt{\\frac{z x}{y}}+\\sqrt{y} \\text { and } \\sqrt{z+x y} \\geq \\sqrt{\\frac{x y}{z}}+\\sqrt{z}\n$$\n\nAddition yields\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$\n\n[2 marks.] Using the condition $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1$ again, we have\n\n$$\n\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}=\\sqrt{x y z}\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)=\\sqrt{x y z}, \\quad[1 \\text { mark. }]\n$$\n\nand thus\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z} . \\quad[1 \\text { mark. }]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 3."}}
|
| 8 |
+
{"year": "2002", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y, z$ be positive numbers such that\n\n$$\n\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=1\n$$\n\nShow that\n\n$$\n\\sqrt{x+y z}+\\sqrt{y+z x}+\\sqrt{z+x y} \\geq \\sqrt{x y z}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z}\n$$", "solution": "This is also another way of presenting the idea in the first solution.\nWe make the substitution $a=\\frac{1}{x}, b=\\frac{1}{y}, c=\\frac{1}{z}$. Then it is enough to show that\n\n$$\n\\sqrt{\\frac{1}{a}+\\frac{1}{b c}}+\\sqrt{\\frac{1}{b}+\\frac{1}{c a}}+\\sqrt{\\frac{1}{c}+\\frac{1}{a b}} \\geq \\sqrt{\\frac{1}{a b c}}+\\sqrt{\\frac{1}{a}}+\\sqrt{\\frac{1}{b}}+\\sqrt{\\frac{1}{c}},\n$$\n\nwhere $a+b+c=1$. Multiplying this inequality by $\\sqrt{a b c}$, we find that it can be written\n\n$$\n\\sqrt{a+b c}+\\sqrt{b+c a}+\\sqrt{c+a b} \\geq 1+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b} . \\quad[1 \\text { mark. }]\n$$\n\nThis is equivalent to\n\n$$\n\\begin{aligned}\n& \\sqrt{a(a+b+c)+b c}+\\sqrt{b(a+b+c)+c a}+\\sqrt{c(a+b+c)+a b} \\\\\n& \\geq a+b+c+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b}, \\quad[1 \\text { mark. }]\n\\end{aligned}\n$$\n\nwhich in turn is equivalent to\n\n$$\n\\sqrt{(a+b)(a+c)}+\\sqrt{(b+c)(b+a)}+\\sqrt{(c+a)(c+b)} \\geq a+b+c+\\sqrt{b c}+\\sqrt{c a}+\\sqrt{a b}\n$$\n\n[1 mark.] (This is a homogeneous version of the original inequality.) By the Cauchy-Schwarz inequality (or since $b+c \\geq 2 \\sqrt{b c}$ ), we have\n\n$$\n\\left[(\\sqrt{a})^{2}+(\\sqrt{b})^{2}\\right]\\left[(\\sqrt{a})^{2}+(\\sqrt{c})^{2}\\right] \\geq(\\sqrt{a} \\sqrt{a}+\\sqrt{b} \\sqrt{c})^{2}\n$$\n\nor\n\n$$\n\\sqrt{(a+b)(a+c)} \\geq a+\\sqrt{b c} . \\quad[2 \\text { marks. }]\n$$\n\nTaking the cyclic sum of this inequality over $a, b, c$, we get the desired inequality. [2 marks.]", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n4. ", "solution_match": "# Solution 4."}}
|
| 9 |
+
{"year": "2002", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:\n(i) there are only finitely many $s$ in R such that $f(s)=0$, and\n(ii) $f\\left(x^{4}+y\\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\\mathbf{R}$.", "solution": "The only such function is the identity function on $R$.\nSetting $(x, y)=(1,0)$ in the given functional equation (ii), we have $f(f(0))=0$. Setting $x=0$ in (ii), we find\n\n$$\nf(y)=f(f(y))\n$$\n\n[1 mark.] and thus $f(0)=f(f(0))=0$ [1 mark.]. It follows from (ii) that $f\\left(x^{4}+y\\right)=$ $x^{3} f(x)+f(y)$ for all $x, y \\in \\mathbf{R}$. Set $y=0$ to obtain\n\n$$\nf\\left(x^{4}\\right)=x^{3} f(x)\n$$\n\nfor all $x \\in \\mathrm{R}$, and so\n\n$$\nf\\left(x^{4}+y\\right)=f\\left(x^{4}\\right)+f(y)\n$$\n\nfor all $x, y \\in \\mathbf{R}$. The functional equation (3) suggests that $f$ is additive, that is, $f(a+b)=$ $f(a)+f(b)$ for all $a, b \\in \\mathbf{R}$. [1 mark.] We now show this.\n\nFirst assume that $a \\geq 0$ and $b \\in R$. It follows from (3) that\n\n$$\nf(a+b)=f\\left(\\left(a^{1 / 4}\\right)^{4}+b\\right)=f\\left(\\left(a^{1 / 4}\\right)^{4}\\right)+f(b)=f(a)+f(b)\n$$\n\nWe next note that $f$ is an odd function, since from (2)\n\n$$\nf(-x)=\\frac{f\\left(x^{4}\\right)}{(-x)^{3}}=\\frac{f\\left(x^{4}\\right)}{-x^{3}}=-f(x), \\quad x \\neq 0\n$$\n\nSince $f$ is odd, we have that, for $a<0$ and $b \\in R$,\n\n$$\n\\begin{aligned}\nf(a+b) & =-f((-a)+(-b))=-(f(-a)+f(-b)) \\\\\n& =-(-f(a)-f(b))=f(a)+f(b)\n\\end{aligned}\n$$\n\nTherefore, we conclude that $f(a+b)=f(a)+f(b)$ for all $a, b \\in R$. [2 mers.].]\nWe now show that $\\{s \\in \\mathrm{R} \\mid f(s)=0\\}=\\{0\\}$. Recall that $f(0)=0$. Assume that there is a nonzero $h \\in \\mathrm{R}$ such that $f(h)=0$. Then, using the fact that $f$ is additive, we inductively have $f(n h)=0$ or $n h \\in\\{s \\in R \\mid f(s)=0\\}$ for all $n \\in \\mathbf{N}$. However, this is a contradiction to the given condition (i). [1 mark.]\n\nIt's now easy to check that $f$ is one-to-one. Assume that $f(a)=f^{\\prime}(b)$ for some $a, b \\in \\mathbb{P}$. Then, we have $f(b)=f(a)=f(a-b)+f(b)$ or $f(a-b)=0$. This implies that $a-b \\in\\{s \\in$ $\\mathbf{R} \\mid f(s)=0\\}=\\{0\\}$ or $a=b$, as desired. From (1) and the fact that $f$ is one-to-one, we deduce that $f(x)=x$ for all $x \\in \\mathbf{R}$. [1 mark.] This completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution 1."}}
|
| 10 |
+
{"year": "2002", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:\n(i) there are only finitely many $s$ in R such that $f(s)=0$, and\n(ii) $f\\left(x^{4}+y\\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\\mathbf{R}$.", "solution": "Again, the only such function is the identity function on R .\nAs in Solution 1, we first show that $f(f(y))=f(y), f(0)=0$, and $f\\left(x^{4}\\right)=x^{3} f(x)$. [2 marks.] From the latter follows\n\n$$\nf(x)=0 \\Longrightarrow f\\left(x^{4}\\right)=0\n$$\n\nand from condition (i) we get that $f(x)=0$ only possibly for $x \\in\\{0,1,-1\\}$. [1 mark.]\nNext we prove\n\n$$\nf(a)=b \\Longrightarrow f(\\sqrt[4]{|a-b|})=0\n$$\n\nThis is clear if $a=b$. If $a>b$ then\n\n$$\n\\begin{aligned}\nf(a) & =f((a-b)+b)=(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(f(b)) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(b) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(f(a)) \\\\\n& =(a-b)^{3 / 4} f(\\sqrt[4]{a-b})+f(a),\n\\end{aligned}\n$$\n\nso $(a-b)^{3 / 4} f(\\sqrt[4]{a-b})=0$ which means $f(\\sqrt[4]{|a-b|})=0$. If $a<b$ we get similarly\n\n$$\n\\begin{aligned}\nf(b) & =f((b-a)+a)=(b-a)^{3 / 4} f(\\sqrt[4]{b-a})+f(f(a)) \\\\\n& =(b-a)^{3 / 4} f(\\sqrt[4]{b-a})+f(b)\n\\end{aligned}\n$$\n\nand again $f(\\sqrt[4]{|a-b|})=0$. [2 marks.]\nThus $f(a)=b \\Longrightarrow|a-b| \\in\\{0,1\\}$. Suppose that $f(x)=x+b$ for some $x$, where $|b|=1$. Then from $f\\left(x^{4}\\right)=x^{3} f(x)$ and $f\\left(x^{4}\\right)=x^{4}+a$ for some $|a| \\leq 1$ we get $x^{3}=a / b$, so $|x| \\leq 1$. Thus $f(x)=x$ for all $x$ except possibly $x= \\pm 1$. [ 1 mark.] But for example,\n\n$$\nf(1)=f\\left(2^{4}-15\\right)=2^{3} f(2)+f(f(-15))=2^{3} \\cdot 2-15=1\n$$\n\nand\n\n$$\nf(-1)=f\\left(2^{4}-17\\right)=2^{3} f(2)+f(f(-17))=2^{3} \\cdot 2-17=-1\n$$\n\n[1 mark.] This finishes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution 2."}}
|
APMO/segmented/en-apmo2003_sol.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "2003", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $a, b, c, d, e, f$ be real numbers such that the polynomial\n\n$$\np(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f\n$$\n\nfactorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \\ldots, 8$. Determine all possible values of $f$.", "solution": "From\n\n$$\nx^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\\left(x-x_{1}\\right)\\left(x-x_{2}\\right) \\ldots\\left(x-x_{8}\\right)\n$$\n\nwe have\n\n$$\n\\sum_{i=1}^{8} x_{i}=4 \\quad \\text { and } \\quad \\sum x_{i} x_{j}=7\n$$\n\nwhere the second sum is over all pairs $(i, j)$ of integers where $1 \\leq i<j \\leq 8$. Since this sum can also be written\n\n$$\n\\frac{1}{2}\\left[\\left(\\sum_{i=1}^{8} x_{i}\\right)^{2}-\\sum_{i=1}^{8} x_{i}^{2}\\right]\n$$\n\nwe get\n\n$$\n14=\\left(\\sum_{i=1}^{8} x_{i}\\right)^{2}-\\sum_{i=1}^{8} x_{i}^{2}=16-\\sum_{i=1}^{8} x_{i}^{2}\n$$\n\nso\n\n$$\n\\sum_{i=1}^{8} x_{i}^{2}=2 \\quad \\text { while } \\quad \\sum_{i=1}^{8} x_{i}=4 . \\quad[3 \\text { marks }]\n$$\n\nNow\n\n$$\n\\sum_{i=1}^{8}\\left(2 x_{i}-1\\right)^{2}=4 \\sum_{i=1}^{8} x_{i}^{2}-4 \\sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0\n$$\n\nwhich forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore\n\n$$\nf=\\prod_{i=1}^{8} x_{i}=\\left(\\frac{1}{2}\\right)^{8}=\\frac{1}{256} . \\quad[1 m x]\n$$\n\nAlternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get\n\n$$\n16=\\left(x_{1} \\cdot 1+x_{2} \\cdot 1+\\cdots+x_{8} \\cdot 1\\right)^{2} \\leq\\left(x_{1}^{2-}+x_{2}^{2}+\\cdots+x_{8}^{2}\\right)\\left(1^{2}+1^{2}+\\cdots+1^{2}\\right)=8 \\cdot 2=16\n$$\n\nor the power mean inequality to get\n\n$$\n\\frac{1}{2}=\\frac{1}{8} \\sum_{i=1}^{8} x_{i} \\leq\\left(\\frac{1}{8} \\sum_{i=1}^{8} x_{i}^{2}\\right)^{1 / 2}=\\frac{1}{2} . \\quad[2 \\text { marks }]\n$$\n\nEither way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n1. ", "solution_match": "# Solution."}}
|
| 2 |
-
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Let $E H$ intersect $F G$ at $O$. The distance from $G$ to line $F D$ and line $E F$ are both $a$. So $F G$ bisects $\\angle E F D$. Similarly, $E H$ bisects $\\angle B E F$. So $O$ is an excentre of $\\triangle A E F$. Similarly, $O$ is an excentre of $\\triangle C G H$. [2 marks] Construct these excircles with centre $O$. Let $M, N, P, Q$ be on sides $A B, B C, C D, D A$ respectively, where these excircles touch the square. Then $O M \\perp A B, O N \\perp B C, O P \\perp C D$, and $O Q \\perp D A$. Since $A B \\| C D$ and $A D \\| B C, M, O, P$ are collinear and $N, O, Q$ are collinear. Now $M P=N Q=a$. [2 marks] Using the fact that the two tangents from a point to a circle have the same length, we get $E F=E M+F Q$ and $G H=G N+H P$. [1 mark] Then\n\n$$\nm_{1}=A E+A F+E F=A E+A F+(E M+F Q)=A M+A Q=O Q+O M\n$$\n\nand\n\n$$\nm_{2}=C G+C H+G H=C G+C H+(G N+H P)=C N+C P=O P+O N . \\quad[1 \\text { mark }]\n$$\n\nTherefore\n\n$$\nm_{1}+m_{2}=(O Q+O M)+(O P+O N)=M P+N Q=2 a . \\quad[1 \\mathrm{mark}]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
-
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Extend $A B$ to $I$ and $D C$ to $J$ so that $A E=B I=C J$. Let $\\ell_{2}$ intersect $I J$ at $M$, and let $K$ lie on $I J$ so that $G K \\perp I J$. Then, since $A E=G K, \\triangle A E F$ and $\\triangle K G M$ are congruent. [1 mark] Thus, since $G K=C J$ and $G C=K J$,\n\n$$\nm_{1}+m_{2}=\\operatorname{perimeter}(K G M)+\\operatorname{perimeter}(C G H)=\\operatorname{perimeter}(H M J) . \\quad[\\mathbf{2} \\text { marks }]\n$$\n\nLet $L$ lie on $C D$ so that $E L \\perp C D$. Then a circle with centre $E$ and radius $a$ will touch $D C$ at $L, I J$ at $I$, and the interior of $H M$ at some point $N$, so\n\n$$\n\\operatorname{perimeter}(H M J)=J H+(H N+N M)+J M=(J H+H L)+(M I+J M)=J L+I J=a+a=2 a\n$$\n\n[4 marks] Thus $m_{1}+m_{2}=2 a$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "# Solution 2."}}
|
| 4 |
-
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Without loss of generality, assume the square has side $a=1$. Let $\\theta$ be the acute angle between $\\ell_{1}$ (or $\\ell_{2}$ ) and the sides $A B$ and $C D$ of the square. Then, letting $E F=x$ and $G H=y$, we have\n\n$$\nE A=x \\cos \\theta, \\quad A F=x \\sin \\theta, \\quad C H=y \\cos \\theta, \\quad C G=y \\sin \\theta\n$$\n\nThus\n\n$$\nm_{1}+m_{2}=(x+y)(\\sin \\theta+\\cos \\theta+1) . \\quad[2 \\text { marks }]\n$$\n\nDraw lines parallel to $\\ell_{1}, \\ell_{2}$ through $A$ and $C$ respectively. The distance between these lines is $\\sin \\theta+\\cos \\theta$ [1 mark], as can be seen by drawing a mutual perpendicular to these lines through $B$, say. Also, the altitudes from $A$ to $E F$ and from $C$ to $G H$ have lengths $x \\sin \\theta \\cos \\theta$ and $y \\sin \\theta \\cos \\theta$ respectively [ 1 mark]. Therefore the distance between $\\ell_{1}$ and $\\ell_{2}$ must be\n\n$$\n(\\sin \\theta+\\cos \\theta)-x \\sin \\theta \\cos \\theta-y \\sin \\theta \\cos \\theta\n$$\n\nBut we are given that this distance is $a=1$, so\n\n$$\n(x+y) \\sin \\theta \\cos \\theta+1=\\sin \\theta+\\cos \\theta\n$$\n\nor\n\n$$\nx+y=\\frac{\\sin \\theta+\\cos \\theta-1}{\\sin \\theta \\cos \\theta} \\cdot \\quad[1 \\text { mark }]\n$$\n\nTherefore, by (1),\n\n$$\n\\begin{aligned}\nm_{1}+m_{2} & =\\frac{(\\sin \\theta+\\cos \\theta-1)(\\sin \\theta+\\cos \\theta+1)}{\\sin \\theta \\cos \\theta} \\\\\n& =\\frac{\\left(\\sin ^{2} \\theta+\\cos ^{2} \\theta+2 \\sin \\theta \\cos \\theta\\right)-1}{\\sin \\theta \\cos \\theta} \\\\\n& =\\frac{1+2 \\sin \\theta \\cos \\theta-1}{\\sin \\theta \\cos \\theta}=2 . \\quad[2 \\text { marks }]\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 3."}}
|
| 5 |
-
{"year": "2003", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $k \\geq 14$ be an integer, and let $p_{k}$ be the largest prime number which is strictly less than $k$. You may assume that $p_{k} \\geq 3 k / 4$. Let $n$ be a composite integer. Prove:\n(a) if $n=2 p_{k}$, then $n$ does not divide $(n-k)$ !;\n(b) if $n>2 p_{k}$, then $n$ divides $(n-k)$ !.", "solution": "(a) Note that $n-k=2 p_{k}-k<2 p_{k}-p_{k}=p_{k}$, so $p_{k} \\nmid(n-k)$ !, so $2 p_{k} \\nless(n-k)$ !. [1 mark]\n(b) Note that $n>2 p_{k} \\geq 3 k / 2$ implies $k<2 n / 3$, so $n-k>n / 3$. So if we can find integers $a, b \\geq 3$ such that $n=a b$ and $a \\neq b$, then both $a$ and $b$ will appear separately in the product $(n-k)!=1 \\times 2 \\times \\cdots \\times(n-k)$, which means $n \\mid(n-k)!$. Observe that $k \\geq 14$ implies $p_{k} \\geq 13$, so that $n>2 p_{k} \\geq 26$.\n\nIf $n=2^{\\alpha}$ for some integer $\\alpha \\geq 5$, then take $a=2^{2}, b=2^{\\alpha-2}$. [ 1 mark] Otherwise, since $n \\geq 26>16$, we can take $a$ to be an odd prime factor of $n$ and $b=n / a$ [1 mark], unless $b<3$ or $b=a$.\n\nCase (i): $b<3$. Since $n$ is composite, this means $b=2$, so that $2 a=n>2 p_{k}$. As $a$ is a prime number and $p_{k}$ is the largest prime number which is strictly less than $k$, it follows that $a \\geq k$. From $n-k=2 a-k \\geq$ $2 a-a=a>2$ we see that $n=2 a$ divides into $(n-k)$. [ 2 marks]\n\nCase (ii): $b=a$. Then $n=a^{2}$ and $a>6$ since $n \\geq 26$. Thus $n-k>n / 3=a^{2} / 3>2 a$, so that both $a$ and $2 a$ appear among $\\{1,2, \\ldots, n-k\\}$. Hence $n=a^{2}$ divides into $(n-k)!$. [2 marks]", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2003", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $a, b, c$ be the sides of a triangle, with $a+b+c=1$, and let $n \\geq 2$ be an integer. Show that\n\n$$\n\\sqrt[n]{a^{n}+b^{n}}+\\sqrt[n]{b^{n}+c^{n}}+\\sqrt[n]{c^{n}+a^{n}}<1+\\frac{\\sqrt[n]{2}}{2}\n$$", "solution": "Without loss of generality, assume $a \\leq b \\leq c$. As $a+b>c$, we have\n\n$$\n\\frac{\\sqrt[n]{2}}{2}=\\frac{\\sqrt[n]{2}}{2}(a+b+c)>\\frac{\\sqrt[n]{2}}{2}(c+c)=\\sqrt[n]{2 c^{n}} \\geq \\sqrt[n]{b^{n}+c^{n}} \\quad \\quad[2 \\text { marks }]\n$$\n\nAs $a \\leq c$ and $n \\geq 2$, we have\n\n$$\n\\begin{aligned}\n\\left(c^{n}+a^{n}\\right)-\\left(c+\\frac{a}{2}\\right)^{n} & =a^{n}-\\sum_{k=1}^{n}\\binom{n}{k} c^{n-k}\\left(\\frac{a}{2}\\right)^{k} \\\\\n& \\leq\\left[1-\\sum_{k=1}^{n}\\binom{n}{k}\\left(\\frac{1}{2}\\right)^{k}\\right] a^{n} \\quad\\left(\\text { since } c^{n-k} \\geq a^{n-k}\\right) \\\\\n& =\\left[\\left(1-\\frac{n}{2}\\right)-\\sum_{k=2}^{n}\\binom{n}{k}\\left(\\frac{1}{2}\\right)^{k}\\right] a^{n}<0\n\\end{aligned}\n$$\n\nThus\n\n$$\n\\sqrt[n]{c^{n}+a^{n}}<c+\\frac{a}{2} . \\quad[3 \\text { marks }]\n$$\n\nLikewise\n\n$$\n\\sqrt[n]{b^{n}+a^{n}}<b+\\frac{a}{2} \\quad \\quad[1 \\text { mark }]\n$$\n\nAdding (1), (2) and (3), we get\n\n$$\n\\sqrt[n]{a^{n}+b^{n}}+\\sqrt[n]{b^{n}+c^{n}}+\\sqrt[n]{c^{n}+a^{n}}<\\frac{\\sqrt[n]{2}}{2}+c+\\frac{a}{2}+b+\\frac{a}{2}=1+\\frac{\\sqrt[n]{2}}{2} . \\quad[1 \\text { mark }]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n4. ", "solution_match": "# Solution."}}
|
| 7 |
-
{"year": "2003", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Given two positive integers $m$ and $n$, find the smallest positive integer $k$ such that among any $k$ people, either there are $2 m$ of them who form $m$ pairs of mutually acquainted people or there are $2 n$ of them forming $n$ pairs of mutually unacquainted people.", "solution": "Let the smallest positive integer $k$ satisfying the condition of the problem be denoted $r(m, n)$. We shall show that\n\n$$\nr(m, n)=2(m+n)-\\min \\{m, n\\}-1\n$$\n\nObserve that, by symmetry, $r(m, n)=r(n, m)$. Therefore it suffices to consider the case where $m \\geq n$, and to prove that\n\n$$\nr(m, n)=2 m+n-1 . \\quad[1 \\text { mark }]\n$$\n\nFirst we prove that\n\n$$\nr(m, n) \\geq 2 m+n-1\n$$\n\nby an example. Call a group of $k$ people, every two of whom are mutually acquainted, a $k$-clique. Consider a set of $2 m+n-2$ people consisting of a $(2 m-1)$-clique together with an additional $n-1$ people none of whom know anyone else. (Call such people isolated.) Then there are not $2 m$ people forming $m$ mutually acquainted pairs, and there also are not $2 n$ people forming $n$ mutually unacquainted pairs. Thus $r(m, n) \\geq$ $(2 m-1)+(n-1)+1=2 m+n-1$ by the definition of $r(m, n)$. [1 mark]\n\nTo establish (1), we need to prove that $r(m, n) \\leq 2 m+n-1$. To do this, we now show that\n\n$$\nr(m, n) \\leq r(m-1, n-1)+3 \\quad \\text { for all } m \\geq n \\geq 2\n$$\n\nLet $G$ be a group of $t=r(m-1, n-1)+3$ people. Notice that\n\n$$\nt \\geq 2(m-1)+(n-1)-1+3=2 m+n-1 \\geq 2 m \\geq 2 n\n$$\n\nIf $G$ is a $t$-clique, then $G$ contains $2 m$ people forming $m$ mutually acquainted pairs, and if $G$ has only isolated people, then $G$ contains $2 n$ people forming $n$ mutually unacquainted pairs. Otherwise, there are three people in $G$, say $a, b$ and $c$, such that $a, b$ are acquainted but $a, c$ are not. Now consider the group $A$ obtained byremoving $a, b$ and $c$ from $G$. A has $t-3=r(m-1, n-1)$ people, so by the definition of $r(m-1, n-1)$, A either contains $2(m-1)$ people forming $m-1$ mutually acquainted pairs, or else contains $2(n-1)$ people forming $n-1$ mutually unacquainted pairs. In the former case, we add the acquainted pair $a, b$ to $A$ to form $m$ mutually acquainted pairs in $G$. In the latter case, we add the unacquainted pair $a, c$ to $A$ to form $n$ mutually unacquainted pairs in $G$. This proves (2). [3 marks]\n\nTrivially, $r(s, 1)=2 s$ for all $s[\\mathbf{1}$ mark], so $r(m, n) \\leq 2 m+n-1$ holds whenever $n=1$. Proceeding by induction on $n$, by (2) we obtain\n\n$$\nr(m, n) \\leq r(m-1, n-1)+3 \\leq 2(m-1)+(n-1)-1+3=2 m+n-1\n$$\n\nwhich completes the proof. [1 mark]\nNote. Give an additional 1 mark to any student who gets at most 5 marks by the above marking scheme, but in addition gives a valid argument that $r(2,2)=5$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution."}}
|
|
|
|
| 1 |
+
{"year": "2003", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c, d, e, f$ be real numbers such that the polynomial\n\n$$\np(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f\n$$\n\nfactorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \\ldots, 8$. Determine all possible values of $f$.", "solution": "From\n\n$$\nx^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\\left(x-x_{1}\\right)\\left(x-x_{2}\\right) \\ldots\\left(x-x_{8}\\right)\n$$\n\nwe have\n\n$$\n\\sum_{i=1}^{8} x_{i}=4 \\quad \\text { and } \\quad \\sum x_{i} x_{j}=7\n$$\n\nwhere the second sum is over all pairs $(i, j)$ of integers where $1 \\leq i<j \\leq 8$. Since this sum can also be written\n\n$$\n\\frac{1}{2}\\left[\\left(\\sum_{i=1}^{8} x_{i}\\right)^{2}-\\sum_{i=1}^{8} x_{i}^{2}\\right]\n$$\n\nwe get\n\n$$\n14=\\left(\\sum_{i=1}^{8} x_{i}\\right)^{2}-\\sum_{i=1}^{8} x_{i}^{2}=16-\\sum_{i=1}^{8} x_{i}^{2}\n$$\n\nso\n\n$$\n\\sum_{i=1}^{8} x_{i}^{2}=2 \\quad \\text { while } \\quad \\sum_{i=1}^{8} x_{i}=4 . \\quad[3 \\text { marks }]\n$$\n\nNow\n\n$$\n\\sum_{i=1}^{8}\\left(2 x_{i}-1\\right)^{2}=4 \\sum_{i=1}^{8} x_{i}^{2}-4 \\sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0\n$$\n\nwhich forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore\n\n$$\nf=\\prod_{i=1}^{8} x_{i}=\\left(\\frac{1}{2}\\right)^{8}=\\frac{1}{256} . \\quad[1 m x]\n$$\n\nAlternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get\n\n$$\n16=\\left(x_{1} \\cdot 1+x_{2} \\cdot 1+\\cdots+x_{8} \\cdot 1\\right)^{2} \\leq\\left(x_{1}^{2-}+x_{2}^{2}+\\cdots+x_{8}^{2}\\right)\\left(1^{2}+1^{2}+\\cdots+1^{2}\\right)=8 \\cdot 2=16\n$$\n\nor the power mean inequality to get\n\n$$\n\\frac{1}{2}=\\frac{1}{8} \\sum_{i=1}^{8} x_{i} \\leq\\left(\\frac{1}{8} \\sum_{i=1}^{8} x_{i}^{2}\\right)^{1 / 2}=\\frac{1}{2} . \\quad[2 \\text { marks }]\n$$\n\nEither way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n1. ", "solution_match": "# Solution."}}
|
| 2 |
+
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Let $E H$ intersect $F G$ at $O$. The distance from $G$ to line $F D$ and line $E F$ are both $a$. So $F G$ bisects $\\angle E F D$. Similarly, $E H$ bisects $\\angle B E F$. So $O$ is an excentre of $\\triangle A E F$. Similarly, $O$ is an excentre of $\\triangle C G H$. [2 marks] Construct these excircles with centre $O$. Let $M, N, P, Q$ be on sides $A B, B C, C D, D A$ respectively, where these excircles touch the square. Then $O M \\perp A B, O N \\perp B C, O P \\perp C D$, and $O Q \\perp D A$. Since $A B \\| C D$ and $A D \\| B C, M, O, P$ are collinear and $N, O, Q$ are collinear. Now $M P=N Q=a$. [2 marks] Using the fact that the two tangents from a point to a circle have the same length, we get $E F=E M+F Q$ and $G H=G N+H P$. [1 mark] Then\n\n$$\nm_{1}=A E+A F+E F=A E+A F+(E M+F Q)=A M+A Q=O Q+O M\n$$\n\nand\n\n$$\nm_{2}=C G+C H+G H=C G+C H+(G N+H P)=C N+C P=O P+O N . \\quad[1 \\text { mark }]\n$$\n\nTherefore\n\n$$\nm_{1}+m_{2}=(O Q+O M)+(O P+O N)=M P+N Q=2 a . \\quad[1 \\mathrm{mark}]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
+
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Extend $A B$ to $I$ and $D C$ to $J$ so that $A E=B I=C J$. Let $\\ell_{2}$ intersect $I J$ at $M$, and let $K$ lie on $I J$ so that $G K \\perp I J$. Then, since $A E=G K, \\triangle A E F$ and $\\triangle K G M$ are congruent. [1 mark] Thus, since $G K=C J$ and $G C=K J$,\n\n$$\nm_{1}+m_{2}=\\operatorname{perimeter}(K G M)+\\operatorname{perimeter}(C G H)=\\operatorname{perimeter}(H M J) . \\quad[\\mathbf{2} \\text { marks }]\n$$\n\nLet $L$ lie on $C D$ so that $E L \\perp C D$. Then a circle with centre $E$ and radius $a$ will touch $D C$ at $L, I J$ at $I$, and the interior of $H M$ at some point $N$, so\n\n$$\n\\operatorname{perimeter}(H M J)=J H+(H N+N M)+J M=(J H+H L)+(M I+J M)=J L+I J=a+a=2 a\n$$\n\n[4 marks] Thus $m_{1}+m_{2}=2 a$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "# Solution 2."}}
|
| 4 |
+
{"year": "2003", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\\ell_{1}$ and $\\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\\triangle A E F$ and $\\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.", "solution": "Without loss of generality, assume the square has side $a=1$. Let $\\theta$ be the acute angle between $\\ell_{1}$ (or $\\ell_{2}$ ) and the sides $A B$ and $C D$ of the square. Then, letting $E F=x$ and $G H=y$, we have\n\n$$\nE A=x \\cos \\theta, \\quad A F=x \\sin \\theta, \\quad C H=y \\cos \\theta, \\quad C G=y \\sin \\theta\n$$\n\nThus\n\n$$\nm_{1}+m_{2}=(x+y)(\\sin \\theta+\\cos \\theta+1) . \\quad[2 \\text { marks }]\n$$\n\nDraw lines parallel to $\\ell_{1}, \\ell_{2}$ through $A$ and $C$ respectively. The distance between these lines is $\\sin \\theta+\\cos \\theta$ [1 mark], as can be seen by drawing a mutual perpendicular to these lines through $B$, say. Also, the altitudes from $A$ to $E F$ and from $C$ to $G H$ have lengths $x \\sin \\theta \\cos \\theta$ and $y \\sin \\theta \\cos \\theta$ respectively [ 1 mark]. Therefore the distance between $\\ell_{1}$ and $\\ell_{2}$ must be\n\n$$\n(\\sin \\theta+\\cos \\theta)-x \\sin \\theta \\cos \\theta-y \\sin \\theta \\cos \\theta\n$$\n\nBut we are given that this distance is $a=1$, so\n\n$$\n(x+y) \\sin \\theta \\cos \\theta+1=\\sin \\theta+\\cos \\theta\n$$\n\nor\n\n$$\nx+y=\\frac{\\sin \\theta+\\cos \\theta-1}{\\sin \\theta \\cos \\theta} \\cdot \\quad[1 \\text { mark }]\n$$\n\nTherefore, by (1),\n\n$$\n\\begin{aligned}\nm_{1}+m_{2} & =\\frac{(\\sin \\theta+\\cos \\theta-1)(\\sin \\theta+\\cos \\theta+1)}{\\sin \\theta \\cos \\theta} \\\\\n& =\\frac{\\left(\\sin ^{2} \\theta+\\cos ^{2} \\theta+2 \\sin \\theta \\cos \\theta\\right)-1}{\\sin \\theta \\cos \\theta} \\\\\n& =\\frac{1+2 \\sin \\theta \\cos \\theta-1}{\\sin \\theta \\cos \\theta}=2 . \\quad[2 \\text { marks }]\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 3."}}
|
| 5 |
+
{"year": "2003", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $k \\geq 14$ be an integer, and let $p_{k}$ be the largest prime number which is strictly less than $k$. You may assume that $p_{k} \\geq 3 k / 4$. Let $n$ be a composite integer. Prove:\n(a) if $n=2 p_{k}$, then $n$ does not divide $(n-k)$ !;\n(b) if $n>2 p_{k}$, then $n$ divides $(n-k)$ !.", "solution": "(a) Note that $n-k=2 p_{k}-k<2 p_{k}-p_{k}=p_{k}$, so $p_{k} \\nmid(n-k)$ !, so $2 p_{k} \\nless(n-k)$ !. [1 mark]\n(b) Note that $n>2 p_{k} \\geq 3 k / 2$ implies $k<2 n / 3$, so $n-k>n / 3$. So if we can find integers $a, b \\geq 3$ such that $n=a b$ and $a \\neq b$, then both $a$ and $b$ will appear separately in the product $(n-k)!=1 \\times 2 \\times \\cdots \\times(n-k)$, which means $n \\mid(n-k)!$. Observe that $k \\geq 14$ implies $p_{k} \\geq 13$, so that $n>2 p_{k} \\geq 26$.\n\nIf $n=2^{\\alpha}$ for some integer $\\alpha \\geq 5$, then take $a=2^{2}, b=2^{\\alpha-2}$. [ 1 mark] Otherwise, since $n \\geq 26>16$, we can take $a$ to be an odd prime factor of $n$ and $b=n / a$ [1 mark], unless $b<3$ or $b=a$.\n\nCase (i): $b<3$. Since $n$ is composite, this means $b=2$, so that $2 a=n>2 p_{k}$. As $a$ is a prime number and $p_{k}$ is the largest prime number which is strictly less than $k$, it follows that $a \\geq k$. From $n-k=2 a-k \\geq$ $2 a-a=a>2$ we see that $n=2 a$ divides into $(n-k)$. [ 2 marks]\n\nCase (ii): $b=a$. Then $n=a^{2}$ and $a>6$ since $n \\geq 26$. Thus $n-k>n / 3=a^{2} / 3>2 a$, so that both $a$ and $2 a$ appear among $\\{1,2, \\ldots, n-k\\}$. Hence $n=a^{2}$ divides into $(n-k)!$. [2 marks]", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2003", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c$ be the sides of a triangle, with $a+b+c=1$, and let $n \\geq 2$ be an integer. Show that\n\n$$\n\\sqrt[n]{a^{n}+b^{n}}+\\sqrt[n]{b^{n}+c^{n}}+\\sqrt[n]{c^{n}+a^{n}}<1+\\frac{\\sqrt[n]{2}}{2}\n$$", "solution": "Without loss of generality, assume $a \\leq b \\leq c$. As $a+b>c$, we have\n\n$$\n\\frac{\\sqrt[n]{2}}{2}=\\frac{\\sqrt[n]{2}}{2}(a+b+c)>\\frac{\\sqrt[n]{2}}{2}(c+c)=\\sqrt[n]{2 c^{n}} \\geq \\sqrt[n]{b^{n}+c^{n}} \\quad \\quad[2 \\text { marks }]\n$$\n\nAs $a \\leq c$ and $n \\geq 2$, we have\n\n$$\n\\begin{aligned}\n\\left(c^{n}+a^{n}\\right)-\\left(c+\\frac{a}{2}\\right)^{n} & =a^{n}-\\sum_{k=1}^{n}\\binom{n}{k} c^{n-k}\\left(\\frac{a}{2}\\right)^{k} \\\\\n& \\leq\\left[1-\\sum_{k=1}^{n}\\binom{n}{k}\\left(\\frac{1}{2}\\right)^{k}\\right] a^{n} \\quad\\left(\\text { since } c^{n-k} \\geq a^{n-k}\\right) \\\\\n& =\\left[\\left(1-\\frac{n}{2}\\right)-\\sum_{k=2}^{n}\\binom{n}{k}\\left(\\frac{1}{2}\\right)^{k}\\right] a^{n}<0\n\\end{aligned}\n$$\n\nThus\n\n$$\n\\sqrt[n]{c^{n}+a^{n}}<c+\\frac{a}{2} . \\quad[3 \\text { marks }]\n$$\n\nLikewise\n\n$$\n\\sqrt[n]{b^{n}+a^{n}}<b+\\frac{a}{2} \\quad \\quad[1 \\text { mark }]\n$$\n\nAdding (1), (2) and (3), we get\n\n$$\n\\sqrt[n]{a^{n}+b^{n}}+\\sqrt[n]{b^{n}+c^{n}}+\\sqrt[n]{c^{n}+a^{n}}<\\frac{\\sqrt[n]{2}}{2}+c+\\frac{a}{2}+b+\\frac{a}{2}=1+\\frac{\\sqrt[n]{2}}{2} . \\quad[1 \\text { mark }]\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n4. ", "solution_match": "# Solution."}}
|
| 7 |
+
{"year": "2003", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Given two positive integers $m$ and $n$, find the smallest positive integer $k$ such that among any $k$ people, either there are $2 m$ of them who form $m$ pairs of mutually acquainted people or there are $2 n$ of them forming $n$ pairs of mutually unacquainted people.", "solution": "Let the smallest positive integer $k$ satisfying the condition of the problem be denoted $r(m, n)$. We shall show that\n\n$$\nr(m, n)=2(m+n)-\\min \\{m, n\\}-1\n$$\n\nObserve that, by symmetry, $r(m, n)=r(n, m)$. Therefore it suffices to consider the case where $m \\geq n$, and to prove that\n\n$$\nr(m, n)=2 m+n-1 . \\quad[1 \\text { mark }]\n$$\n\nFirst we prove that\n\n$$\nr(m, n) \\geq 2 m+n-1\n$$\n\nby an example. Call a group of $k$ people, every two of whom are mutually acquainted, a $k$-clique. Consider a set of $2 m+n-2$ people consisting of a $(2 m-1)$-clique together with an additional $n-1$ people none of whom know anyone else. (Call such people isolated.) Then there are not $2 m$ people forming $m$ mutually acquainted pairs, and there also are not $2 n$ people forming $n$ mutually unacquainted pairs. Thus $r(m, n) \\geq$ $(2 m-1)+(n-1)+1=2 m+n-1$ by the definition of $r(m, n)$. [1 mark]\n\nTo establish (1), we need to prove that $r(m, n) \\leq 2 m+n-1$. To do this, we now show that\n\n$$\nr(m, n) \\leq r(m-1, n-1)+3 \\quad \\text { for all } m \\geq n \\geq 2\n$$\n\nLet $G$ be a group of $t=r(m-1, n-1)+3$ people. Notice that\n\n$$\nt \\geq 2(m-1)+(n-1)-1+3=2 m+n-1 \\geq 2 m \\geq 2 n\n$$\n\nIf $G$ is a $t$-clique, then $G$ contains $2 m$ people forming $m$ mutually acquainted pairs, and if $G$ has only isolated people, then $G$ contains $2 n$ people forming $n$ mutually unacquainted pairs. Otherwise, there are three people in $G$, say $a, b$ and $c$, such that $a, b$ are acquainted but $a, c$ are not. Now consider the group $A$ obtained byremoving $a, b$ and $c$ from $G$. A has $t-3=r(m-1, n-1)$ people, so by the definition of $r(m-1, n-1)$, A either contains $2(m-1)$ people forming $m-1$ mutually acquainted pairs, or else contains $2(n-1)$ people forming $n-1$ mutually unacquainted pairs. In the former case, we add the acquainted pair $a, b$ to $A$ to form $m$ mutually acquainted pairs in $G$. In the latter case, we add the unacquainted pair $a, c$ to $A$ to form $n$ mutually unacquainted pairs in $G$. This proves (2). [3 marks]\n\nTrivially, $r(s, 1)=2 s$ for all $s[\\mathbf{1}$ mark], so $r(m, n) \\leq 2 m+n-1$ holds whenever $n=1$. Proceeding by induction on $n$, by (2) we obtain\n\n$$\nr(m, n) \\leq r(m-1, n-1)+3 \\leq 2(m-1)+(n-1)-1+3=2 m+n-1\n$$\n\nwhich completes the proof. [1 mark]\nNote. Give an additional 1 mark to any student who gets at most 5 marks by the above marking scheme, but in addition gives a valid argument that $r(2,2)=5$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl", "problem_match": "\n5. ", "solution_match": "# Solution."}}
|
APMO/segmented/en-apmo2004_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2004", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Determine all finite nonempty sets $S$ of positive integers satisfying\n\n$$\n\\frac{i+j}{(i, j)} \\text { is an element of } S \\text { for all } i, j \\text { in } S \\text {, }\n$$\n\nwhere $(i, j)$ is the greatest common divisor of $i$ and $j$.\nAnswer: $S=\\{2\\}$.", "solution": "Let $k \\in S$. Then $\\frac{k+k}{(k, k)}=2$ is in $S$ as well.\nSuppose for the sake of contradiction that there is an odd number in $S$, and let $k$ be the largest such odd number. Since $(k, 2)=1, \\frac{k+2}{(k, 2)}=k+2>k$ is in $S$ as well, a contradiction. Hence $S$ has no odd numbers.\nNow suppose that $\\ell>2$ is the second smallest number in $S$. Then $\\ell$ is even and $\\frac{\\ell+2}{(\\ell, 2)}=\\frac{\\ell}{2}+1$ is in $S$. Since $\\ell>2 \\Longrightarrow \\frac{\\ell}{2}+1>2, \\frac{\\ell}{2}+1 \\geq \\ell \\Longleftrightarrow \\ell \\leq 2$, a contradiction again.\nTherefore $S$ can only contain 2 , and $S=\\{2\\}$ is the only solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
-
{"year": "2004", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\\mathrm{AOH}, \\mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.", "solution": "Suppose, without loss of generality, that $B$ and $C$ lies in the same side of line $O H$. Such line is the Euler line of $A B C$, so the centroid $G$ lies in this line.\n\n\nLet $M$ be the midpoint of $B C$. Then the distance between $M$ and the line $O H$ is the average of the distances from $B$ and C to OH , and the sum of the areas of triangles BOH and COH is\n\n$$\n[B O H]+[C O H]=\\frac{O H \\cdot d(B, O H)}{2}+\\frac{O H \\cdot d(C, O H)}{2}=\\frac{O H \\cdot 2 d(M, O H)}{2} .\n$$\n\nSince $A G=2 G M, d(A, O H)=2 d(M, O H)$. Hence\n\n$$\n[B O H]+[C O H]=\\frac{O H \\cdot d(A, O H)}{2}=[A O H]\n$$\n\nand the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 1"}}
|
| 3 |
-
{"year": "2004", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\\mathrm{AOH}, \\mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.", "solution": "One can use barycentric coordinates: it is well known that\n\n$$\n\\begin{gathered}\nA=(1: 0: 0), \\quad B=(0: 1: 0), \\quad C=(0: 0: 1), \\\\\nO=(\\sin 2 A: \\sin 2 B: \\sin 2 C) \\quad \\text { and } \\quad H=(\\tan A: \\tan B: \\tan C) .\n\\end{gathered}\n$$\n\nThen the (signed) area of $A O H$ is proportional to\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 0 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nAdding all three expressions we find that the sum of the signed sums of the areas is a constant times\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 0 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|+\\left|\\begin{array}{ccc}\n0 & 1 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|+\\left|\\begin{array}{ccc}\n0 & 0 & 1 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nBy multilinearity of the determinant, this sum equals\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 1 & 1 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nwhich contains, in its rows, the coordinates of the centroid, the circumcenter, and the orthocenter. Since these three points lie in the Euler line of $A B C$, the signed sum of the areas is 0 , which means that one of the areas of $A O H, B O H, C O H$ is the sum of the other two areas.\nComment: Both solutions can be adapted to prove a stronger result: if the centroid $G$ of triangle $A B C$ belongs to line $X Y$ then one of the areas of triangles $A X Y, B X Y$, and $C X Y$ is equal to the sum of the other two.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 2"}}
|
| 4 |
-
{"year": "2004", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let a set $S$ of 2004 points in the plane be given, no three of which are collinear. Let $\\mathcal{L}$ denote the set of all lines (extended indefinitely in both directions) determined by pairs of points from the set. Show that it is possible to colour the points of $S$ with at most two colours, such that for any points $p, q$ of $S$, the number of lines in $\\mathcal{L}$ which separate $p$ from $q$ is odd if and only if $p$ and $q$ have the same colour.\nNote: A line $\\ell$ separates two points $p$ and $q$ if $p$ and $q$ lie on opposite sides of $\\ell$ with neither point on $\\ell$.", "solution": "Choose any point $p$ from $S$ and color it, say, blue. Let $n(q, r)$ be the number of lines from $\\mathcal{L}$ that separates $q$ and $r$. Then color any other point $q$ blue if $n(p, q)$ is odd and red if $n(p, q)$ is even.\nNow it remains to show that $q$ and $r$ have the same color if and only if $n(q, r)$ is odd for all $q \\neq p$ and $r \\neq p$, which is equivalent to proving that $n(p, q)+n(p, r)+n(q, r)$ is always odd. For this purpose, consider the seven numbered regions defined by lines $p q$, $p r$, and $q r$ :\n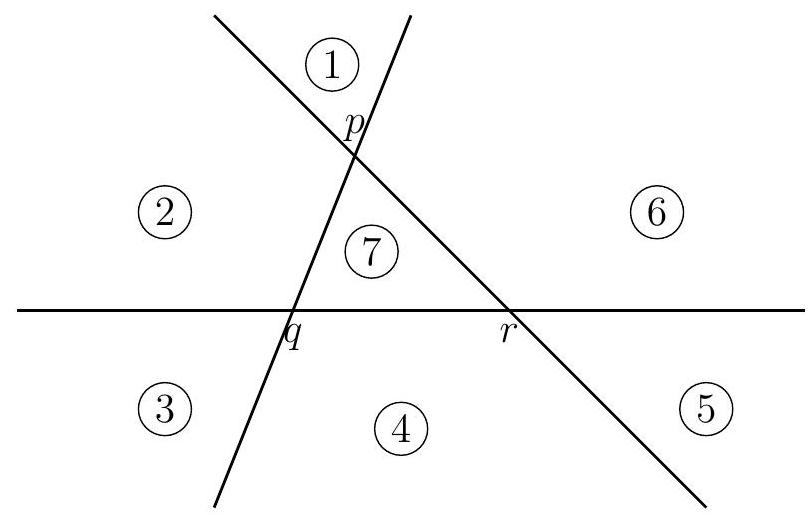\n\nAny line that do not pass through any of points $p, q, r$ meets the sides $p q, q r, p r$ of triangle $p q r$ in an even number of points (two sides or no sides), so these lines do not affect the parity of $n(p, q)+n(p, r)+n(q, r)$. Hence the only lines that need to be considered are the ones that pass through one of vertices $p, q, r$ and cuts the opposite side in the triangle $p q r$.\nLet $n_{i}$ be the number of points in region $i, p, q$, and $r$ excluded, as depicted in the diagram. Then the lines through $p$ that separate $q$ and $r$ are the lines passing through $p$ and points from regions 1,4 , and 7 . The same applies for $p, q$ and regions 2,5 , and 7 ; and $p, r$ and regions 3,6 , and 7. Therefore\n\n$$\n\\begin{aligned}\nn(p, q)+n(q, r)+n(p, r) & \\equiv\\left(n_{2}+n_{5}+n_{7}\\right)+\\left(n_{1}+n_{4}+n_{7}\\right)+\\left(n_{3}+n_{6}+n_{7}\\right) \\\\\n& \\equiv n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}+n_{7}=2004-3 \\equiv 1 \\quad(\\bmod 2)\n\\end{aligned}\n$$\n\nand the result follows.\nComment: The problem statement is also true if 2004 is replaced by any even number and is not true if 2004 is replaced by any odd number greater than 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "2004", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "For a real number $x$, let $\\lfloor x\\rfloor$ stand for the largest integer that is less than or equal to $x$. Prove that\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor\n$$\n\nis even for every positive integer $n$.", "solution": "Consider four cases:\n\n- $n \\leq 5$. Then $\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=0$ is an even number.\n- $n$ and $n+1$ are both composite (in particular, $n \\geq 8$ ). Then $n=a b$ and $n+1=c d$ for $a, b, c, d \\geq 2$. Moreover, since $n$ and $n+1$ are coprime, $a, b, c, d$ are all distinct and smaller than $n$, and one can choose $a, b, c, d$ such that exactly one of these four numbers is even. Hence $\\frac{(n-1)!}{n(n+1)}$ is an integer. As $n \\geq 8>6,(n-1)!$ has at least three even factors, so $\\frac{(n-1)!}{n(n+1)}$ is an even integer.\n- $n \\geq 7$ is an odd prime. By Wilson's theorem, $(n-1)!\\equiv-1(\\bmod n)$, that is, $\\frac{(n-1)!+1}{n}$ is an integer, as $\\frac{(n-1)!+n+1}{n}=\\frac{(n-1)!+1}{n}+1$ is. As before, $\\frac{(n-1)!}{n+1}$ is an even integer; therefore $\\frac{(n-1)!+n+1}{n+1}=\\frac{(n-1)!}{n+1}+1$ is an odd integer.\nAlso, $n$ and $n+1$ are coprime and $n$ divides the odd integer $\\frac{(n-1)!+n+1}{n+1}$, so $\\frac{(n-1)!+n+1}{n(n+1)}$ is also an odd integer. Then\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=\\frac{(n-1)!+n+1}{n(n+1)}-1\n$$\n\nis even.\n\n- $n+1 \\geq 7$ is an odd prime. Again, since $n$ is composite, $\\frac{(n-1)!}{n}$ is an even integer, and $\\frac{(n-1)!+n}{n}$ is an odd integer. By Wilson's theorem, $n!\\equiv-1(\\bmod n+1) \\Longleftrightarrow(n-1)!\\equiv 1$ $(\\bmod n+1)$. This means that $n+1$ divides $(n-1)!+n$, and since $n$ and $n+1$ are coprime, $n+1$ also divides $\\frac{(n-1)!+n}{n}$. Then $\\frac{(n-1)!+n}{n(n+1)}$ is also an odd integer and\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=\\frac{(n-1)!+n}{n(n+1)}-1\n$$\n\nis even.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
-
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "Let $p=a+b+c, q=a b+b c+c a$, and $r=a b c$. The inequality simplifies to\n\n$$\na^{2} b^{2} c^{2}+2\\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\\right)+4\\left(a^{2}+b^{2}+c^{2}\\right)+8-9(a b+b c+c a) \\geq 0\n$$\n\nSince $a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}=q^{2}-2 p r$ and $a^{2}+b^{2}+c^{2}=p^{2}-2 q$,\n\n$$\nr^{2}+2 q^{2}-4 p r+4 p^{2}-8 q+8-9 q \\geq 0\n$$\n\nwhich simplifies to\n\n$$\nr^{2}+2 q^{2}+4 p^{2}-17 q-4 p r+8 \\geq 0\n$$\n\nBearing in mind that equality occurs for $a=b=c=1$, which means that, for instance, $p=3 r$, one can rewrite $(I)$ as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}-\\frac{10}{3} p r+\\frac{35}{9} p^{2}+2 q^{2}-17 q+8 \\geq 0\n$$\n\nSince $(a b-b c)^{2}+(b c-c a)^{2}+(c a-a b)^{2} \\geq 0$ is equivalent to $q^{2} \\geq 3 p r$, rewrite $(I I)$ as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}+\\frac{10}{9}\\left(q^{2}-3 p r\\right)+\\frac{35}{9} p^{2}+\\frac{8}{9} q^{2}-17 q+8 \\geq 0\n$$\n\nFinally, $a=b=c=1$ implies $q=3$; then rewrite (III) as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}+\\frac{10}{9}\\left(q^{2}-3 p r\\right)+\\frac{35}{9}\\left(p^{2}-3 q\\right)+\\frac{8}{9}(q-3)^{2} \\geq 0\n$$\n\nThis final inequality is true because $q^{2} \\geq 3 p r$ and $p^{2}-3 q=\\frac{1}{2}\\left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\\right] \\geq 0$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 7 |
-
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "We prove the stronger inequality\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 3(a+b+c)^{2}\n$$\n\nwhich implies the proposed inequality because $(a+b+c)^{2} \\geq 3(a b+b c+c a)$ is equivalent to $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \\geq 0$, which is immediate.\nThe inequality $(*)$ is equivalent to\n\n$$\n\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right) a^{2}-6(b+c) a+2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3(b+c)^{2} \\geq 0\n$$\n\nSeeing this inequality as a quadratic inequality in $a$ with positive leading coefficient $\\left(b^{2}+2\\right)\\left(c^{2}+\\right.$ 2) $-3=b^{2} c^{2}+2 b^{2}+2 c^{2}+1$, it suffices to prove that its discriminant is non-positive, which is equivalent to\n\n$$\n(3(b+c))^{2}-\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right)\\left(2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3(b+c)^{2}\\right) \\leq 0\n$$\n\nThis simplifies to\n\n$$\n-2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)+3(b+c)^{2}+6 \\leq 0\n$$\n\nNow we look $(* *)$ as a quadratic inequality in $b$ with negative leading coefficient $-2 c^{2}-1$ :\n\n$$\n\\left(-2 c^{2}-1\\right) b^{2}+6 c b-c^{2}-2 \\leq 0\n$$\n\nIf suffices to show that the discriminant of $(* *)$ is non-positive, which is equivalent to\n\n$$\n9 c^{2}-\\left(2 c^{2}+1\\right)\\left(c^{2}+2\\right) \\leq 0\n$$\n\nIt simplifies to $-2\\left(c^{2}-1\\right)^{2} \\leq 0$, which is true. The equality occurs for $c^{2}=1$, that is, $c=1$, for which $b=\\frac{6 c}{2\\left(2 c^{2}+1\\right)}=1$, and $a=\\frac{6(b+c)}{2\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right)}=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
| 8 |
-
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "Let $A, B, C$ angles in $(0, \\pi / 2)$ such that $a=\\sqrt{2} \\tan A, b=\\sqrt{2} \\tan B$, and $c=\\sqrt{2} \\tan C$. Then the inequality is equivalent to\n\n$$\n4 \\sec ^{2} A \\sec ^{2} B \\sec ^{2} C \\geq 9(\\tan A \\tan B+\\tan B \\tan C+\\tan C \\tan A)\n$$\n\nSubstituting $\\sec x=\\frac{1}{\\cos x}$ for $x \\in\\{A, B, C\\}$ and clearing denominators, the inequality is equivalent to\n\n$$\n\\cos A \\cos B \\cos C(\\sin A \\sin B \\cos C+\\cos A \\sin B \\sin C+\\sin A \\cos B \\sin C) \\leq \\frac{4}{9}\n$$\n\nSince\n\n$$\n\\begin{aligned}\n& \\cos (A+B+C)=\\cos A \\cos (B+C)-\\sin A \\sin (B+C) \\\\\n= & \\cos A \\cos B \\cos C-\\cos A \\sin B \\sin C-\\sin A \\cos B \\sin C-\\sin A \\sin B \\cos C,\n\\end{aligned}\n$$\n\nwe rewrite our inequality as\n\n$$\n\\cos A \\cos B \\cos C(\\cos A \\cos B \\cos C-\\cos (A+B+C)) \\leq \\frac{4}{9}\n$$\n\nThe cosine function is concave down on $(0, \\pi / 2)$. Therefore, if $\\theta=\\frac{A+B+C}{3}$, by the AM-GM inequality and Jensen's inequality,\n\n$$\n\\cos A \\cos B \\cos C \\leq\\left(\\frac{\\cos A+\\cos B+\\cos C}{3}\\right)^{3} \\leq \\cos ^{3} \\frac{A+B+C}{3}=\\cos ^{3} \\theta\n$$\n\nTherefore, since $\\cos A \\cos B \\cos C-\\cos (A+B+C)=\\sin A \\sin B \\cos C+\\cos A \\sin B \\sin C+$ $\\sin A \\cos B \\sin C>0$, and recalling that $\\cos 3 \\theta=4 \\cos ^{3} \\theta-3 \\cos \\theta$,\n$\\cos A \\cos B \\cos C(\\cos A \\cos B \\cos C-\\cos (A+B+C)) \\leq \\cos ^{3} \\theta\\left(\\cos ^{3} \\theta-\\cos 3 \\theta\\right)=3 \\cos ^{4} \\theta\\left(1-\\cos ^{2} \\theta\\right)$. Finally, by AM-GM (notice that $1-\\cos ^{2} \\theta=\\sin ^{2} \\theta>0$ ),\n$3 \\cos ^{4} \\theta\\left(1-\\cos ^{2} \\theta\\right)=\\frac{3}{2} \\cos ^{2} \\theta \\cdot \\cos ^{2} \\theta\\left(2-2 \\cos ^{2} \\theta\\right) \\leq \\frac{3}{2}\\left(\\frac{\\cos ^{2} \\theta+\\cos ^{2} \\theta+\\left(2-2 \\cos ^{2} \\theta\\right)}{3}\\right)^{3}=\\frac{4}{9}$,\nand the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 3"}}
|
|
|
|
| 1 |
+
{"year": "2004", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Determine all finite nonempty sets $S$ of positive integers satisfying\n\n$$\n\\frac{i+j}{(i, j)} \\text { is an element of } S \\text { for all } i, j \\text { in } S \\text {, }\n$$\n\nwhere $(i, j)$ is the greatest common divisor of $i$ and $j$.\nAnswer: $S=\\{2\\}$.", "solution": "Let $k \\in S$. Then $\\frac{k+k}{(k, k)}=2$ is in $S$ as well.\nSuppose for the sake of contradiction that there is an odd number in $S$, and let $k$ be the largest such odd number. Since $(k, 2)=1, \\frac{k+2}{(k, 2)}=k+2>k$ is in $S$ as well, a contradiction. Hence $S$ has no odd numbers.\nNow suppose that $\\ell>2$ is the second smallest number in $S$. Then $\\ell$ is even and $\\frac{\\ell+2}{(\\ell, 2)}=\\frac{\\ell}{2}+1$ is in $S$. Since $\\ell>2 \\Longrightarrow \\frac{\\ell}{2}+1>2, \\frac{\\ell}{2}+1 \\geq \\ell \\Longleftrightarrow \\ell \\leq 2$, a contradiction again.\nTherefore $S$ can only contain 2 , and $S=\\{2\\}$ is the only solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution\n\n"}}
|
| 2 |
+
{"year": "2004", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\\mathrm{AOH}, \\mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.", "solution": "Suppose, without loss of generality, that $B$ and $C$ lies in the same side of line $O H$. Such line is the Euler line of $A B C$, so the centroid $G$ lies in this line.\n\n\nLet $M$ be the midpoint of $B C$. Then the distance between $M$ and the line $O H$ is the average of the distances from $B$ and C to OH , and the sum of the areas of triangles BOH and COH is\n\n$$\n[B O H]+[C O H]=\\frac{O H \\cdot d(B, O H)}{2}+\\frac{O H \\cdot d(C, O H)}{2}=\\frac{O H \\cdot 2 d(M, O H)}{2} .\n$$\n\nSince $A G=2 G M, d(A, O H)=2 d(M, O H)$. Hence\n\n$$\n[B O H]+[C O H]=\\frac{O H \\cdot d(A, O H)}{2}=[A O H]\n$$\n\nand the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 1"}}
|
| 3 |
+
{"year": "2004", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\\mathrm{AOH}, \\mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.", "solution": "One can use barycentric coordinates: it is well known that\n\n$$\n\\begin{gathered}\nA=(1: 0: 0), \\quad B=(0: 1: 0), \\quad C=(0: 0: 1), \\\\\nO=(\\sin 2 A: \\sin 2 B: \\sin 2 C) \\quad \\text { and } \\quad H=(\\tan A: \\tan B: \\tan C) .\n\\end{gathered}\n$$\n\nThen the (signed) area of $A O H$ is proportional to\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 0 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nAdding all three expressions we find that the sum of the signed sums of the areas is a constant times\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 0 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|+\\left|\\begin{array}{ccc}\n0 & 1 & 0 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|+\\left|\\begin{array}{ccc}\n0 & 0 & 1 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nBy multilinearity of the determinant, this sum equals\n\n$$\n\\left|\\begin{array}{ccc}\n1 & 1 & 1 \\\\\n\\sin 2 A & \\sin 2 B & \\sin 2 C \\\\\n\\tan A & \\tan B & \\tan C\n\\end{array}\\right|\n$$\n\nwhich contains, in its rows, the coordinates of the centroid, the circumcenter, and the orthocenter. Since these three points lie in the Euler line of $A B C$, the signed sum of the areas is 0 , which means that one of the areas of $A O H, B O H, C O H$ is the sum of the other two areas.\nComment: Both solutions can be adapted to prove a stronger result: if the centroid $G$ of triangle $A B C$ belongs to line $X Y$ then one of the areas of triangles $A X Y, B X Y$, and $C X Y$ is equal to the sum of the other two.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution 2"}}
|
| 4 |
+
{"year": "2004", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let a set $S$ of 2004 points in the plane be given, no three of which are collinear. Let $\\mathcal{L}$ denote the set of all lines (extended indefinitely in both directions) determined by pairs of points from the set. Show that it is possible to colour the points of $S$ with at most two colours, such that for any points $p, q$ of $S$, the number of lines in $\\mathcal{L}$ which separate $p$ from $q$ is odd if and only if $p$ and $q$ have the same colour.\nNote: A line $\\ell$ separates two points $p$ and $q$ if $p$ and $q$ lie on opposite sides of $\\ell$ with neither point on $\\ell$.", "solution": "Choose any point $p$ from $S$ and color it, say, blue. Let $n(q, r)$ be the number of lines from $\\mathcal{L}$ that separates $q$ and $r$. Then color any other point $q$ blue if $n(p, q)$ is odd and red if $n(p, q)$ is even.\nNow it remains to show that $q$ and $r$ have the same color if and only if $n(q, r)$ is odd for all $q \\neq p$ and $r \\neq p$, which is equivalent to proving that $n(p, q)+n(p, r)+n(q, r)$ is always odd. For this purpose, consider the seven numbered regions defined by lines $p q$, $p r$, and $q r$ :\n\n\nAny line that do not pass through any of points $p, q, r$ meets the sides $p q, q r, p r$ of triangle $p q r$ in an even number of points (two sides or no sides), so these lines do not affect the parity of $n(p, q)+n(p, r)+n(q, r)$. Hence the only lines that need to be considered are the ones that pass through one of vertices $p, q, r$ and cuts the opposite side in the triangle $p q r$.\nLet $n_{i}$ be the number of points in region $i, p, q$, and $r$ excluded, as depicted in the diagram. Then the lines through $p$ that separate $q$ and $r$ are the lines passing through $p$ and points from regions 1,4 , and 7 . The same applies for $p, q$ and regions 2,5 , and 7 ; and $p, r$ and regions 3,6 , and 7. Therefore\n\n$$\n\\begin{aligned}\nn(p, q)+n(q, r)+n(p, r) & \\equiv\\left(n_{2}+n_{5}+n_{7}\\right)+\\left(n_{1}+n_{4}+n_{7}\\right)+\\left(n_{3}+n_{6}+n_{7}\\right) \\\\\n& \\equiv n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}+n_{7}=2004-3 \\equiv 1 \\quad(\\bmod 2)\n\\end{aligned}\n$$\n\nand the result follows.\nComment: The problem statement is also true if 2004 is replaced by any even number and is not true if 2004 is replaced by any odd number greater than 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "2004", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "For a real number $x$, let $\\lfloor x\\rfloor$ stand for the largest integer that is less than or equal to $x$. Prove that\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor\n$$\n\nis even for every positive integer $n$.", "solution": "Consider four cases:\n\n- $n \\leq 5$. Then $\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=0$ is an even number.\n- $n$ and $n+1$ are both composite (in particular, $n \\geq 8$ ). Then $n=a b$ and $n+1=c d$ for $a, b, c, d \\geq 2$. Moreover, since $n$ and $n+1$ are coprime, $a, b, c, d$ are all distinct and smaller than $n$, and one can choose $a, b, c, d$ such that exactly one of these four numbers is even. Hence $\\frac{(n-1)!}{n(n+1)}$ is an integer. As $n \\geq 8>6,(n-1)!$ has at least three even factors, so $\\frac{(n-1)!}{n(n+1)}$ is an even integer.\n- $n \\geq 7$ is an odd prime. By Wilson's theorem, $(n-1)!\\equiv-1(\\bmod n)$, that is, $\\frac{(n-1)!+1}{n}$ is an integer, as $\\frac{(n-1)!+n+1}{n}=\\frac{(n-1)!+1}{n}+1$ is. As before, $\\frac{(n-1)!}{n+1}$ is an even integer; therefore $\\frac{(n-1)!+n+1}{n+1}=\\frac{(n-1)!}{n+1}+1$ is an odd integer.\nAlso, $n$ and $n+1$ are coprime and $n$ divides the odd integer $\\frac{(n-1)!+n+1}{n+1}$, so $\\frac{(n-1)!+n+1}{n(n+1)}$ is also an odd integer. Then\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=\\frac{(n-1)!+n+1}{n(n+1)}-1\n$$\n\nis even.\n\n- $n+1 \\geq 7$ is an odd prime. Again, since $n$ is composite, $\\frac{(n-1)!}{n}$ is an even integer, and $\\frac{(n-1)!+n}{n}$ is an odd integer. By Wilson's theorem, $n!\\equiv-1(\\bmod n+1) \\Longleftrightarrow(n-1)!\\equiv 1$ $(\\bmod n+1)$. This means that $n+1$ divides $(n-1)!+n$, and since $n$ and $n+1$ are coprime, $n+1$ also divides $\\frac{(n-1)!+n}{n}$. Then $\\frac{(n-1)!+n}{n(n+1)}$ is also an odd integer and\n\n$$\n\\left\\lfloor\\frac{(n-1)!}{n(n+1)}\\right\\rfloor=\\frac{(n-1)!+n}{n(n+1)}-1\n$$\n\nis even.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 6 |
+
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "Let $p=a+b+c, q=a b+b c+c a$, and $r=a b c$. The inequality simplifies to\n\n$$\na^{2} b^{2} c^{2}+2\\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\\right)+4\\left(a^{2}+b^{2}+c^{2}\\right)+8-9(a b+b c+c a) \\geq 0\n$$\n\nSince $a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}=q^{2}-2 p r$ and $a^{2}+b^{2}+c^{2}=p^{2}-2 q$,\n\n$$\nr^{2}+2 q^{2}-4 p r+4 p^{2}-8 q+8-9 q \\geq 0\n$$\n\nwhich simplifies to\n\n$$\nr^{2}+2 q^{2}+4 p^{2}-17 q-4 p r+8 \\geq 0\n$$\n\nBearing in mind that equality occurs for $a=b=c=1$, which means that, for instance, $p=3 r$, one can rewrite $(I)$ as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}-\\frac{10}{3} p r+\\frac{35}{9} p^{2}+2 q^{2}-17 q+8 \\geq 0\n$$\n\nSince $(a b-b c)^{2}+(b c-c a)^{2}+(c a-a b)^{2} \\geq 0$ is equivalent to $q^{2} \\geq 3 p r$, rewrite $(I I)$ as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}+\\frac{10}{9}\\left(q^{2}-3 p r\\right)+\\frac{35}{9} p^{2}+\\frac{8}{9} q^{2}-17 q+8 \\geq 0\n$$\n\nFinally, $a=b=c=1$ implies $q=3$; then rewrite (III) as\n\n$$\n\\left(r-\\frac{p}{3}\\right)^{2}+\\frac{10}{9}\\left(q^{2}-3 p r\\right)+\\frac{35}{9}\\left(p^{2}-3 q\\right)+\\frac{8}{9}(q-3)^{2} \\geq 0\n$$\n\nThis final inequality is true because $q^{2} \\geq 3 p r$ and $p^{2}-3 q=\\frac{1}{2}\\left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\\right] \\geq 0$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 7 |
+
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "We prove the stronger inequality\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 3(a+b+c)^{2}\n$$\n\nwhich implies the proposed inequality because $(a+b+c)^{2} \\geq 3(a b+b c+c a)$ is equivalent to $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \\geq 0$, which is immediate.\nThe inequality $(*)$ is equivalent to\n\n$$\n\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right) a^{2}-6(b+c) a+2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3(b+c)^{2} \\geq 0\n$$\n\nSeeing this inequality as a quadratic inequality in $a$ with positive leading coefficient $\\left(b^{2}+2\\right)\\left(c^{2}+\\right.$ 2) $-3=b^{2} c^{2}+2 b^{2}+2 c^{2}+1$, it suffices to prove that its discriminant is non-positive, which is equivalent to\n\n$$\n(3(b+c))^{2}-\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right)\\left(2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3(b+c)^{2}\\right) \\leq 0\n$$\n\nThis simplifies to\n\n$$\n-2\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)+3(b+c)^{2}+6 \\leq 0\n$$\n\nNow we look $(* *)$ as a quadratic inequality in $b$ with negative leading coefficient $-2 c^{2}-1$ :\n\n$$\n\\left(-2 c^{2}-1\\right) b^{2}+6 c b-c^{2}-2 \\leq 0\n$$\n\nIf suffices to show that the discriminant of $(* *)$ is non-positive, which is equivalent to\n\n$$\n9 c^{2}-\\left(2 c^{2}+1\\right)\\left(c^{2}+2\\right) \\leq 0\n$$\n\nIt simplifies to $-2\\left(c^{2}-1\\right)^{2} \\leq 0$, which is true. The equality occurs for $c^{2}=1$, that is, $c=1$, for which $b=\\frac{6 c}{2\\left(2 c^{2}+1\\right)}=1$, and $a=\\frac{6(b+c)}{2\\left(\\left(b^{2}+2\\right)\\left(c^{2}+2\\right)-3\\right)}=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
| 8 |
+
{"year": "2004", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Prove that\n\n$$\n\\left(a^{2}+2\\right)\\left(b^{2}+2\\right)\\left(c^{2}+2\\right) \\geq 9(a b+b c+c a)\n$$\n\nfor all real numbers $a, b, c>0$.", "solution": "Let $A, B, C$ angles in $(0, \\pi / 2)$ such that $a=\\sqrt{2} \\tan A, b=\\sqrt{2} \\tan B$, and $c=\\sqrt{2} \\tan C$. Then the inequality is equivalent to\n\n$$\n4 \\sec ^{2} A \\sec ^{2} B \\sec ^{2} C \\geq 9(\\tan A \\tan B+\\tan B \\tan C+\\tan C \\tan A)\n$$\n\nSubstituting $\\sec x=\\frac{1}{\\cos x}$ for $x \\in\\{A, B, C\\}$ and clearing denominators, the inequality is equivalent to\n\n$$\n\\cos A \\cos B \\cos C(\\sin A \\sin B \\cos C+\\cos A \\sin B \\sin C+\\sin A \\cos B \\sin C) \\leq \\frac{4}{9}\n$$\n\nSince\n\n$$\n\\begin{aligned}\n& \\cos (A+B+C)=\\cos A \\cos (B+C)-\\sin A \\sin (B+C) \\\\\n= & \\cos A \\cos B \\cos C-\\cos A \\sin B \\sin C-\\sin A \\cos B \\sin C-\\sin A \\sin B \\cos C,\n\\end{aligned}\n$$\n\nwe rewrite our inequality as\n\n$$\n\\cos A \\cos B \\cos C(\\cos A \\cos B \\cos C-\\cos (A+B+C)) \\leq \\frac{4}{9}\n$$\n\nThe cosine function is concave down on $(0, \\pi / 2)$. Therefore, if $\\theta=\\frac{A+B+C}{3}$, by the AM-GM inequality and Jensen's inequality,\n\n$$\n\\cos A \\cos B \\cos C \\leq\\left(\\frac{\\cos A+\\cos B+\\cos C}{3}\\right)^{3} \\leq \\cos ^{3} \\frac{A+B+C}{3}=\\cos ^{3} \\theta\n$$\n\nTherefore, since $\\cos A \\cos B \\cos C-\\cos (A+B+C)=\\sin A \\sin B \\cos C+\\cos A \\sin B \\sin C+$ $\\sin A \\cos B \\sin C>0$, and recalling that $\\cos 3 \\theta=4 \\cos ^{3} \\theta-3 \\cos \\theta$,\n$\\cos A \\cos B \\cos C(\\cos A \\cos B \\cos C-\\cos (A+B+C)) \\leq \\cos ^{3} \\theta\\left(\\cos ^{3} \\theta-\\cos 3 \\theta\\right)=3 \\cos ^{4} \\theta\\left(1-\\cos ^{2} \\theta\\right)$. Finally, by AM-GM (notice that $1-\\cos ^{2} \\theta=\\sin ^{2} \\theta>0$ ),\n$3 \\cos ^{4} \\theta\\left(1-\\cos ^{2} \\theta\\right)=\\frac{3}{2} \\cos ^{2} \\theta \\cdot \\cos ^{2} \\theta\\left(2-2 \\cos ^{2} \\theta\\right) \\leq \\frac{3}{2}\\left(\\frac{\\cos ^{2} \\theta+\\cos ^{2} \\theta+\\left(2-2 \\cos ^{2} \\theta\\right)}{3}\\right)^{3}=\\frac{4}{9}$,\nand the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 3"}}
|
APMO/segmented/en-apmo2005_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2005", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Prove that for every irrational real number $a$, there are irrational real numbers $b$ and $b^{\\prime}$ so that $a+b$ and $a b^{\\prime}$ are both rational while $a b$ and $a+b^{\\prime}$ are both irrational.", "solution": "Let $a$ be an irrational number. If $a^{2}$ is irrational, we let $b=-a$. Then, $a+b=0$ is rational and $a b=-a^{2}$ is irrational. If $a^{2}$ is rational, we let $b=a^{2}-a$. Then, $a+b=a^{2}$ is rational and $a b=a^{2}(a-1)$. Since\n\n$$\na=\\frac{a b}{a^{2}}+1\n$$\n\nis irrational, so is $a b$.\nNow, we let $b^{\\prime}=\\frac{1}{a}$ or $b^{\\prime}=\\frac{2}{a}$. Then $a b^{\\prime}=1$ or 2 , which is rational. Note that\n\n$$\na+b^{\\prime}=\\frac{a^{2}+1}{a} \\quad \\text { or } \\quad a+b^{\\prime}=\\frac{a^{2}+2}{a} .\n$$\n\nSince,\n\n$$\n\\frac{a^{2}+2}{a}-\\frac{a^{2}+1}{a}=\\frac{1}{a}\n$$\n\nat least one of them is irrational.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
-
{"year": "2005", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a, b$ and $c$ be positive real numbers such that $a b c=8$. Prove that\n\n$$\n\\frac{a^{2}}{\\sqrt{\\left(1+a^{3}\\right)\\left(1+b^{3}\\right)}}+\\frac{b^{2}}{\\sqrt{\\left(1+b^{3}\\right)\\left(1+c^{3}\\right)}}+\\frac{c^{2}}{\\sqrt{\\left(1+c^{3}\\right)\\left(1+a^{3}\\right)}} \\geq \\frac{4}{3} .\n$$", "solution": "Observe that\n\n$$\n\\frac{1}{\\sqrt{1+x^{3}}} \\geq \\frac{2}{2+x^{2}}\n$$\n\nIn fact, this is equivalent to $\\left(2+x^{2}\\right)^{2} \\geq 4\\left(1+x^{3}\\right)$, or $x^{2}(x-2)^{2} \\geq 0$. Notice that equality holds in (1) if and only if $x=2$.\n\nWe substitute $x$ by $a, b, c$ in (1), respectively, to find\n\n$$\n\\begin{gathered}\n\\frac{a^{2}}{\\sqrt{\\left(1+a^{3}\\right)\\left(1+b^{3}\\right)}}+\\frac{b^{2}}{\\sqrt{\\left(1+b^{3}\\right)\\left(1+c^{3}\\right)}}+\\frac{c^{2}}{\\sqrt{\\left(1+c^{3}\\right)\\left(1+a^{3}\\right)}} \\\\\n\\geq \\frac{4 a^{2}}{\\left(2+a^{2}\\right)\\left(2+b^{2}\\right)}+\\frac{4 b^{2}}{\\left(2+b^{2}\\right)\\left(2+c^{2}\\right)}+\\frac{4 c^{2}}{\\left(2+c^{2}\\right)\\left(2+a^{2}\\right)}\n\\end{gathered}\n$$\n\nWe combine the terms on the right hand side of (2) to obtain\n\n$$\n\\text { Left hand side of }(2) \\geq \\frac{2 S(a, b, c)}{36+S(a, b, c)}=\\frac{2}{1+36 / S(a, b, c)}\n$$\n\nwhere $S(a, b, c):=2\\left(a^{2}+b^{2}+c^{2}\\right)+(a b)^{2}+(b c)^{2}+(c a)^{2}$. By AM-GM inequality, we have\n\n$$\n\\begin{aligned}\na^{2}+b^{2}+c^{2} & \\geq 3 \\sqrt[3]{(a b c)^{2}}=12 \\\\\n(a b)^{2}+(b c)^{2}+(c a)^{2} & \\geq 3 \\sqrt[3]{(a b c)^{4}}=48\n\\end{aligned}\n$$\n\nNote that the equalities holds if and only if $a=b=c=2$. The above inequalities yield\n\n$$\nS(a, b, c)=2\\left(a^{2}+b^{2}+c^{2}\\right)+(a b)^{2}+(b c)^{2}+(c a)^{2} \\geq 72\n$$\n\nTherefore\n\n$$\n\\frac{2}{1+36 / S(a, b, c)} \\geq \\frac{2}{1+36 / 72}=\\frac{4}{3}\n$$\n\nwhich is the required inequality.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
-
{"year": "2005", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Prove that there exists a triangle which can be cut into 2005 congruent triangles.", "solution": "Suppose that one side of a triangle has length $n$. Then it can be cut into $n^{2}$ congruent triangles which are similar to the original one and whose corresponding sides to the side of length $n$ have lengths 1 .\n\nSince $2005=5 \\times 401$ where 5 and 401 are primes and both primes are of the type $4 k+1$, it is representable as a sum of two integer squares. Indeed, it is easy to see that\n\n$$\n\\begin{aligned}\n2005 & =5 \\times 401=\\left(2^{2}+1\\right)\\left(20^{2}+1\\right) \\\\\n& =40^{2}+20^{2}+2^{2}+1 \\\\\n& =(40-1)^{2}+2 \\times 40+20^{2}+2^{2} \\\\\n& =39^{2}+22^{2}\n\\end{aligned}\n$$\n\nLet $A B C$ be a right-angled triangle with the legs $A B$ and $B C$ having lengths 39 and 22 , respectively. We draw the altitude $B K$, which divides $A B C$ into two similar triangles. Now we divide $A B K$ into $39^{2}$ congruent triangles as described above and $B C K$ into $22^{2}$ congruent triangles. Since $A B K$ is similar to $B K C$, all 2005 triangles will be congruent.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
-
{"year": "2005", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "In a small town, there are $n \\times n$ houses indexed by $(i, j)$ for $1 \\leq i, j \\leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \\leq \\frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \\ell)$ if $|i-k|+|j-\\ell|=1$.", "solution": "At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:\n\n$$\n\\begin{gathered}\n(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \\ldots \\\\\n(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \\ldots,(c+1, n)\n\\end{gathered}\n$$\n\nUnder this strategy, there are\n2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved\n2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved\n...\n2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved\n$n-2 c$ columns (column numbers $n-2 c+1, \\ldots, n$ ) at which $n-c$ houses are saved\nAdding all these we obtain :\n\n$$\n2[(n-1)+(n-2)+\\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c\n$$\n\nWe say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that\n\n$$\np(t)+\\sum_{i=1}^{t} d(i) \\leq t \\text { and } p(t+1)+d(t+1) \\leq p(t)+1\n$$\n\nLet $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that\n\n$$\ns(t) \\leq t-p(t) \\leq t\n$$\n\nfor $1 \\leq t \\leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \\leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have\n\n$$\n\\begin{aligned}\ns(k+1) & \\leq k-p(k)+d(k+1) \\\\\n& =(k+1)-(p(k)+1-d(k+1)) \\\\\n& \\leq(k+1)-p(k+1)\n\\end{aligned}\n$$\n\nWe now prove that the strategy given above is optimal. Since\n\n$$\n\\sum_{t=1}^{n-1} s(t) \\leq\\binom{ n}{2}\n$$\n\nthe maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.\n\nThe following is an example when $n=11$ and $c=4$. The houses with $\\bigcirc$ mark are burned. The houses with $\\otimes$ mark are blocked ones and hence those and the houses below them are saved.\n", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
-
{"year": "2005", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "In a triangle $A B C$, points $M$ and $N$ are on sides $A B$ and $A C$, respectively, such that $M B=B C=C N$. Let $R$ and $r$ denote the circumradius and the inradius of the triangle $A B C$, respectively. Express the ratio $M N / B C$ in terms of $R$ and $r$.", "solution": "Let $\\omega, O$ and $I$ be the circumcircle, the circumcenter and the incenter of $A B C$, respectively. Let $D$ be the point of intersection of the line $B I$ and the circle $\\omega$ such that $D \\neq B$. Then $D$ is the midpoint of the arc $A C$. Hence $O D \\perp C N$ and $O D=R$.\n\nWe first show that triangles $M N C$ and $I O D$ are similar. Because $B C=B M$, the line $B I$ (the bisector of $\\angle M B C$ ) is perpendicular to the line $C M$. Because $O D \\perp C N$ and $I D \\perp M C$, it follows that\n\n$$\n\\angle O D I=\\angle N C M\n$$\n\nLet $\\angle A B C=2 \\beta$. In the triangle $B C M$, we have\n\n$$\n\\frac{C M}{N C}=\\frac{C M}{B C}=2 \\sin \\beta\n$$\n\nSince $\\angle D I C=\\angle D C I$, we have $I D=C D=A D$. Let $E$ be the point of intersection of the line $D O$ and the circle $\\omega$ such that $E \\neq D$. Then $D E$ is a diameter of $\\omega$ and $\\angle D E C=\\angle D B C=\\beta$. Thus we have\n\n$$\n\\frac{D I}{O D}=\\frac{C D}{O D}=\\frac{2 R \\sin \\beta}{R}=2 \\sin \\beta .\n$$\n\nCombining equations (8), (9), and (10) shows that triangles $M N C$ and $I O D$ are similar. It follows that\n\n$$\n\\frac{M N}{B C}=\\frac{M N}{N C}=\\frac{I O}{O D}=\\frac{I O}{R} .\n$$\n\nThe well-known Euler's formula states that\n\n$$\nO I^{2}=R^{2}-2 R r .\n$$\n\nTherefore,\n\n$$\n\\frac{M N}{B C}=\\sqrt{1-\\frac{2 r}{R}}\n$$\n\n(Alternative Solution) Let $a$ (resp., $b, c$ ) be the length of $B C$ (resp., $A C, A B$ ). Let $\\alpha$ (resp., $\\beta, \\gamma$ ) denote the angle $\\angle B A C$ (resp., $\\angle A B C, \\angle A C B$ ). By introducing coordinates $B=(0,0), C=(a, 0)$, it is immediate that the coordinates of $M$ and $N$ are\n\n$$\nM=(a \\cos \\beta, a \\sin \\beta), \\quad N=(a-a \\cos \\gamma, a \\sin \\gamma)\n$$\n\nrespectively. Therefore,\n\n$$\n\\begin{aligned}\n(M N / B C)^{2} & =\\left[(a-a \\cos \\gamma-a \\cos \\beta)^{2}+(a \\sin \\gamma-a \\sin \\beta)^{2}\\right] / a^{2} \\\\\n& =(1-\\cos \\gamma-\\cos \\beta)^{2}+(\\sin \\gamma-\\sin \\beta)^{2} \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta+2(\\cos \\gamma \\cos \\beta-\\sin \\gamma \\sin \\beta) \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta+2 \\cos (\\gamma+\\beta) \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta-2 \\cos \\alpha \\\\\n& =3-2(\\cos \\gamma+\\cos \\beta+\\cos \\alpha) .\n\\end{aligned}\n$$\n\nNow we claim\n\n$$\n\\cos \\gamma+\\cos \\beta+\\cos \\alpha=\\frac{r}{R}+1\n$$\n\nFrom\n\n$$\n\\begin{aligned}\n& a=b \\cos \\gamma+c \\cos \\beta \\\\\n& b=c \\cos \\alpha+a \\cos \\gamma \\\\\n& c=a \\cos \\beta+b \\cos \\alpha\n\\end{aligned}\n$$\n\nwe get\n\n$$\na(1+\\cos \\alpha)+b(1+\\cos \\beta)+c(1+\\cos \\gamma)=(a+b+c)(\\cos \\alpha+\\cos \\beta+\\cos \\gamma)\n$$\n\nThus\n\n$$\n\\begin{aligned}\n& \\cos \\alpha+\\cos \\beta+\\cos \\gamma \\\\\n& =\\frac{1}{a+b+c}(a(1+\\cos \\alpha)+b(1+\\cos \\beta)+c(1+\\cos \\gamma)) \\\\\n& =\\frac{1}{a+b+c}\\left(a\\left(1+\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)+b\\left(1+\\frac{a^{2}+c^{2}-b^{2}}{2 a c}\\right)+c\\left(1+\\frac{a^{2}+b^{2}-c^{2}}{2 a b}\\right)\\right) \\\\\n& =\\frac{1}{a+b+c}\\left(a+b+c+\\frac{a^{2}\\left(b^{2}+c^{2}-a^{2}\\right)+b^{2}\\left(a^{2}+c^{2}-b^{2}\\right)+c^{2}\\left(a^{2}+b^{2}-c^{2}\\right)}{2 a b c}\\right) \\\\\n& =1+\\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2 a b c(a+b+c)}\n\\end{aligned}\n$$\n\nOn the other hand, from $R=\\frac{a}{2 \\sin \\alpha}$ it follows that\n\n$$\n\\begin{aligned}\nR^{2} & =\\frac{a^{2}}{4\\left(1-\\cos ^{2} \\alpha\\right)}=\\frac{a^{2}}{4\\left(1-\\left(\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)^{2}\\right)} \\\\\n& =\\frac{a^{2} b^{2} c^{2}}{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}\n\\end{aligned}\n$$\n\nAlso from $\\frac{1}{2}(a+b+c) r=\\frac{1}{2} b c \\sin \\alpha$, it follows that\n\n$$\n\\begin{aligned}\nr^{2} & =\\frac{b^{2} c^{2}\\left(1-\\cos ^{2} \\alpha\\right)}{(a+b+c)^{2}}=\\frac{b^{2} c^{2}\\left(1-\\left(\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)^{2}\\right)}{(a+b+c)^{2}} \\\\\n& =\\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{4(a+b+c)^{2}}\n\\end{aligned}\n$$\n\nCombining (19), (20) and (21), we get (16) as desired.\nFinally, by (15) and (16) we have\n\n$$\n\\frac{M N}{B C}=\\sqrt{1-\\frac{2 r}{R}}\n$$\n\nAnother proof of (16) from R.A. Johnson's \"Advanced Euclidean Geometry\" ${ }^{1}$ :\nConstruct the perpendicular bisectors $O D, O E, O F$, where $D, E, F$ are the midpoints of $B C, C A, A B$, respectively. By Ptolemy's Theorem applied to the cyclic quadrilateral $O E A F$, we get\n\n$$\n\\frac{a}{2} \\cdot R=\\frac{b}{2} \\cdot O F+\\frac{c}{2} \\cdot O E\n$$\n\nSimilarly\n\n$$\n\\frac{b}{2} \\cdot R=\\frac{c}{2} \\cdot O D+\\frac{a}{2} \\cdot O F, \\quad \\frac{c}{2} \\cdot R=\\frac{a}{2} \\cdot O E+\\frac{b}{2} \\cdot O D .\n$$\n\nAdding, we get\n\n$$\ns R=O D \\cdot \\frac{b+c}{2}+O E \\cdot \\frac{c+a}{2}+O F \\cdot \\frac{a+b}{2}\n$$\n\nwhere $s$ is the semiperimeter. But also, the area of triangle $O B C$ is $O D \\cdot \\frac{a}{2}$, and adding similar formulas for the areas of triangles $O C A$ and $O A B$ gives\n\n$$\nr s=\\triangle A B C=O D \\cdot \\frac{a}{2}+O E \\cdot \\frac{b}{2}+O F \\cdot \\frac{c}{2}\n$$\n\nAdding (23) and (24) gives $s(R+r)=s(O D+O E+O F)$, or\n\n$$\nO D+O E+O F=R+r .\n$$\n\nSince $O D=R \\cos A$ etc., (16) follows.\n\n[^0]\n[^0]: ${ }^{1}$ This proof was introduced to the coordinating country by Professor Bill Sands of Canada.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
|
|
|
| 1 |
+
{"year": "2005", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Prove that for every irrational real number $a$, there are irrational real numbers $b$ and $b^{\\prime}$ so that $a+b$ and $a b^{\\prime}$ are both rational while $a b$ and $a+b^{\\prime}$ are both irrational.", "solution": "Let $a$ be an irrational number. If $a^{2}$ is irrational, we let $b=-a$. Then, $a+b=0$ is rational and $a b=-a^{2}$ is irrational. If $a^{2}$ is rational, we let $b=a^{2}-a$. Then, $a+b=a^{2}$ is rational and $a b=a^{2}(a-1)$. Since\n\n$$\na=\\frac{a b}{a^{2}}+1\n$$\n\nis irrational, so is $a b$.\nNow, we let $b^{\\prime}=\\frac{1}{a}$ or $b^{\\prime}=\\frac{2}{a}$. Then $a b^{\\prime}=1$ or 2 , which is rational. Note that\n\n$$\na+b^{\\prime}=\\frac{a^{2}+1}{a} \\quad \\text { or } \\quad a+b^{\\prime}=\\frac{a^{2}+2}{a} .\n$$\n\nSince,\n\n$$\n\\frac{a^{2}+2}{a}-\\frac{a^{2}+1}{a}=\\frac{1}{a}\n$$\n\nat least one of them is irrational.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
+
{"year": "2005", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $a, b$ and $c$ be positive real numbers such that $a b c=8$. Prove that\n\n$$\n\\frac{a^{2}}{\\sqrt{\\left(1+a^{3}\\right)\\left(1+b^{3}\\right)}}+\\frac{b^{2}}{\\sqrt{\\left(1+b^{3}\\right)\\left(1+c^{3}\\right)}}+\\frac{c^{2}}{\\sqrt{\\left(1+c^{3}\\right)\\left(1+a^{3}\\right)}} \\geq \\frac{4}{3} .\n$$", "solution": "Observe that\n\n$$\n\\frac{1}{\\sqrt{1+x^{3}}} \\geq \\frac{2}{2+x^{2}}\n$$\n\nIn fact, this is equivalent to $\\left(2+x^{2}\\right)^{2} \\geq 4\\left(1+x^{3}\\right)$, or $x^{2}(x-2)^{2} \\geq 0$. Notice that equality holds in (1) if and only if $x=2$.\n\nWe substitute $x$ by $a, b, c$ in (1), respectively, to find\n\n$$\n\\begin{gathered}\n\\frac{a^{2}}{\\sqrt{\\left(1+a^{3}\\right)\\left(1+b^{3}\\right)}}+\\frac{b^{2}}{\\sqrt{\\left(1+b^{3}\\right)\\left(1+c^{3}\\right)}}+\\frac{c^{2}}{\\sqrt{\\left(1+c^{3}\\right)\\left(1+a^{3}\\right)}} \\\\\n\\geq \\frac{4 a^{2}}{\\left(2+a^{2}\\right)\\left(2+b^{2}\\right)}+\\frac{4 b^{2}}{\\left(2+b^{2}\\right)\\left(2+c^{2}\\right)}+\\frac{4 c^{2}}{\\left(2+c^{2}\\right)\\left(2+a^{2}\\right)}\n\\end{gathered}\n$$\n\nWe combine the terms on the right hand side of (2) to obtain\n\n$$\n\\text { Left hand side of }(2) \\geq \\frac{2 S(a, b, c)}{36+S(a, b, c)}=\\frac{2}{1+36 / S(a, b, c)}\n$$\n\nwhere $S(a, b, c):=2\\left(a^{2}+b^{2}+c^{2}\\right)+(a b)^{2}+(b c)^{2}+(c a)^{2}$. By AM-GM inequality, we have\n\n$$\n\\begin{aligned}\na^{2}+b^{2}+c^{2} & \\geq 3 \\sqrt[3]{(a b c)^{2}}=12 \\\\\n(a b)^{2}+(b c)^{2}+(c a)^{2} & \\geq 3 \\sqrt[3]{(a b c)^{4}}=48\n\\end{aligned}\n$$\n\nNote that the equalities holds if and only if $a=b=c=2$. The above inequalities yield\n\n$$\nS(a, b, c)=2\\left(a^{2}+b^{2}+c^{2}\\right)+(a b)^{2}+(b c)^{2}+(c a)^{2} \\geq 72\n$$\n\nTherefore\n\n$$\n\\frac{2}{1+36 / S(a, b, c)} \\geq \\frac{2}{1+36 / 72}=\\frac{4}{3}\n$$\n\nwhich is the required inequality.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
+
{"year": "2005", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Prove that there exists a triangle which can be cut into 2005 congruent triangles.", "solution": "Suppose that one side of a triangle has length $n$. Then it can be cut into $n^{2}$ congruent triangles which are similar to the original one and whose corresponding sides to the side of length $n$ have lengths 1 .\n\nSince $2005=5 \\times 401$ where 5 and 401 are primes and both primes are of the type $4 k+1$, it is representable as a sum of two integer squares. Indeed, it is easy to see that\n\n$$\n\\begin{aligned}\n2005 & =5 \\times 401=\\left(2^{2}+1\\right)\\left(20^{2}+1\\right) \\\\\n& =40^{2}+20^{2}+2^{2}+1 \\\\\n& =(40-1)^{2}+2 \\times 40+20^{2}+2^{2} \\\\\n& =39^{2}+22^{2}\n\\end{aligned}\n$$\n\nLet $A B C$ be a right-angled triangle with the legs $A B$ and $B C$ having lengths 39 and 22 , respectively. We draw the altitude $B K$, which divides $A B C$ into two similar triangles. Now we divide $A B K$ into $39^{2}$ congruent triangles as described above and $B C K$ into $22^{2}$ congruent triangles. Since $A B K$ is similar to $B K C$, all 2005 triangles will be congruent.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
+
{"year": "2005", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "In a small town, there are $n \\times n$ houses indexed by $(i, j)$ for $1 \\leq i, j \\leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \\leq \\frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \\ell)$ if $|i-k|+|j-\\ell|=1$.", "solution": "At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:\n\n$$\n\\begin{gathered}\n(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \\ldots \\\\\n(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \\ldots,(c+1, n)\n\\end{gathered}\n$$\n\nUnder this strategy, there are\n2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved\n2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved\n...\n2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved\n$n-2 c$ columns (column numbers $n-2 c+1, \\ldots, n$ ) at which $n-c$ houses are saved\nAdding all these we obtain :\n\n$$\n2[(n-1)+(n-2)+\\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c\n$$\n\nWe say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that\n\n$$\np(t)+\\sum_{i=1}^{t} d(i) \\leq t \\text { and } p(t+1)+d(t+1) \\leq p(t)+1\n$$\n\nLet $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that\n\n$$\ns(t) \\leq t-p(t) \\leq t\n$$\n\nfor $1 \\leq t \\leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \\leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have\n\n$$\n\\begin{aligned}\ns(k+1) & \\leq k-p(k)+d(k+1) \\\\\n& =(k+1)-(p(k)+1-d(k+1)) \\\\\n& \\leq(k+1)-p(k+1)\n\\end{aligned}\n$$\n\nWe now prove that the strategy given above is optimal. Since\n\n$$\n\\sum_{t=1}^{n-1} s(t) \\leq\\binom{ n}{2}\n$$\n\nthe maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.\n\nThe following is an example when $n=11$ and $c=4$. The houses with $\\bigcirc$ mark are burned. The houses with $\\otimes$ mark are blocked ones and hence those and the houses below them are saved.\n", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
+
{"year": "2005", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "In a triangle $A B C$, points $M$ and $N$ are on sides $A B$ and $A C$, respectively, such that $M B=B C=C N$. Let $R$ and $r$ denote the circumradius and the inradius of the triangle $A B C$, respectively. Express the ratio $M N / B C$ in terms of $R$ and $r$.", "solution": "Let $\\omega, O$ and $I$ be the circumcircle, the circumcenter and the incenter of $A B C$, respectively. Let $D$ be the point of intersection of the line $B I$ and the circle $\\omega$ such that $D \\neq B$. Then $D$ is the midpoint of the arc $A C$. Hence $O D \\perp C N$ and $O D=R$.\n\nWe first show that triangles $M N C$ and $I O D$ are similar. Because $B C=B M$, the line $B I$ (the bisector of $\\angle M B C$ ) is perpendicular to the line $C M$. Because $O D \\perp C N$ and $I D \\perp M C$, it follows that\n\n$$\n\\angle O D I=\\angle N C M\n$$\n\nLet $\\angle A B C=2 \\beta$. In the triangle $B C M$, we have\n\n$$\n\\frac{C M}{N C}=\\frac{C M}{B C}=2 \\sin \\beta\n$$\n\nSince $\\angle D I C=\\angle D C I$, we have $I D=C D=A D$. Let $E$ be the point of intersection of the line $D O$ and the circle $\\omega$ such that $E \\neq D$. Then $D E$ is a diameter of $\\omega$ and $\\angle D E C=\\angle D B C=\\beta$. Thus we have\n\n$$\n\\frac{D I}{O D}=\\frac{C D}{O D}=\\frac{2 R \\sin \\beta}{R}=2 \\sin \\beta .\n$$\n\nCombining equations (8), (9), and (10) shows that triangles $M N C$ and $I O D$ are similar. It follows that\n\n$$\n\\frac{M N}{B C}=\\frac{M N}{N C}=\\frac{I O}{O D}=\\frac{I O}{R} .\n$$\n\nThe well-known Euler's formula states that\n\n$$\nO I^{2}=R^{2}-2 R r .\n$$\n\nTherefore,\n\n$$\n\\frac{M N}{B C}=\\sqrt{1-\\frac{2 r}{R}}\n$$\n\n(Alternative Solution) Let $a$ (resp., $b, c$ ) be the length of $B C$ (resp., $A C, A B$ ). Let $\\alpha$ (resp., $\\beta, \\gamma$ ) denote the angle $\\angle B A C$ (resp., $\\angle A B C, \\angle A C B$ ). By introducing coordinates $B=(0,0), C=(a, 0)$, it is immediate that the coordinates of $M$ and $N$ are\n\n$$\nM=(a \\cos \\beta, a \\sin \\beta), \\quad N=(a-a \\cos \\gamma, a \\sin \\gamma)\n$$\n\nrespectively. Therefore,\n\n$$\n\\begin{aligned}\n(M N / B C)^{2} & =\\left[(a-a \\cos \\gamma-a \\cos \\beta)^{2}+(a \\sin \\gamma-a \\sin \\beta)^{2}\\right] / a^{2} \\\\\n& =(1-\\cos \\gamma-\\cos \\beta)^{2}+(\\sin \\gamma-\\sin \\beta)^{2} \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta+2(\\cos \\gamma \\cos \\beta-\\sin \\gamma \\sin \\beta) \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta+2 \\cos (\\gamma+\\beta) \\\\\n& =3-2 \\cos \\gamma-2 \\cos \\beta-2 \\cos \\alpha \\\\\n& =3-2(\\cos \\gamma+\\cos \\beta+\\cos \\alpha) .\n\\end{aligned}\n$$\n\nNow we claim\n\n$$\n\\cos \\gamma+\\cos \\beta+\\cos \\alpha=\\frac{r}{R}+1\n$$\n\nFrom\n\n$$\n\\begin{aligned}\n& a=b \\cos \\gamma+c \\cos \\beta \\\\\n& b=c \\cos \\alpha+a \\cos \\gamma \\\\\n& c=a \\cos \\beta+b \\cos \\alpha\n\\end{aligned}\n$$\n\nwe get\n\n$$\na(1+\\cos \\alpha)+b(1+\\cos \\beta)+c(1+\\cos \\gamma)=(a+b+c)(\\cos \\alpha+\\cos \\beta+\\cos \\gamma)\n$$\n\nThus\n\n$$\n\\begin{aligned}\n& \\cos \\alpha+\\cos \\beta+\\cos \\gamma \\\\\n& =\\frac{1}{a+b+c}(a(1+\\cos \\alpha)+b(1+\\cos \\beta)+c(1+\\cos \\gamma)) \\\\\n& =\\frac{1}{a+b+c}\\left(a\\left(1+\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)+b\\left(1+\\frac{a^{2}+c^{2}-b^{2}}{2 a c}\\right)+c\\left(1+\\frac{a^{2}+b^{2}-c^{2}}{2 a b}\\right)\\right) \\\\\n& =\\frac{1}{a+b+c}\\left(a+b+c+\\frac{a^{2}\\left(b^{2}+c^{2}-a^{2}\\right)+b^{2}\\left(a^{2}+c^{2}-b^{2}\\right)+c^{2}\\left(a^{2}+b^{2}-c^{2}\\right)}{2 a b c}\\right) \\\\\n& =1+\\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2 a b c(a+b+c)}\n\\end{aligned}\n$$\n\nOn the other hand, from $R=\\frac{a}{2 \\sin \\alpha}$ it follows that\n\n$$\n\\begin{aligned}\nR^{2} & =\\frac{a^{2}}{4\\left(1-\\cos ^{2} \\alpha\\right)}=\\frac{a^{2}}{4\\left(1-\\left(\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)^{2}\\right)} \\\\\n& =\\frac{a^{2} b^{2} c^{2}}{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}\n\\end{aligned}\n$$\n\nAlso from $\\frac{1}{2}(a+b+c) r=\\frac{1}{2} b c \\sin \\alpha$, it follows that\n\n$$\n\\begin{aligned}\nr^{2} & =\\frac{b^{2} c^{2}\\left(1-\\cos ^{2} \\alpha\\right)}{(a+b+c)^{2}}=\\frac{b^{2} c^{2}\\left(1-\\left(\\frac{b^{2}+c^{2}-a^{2}}{2 b c}\\right)^{2}\\right)}{(a+b+c)^{2}} \\\\\n& =\\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{4(a+b+c)^{2}}\n\\end{aligned}\n$$\n\nCombining (19), (20) and (21), we get (16) as desired.\nFinally, by (15) and (16) we have\n\n$$\n\\frac{M N}{B C}=\\sqrt{1-\\frac{2 r}{R}}\n$$\n\nAnother proof of (16) from R.A. Johnson's \"Advanced Euclidean Geometry\" ${ }^{1}$ :\nConstruct the perpendicular bisectors $O D, O E, O F$, where $D, E, F$ are the midpoints of $B C, C A, A B$, respectively. By Ptolemy's Theorem applied to the cyclic quadrilateral $O E A F$, we get\n\n$$\n\\frac{a}{2} \\cdot R=\\frac{b}{2} \\cdot O F+\\frac{c}{2} \\cdot O E\n$$\n\nSimilarly\n\n$$\n\\frac{b}{2} \\cdot R=\\frac{c}{2} \\cdot O D+\\frac{a}{2} \\cdot O F, \\quad \\frac{c}{2} \\cdot R=\\frac{a}{2} \\cdot O E+\\frac{b}{2} \\cdot O D .\n$$\n\nAdding, we get\n\n$$\ns R=O D \\cdot \\frac{b+c}{2}+O E \\cdot \\frac{c+a}{2}+O F \\cdot \\frac{a+b}{2}\n$$\n\nwhere $s$ is the semiperimeter. But also, the area of triangle $O B C$ is $O D \\cdot \\frac{a}{2}$, and adding similar formulas for the areas of triangles $O C A$ and $O A B$ gives\n\n$$\nr s=\\triangle A B C=O D \\cdot \\frac{a}{2}+O E \\cdot \\frac{b}{2}+O F \\cdot \\frac{c}{2}\n$$\n\nAdding (23) and (24) gives $s(R+r)=s(O D+O E+O F)$, or\n\n$$\nO D+O E+O F=R+r .\n$$\n\nSince $O D=R \\cos A$ etc., (16) follows.\n\n[^0]\n[^0]: ${ }^{1}$ This proof was introduced to the coordinating country by Professor Bill Sands of Canada.", "metadata": {"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
APMO/segmented/en-apmo2006_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2006", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $n$ be a positive integer. Find the largest nonnegative real number $f(n)$ (depending on $n$ ) with the following property: whenever $a_{1}, a_{2}, \\ldots, a_{n}$ are real numbers such that $a_{1}+a_{2}+\\cdots+a_{n}$ is an integer, there exists some $i$ such that $\\left|a_{i}-\\frac{1}{2}\\right| \\geq f(n)$.", "solution": "The answer is\n\n$$\nf(n)=\\left\\{\\begin{array}{cl}\n0 & \\text { if } n \\text { is even, } \\\\\n\\frac{1}{2 n} & \\text { if } n \\text { is odd. }\n\\end{array}\\right.\n$$\n\nFirst, assume that $n$ is even. If $a_{i}=\\frac{1}{2}$ for all $i$, then the sum $a_{1}+a_{2}+\\cdots+a_{n}$ is an integer. Since $\\left|a_{i}-\\frac{1}{2}\\right|=0$ for all $i$, we may conclude $f(n)=0$ for any even $n$.\n\nNow assume that $n$ is odd. Suppose that $\\left|a_{i}-\\frac{1}{2}\\right|<\\frac{1}{2 n}$ for all $1 \\leq i \\leq n$. Then, since $\\sum_{i=1}^{n} a_{i}$ is an integer,\n\n$$\n\\frac{1}{2} \\leq\\left|\\sum_{i=1}^{n} a_{i}-\\frac{n}{2}\\right| \\leq \\sum_{i=1}^{n}\\left|a_{i}-\\frac{1}{2}\\right|<\\frac{1}{2 n} \\cdot n=\\frac{1}{2}\n$$\n\na contradiction. Thus $\\left|a_{i}-\\frac{1}{2}\\right| \\geq \\frac{1}{2 n}$ for some $i$, as required. On the other hand, putting $n=2 m+1$ and $a_{i}=\\frac{m}{2 m+1}$ for all $i$ gives $\\sum a_{i}=m$, while\n\n$$\n\\left|a_{i}-\\frac{1}{2}\\right|=\\frac{1}{2}-\\frac{m}{2 m+1}=\\frac{1}{2(2 m+1)}=\\frac{1}{2 n}\n$$\n\nfor all $i$. Therefore, $f(n)=\\frac{1}{2 n}$ is the best possible for any odd $n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
-
{"year": "2006", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Prove that every positive integer can be written as a finite sum of distinct integral powers of the golden mean $\\tau=\\frac{1+\\sqrt{5}}{2}$. Here, an integral power of $\\tau$ is of the form $\\tau^{i}$, where $i$ is an integer (not necessarily positive).", "solution": "We will prove this statement by induction using the equality\n\n$$\n\\tau^{2}=\\tau+1\n$$\n\nIf $n=1$, then $1=\\tau^{0}$. Suppose that $n-1$ can be written as a finite sum of integral powers of $\\tau$, say\n\n$$\nn-1=\\sum_{i=-k}^{k} a_{i} \\tau^{i}\n$$\n\nwhere $a_{i} \\in\\{0,1\\}$ and $n \\geq 2$. We will write (1) as\n\n$$\nn-1=a_{k} \\cdots a_{1} a_{0} \\cdot a_{-1} a_{-2} \\cdots a_{-k}\n$$\n\nFor example,\n\n$$\n1=1.0=0.11=0.1011=0.101011\n$$\n\nFirstly, we will prove that we may assume that in (2) we have $a_{i} a_{i+1}=0$ for all $i$ with $-k \\leq i \\leq k-1$. Indeed, if we have several occurrences of 11 , then we take the leftmost such occurrence. Since we may assume that it is preceded by a 0 , we can replace 011 with 100 using the identity $\\tau^{i+1}+\\tau^{i}=\\tau^{i+2}$. By doing so repeatedly, if necessary, we will eliminate all occurrences of two 1's standing together. Now we have the representation\n\n$$\nn-1=\\sum_{i=-K}^{K} b_{i} \\tau^{i}\n$$\n\nwhere $b_{i} \\in\\{0,1\\}$ and $b_{i} b_{i+1}=0$.\nIf $b_{0}=0$ in (3), then we just add $1=\\tau^{0}$ to both sides of (3) and we are done.\nSuppose now that there is 1 in the unit position of (3), that is $b_{0}=1$. If there are two 0 's to the right of it, i.e.\n\n$$\nn-1=\\cdots 1.00 \\cdots\n$$\n\nthen we can replace 1.00 with 0.11 because $1=\\tau^{-1}+\\tau^{-2}$, and we are done because we obtain 0 in the unit position. Thus we may assume that\n\n$$\nn-1=\\cdots 1.010 \\cdots\n$$\n\nAgain, if we have $n-1=\\cdots 1.0100 \\cdots$, we may rewrite it as\n\n$$\nn-1=\\cdots 1.0100 \\cdots=\\cdots 1.0011 \\cdots=\\cdots 0.1111 \\cdots\n$$\n\nand obtain 0 in the unit position. Therefore, we may assume that\n\n$$\nn-1=\\cdots 1.01010 \\cdots\n$$\n\nSince the number of 1's is finite, eventually we will obtain an occurrence of 100 at the end, i.e.\n\n$$\nn-1=\\cdots 1.01010 \\cdots 100\n$$\n\nThen we can shift all 1's to the right to obtain 0 in the unit position, i.e.\n\n$$\nn-1=\\cdots 0.11 \\cdots 11\n$$\n\nand we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
-
{"year": "2006", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $p \\geq 5$ be a prime and let $r$ be the number of ways of placing $p$ checkers on a $p \\times p$ checkerboard so that not all checkers are in the same row (but they may all be in the same column). Show that $r$ is divisible by $p^{5}$. Here, we assume that all the checkers are identical.", "solution": "Note that $r=\\binom{p^{2}}{p}-p$. Hence, it suffices to show that\n\n$$\n\\left(p^{2}-1\\right)\\left(p^{2}-2\\right) \\cdots\\left(p^{2}-(p-1)\\right)-(p-1)!\\equiv 0 \\quad\\left(\\bmod p^{4}\\right)\n$$\n\nNow, let\n\n$$\nf(x):=(x-1)(x-2) \\cdots(x-(p-1))=x^{p-1}+s_{p-2} x^{p-2}+\\cdots+s_{1} x+s_{0} .\n$$\n\nThen the congruence equation (1) is same as $f\\left(p^{2}\\right)-s_{0} \\equiv 0\\left(\\bmod p^{4}\\right)$. Therefore, it suffices to show that $s_{1} p^{2} \\equiv 0\\left(\\bmod p^{4}\\right)$ or $s_{1} \\equiv 0\\left(\\bmod p^{2}\\right)$.\n\nSince $a^{p-1} \\equiv 1(\\bmod p)$ for all $1 \\leq a \\leq p-1$, we can factor\n\n$$\nx^{p-1}-1 \\equiv(x-1)(x-2) \\cdots(x-(p-1)) \\quad(\\bmod p)\n$$\n\nComparing the coefficients of the left hand side of (3) with those of the right hand side of (2), we obtain $p \\mid s_{i}$ for all $1 \\leq i \\leq p-2$ and $s_{0} \\equiv-1(\\bmod p)$. On the other hand, plugging $p$ for $x$ in (2), we get\n\n$$\nf(p)=(p-1)!=s_{0}=p^{p-1}+s_{p-2} p^{p-2}+\\cdots+s_{1} p+s_{0}\n$$\n\nwhich implies\n\n$$\np^{p-1}+s_{p-2} p^{p-2}+\\cdots+s_{2} p^{2}=-s_{1} p\n$$\n\nSince $p \\geq 5, p \\mid s_{2}$ and hence $s_{1} \\equiv 0\\left(\\bmod p^{2}\\right)$ as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
-
{"year": "2006", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $A, B$ be two distinct points on a given circle $O$ and let $P$ be the midpoint of the line segment $A B$. Let $O_{1}$ be the circle tangent to the line $A B$ at $P$ and tangent to the circle $O$. Let $\\ell$ be the tangent line, different from the line $A B$, to $O_{1}$ passing through $A$. Let $C$ be the intersection point, different from $A$, of $\\ell$ and $O$. Let $Q$ be the midpoint of the line segment $B C$ and $O_{2}$ be the circle tangent to the line $B C$ at $Q$ and tangent to the line segment $A C$. Prove that the circle $O_{2}$ is tangent to the circle $O$.", "solution": "Let $S$ be the tangent point of the circles $O$ and $O_{1}$ and let $T$ be the intersection point, different from $S$, of the circle $O$ and the line $S P$. Let $X$ be the tangent point of $\\ell$ to $O_{1}$ and let $M$ be the midpoint of the line segment $X P$. Since $\\angle T B P=\\angle A S P$, the triangle $T B P$ is similar to the triangle $A S P$. Therefore,\n\n$$\n\\frac{P T}{P B}=\\frac{P A}{P S}\n$$\n\nSince the line $\\ell$ is tangent to the circle $O_{1}$ at $X$, we have\n\n$$\n\\angle S P X=90^{\\circ}-\\angle X S P=90^{\\circ}-\\angle A P M=\\angle P A M\n$$\n\nwhich implies that the triangle $P A M$ is similar to the triangle $S P X$. Consequently,\n\n$$\n\\frac{X S}{X P}=\\frac{M P}{M A}=\\frac{X P}{2 M A} \\quad \\text { and } \\quad \\frac{X P}{P S}=\\frac{M A}{A P}\n$$\n\nFrom this and the above observation follows\n\n$$\n\\frac{X S}{X P} \\cdot \\frac{P T}{P B}=\\frac{X P}{2 M A} \\cdot \\frac{P A}{P S}=\\frac{X P}{2 M A} \\cdot \\frac{M A}{X P}=\\frac{1}{2} .\n$$\n\nLet $A^{\\prime}$ be the intersection point of the circle $O$ and the perpendicular bisector of the chord $B C$ such that $A, A^{\\prime}$ are on the same side of the line $B C$, and $N$ be the intersection point of the lines $A^{\\prime} Q$ and $C T$. Since\n\n$$\n\\angle N C Q=\\angle T C B=\\angle T C A=\\angle T B A=\\angle T B P\n$$\n\nand\n\n$$\n\\angle C A^{\\prime} Q=\\frac{\\angle C A B}{2}=\\frac{\\angle X A P}{2}=\\angle P A M=\\angle S P X,\n$$\n\nthe triangle $N C Q$ is similar to the triangle $T B P$ and the triangle $C A^{\\prime} Q$ is similar to the triangle $S P X$. Therefore\n\n$$\n\\frac{Q N}{Q C}=\\frac{P T}{P B} \\quad \\text { and } \\quad \\frac{Q C}{Q A^{\\prime}}=\\frac{X S}{X P} .\n$$\n\nand hence $Q A^{\\prime}=2 Q N$ by (1). This implies that $N$ is the midpoint of the line segment $Q A^{\\prime}$. Let the circle $O_{2}$ touch the line segment $A C$ at $Y$. Since\n\n$$\n\\angle A C N=\\angle A C T=\\angle B C T=\\angle Q C N\n$$\n\nand $|C Y|=|C Q|$, the triangles $Y C N$ and $Q C N$ are congruent and hence $N Y \\perp A C$ and $N Y=N Q=N A^{\\prime}$. Therefore, $N$ is the center of the circle $O_{2}$, which completes the proof.\n\nRemark: Analytic solutions are possible: For example, one can prove for a triangle $A B C$ inscribed in a circle $O$ that $A B=k(2+2 t), A C=k(1+2 t), B C=k(1+4 t)$ for some positive numbers $k, t$ if and only if there exists a circle $O_{1}$ such that $O_{1}$ is tangent to the side $A B$ at its midpoint, the side $A C$ and the circle $O$.\n\nOne obtains $A B=k^{\\prime}\\left(1+4 t^{\\prime}\\right), A C=k^{\\prime}\\left(1+2 t^{\\prime}\\right), B C=k^{\\prime}\\left(2+2 t^{\\prime}\\right)$ by substituting $t=1 / 4 t^{\\prime}$ and $k=2 k^{\\prime} t^{\\prime}$. So, there exists a circle $O_{2}$ such that $O_{2}$ is tangent to the side $B C$ at its midpoint, the side $A C$ and the circle $O$.\n\nIn the above, $t=\\tan ^{2} \\alpha$ and $k=\\frac{4 R \\tan \\alpha}{\\left(1+\\tan ^{2} \\alpha\\right)\\left(1+4 \\tan ^{2} \\alpha\\right)}$, where $R$ is the radius of $O$ and $\\angle A=2 \\alpha$. Furthermore, $t^{\\prime}=\\tan ^{2} \\gamma$ and $k^{\\prime}=\\frac{4 R \\tan \\gamma}{\\left(1+\\tan ^{2} \\gamma\\right)\\left(1+4 \\tan ^{2} \\gamma\\right)}$, where $\\angle C=2 \\gamma$. Observe that $\\sqrt{t t^{\\prime}}=\\tan \\alpha \\cdot \\tan \\gamma=\\frac{X S}{X P} \\cdot \\frac{P T}{P B}=\\frac{1}{2}$, which implies $t t^{\\prime}=\\frac{1}{4}$. It is now routine easy to check that $k=2 k^{\\prime} t^{\\prime}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
-
{"year": "2006", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set\nof colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.", "solution": "Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \\ldots, 12$. For each $i=1,2, \\ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\\{1,2, \\ldots, 12\\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \\neq S^{\\prime}$ implies $E_{S} \\cap E_{S^{\\prime}}=\\emptyset$, we have\n\n$$\n\\sum_{S}\\left|E_{S}\\right|=|C|=n\n$$\n\nwhere $S$ runs over all subsets of $\\{1,2, \\ldots, 12\\}$. Now for each $i$,\n\n$$\nE_{S} \\subseteq E_{i} \\quad \\text { if and only if } \\quad i \\in S\n$$\n\nand hence\n\n$$\n\\left|E_{i}\\right|=\\sum_{i \\in S}\\left|E_{S}\\right|\n$$\n\nBy assumption, we know that $\\left|E_{i}\\right| \\leq 20$ and that if $E_{S} \\neq \\emptyset$, then $|S| \\geq 5$. From this we obtain\n\n$$\n20 \\times 12 \\geq \\sum_{i=1}^{12}\\left|E_{i}\\right|=\\sum_{i=1}^{12}\\left(\\sum_{i \\in S}\\left|E_{S}\\right|\\right) \\geq 5 \\sum_{S}\\left|E_{S}\\right|=5 n\n$$\n\nTherefore $n \\leq 48$.\nNow, define a sequence $\\left\\{c_{i}\\right\\}_{i=1}^{52}$ of colours in the following way:\n$1234|5678| 9101112 \\mid$\n$4123|8567| 1291011 \\mid$\n$3412|7856| 1112910 \\mid$\n$2341|6785| 1011129 \\mid 1234$\n\nThe first row lists $c_{1}, \\ldots, c_{12}$ in order, the second row lists $c_{13}, \\ldots, c_{24}$ in order, the third row lists $c_{25}, \\ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \\ldots, c_{52}$ in order. For each $j, 1 \\leq j \\leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.\n\nRemark: The fact that $n \\leq 48$ can be obtained in a much simpler observation that\n\n$$\n5 n \\leq 12 \\times 20=240\n$$\n\nThere are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets\n\n$$\n\\begin{array}{cccc}\n\\{1,2,3,4,5,6\\}, & \\{3,4,5,6,7,8\\}, & \\{5,6,7,8,9,10\\}, & \\{7,8,9,10,11,12\\}, \\\\\n\\{9,10,11,12,1,2\\}, & \\{11,12,1,2,3,4\\}, & \\{1,2,5,6,9,10\\}, & \\{3,4,7,8,11,12\\} .\n\\end{array}\n$$\n\nEach of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
|
|
|
| 1 |
+
{"year": "2006", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be a positive integer. Find the largest nonnegative real number $f(n)$ (depending on $n$ ) with the following property: whenever $a_{1}, a_{2}, \\ldots, a_{n}$ are real numbers such that $a_{1}+a_{2}+\\cdots+a_{n}$ is an integer, there exists some $i$ such that $\\left|a_{i}-\\frac{1}{2}\\right| \\geq f(n)$.", "solution": "The answer is\n\n$$\nf(n)=\\left\\{\\begin{array}{cl}\n0 & \\text { if } n \\text { is even, } \\\\\n\\frac{1}{2 n} & \\text { if } n \\text { is odd. }\n\\end{array}\\right.\n$$\n\nFirst, assume that $n$ is even. If $a_{i}=\\frac{1}{2}$ for all $i$, then the sum $a_{1}+a_{2}+\\cdots+a_{n}$ is an integer. Since $\\left|a_{i}-\\frac{1}{2}\\right|=0$ for all $i$, we may conclude $f(n)=0$ for any even $n$.\n\nNow assume that $n$ is odd. Suppose that $\\left|a_{i}-\\frac{1}{2}\\right|<\\frac{1}{2 n}$ for all $1 \\leq i \\leq n$. Then, since $\\sum_{i=1}^{n} a_{i}$ is an integer,\n\n$$\n\\frac{1}{2} \\leq\\left|\\sum_{i=1}^{n} a_{i}-\\frac{n}{2}\\right| \\leq \\sum_{i=1}^{n}\\left|a_{i}-\\frac{1}{2}\\right|<\\frac{1}{2 n} \\cdot n=\\frac{1}{2}\n$$\n\na contradiction. Thus $\\left|a_{i}-\\frac{1}{2}\\right| \\geq \\frac{1}{2 n}$ for some $i$, as required. On the other hand, putting $n=2 m+1$ and $a_{i}=\\frac{m}{2 m+1}$ for all $i$ gives $\\sum a_{i}=m$, while\n\n$$\n\\left|a_{i}-\\frac{1}{2}\\right|=\\frac{1}{2}-\\frac{m}{2 m+1}=\\frac{1}{2(2 m+1)}=\\frac{1}{2 n}\n$$\n\nfor all $i$. Therefore, $f(n)=\\frac{1}{2 n}$ is the best possible for any odd $n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
+
{"year": "2006", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Prove that every positive integer can be written as a finite sum of distinct integral powers of the golden mean $\\tau=\\frac{1+\\sqrt{5}}{2}$. Here, an integral power of $\\tau$ is of the form $\\tau^{i}$, where $i$ is an integer (not necessarily positive).", "solution": "We will prove this statement by induction using the equality\n\n$$\n\\tau^{2}=\\tau+1\n$$\n\nIf $n=1$, then $1=\\tau^{0}$. Suppose that $n-1$ can be written as a finite sum of integral powers of $\\tau$, say\n\n$$\nn-1=\\sum_{i=-k}^{k} a_{i} \\tau^{i}\n$$\n\nwhere $a_{i} \\in\\{0,1\\}$ and $n \\geq 2$. We will write (1) as\n\n$$\nn-1=a_{k} \\cdots a_{1} a_{0} \\cdot a_{-1} a_{-2} \\cdots a_{-k}\n$$\n\nFor example,\n\n$$\n1=1.0=0.11=0.1011=0.101011\n$$\n\nFirstly, we will prove that we may assume that in (2) we have $a_{i} a_{i+1}=0$ for all $i$ with $-k \\leq i \\leq k-1$. Indeed, if we have several occurrences of 11 , then we take the leftmost such occurrence. Since we may assume that it is preceded by a 0 , we can replace 011 with 100 using the identity $\\tau^{i+1}+\\tau^{i}=\\tau^{i+2}$. By doing so repeatedly, if necessary, we will eliminate all occurrences of two 1's standing together. Now we have the representation\n\n$$\nn-1=\\sum_{i=-K}^{K} b_{i} \\tau^{i}\n$$\n\nwhere $b_{i} \\in\\{0,1\\}$ and $b_{i} b_{i+1}=0$.\nIf $b_{0}=0$ in (3), then we just add $1=\\tau^{0}$ to both sides of (3) and we are done.\nSuppose now that there is 1 in the unit position of (3), that is $b_{0}=1$. If there are two 0 's to the right of it, i.e.\n\n$$\nn-1=\\cdots 1.00 \\cdots\n$$\n\nthen we can replace 1.00 with 0.11 because $1=\\tau^{-1}+\\tau^{-2}$, and we are done because we obtain 0 in the unit position. Thus we may assume that\n\n$$\nn-1=\\cdots 1.010 \\cdots\n$$\n\nAgain, if we have $n-1=\\cdots 1.0100 \\cdots$, we may rewrite it as\n\n$$\nn-1=\\cdots 1.0100 \\cdots=\\cdots 1.0011 \\cdots=\\cdots 0.1111 \\cdots\n$$\n\nand obtain 0 in the unit position. Therefore, we may assume that\n\n$$\nn-1=\\cdots 1.01010 \\cdots\n$$\n\nSince the number of 1's is finite, eventually we will obtain an occurrence of 100 at the end, i.e.\n\n$$\nn-1=\\cdots 1.01010 \\cdots 100\n$$\n\nThen we can shift all 1's to the right to obtain 0 in the unit position, i.e.\n\n$$\nn-1=\\cdots 0.11 \\cdots 11\n$$\n\nand we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
+
{"year": "2006", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $p \\geq 5$ be a prime and let $r$ be the number of ways of placing $p$ checkers on a $p \\times p$ checkerboard so that not all checkers are in the same row (but they may all be in the same column). Show that $r$ is divisible by $p^{5}$. Here, we assume that all the checkers are identical.", "solution": "Note that $r=\\binom{p^{2}}{p}-p$. Hence, it suffices to show that\n\n$$\n\\left(p^{2}-1\\right)\\left(p^{2}-2\\right) \\cdots\\left(p^{2}-(p-1)\\right)-(p-1)!\\equiv 0 \\quad\\left(\\bmod p^{4}\\right)\n$$\n\nNow, let\n\n$$\nf(x):=(x-1)(x-2) \\cdots(x-(p-1))=x^{p-1}+s_{p-2} x^{p-2}+\\cdots+s_{1} x+s_{0} .\n$$\n\nThen the congruence equation (1) is same as $f\\left(p^{2}\\right)-s_{0} \\equiv 0\\left(\\bmod p^{4}\\right)$. Therefore, it suffices to show that $s_{1} p^{2} \\equiv 0\\left(\\bmod p^{4}\\right)$ or $s_{1} \\equiv 0\\left(\\bmod p^{2}\\right)$.\n\nSince $a^{p-1} \\equiv 1(\\bmod p)$ for all $1 \\leq a \\leq p-1$, we can factor\n\n$$\nx^{p-1}-1 \\equiv(x-1)(x-2) \\cdots(x-(p-1)) \\quad(\\bmod p)\n$$\n\nComparing the coefficients of the left hand side of (3) with those of the right hand side of (2), we obtain $p \\mid s_{i}$ for all $1 \\leq i \\leq p-2$ and $s_{0} \\equiv-1(\\bmod p)$. On the other hand, plugging $p$ for $x$ in (2), we get\n\n$$\nf(p)=(p-1)!=s_{0}=p^{p-1}+s_{p-2} p^{p-2}+\\cdots+s_{1} p+s_{0}\n$$\n\nwhich implies\n\n$$\np^{p-1}+s_{p-2} p^{p-2}+\\cdots+s_{2} p^{2}=-s_{1} p\n$$\n\nSince $p \\geq 5, p \\mid s_{2}$ and hence $s_{1} \\equiv 0\\left(\\bmod p^{2}\\right)$ as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
+
{"year": "2006", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $A, B$ be two distinct points on a given circle $O$ and let $P$ be the midpoint of the line segment $A B$. Let $O_{1}$ be the circle tangent to the line $A B$ at $P$ and tangent to the circle $O$. Let $\\ell$ be the tangent line, different from the line $A B$, to $O_{1}$ passing through $A$. Let $C$ be the intersection point, different from $A$, of $\\ell$ and $O$. Let $Q$ be the midpoint of the line segment $B C$ and $O_{2}$ be the circle tangent to the line $B C$ at $Q$ and tangent to the line segment $A C$. Prove that the circle $O_{2}$ is tangent to the circle $O$.", "solution": "Let $S$ be the tangent point of the circles $O$ and $O_{1}$ and let $T$ be the intersection point, different from $S$, of the circle $O$ and the line $S P$. Let $X$ be the tangent point of $\\ell$ to $O_{1}$ and let $M$ be the midpoint of the line segment $X P$. Since $\\angle T B P=\\angle A S P$, the triangle $T B P$ is similar to the triangle $A S P$. Therefore,\n\n$$\n\\frac{P T}{P B}=\\frac{P A}{P S}\n$$\n\nSince the line $\\ell$ is tangent to the circle $O_{1}$ at $X$, we have\n\n$$\n\\angle S P X=90^{\\circ}-\\angle X S P=90^{\\circ}-\\angle A P M=\\angle P A M\n$$\n\nwhich implies that the triangle $P A M$ is similar to the triangle $S P X$. Consequently,\n\n$$\n\\frac{X S}{X P}=\\frac{M P}{M A}=\\frac{X P}{2 M A} \\quad \\text { and } \\quad \\frac{X P}{P S}=\\frac{M A}{A P}\n$$\n\nFrom this and the above observation follows\n\n$$\n\\frac{X S}{X P} \\cdot \\frac{P T}{P B}=\\frac{X P}{2 M A} \\cdot \\frac{P A}{P S}=\\frac{X P}{2 M A} \\cdot \\frac{M A}{X P}=\\frac{1}{2} .\n$$\n\nLet $A^{\\prime}$ be the intersection point of the circle $O$ and the perpendicular bisector of the chord $B C$ such that $A, A^{\\prime}$ are on the same side of the line $B C$, and $N$ be the intersection point of the lines $A^{\\prime} Q$ and $C T$. Since\n\n$$\n\\angle N C Q=\\angle T C B=\\angle T C A=\\angle T B A=\\angle T B P\n$$\n\nand\n\n$$\n\\angle C A^{\\prime} Q=\\frac{\\angle C A B}{2}=\\frac{\\angle X A P}{2}=\\angle P A M=\\angle S P X,\n$$\n\nthe triangle $N C Q$ is similar to the triangle $T B P$ and the triangle $C A^{\\prime} Q$ is similar to the triangle $S P X$. Therefore\n\n$$\n\\frac{Q N}{Q C}=\\frac{P T}{P B} \\quad \\text { and } \\quad \\frac{Q C}{Q A^{\\prime}}=\\frac{X S}{X P} .\n$$\n\nand hence $Q A^{\\prime}=2 Q N$ by (1). This implies that $N$ is the midpoint of the line segment $Q A^{\\prime}$. Let the circle $O_{2}$ touch the line segment $A C$ at $Y$. Since\n\n$$\n\\angle A C N=\\angle A C T=\\angle B C T=\\angle Q C N\n$$\n\nand $|C Y|=|C Q|$, the triangles $Y C N$ and $Q C N$ are congruent and hence $N Y \\perp A C$ and $N Y=N Q=N A^{\\prime}$. Therefore, $N$ is the center of the circle $O_{2}$, which completes the proof.\n\nRemark: Analytic solutions are possible: For example, one can prove for a triangle $A B C$ inscribed in a circle $O$ that $A B=k(2+2 t), A C=k(1+2 t), B C=k(1+4 t)$ for some positive numbers $k, t$ if and only if there exists a circle $O_{1}$ such that $O_{1}$ is tangent to the side $A B$ at its midpoint, the side $A C$ and the circle $O$.\n\nOne obtains $A B=k^{\\prime}\\left(1+4 t^{\\prime}\\right), A C=k^{\\prime}\\left(1+2 t^{\\prime}\\right), B C=k^{\\prime}\\left(2+2 t^{\\prime}\\right)$ by substituting $t=1 / 4 t^{\\prime}$ and $k=2 k^{\\prime} t^{\\prime}$. So, there exists a circle $O_{2}$ such that $O_{2}$ is tangent to the side $B C$ at its midpoint, the side $A C$ and the circle $O$.\n\nIn the above, $t=\\tan ^{2} \\alpha$ and $k=\\frac{4 R \\tan \\alpha}{\\left(1+\\tan ^{2} \\alpha\\right)\\left(1+4 \\tan ^{2} \\alpha\\right)}$, where $R$ is the radius of $O$ and $\\angle A=2 \\alpha$. Furthermore, $t^{\\prime}=\\tan ^{2} \\gamma$ and $k^{\\prime}=\\frac{4 R \\tan \\gamma}{\\left(1+\\tan ^{2} \\gamma\\right)\\left(1+4 \\tan ^{2} \\gamma\\right)}$, where $\\angle C=2 \\gamma$. Observe that $\\sqrt{t t^{\\prime}}=\\tan \\alpha \\cdot \\tan \\gamma=\\frac{X S}{X P} \\cdot \\frac{P T}{P B}=\\frac{1}{2}$, which implies $t t^{\\prime}=\\frac{1}{4}$. It is now routine easy to check that $k=2 k^{\\prime} t^{\\prime}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
+
{"year": "2006", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set\nof colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.", "solution": "Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \\ldots, 12$. For each $i=1,2, \\ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\\{1,2, \\ldots, 12\\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \\neq S^{\\prime}$ implies $E_{S} \\cap E_{S^{\\prime}}=\\emptyset$, we have\n\n$$\n\\sum_{S}\\left|E_{S}\\right|=|C|=n\n$$\n\nwhere $S$ runs over all subsets of $\\{1,2, \\ldots, 12\\}$. Now for each $i$,\n\n$$\nE_{S} \\subseteq E_{i} \\quad \\text { if and only if } \\quad i \\in S\n$$\n\nand hence\n\n$$\n\\left|E_{i}\\right|=\\sum_{i \\in S}\\left|E_{S}\\right|\n$$\n\nBy assumption, we know that $\\left|E_{i}\\right| \\leq 20$ and that if $E_{S} \\neq \\emptyset$, then $|S| \\geq 5$. From this we obtain\n\n$$\n20 \\times 12 \\geq \\sum_{i=1}^{12}\\left|E_{i}\\right|=\\sum_{i=1}^{12}\\left(\\sum_{i \\in S}\\left|E_{S}\\right|\\right) \\geq 5 \\sum_{S}\\left|E_{S}\\right|=5 n\n$$\n\nTherefore $n \\leq 48$.\nNow, define a sequence $\\left\\{c_{i}\\right\\}_{i=1}^{52}$ of colours in the following way:\n$1234|5678| 9101112 \\mid$\n$4123|8567| 1291011 \\mid$\n$3412|7856| 1112910 \\mid$\n$2341|6785| 1011129 \\mid 1234$\n\nThe first row lists $c_{1}, \\ldots, c_{12}$ in order, the second row lists $c_{13}, \\ldots, c_{24}$ in order, the third row lists $c_{25}, \\ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \\ldots, c_{52}$ in order. For each $j, 1 \\leq j \\leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.\n\nRemark: The fact that $n \\leq 48$ can be obtained in a much simpler observation that\n\n$$\n5 n \\leq 12 \\times 20=240\n$$\n\nThere are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets\n\n$$\n\\begin{array}{cccc}\n\\{1,2,3,4,5,6\\}, & \\{3,4,5,6,7,8\\}, & \\{5,6,7,8,9,10\\}, & \\{7,8,9,10,11,12\\}, \\\\\n\\{9,10,11,12,1,2\\}, & \\{11,12,1,2,3,4\\}, & \\{1,2,5,6,9,10\\}, & \\{3,4,7,8,11,12\\} .\n\\end{array}\n$$\n\nEach of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.", "metadata": {"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
APMO/segmented/en-apmo2007_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2007", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.", "solution": "Without loss of generality, we may assume that $S$ contains only positive integers. Let\n\n$$\nS=\\left\\{2^{a_{i}} 3^{b_{i}} \\mid a_{i}, b_{i} \\in \\mathbb{Z}, a_{i}, b_{i} \\geq 0,1 \\leq i \\leq 9\\right\\}\n$$\n\nIt suffices to show that there are $1 \\leq i_{1}, i_{2}, i_{3} \\leq 9$ such that\n\n$$\na_{i_{1}}+a_{i_{2}}+a_{i_{3}} \\equiv b_{i_{1}}+b_{i_{2}}+b_{i_{3}} \\equiv 0 \\quad(\\bmod 3) .\n$$\n\nFor $n=2^{a} 3^{b} \\in S$, let's call $(a(\\bmod 3), b(\\bmod 3))$ the type of $n$. Then there are 9 possible types:\n\n$$\n(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\n$$\n\nLet $N(i, j)$ be the number of integers in $S$ of type $(i, j)$. We obtain 3 distinct integers whose product is a perfect cube when\n(1) $N(i, j) \\geq 3$ for some $i, j$, or\n(2) $N(i, 0) N(i, 1) N(i, 2) \\neq 0$ for some $i=0,1,2$, or\n(3) $N(0, j) N(1, j) N(2, j) \\neq 0$ for some $j=0,1,2$, or\n(4) $N\\left(i_{1}, j_{1}\\right) N\\left(i_{2}, j_{2}\\right) N\\left(i_{3}, j_{3}\\right) \\neq 0$, where $\\left\\{i_{1}, i_{2}, i_{3}\\right\\}=\\left\\{j_{1}, j_{2}, j_{3}\\right\\}=\\{0,1,2\\}$.\n\nAssume that none of the conditions (1) (3) holds. Since $N(i, j) \\leq 2$ for all $(i, j)$, there are at least five $N(i, j)$ 's that are nonzero. Furthermore, among those nonzero $N(i, j)$ 's, no three have the same $i$ nor the same $j$. Using these facts, one may easily conclude that the condition (4) should hold. (For example, if one places each nonzero $N(i, j)$ in the $(i, j)$-th box of a regular $3 \\times 3$ array of boxes whose rows and columns are indexed by 0,1 and 2 , then one can always find three boxes, occupied by at least one nonzero $N(i, j)$, whose rows and columns are all distinct. This implies (4).)", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2007", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.", "solution": "Up to $(\\dagger)$, we do the same as above and get 9 possible types:\n\n$$\n(a(\\bmod 3), b(\\bmod 3))=(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\n$$\n\nfor $n=2^{a} 3^{b} \\in S$.\nNote that (i) among any 5 integers, there exist 3 whose sum is $0(\\bmod 3)$, and that (ii) if $i, j, k \\in\\{0,1,2\\}$, then $i+j+k \\equiv 0(\\bmod 3)$ if and only if $i=j=k$ or $\\{i, j, k\\}=\\{0,1,2\\}$.\n\nLet's define\n$T$ : the set of types of the integers in $S$;\n$N(i)$ : the number of integers in $S$ of the type $(i, \\cdot)$;\n$M(i)$ : the number of integers $j \\in\\{0,1,2\\}$ such that $(i, j) \\in T$.\nIf $N(i) \\geq 5$ for some $i$, the result follows from (i). Otherwise, for some permutation $(i, j, k)$ of $(0,1,2)$,\n\n$$\nN(i) \\geq 3, \\quad N(j) \\geq 3, \\quad N(k) \\geq 1\n$$\n\nIf $M(i)$ or $M(j)$ is 1 or 3 , the result follows from (ii). Otherwise $M(i)=M(j)=2$. Then either\n\n$$\n(i, x),(i, y),(j, x),(j, y) \\in T \\quad \\text { or } \\quad(i, x),(i, y),(j, x),(j, z) \\in T\n$$\n\nfor some permutation $(x, y, z)$ of $(0,1,2)$. Since $N(k) \\geq 1$, at least one of $(k, x),(k, y)$ and $(k, z)$ contained in $T$. Therefore, in any case, the result follows from (ii). (For example, if $(k, y) \\in T$, then take $(i, y),(j, y),(k, y)$ or $(i, x),(j, z),(k, y)$ from T.)", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSecond solution."}}
|
| 3 |
-
{"year": "2007", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be an acute angled triangle with $\\angle B A C=60^{\\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that\n\n$$\n2 \\angle A H I=3 \\angle A B C .\n$$", "solution": "Let $D$ be the intersection point of the lines $A H$ and $B C$. Let $K$ be the intersection point of the circumcircle $O$ of the triangle $A B C$ and the line $A H$. Let the line through $I$ perpendicular to $B C$ meet $B C$ and the minor arc $B C$ of the circumcircle $O$ at $E$ and $N$, respectively. We have\n$\\angle B I C=180^{\\circ}-(\\angle I B C+\\angle I C B)=180^{\\circ}-\\frac{1}{2}(\\angle A B C+\\angle A C B)=90^{\\circ}+\\frac{1}{2} \\angle B A C=120^{\\circ}$\nand also $\\angle B N C=180^{\\circ}-\\angle B A C=120^{\\circ}=\\angle B I C$. Since $I N \\perp B C$, the quadrilateral $B I C N$ is a kite and thus $I E=E N$.\n\nNow, since $H$ is the orthocenter of the triangle $A B C, H D=D K$. Also because $E D \\perp I N$ and $E D \\perp H K$, we conclude that $I H K N$ is an isosceles trapezoid with $I H=N K$.\n\nHence\n\n$$\n\\angle A H I=180^{\\circ}-\\angle I H K=180^{\\circ}-\\angle A K N=\\angle A B N .\n$$\n\nSince $I E=E N$ and $B E \\perp I N$, the triangles $I B E$ and $N B E$ are congruent. Therefore\n\n$$\n\\angle N B E=\\angle I B E=\\angle I B C=\\angle I B A=\\frac{1}{2} \\angle A B C\n$$\n\nand thus\n\n$$\n\\angle A H I=\\angle A B N=\\frac{3}{2} \\angle A B C .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2007", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be an acute angled triangle with $\\angle B A C=60^{\\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that\n\n$$\n2 \\angle A H I=3 \\angle A B C .\n$$", "solution": "Let $P, Q$ and $R$ be the intersection points of $B H, C H$ and $A H$ with $A C, A B$ and $B C$, respectively. Then we have $\\angle I B H=\\angle I C H$. Indeed,\n\n$$\n\\angle I B H=\\angle A B P-\\angle A B I=30^{\\circ}-\\frac{1}{2} \\angle A B C\n$$\n\nand\n\n$$\n\\angle I C H=\\angle A C I-\\angle A C H=\\frac{1}{2} \\angle A C B-30^{\\circ}=30^{\\circ}-\\frac{1}{2} \\angle A B C,\n$$\n\nbecause $\\angle A B H=\\angle A C H=30^{\\circ}$ and $\\angle A C B+\\angle A B C=120^{\\circ}$. (Note that $\\angle A B P>\\angle A B I$ and $\\angle A C I>\\angle A C H$ because $A B$ is the longest side of the triangle $A B C$ under the given conditions.) Therefore BIHC is a cyclic quadrilateral and thus\n\n$$\n\\angle B H I=\\angle B C I=\\frac{1}{2} \\angle A C B .\n$$\n\nOn the other hand,\n\n$$\n\\angle B H R=90^{\\circ}-\\angle H B R=90^{\\circ}-(\\angle A B C-\\angle A B H)=120^{\\circ}-\\angle A B C\n$$\n\nTherefore,\n\n$$\n\\begin{aligned}\n\\angle A H I & =180^{\\circ}-\\angle B H I-\\angle B H R=60^{\\circ}-\\frac{1}{2} \\angle A C B+\\angle A B C \\\\\n& =60^{\\circ}-\\frac{1}{2}\\left(120^{\\circ}-\\angle A B C\\right)+\\angle A B C=\\frac{3}{2} \\angle A B C .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSecond solution."}}
|
| 5 |
-
{"year": "2007", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Consider $n$ disks $C_{1}, C_{2}, \\ldots, C_{n}$ in a plane such that for each $1 \\leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.", "solution": "The answer is $(n-1)(n-2) / 2$.\nLet's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\\mathcal{C}=\\left\\{C_{1}, \\ldots, C_{n}\\right\\}$, let $S_{\\mathcal{C}}=\\left\\{(i, j) \\mid C_{i}\\right.$ properly contains $\\left.C_{j}\\right\\}$. So, the score of an $n$-configuration $\\mathcal{C}$ is $\\left|S_{\\mathcal{C}}\\right|$.\n\nWe'll show that (i) there is an $n$-configuration $\\mathcal{C}$ for which $\\left|S_{\\mathcal{C}}\\right|=(n-1)(n-2) / 2$, and that (ii) $\\left|S_{\\mathcal{C}}\\right| \\leq(n-1)(n-2) / 2$ for any $n$-configuration $\\mathcal{C}$.\n\nLet $C_{1}$ be any disk. Then for $i=2, \\ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\\mathcal{C}}=\\{(i, j) \\mid 1 \\leq i<j \\leq n-1\\}$ of size $(n-1)(n-2) / 2$, which proves (i).\n\nFor any $n$-configuration $\\mathcal{C}, S_{\\mathcal{C}}$ must satisfy the following properties:\n(1) $(i, i) \\notin S_{\\mathcal{C}}$,\n(2) $(i+1, i) \\notin S_{\\mathcal{C}},(1, n) \\notin S_{\\mathcal{C}}$,\n(3) if $(i, j),(j, k) \\in S_{\\mathcal{C}}$, then $(i, k) \\in S_{\\mathcal{C}}$,\n(4) if $(i, j) \\in S_{\\mathcal{C}}$, then $(j, i) \\notin S_{\\mathcal{C}}$.\n\nNow we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \\sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \\leq i \\leq n$ or $(n, 1)$, since otherwise $G$ can have at most\n\n$$\n\\binom{n}{2}-n=\\frac{n(n-3)}{2}<\\frac{(n-1)(n-2)}{2}\n$$\n\nelements. Without loss of generality we may assume that $(n, 1) \\in G$. Then $(1, n-1) \\notin G$, since otherwise the condition (3) yields $(n, n-1) \\in G$ contradicting the condition (2). Now let $G^{\\prime}=\\{(i, j) \\in G \\mid 1 \\leq i, j \\leq n-1\\}$, then $G^{\\prime}$ satisfies the conditions (1) (4), with $n-1$.\n\nWe now claim that $\\left|G-G^{\\prime}\\right| \\leq n-2$ :\nSuppose that $\\left|G-G^{\\prime}\\right|>n-2$, then $\\left|G-G^{\\prime}\\right|=n-1$ and hence for each $1 \\leq i \\leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \\in G$ and $(n-1, n) \\in G$ (because $(n, n-1) \\notin G$ ) and this implies that $(n, n-2) \\notin G$ and $(n-2, n) \\in G$. If we keep doing this process, we obtain $(1, n) \\in G$, which is a contradiction.\n\nSince $\\left|G-G^{\\prime}\\right| \\leq n-2$, we obtain\n\n$$\n\\left|G^{\\prime}\\right| \\geq \\frac{(n-1)(n-2)}{2}-(n-2)=\\frac{(n-2)(n-3)}{2}\n$$\n\nThis, however, contradicts the minimality of $n$, and hence proves (ii).", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2007", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y$ and $z$ be positive real numbers such that $\\sqrt{x}+\\sqrt{y}+\\sqrt{z}=1$. Prove that\n\n$$\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq 1\n$$", "solution": "We first note that\n\n$$\n\\begin{aligned}\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}} & =\\frac{x^{2}-x(y+z)+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{x(y+z)}{\\sqrt{2 x^{2}(y+z)}} \\\\\n& =\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\sqrt{\\frac{y+z}{2}} \\\\\n& \\geq \\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{\\sqrt{y}+\\sqrt{z}}{2} .\n\\end{aligned}\n$$\n\nSimilarly, we have\n\n$$\n\\begin{aligned}\n& \\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}} \\geq \\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{\\sqrt{z}+\\sqrt{x}}{2}, \\\\\n& \\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq \\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\frac{\\sqrt{x}+\\sqrt{y}}{2} .\n\\end{aligned}\n$$\n\nWe now add (1) (3) to get\n\n$$\n\\begin{aligned}\n& \\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\\\\n& \\geq \\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z} \\\\\n& =\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+1 .\n\\end{aligned}\n$$\n\nThus, it suffices to show that\n\n$$\n\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}} \\geq 0 .\n$$\n\nNow, assume without loss of generality, that $x \\geq y \\geq z$. Then we have\n\n$$\n\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}} \\geq 0\n$$\n\nand\n\n$$\n\\begin{aligned}\n& \\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}=\\frac{(y-z)(x-z)}{\\sqrt{2 z^{2}(x+y)}}-\\frac{(y-z)(x-y)}{\\sqrt{2 y^{2}(z+x)}} \\\\\n& \\geq \\frac{(y-z)(x-y)}{\\sqrt{2 z^{2}(x+y)}}-\\frac{(y-z)(x-y)}{\\sqrt{2 y^{2}(z+x)}}=(y-z)(x-y)\\left(\\frac{1}{\\sqrt{2 z^{2}(x+y)}}-\\frac{1}{\\sqrt{2 y^{2}(z+x)}}\\right)\n\\end{aligned}\n$$\n\nThe last quantity is non-negative due to the fact that\n\n$$\ny^{2}(z+x)=y^{2} z+y^{2} x \\geq y z^{2}+z^{2} x=z^{2}(x+y)\n$$\n\nThis completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 7 |
-
{"year": "2007", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $x, y$ and $z$ be positive real numbers such that $\\sqrt{x}+\\sqrt{y}+\\sqrt{z}=1$. Prove that\n\n$$\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq 1\n$$", "solution": "By Cauchy-Schwarz inequality,\n\n$$\n\\begin{aligned}\n& \\left(\\frac{x^{2}}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}) \\geq(\\sqrt{x}+\\sqrt{y}+\\sqrt{z})^{2}=1\n\\end{aligned}\n$$\n\nand\n\n$$\n\\begin{aligned}\n& \\left(\\frac{y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{x y}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}) \\geq\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right)^{2}\n\\end{aligned}\n$$\n\nWe now combine (5) and (6) to find\n\n$$\n\\begin{aligned}\n& \\left(\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(x+y)}+\\sqrt{2(y+z)}+\\sqrt{2(z+x)}) \\\\\n& \\geq 1+\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right)^{2} \\geq 2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) .\n\\end{aligned}\n$$\n\nThus, it suffices to show that\n\n$$\n2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}\n$$\n\nConsider the following inequality using AM-GM inequality\n\n$$\n\\left[\\sqrt{\\frac{y z}{x}}+\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right)\\right]^{2} \\geq 4 \\sqrt{\\frac{y z}{x}}\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right)=2(y+z)\n$$\n\nor equivalently\n\n$$\n\\sqrt{\\frac{y z}{x}}+\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)} .\n$$\n\nSimilarly, we have\n\n$$\n\\begin{aligned}\n& \\sqrt{\\frac{z x}{y}}+\\left(\\frac{1}{2} \\sqrt{\\frac{x y}{z}}+\\frac{1}{2} \\sqrt{\\frac{y z}{x}}\\right) \\geq \\sqrt{2(z+x)} \\\\\n& \\sqrt{\\frac{x y}{z}}+\\left(\\frac{1}{2} \\sqrt{\\frac{y z}{x}}+\\frac{1}{2} \\sqrt{\\frac{z x}{y}}\\right) \\geq \\sqrt{2(x+y)}\n\\end{aligned}\n$$\n\nAdding the last three inequalities, we get\n\n$$\n2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)} .\n$$\n\nThis completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSecond solution."}}
|
| 8 |
-
{"year": "2007", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "A regular $(5 \\times 5)$-array of lights is defective, so that toggling the switch for one light causes each adjacent light in the same row and in the same column as well as the light itself to change state, from on to off, or from off to on. Initially all the lights are switched off. After a certain number of toggles, exactly one light is switched on. Find all the possible positions of this light.", "solution": "We assign the following first labels to the 25 positions of the lights:\n\n| 1 | 1 | 0 | 1 | 1 |\n| :--- | :--- | :--- | :--- | :--- |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 1 | 0 | 1 | 1 |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 1 | 0 | 1 | 1 |\n\nFor each on-off combination of lights in the array, define its first value to be the sum of the first labels of those positions at which the lights are switched on. It is easy to check that toggling any switch always leads to an on-off combination of lights whose first value has the same parity(the remainder when divided by 2) as that of the previous on-off combination.\n\nThe $90^{\\circ}$ rotation of the first labels gives us another labels (let us call it the second labels) which also makes the parity of the second value(the sum of the second labels of those positions at which the lights are switched on) invariant under toggling.\n\n| 1 | 0 | 1 | 0 | 1 |\n| :--- | :--- | :--- | :--- | :--- |\n| 1 | 0 | 1 | 0 | 1 |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 0 | 1 | 0 | 1 |\n| 1 | 0 | 1 | 0 | 1 |\n\nSince the parity of the first and the second values of the initial status is 0 , after certain number of toggles the parity must remain unchanged with respect to the first labels and the second labels as well. Therefore, if exactly one light is on after some number of toggles, the label of that position must be 0 with respect to both labels. Hence according to the above pictures, the possible positions are the ones marked with $*_{i}$ 's in the following picture:\n\n| | | | | |\n| :--- | :--- | :--- | :--- | :--- |\n| | $*_{2}$ | | $*_{1}$ | |\n| | | $*_{0}$ | | |\n| | $*_{3}$ | | $*_{4}$ | |\n| | | | | |\n\nNow we demonstrate that all five positions are possible:\nToggling the positions checked by t (the order of toggling is irrelevant) in the first picture makes the center $\\left(*_{0}\\right)$ the only position with light on and the second picture makes the position $*_{1}$ the only position with light on. The other $*_{i}$ 's can be obtained by rotating the second picture appropriately.\n\n\n| | t | | t | |\n| :---: | :---: | :---: | :---: | :---: |\n| t | t | | t | t |\n| | t | | | |\n| | | t | t | t |\n| | | | t | |", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2007", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.", "solution": "Without loss of generality, we may assume that $S$ contains only positive integers. Let\n\n$$\nS=\\left\\{2^{a_{i}} 3^{b_{i}} \\mid a_{i}, b_{i} \\in \\mathbb{Z}, a_{i}, b_{i} \\geq 0,1 \\leq i \\leq 9\\right\\}\n$$\n\nIt suffices to show that there are $1 \\leq i_{1}, i_{2}, i_{3} \\leq 9$ such that\n\n$$\na_{i_{1}}+a_{i_{2}}+a_{i_{3}} \\equiv b_{i_{1}}+b_{i_{2}}+b_{i_{3}} \\equiv 0 \\quad(\\bmod 3) .\n$$\n\nFor $n=2^{a} 3^{b} \\in S$, let's call $(a(\\bmod 3), b(\\bmod 3))$ the type of $n$. Then there are 9 possible types:\n\n$$\n(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\n$$\n\nLet $N(i, j)$ be the number of integers in $S$ of type $(i, j)$. We obtain 3 distinct integers whose product is a perfect cube when\n(1) $N(i, j) \\geq 3$ for some $i, j$, or\n(2) $N(i, 0) N(i, 1) N(i, 2) \\neq 0$ for some $i=0,1,2$, or\n(3) $N(0, j) N(1, j) N(2, j) \\neq 0$ for some $j=0,1,2$, or\n(4) $N\\left(i_{1}, j_{1}\\right) N\\left(i_{2}, j_{2}\\right) N\\left(i_{3}, j_{3}\\right) \\neq 0$, where $\\left\\{i_{1}, i_{2}, i_{3}\\right\\}=\\left\\{j_{1}, j_{2}, j_{3}\\right\\}=\\{0,1,2\\}$.\n\nAssume that none of the conditions (1) (3) holds. Since $N(i, j) \\leq 2$ for all $(i, j)$, there are at least five $N(i, j)$ 's that are nonzero. Furthermore, among those nonzero $N(i, j)$ 's, no three have the same $i$ nor the same $j$. Using these facts, one may easily conclude that the condition (4) should hold. (For example, if one places each nonzero $N(i, j)$ in the $(i, j)$-th box of a regular $3 \\times 3$ array of boxes whose rows and columns are indexed by 0,1 and 2 , then one can always find three boxes, occupied by at least one nonzero $N(i, j)$, whose rows and columns are all distinct. This implies (4).)", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2007", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.", "solution": "Up to $(\\dagger)$, we do the same as above and get 9 possible types:\n\n$$\n(a(\\bmod 3), b(\\bmod 3))=(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\n$$\n\nfor $n=2^{a} 3^{b} \\in S$.\nNote that (i) among any 5 integers, there exist 3 whose sum is $0(\\bmod 3)$, and that (ii) if $i, j, k \\in\\{0,1,2\\}$, then $i+j+k \\equiv 0(\\bmod 3)$ if and only if $i=j=k$ or $\\{i, j, k\\}=\\{0,1,2\\}$.\n\nLet's define\n$T$ : the set of types of the integers in $S$;\n$N(i)$ : the number of integers in $S$ of the type $(i, \\cdot)$;\n$M(i)$ : the number of integers $j \\in\\{0,1,2\\}$ such that $(i, j) \\in T$.\nIf $N(i) \\geq 5$ for some $i$, the result follows from (i). Otherwise, for some permutation $(i, j, k)$ of $(0,1,2)$,\n\n$$\nN(i) \\geq 3, \\quad N(j) \\geq 3, \\quad N(k) \\geq 1\n$$\n\nIf $M(i)$ or $M(j)$ is 1 or 3 , the result follows from (ii). Otherwise $M(i)=M(j)=2$. Then either\n\n$$\n(i, x),(i, y),(j, x),(j, y) \\in T \\quad \\text { or } \\quad(i, x),(i, y),(j, x),(j, z) \\in T\n$$\n\nfor some permutation $(x, y, z)$ of $(0,1,2)$. Since $N(k) \\geq 1$, at least one of $(k, x),(k, y)$ and $(k, z)$ contained in $T$. Therefore, in any case, the result follows from (ii). (For example, if $(k, y) \\in T$, then take $(i, y),(j, y),(k, y)$ or $(i, x),(j, z),(k, y)$ from T.)", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSecond solution."}}
|
| 3 |
+
{"year": "2007", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute angled triangle with $\\angle B A C=60^{\\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that\n\n$$\n2 \\angle A H I=3 \\angle A B C .\n$$", "solution": "Let $D$ be the intersection point of the lines $A H$ and $B C$. Let $K$ be the intersection point of the circumcircle $O$ of the triangle $A B C$ and the line $A H$. Let the line through $I$ perpendicular to $B C$ meet $B C$ and the minor arc $B C$ of the circumcircle $O$ at $E$ and $N$, respectively. We have\n$\\angle B I C=180^{\\circ}-(\\angle I B C+\\angle I C B)=180^{\\circ}-\\frac{1}{2}(\\angle A B C+\\angle A C B)=90^{\\circ}+\\frac{1}{2} \\angle B A C=120^{\\circ}$\nand also $\\angle B N C=180^{\\circ}-\\angle B A C=120^{\\circ}=\\angle B I C$. Since $I N \\perp B C$, the quadrilateral $B I C N$ is a kite and thus $I E=E N$.\n\nNow, since $H$ is the orthocenter of the triangle $A B C, H D=D K$. Also because $E D \\perp I N$ and $E D \\perp H K$, we conclude that $I H K N$ is an isosceles trapezoid with $I H=N K$.\n\nHence\n\n$$\n\\angle A H I=180^{\\circ}-\\angle I H K=180^{\\circ}-\\angle A K N=\\angle A B N .\n$$\n\nSince $I E=E N$ and $B E \\perp I N$, the triangles $I B E$ and $N B E$ are congruent. Therefore\n\n$$\n\\angle N B E=\\angle I B E=\\angle I B C=\\angle I B A=\\frac{1}{2} \\angle A B C\n$$\n\nand thus\n\n$$\n\\angle A H I=\\angle A B N=\\frac{3}{2} \\angle A B C .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2007", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute angled triangle with $\\angle B A C=60^{\\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that\n\n$$\n2 \\angle A H I=3 \\angle A B C .\n$$", "solution": "Let $P, Q$ and $R$ be the intersection points of $B H, C H$ and $A H$ with $A C, A B$ and $B C$, respectively. Then we have $\\angle I B H=\\angle I C H$. Indeed,\n\n$$\n\\angle I B H=\\angle A B P-\\angle A B I=30^{\\circ}-\\frac{1}{2} \\angle A B C\n$$\n\nand\n\n$$\n\\angle I C H=\\angle A C I-\\angle A C H=\\frac{1}{2} \\angle A C B-30^{\\circ}=30^{\\circ}-\\frac{1}{2} \\angle A B C,\n$$\n\nbecause $\\angle A B H=\\angle A C H=30^{\\circ}$ and $\\angle A C B+\\angle A B C=120^{\\circ}$. (Note that $\\angle A B P>\\angle A B I$ and $\\angle A C I>\\angle A C H$ because $A B$ is the longest side of the triangle $A B C$ under the given conditions.) Therefore BIHC is a cyclic quadrilateral and thus\n\n$$\n\\angle B H I=\\angle B C I=\\frac{1}{2} \\angle A C B .\n$$\n\nOn the other hand,\n\n$$\n\\angle B H R=90^{\\circ}-\\angle H B R=90^{\\circ}-(\\angle A B C-\\angle A B H)=120^{\\circ}-\\angle A B C\n$$\n\nTherefore,\n\n$$\n\\begin{aligned}\n\\angle A H I & =180^{\\circ}-\\angle B H I-\\angle B H R=60^{\\circ}-\\frac{1}{2} \\angle A C B+\\angle A B C \\\\\n& =60^{\\circ}-\\frac{1}{2}\\left(120^{\\circ}-\\angle A B C\\right)+\\angle A B C=\\frac{3}{2} \\angle A B C .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSecond solution."}}
|
| 5 |
+
{"year": "2007", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Consider $n$ disks $C_{1}, C_{2}, \\ldots, C_{n}$ in a plane such that for each $1 \\leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.", "solution": "The answer is $(n-1)(n-2) / 2$.\nLet's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\\mathcal{C}=\\left\\{C_{1}, \\ldots, C_{n}\\right\\}$, let $S_{\\mathcal{C}}=\\left\\{(i, j) \\mid C_{i}\\right.$ properly contains $\\left.C_{j}\\right\\}$. So, the score of an $n$-configuration $\\mathcal{C}$ is $\\left|S_{\\mathcal{C}}\\right|$.\n\nWe'll show that (i) there is an $n$-configuration $\\mathcal{C}$ for which $\\left|S_{\\mathcal{C}}\\right|=(n-1)(n-2) / 2$, and that (ii) $\\left|S_{\\mathcal{C}}\\right| \\leq(n-1)(n-2) / 2$ for any $n$-configuration $\\mathcal{C}$.\n\nLet $C_{1}$ be any disk. Then for $i=2, \\ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\\mathcal{C}}=\\{(i, j) \\mid 1 \\leq i<j \\leq n-1\\}$ of size $(n-1)(n-2) / 2$, which proves (i).\n\nFor any $n$-configuration $\\mathcal{C}, S_{\\mathcal{C}}$ must satisfy the following properties:\n(1) $(i, i) \\notin S_{\\mathcal{C}}$,\n(2) $(i+1, i) \\notin S_{\\mathcal{C}},(1, n) \\notin S_{\\mathcal{C}}$,\n(3) if $(i, j),(j, k) \\in S_{\\mathcal{C}}$, then $(i, k) \\in S_{\\mathcal{C}}$,\n(4) if $(i, j) \\in S_{\\mathcal{C}}$, then $(j, i) \\notin S_{\\mathcal{C}}$.\n\nNow we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \\sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \\leq i \\leq n$ or $(n, 1)$, since otherwise $G$ can have at most\n\n$$\n\\binom{n}{2}-n=\\frac{n(n-3)}{2}<\\frac{(n-1)(n-2)}{2}\n$$\n\nelements. Without loss of generality we may assume that $(n, 1) \\in G$. Then $(1, n-1) \\notin G$, since otherwise the condition (3) yields $(n, n-1) \\in G$ contradicting the condition (2). Now let $G^{\\prime}=\\{(i, j) \\in G \\mid 1 \\leq i, j \\leq n-1\\}$, then $G^{\\prime}$ satisfies the conditions (1) (4), with $n-1$.\n\nWe now claim that $\\left|G-G^{\\prime}\\right| \\leq n-2$ :\nSuppose that $\\left|G-G^{\\prime}\\right|>n-2$, then $\\left|G-G^{\\prime}\\right|=n-1$ and hence for each $1 \\leq i \\leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \\in G$ and $(n-1, n) \\in G$ (because $(n, n-1) \\notin G$ ) and this implies that $(n, n-2) \\notin G$ and $(n-2, n) \\in G$. If we keep doing this process, we obtain $(1, n) \\in G$, which is a contradiction.\n\nSince $\\left|G-G^{\\prime}\\right| \\leq n-2$, we obtain\n\n$$\n\\left|G^{\\prime}\\right| \\geq \\frac{(n-1)(n-2)}{2}-(n-2)=\\frac{(n-2)(n-3)}{2}\n$$\n\nThis, however, contradicts the minimality of $n$, and hence proves (ii).", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2007", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y$ and $z$ be positive real numbers such that $\\sqrt{x}+\\sqrt{y}+\\sqrt{z}=1$. Prove that\n\n$$\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq 1\n$$", "solution": "We first note that\n\n$$\n\\begin{aligned}\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}} & =\\frac{x^{2}-x(y+z)+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{x(y+z)}{\\sqrt{2 x^{2}(y+z)}} \\\\\n& =\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\sqrt{\\frac{y+z}{2}} \\\\\n& \\geq \\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{\\sqrt{y}+\\sqrt{z}}{2} .\n\\end{aligned}\n$$\n\nSimilarly, we have\n\n$$\n\\begin{aligned}\n& \\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}} \\geq \\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{\\sqrt{z}+\\sqrt{x}}{2}, \\\\\n& \\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq \\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\frac{\\sqrt{x}+\\sqrt{y}}{2} .\n\\end{aligned}\n$$\n\nWe now add (1) (3) to get\n\n$$\n\\begin{aligned}\n& \\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\\\\n& \\geq \\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\sqrt{x}+\\sqrt{y}+\\sqrt{z} \\\\\n& =\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+1 .\n\\end{aligned}\n$$\n\nThus, it suffices to show that\n\n$$\n\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}+\\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}} \\geq 0 .\n$$\n\nNow, assume without loss of generality, that $x \\geq y \\geq z$. Then we have\n\n$$\n\\frac{(x-y)(x-z)}{\\sqrt{2 x^{2}(y+z)}} \\geq 0\n$$\n\nand\n\n$$\n\\begin{aligned}\n& \\frac{(z-x)(z-y)}{\\sqrt{2 z^{2}(x+y)}}+\\frac{(y-z)(y-x)}{\\sqrt{2 y^{2}(z+x)}}=\\frac{(y-z)(x-z)}{\\sqrt{2 z^{2}(x+y)}}-\\frac{(y-z)(x-y)}{\\sqrt{2 y^{2}(z+x)}} \\\\\n& \\geq \\frac{(y-z)(x-y)}{\\sqrt{2 z^{2}(x+y)}}-\\frac{(y-z)(x-y)}{\\sqrt{2 y^{2}(z+x)}}=(y-z)(x-y)\\left(\\frac{1}{\\sqrt{2 z^{2}(x+y)}}-\\frac{1}{\\sqrt{2 y^{2}(z+x)}}\\right)\n\\end{aligned}\n$$\n\nThe last quantity is non-negative due to the fact that\n\n$$\ny^{2}(z+x)=y^{2} z+y^{2} x \\geq y z^{2}+z^{2} x=z^{2}(x+y)\n$$\n\nThis completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 7 |
+
{"year": "2007", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $x, y$ and $z$ be positive real numbers such that $\\sqrt{x}+\\sqrt{y}+\\sqrt{z}=1$. Prove that\n\n$$\n\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}} \\geq 1\n$$", "solution": "By Cauchy-Schwarz inequality,\n\n$$\n\\begin{aligned}\n& \\left(\\frac{x^{2}}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}) \\geq(\\sqrt{x}+\\sqrt{y}+\\sqrt{z})^{2}=1\n\\end{aligned}\n$$\n\nand\n\n$$\n\\begin{aligned}\n& \\left(\\frac{y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{x y}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}) \\geq\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right)^{2}\n\\end{aligned}\n$$\n\nWe now combine (5) and (6) to find\n\n$$\n\\begin{aligned}\n& \\left(\\frac{x^{2}+y z}{\\sqrt{2 x^{2}(y+z)}}+\\frac{y^{2}+z x}{\\sqrt{2 y^{2}(z+x)}}+\\frac{z^{2}+x y}{\\sqrt{2 z^{2}(x+y)}}\\right) \\\\\n& \\quad \\times(\\sqrt{2(x+y)}+\\sqrt{2(y+z)}+\\sqrt{2(z+x)}) \\\\\n& \\geq 1+\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right)^{2} \\geq 2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) .\n\\end{aligned}\n$$\n\nThus, it suffices to show that\n\n$$\n2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)}\n$$\n\nConsider the following inequality using AM-GM inequality\n\n$$\n\\left[\\sqrt{\\frac{y z}{x}}+\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right)\\right]^{2} \\geq 4 \\sqrt{\\frac{y z}{x}}\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right)=2(y+z)\n$$\n\nor equivalently\n\n$$\n\\sqrt{\\frac{y z}{x}}+\\left(\\frac{1}{2} \\sqrt{\\frac{z x}{y}}+\\frac{1}{2} \\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)} .\n$$\n\nSimilarly, we have\n\n$$\n\\begin{aligned}\n& \\sqrt{\\frac{z x}{y}}+\\left(\\frac{1}{2} \\sqrt{\\frac{x y}{z}}+\\frac{1}{2} \\sqrt{\\frac{y z}{x}}\\right) \\geq \\sqrt{2(z+x)} \\\\\n& \\sqrt{\\frac{x y}{z}}+\\left(\\frac{1}{2} \\sqrt{\\frac{y z}{x}}+\\frac{1}{2} \\sqrt{\\frac{z x}{y}}\\right) \\geq \\sqrt{2(x+y)}\n\\end{aligned}\n$$\n\nAdding the last three inequalities, we get\n\n$$\n2\\left(\\sqrt{\\frac{y z}{x}}+\\sqrt{\\frac{z x}{y}}+\\sqrt{\\frac{x y}{z}}\\right) \\geq \\sqrt{2(y+z)}+\\sqrt{2(z+x)}+\\sqrt{2(x+y)} .\n$$\n\nThis completes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSecond solution."}}
|
| 8 |
+
{"year": "2007", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "A regular $(5 \\times 5)$-array of lights is defective, so that toggling the switch for one light causes each adjacent light in the same row and in the same column as well as the light itself to change state, from on to off, or from off to on. Initially all the lights are switched off. After a certain number of toggles, exactly one light is switched on. Find all the possible positions of this light.", "solution": "We assign the following first labels to the 25 positions of the lights:\n\n| 1 | 1 | 0 | 1 | 1 |\n| :--- | :--- | :--- | :--- | :--- |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 1 | 0 | 1 | 1 |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 1 | 0 | 1 | 1 |\n\nFor each on-off combination of lights in the array, define its first value to be the sum of the first labels of those positions at which the lights are switched on. It is easy to check that toggling any switch always leads to an on-off combination of lights whose first value has the same parity(the remainder when divided by 2) as that of the previous on-off combination.\n\nThe $90^{\\circ}$ rotation of the first labels gives us another labels (let us call it the second labels) which also makes the parity of the second value(the sum of the second labels of those positions at which the lights are switched on) invariant under toggling.\n\n| 1 | 0 | 1 | 0 | 1 |\n| :--- | :--- | :--- | :--- | :--- |\n| 1 | 0 | 1 | 0 | 1 |\n| 0 | 0 | 0 | 0 | 0 |\n| 1 | 0 | 1 | 0 | 1 |\n| 1 | 0 | 1 | 0 | 1 |\n\nSince the parity of the first and the second values of the initial status is 0 , after certain number of toggles the parity must remain unchanged with respect to the first labels and the second labels as well. Therefore, if exactly one light is on after some number of toggles, the label of that position must be 0 with respect to both labels. Hence according to the above pictures, the possible positions are the ones marked with $*_{i}$ 's in the following picture:\n\n| | | | | |\n| :--- | :--- | :--- | :--- | :--- |\n| | $*_{2}$ | | $*_{1}$ | |\n| | | $*_{0}$ | | |\n| | $*_{3}$ | | $*_{4}$ | |\n| | | | | |\n\nNow we demonstrate that all five positions are possible:\nToggling the positions checked by t (the order of toggling is irrelevant) in the first picture makes the center $\\left(*_{0}\\right)$ the only position with light on and the second picture makes the position $*_{1}$ the only position with light on. The other $*_{i}$ 's can be obtained by rotating the second picture appropriately.\n\n\n| | t | | t | |\n| :---: | :---: | :---: | :---: | :---: |\n| t | t | | t | t |\n| | t | | | |\n| | | t | t | t |\n| | | | t | |", "metadata": {"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2008_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2008", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with $\\angle A<60^{\\circ}$. Let $X$ and $Y$ be the points on the sides $A B$ and $A C$, respectively, such that $C A+A X=C B+B X$ and $B A+A Y=B C+C Y$. Let $P$ be the point in the plane such that the lines $P X$ and $P Y$ are perpendicular to $A B$ and $A C$, respectively. Prove that $\\angle B P C<120^{\\circ}$.", "solution": "Let $I$ be the incenter of $\\triangle A B C$, and let the feet of the perpendiculars from $I$ to $A B$ and to $A C$ be $D$ and $E$, respectively. (Without loss of generality, we may assume that $A C$ is the longest side. Then $X$ lies on the line segment $A D$. Although $P$ may or may not lie inside $\\triangle A B C$, the proof below works for both cases. Note that $P$ is on the line perpendicular to $A B$ passing through $X$.) Let $O$ be the midpoint of $I P$, and let the feet of the perpendiculars from $O$ to $A B$ and to $A C$ be $M$ and $N$, respectively. Then $M$ and $N$ are the midpoints of $D X$ and $E Y$, respectively.\n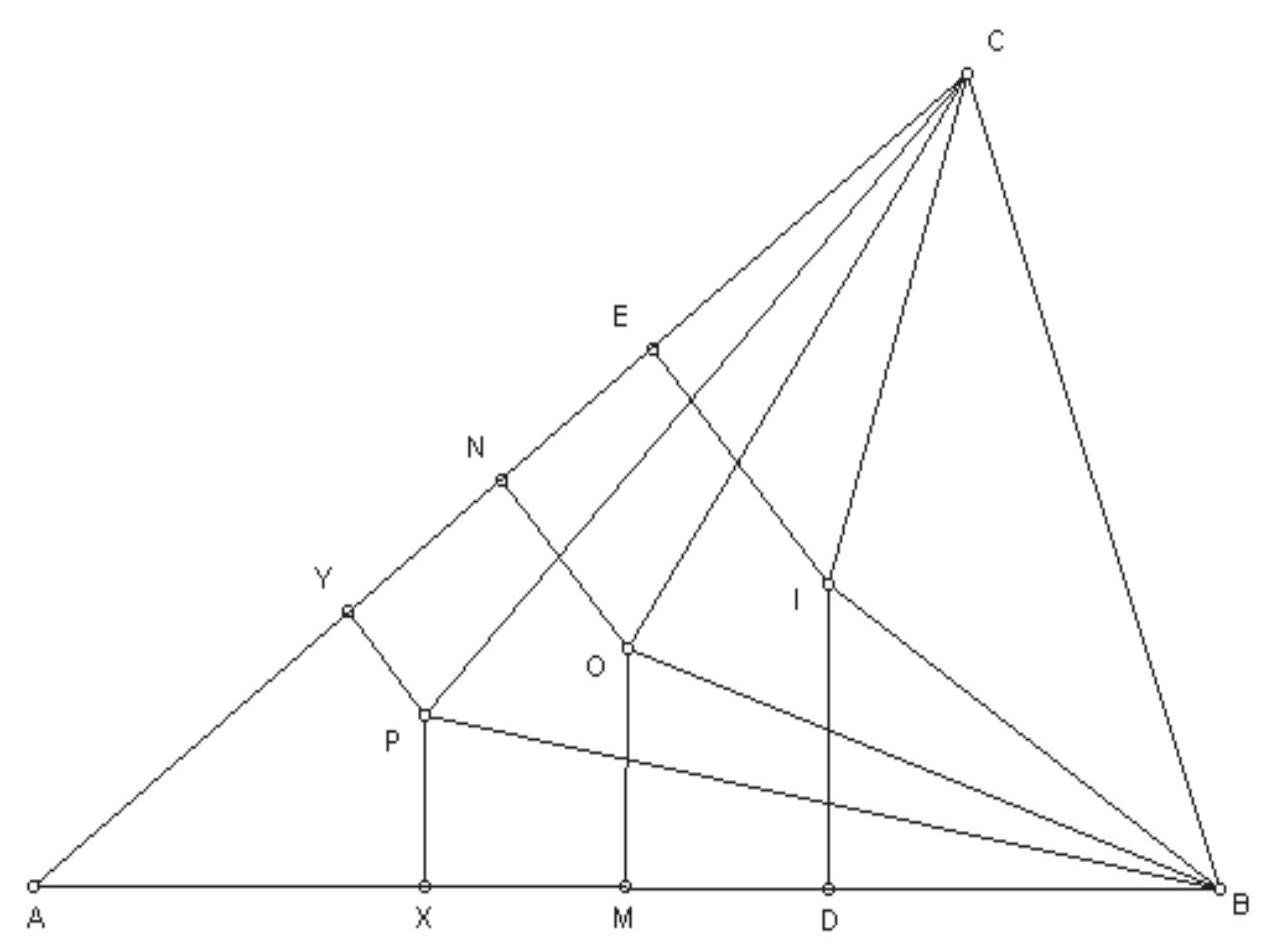\n\nThe conditions on the points $X$ and $Y$ yield the equations\n\n$$\nA X=\\frac{A B+B C-C A}{2} \\quad \\text { and } \\quad A Y=\\frac{B C+C A-A B}{2} .\n$$\n\nFrom $A D=A E=\\frac{C A+A B-B C}{2}$, we obtain\n\n$$\nB D=A B-A D=A B-\\frac{C A+A B-B C}{2}=\\frac{A B+B C-C A}{2}=A X .\n$$\n\nSince $M$ is the midpoint of $D X$, it follows that $M$ is the midpoint of $A B$. Similarly, $N$ is the midpoint of $A C$. Therefore, the perpendicular bisectors of $A B$ and $A C$ meet at $O$, that is, $O$ is the circumcenter of $\\triangle A B C$. Since $\\angle B A C<60^{\\circ}, O$ lies on the same side of $B C$ as the point $A$ and\n\n$$\n\\angle B O C=2 \\angle B A C\n$$\n\nWe can compute $\\angle B I C$ as follows:\n\n$$\n\\begin{aligned}\n\\angle B I C & =180^{\\circ}-\\angle I B C-\\angle I C B=180^{\\circ}-\\frac{1}{2} \\angle A B C-\\frac{1}{2} \\angle A C B \\\\\n& =180^{\\circ}-\\frac{1}{2}(\\angle A B C+\\angle A C B)=180^{\\circ}-\\frac{1}{2}\\left(180^{\\circ}-\\angle B A C\\right)=90^{\\circ}+\\frac{1}{2} \\angle B A C\n\\end{aligned}\n$$\n\nIt follows from $\\angle B A C<60^{\\circ}$ that\n\n$$\n2 \\angle B A C<90^{\\circ}+\\frac{1}{2} \\angle B A C, \\quad \\text { i.e., } \\quad \\angle B O C<\\angle B I C \\text {. }\n$$\n\nFrom this it follows that $I$ lies inside the circumcircle of the isosceles triangle $B O C$ because $O$ and $I$ lie on the same side of $B C$. However, as $O$ is the midpoint of $I P, P$ must lie outside the circumcircle of triangle $B O C$ and on the same side of $B C$ as $O$. Therefore\n\n$$\n\\angle B P C<\\angle B O C=2 \\angle B A C<120^{\\circ} .\n$$\n\nRemark. If one assumes that $\\angle A$ is smaller than the other two, then it is clear that the line $P X$ (or the line perpendicular to $A B$ at $X$ if $P=X$ ) runs through the excenter $I_{C}$ of the excircle tangent to the side $A B$. Since $2 \\angle A C I_{C}=\\angle A C B$ and $B C<A C$, we have $2 \\angle P C B>\\angle C$. Similarly, $2 \\angle P B C>\\angle B$. Therefore,\n\n$$\n\\angle B P C=180^{\\circ}-(\\angle P B C+\\angle P C B)<180^{\\circ}-\\left(\\frac{\\angle B+\\angle C}{2}\\right)=90+\\frac{\\angle A}{2}<120^{\\circ}\n$$\n\nIn this way, a special case of the problem can be easily proved.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
-
{"year": "2008", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Students in a class form groups each of which contains exactly three members such that any two distinct groups have at most one member in common. Prove that, when the class size is 46 , there is a set of 10 students in which no group is properly contained.", "solution": "We let $C$ be the set of all 46 students in the class and let\n\n$$\ns:=\\max \\{|S|: S \\subseteq C \\text { such that } S \\text { contains no group properly }\\}\n$$\n\nThen it suffices to prove that $s \\geq 10$. (If $|S|=s>10$, we may choose a subset of $S$ consisting of 10 students.)\n\nSuppose that $s \\leq 9$ and let $S$ be a set of size $s$ in which no group is properly contained. Take any student, say $v$, from outside $S$. Because of the maximality of $s$, there should be a group containing the student $v$ and two other students in $S$. The number of ways to choose two students from $S$ is\n\n$$\n\\binom{s}{2} \\leq\\binom{ 9}{2}=36\n$$\n\nOn the other hand, there are at least $37=46-9$ students outside of $S$. Thus, among those 37 students outside, there is at least one student, say $u$, who does not belong to any group containing two students in $S$ and one outside. This is because no two distinct groups have two members in common. But then, $S$ can be enlarged by including $u$, which is a contradiction.\n\nRemark. One may choose a subset $S$ of $C$ that contains no group properly. Then, assuming $|S|<10$, prove that there is a student outside $S$, say $u$, who does not belong to any group containing two students in $S$. After enlarging $S$ by including $u$, prove that the enlarged $S$ still contains no group properly.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
-
{"year": "2008", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of a triangle $A B C$. A circle passing through points $A$ and $C$ meets the sides $B C$ and $B A$ at $D$ and $E$, respectively. The lines $A D$ and $C E$ meet $\\Gamma$ again at $G$ and $H$, respectively. The tangent lines of $\\Gamma$ at $A$ and $C$ meet the line $D E$ at $L$ and $M$, respectively. Prove that the lines $L H$ and $M G$ meet at $\\Gamma$.", "solution": "Let $M G$ meet $\\Gamma$ at $P$. Since $\\angle M C D=\\angle C A E$ and $\\angle M D C=\\angle C A E$, we have $M C=M D$. Thus\n\n$$\nM D^{2}=M C^{2}=M G \\cdot M P\n$$\n\nand hence $M D$ is tangent to the circumcircle of $\\triangle D G P$. Therefore $\\angle D G P=\\angle E D P$.\nLet $\\Gamma^{\\prime}$ be the circumcircle of $\\triangle B D E$. If $B=P$, then, since $\\angle B G D=\\angle B D E$, the tangent lines of $\\Gamma^{\\prime}$ and $\\Gamma$ at $B$ should coincide, that is $\\Gamma^{\\prime}$ is tangent to $\\Gamma$ from inside. Let $B \\neq P$. If $P$ lies in the same side of the line $B C$ as $G$, then we have\n\n$$\n\\angle E D P+\\angle A B P=180^{\\circ}\n$$\n\nbecause $\\angle D G P+\\angle A B P=180^{\\circ}$. That is, the quadrilateral $B P D E$ is cyclic, and hence $P$ is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$.\n\n\nOtherwise,\n\n$$\n\\angle E D P=\\angle D G P=\\angle A G P=\\angle A B P=\\angle E B P .\n$$\n\nTherefore the quadrilateral $P B D E$ is cyclic, and hence $P$ again is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$.\n\nSimilarly, if $L H$ meets $\\Gamma$ at $Q$, we either have $Q=B$, in which case $\\Gamma^{\\prime}$ is tangent to $\\Gamma$ from inside, or $Q \\neq B$. In the latter case, $Q$ is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$. In either case, we have $P=Q$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
-
{"year": "2008", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Consider the function $f: \\mathbb{N}_{0} \\rightarrow \\mathbb{N}_{0}$, where $\\mathbb{N}_{0}$ is the set of all non-negative integers, defined by the following conditions:\n(i) $f(0)=0$,\n(ii) $f(2 n)=2 f(n)$ and\n(iii) $f(2 n+1)=n+2 f(n)$ for all $n \\geq 0$.\n(a) Determine the three sets $L:=\\{n \\mid f(n)<f(n+1)\\}, E:=\\{n \\mid f(n)=f(n+1)\\}$, and $G:=\\{n \\mid f(n)>f(n+1)\\}$.\n(b) For each $k \\geq 0$, find a formula for $a_{k}:=\\max \\left\\{f(n): 0 \\leq n \\leq 2^{k}\\right\\}$ in terms of $k$.", "solution": "(a) Let\n\n$$\nL_{1}:=\\{2 k: k>0\\}, \\quad E_{1}:=\\{0\\} \\cup\\{4 k+1: k \\geq 0\\}, \\quad \\text { and } G_{1}:=\\{4 k+3: k \\geq 0\\} .\n$$\n\nWe will show that $L_{1}=L, E_{1}=E$, and $G_{1}=G$. It suffices to verify that $L_{1} \\subseteq E, E_{1} \\subseteq E$, and $G_{1} \\subseteq G$ because $L_{1}, E_{1}$, and $G_{1}$ are mutually disjoint and $L_{1} \\cup E_{1} \\cup G_{1}=\\mathbb{N}_{0}$.\n\nFirstly, if $k>0$, then $f(2 k)-f(2 k+1)=-k<0$ and therefore $L_{1} \\subseteq L$.\nSecondly, $f(0)=0$ and\n\n$$\n\\begin{aligned}\n& f(4 k+1)=2 k+2 f(2 k)=2 k+4 f(k) \\\\\n& f(4 k+2)=2 f(2 k+1)=2(k+2 f(k))=2 k+4 f(k)\n\\end{aligned}\n$$\n\nfor all $k \\geq 0$. Thus, $E_{1} \\subseteq E$.\nLastly, in order to prove $G_{1} \\subset G$, we claim that $f(n+1)-f(n) \\leq n$ for all $n$. (In fact, one can prove a stronger inequality : $f(n+1)-f(n) \\leq n / 2$.) This is clearly true for even $n$ from the definition since for $n=2 t$,\n\n$$\nf(2 t+1)-f(2 t)=t \\leq n\n$$\n\nIf $n=2 t+1$ is odd, then (assuming inductively that the result holds for all nonnegative $m<n$ ), we have\n\n$$\n\\begin{aligned}\nf(n+1)-f(n) & =f(2 t+2)-f(2 t+1)=2 f(t+1)-t-2 f(t) \\\\\n& =2(f(t+1)-f(t))-t \\leq 2 t-t=t<n .\n\\end{aligned}\n$$\n\nFor all $k \\geq 0$,\n\n$$\n\\begin{aligned}\n& f(4 k+4)-f(4 k+3)=f(2(2 k+2))-f(2(2 k+1)+1) \\\\\n& =4 f(k+1)-(2 k+1+2 f(2 k+1))=4 f(k+1)-(2 k+1+2 k+4 f(k)) \\\\\n& =4(f(k+1)-f(k))-(4 k+1) \\leq 4 k-(4 k+1)<0 .\n\\end{aligned}\n$$\n\nThis proves $G_{1} \\subseteq G$.\n(b) Note that $a_{0}=a_{1}=f(1)=0$. Let $k \\geq 2$ and let $N_{k}=\\left\\{0,1,2, \\ldots, 2^{k}\\right\\}$. First we claim that the maximum $a_{k}$ occurs at the largest number in $G \\cap N_{k}$, that is, $a_{k}=f\\left(2^{k}-1\\right)$. We use mathematical induction on $k$ to prove the claim. Note that $a_{2}=f(3)=f\\left(2^{2}-1\\right)$.\n\nNow let $k \\geq 3$. For every even number $2 t$ with $2^{k-1}+1<2 t \\leq 2^{k}$,\n\n$$\nf(2 t)=2 f(t) \\leq 2 a_{k-1}=2 f\\left(2^{k-1}-1\\right)\n$$\n\nby induction hypothesis. For every odd number $2 t+1$ with $2^{k-1}+1 \\leq 2 t+1<2^{k}$,\n\n$$\n\\begin{aligned}\nf(2 t+1) & =t+2 f(t) \\leq 2^{k-1}-1+2 f(t) \\\\\n& \\leq 2^{k-1}-1+2 a_{k-1}=2^{k-1}-1+2 f\\left(2^{k-1}-1\\right)\n\\end{aligned}\n$$\n\nagain by induction hypothesis. Combining ( $\\dagger$ ), ( $\\ddagger$ ) and\n\n$$\nf\\left(2^{k}-1\\right)=f\\left(2\\left(2^{k-1}-1\\right)+1\\right)=2^{k-1}-1+2 f\\left(2^{k-1}-1\\right)\n$$\n\nwe may conclude that $a_{k}=f\\left(2^{k}-1\\right)$ as desired.\nFurthermore, we obtain\n\n$$\na_{k}=2 a_{k-1}+2^{k-1}-1\n$$\n\nfor all $k \\geq 3$. Note that this recursive formula for $a_{k}$ also holds for $k \\geq 0,1$ and 2 . Unwinding this recursive formula, we finally get\n\n$$\n\\begin{aligned}\na_{k} & =2 a_{k-1}+2^{k-1}-1=2\\left(2 a_{k-2}+2^{k-2}-1\\right)+2^{k-1}-1 \\\\\n& =2^{2} a_{k-2}+2 \\cdot 2^{k-1}-2-1=2^{2}\\left(2 a_{k-3}+2^{k-3}-1\\right)+2 \\cdot 2^{k-1}-2-1 \\\\\n& =2^{3} a_{k-3}+3 \\cdot 2^{k-1}-2^{2}-2-1 \\\\\n& \\vdots \\\\\n& =2^{k} a_{0}+k 2^{k-1}-2^{k-1}-2^{k-2}-\\ldots-2-1 \\\\\n& =k 2^{k-1}-2^{k}+1 \\quad \\text { for all } k \\geq 0 .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
-
{"year": "2008", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $a, b, c$ be integers satisfying $0<a<c-1$ and $1<b<c$. For each $k$, $0 \\leq k \\leq a$, let $r_{k}, 0 \\leq r_{k}<c$, be the remainder of $k b$ when divided by $c$. Prove that the two sets $\\left\\{r_{0}, r_{1}, r_{2}, \\ldots, r_{a}\\right\\}$ and $\\{0,1,2, \\ldots, a\\}$ are different.", "solution": "Suppose that two sets are equal. Then $\\operatorname{gcd}(b, c)=1$ and the polynomial\n\n$$\nf(x):=\\left(1+x^{b}+x^{2 b}+\\cdots+x^{a b}\\right)-\\left(1+x+x^{2}+\\cdots+x^{a-1}+x^{a}\\right)\n$$\n\nis divisible by $x^{c}-1$. (This is because: $m=n+c q \\Longrightarrow x^{m}-x^{n}=x^{n+c q}-x^{n}=x^{n}\\left(x^{c q}-1\\right)$ and $\\left(x^{c q}-1\\right)=\\left(x^{c}-1\\right)\\left(\\left(x^{c}\\right)^{q-1}+\\left(x^{c}\\right)^{q-2}+\\cdots+1\\right)$.) From\n\n$$\nf(x)=\\frac{x^{(a+1) b}-1}{x^{b}-1}-\\frac{x^{a+1}-1}{x-1}=\\frac{F(x)}{(x-1)\\left(x^{b}-1\\right)}\n$$\n\nwhere $F(x)=x^{a b+b+1}+x^{b}+x^{a+1}-x^{a b+b}-x^{a+b+1}-x$, we have\n\n$$\nF(x) \\equiv 0 \\quad\\left(\\bmod x^{c}-1\\right)\n$$\n\nSince $x^{c} \\equiv 1\\left(\\bmod x^{c}-1\\right)$, we may conclude that\n\n$$\n\\{a b+b+1, b, a+1\\} \\equiv\\{a b+b, a+b+1,1\\} \\quad(\\bmod c)\n$$\n\nThus,\n\n$$\nb \\equiv a b+b, a+b+1 \\text { or } 1(\\bmod c)\n$$\n\nBut neither $b \\equiv 1(\\bmod c)$ nor $b \\equiv a+b+1(\\bmod c)$ are possible by the given conditions. Therefore, $b \\equiv a b+b(\\bmod c)$. But this is also impossible because $\\operatorname{gcd}(b, c)=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
|
|
|
| 1 |
+
{"year": "2008", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle with $\\angle A<60^{\\circ}$. Let $X$ and $Y$ be the points on the sides $A B$ and $A C$, respectively, such that $C A+A X=C B+B X$ and $B A+A Y=B C+C Y$. Let $P$ be the point in the plane such that the lines $P X$ and $P Y$ are perpendicular to $A B$ and $A C$, respectively. Prove that $\\angle B P C<120^{\\circ}$.", "solution": "Let $I$ be the incenter of $\\triangle A B C$, and let the feet of the perpendiculars from $I$ to $A B$ and to $A C$ be $D$ and $E$, respectively. (Without loss of generality, we may assume that $A C$ is the longest side. Then $X$ lies on the line segment $A D$. Although $P$ may or may not lie inside $\\triangle A B C$, the proof below works for both cases. Note that $P$ is on the line perpendicular to $A B$ passing through $X$.) Let $O$ be the midpoint of $I P$, and let the feet of the perpendiculars from $O$ to $A B$ and to $A C$ be $M$ and $N$, respectively. Then $M$ and $N$ are the midpoints of $D X$ and $E Y$, respectively.\n\n\nThe conditions on the points $X$ and $Y$ yield the equations\n\n$$\nA X=\\frac{A B+B C-C A}{2} \\quad \\text { and } \\quad A Y=\\frac{B C+C A-A B}{2} .\n$$\n\nFrom $A D=A E=\\frac{C A+A B-B C}{2}$, we obtain\n\n$$\nB D=A B-A D=A B-\\frac{C A+A B-B C}{2}=\\frac{A B+B C-C A}{2}=A X .\n$$\n\nSince $M$ is the midpoint of $D X$, it follows that $M$ is the midpoint of $A B$. Similarly, $N$ is the midpoint of $A C$. Therefore, the perpendicular bisectors of $A B$ and $A C$ meet at $O$, that is, $O$ is the circumcenter of $\\triangle A B C$. Since $\\angle B A C<60^{\\circ}, O$ lies on the same side of $B C$ as the point $A$ and\n\n$$\n\\angle B O C=2 \\angle B A C\n$$\n\nWe can compute $\\angle B I C$ as follows:\n\n$$\n\\begin{aligned}\n\\angle B I C & =180^{\\circ}-\\angle I B C-\\angle I C B=180^{\\circ}-\\frac{1}{2} \\angle A B C-\\frac{1}{2} \\angle A C B \\\\\n& =180^{\\circ}-\\frac{1}{2}(\\angle A B C+\\angle A C B)=180^{\\circ}-\\frac{1}{2}\\left(180^{\\circ}-\\angle B A C\\right)=90^{\\circ}+\\frac{1}{2} \\angle B A C\n\\end{aligned}\n$$\n\nIt follows from $\\angle B A C<60^{\\circ}$ that\n\n$$\n2 \\angle B A C<90^{\\circ}+\\frac{1}{2} \\angle B A C, \\quad \\text { i.e., } \\quad \\angle B O C<\\angle B I C \\text {. }\n$$\n\nFrom this it follows that $I$ lies inside the circumcircle of the isosceles triangle $B O C$ because $O$ and $I$ lie on the same side of $B C$. However, as $O$ is the midpoint of $I P, P$ must lie outside the circumcircle of triangle $B O C$ and on the same side of $B C$ as $O$. Therefore\n\n$$\n\\angle B P C<\\angle B O C=2 \\angle B A C<120^{\\circ} .\n$$\n\nRemark. If one assumes that $\\angle A$ is smaller than the other two, then it is clear that the line $P X$ (or the line perpendicular to $A B$ at $X$ if $P=X$ ) runs through the excenter $I_{C}$ of the excircle tangent to the side $A B$. Since $2 \\angle A C I_{C}=\\angle A C B$ and $B C<A C$, we have $2 \\angle P C B>\\angle C$. Similarly, $2 \\angle P B C>\\angle B$. Therefore,\n\n$$\n\\angle B P C=180^{\\circ}-(\\angle P B C+\\angle P C B)<180^{\\circ}-\\left(\\frac{\\angle B+\\angle C}{2}\\right)=90+\\frac{\\angle A}{2}<120^{\\circ}\n$$\n\nIn this way, a special case of the problem can be easily proved.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
+
{"year": "2008", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Students in a class form groups each of which contains exactly three members such that any two distinct groups have at most one member in common. Prove that, when the class size is 46 , there is a set of 10 students in which no group is properly contained.", "solution": "We let $C$ be the set of all 46 students in the class and let\n\n$$\ns:=\\max \\{|S|: S \\subseteq C \\text { such that } S \\text { contains no group properly }\\}\n$$\n\nThen it suffices to prove that $s \\geq 10$. (If $|S|=s>10$, we may choose a subset of $S$ consisting of 10 students.)\n\nSuppose that $s \\leq 9$ and let $S$ be a set of size $s$ in which no group is properly contained. Take any student, say $v$, from outside $S$. Because of the maximality of $s$, there should be a group containing the student $v$ and two other students in $S$. The number of ways to choose two students from $S$ is\n\n$$\n\\binom{s}{2} \\leq\\binom{ 9}{2}=36\n$$\n\nOn the other hand, there are at least $37=46-9$ students outside of $S$. Thus, among those 37 students outside, there is at least one student, say $u$, who does not belong to any group containing two students in $S$ and one outside. This is because no two distinct groups have two members in common. But then, $S$ can be enlarged by including $u$, which is a contradiction.\n\nRemark. One may choose a subset $S$ of $C$ that contains no group properly. Then, assuming $|S|<10$, prove that there is a student outside $S$, say $u$, who does not belong to any group containing two students in $S$. After enlarging $S$ by including $u$, prove that the enlarged $S$ still contains no group properly.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
+
{"year": "2008", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $\\Gamma$ be the circumcircle of a triangle $A B C$. A circle passing through points $A$ and $C$ meets the sides $B C$ and $B A$ at $D$ and $E$, respectively. The lines $A D$ and $C E$ meet $\\Gamma$ again at $G$ and $H$, respectively. The tangent lines of $\\Gamma$ at $A$ and $C$ meet the line $D E$ at $L$ and $M$, respectively. Prove that the lines $L H$ and $M G$ meet at $\\Gamma$.", "solution": "Let $M G$ meet $\\Gamma$ at $P$. Since $\\angle M C D=\\angle C A E$ and $\\angle M D C=\\angle C A E$, we have $M C=M D$. Thus\n\n$$\nM D^{2}=M C^{2}=M G \\cdot M P\n$$\n\nand hence $M D$ is tangent to the circumcircle of $\\triangle D G P$. Therefore $\\angle D G P=\\angle E D P$.\nLet $\\Gamma^{\\prime}$ be the circumcircle of $\\triangle B D E$. If $B=P$, then, since $\\angle B G D=\\angle B D E$, the tangent lines of $\\Gamma^{\\prime}$ and $\\Gamma$ at $B$ should coincide, that is $\\Gamma^{\\prime}$ is tangent to $\\Gamma$ from inside. Let $B \\neq P$. If $P$ lies in the same side of the line $B C$ as $G$, then we have\n\n$$\n\\angle E D P+\\angle A B P=180^{\\circ}\n$$\n\nbecause $\\angle D G P+\\angle A B P=180^{\\circ}$. That is, the quadrilateral $B P D E$ is cyclic, and hence $P$ is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$.\n\n\nOtherwise,\n\n$$\n\\angle E D P=\\angle D G P=\\angle A G P=\\angle A B P=\\angle E B P .\n$$\n\nTherefore the quadrilateral $P B D E$ is cyclic, and hence $P$ again is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$.\n\nSimilarly, if $L H$ meets $\\Gamma$ at $Q$, we either have $Q=B$, in which case $\\Gamma^{\\prime}$ is tangent to $\\Gamma$ from inside, or $Q \\neq B$. In the latter case, $Q$ is on the intersection of $\\Gamma^{\\prime}$ with $\\Gamma$. In either case, we have $P=Q$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
+
{"year": "2008", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Consider the function $f: \\mathbb{N}_{0} \\rightarrow \\mathbb{N}_{0}$, where $\\mathbb{N}_{0}$ is the set of all non-negative integers, defined by the following conditions:\n(i) $f(0)=0$,\n(ii) $f(2 n)=2 f(n)$ and\n(iii) $f(2 n+1)=n+2 f(n)$ for all $n \\geq 0$.\n(a) Determine the three sets $L:=\\{n \\mid f(n)<f(n+1)\\}, E:=\\{n \\mid f(n)=f(n+1)\\}$, and $G:=\\{n \\mid f(n)>f(n+1)\\}$.\n(b) For each $k \\geq 0$, find a formula for $a_{k}:=\\max \\left\\{f(n): 0 \\leq n \\leq 2^{k}\\right\\}$ in terms of $k$.", "solution": "(a) Let\n\n$$\nL_{1}:=\\{2 k: k>0\\}, \\quad E_{1}:=\\{0\\} \\cup\\{4 k+1: k \\geq 0\\}, \\quad \\text { and } G_{1}:=\\{4 k+3: k \\geq 0\\} .\n$$\n\nWe will show that $L_{1}=L, E_{1}=E$, and $G_{1}=G$. It suffices to verify that $L_{1} \\subseteq E, E_{1} \\subseteq E$, and $G_{1} \\subseteq G$ because $L_{1}, E_{1}$, and $G_{1}$ are mutually disjoint and $L_{1} \\cup E_{1} \\cup G_{1}=\\mathbb{N}_{0}$.\n\nFirstly, if $k>0$, then $f(2 k)-f(2 k+1)=-k<0$ and therefore $L_{1} \\subseteq L$.\nSecondly, $f(0)=0$ and\n\n$$\n\\begin{aligned}\n& f(4 k+1)=2 k+2 f(2 k)=2 k+4 f(k) \\\\\n& f(4 k+2)=2 f(2 k+1)=2(k+2 f(k))=2 k+4 f(k)\n\\end{aligned}\n$$\n\nfor all $k \\geq 0$. Thus, $E_{1} \\subseteq E$.\nLastly, in order to prove $G_{1} \\subset G$, we claim that $f(n+1)-f(n) \\leq n$ for all $n$. (In fact, one can prove a stronger inequality : $f(n+1)-f(n) \\leq n / 2$.) This is clearly true for even $n$ from the definition since for $n=2 t$,\n\n$$\nf(2 t+1)-f(2 t)=t \\leq n\n$$\n\nIf $n=2 t+1$ is odd, then (assuming inductively that the result holds for all nonnegative $m<n$ ), we have\n\n$$\n\\begin{aligned}\nf(n+1)-f(n) & =f(2 t+2)-f(2 t+1)=2 f(t+1)-t-2 f(t) \\\\\n& =2(f(t+1)-f(t))-t \\leq 2 t-t=t<n .\n\\end{aligned}\n$$\n\nFor all $k \\geq 0$,\n\n$$\n\\begin{aligned}\n& f(4 k+4)-f(4 k+3)=f(2(2 k+2))-f(2(2 k+1)+1) \\\\\n& =4 f(k+1)-(2 k+1+2 f(2 k+1))=4 f(k+1)-(2 k+1+2 k+4 f(k)) \\\\\n& =4(f(k+1)-f(k))-(4 k+1) \\leq 4 k-(4 k+1)<0 .\n\\end{aligned}\n$$\n\nThis proves $G_{1} \\subseteq G$.\n(b) Note that $a_{0}=a_{1}=f(1)=0$. Let $k \\geq 2$ and let $N_{k}=\\left\\{0,1,2, \\ldots, 2^{k}\\right\\}$. First we claim that the maximum $a_{k}$ occurs at the largest number in $G \\cap N_{k}$, that is, $a_{k}=f\\left(2^{k}-1\\right)$. We use mathematical induction on $k$ to prove the claim. Note that $a_{2}=f(3)=f\\left(2^{2}-1\\right)$.\n\nNow let $k \\geq 3$. For every even number $2 t$ with $2^{k-1}+1<2 t \\leq 2^{k}$,\n\n$$\nf(2 t)=2 f(t) \\leq 2 a_{k-1}=2 f\\left(2^{k-1}-1\\right)\n$$\n\nby induction hypothesis. For every odd number $2 t+1$ with $2^{k-1}+1 \\leq 2 t+1<2^{k}$,\n\n$$\n\\begin{aligned}\nf(2 t+1) & =t+2 f(t) \\leq 2^{k-1}-1+2 f(t) \\\\\n& \\leq 2^{k-1}-1+2 a_{k-1}=2^{k-1}-1+2 f\\left(2^{k-1}-1\\right)\n\\end{aligned}\n$$\n\nagain by induction hypothesis. Combining ( $\\dagger$ ), ( $\\ddagger$ ) and\n\n$$\nf\\left(2^{k}-1\\right)=f\\left(2\\left(2^{k-1}-1\\right)+1\\right)=2^{k-1}-1+2 f\\left(2^{k-1}-1\\right)\n$$\n\nwe may conclude that $a_{k}=f\\left(2^{k}-1\\right)$ as desired.\nFurthermore, we obtain\n\n$$\na_{k}=2 a_{k-1}+2^{k-1}-1\n$$\n\nfor all $k \\geq 3$. Note that this recursive formula for $a_{k}$ also holds for $k \\geq 0,1$ and 2 . Unwinding this recursive formula, we finally get\n\n$$\n\\begin{aligned}\na_{k} & =2 a_{k-1}+2^{k-1}-1=2\\left(2 a_{k-2}+2^{k-2}-1\\right)+2^{k-1}-1 \\\\\n& =2^{2} a_{k-2}+2 \\cdot 2^{k-1}-2-1=2^{2}\\left(2 a_{k-3}+2^{k-3}-1\\right)+2 \\cdot 2^{k-1}-2-1 \\\\\n& =2^{3} a_{k-3}+3 \\cdot 2^{k-1}-2^{2}-2-1 \\\\\n& \\vdots \\\\\n& =2^{k} a_{0}+k 2^{k-1}-2^{k-1}-2^{k-2}-\\ldots-2-1 \\\\\n& =k 2^{k-1}-2^{k}+1 \\quad \\text { for all } k \\geq 0 .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
+
{"year": "2008", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c$ be integers satisfying $0<a<c-1$ and $1<b<c$. For each $k$, $0 \\leq k \\leq a$, let $r_{k}, 0 \\leq r_{k}<c$, be the remainder of $k b$ when divided by $c$. Prove that the two sets $\\left\\{r_{0}, r_{1}, r_{2}, \\ldots, r_{a}\\right\\}$ and $\\{0,1,2, \\ldots, a\\}$ are different.", "solution": "Suppose that two sets are equal. Then $\\operatorname{gcd}(b, c)=1$ and the polynomial\n\n$$\nf(x):=\\left(1+x^{b}+x^{2 b}+\\cdots+x^{a b}\\right)-\\left(1+x+x^{2}+\\cdots+x^{a-1}+x^{a}\\right)\n$$\n\nis divisible by $x^{c}-1$. (This is because: $m=n+c q \\Longrightarrow x^{m}-x^{n}=x^{n+c q}-x^{n}=x^{n}\\left(x^{c q}-1\\right)$ and $\\left(x^{c q}-1\\right)=\\left(x^{c}-1\\right)\\left(\\left(x^{c}\\right)^{q-1}+\\left(x^{c}\\right)^{q-2}+\\cdots+1\\right)$.) From\n\n$$\nf(x)=\\frac{x^{(a+1) b}-1}{x^{b}-1}-\\frac{x^{a+1}-1}{x-1}=\\frac{F(x)}{(x-1)\\left(x^{b}-1\\right)}\n$$\n\nwhere $F(x)=x^{a b+b+1}+x^{b}+x^{a+1}-x^{a b+b}-x^{a+b+1}-x$, we have\n\n$$\nF(x) \\equiv 0 \\quad\\left(\\bmod x^{c}-1\\right)\n$$\n\nSince $x^{c} \\equiv 1\\left(\\bmod x^{c}-1\\right)$, we may conclude that\n\n$$\n\\{a b+b+1, b, a+1\\} \\equiv\\{a b+b, a+b+1,1\\} \\quad(\\bmod c)\n$$\n\nThus,\n\n$$\nb \\equiv a b+b, a+b+1 \\text { or } 1(\\bmod c)\n$$\n\nBut neither $b \\equiv 1(\\bmod c)$ nor $b \\equiv a+b+1(\\bmod c)$ are possible by the given conditions. Therefore, $b \\equiv a b+b(\\bmod c)$. But this is also impossible because $\\operatorname{gcd}(b, c)=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
APMO/segmented/en-apmo2009_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2009", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Consider the following operation on positive real numbers written on a blackboard:\n\nChoose a number $r$ written on the blackboard, erase that number, and then write a pair of positive real numbers $a$ and $b$ satisfying the condition $2 r^{2}=a b$ on the board.\n\nAssume that you start out with just one positive real number $r$ on the blackboard, and apply this operation $k^{2}-1$ times to end up with $k^{2}$ positive real numbers, not necessarily distinct. Show that there exists a number on the board which does not exceed $k r$.", "solution": "Using AM-GM inequality, we obtain\n\n$$\n\\frac{1}{r^{2}}=\\frac{2}{a b}=\\frac{2 a b}{a^{2} b^{2}} \\leq \\frac{a^{2}+b^{2}}{a^{2} b^{2}} \\leq \\frac{1}{a^{2}}+\\frac{1}{b^{2}}\n$$\n\nConsequently, if we let $S_{\\ell}$ be the sum of the squares of the reciprocals of the numbers written on the board after $\\ell$ operations, then $S_{\\ell}$ increases as $\\ell$ increases, that is,\n\n$$\nS_{0} \\leq S_{1} \\leq \\cdots \\leq S_{k^{2}-1}\n$$\n\nTherefore if we let $s$ be the smallest real number written on the board after $k^{2}-1$ operations, then $\\frac{1}{s^{2}} \\geq \\frac{1}{t^{2}}$ for any number $t$ among $k^{2}$ numbers on the board and hence\n\n$$\nk^{2} \\times \\frac{1}{s^{2}} \\geq S_{k^{2}-1} \\geq S_{0}=\\frac{1}{r^{2}}\n$$\n\nwhich implies that $s \\leq k r$ as desired.\n\nRemark. The nature of the problem does not change at all if the numbers on the board are restricted to be positive integers. But that may mislead some contestants to think the problem is a number theoretic problem rather than a combinatorial problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
-
{"year": "2009", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:\n\n$$\n\\frac{a_{1}}{k^{2}+1}+\\frac{a_{2}}{k^{2}+2}+\\frac{a_{3}}{k^{2}+3}+\\frac{a_{4}}{k^{2}+4}+\\frac{a_{5}}{k^{2}+5}=\\frac{1}{k^{2}} \\text { for } k=1,2,3,4,5\n$$\n\nFind the value of $\\frac{a_{1}}{37}+\\frac{a_{2}}{38}+\\frac{a_{3}}{39}+\\frac{a_{4}}{40}+\\frac{a_{5}}{41}$. (Express the value in a single fraction.)", "solution": "Let $R(x):=\\frac{a_{1}}{x^{2}+1}+\\frac{a_{2}}{x^{2}+2}+\\frac{a_{3}}{x^{2}+3}+\\frac{a_{4}}{x^{2}+4}+\\frac{a_{5}}{x^{2}+5}$. Then $R( \\pm 1)=1$, $R( \\pm 2)=\\frac{1}{4}, R( \\pm 3)=\\frac{1}{9}, R( \\pm 4)=\\frac{1}{16}, R( \\pm 5)=\\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\\left(x^{2}+1\\right)\\left(x^{2}+2\\right)\\left(x^{2}+3\\right)\\left(x^{2}+4\\right)\\left(x^{2}+5\\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \\pm 1, \\pm 2, \\pm 3, \\pm 4, \\pm 5$, we get $Q(k)=R(k) P(k)=\\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\\pm 1, \\pm 2, \\pm 3, \\pm 4, \\pm 5$, we get\n\n$$\nP(x)-x^{2} Q(x)=A\\left(x^{2}-1\\right)\\left(x^{2}-4\\right)\\left(x^{2}-9\\right)\\left(x^{2}-16\\right)\\left(x^{2}-25\\right)\n$$\n\nPutting $x=0$, we get $A=\\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields\n\n$$\n1-x^{2} R(x)=1-x^{2} \\frac{Q(x)}{P(x)}=-\\frac{1}{120} \\cdot \\frac{\\left(x^{2}-1\\right)\\left(x^{2}-4\\right)\\left(x^{2}-9\\right)\\left(x^{2}-16\\right)\\left(x^{2}-25\\right)}{\\left(x^{2}+1\\right)\\left(x^{2}+2\\right)\\left(x^{2}+3\\right)\\left(x^{2}+4\\right)\\left(x^{2}+5\\right)}\n$$\n\nand hence that\n\n$$\n1-36 R(6)=-\\frac{35 \\times 32 \\times 27 \\times 20 \\times 11}{120 \\times 37 \\times 38 \\times 39 \\times 40 \\times 41}=-\\frac{3 \\times 7 \\times 11}{13 \\times 19 \\times 37 \\times 41}=-\\frac{231}{374699}\n$$\n\nwhich implies $R(6)=\\frac{187465}{6744582}$.\nRemark. We can get $a_{1}=\\frac{1105}{72}, a_{2}=-\\frac{2673}{40}, a_{3}=\\frac{1862}{15}, a_{4}=-\\frac{1885}{18}, a_{5}=\\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
-
{"year": "2009", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let three circles $\\Gamma_{1}, \\Gamma_{2}, \\Gamma_{3}$, which are non-overlapping and mutually external, be given in the plane. For each point $P$ in the plane, outside the three circles, construct six points $A_{1}, B_{1}, A_{2}, B_{2}, A_{3}, B_{3}$ as follows: For each $i=1,2,3, A_{i}, B_{i}$ are distinct points on the circle $\\Gamma_{i}$ such that the lines $P A_{i}$ and $P B_{i}$ are both tangents to $\\Gamma_{i}$. Call the point $P$ exceptional if, from the construction, three lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ are concurrent. Show that every exceptional point of the plane, if exists, lies on the same circle.", "solution": "Let $O_{i}$ be the center and $r_{i}$ the radius of circle $\\Gamma_{i}$ for each $i=1,2,3$. Let $P$ be an exceptional point, and let the three corresponding lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ concur at $Q$. Construct the circle with diameter $P Q$. Call the circle $\\Gamma$, its center $O$ and its radius $r$. We now claim that all exceptional points lie on $\\Gamma$.\n\n\nLet $P O_{1}$ intersect $A_{1} B_{1}$ in $X_{1}$. As $P O_{1} \\perp A_{1} B_{1}$, we see that $X_{1}$ lies on $\\Gamma$. As $P A_{1}$ is a tangent to $\\Gamma_{1}$, triangle $P A_{1} O_{1}$ is right-angled and similar to triangle $A_{1} X_{1} O_{1}$. It follows that\n\n$$\n\\frac{O_{1} X_{1}}{O_{1} A_{1}}=\\frac{O_{1} A_{1}}{O_{1} P}, \\quad \\text { i.e., } \\quad O_{1} X_{1} \\cdot O_{1} P=O_{1} A_{1}^{2}=r_{1}^{2}\n$$\n\nOn the other hand, $O_{1} X_{1} \\cdot O_{1} P$ is also the power of $O_{1}$ with respect to $\\Gamma$, so that\n\n$$\nr_{1}^{2}=O_{1} X_{1} \\cdot O_{1} P=\\left(O_{1} O-r\\right)\\left(O_{1} O+r\\right)=O_{1} O^{2}-r^{2}\n$$\n\nand hence\n\n$$\nr^{2}=O O_{1}^{2}-r_{1}^{2}=\\left(O O_{1}-r_{1}\\right)\\left(O O_{1}+r_{1}\\right)\n$$\n\nThus, $r^{2}$ is the power of $O$ with respect to $\\Gamma_{1}$. By the same token, $r^{2}$ is also the power of $O$ with respect to $\\Gamma_{2}$ and $\\Gamma_{3}$. Hence $O$ must be the radical center of the three given circles. Since $r$, as the square root of the power of $O$ with respect to the three given circles, does not depend on $P$, it follows that all exceptional points lie on $\\Gamma$.\n\nRemark. In the event of the radical point being at infinity (and hence the three radical axes being parallel), there are no exceptional points in the plane, which is consistent with the statement of the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
-
{"year": "2009", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Prove that for any positive integer $k$, there exists an arithmetic sequence\n\n$$\n\\frac{a_{1}}{b_{1}}, \\quad \\frac{a_{2}}{b_{2}}, \\ldots, \\quad \\frac{a_{k}}{b_{k}}\n$$\n\nof rational numbers, where $a_{i}, b_{i}$ are relatively prime positive integers for each $i=1,2, \\ldots, k$, such that the positive integers $a_{1}, b_{1}, a_{2}, b_{2}, \\ldots, a_{k}, b_{k}$ are all distinct.", "solution": "For $k=1$, there is nothing to prove. Henceforth assume $k \\geq 2$.\nLet $p_{1}, p_{2}, \\ldots, p_{k}$ be $k$ distinct primes such that\n\n$$\nk<p_{k}<\\cdots<p_{2}<p_{1}\n$$\n\nand let $N=p_{1} p_{2} \\cdots p_{k}$. By Chinese Remainder Theorem, there exists a positive integer $x$ satisfying\n\n$$\nx \\equiv-i \\quad\\left(\\bmod p_{i}\\right)\n$$\n\nfor all $i=1,2, \\ldots, k$ and $x>N^{2}$. Consider the following sequence:\n\n$$\n\\frac{x+1}{N}, \\frac{x+2}{N}, \\quad, \\ldots, \\frac{x+k}{N}\n$$\n\nThis sequence is obviously an arithmetic sequence of positive rational numbers of length $k$. For each $i=1,2, \\ldots, k$, the numerator $x+i$ is divisible by $p_{i}$ but not by $p_{j}$ for $j \\neq i$, for otherwise $p_{j}$ divides $|i-j|$, which is not possible because $p_{j}>k>|i-j|$. Let\n\n$$\na_{i}:=\\frac{x+i}{p_{i}}, \\quad b_{i}:=\\frac{N}{p_{i}} \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nThen\n\n$$\n\\frac{x+i}{N}=\\frac{a_{i}}{b_{i}}, \\quad \\operatorname{gcd}\\left(a_{i}, b_{i}\\right)=1 \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nand all $b_{i}$ 's are distinct from each other. Moreover, $x>N^{2}$ implies\n\n$$\na_{i}=\\frac{x+i}{p_{i}}>\\frac{N^{2}}{p_{i}}>N>\\frac{N}{p_{j}}=b_{j} \\quad \\text { for all } i, j=1,2, \\ldots, k\n$$\n\nand hence all $a_{i}$ 's are distinct from $b_{i}$ 's. It only remains to show that all $a_{i}$ 's are distinct from each other. This follows from\n\n$$\na_{j}=\\frac{x+j}{p_{j}}>\\frac{x+i}{p_{j}}>\\frac{x+i}{p_{i}}=a_{i} \\quad \\text { for all } i<j\n$$\n\nby our choice of $p_{1}, p_{2}, \\ldots, p_{k}$. Thus, the arithmetic sequence\n\n$$\n\\frac{a_{1}}{b_{1}}, \\quad \\frac{a_{2}}{b_{2}}, \\ldots, \\quad \\frac{a_{k}}{b_{k}}\n$$\n\nof positive rational numbers satisfies the conditions of the problem.\n\nRemark. Here is a much easier solution :\n\nFor any positive integer $k \\geq 2$, consider the sequence\n\n$$\n\\frac{(k!)^{2}+1}{k!}, \\frac{(k!)^{2}+2}{k!}, \\ldots, \\frac{(k!)^{2}+k}{k!}\n$$\n\nNote that $\\operatorname{gcd}\\left(k!,(k!)^{2}+i\\right)=i$ for all $i=1,2, \\ldots, k$. So, taking\n\n$$\na_{i}:=\\frac{(k!)^{2}+i}{i}, \\quad b_{i}:=\\frac{k!}{i} \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nwe have $\\operatorname{gcd}\\left(a_{i}, b_{i}\\right)=1$ and\n\n$$\na_{i}=\\frac{(k!)^{2}+i}{i}>a_{j}=\\frac{(k!)^{2}+j}{j}>b_{i}=\\frac{k!}{i}>b_{j}=\\frac{k!}{j}\n$$\n\nfor any $1 \\leq i<j \\leq k$. Therefore this sequence satisfies every condition given in the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
-
{"year": "2009", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Larry and Rob are two robots travelling in one car from Argovia to Zillis. Both robots have control over the steering and steer according to the following algorithm: Larry makes a $90^{\\circ}$ left turn after every $\\ell$ kilometer driving from start; Rob makes a $90^{\\circ}$ right turn after every $r$ kilometer driving from start, where $\\ell$ and $r$ are relatively prime positive integers. In the event of both turns occurring simultaneously, the car will keep going without changing direction. Assume that the ground is flat and the car can move in any direction.\n\nLet the car start from Argovia facing towards Zillis. For which choices of the pair $(\\ell, r)$ is the car guaranteed to reach Zillis, regardless of how far it is from Argovia?", "solution": "Let Zillis be $d$ kilometers away from Argovia, where $d$ is a positive real number. For simplicity, we will position Argovia at $(0,0)$ and Zillis at $(d, 0)$, so that the car starts out facing east. We will investigate how the car moves around in the period of travelling the first $\\ell r$ kilometers, the second $\\ell r$ kilometers, ..., and so on. We call each period of travelling $\\ell r$ kilometers a section. It is clear that the car will have identical behavior in every section except the direction of the car at the beginning.\n\nCase 1: $\\underline{\\ell-r \\equiv 2(\\bmod 4)}$. After the first section, the car has made $\\ell-1$ right turns and $r-1$ left turns, which is a net of $2(\\equiv \\ell-r(\\bmod 4))$ right turns. Let the displacement vector for the first section be $(x, y)$. Since the car has rotated $180^{\\circ}$, the displacement vector for the second section will be $(-x,-y)$, which will take the car back to $(0,0)$ facing east again. We now have our original situation, and the car has certainly never travelled further than lr kilometers from Argovia. So, the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 2: $\\ell-r \\equiv 1(\\bmod 4)$. After the first section, the car has made a net of 1 right turn. Let the displacement vector for the first section again be $(x, y)$. This time the car has rotated $90^{\\circ}$ clockwise. We can see that the displacements for the second, third and fourth section will be $(y,-x),(-x,-y)$ and $(-y, x)$, respectively, so after four sections the car is back at $(0,0)$ facing east. Since the car has certainly never travelled further than $2 \\ell r$ kilometers from Argovia, the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 3: $\\quad \\ell-r \\equiv 3(\\bmod 4)$. An argument similar to that in Case 2 (switching the roles of left and right) shows that the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 4: $\\quad \\ell \\equiv r(\\bmod 4)$. The car makes a net turn of $0^{\\circ}$ after each section, so it must be facing east. We are going to show that, after traversing the first section, the car will be at $(1,0)$. It will be useful to interpret the Cartesian plane as the complex plane, i.e. writing $x+i y$ for $(x, y)$, where $i=\\sqrt{-1}$. We will denote the $k$-th kilometer of movement by $m_{k-1}$,\nwhich takes values from the set $\\{1, i,-1,-i\\}$, depending on the direction. We then just have to show that\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=1\n$$\n\nwhich implies that the car will get to Zillis no matter how far it is apart from Argovia.\nCase $4 \\mathrm{a}: \\underline{\\ell \\equiv r \\equiv 1(\\bmod 4)}$. First note that for $k=0,1, \\ldots, \\ell r-1$,\n\n$$\nm_{k}=i^{\\lfloor k / \\ell\\rfloor}(-i)^{\\lfloor k / r\\rfloor}\n$$\n\nsince $\\lfloor k / \\ell\\rfloor$ and $\\lfloor k / r\\rfloor$ are the exact numbers of left and right turns before the $(k+1)$ st kilometer, respectively. Let $a_{k}(\\equiv k(\\bmod \\ell))$ and $b_{k}(\\equiv k(\\bmod r))$ be the remainders of $k$ when divided by $\\ell$ and $r$, respectively. Then, since\n\n$$\na_{k}=k-\\left\\lfloor\\frac{k}{\\ell}\\right\\rfloor \\ell \\equiv k-\\left\\lfloor\\frac{k}{\\ell}\\right\\rfloor \\quad(\\bmod 4) \\quad \\text { and } \\quad b_{k}=k-\\left\\lfloor\\frac{k}{r}\\right\\rfloor r \\equiv k-\\left\\lfloor\\frac{k}{r}\\right\\rfloor \\quad(\\bmod 4),\n$$\n\nwe have $\\lfloor k / \\ell\\rfloor \\equiv k-a_{k}(\\bmod 4)$ and $\\lfloor k / r\\rfloor \\equiv k-b_{k}(\\bmod 4)$. We therefore have\n\n$$\nm_{k}=i^{k-a_{k}}(-i)^{k-b_{k}}=\\left(-i^{2}\\right)^{k} i^{-a_{k}}(-i)^{-b_{k}}=(-i)^{a_{k}} i^{b_{k}} .\n$$\n\nAs $\\ell$ and $r$ are relatively prime, by Chinese Remainder Theorem, there is a bijection between pairs $\\left(a_{k}, b_{k}\\right)=(k(\\bmod \\ell), k(\\bmod r))$ and the numbers $k=0,1,2, \\ldots, \\ell r-1$. Hence\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=\\sum_{k=0}^{\\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\\left(\\sum_{k=0}^{\\ell-1}(-i)^{a_{k}}\\right)\\left(\\sum_{k=0}^{r-1} i^{b_{k}}\\right)=1 \\times 1=1\n$$\n\nas required because $\\ell \\equiv r \\equiv 1(\\bmod 4)$.\nCase $4 \\mathrm{~b}: \\underline{\\ell \\equiv r \\equiv 3(\\bmod 4)}$. In this case, we get\n\n$$\nm_{k}=i^{a_{k}}(-i)^{b_{k}}\n$$\n\nwhere $a_{k}(\\equiv k(\\bmod \\ell))$ and $b_{k}(\\equiv k(\\bmod r))$ for $k=0,1, \\ldots, \\ell r-1$. Then we can proceed analogously to Case 4a to obtain\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=\\sum_{k=0}^{\\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\\left(\\sum_{k=0}^{\\ell-1}(-i)^{a_{k}}\\right)\\left(\\sum_{k=0}^{r-1} i^{b_{k}}\\right)=i \\times(-i)=1\n$$\n\nas required because $\\ell \\equiv r \\equiv 3(\\bmod 4)$.\nNow clearly the car traverses through all points between $(0,0)$ and $(1,0)$ during the first section and, in fact, covers all points between $(n-1,0)$ and $(n, 0)$ during the $n$-th section. Hence it will eventually reach $(d, 0)$ for any positive $d$.\n\nTo summarize: $(\\ell, r)$ satisfies the required conditions if and only if\n\n$$\n\\ell \\equiv r \\equiv 1 \\quad \\text { or } \\quad \\ell \\equiv r \\equiv 3 \\quad(\\bmod 4)\n$$\n\nRemark. In case $\\operatorname{gcd}(\\ell, r)=d \\neq 1$, the answer is :\n\n$$\n\\frac{\\ell}{d} \\equiv \\frac{r}{d} \\equiv 1 \\quad \\text { or } \\quad \\frac{\\ell}{d} \\equiv \\frac{r}{d} \\equiv 3 \\quad(\\bmod 4)\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
|
|
|
| 1 |
+
{"year": "2009", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Consider the following operation on positive real numbers written on a blackboard:\n\nChoose a number $r$ written on the blackboard, erase that number, and then write a pair of positive real numbers $a$ and $b$ satisfying the condition $2 r^{2}=a b$ on the board.\n\nAssume that you start out with just one positive real number $r$ on the blackboard, and apply this operation $k^{2}-1$ times to end up with $k^{2}$ positive real numbers, not necessarily distinct. Show that there exists a number on the board which does not exceed $k r$.", "solution": "Using AM-GM inequality, we obtain\n\n$$\n\\frac{1}{r^{2}}=\\frac{2}{a b}=\\frac{2 a b}{a^{2} b^{2}} \\leq \\frac{a^{2}+b^{2}}{a^{2} b^{2}} \\leq \\frac{1}{a^{2}}+\\frac{1}{b^{2}}\n$$\n\nConsequently, if we let $S_{\\ell}$ be the sum of the squares of the reciprocals of the numbers written on the board after $\\ell$ operations, then $S_{\\ell}$ increases as $\\ell$ increases, that is,\n\n$$\nS_{0} \\leq S_{1} \\leq \\cdots \\leq S_{k^{2}-1}\n$$\n\nTherefore if we let $s$ be the smallest real number written on the board after $k^{2}-1$ operations, then $\\frac{1}{s^{2}} \\geq \\frac{1}{t^{2}}$ for any number $t$ among $k^{2}$ numbers on the board and hence\n\n$$\nk^{2} \\times \\frac{1}{s^{2}} \\geq S_{k^{2}-1} \\geq S_{0}=\\frac{1}{r^{2}}\n$$\n\nwhich implies that $s \\leq k r$ as desired.\n\nRemark. The nature of the problem does not change at all if the numbers on the board are restricted to be positive integers. But that may mislead some contestants to think the problem is a number theoretic problem rather than a combinatorial problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "(Solution)"}}
|
| 2 |
+
{"year": "2009", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:\n\n$$\n\\frac{a_{1}}{k^{2}+1}+\\frac{a_{2}}{k^{2}+2}+\\frac{a_{3}}{k^{2}+3}+\\frac{a_{4}}{k^{2}+4}+\\frac{a_{5}}{k^{2}+5}=\\frac{1}{k^{2}} \\text { for } k=1,2,3,4,5\n$$\n\nFind the value of $\\frac{a_{1}}{37}+\\frac{a_{2}}{38}+\\frac{a_{3}}{39}+\\frac{a_{4}}{40}+\\frac{a_{5}}{41}$. (Express the value in a single fraction.)", "solution": "Let $R(x):=\\frac{a_{1}}{x^{2}+1}+\\frac{a_{2}}{x^{2}+2}+\\frac{a_{3}}{x^{2}+3}+\\frac{a_{4}}{x^{2}+4}+\\frac{a_{5}}{x^{2}+5}$. Then $R( \\pm 1)=1$, $R( \\pm 2)=\\frac{1}{4}, R( \\pm 3)=\\frac{1}{9}, R( \\pm 4)=\\frac{1}{16}, R( \\pm 5)=\\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\\left(x^{2}+1\\right)\\left(x^{2}+2\\right)\\left(x^{2}+3\\right)\\left(x^{2}+4\\right)\\left(x^{2}+5\\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \\pm 1, \\pm 2, \\pm 3, \\pm 4, \\pm 5$, we get $Q(k)=R(k) P(k)=\\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\\pm 1, \\pm 2, \\pm 3, \\pm 4, \\pm 5$, we get\n\n$$\nP(x)-x^{2} Q(x)=A\\left(x^{2}-1\\right)\\left(x^{2}-4\\right)\\left(x^{2}-9\\right)\\left(x^{2}-16\\right)\\left(x^{2}-25\\right)\n$$\n\nPutting $x=0$, we get $A=\\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields\n\n$$\n1-x^{2} R(x)=1-x^{2} \\frac{Q(x)}{P(x)}=-\\frac{1}{120} \\cdot \\frac{\\left(x^{2}-1\\right)\\left(x^{2}-4\\right)\\left(x^{2}-9\\right)\\left(x^{2}-16\\right)\\left(x^{2}-25\\right)}{\\left(x^{2}+1\\right)\\left(x^{2}+2\\right)\\left(x^{2}+3\\right)\\left(x^{2}+4\\right)\\left(x^{2}+5\\right)}\n$$\n\nand hence that\n\n$$\n1-36 R(6)=-\\frac{35 \\times 32 \\times 27 \\times 20 \\times 11}{120 \\times 37 \\times 38 \\times 39 \\times 40 \\times 41}=-\\frac{3 \\times 7 \\times 11}{13 \\times 19 \\times 37 \\times 41}=-\\frac{231}{374699}\n$$\n\nwhich implies $R(6)=\\frac{187465}{6744582}$.\nRemark. We can get $a_{1}=\\frac{1105}{72}, a_{2}=-\\frac{2673}{40}, a_{3}=\\frac{1862}{15}, a_{4}=-\\frac{1885}{18}, a_{5}=\\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "(Solution)"}}
|
| 3 |
+
{"year": "2009", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let three circles $\\Gamma_{1}, \\Gamma_{2}, \\Gamma_{3}$, which are non-overlapping and mutually external, be given in the plane. For each point $P$ in the plane, outside the three circles, construct six points $A_{1}, B_{1}, A_{2}, B_{2}, A_{3}, B_{3}$ as follows: For each $i=1,2,3, A_{i}, B_{i}$ are distinct points on the circle $\\Gamma_{i}$ such that the lines $P A_{i}$ and $P B_{i}$ are both tangents to $\\Gamma_{i}$. Call the point $P$ exceptional if, from the construction, three lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ are concurrent. Show that every exceptional point of the plane, if exists, lies on the same circle.", "solution": "Let $O_{i}$ be the center and $r_{i}$ the radius of circle $\\Gamma_{i}$ for each $i=1,2,3$. Let $P$ be an exceptional point, and let the three corresponding lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ concur at $Q$. Construct the circle with diameter $P Q$. Call the circle $\\Gamma$, its center $O$ and its radius $r$. We now claim that all exceptional points lie on $\\Gamma$.\n\n\nLet $P O_{1}$ intersect $A_{1} B_{1}$ in $X_{1}$. As $P O_{1} \\perp A_{1} B_{1}$, we see that $X_{1}$ lies on $\\Gamma$. As $P A_{1}$ is a tangent to $\\Gamma_{1}$, triangle $P A_{1} O_{1}$ is right-angled and similar to triangle $A_{1} X_{1} O_{1}$. It follows that\n\n$$\n\\frac{O_{1} X_{1}}{O_{1} A_{1}}=\\frac{O_{1} A_{1}}{O_{1} P}, \\quad \\text { i.e., } \\quad O_{1} X_{1} \\cdot O_{1} P=O_{1} A_{1}^{2}=r_{1}^{2}\n$$\n\nOn the other hand, $O_{1} X_{1} \\cdot O_{1} P$ is also the power of $O_{1}$ with respect to $\\Gamma$, so that\n\n$$\nr_{1}^{2}=O_{1} X_{1} \\cdot O_{1} P=\\left(O_{1} O-r\\right)\\left(O_{1} O+r\\right)=O_{1} O^{2}-r^{2}\n$$\n\nand hence\n\n$$\nr^{2}=O O_{1}^{2}-r_{1}^{2}=\\left(O O_{1}-r_{1}\\right)\\left(O O_{1}+r_{1}\\right)\n$$\n\nThus, $r^{2}$ is the power of $O$ with respect to $\\Gamma_{1}$. By the same token, $r^{2}$ is also the power of $O$ with respect to $\\Gamma_{2}$ and $\\Gamma_{3}$. Hence $O$ must be the radical center of the three given circles. Since $r$, as the square root of the power of $O$ with respect to the three given circles, does not depend on $P$, it follows that all exceptional points lie on $\\Gamma$.\n\nRemark. In the event of the radical point being at infinity (and hence the three radical axes being parallel), there are no exceptional points in the plane, which is consistent with the statement of the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "(Solution)"}}
|
| 4 |
+
{"year": "2009", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Prove that for any positive integer $k$, there exists an arithmetic sequence\n\n$$\n\\frac{a_{1}}{b_{1}}, \\quad \\frac{a_{2}}{b_{2}}, \\ldots, \\quad \\frac{a_{k}}{b_{k}}\n$$\n\nof rational numbers, where $a_{i}, b_{i}$ are relatively prime positive integers for each $i=1,2, \\ldots, k$, such that the positive integers $a_{1}, b_{1}, a_{2}, b_{2}, \\ldots, a_{k}, b_{k}$ are all distinct.", "solution": "For $k=1$, there is nothing to prove. Henceforth assume $k \\geq 2$.\nLet $p_{1}, p_{2}, \\ldots, p_{k}$ be $k$ distinct primes such that\n\n$$\nk<p_{k}<\\cdots<p_{2}<p_{1}\n$$\n\nand let $N=p_{1} p_{2} \\cdots p_{k}$. By Chinese Remainder Theorem, there exists a positive integer $x$ satisfying\n\n$$\nx \\equiv-i \\quad\\left(\\bmod p_{i}\\right)\n$$\n\nfor all $i=1,2, \\ldots, k$ and $x>N^{2}$. Consider the following sequence:\n\n$$\n\\frac{x+1}{N}, \\frac{x+2}{N}, \\quad, \\ldots, \\frac{x+k}{N}\n$$\n\nThis sequence is obviously an arithmetic sequence of positive rational numbers of length $k$. For each $i=1,2, \\ldots, k$, the numerator $x+i$ is divisible by $p_{i}$ but not by $p_{j}$ for $j \\neq i$, for otherwise $p_{j}$ divides $|i-j|$, which is not possible because $p_{j}>k>|i-j|$. Let\n\n$$\na_{i}:=\\frac{x+i}{p_{i}}, \\quad b_{i}:=\\frac{N}{p_{i}} \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nThen\n\n$$\n\\frac{x+i}{N}=\\frac{a_{i}}{b_{i}}, \\quad \\operatorname{gcd}\\left(a_{i}, b_{i}\\right)=1 \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nand all $b_{i}$ 's are distinct from each other. Moreover, $x>N^{2}$ implies\n\n$$\na_{i}=\\frac{x+i}{p_{i}}>\\frac{N^{2}}{p_{i}}>N>\\frac{N}{p_{j}}=b_{j} \\quad \\text { for all } i, j=1,2, \\ldots, k\n$$\n\nand hence all $a_{i}$ 's are distinct from $b_{i}$ 's. It only remains to show that all $a_{i}$ 's are distinct from each other. This follows from\n\n$$\na_{j}=\\frac{x+j}{p_{j}}>\\frac{x+i}{p_{j}}>\\frac{x+i}{p_{i}}=a_{i} \\quad \\text { for all } i<j\n$$\n\nby our choice of $p_{1}, p_{2}, \\ldots, p_{k}$. Thus, the arithmetic sequence\n\n$$\n\\frac{a_{1}}{b_{1}}, \\quad \\frac{a_{2}}{b_{2}}, \\ldots, \\quad \\frac{a_{k}}{b_{k}}\n$$\n\nof positive rational numbers satisfies the conditions of the problem.\n\nRemark. Here is a much easier solution :\n\nFor any positive integer $k \\geq 2$, consider the sequence\n\n$$\n\\frac{(k!)^{2}+1}{k!}, \\frac{(k!)^{2}+2}{k!}, \\ldots, \\frac{(k!)^{2}+k}{k!}\n$$\n\nNote that $\\operatorname{gcd}\\left(k!,(k!)^{2}+i\\right)=i$ for all $i=1,2, \\ldots, k$. So, taking\n\n$$\na_{i}:=\\frac{(k!)^{2}+i}{i}, \\quad b_{i}:=\\frac{k!}{i} \\quad \\text { for all } i=1,2, \\ldots, k\n$$\n\nwe have $\\operatorname{gcd}\\left(a_{i}, b_{i}\\right)=1$ and\n\n$$\na_{i}=\\frac{(k!)^{2}+i}{i}>a_{j}=\\frac{(k!)^{2}+j}{j}>b_{i}=\\frac{k!}{i}>b_{j}=\\frac{k!}{j}\n$$\n\nfor any $1 \\leq i<j \\leq k$. Therefore this sequence satisfies every condition given in the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "(Solution)"}}
|
| 5 |
+
{"year": "2009", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Larry and Rob are two robots travelling in one car from Argovia to Zillis. Both robots have control over the steering and steer according to the following algorithm: Larry makes a $90^{\\circ}$ left turn after every $\\ell$ kilometer driving from start; Rob makes a $90^{\\circ}$ right turn after every $r$ kilometer driving from start, where $\\ell$ and $r$ are relatively prime positive integers. In the event of both turns occurring simultaneously, the car will keep going without changing direction. Assume that the ground is flat and the car can move in any direction.\n\nLet the car start from Argovia facing towards Zillis. For which choices of the pair $(\\ell, r)$ is the car guaranteed to reach Zillis, regardless of how far it is from Argovia?", "solution": "Let Zillis be $d$ kilometers away from Argovia, where $d$ is a positive real number. For simplicity, we will position Argovia at $(0,0)$ and Zillis at $(d, 0)$, so that the car starts out facing east. We will investigate how the car moves around in the period of travelling the first $\\ell r$ kilometers, the second $\\ell r$ kilometers, ..., and so on. We call each period of travelling $\\ell r$ kilometers a section. It is clear that the car will have identical behavior in every section except the direction of the car at the beginning.\n\nCase 1: $\\underline{\\ell-r \\equiv 2(\\bmod 4)}$. After the first section, the car has made $\\ell-1$ right turns and $r-1$ left turns, which is a net of $2(\\equiv \\ell-r(\\bmod 4))$ right turns. Let the displacement vector for the first section be $(x, y)$. Since the car has rotated $180^{\\circ}$, the displacement vector for the second section will be $(-x,-y)$, which will take the car back to $(0,0)$ facing east again. We now have our original situation, and the car has certainly never travelled further than lr kilometers from Argovia. So, the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 2: $\\ell-r \\equiv 1(\\bmod 4)$. After the first section, the car has made a net of 1 right turn. Let the displacement vector for the first section again be $(x, y)$. This time the car has rotated $90^{\\circ}$ clockwise. We can see that the displacements for the second, third and fourth section will be $(y,-x),(-x,-y)$ and $(-y, x)$, respectively, so after four sections the car is back at $(0,0)$ facing east. Since the car has certainly never travelled further than $2 \\ell r$ kilometers from Argovia, the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 3: $\\quad \\ell-r \\equiv 3(\\bmod 4)$. An argument similar to that in Case 2 (switching the roles of left and right) shows that the car cannot reach Zillis if it is further apart from Argovia.\n\nCase 4: $\\quad \\ell \\equiv r(\\bmod 4)$. The car makes a net turn of $0^{\\circ}$ after each section, so it must be facing east. We are going to show that, after traversing the first section, the car will be at $(1,0)$. It will be useful to interpret the Cartesian plane as the complex plane, i.e. writing $x+i y$ for $(x, y)$, where $i=\\sqrt{-1}$. We will denote the $k$-th kilometer of movement by $m_{k-1}$,\nwhich takes values from the set $\\{1, i,-1,-i\\}$, depending on the direction. We then just have to show that\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=1\n$$\n\nwhich implies that the car will get to Zillis no matter how far it is apart from Argovia.\nCase $4 \\mathrm{a}: \\underline{\\ell \\equiv r \\equiv 1(\\bmod 4)}$. First note that for $k=0,1, \\ldots, \\ell r-1$,\n\n$$\nm_{k}=i^{\\lfloor k / \\ell\\rfloor}(-i)^{\\lfloor k / r\\rfloor}\n$$\n\nsince $\\lfloor k / \\ell\\rfloor$ and $\\lfloor k / r\\rfloor$ are the exact numbers of left and right turns before the $(k+1)$ st kilometer, respectively. Let $a_{k}(\\equiv k(\\bmod \\ell))$ and $b_{k}(\\equiv k(\\bmod r))$ be the remainders of $k$ when divided by $\\ell$ and $r$, respectively. Then, since\n\n$$\na_{k}=k-\\left\\lfloor\\frac{k}{\\ell}\\right\\rfloor \\ell \\equiv k-\\left\\lfloor\\frac{k}{\\ell}\\right\\rfloor \\quad(\\bmod 4) \\quad \\text { and } \\quad b_{k}=k-\\left\\lfloor\\frac{k}{r}\\right\\rfloor r \\equiv k-\\left\\lfloor\\frac{k}{r}\\right\\rfloor \\quad(\\bmod 4),\n$$\n\nwe have $\\lfloor k / \\ell\\rfloor \\equiv k-a_{k}(\\bmod 4)$ and $\\lfloor k / r\\rfloor \\equiv k-b_{k}(\\bmod 4)$. We therefore have\n\n$$\nm_{k}=i^{k-a_{k}}(-i)^{k-b_{k}}=\\left(-i^{2}\\right)^{k} i^{-a_{k}}(-i)^{-b_{k}}=(-i)^{a_{k}} i^{b_{k}} .\n$$\n\nAs $\\ell$ and $r$ are relatively prime, by Chinese Remainder Theorem, there is a bijection between pairs $\\left(a_{k}, b_{k}\\right)=(k(\\bmod \\ell), k(\\bmod r))$ and the numbers $k=0,1,2, \\ldots, \\ell r-1$. Hence\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=\\sum_{k=0}^{\\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\\left(\\sum_{k=0}^{\\ell-1}(-i)^{a_{k}}\\right)\\left(\\sum_{k=0}^{r-1} i^{b_{k}}\\right)=1 \\times 1=1\n$$\n\nas required because $\\ell \\equiv r \\equiv 1(\\bmod 4)$.\nCase $4 \\mathrm{~b}: \\underline{\\ell \\equiv r \\equiv 3(\\bmod 4)}$. In this case, we get\n\n$$\nm_{k}=i^{a_{k}}(-i)^{b_{k}}\n$$\n\nwhere $a_{k}(\\equiv k(\\bmod \\ell))$ and $b_{k}(\\equiv k(\\bmod r))$ for $k=0,1, \\ldots, \\ell r-1$. Then we can proceed analogously to Case 4a to obtain\n\n$$\n\\sum_{k=0}^{\\ell r-1} m_{k}=\\sum_{k=0}^{\\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\\left(\\sum_{k=0}^{\\ell-1}(-i)^{a_{k}}\\right)\\left(\\sum_{k=0}^{r-1} i^{b_{k}}\\right)=i \\times(-i)=1\n$$\n\nas required because $\\ell \\equiv r \\equiv 3(\\bmod 4)$.\nNow clearly the car traverses through all points between $(0,0)$ and $(1,0)$ during the first section and, in fact, covers all points between $(n-1,0)$ and $(n, 0)$ during the $n$-th section. Hence it will eventually reach $(d, 0)$ for any positive $d$.\n\nTo summarize: $(\\ell, r)$ satisfies the required conditions if and only if\n\n$$\n\\ell \\equiv r \\equiv 1 \\quad \\text { or } \\quad \\ell \\equiv r \\equiv 3 \\quad(\\bmod 4)\n$$\n\nRemark. In case $\\operatorname{gcd}(\\ell, r)=d \\neq 1$, the answer is :\n\n$$\n\\frac{\\ell}{d} \\equiv \\frac{r}{d} \\equiv 1 \\quad \\text { or } \\quad \\frac{\\ell}{d} \\equiv \\frac{r}{d} \\equiv 3 \\quad(\\bmod 4)\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "(Solution)"}}
|
APMO/segmented/en-apmo2010_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2010", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with $\\angle B A C \\neq 90^{\\circ}$. Let $O$ be the circumcenter of the triangle $A B C$ and let $\\Gamma$ be the circumcircle of the triangle $B O C$. Suppose that $\\Gamma$ intersects the line segment $A B$ at $P$ different from $B$, and the line segment $A C$ at $Q$ different from $C$. Let $O N$ be a diameter of the circle $\\Gamma$. Prove that the quadrilateral $A P N Q$ is a parallelogram.", "solution": "From the assumption that the circle $\\Gamma$ intersects both of the line segments $A B$ and $A C$, it follows that the 4 points $N, C, Q, O$ are located on $\\Gamma$ in the order of $N, C, Q, O$ or in the order of $N, C, O, Q$. The following argument for the proof of the assertion of the problem is valid in either case. Since $\\angle N Q C$ and $\\angle N O C$ are subtended by the same arc $\\widehat{N C}$ of $\\Gamma$ at the points $Q$ and $O$, respectively, on $\\Gamma$, we have $\\angle N Q C=\\angle N O C$. We also have $\\angle B O C=2 \\angle B A C$, since $\\angle B O C$ and $\\angle B A C$ are subtended by the same arc $\\widehat{B C}$ of the circum-circle of the triangle $A B C$ at the center $O$ of the circle and at the point $A$ on the circle, respectively. From $O B=O C$ and the fact that $O N$ is a diameter of $\\Gamma$, it follows that the triangles $O B N$ and $O C N$ are congruent, and therefore we obtain $2 \\angle N O C=\\angle B O C$. Consequently, we have $\\angle N Q C=\\frac{1}{2} \\angle B O C=\\angle B A C$, which shows that the 2 lines $A P, Q N$ are parallel.\n\nIn the same manner, we can show that the 2 lines $A Q, P N$ are also parallel. Thus, the quadrilateral $A P N Q$ is a parallelogram.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution:"}}
|
| 2 |
-
{"year": "2010", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "For a positive integer $k$, call an integer a pure $k$-th power if it can be represented as $m^{k}$ for some integer $m$. Show that for every positive integer $n$ there exist $n$ distinct positive integers such that their sum is a pure 2009-th power, and their product is a pure 2010-th power.", "solution": "For the sake of simplicity, let us set $k=2009$.\nFirst of all, choose $n$ distinct positive integers $b_{1}, \\cdots, b_{n}$ suitably so that their product is a pure $k+1$-th power (for example, let $b_{i}=i^{k+1}$ for $i=1, \\cdots, n$ ). Then we have $b_{1} \\cdots b_{n}=t^{k+1}$ for some positive integer $t$. Set $b_{1}+\\cdots+b_{n}=s$.\n\nNow we set $a_{i}=b_{i} s^{k^{2}-1}$ for $i=1, \\cdots, n$, and show that $a_{1}, \\cdots, a_{n}$ satisfy the required conditions. Since $b_{1}, \\cdots, b_{n}$ are distinct positive integers, it is clear that so are $a_{1}, \\cdots, a_{n}$. From\n\n$$\n\\begin{aligned}\na_{1}+\\cdots+a_{n} & =s^{k^{2}-1}\\left(b_{1}+\\cdots+b_{n}\\right)=s^{k^{2}}=\\left(s^{k}\\right)^{2009} \\\\\na_{1} \\cdots a_{n} & =\\left(s^{k^{2}-1}\\right)^{n} b_{1} \\cdots b_{n}=\\left(s^{k^{2}-1}\\right)^{n} t^{k+1}=\\left(s^{(k-1) n} t\\right)^{2010}\n\\end{aligned}\n$$\n\nwe can see that $a_{1}, \\cdots, a_{n}$ satisfy the conditions on the sum and the product as well. This ends the proof of the assertion.\nRemark: We can find the appropriate exponent $k^{2}-1$ needed for the construction of the $a_{i}$ 's by solving the simultaneous congruence relations: $x \\equiv 0(\\bmod k+1), x \\equiv-1(\\bmod k)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution:"}}
|
| 3 |
-
{"year": "2010", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?", "solution": "When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\\frac{(n-1)(n-2)}{2}=\\frac{n^{2}-3 n+2}{2}$.\n\nLet us show that $\\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \\in T$ and $B \\in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.\n\nLet us now call a set of participants a group if it satisfies the following 2 conditions:\n\n- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \\cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \\leq i \\leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.\n- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.\n\nIn view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.\nLemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.\nProof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.\n\nThe lemma implies that there are at most $\\frac{n(n-1)}{2}-(n-1)=\\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\\frac{n^{2}-3 n+2}{2}$.\nRemark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.\n\nAlternate Solution 1: The construction of an example for the case for which the number $\\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.\n\nSuppose, then, $n$ participants are separated into $k(k \\geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \\cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \\leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\\sum_{i=1}^{k} a_{i} C_{2} \\leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From\n\n$$\n{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\\frac{n^{2}-n}{2}=\\left(a_{1}-\\frac{n}{2}\\right)^{2}+\\frac{n^{2}-2 n}{4}\n$$\n\nit follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\\sum_{i=1}^{k}{ }_{a} C_{2} \\leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\\frac{n^{2}-3 n+2}{2}$.\nAlternate Solution 2: Construction of an example would be the same as the preceding proof.\n\nFor a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.\n\nSuppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.\n\nThen the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since\n\n$$\ne+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\\frac{n^{2}-3 n+2}{2}\n$$\n\nthe number we seek is at most $\\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution:"}}
|
| 4 |
-
{"year": "2010", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $A B C$ be an acute triangle satisfying the condition $A B>B C$ and $A C>B C$. Denote by $O$ and $H$ the circumcenter and the orthocenter, respectively, of the triangle $A B C$. Suppose that the circumcircle of the triangle $A H C$ intersects the line $A B$ at $M$ different from $A$, and that the circumcircle of the triangle $A H B$ intersects the line $A C$ at $N$ different from $A$. Prove that the circumcenter of the triangle $M N H$ lies on the line $O H$.", "solution": "In the sequel, we denote $\\angle B A C=\\alpha, \\angle C B A=\\beta, \\angle A C B=\\gamma$. Let $O^{\\prime}$ be the circumcenter of the triangle $M N H$. The lengths of line segments starting from the point $H$ will be treated as signed quantities.\n\nLet us denote by $M^{\\prime}, N^{\\prime}$ the point of intersection of $C H, B H$, respectively, with the circumcircle of the triangle $A B C$ (distinct from $C, B$, respectively.) From the fact that 4 points $A, M, H, C$ lie on the same circle, we see that $\\angle M H M^{\\prime}=\\alpha$ holds. Furthermore, $\\angle B M^{\\prime} C, \\angle B N^{\\prime} C$ and $\\alpha$ are all subtended by the same arc $\\widehat{B C}$ of the circumcircle of the triangle $A B C$ at points on the circle, and therefore, we have $\\angle B M^{\\prime} C=\\alpha$, and $\\angle B N^{\\prime} C=\\alpha$ as well. We also have $\\angle A B H=\\angle A C N^{\\prime}$ as they are subtended by the same $\\operatorname{arc} A N^{\\prime}$ of the circumcircle of the triangle $A B C$ at points on the circle. Since $H M^{\\prime} \\perp B M, H N^{\\prime} \\perp A C$, we conclude that\n\n$$\n\\angle M^{\\prime} H B=90^{\\circ}-\\angle A B H=90^{\\circ}-\\angle A C N^{\\prime}=\\alpha\n$$\n\nis valid as well. Putting these facts together, we obtain the fact that the quadrilateral $H B M^{\\prime} M$ is a rhombus. In a similar manner, we can conclude that the quadrilateral $H C N^{\\prime} N$ is also a rhombus. Since both of these rhombuses are made up of 4 right triangles with an angle of magnitude $\\alpha$, we also see that these rhombuses are similar.\n\nLet us denote by $P, Q$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O^{\\prime}$. Since $O^{\\prime}$ is the circumcenter of the triangle $M N H, P, Q$ are respectively, the midpoints of the line segments $H M, H N$. Furthermore, if we denote by $R, S$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O$, then since $O$ is the circumcenter of both the triangle $M^{\\prime} B C$ and the triangle $N^{\\prime} B C$, we see that $R$ is the intersection point of $H M$ and the perpendicular bisector of $B M^{\\prime}$, and $S$ is the intersection point of $H N$ and the perpendicular bisector of $C N^{\\prime}$.\n\nWe note that the similarity map $\\phi$ between the rhombuses $H B M^{\\prime} M$ and $H C N^{\\prime} N$ carries the perpendicular bisector of $B M^{\\prime}$ onto the perpendicular bisector of $C N^{\\prime}$, and straight line $H M$ onto the straight line $H N$, and hence $\\phi$ maps $R$ onto $S$, and $P$ onto $Q$. Therefore, we get $H P: H R=H Q: H S$. If we now denote by $X, Y$ the intersection points of the line $H O^{\\prime}$ with the line through $R$ and perpendicular to $H P$, and with the line through $S$ and perpendicular to $H Q$, respectively, then we get\n\n$$\nH O^{\\prime}: H X=H P: H R=H Q: H S=H O^{\\prime}: H Y\n$$\n\nso that we must have $H X=H Y$, and therefore, $X=Y$. But it is obvious that the point of intersection of the line through $R$ and perpendicular to $H P$ with the line through $S$ and perpendicular to $H Q$ must be $O$, and therefore, we conclude that $X=Y=O$ and that the points $H, O^{\\prime}, O$ are collinear.\n\nAlternate Solution: Deduction of the fact that both of the quadrilaterals $H B M^{\\prime} M$ and $H C N^{\\prime} N$ are rhombuses is carried out in the same way as in the preceding proof.\n\nWe then see that the point $M$ is located in a symmetric position with the point $B$ with respect to the line $C H$, we conclude that we have $\\angle C M B=\\beta$. Similarly, we have $\\angle C N B=\\gamma$. If we now put $x=\\angle A H O^{\\prime}$, then we get\n\n$$\n\\angle O^{\\prime}=\\beta-\\alpha-x, \\angle M N H=90^{\\circ}-\\beta-\\alpha+x\n$$\n\nfrom which it follows that\n\n$$\n\\angle A N M=180^{\\circ}-\\angle M N H-\\left(90^{\\circ}-\\alpha\\right)=\\beta-x\n$$\n\nSimilarly, we get\n\n$$\n\\angle N M A=\\gamma+x\n$$\n\nUsing the laws of sines, we then get\n\n$$\n\\begin{aligned}\n\\frac{\\sin (\\gamma+x)}{\\sin (\\beta-x)} & =\\frac{A N}{A M}=\\frac{A C}{A M} \\cdot \\frac{A B}{A C} \\cdot \\frac{A N}{A B} \\\\\n& =\\frac{\\sin \\beta}{\\sin (\\beta-\\alpha)} \\cdot \\frac{\\sin \\gamma}{\\sin \\beta} \\cdot \\frac{\\sin (\\gamma-\\alpha)}{\\sin \\gamma}=\\frac{\\sin (\\gamma-\\alpha)}{\\sin (\\beta-\\alpha)}\n\\end{aligned}\n$$\n\nOn the other hand, if we let $y=\\angle A H O$, we then get\n\n$$\n\\angle O H B=180^{\\circ}-\\gamma-y, \\angle C H O=180^{\\circ}-\\beta+y,\n$$\n\nand since\n\n$$\n\\angle H B O=\\gamma-\\alpha, \\angle O C H=\\beta-\\alpha,\n$$\n\nusing the laws of sines and observing that $O B=O C$, we get\n\n$$\n\\begin{aligned}\n\\frac{\\sin (\\gamma-\\alpha)}{\\sin (\\beta-\\alpha)}=\\frac{\\sin \\angle H B O}{\\sin \\angle O C H} & =\\frac{\\sin \\left(180^{\\circ}-\\gamma-y\\right) \\cdot \\frac{O H}{O B}}{\\sin \\left(180^{\\circ}-\\beta+y\\right) \\cdot \\frac{O H}{O C}} \\\\\n& =\\frac{\\sin \\left(180^{\\circ}-\\gamma-y\\right)}{\\sin \\left(180^{\\circ}-\\beta+y\\right)}=\\frac{\\sin (\\gamma+y)}{\\sin (\\beta-y)}\n\\end{aligned}\n$$\n\nWe then get $\\sin (\\gamma+x) \\sin (\\beta-y)=\\sin (\\beta-x) \\sin (\\gamma+y)$. Expanding both sides of the last identity by using the addition formula for the sine function and after factoring and using again the addition formula we obtain that $\\sin (x-y) \\sin (\\beta+\\gamma)=0$. This implies that $x-y$ must be an integral multiple of $180^{\\circ}$, and hence we conclude that $H, O, O^{\\prime}$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution:"}}
|
| 5 |
-
{"year": "2010", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Find all functions $f$ from the set $\\mathbf{R}$ of real numbers into $\\mathbf{R}$ which satisfy for all $x, y, z \\in \\mathbf{R}$ the identity\n\n$$\nf(f(x)+f(y)+f(z))=f(f(x)-f(y))+f(2 x y+f(z))+2 f(x z-y z) .\n$$", "solution": "It is clear that if $f$ is a constant function which satisfies the given equation, then the constant must be 0 . Conversely, $f(x)=0$ clearly satisfies the given equation, so, the identically 0 function is a solution. In the sequel, we consider the case where $f$ is not a constant function.\n\nLet $t \\in \\mathbf{R}$ and substitute $(x, y, z)=(t, 0,0)$ and $(x, y, z)=(0, t, 0)$ into the given functional equation. Then, we obtain, respectively,\n\n$$\n\\begin{aligned}\n& f(f(t)+2 f(0))=f(f(t)-f(0))+f(f(0))+2 f(0), \\\\\n& f(f(t)+2 f(0))=f(f(0)-f(t))+f(f(0))+2 f(0)\n\\end{aligned}\n$$\n\nfrom which we conclude that $f(f(t)-f(0))=f(f(0)-f(t))$ holds for all $t \\in \\mathbf{R}$. Now, suppose for some pair $u_{1}, u_{2}, f\\left(u_{1}\\right)=f\\left(u_{2}\\right)$ is satisfied. Then by substituting $(x, y, z)=\\left(s, 0, u_{1}\\right)$ and $(x, y, z)=\\left(s, 0, u_{2}\\right)$ into the functional equation and comparing the resulting identities, we can easily conclude that\n\n$$\nf\\left(s u_{1}\\right)=f\\left(s u_{2}\\right)\n$$\n\nholds for all $s \\in \\mathbf{R}$. Since $f$ is not a constant function there exists an $s_{0}$ such that $f\\left(s_{0}\\right)-f(0) \\neq$ 0 . If we put $u_{1}=f\\left(s_{0}\\right)-f(0), u_{2}=-u_{1}$, then $f\\left(u_{1}\\right)=f\\left(u_{2}\\right)$, so we have by $(*)$\n\n$$\nf\\left(s u_{1}\\right)=f\\left(s u_{2}\\right)=f\\left(-s u_{1}\\right)\n$$\n\nfor all $s \\in \\mathbf{R}$. Since $u_{1} \\neq 0$, we conclude that\n\n$$\nf(x)=f(-x)\n$$\n\nholds for all $x \\in \\mathbf{R}$.\nNext, if $f(u)=f(0)$ for some $u \\neq 0$, then by $(*)$, we have $f(s u)=f(s 0)=f(0)$ for all $s$, which implies that $f$ is a constant function, contradicting our assumption. Therefore, we must have $f(s) \\neq f(0)$ whenever $s \\neq 0$.\n\nWe will now show that if $f(x)=f(y)$ holds, then either $x=y$ or $x=-y$ must hold. Suppose on the contrary that $f\\left(x_{0}\\right)=f\\left(y_{0}\\right)$ holds for some pair of non-zero numbers $x_{0}, y_{0}$ for which $x_{0} \\neq y_{0}, x_{0} \\neq-y_{0}$. Since $f\\left(-y_{0}\\right)=f\\left(y_{0}\\right)$, we may assume, by replacing $y_{0}$ by $-y_{0}$ if necessary, that $x_{0}$ and $y_{0}$ have the same sign. In view of $(*)$, we see that $f\\left(s x_{0}\\right)=f\\left(s y_{0}\\right)$ holds for all $s$, and therefore, there exists some $r>0, r \\neq 1$ such that\n\n$$\nf(x)=f(r x)\n$$\n\nholds for all $x$. Replacing $x$ by $r x$ and $y$ by $r y$ in the given functional equation, we obtain\n\n$$\nf(f(r x)+f(r y)+f(z))=f(f(r x)-f(r y))+f\\left(2 r^{2} x y+f(z)\\right)+2 f(r(x-y) z)\n$$\n\nand replacing $x$ by $r^{2} x$ in the functional equation, we get\n\n$$\nf\\left(f\\left(r^{2} x\\right)+f(y)+f(z)\\right)=f\\left(f\\left(r^{2} x\\right)-f(y)\\right)+f\\left(2 r^{2} x y+f(z)\\right)+2 f\\left(\\left(r^{2} x-y\\right) z\\right)\n$$\n\nSince $f(r x)=f(x)$ holds for all $x \\in \\mathbf{R}$, we see that except for the last term on the right-hand side, all the corresponding terms appearing in the identities (i) and (ii) above are equal, and hence we conclude that\n\n$$\n\\left.f(r(x-y) z)=f\\left(\\left(r^{2} x-y\\right) z\\right)\\right)\n$$\n\nmust hold for arbitrary choice of $x, y, z \\in \\mathbf{R}$. For arbitrarily fixed pair $u, v \\in \\mathbf{R}$, substitute $(x, y, z)=\\left(\\frac{v-u}{r^{2}-1}, \\frac{v-r^{2} u}{r^{2}-1}, 1\\right)$ into the identity (iii). Then we obtain $f(v)=f(r u)=f(u)$, since $x-y=u, r^{2} x-y=v, z=1$. But this implies that the function $f$ is a constant, contradicting our assumption. Thus we conclude that if $f(x)=f(y)$ then either $x=y$ or $x=-y$ must hold.\n\nBy substituting $z=0$ in the functional equation, we get\n\n$$\nf(f(x)+f(y)+f(0))=f(f(x)-f(y)+f(0))=f((f(x)-f(y))+f(2 x y+f(0))+2 f(0)\n$$\n\nChanging $y$ to $-y$ in the identity above and using the fact that $f(y)=f(-y)$, we see that all the terms except the second term on the right-hand side in the identity above remain the same. Thus we conclude that $f(2 x y+f(0))=f(-2 x y+f(0))$, from which we get either $2 x y+f(0)=-2 x y+f(0)$ or $2 x y+f(0)=2 x y-f(0)$ for all $x, y \\in \\mathbf{R}$. The first of these alternatives says that $4 x y=0$, which is impossible if $x y \\neq 0$. Therefore the second alternative must be valid and we get that $f(0)=0$.\n\nFinally, let us show that if $f$ satisfies the given functional equation and is not a constant function, then $f(x)=x^{2}$. Let $x=y$ in the functional equation, then since $f(0)=0$, we get\n\n$$\nf(2 f(x)+f(z))=f\\left(2 x^{2}+f(z)\\right)\n$$\n\nfrom which we conclude that either $2 f(x)+f(z)=2 x^{2}+f(z)$ or $2 f(x)+f(z)=-2 x^{2}-f(z)$ must hold. Suppose there exists $x_{0}$ for which $f\\left(x_{0}\\right) \\neq x_{0}^{2}$, then from the second alternative, we see that $f(z)=-f\\left(x_{0}\\right)-x_{0}^{2}$ must hold for all $z$, which means that $f$ must be a constant function, contrary to our assumption. Therefore, the first alternative above must hold, and we have $f(x)=x^{2}$ for all $x$, establishing our claim.\n\nIt is easy to check that $f(x)=x^{2}$ does satisfy the given functional equation, so we conclude that $f(x)=0$ and $f(x)=x^{2}$ are the only functions that satisfy the requirement.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution:"}}
|
|
|
|
| 1 |
+
{"year": "2010", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle with $\\angle B A C \\neq 90^{\\circ}$. Let $O$ be the circumcenter of the triangle $A B C$ and let $\\Gamma$ be the circumcircle of the triangle $B O C$. Suppose that $\\Gamma$ intersects the line segment $A B$ at $P$ different from $B$, and the line segment $A C$ at $Q$ different from $C$. Let $O N$ be a diameter of the circle $\\Gamma$. Prove that the quadrilateral $A P N Q$ is a parallelogram.", "solution": "From the assumption that the circle $\\Gamma$ intersects both of the line segments $A B$ and $A C$, it follows that the 4 points $N, C, Q, O$ are located on $\\Gamma$ in the order of $N, C, Q, O$ or in the order of $N, C, O, Q$. The following argument for the proof of the assertion of the problem is valid in either case. Since $\\angle N Q C$ and $\\angle N O C$ are subtended by the same arc $\\widehat{N C}$ of $\\Gamma$ at the points $Q$ and $O$, respectively, on $\\Gamma$, we have $\\angle N Q C=\\angle N O C$. We also have $\\angle B O C=2 \\angle B A C$, since $\\angle B O C$ and $\\angle B A C$ are subtended by the same arc $\\widehat{B C}$ of the circum-circle of the triangle $A B C$ at the center $O$ of the circle and at the point $A$ on the circle, respectively. From $O B=O C$ and the fact that $O N$ is a diameter of $\\Gamma$, it follows that the triangles $O B N$ and $O C N$ are congruent, and therefore we obtain $2 \\angle N O C=\\angle B O C$. Consequently, we have $\\angle N Q C=\\frac{1}{2} \\angle B O C=\\angle B A C$, which shows that the 2 lines $A P, Q N$ are parallel.\n\nIn the same manner, we can show that the 2 lines $A Q, P N$ are also parallel. Thus, the quadrilateral $A P N Q$ is a parallelogram.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution:"}}
|
| 2 |
+
{"year": "2010", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "For a positive integer $k$, call an integer a pure $k$-th power if it can be represented as $m^{k}$ for some integer $m$. Show that for every positive integer $n$ there exist $n$ distinct positive integers such that their sum is a pure 2009-th power, and their product is a pure 2010-th power.", "solution": "For the sake of simplicity, let us set $k=2009$.\nFirst of all, choose $n$ distinct positive integers $b_{1}, \\cdots, b_{n}$ suitably so that their product is a pure $k+1$-th power (for example, let $b_{i}=i^{k+1}$ for $i=1, \\cdots, n$ ). Then we have $b_{1} \\cdots b_{n}=t^{k+1}$ for some positive integer $t$. Set $b_{1}+\\cdots+b_{n}=s$.\n\nNow we set $a_{i}=b_{i} s^{k^{2}-1}$ for $i=1, \\cdots, n$, and show that $a_{1}, \\cdots, a_{n}$ satisfy the required conditions. Since $b_{1}, \\cdots, b_{n}$ are distinct positive integers, it is clear that so are $a_{1}, \\cdots, a_{n}$. From\n\n$$\n\\begin{aligned}\na_{1}+\\cdots+a_{n} & =s^{k^{2}-1}\\left(b_{1}+\\cdots+b_{n}\\right)=s^{k^{2}}=\\left(s^{k}\\right)^{2009} \\\\\na_{1} \\cdots a_{n} & =\\left(s^{k^{2}-1}\\right)^{n} b_{1} \\cdots b_{n}=\\left(s^{k^{2}-1}\\right)^{n} t^{k+1}=\\left(s^{(k-1) n} t\\right)^{2010}\n\\end{aligned}\n$$\n\nwe can see that $a_{1}, \\cdots, a_{n}$ satisfy the conditions on the sum and the product as well. This ends the proof of the assertion.\nRemark: We can find the appropriate exponent $k^{2}-1$ needed for the construction of the $a_{i}$ 's by solving the simultaneous congruence relations: $x \\equiv 0(\\bmod k+1), x \\equiv-1(\\bmod k)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution:"}}
|
| 3 |
+
{"year": "2010", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?", "solution": "When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\\frac{(n-1)(n-2)}{2}=\\frac{n^{2}-3 n+2}{2}$.\n\nLet us show that $\\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \\in T$ and $B \\in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.\n\nLet us now call a set of participants a group if it satisfies the following 2 conditions:\n\n- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \\cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \\leq i \\leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.\n- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.\n\nIn view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.\nLemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.\nProof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.\n\nThe lemma implies that there are at most $\\frac{n(n-1)}{2}-(n-1)=\\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\\frac{n^{2}-3 n+2}{2}$.\nRemark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.\n\nAlternate Solution 1: The construction of an example for the case for which the number $\\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.\n\nSuppose, then, $n$ participants are separated into $k(k \\geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \\cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \\leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\\sum_{i=1}^{k} a_{i} C_{2} \\leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From\n\n$$\n{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\\frac{n^{2}-n}{2}=\\left(a_{1}-\\frac{n}{2}\\right)^{2}+\\frac{n^{2}-2 n}{4}\n$$\n\nit follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\\sum_{i=1}^{k}{ }_{a} C_{2} \\leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\\frac{n^{2}-3 n+2}{2}$.\nAlternate Solution 2: Construction of an example would be the same as the preceding proof.\n\nFor a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.\n\nSuppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.\n\nThen the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since\n\n$$\ne+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\\frac{n^{2}-3 n+2}{2}\n$$\n\nthe number we seek is at most $\\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution:"}}
|
| 4 |
+
{"year": "2010", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute triangle satisfying the condition $A B>B C$ and $A C>B C$. Denote by $O$ and $H$ the circumcenter and the orthocenter, respectively, of the triangle $A B C$. Suppose that the circumcircle of the triangle $A H C$ intersects the line $A B$ at $M$ different from $A$, and that the circumcircle of the triangle $A H B$ intersects the line $A C$ at $N$ different from $A$. Prove that the circumcenter of the triangle $M N H$ lies on the line $O H$.", "solution": "In the sequel, we denote $\\angle B A C=\\alpha, \\angle C B A=\\beta, \\angle A C B=\\gamma$. Let $O^{\\prime}$ be the circumcenter of the triangle $M N H$. The lengths of line segments starting from the point $H$ will be treated as signed quantities.\n\nLet us denote by $M^{\\prime}, N^{\\prime}$ the point of intersection of $C H, B H$, respectively, with the circumcircle of the triangle $A B C$ (distinct from $C, B$, respectively.) From the fact that 4 points $A, M, H, C$ lie on the same circle, we see that $\\angle M H M^{\\prime}=\\alpha$ holds. Furthermore, $\\angle B M^{\\prime} C, \\angle B N^{\\prime} C$ and $\\alpha$ are all subtended by the same arc $\\widehat{B C}$ of the circumcircle of the triangle $A B C$ at points on the circle, and therefore, we have $\\angle B M^{\\prime} C=\\alpha$, and $\\angle B N^{\\prime} C=\\alpha$ as well. We also have $\\angle A B H=\\angle A C N^{\\prime}$ as they are subtended by the same $\\operatorname{arc} A N^{\\prime}$ of the circumcircle of the triangle $A B C$ at points on the circle. Since $H M^{\\prime} \\perp B M, H N^{\\prime} \\perp A C$, we conclude that\n\n$$\n\\angle M^{\\prime} H B=90^{\\circ}-\\angle A B H=90^{\\circ}-\\angle A C N^{\\prime}=\\alpha\n$$\n\nis valid as well. Putting these facts together, we obtain the fact that the quadrilateral $H B M^{\\prime} M$ is a rhombus. In a similar manner, we can conclude that the quadrilateral $H C N^{\\prime} N$ is also a rhombus. Since both of these rhombuses are made up of 4 right triangles with an angle of magnitude $\\alpha$, we also see that these rhombuses are similar.\n\nLet us denote by $P, Q$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O^{\\prime}$. Since $O^{\\prime}$ is the circumcenter of the triangle $M N H, P, Q$ are respectively, the midpoints of the line segments $H M, H N$. Furthermore, if we denote by $R, S$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O$, then since $O$ is the circumcenter of both the triangle $M^{\\prime} B C$ and the triangle $N^{\\prime} B C$, we see that $R$ is the intersection point of $H M$ and the perpendicular bisector of $B M^{\\prime}$, and $S$ is the intersection point of $H N$ and the perpendicular bisector of $C N^{\\prime}$.\n\nWe note that the similarity map $\\phi$ between the rhombuses $H B M^{\\prime} M$ and $H C N^{\\prime} N$ carries the perpendicular bisector of $B M^{\\prime}$ onto the perpendicular bisector of $C N^{\\prime}$, and straight line $H M$ onto the straight line $H N$, and hence $\\phi$ maps $R$ onto $S$, and $P$ onto $Q$. Therefore, we get $H P: H R=H Q: H S$. If we now denote by $X, Y$ the intersection points of the line $H O^{\\prime}$ with the line through $R$ and perpendicular to $H P$, and with the line through $S$ and perpendicular to $H Q$, respectively, then we get\n\n$$\nH O^{\\prime}: H X=H P: H R=H Q: H S=H O^{\\prime}: H Y\n$$\n\nso that we must have $H X=H Y$, and therefore, $X=Y$. But it is obvious that the point of intersection of the line through $R$ and perpendicular to $H P$ with the line through $S$ and perpendicular to $H Q$ must be $O$, and therefore, we conclude that $X=Y=O$ and that the points $H, O^{\\prime}, O$ are collinear.\n\nAlternate Solution: Deduction of the fact that both of the quadrilaterals $H B M^{\\prime} M$ and $H C N^{\\prime} N$ are rhombuses is carried out in the same way as in the preceding proof.\n\nWe then see that the point $M$ is located in a symmetric position with the point $B$ with respect to the line $C H$, we conclude that we have $\\angle C M B=\\beta$. Similarly, we have $\\angle C N B=\\gamma$. If we now put $x=\\angle A H O^{\\prime}$, then we get\n\n$$\n\\angle O^{\\prime}=\\beta-\\alpha-x, \\angle M N H=90^{\\circ}-\\beta-\\alpha+x\n$$\n\nfrom which it follows that\n\n$$\n\\angle A N M=180^{\\circ}-\\angle M N H-\\left(90^{\\circ}-\\alpha\\right)=\\beta-x\n$$\n\nSimilarly, we get\n\n$$\n\\angle N M A=\\gamma+x\n$$\n\nUsing the laws of sines, we then get\n\n$$\n\\begin{aligned}\n\\frac{\\sin (\\gamma+x)}{\\sin (\\beta-x)} & =\\frac{A N}{A M}=\\frac{A C}{A M} \\cdot \\frac{A B}{A C} \\cdot \\frac{A N}{A B} \\\\\n& =\\frac{\\sin \\beta}{\\sin (\\beta-\\alpha)} \\cdot \\frac{\\sin \\gamma}{\\sin \\beta} \\cdot \\frac{\\sin (\\gamma-\\alpha)}{\\sin \\gamma}=\\frac{\\sin (\\gamma-\\alpha)}{\\sin (\\beta-\\alpha)}\n\\end{aligned}\n$$\n\nOn the other hand, if we let $y=\\angle A H O$, we then get\n\n$$\n\\angle O H B=180^{\\circ}-\\gamma-y, \\angle C H O=180^{\\circ}-\\beta+y,\n$$\n\nand since\n\n$$\n\\angle H B O=\\gamma-\\alpha, \\angle O C H=\\beta-\\alpha,\n$$\n\nusing the laws of sines and observing that $O B=O C$, we get\n\n$$\n\\begin{aligned}\n\\frac{\\sin (\\gamma-\\alpha)}{\\sin (\\beta-\\alpha)}=\\frac{\\sin \\angle H B O}{\\sin \\angle O C H} & =\\frac{\\sin \\left(180^{\\circ}-\\gamma-y\\right) \\cdot \\frac{O H}{O B}}{\\sin \\left(180^{\\circ}-\\beta+y\\right) \\cdot \\frac{O H}{O C}} \\\\\n& =\\frac{\\sin \\left(180^{\\circ}-\\gamma-y\\right)}{\\sin \\left(180^{\\circ}-\\beta+y\\right)}=\\frac{\\sin (\\gamma+y)}{\\sin (\\beta-y)}\n\\end{aligned}\n$$\n\nWe then get $\\sin (\\gamma+x) \\sin (\\beta-y)=\\sin (\\beta-x) \\sin (\\gamma+y)$. Expanding both sides of the last identity by using the addition formula for the sine function and after factoring and using again the addition formula we obtain that $\\sin (x-y) \\sin (\\beta+\\gamma)=0$. This implies that $x-y$ must be an integral multiple of $180^{\\circ}$, and hence we conclude that $H, O, O^{\\prime}$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution:"}}
|
| 5 |
+
{"year": "2010", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Find all functions $f$ from the set $\\mathbf{R}$ of real numbers into $\\mathbf{R}$ which satisfy for all $x, y, z \\in \\mathbf{R}$ the identity\n\n$$\nf(f(x)+f(y)+f(z))=f(f(x)-f(y))+f(2 x y+f(z))+2 f(x z-y z) .\n$$", "solution": "It is clear that if $f$ is a constant function which satisfies the given equation, then the constant must be 0 . Conversely, $f(x)=0$ clearly satisfies the given equation, so, the identically 0 function is a solution. In the sequel, we consider the case where $f$ is not a constant function.\n\nLet $t \\in \\mathbf{R}$ and substitute $(x, y, z)=(t, 0,0)$ and $(x, y, z)=(0, t, 0)$ into the given functional equation. Then, we obtain, respectively,\n\n$$\n\\begin{aligned}\n& f(f(t)+2 f(0))=f(f(t)-f(0))+f(f(0))+2 f(0), \\\\\n& f(f(t)+2 f(0))=f(f(0)-f(t))+f(f(0))+2 f(0)\n\\end{aligned}\n$$\n\nfrom which we conclude that $f(f(t)-f(0))=f(f(0)-f(t))$ holds for all $t \\in \\mathbf{R}$. Now, suppose for some pair $u_{1}, u_{2}, f\\left(u_{1}\\right)=f\\left(u_{2}\\right)$ is satisfied. Then by substituting $(x, y, z)=\\left(s, 0, u_{1}\\right)$ and $(x, y, z)=\\left(s, 0, u_{2}\\right)$ into the functional equation and comparing the resulting identities, we can easily conclude that\n\n$$\nf\\left(s u_{1}\\right)=f\\left(s u_{2}\\right)\n$$\n\nholds for all $s \\in \\mathbf{R}$. Since $f$ is not a constant function there exists an $s_{0}$ such that $f\\left(s_{0}\\right)-f(0) \\neq$ 0 . If we put $u_{1}=f\\left(s_{0}\\right)-f(0), u_{2}=-u_{1}$, then $f\\left(u_{1}\\right)=f\\left(u_{2}\\right)$, so we have by $(*)$\n\n$$\nf\\left(s u_{1}\\right)=f\\left(s u_{2}\\right)=f\\left(-s u_{1}\\right)\n$$\n\nfor all $s \\in \\mathbf{R}$. Since $u_{1} \\neq 0$, we conclude that\n\n$$\nf(x)=f(-x)\n$$\n\nholds for all $x \\in \\mathbf{R}$.\nNext, if $f(u)=f(0)$ for some $u \\neq 0$, then by $(*)$, we have $f(s u)=f(s 0)=f(0)$ for all $s$, which implies that $f$ is a constant function, contradicting our assumption. Therefore, we must have $f(s) \\neq f(0)$ whenever $s \\neq 0$.\n\nWe will now show that if $f(x)=f(y)$ holds, then either $x=y$ or $x=-y$ must hold. Suppose on the contrary that $f\\left(x_{0}\\right)=f\\left(y_{0}\\right)$ holds for some pair of non-zero numbers $x_{0}, y_{0}$ for which $x_{0} \\neq y_{0}, x_{0} \\neq-y_{0}$. Since $f\\left(-y_{0}\\right)=f\\left(y_{0}\\right)$, we may assume, by replacing $y_{0}$ by $-y_{0}$ if necessary, that $x_{0}$ and $y_{0}$ have the same sign. In view of $(*)$, we see that $f\\left(s x_{0}\\right)=f\\left(s y_{0}\\right)$ holds for all $s$, and therefore, there exists some $r>0, r \\neq 1$ such that\n\n$$\nf(x)=f(r x)\n$$\n\nholds for all $x$. Replacing $x$ by $r x$ and $y$ by $r y$ in the given functional equation, we obtain\n\n$$\nf(f(r x)+f(r y)+f(z))=f(f(r x)-f(r y))+f\\left(2 r^{2} x y+f(z)\\right)+2 f(r(x-y) z)\n$$\n\nand replacing $x$ by $r^{2} x$ in the functional equation, we get\n\n$$\nf\\left(f\\left(r^{2} x\\right)+f(y)+f(z)\\right)=f\\left(f\\left(r^{2} x\\right)-f(y)\\right)+f\\left(2 r^{2} x y+f(z)\\right)+2 f\\left(\\left(r^{2} x-y\\right) z\\right)\n$$\n\nSince $f(r x)=f(x)$ holds for all $x \\in \\mathbf{R}$, we see that except for the last term on the right-hand side, all the corresponding terms appearing in the identities (i) and (ii) above are equal, and hence we conclude that\n\n$$\n\\left.f(r(x-y) z)=f\\left(\\left(r^{2} x-y\\right) z\\right)\\right)\n$$\n\nmust hold for arbitrary choice of $x, y, z \\in \\mathbf{R}$. For arbitrarily fixed pair $u, v \\in \\mathbf{R}$, substitute $(x, y, z)=\\left(\\frac{v-u}{r^{2}-1}, \\frac{v-r^{2} u}{r^{2}-1}, 1\\right)$ into the identity (iii). Then we obtain $f(v)=f(r u)=f(u)$, since $x-y=u, r^{2} x-y=v, z=1$. But this implies that the function $f$ is a constant, contradicting our assumption. Thus we conclude that if $f(x)=f(y)$ then either $x=y$ or $x=-y$ must hold.\n\nBy substituting $z=0$ in the functional equation, we get\n\n$$\nf(f(x)+f(y)+f(0))=f(f(x)-f(y)+f(0))=f((f(x)-f(y))+f(2 x y+f(0))+2 f(0)\n$$\n\nChanging $y$ to $-y$ in the identity above and using the fact that $f(y)=f(-y)$, we see that all the terms except the second term on the right-hand side in the identity above remain the same. Thus we conclude that $f(2 x y+f(0))=f(-2 x y+f(0))$, from which we get either $2 x y+f(0)=-2 x y+f(0)$ or $2 x y+f(0)=2 x y-f(0)$ for all $x, y \\in \\mathbf{R}$. The first of these alternatives says that $4 x y=0$, which is impossible if $x y \\neq 0$. Therefore the second alternative must be valid and we get that $f(0)=0$.\n\nFinally, let us show that if $f$ satisfies the given functional equation and is not a constant function, then $f(x)=x^{2}$. Let $x=y$ in the functional equation, then since $f(0)=0$, we get\n\n$$\nf(2 f(x)+f(z))=f\\left(2 x^{2}+f(z)\\right)\n$$\n\nfrom which we conclude that either $2 f(x)+f(z)=2 x^{2}+f(z)$ or $2 f(x)+f(z)=-2 x^{2}-f(z)$ must hold. Suppose there exists $x_{0}$ for which $f\\left(x_{0}\\right) \\neq x_{0}^{2}$, then from the second alternative, we see that $f(z)=-f\\left(x_{0}\\right)-x_{0}^{2}$ must hold for all $z$, which means that $f$ must be a constant function, contrary to our assumption. Therefore, the first alternative above must hold, and we have $f(x)=x^{2}$ for all $x$, establishing our claim.\n\nIt is easy to check that $f(x)=x^{2}$ does satisfy the given functional equation, so we conclude that $f(x)=0$ and $f(x)=x^{2}$ are the only functions that satisfy the requirement.", "metadata": {"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution:"}}
|
APMO/segmented/en-apmo2013_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2013", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with altitudes $A D, B E$ and $C F$, and let $O$ be the center of its circumcircle. Show that the segments $O A, O F, O B, O D, O C, O E$ dissect the triangle $A B C$ into three pairs of triangles that have equal areas.", "solution": "Let $M$ and $N$ be midpoints of sides $B C$ and $A C$, respectively. Notice that $\\angle M O C=\\frac{1}{2} \\angle B O C=\\angle E A B, \\angle O M C=90^{\\circ}=\\angle A E B$, so triangles $O M C$ and $A E B$ are similar and we get $\\frac{O M}{A E}=\\frac{O C}{A B}$. For triangles $O N A$ and $B D A$ we also have $\\frac{O N}{B D}=\\frac{O A}{B A}$. Then $\\frac{O M}{A E}=\\frac{O N}{B D}$ or $B D \\cdot O M=A E \\cdot O N$.\n\nDenote by $S(\\Phi)$ the area of the figure $\\Phi$. So, we see that $S(O B D)=\\frac{1}{2} B D \\cdot O M=$ $\\frac{1}{2} A E \\cdot O N=S(O A E)$. Analogously, $S(O C D)=S(O A F)$ and $S(O C E)=S(O B F)$.\n\nAlternative solution. Let $R$ be the circumradius of triangle $A B C$, and as usual write $A, B, C$ for angles $\\angle C A B, \\angle A B C, \\angle B C A$ respectively, and $a, b, c$ for sides $B C, C A, A B$ respectively. Then the area of triangle $O C D$ is\n\n$$\nS(O C D)=\\frac{1}{2} \\cdot O C \\cdot C D \\cdot \\sin (\\angle O C D)=\\frac{1}{2} R \\cdot C D \\cdot \\sin (\\angle O C D)\n$$\n\nNow $C D=b \\cos C$, and\n\n$$\n\\angle O C D=\\frac{180^{\\circ}-2 A}{2}=90^{\\circ}-A\n$$\n\n(since triangle $O B C$ is isosceles, and $\\angle B O C=2 A$ ). So\n\n$$\nS(O C D)=\\frac{1}{2} R b \\cos C \\sin \\left(90^{\\circ}-A\\right)=\\frac{1}{2} R b \\cos C \\cos A\n$$\n\nA similar calculation gives\n\n$$\n\\begin{aligned}\nS(O A F) & =\\frac{1}{2} O A \\cdot A F \\cdot \\sin (\\angle O A F) \\\\\n& =\\frac{1}{2} R \\cdot(b \\cos A) \\sin \\left(90^{\\circ}-C\\right) \\\\\n& =\\frac{1}{2} R b \\cos A \\cos C\n\\end{aligned}\n$$\n\nso $O C D$ and $O A F$ have the same area. In the same way we find that $O B D$ and $O A E$ have the same area, as do $O C E$ and $O B F$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2013", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Determine all positive integers $n$ for which $\\frac{n^{2}+1}{[\\sqrt{n}]^{2}+2}$ is an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.", "solution": "We will show that there are no positive integers $n$ satisfying the condition of the problem.\n\nLet $m=[\\sqrt{n}]$ and $a=n-m^{2}$. We have $m \\geq 1$ since $n \\geq 1$. From $n^{2}+1=\\left(m^{2}+a\\right)^{2}+1 \\equiv$ $(a-2)^{2}+1\\left(\\bmod \\left(m^{2}+2\\right)\\right)$, it follows that the condition of the problem is equivalent to the fact that $(a-2)^{2}+1$ is divisible by $m^{2}+2$. Since we have\n\n$$\n0<(a-2)^{2}+1 \\leq \\max \\left\\{2^{2},(2 m-2)^{2}\\right\\}+1 \\leq 4 m^{2}+1<4\\left(m^{2}+2\\right)\n$$\n\nwe see that $(a-2)^{2}+1=k\\left(m^{2}+2\\right)$ must hold with $k=1,2$ or 3 . We will show that none of these can occur.\n\nCase 1. When $k=1$. We get $(a-2)^{2}-m^{2}=1$, and this implies that $a-2= \\pm 1, m=0$ must hold, but this contradicts with fact $m \\geq 1$.\n\nCase 2. When $k=2$. We have $(a-2)^{2}+1=2\\left(m^{2}+2\\right)$ in this case, but any perfect square is congruent to $0,1,4 \\bmod 8$, and therefore, we have $(a-2)^{2}+1 \\equiv 1,2,5(\\bmod 8)$, while $2\\left(m^{2}+2\\right) \\equiv 4,6(\\bmod 8)$. Thus, this case cannot occur either.\n\nCase 3. When $k=3$. We have $(a-2)^{2}+1=3\\left(m^{2}+2\\right)$ in this case. Since any perfect square is congruent to 0 or $1 \\bmod 3$, we have $(a-2)^{2}+1 \\equiv 1,2(\\bmod 3)$, while $3\\left(m^{2}+2\\right) \\equiv 0$ $(\\bmod 3)$, which shows that this case cannot occur either.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2013", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "For $2 k$ real numbers $a_{1}, a_{2}, \\ldots, a_{k}, b_{1}, b_{2}, \\ldots, b_{k}$ define the sequence of numbers $X_{n}$ by\n\n$$\nX_{n}=\\sum_{i=1}^{k}\\left[a_{i} n+b_{i}\\right] \\quad(n=1,2, \\ldots)\n$$\n\nIf the sequence $X_{n}$ forms an arithmetic progression, show that $\\sum_{i=1}^{k} a_{i}$ must be an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.", "solution": "Let us write $A=\\sum_{i=1}^{k} a_{i}$ and $B=\\sum_{i=1}^{k} b_{i}$. Summing the corresponding terms of the following inequalities over $i$,\n\n$$\na_{i} n+b_{i}-1<\\left[a_{i} n+b_{i}\\right] \\leq a_{i} n+b_{i}\n$$\n\nwe obtain $A n+B-k<X_{n}<A n+B$. Now suppose that $\\left\\{X_{n}\\right\\}$ is an arithmetic progression with the common difference $d$, then we have $n d=X_{n+1}-X_{1}$ and $A+B-k<X_{1} \\leq A+B$ Combining with the inequalities obtained above, we get\n\n$$\nA(n+1)+B-k<n d+X_{1}<A(n+1)+B,\n$$\n\nor\n\n$$\nA n-k \\leq A n+\\left(A+B-X_{1}\\right)-k<n d<A n+\\left(A+B-X_{1}\\right)<A n+k,\n$$\n\nfrom which we conclude that $|A-d|<\\frac{k}{n}$ must hold. Since this inequality holds for any positive integer $n$, we must have $A=d$. Since $\\left\\{X_{n}\\right\\}$ is a sequence of integers, $d$ must be an integer also, and thus we conclude that $A$ is also an integer.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2013", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $a$ and $b$ be positive integers, and let $A$ and $B$ be finite sets of integers satisfying:\n(i) $A$ and $B$ are disjoint;\n(ii) if an integer $i$ belongs either to $A$ or to $B$, then $i+a$ belongs to $A$ or $i-b$ belongs to $B$.\n\nProve that $a|A|=b|B|$. (Here $|X|$ denotes the number of elements in the set $X$.)", "solution": "Let $A^{*}=\\{n-a: n \\in A\\}$ and $B^{*}=\\{n+b: n \\in B\\}$. Then, by (ii), $A \\cup B \\subseteq A^{*} \\cup B^{*}$ and by (i),\n\n$$\n|A \\cup B| \\leq\\left|A^{*} \\cup B^{*}\\right| \\leq\\left|A^{*}\\right|+\\left|B^{*}\\right|=|A|+|B|=|A \\cup B|\n$$\n\nThus, $A \\cup B=A^{*} \\cup B^{*}$ and $A^{*}$ and $B^{*}$ have no element in common. For each finite set $X$ of integers, let $\\sum(X)=\\sum_{x \\in X} x$. Then\n\n$$\n\\begin{aligned}\n\\sum(A)+\\sum(B) & =\\sum(A \\cup B) \\\\\n& =\\sum\\left(A^{*} \\cup B^{*}\\right)=\\sum\\left(A^{*}\\right)+\\sum\\left(B^{*}\\right) \\\\\n& =\\sum(A)-a|A|+\\sum(B)+b|B|\n\\end{aligned}\n$$\n\nwhich implies $a|A|=b|B|$.\nAlternative solution. Let us construct a directed graph whose vertices are labelled by the members of $A \\cup B$ and such that there is an edge from $i$ to $j$ iff $j \\in A$ and $j=i+a$ or $j \\in B$ and $j=i-b$. From (ii), each vertex has out-degree $\\geq 1$ and, from (i), each vertex has in-degree $\\leq 1$. Since the sum of the out-degrees equals the sum of the in-degrees, each vertex has in-degree and out-degree equal to 1. This is only possible if the graph is the union of disjoint cycles, say $G_{1}, G_{2}, \\ldots, G_{n}$. Let $\\left|A_{k}\\right|$ be the number of elements of $A$ in $G_{k}$ and $\\left|B_{k}\\right|$ be the number of elements of $B$ in $G_{k}$. The cycle $G_{k}$ will involve increasing vertex labels by $a$ a total of $\\left|A_{k}\\right|$ times and decreasing them by $b$ a total of $\\left|B_{k}\\right|$ times. Since it is a cycle, we have $a\\left|A_{k}\\right|=b\\left|B_{k}\\right|$. Summing over all cycles gives the result.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 5 |
-
{"year": "2013", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle $\\omega$, and let $P$ be a point on the extension of $A C$ such that $P B$ and $P D$ are tangent to $\\omega$. The tangent at $C$ intersects $P D$ at $Q$ and the line $A D$ at $R$. Let $E$ be the second point of intersection between $A Q$ and $\\omega$. Prove that $B, E, R$ are collinear.", "solution": "To show $B, E, R$ are collinear, it is equivalent to show the lines $A D, B E, C Q$ are concurrent. Let $C Q$ intersect $A D$ at $R$ and $B E$ intersect $A D$ at $R^{\\prime}$. We shall show $R D / R A=R^{\\prime} D / R^{\\prime} A$ so that $R=R^{\\prime}$.\n\nSince $\\triangle P A D$ is similar to $\\triangle P D C$ and $\\triangle P A B$ is similar to $\\triangle P B C$, we have $A D / D C=$ $P A / P D=P A / P B=A B / B C$. Hence, $A B \\cdot D C=B C \\cdot A D$. By Ptolemy's theorem, $A B \\cdot D C=B C \\cdot A D=\\frac{1}{2} C A \\cdot D B$. Similarly $C A \\cdot E D=C E \\cdot A D=\\frac{1}{2} A E \\cdot D C$.\n\nThus\n\n$$\n\\frac{D B}{A B}=\\frac{2 D C}{C A}\n$$\n\nand\n\n$$\n\\frac{D C}{C A}=\\frac{2 E D}{A E}\n$$\n\n\n\nSince the triangles $R D C$ and $R C A$ are similar, we have $\\frac{R D}{R C}=\\frac{D C}{C A}=\\frac{R C}{R A}$. Thus using (4)\n\n$$\n\\frac{R D}{R A}=\\frac{R D \\cdot R A}{R A^{2}}=\\left(\\frac{R C}{R A}\\right)^{2}=\\left(\\frac{D C}{C A}\\right)^{2}=\\left(\\frac{2 E D}{A E}\\right)^{2}\n$$\n\nUsing the similar triangles $A B R^{\\prime}$ and $E D R^{\\prime}$, we have $R^{\\prime} D / R^{\\prime} B=E D / A B$. Using the similar triangles $D B R^{\\prime}$ and $E A R^{\\prime}$ we have $R^{\\prime} A / R^{\\prime} B=E A / D B$. Thus using (3) and (4),\n\n$$\n\\frac{R^{\\prime} D}{R^{\\prime} A}=\\frac{E D \\cdot D B}{E A \\cdot A B}=\\left(\\frac{2 E D}{A E}\\right)^{2}\n$$\n\nIt follows from (5) and (6) that $R=R^{\\prime}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2013", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute triangle with altitudes $A D, B E$ and $C F$, and let $O$ be the center of its circumcircle. Show that the segments $O A, O F, O B, O D, O C, O E$ dissect the triangle $A B C$ into three pairs of triangles that have equal areas.", "solution": "Let $M$ and $N$ be midpoints of sides $B C$ and $A C$, respectively. Notice that $\\angle M O C=\\frac{1}{2} \\angle B O C=\\angle E A B, \\angle O M C=90^{\\circ}=\\angle A E B$, so triangles $O M C$ and $A E B$ are similar and we get $\\frac{O M}{A E}=\\frac{O C}{A B}$. For triangles $O N A$ and $B D A$ we also have $\\frac{O N}{B D}=\\frac{O A}{B A}$. Then $\\frac{O M}{A E}=\\frac{O N}{B D}$ or $B D \\cdot O M=A E \\cdot O N$.\n\nDenote by $S(\\Phi)$ the area of the figure $\\Phi$. So, we see that $S(O B D)=\\frac{1}{2} B D \\cdot O M=$ $\\frac{1}{2} A E \\cdot O N=S(O A E)$. Analogously, $S(O C D)=S(O A F)$ and $S(O C E)=S(O B F)$.\n\nAlternative solution. Let $R$ be the circumradius of triangle $A B C$, and as usual write $A, B, C$ for angles $\\angle C A B, \\angle A B C, \\angle B C A$ respectively, and $a, b, c$ for sides $B C, C A, A B$ respectively. Then the area of triangle $O C D$ is\n\n$$\nS(O C D)=\\frac{1}{2} \\cdot O C \\cdot C D \\cdot \\sin (\\angle O C D)=\\frac{1}{2} R \\cdot C D \\cdot \\sin (\\angle O C D)\n$$\n\nNow $C D=b \\cos C$, and\n\n$$\n\\angle O C D=\\frac{180^{\\circ}-2 A}{2}=90^{\\circ}-A\n$$\n\n(since triangle $O B C$ is isosceles, and $\\angle B O C=2 A$ ). So\n\n$$\nS(O C D)=\\frac{1}{2} R b \\cos C \\sin \\left(90^{\\circ}-A\\right)=\\frac{1}{2} R b \\cos C \\cos A\n$$\n\nA similar calculation gives\n\n$$\n\\begin{aligned}\nS(O A F) & =\\frac{1}{2} O A \\cdot A F \\cdot \\sin (\\angle O A F) \\\\\n& =\\frac{1}{2} R \\cdot(b \\cos A) \\sin \\left(90^{\\circ}-C\\right) \\\\\n& =\\frac{1}{2} R b \\cos A \\cos C\n\\end{aligned}\n$$\n\nso $O C D$ and $O A F$ have the same area. In the same way we find that $O B D$ and $O A E$ have the same area, as do $O C E$ and $O B F$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2013", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Determine all positive integers $n$ for which $\\frac{n^{2}+1}{[\\sqrt{n}]^{2}+2}$ is an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.", "solution": "We will show that there are no positive integers $n$ satisfying the condition of the problem.\n\nLet $m=[\\sqrt{n}]$ and $a=n-m^{2}$. We have $m \\geq 1$ since $n \\geq 1$. From $n^{2}+1=\\left(m^{2}+a\\right)^{2}+1 \\equiv$ $(a-2)^{2}+1\\left(\\bmod \\left(m^{2}+2\\right)\\right)$, it follows that the condition of the problem is equivalent to the fact that $(a-2)^{2}+1$ is divisible by $m^{2}+2$. Since we have\n\n$$\n0<(a-2)^{2}+1 \\leq \\max \\left\\{2^{2},(2 m-2)^{2}\\right\\}+1 \\leq 4 m^{2}+1<4\\left(m^{2}+2\\right)\n$$\n\nwe see that $(a-2)^{2}+1=k\\left(m^{2}+2\\right)$ must hold with $k=1,2$ or 3 . We will show that none of these can occur.\n\nCase 1. When $k=1$. We get $(a-2)^{2}-m^{2}=1$, and this implies that $a-2= \\pm 1, m=0$ must hold, but this contradicts with fact $m \\geq 1$.\n\nCase 2. When $k=2$. We have $(a-2)^{2}+1=2\\left(m^{2}+2\\right)$ in this case, but any perfect square is congruent to $0,1,4 \\bmod 8$, and therefore, we have $(a-2)^{2}+1 \\equiv 1,2,5(\\bmod 8)$, while $2\\left(m^{2}+2\\right) \\equiv 4,6(\\bmod 8)$. Thus, this case cannot occur either.\n\nCase 3. When $k=3$. We have $(a-2)^{2}+1=3\\left(m^{2}+2\\right)$ in this case. Since any perfect square is congruent to 0 or $1 \\bmod 3$, we have $(a-2)^{2}+1 \\equiv 1,2(\\bmod 3)$, while $3\\left(m^{2}+2\\right) \\equiv 0$ $(\\bmod 3)$, which shows that this case cannot occur either.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2013", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "For $2 k$ real numbers $a_{1}, a_{2}, \\ldots, a_{k}, b_{1}, b_{2}, \\ldots, b_{k}$ define the sequence of numbers $X_{n}$ by\n\n$$\nX_{n}=\\sum_{i=1}^{k}\\left[a_{i} n+b_{i}\\right] \\quad(n=1,2, \\ldots)\n$$\n\nIf the sequence $X_{n}$ forms an arithmetic progression, show that $\\sum_{i=1}^{k} a_{i}$ must be an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.", "solution": "Let us write $A=\\sum_{i=1}^{k} a_{i}$ and $B=\\sum_{i=1}^{k} b_{i}$. Summing the corresponding terms of the following inequalities over $i$,\n\n$$\na_{i} n+b_{i}-1<\\left[a_{i} n+b_{i}\\right] \\leq a_{i} n+b_{i}\n$$\n\nwe obtain $A n+B-k<X_{n}<A n+B$. Now suppose that $\\left\\{X_{n}\\right\\}$ is an arithmetic progression with the common difference $d$, then we have $n d=X_{n+1}-X_{1}$ and $A+B-k<X_{1} \\leq A+B$ Combining with the inequalities obtained above, we get\n\n$$\nA(n+1)+B-k<n d+X_{1}<A(n+1)+B,\n$$\n\nor\n\n$$\nA n-k \\leq A n+\\left(A+B-X_{1}\\right)-k<n d<A n+\\left(A+B-X_{1}\\right)<A n+k,\n$$\n\nfrom which we conclude that $|A-d|<\\frac{k}{n}$ must hold. Since this inequality holds for any positive integer $n$, we must have $A=d$. Since $\\left\\{X_{n}\\right\\}$ is a sequence of integers, $d$ must be an integer also, and thus we conclude that $A$ is also an integer.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2013", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $a$ and $b$ be positive integers, and let $A$ and $B$ be finite sets of integers satisfying:\n(i) $A$ and $B$ are disjoint;\n(ii) if an integer $i$ belongs either to $A$ or to $B$, then $i+a$ belongs to $A$ or $i-b$ belongs to $B$.\n\nProve that $a|A|=b|B|$. (Here $|X|$ denotes the number of elements in the set $X$.)", "solution": "Let $A^{*}=\\{n-a: n \\in A\\}$ and $B^{*}=\\{n+b: n \\in B\\}$. Then, by (ii), $A \\cup B \\subseteq A^{*} \\cup B^{*}$ and by (i),\n\n$$\n|A \\cup B| \\leq\\left|A^{*} \\cup B^{*}\\right| \\leq\\left|A^{*}\\right|+\\left|B^{*}\\right|=|A|+|B|=|A \\cup B|\n$$\n\nThus, $A \\cup B=A^{*} \\cup B^{*}$ and $A^{*}$ and $B^{*}$ have no element in common. For each finite set $X$ of integers, let $\\sum(X)=\\sum_{x \\in X} x$. Then\n\n$$\n\\begin{aligned}\n\\sum(A)+\\sum(B) & =\\sum(A \\cup B) \\\\\n& =\\sum\\left(A^{*} \\cup B^{*}\\right)=\\sum\\left(A^{*}\\right)+\\sum\\left(B^{*}\\right) \\\\\n& =\\sum(A)-a|A|+\\sum(B)+b|B|\n\\end{aligned}\n$$\n\nwhich implies $a|A|=b|B|$.\nAlternative solution. Let us construct a directed graph whose vertices are labelled by the members of $A \\cup B$ and such that there is an edge from $i$ to $j$ iff $j \\in A$ and $j=i+a$ or $j \\in B$ and $j=i-b$. From (ii), each vertex has out-degree $\\geq 1$ and, from (i), each vertex has in-degree $\\leq 1$. Since the sum of the out-degrees equals the sum of the in-degrees, each vertex has in-degree and out-degree equal to 1. This is only possible if the graph is the union of disjoint cycles, say $G_{1}, G_{2}, \\ldots, G_{n}$. Let $\\left|A_{k}\\right|$ be the number of elements of $A$ in $G_{k}$ and $\\left|B_{k}\\right|$ be the number of elements of $B$ in $G_{k}$. The cycle $G_{k}$ will involve increasing vertex labels by $a$ a total of $\\left|A_{k}\\right|$ times and decreasing them by $b$ a total of $\\left|B_{k}\\right|$ times. Since it is a cycle, we have $a\\left|A_{k}\\right|=b\\left|B_{k}\\right|$. Summing over all cycles gives the result.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 5 |
+
{"year": "2013", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $A B C D$ be a quadrilateral inscribed in a circle $\\omega$, and let $P$ be a point on the extension of $A C$ such that $P B$ and $P D$ are tangent to $\\omega$. The tangent at $C$ intersects $P D$ at $Q$ and the line $A D$ at $R$. Let $E$ be the second point of intersection between $A Q$ and $\\omega$. Prove that $B, E, R$ are collinear.", "solution": "To show $B, E, R$ are collinear, it is equivalent to show the lines $A D, B E, C Q$ are concurrent. Let $C Q$ intersect $A D$ at $R$ and $B E$ intersect $A D$ at $R^{\\prime}$. We shall show $R D / R A=R^{\\prime} D / R^{\\prime} A$ so that $R=R^{\\prime}$.\n\nSince $\\triangle P A D$ is similar to $\\triangle P D C$ and $\\triangle P A B$ is similar to $\\triangle P B C$, we have $A D / D C=$ $P A / P D=P A / P B=A B / B C$. Hence, $A B \\cdot D C=B C \\cdot A D$. By Ptolemy's theorem, $A B \\cdot D C=B C \\cdot A D=\\frac{1}{2} C A \\cdot D B$. Similarly $C A \\cdot E D=C E \\cdot A D=\\frac{1}{2} A E \\cdot D C$.\n\nThus\n\n$$\n\\frac{D B}{A B}=\\frac{2 D C}{C A}\n$$\n\nand\n\n$$\n\\frac{D C}{C A}=\\frac{2 E D}{A E}\n$$\n\n\n\nSince the triangles $R D C$ and $R C A$ are similar, we have $\\frac{R D}{R C}=\\frac{D C}{C A}=\\frac{R C}{R A}$. Thus using (4)\n\n$$\n\\frac{R D}{R A}=\\frac{R D \\cdot R A}{R A^{2}}=\\left(\\frac{R C}{R A}\\right)^{2}=\\left(\\frac{D C}{C A}\\right)^{2}=\\left(\\frac{2 E D}{A E}\\right)^{2}\n$$\n\nUsing the similar triangles $A B R^{\\prime}$ and $E D R^{\\prime}$, we have $R^{\\prime} D / R^{\\prime} B=E D / A B$. Using the similar triangles $D B R^{\\prime}$ and $E A R^{\\prime}$ we have $R^{\\prime} A / R^{\\prime} B=E A / D B$. Thus using (3) and (4),\n\n$$\n\\frac{R^{\\prime} D}{R^{\\prime} A}=\\frac{E D \\cdot D B}{E A \\cdot A B}=\\left(\\frac{2 E D}{A E}\\right)^{2}\n$$\n\nIt follows from (5) and (6) that $R=R^{\\prime}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2014_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2014", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "For a positive integer $m$ denote by $S(m)$ and $P(m)$ the sum and product, respectively, of the digits of $m$. Show that for each positive integer $n$, there exist positive integers $a_{1}, a_{2}, \\ldots, a_{n}$ satisfying the following conditions:\n\n$$\nS\\left(a_{1}\\right)<S\\left(a_{2}\\right)<\\cdots<S\\left(a_{n}\\right) \\text { and } S\\left(a_{i}\\right)=P\\left(a_{i+1}\\right) \\quad(i=1,2, \\ldots, n)\n$$\n\n(We let $\\left.a_{n+1}=a_{1}.\\right)$ (Problem Committee of the Japan Mathematical Olympiad Foundation)", "solution": "Let $k$ be a sufficiently large positive integer. Choose for each $i=2,3, \\ldots, n$, $a_{i}$ to be a positive integer among whose digits the number 2 appears exactly $k+i-2$ times and the number 1 appears exactly $2^{k+i-1}-2(k+i-2)$ times, and nothing else. Then, we have $S\\left(a_{i}\\right)=2^{k+i-1}$ and $P\\left(a_{i}\\right)=2^{k+i-2}$ for each $i, 2 \\leq i \\leq n$. Then, we let $a_{1}$ be a positive integer among whose digits the number 2 appears exactly $k+n-1$ times and the number 1 appears exactly $2^{k}-2(k+n-1)$ times, and nothing else. Then, we see that $a_{1}$ satisfies $S\\left(a_{1}\\right)=2^{k}$ and $P\\left(a_{1}\\right)=2^{k+n-1}$. Such a choice of $a_{1}$ is possible if we take $k$ to be large enough to satisfy $2^{k}>2(k+n-1)$ and we see that the numbers $a_{1}, \\ldots, a_{n}$ chosen this way satisfy the given requirements.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2014", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $S=\\{1,2, \\ldots, 2014\\}$. For each non-empty subset $T \\subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \\subseteq S$ is a disjoint union of non-empty subsets $A, B, C \\subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)", "solution": "Answer: 108 - 2014!.\nFor any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:\n\n$$\n\\text { If } x_{1} \\in X \\text { and } X \\subseteq S \\text {, then } x_{1}=r(X) \\text {. }\n$$\n\nIf $|X| \\leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \\in X$ and $y \\neq x_{1}$. We can write $X$ as a disjoint union of $\\left\\{x_{1}, y\\right\\}$ and two other subsets. We already proved that $r\\left(\\left\\{x_{1}, y\\right\\}\\right)=x_{1}$ (since $\\left|\\left\\{x_{1}, y\\right\\}\\right|=2<2012$ ) and it follows that $y \\neq r(X)$ for every $y \\in X$ except $x_{1}$. We have proved the fact.\n\nNote that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.\n\nThere are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \\in X \\subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \\backslash\\left\\{x_{1}\\right\\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\\left(S_{1}\\right)$ and for $x_{2} \\in X \\subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \\cdot 2013 \\cdots 5$ ways to choose $x_{1}, x_{2}, \\ldots, x_{2010} \\in S$ so that for all $i=1,2 \\ldots, 2010$, $x_{i}=r(X)$ for each $X \\subseteq S \\backslash\\left\\{x_{1}, \\ldots, x_{i-1}\\right\\}$ and $x_{i} \\in X$.\n\nWe are now left with four elements $Y=\\left\\{y_{1}, y_{2}, y_{3}, y_{4}\\right\\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\\left(\\left\\{y_{1}, y_{2}\\right\\}\\right)=r\\left(\\left\\{y_{1}, y_{3}\\right\\}\\right)=r\\left(\\left\\{y_{1}, y_{4}\\right\\}\\right)$. The only subsets whose representative has not been assigned yet are $\\left\\{y_{1}, y_{2}, y_{3}\\right\\},\\left\\{y_{1}, y_{2}, y_{4}\\right\\}$, $\\left\\{y_{1}, y_{3}, y_{4}\\right\\},\\left\\{y_{2}, y_{3}, y_{4}\\right\\},\\left\\{y_{2}, y_{3}\\right\\},\\left\\{y_{2}, y_{4}\\right\\},\\left\\{y_{3}, y_{4}\\right\\}$. These subsets can be assigned in any way, hence giving $3^{4} \\cdot 2^{3}$ more choices.\n\nIn conclusion, the total number of assignments is $2014 \\cdot 2013 \\cdots 4 \\cdot 3^{4} \\cdot 2^{3}=108 \\cdot 2014$ !.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2014", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Find all positive integers $n$ such that for any integer $k$ there exists an integer $a$ for which $a^{3}+a-k$ is divisible by $n$. (Warut Suksompong, Thailand)", "solution": "Answer: All integers $n=3^{b}$, where $b$ is a nonnegative integer.\nWe are looking for integers $n$ such that the set $A=\\left\\{a^{3}+a \\mid a \\in \\mathbf{Z}\\right\\}$ is a complete residue system by modulo $n$. Let us call this property by $\\left(^{*}\\right)$. It is not hard to see that $n=1$ satisfies $\\left({ }^{*}\\right)$ and $n=2$ does not.\n\nIf $a \\equiv b(\\bmod n)$, then $a^{3}+a \\equiv b^{3}+b(\\bmod n)$. So $n$ satisfies $\\left(^{*}\\right)$ iff there are no $a, b \\in\\{0, \\ldots, n-1\\}$ with $a \\neq b$ and $a^{3}+a \\equiv b^{3}+b(\\bmod n)$.\n\nFirst, let us prove that $3^{j}$ satisfies $\\left(^{*}\\right)$ for all $j \\geq 1$. Suppose that $a^{3}+a \\equiv b^{3}+b\\left(\\bmod 3^{j}\\right)$ for $a \\neq b$. Then $(a-b)\\left(a^{2}+a b+b^{2}+1\\right) \\equiv 0\\left(\\bmod 3^{j}\\right)$. We can easily check mod 3 that $a^{2}+a b+b^{2}+1$ is not divisible by 3 .\n\nNext note that if $A$ is not a complete residue system modulo integer $r$, then it is also not a complete residue system modulo any multiple of $r$. Hence it remains to prove that any prime $p>3$ does not satisfy (*).\n\nIf $p \\equiv 1(\\bmod 4)$, there exists $b$ such that $b^{2} \\equiv-1(\\bmod p)$. We then take $a=0$ to obtain the congruence $a^{3}+a \\equiv b^{3}+b(\\bmod p)$.\n\nSuppose now that $p \\equiv 3(\\bmod 4)$. We will prove that there are integers $a, b \\not \\equiv 0(\\bmod p)$ such that $a^{2}+a b+b^{2} \\equiv-1(\\bmod p)$. Note that we may suppose that $a \\not \\equiv b(\\bmod p)$, since otherwise if $a \\equiv b(\\bmod p)$ satisfies $a^{2}+a b+b^{2}+1 \\equiv 0(\\bmod p)$, then $(2 a)^{2}+(2 a)(-a)+$ $a^{2}+1 \\equiv 0(\\bmod p)$ and $2 a \\not \\equiv-a(\\bmod p)$. Letting $c$ be the inverse of $b$ modulo $p$ (i.e. $b c \\equiv 1(\\bmod p)$ ), the relation is equivalent to $(a c)^{2}+a c+1 \\equiv-c^{2}(\\bmod p)$. Note that $-c^{2}$ can take on the values of all non-quadratic residues modulo $p$. If we can find an integer $x$ such that $x^{2}+x+1$ is a non-quadratic residue modulo $p$, the values of $a$ and $c$ will follow immediately. Hence we focus on this latter task.\n\nNote that if $x, y \\in\\{0, \\ldots, p-1\\}=B$, then $x^{2}+x+1 \\equiv y^{2}+y+1(\\bmod p)$ iff $p$ divides $x+y+1$. We can deduce that $x^{2}+x+1$ takes on $(p+1) / 2$ values as $x$ varies in $B$. Since there are $(p-1) / 2$ non-quadratic residues modulo $p$, the $(p+1) / 2$ values that $x^{2}+x+1$ take on must be 0 and all the quadratic residues.\n\nLet $C$ be the set of quadratic residues modulo $p$ and 0 , and let $y \\in C$. Suppose that $y \\equiv z^{2}(\\bmod p)$ and let $z \\equiv 2 w+1(\\bmod p)$ (we can always choose such $\\left.w\\right)$. Then $y+3 \\equiv$ $4\\left(w^{2}+w+1\\right)(\\bmod p)$. From the previous paragraph, we know that $4\\left(w^{2}+w+1\\right) \\in C$. This means that $y \\in C \\Longrightarrow y+3 \\in C$. Unless $p=3$, the relation implies that all elements of $B$ are in $C$, a contradiction. This concludes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2014", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $n$ and $b$ be positive integers. We say $n$ is $b$-discerning if there exists a set consisting of $n$ different positive integers less than $b$ that has no two different subsets $U$ and $V$ such that the sum of all elements in $U$ equals the sum of all elements in $V$.\n(a) Prove that 8 is a 100 -discerning.\n(b) Prove that 9 is not 100-discerning.\n(Senior Problems Committee of the Australian Mathematical Olympiad Committee)", "solution": "(a) Take $S=\\{3,6,12,24,48,95,96,97\\}$, i.e.\n\n$$\nS=\\left\\{3 \\cdot 2^{k}: 0 \\leq k \\leq 5\\right\\} \\cup\\left\\{3 \\cdot 2^{5}-1,3 \\cdot 2^{5}+1\\right\\}\n$$\n\nAs $k$ ranges between 0 to 5 , the sums obtained from the numbers $3 \\cdot 2^{k}$ are $3 t$, where $1 \\leq t \\leq 63$. These are 63 numbers that are divisible by 3 and are at most $3 \\cdot 63=189$.\n\nSums of elements of $S$ are also the numbers $95+97=192$ and all the numbers that are sums of 192 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all divisible by 3 and at least equal to 192. In addition, sums of elements of $S$ are the numbers 95 and all the numbers that are sums of 95 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all congruent to $-1 \\bmod$ 3.\n\nFinally, sums of elements of $S$ are the numbers 97 and all the numbers that are sums of 97 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all congruent to $1 \\bmod 3$.\n\nHence there are at least $63+64+64+64=255$ different sums from elements of $S$. On the other hand, $S$ has $2^{8}-1=255$ non-empty subsets. Therefore $S$ has no two different subsets with equal sums of elements. Therefore, 8 is 100 -discerning.\n(b) Suppose that 9 is 100 -discerning. Then there is a set $S=\\left\\{s_{1}, \\ldots, s_{9}\\right\\}, s_{i}<100$ that has no two different subsets with equal sums of elements. Assume that $0<s_{1}<\\cdots<s_{9}<$ 100.\n\nLet $X$ be the set of all subsets of $S$ having at least 3 and at most 6 elements and let $Y$ be the set of all subsets of $S$ having exactly 2 or 3 or 4 elements greater than $s_{3}$.\n\nThe set $X$ consists of\n\n$$\n\\binom{9}{3}+\\binom{9}{4}+\\binom{9}{5}+\\binom{9}{6}=84+126+126+84=420\n$$\n\nsubsets of $S$. The set in $X$ with the largest sums of elements is $\\left\\{s_{4}, \\ldots, s_{9}\\right\\}$ and the smallest sums is in $\\left\\{s_{1}, s_{2}, s_{3}\\right\\}$. Thus the sum of the elements of each of the 420 sets in $X$ is at least $s_{1}+s_{2}+s_{3}$ and at most $s_{4}+\\cdots+s_{9}$, which is one of $\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right)+1$ integers. From the pigeonhole principle it follows that $\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right)+1 \\geq 420$, i.e.,\n\n$$\n\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right) \\geq 419\n$$\n\nNow let us calculate the number of subsets in $Y$. Observe that $\\left\\{s_{4}, \\ldots, s_{9}\\right\\}$ has $\\binom{6}{2}$ 2-element subsets, $\\binom{6}{3}$ 3-element subsets and $\\binom{6}{4}$ 4-element subsets, while $\\left\\{s_{1}, s_{2}, s_{3}\\right\\}$ has exactly 8 subsets. Hence the number of subsets of $S$ in $Y$ equals\n\n$$\n8\\left(\\binom{6}{2}+\\binom{6}{3}+\\binom{6}{4}\\right)=8(15+20+15)=400\n$$\n\nThe set in $Y$ with the largest sum of elements is $\\left\\{s_{1}, s_{2}, s_{3}, s_{6}, s_{7}, s_{8}, s_{9}\\right\\}$ and the smallest sum is in $\\left\\{s_{4}, s_{5}\\right\\}$. Again, by the pigeonhole principle it follows that $\\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+\\right.$ $\\left.s_{8}+s_{9}\\right)-\\left(s_{4}+s_{5}\\right)+1 \\geq 400$, i.e.,\n\n$$\n\\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+s_{8}+s_{9}\\right)-\\left(s_{4}+s_{5}\\right) \\geq 399\n$$\n\nAdding (1) and (2) yields $2\\left(s_{6}+s_{7}+s_{8}+s_{9}\\right) \\geq 818$, so that $s_{9}+98+97+96 \\geq$ $s_{9}+s_{8}+s_{7}+s_{6} \\geq 409$, i.e. $s_{9} \\geq 118$, a contradiction with $s_{9}<100$. Therefore, 9 is not 100-discerning.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution."}}
|
| 5 |
-
{"year": "2014", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Circles $\\omega$ and $\\Omega$ meet at points $A$ and $B$. Let $M$ be the midpoint of the $\\operatorname{arc} A B$ of circle $\\omega$ ( $M$ lies inside $\\Omega$ ). A chord $M P$ of circle $\\omega$ intersects $\\Omega$ at $Q(Q$ lies inside $\\omega)$. Let $\\ell_{P}$ be the tangent line to $\\omega$ at $P$, and let $\\ell_{Q}$ be the tangent line to $\\Omega$ at $Q$. Prove that the circumcircle of the triangle formed by the lines $\\ell_{P}, \\ell_{Q}$, and $A B$ is tangent to $\\Omega$. (Ilya Bogdanov, Russia and Medeubek Kungozhin, Kazakhstan)", "solution": "Denote $X=A B \\cap \\ell_{P}, Y=A B \\cap \\ell_{Q}$, and $Z=\\ell_{P} \\cap \\ell_{Q}$. Without loss of generality we have $A X<B X$. Let $F=M P \\cap A B$.\n\n\nDenote by $R$ the second point of intersection of $P Q$ and $\\Omega$; by $S$ the point of $\\Omega$ such that $S R \\| A B$; and by $T$ the point of $\\Omega$ such that $R T \\| \\ell_{P}$. Since $M$ is the midpoint of arc $A B$, the tangent $\\ell_{M}$ at $M$ to $\\omega$ is parallel to $A B$, so $\\angle(A B, P M)=\\angle\\left(P M, \\ell_{P}\\right)$. Therefore we have $\\angle P R T=\\angle M P X=\\angle P F X=\\angle P R S$. Thus the point $Q$ is the midpoint of the $\\operatorname{arc} T Q S$ of $\\Omega$, hence $S T \\| \\ell_{Q}$. So the corresponding sides of the triangles $R S T$ and $X Y Z$ are parallel, and there exist a homothety $h$ mapping $R S T$ to $X Y Z$.\n\nLet $D$ be the second point of intersection of $X R$ and $\\Omega$. We claim that $D$ is the center of the homothety $h$; since $D \\in \\Omega$, this implies that the circumcircles of triangles $R S T$ and $X Y Z$ are tangent, as required. So, it remains to prove this claim. In order to do this, it suffices to show that $D \\in S Y$.\n\nBy $\\angle P F X=\\angle X P F$ we have $X F^{2}=X P^{2}=X A \\cdot X B=X D \\cdot X R$. Therefore, $\\frac{X F}{X D}=\\frac{X R}{X F}$, so the triangles $X D F$ and $X F R$ are similar, hence $\\angle D F X=\\angle X R F=\\angle D R Q=$ $\\angle D Q Y$; thus the points $D, Y, Q$, and $F$ are concyclic. It follows that $\\angle Y D Q=\\angle Y F Q=$ $\\angle S R Q=180^{\\circ}-\\angle S D Q$ which means exactly that the points $Y, D$, and $S$ are collinear, with $D$ between $S$ and $Y$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2014", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "For a positive integer $m$ denote by $S(m)$ and $P(m)$ the sum and product, respectively, of the digits of $m$. Show that for each positive integer $n$, there exist positive integers $a_{1}, a_{2}, \\ldots, a_{n}$ satisfying the following conditions:\n\n$$\nS\\left(a_{1}\\right)<S\\left(a_{2}\\right)<\\cdots<S\\left(a_{n}\\right) \\text { and } S\\left(a_{i}\\right)=P\\left(a_{i+1}\\right) \\quad(i=1,2, \\ldots, n)\n$$\n\n(We let $\\left.a_{n+1}=a_{1}.\\right)$ (Problem Committee of the Japan Mathematical Olympiad Foundation)", "solution": "Let $k$ be a sufficiently large positive integer. Choose for each $i=2,3, \\ldots, n$, $a_{i}$ to be a positive integer among whose digits the number 2 appears exactly $k+i-2$ times and the number 1 appears exactly $2^{k+i-1}-2(k+i-2)$ times, and nothing else. Then, we have $S\\left(a_{i}\\right)=2^{k+i-1}$ and $P\\left(a_{i}\\right)=2^{k+i-2}$ for each $i, 2 \\leq i \\leq n$. Then, we let $a_{1}$ be a positive integer among whose digits the number 2 appears exactly $k+n-1$ times and the number 1 appears exactly $2^{k}-2(k+n-1)$ times, and nothing else. Then, we see that $a_{1}$ satisfies $S\\left(a_{1}\\right)=2^{k}$ and $P\\left(a_{1}\\right)=2^{k+n-1}$. Such a choice of $a_{1}$ is possible if we take $k$ to be large enough to satisfy $2^{k}>2(k+n-1)$ and we see that the numbers $a_{1}, \\ldots, a_{n}$ chosen this way satisfy the given requirements.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2014", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $S=\\{1,2, \\ldots, 2014\\}$. For each non-empty subset $T \\subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \\subseteq S$ is a disjoint union of non-empty subsets $A, B, C \\subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)", "solution": "Answer: 108 - 2014!.\nFor any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:\n\n$$\n\\text { If } x_{1} \\in X \\text { and } X \\subseteq S \\text {, then } x_{1}=r(X) \\text {. }\n$$\n\nIf $|X| \\leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \\in X$ and $y \\neq x_{1}$. We can write $X$ as a disjoint union of $\\left\\{x_{1}, y\\right\\}$ and two other subsets. We already proved that $r\\left(\\left\\{x_{1}, y\\right\\}\\right)=x_{1}$ (since $\\left|\\left\\{x_{1}, y\\right\\}\\right|=2<2012$ ) and it follows that $y \\neq r(X)$ for every $y \\in X$ except $x_{1}$. We have proved the fact.\n\nNote that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.\n\nThere are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \\in X \\subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \\backslash\\left\\{x_{1}\\right\\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\\left(S_{1}\\right)$ and for $x_{2} \\in X \\subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \\cdot 2013 \\cdots 5$ ways to choose $x_{1}, x_{2}, \\ldots, x_{2010} \\in S$ so that for all $i=1,2 \\ldots, 2010$, $x_{i}=r(X)$ for each $X \\subseteq S \\backslash\\left\\{x_{1}, \\ldots, x_{i-1}\\right\\}$ and $x_{i} \\in X$.\n\nWe are now left with four elements $Y=\\left\\{y_{1}, y_{2}, y_{3}, y_{4}\\right\\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\\left(\\left\\{y_{1}, y_{2}\\right\\}\\right)=r\\left(\\left\\{y_{1}, y_{3}\\right\\}\\right)=r\\left(\\left\\{y_{1}, y_{4}\\right\\}\\right)$. The only subsets whose representative has not been assigned yet are $\\left\\{y_{1}, y_{2}, y_{3}\\right\\},\\left\\{y_{1}, y_{2}, y_{4}\\right\\}$, $\\left\\{y_{1}, y_{3}, y_{4}\\right\\},\\left\\{y_{2}, y_{3}, y_{4}\\right\\},\\left\\{y_{2}, y_{3}\\right\\},\\left\\{y_{2}, y_{4}\\right\\},\\left\\{y_{3}, y_{4}\\right\\}$. These subsets can be assigned in any way, hence giving $3^{4} \\cdot 2^{3}$ more choices.\n\nIn conclusion, the total number of assignments is $2014 \\cdot 2013 \\cdots 4 \\cdot 3^{4} \\cdot 2^{3}=108 \\cdot 2014$ !.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2014", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Find all positive integers $n$ such that for any integer $k$ there exists an integer $a$ for which $a^{3}+a-k$ is divisible by $n$. (Warut Suksompong, Thailand)", "solution": "Answer: All integers $n=3^{b}$, where $b$ is a nonnegative integer.\nWe are looking for integers $n$ such that the set $A=\\left\\{a^{3}+a \\mid a \\in \\mathbf{Z}\\right\\}$ is a complete residue system by modulo $n$. Let us call this property by $\\left(^{*}\\right)$. It is not hard to see that $n=1$ satisfies $\\left({ }^{*}\\right)$ and $n=2$ does not.\n\nIf $a \\equiv b(\\bmod n)$, then $a^{3}+a \\equiv b^{3}+b(\\bmod n)$. So $n$ satisfies $\\left(^{*}\\right)$ iff there are no $a, b \\in\\{0, \\ldots, n-1\\}$ with $a \\neq b$ and $a^{3}+a \\equiv b^{3}+b(\\bmod n)$.\n\nFirst, let us prove that $3^{j}$ satisfies $\\left(^{*}\\right)$ for all $j \\geq 1$. Suppose that $a^{3}+a \\equiv b^{3}+b\\left(\\bmod 3^{j}\\right)$ for $a \\neq b$. Then $(a-b)\\left(a^{2}+a b+b^{2}+1\\right) \\equiv 0\\left(\\bmod 3^{j}\\right)$. We can easily check mod 3 that $a^{2}+a b+b^{2}+1$ is not divisible by 3 .\n\nNext note that if $A$ is not a complete residue system modulo integer $r$, then it is also not a complete residue system modulo any multiple of $r$. Hence it remains to prove that any prime $p>3$ does not satisfy (*).\n\nIf $p \\equiv 1(\\bmod 4)$, there exists $b$ such that $b^{2} \\equiv-1(\\bmod p)$. We then take $a=0$ to obtain the congruence $a^{3}+a \\equiv b^{3}+b(\\bmod p)$.\n\nSuppose now that $p \\equiv 3(\\bmod 4)$. We will prove that there are integers $a, b \\not \\equiv 0(\\bmod p)$ such that $a^{2}+a b+b^{2} \\equiv-1(\\bmod p)$. Note that we may suppose that $a \\not \\equiv b(\\bmod p)$, since otherwise if $a \\equiv b(\\bmod p)$ satisfies $a^{2}+a b+b^{2}+1 \\equiv 0(\\bmod p)$, then $(2 a)^{2}+(2 a)(-a)+$ $a^{2}+1 \\equiv 0(\\bmod p)$ and $2 a \\not \\equiv-a(\\bmod p)$. Letting $c$ be the inverse of $b$ modulo $p$ (i.e. $b c \\equiv 1(\\bmod p)$ ), the relation is equivalent to $(a c)^{2}+a c+1 \\equiv-c^{2}(\\bmod p)$. Note that $-c^{2}$ can take on the values of all non-quadratic residues modulo $p$. If we can find an integer $x$ such that $x^{2}+x+1$ is a non-quadratic residue modulo $p$, the values of $a$ and $c$ will follow immediately. Hence we focus on this latter task.\n\nNote that if $x, y \\in\\{0, \\ldots, p-1\\}=B$, then $x^{2}+x+1 \\equiv y^{2}+y+1(\\bmod p)$ iff $p$ divides $x+y+1$. We can deduce that $x^{2}+x+1$ takes on $(p+1) / 2$ values as $x$ varies in $B$. Since there are $(p-1) / 2$ non-quadratic residues modulo $p$, the $(p+1) / 2$ values that $x^{2}+x+1$ take on must be 0 and all the quadratic residues.\n\nLet $C$ be the set of quadratic residues modulo $p$ and 0 , and let $y \\in C$. Suppose that $y \\equiv z^{2}(\\bmod p)$ and let $z \\equiv 2 w+1(\\bmod p)$ (we can always choose such $\\left.w\\right)$. Then $y+3 \\equiv$ $4\\left(w^{2}+w+1\\right)(\\bmod p)$. From the previous paragraph, we know that $4\\left(w^{2}+w+1\\right) \\in C$. This means that $y \\in C \\Longrightarrow y+3 \\in C$. Unless $p=3$, the relation implies that all elements of $B$ are in $C$, a contradiction. This concludes the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2014", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $n$ and $b$ be positive integers. We say $n$ is $b$-discerning if there exists a set consisting of $n$ different positive integers less than $b$ that has no two different subsets $U$ and $V$ such that the sum of all elements in $U$ equals the sum of all elements in $V$.\n(a) Prove that 8 is a 100 -discerning.\n(b) Prove that 9 is not 100-discerning.\n(Senior Problems Committee of the Australian Mathematical Olympiad Committee)", "solution": "(a) Take $S=\\{3,6,12,24,48,95,96,97\\}$, i.e.\n\n$$\nS=\\left\\{3 \\cdot 2^{k}: 0 \\leq k \\leq 5\\right\\} \\cup\\left\\{3 \\cdot 2^{5}-1,3 \\cdot 2^{5}+1\\right\\}\n$$\n\nAs $k$ ranges between 0 to 5 , the sums obtained from the numbers $3 \\cdot 2^{k}$ are $3 t$, where $1 \\leq t \\leq 63$. These are 63 numbers that are divisible by 3 and are at most $3 \\cdot 63=189$.\n\nSums of elements of $S$ are also the numbers $95+97=192$ and all the numbers that are sums of 192 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all divisible by 3 and at least equal to 192. In addition, sums of elements of $S$ are the numbers 95 and all the numbers that are sums of 95 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all congruent to $-1 \\bmod$ 3.\n\nFinally, sums of elements of $S$ are the numbers 97 and all the numbers that are sums of 97 and sums obtained from the numbers $3 \\cdot 2^{k}$ with $0 \\leq k \\leq 5$. These are 64 numbers that are all congruent to $1 \\bmod 3$.\n\nHence there are at least $63+64+64+64=255$ different sums from elements of $S$. On the other hand, $S$ has $2^{8}-1=255$ non-empty subsets. Therefore $S$ has no two different subsets with equal sums of elements. Therefore, 8 is 100 -discerning.\n(b) Suppose that 9 is 100 -discerning. Then there is a set $S=\\left\\{s_{1}, \\ldots, s_{9}\\right\\}, s_{i}<100$ that has no two different subsets with equal sums of elements. Assume that $0<s_{1}<\\cdots<s_{9}<$ 100.\n\nLet $X$ be the set of all subsets of $S$ having at least 3 and at most 6 elements and let $Y$ be the set of all subsets of $S$ having exactly 2 or 3 or 4 elements greater than $s_{3}$.\n\nThe set $X$ consists of\n\n$$\n\\binom{9}{3}+\\binom{9}{4}+\\binom{9}{5}+\\binom{9}{6}=84+126+126+84=420\n$$\n\nsubsets of $S$. The set in $X$ with the largest sums of elements is $\\left\\{s_{4}, \\ldots, s_{9}\\right\\}$ and the smallest sums is in $\\left\\{s_{1}, s_{2}, s_{3}\\right\\}$. Thus the sum of the elements of each of the 420 sets in $X$ is at least $s_{1}+s_{2}+s_{3}$ and at most $s_{4}+\\cdots+s_{9}$, which is one of $\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right)+1$ integers. From the pigeonhole principle it follows that $\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right)+1 \\geq 420$, i.e.,\n\n$$\n\\left(s_{4}+\\cdots+s_{9}\\right)-\\left(s_{1}+s_{2}+s_{3}\\right) \\geq 419\n$$\n\nNow let us calculate the number of subsets in $Y$. Observe that $\\left\\{s_{4}, \\ldots, s_{9}\\right\\}$ has $\\binom{6}{2}$ 2-element subsets, $\\binom{6}{3}$ 3-element subsets and $\\binom{6}{4}$ 4-element subsets, while $\\left\\{s_{1}, s_{2}, s_{3}\\right\\}$ has exactly 8 subsets. Hence the number of subsets of $S$ in $Y$ equals\n\n$$\n8\\left(\\binom{6}{2}+\\binom{6}{3}+\\binom{6}{4}\\right)=8(15+20+15)=400\n$$\n\nThe set in $Y$ with the largest sum of elements is $\\left\\{s_{1}, s_{2}, s_{3}, s_{6}, s_{7}, s_{8}, s_{9}\\right\\}$ and the smallest sum is in $\\left\\{s_{4}, s_{5}\\right\\}$. Again, by the pigeonhole principle it follows that $\\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+\\right.$ $\\left.s_{8}+s_{9}\\right)-\\left(s_{4}+s_{5}\\right)+1 \\geq 400$, i.e.,\n\n$$\n\\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+s_{8}+s_{9}\\right)-\\left(s_{4}+s_{5}\\right) \\geq 399\n$$\n\nAdding (1) and (2) yields $2\\left(s_{6}+s_{7}+s_{8}+s_{9}\\right) \\geq 818$, so that $s_{9}+98+97+96 \\geq$ $s_{9}+s_{8}+s_{7}+s_{6} \\geq 409$, i.e. $s_{9} \\geq 118$, a contradiction with $s_{9}<100$. Therefore, 9 is not 100-discerning.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution."}}
|
| 5 |
+
{"year": "2014", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Circles $\\omega$ and $\\Omega$ meet at points $A$ and $B$. Let $M$ be the midpoint of the $\\operatorname{arc} A B$ of circle $\\omega$ ( $M$ lies inside $\\Omega$ ). A chord $M P$ of circle $\\omega$ intersects $\\Omega$ at $Q(Q$ lies inside $\\omega)$. Let $\\ell_{P}$ be the tangent line to $\\omega$ at $P$, and let $\\ell_{Q}$ be the tangent line to $\\Omega$ at $Q$. Prove that the circumcircle of the triangle formed by the lines $\\ell_{P}, \\ell_{Q}$, and $A B$ is tangent to $\\Omega$. (Ilya Bogdanov, Russia and Medeubek Kungozhin, Kazakhstan)", "solution": "Denote $X=A B \\cap \\ell_{P}, Y=A B \\cap \\ell_{Q}$, and $Z=\\ell_{P} \\cap \\ell_{Q}$. Without loss of generality we have $A X<B X$. Let $F=M P \\cap A B$.\n\n\nDenote by $R$ the second point of intersection of $P Q$ and $\\Omega$; by $S$ the point of $\\Omega$ such that $S R \\| A B$; and by $T$ the point of $\\Omega$ such that $R T \\| \\ell_{P}$. Since $M$ is the midpoint of arc $A B$, the tangent $\\ell_{M}$ at $M$ to $\\omega$ is parallel to $A B$, so $\\angle(A B, P M)=\\angle\\left(P M, \\ell_{P}\\right)$. Therefore we have $\\angle P R T=\\angle M P X=\\angle P F X=\\angle P R S$. Thus the point $Q$ is the midpoint of the $\\operatorname{arc} T Q S$ of $\\Omega$, hence $S T \\| \\ell_{Q}$. So the corresponding sides of the triangles $R S T$ and $X Y Z$ are parallel, and there exist a homothety $h$ mapping $R S T$ to $X Y Z$.\n\nLet $D$ be the second point of intersection of $X R$ and $\\Omega$. We claim that $D$ is the center of the homothety $h$; since $D \\in \\Omega$, this implies that the circumcircles of triangles $R S T$ and $X Y Z$ are tangent, as required. So, it remains to prove this claim. In order to do this, it suffices to show that $D \\in S Y$.\n\nBy $\\angle P F X=\\angle X P F$ we have $X F^{2}=X P^{2}=X A \\cdot X B=X D \\cdot X R$. Therefore, $\\frac{X F}{X D}=\\frac{X R}{X F}$, so the triangles $X D F$ and $X F R$ are similar, hence $\\angle D F X=\\angle X R F=\\angle D R Q=$ $\\angle D Q Y$; thus the points $D, Y, Q$, and $F$ are concyclic. It follows that $\\angle Y D Q=\\angle Y F Q=$ $\\angle S R Q=180^{\\circ}-\\angle S D Q$ which means exactly that the points $Y, D$, and $S$ are collinear, with $D$ between $S$ and $Y$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2015_sol.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2015", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle, and let $D$ be a point on side $B C$. A line through $D$ intersects side $A B$ at $X$ and ray $A C$ at $Y$. The circumcircle of triangle $B X D$ intersects the circumcircle $\\omega$ of triangle $A B C$ again at point $Z \\neq B$. The lines $Z D$ and $Z Y$ intersect $\\omega$ again at $V$ and $W$, respectively. Prove that $A B=V W$.", "solution": "Suppose $X Y$ intersects $\\omega$ at points $P$ and $Q$, where $Q$ lies between $X$ and $Y$. We will show that $V$ and $W$ are the reflections of $A$ and $B$ with respect to the perpendicular bisector of $P Q$. From this, it follows that $A V W B$ is an isosceles trapezoid and hence $A B=V W$.\n\nFirst, note that\n\n$$\n\\angle B Z D=\\angle A X Y=\\angle A P Q+\\angle B A P=\\angle A P Q+\\angle B Z P,\n$$\n\nso $\\angle A P Q=\\angle P Z V=\\angle P Q V$, and hence $V$ is the reflection of $A$ with respect to the perpendicular bisector of $P Q$.\n\nNow, suppose $W^{\\prime}$ is the reflection of $B$ with respect to the perpendicular bisector of $P Q$, and let $Z^{\\prime}$ be the intersection of $Y W^{\\prime}$ and $\\omega$. It suffices to show that $B, X, D, Z^{\\prime}$ are concyclic. Note that\n\n$$\n\\angle Y D C=\\angle P D B=\\angle P C B+\\angle Q P C=\\angle W^{\\prime} P Q+\\angle Q P C=\\angle W^{\\prime} P C=\\angle Y Z^{\\prime} C .\n$$\n\nSo $D, C, Y, Z^{\\prime}$ are concyclic. Next, $\\angle B Z^{\\prime} D=\\angle C Z^{\\prime} B-\\angle C Z^{\\prime} D=180^{\\circ}-\\angle B X D$ and due to the previous concyclicity we are done.\n\nAlternative solution 1. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle Z D Y=\\angle Z B A=\\angle Z C Y$. So $Z D C Y$ is cyclic.\n\nUsing cyclic quadrilaterals $A B Z C$ and $Z D C Y$ in turn, we have $\\angle A Z B=\\angle A C B=\\angle W Z V$ (or $180^{\\circ}-\\angle W Z V$ if $Z$ lies between $W$ and $C$ ).\n\nSo $A B=V W$ because they subtend equal (or supplementary) angles in $\\omega$.\nAlternative solution 2. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle Z D Y=\\angle Z B A=\\angle Z C Y$. So $Z D C Y$ is cyclic.\n\nUsing cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle D X A=\\angle V Z B=$ $180^{\\circ}-B A V$. So $X D \\| A V$.\n\nUsing cyclic quadrilaterals $Z D C Y$ and $B C W Z$ in turn, we have $\\angle Y D C=\\angle Y Z C=$ $\\angle W B C$. So $X D \\| B W$.\n\nHence $B W \\| A V$ which implies that $A V W B$ is an isosceles trapezium with $A B=V W$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2015", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $S=\\{2,3,4, \\ldots\\}$ denote the set of integers that are greater than or equal to 2 . Does there exist a function $f: S \\rightarrow S$ such that\n\n$$\nf(a) f(b)=f\\left(a^{2} b^{2}\\right) \\text { for all } a, b \\in S \\text { with } a \\neq b ?\n$$", "solution": "We prove that there is no such function. For arbitrary elements $a$ and $b$ of $S$, choose an integer $c$ that is greater than both of them. Since $b c>a$ and $c>b$, we have\n\n$$\nf\\left(a^{4} b^{4} c^{4}\\right)=f\\left(a^{2}\\right) f\\left(b^{2} c^{2}\\right)=f\\left(a^{2}\\right) f(b) f(c)\n$$\n\nFurthermore, since $a c>b$ and $c>a$, we have\n\n$$\nf\\left(a^{4} b^{4} c^{4}\\right)=f\\left(b^{2}\\right) f\\left(a^{2} c^{2}\\right)=f\\left(b^{2}\\right) f(a) f(c)\n$$\n\nComparing these two equations, we find that for all elements $a$ and $b$ of $S$,\n\n$$\nf\\left(a^{2}\\right) f(b)=f\\left(b^{2}\\right) f(a) \\quad \\Longrightarrow \\quad \\frac{f\\left(a^{2}\\right)}{f(a)}=\\frac{f\\left(b^{2}\\right)}{f(b)} .\n$$\n\nIt follows that there exists a positive rational number $k$ such that\n\n$$\nf\\left(a^{2}\\right)=k f(a), \\quad \\text { for all } a \\in S\n$$\n\nSubstituting this into the functional equation yields\n\n$$\nf(a b)=\\frac{f(a) f(b)}{k}, \\quad \\text { for all } a, b \\in S \\text { with } a \\neq b .\n$$\n\nNow combine the functional equation with equations (1) and (2) to obtain\n\n$$\nf(a) f\\left(a^{2}\\right)=f\\left(a^{6}\\right)=\\frac{f(a) f\\left(a^{5}\\right)}{k}=\\frac{f(a) f(a) f\\left(a^{4}\\right)}{k^{2}}=\\frac{f(a) f(a) f\\left(a^{2}\\right)}{k}, \\quad \\text { for all } a \\in S .\n$$\n\nIt follows that $f(a)=k$ for all $a \\in S$. Substituting $a=2$ and $b=3$ into the functional equation yields $k=1$, however $1 \\notin S$ and hence we have no solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2015", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "A sequence of real numbers $a_{0}, a_{1}, \\ldots$ is said to be good if the following three conditions hold.\n(i) The value of $a_{0}$ is a positive integer.\n(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\\frac{a_{i}}{a_{i}+2}$.\n(iii) There exists a positive integer $k$ such that $a_{k}=2014$.\n\nFind the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \\ldots$ of real numbers with the property that $a_{n}=2014$.\n\nAnswer: 60.", "solution": "Note that\n\n$$\na_{i+1}+1=2\\left(a_{i}+1\\right) \\text { or } a_{i+1}+1=\\frac{a_{i}+a_{i}+2}{a_{i}+2}=\\frac{2\\left(a_{i}+1\\right)}{a_{i}+2} .\n$$\n\nHence\n\n$$\n\\frac{1}{a_{i+1}+1}=\\frac{1}{2} \\cdot \\frac{1}{a_{i}+1} \\text { or } \\frac{1}{a_{i+1}+1}=\\frac{a_{i}+2}{2\\left(a_{i}+1\\right)}=\\frac{1}{2} \\cdot \\frac{1}{a_{i}+1}+\\frac{1}{2} .\n$$\n\nTherefore,\n\n$$\n\\frac{1}{a_{k}+1}=\\frac{1}{2^{k}} \\cdot \\frac{1}{a_{0}+1}+\\sum_{i=1}^{k} \\frac{\\varepsilon_{i}}{2^{k-i+1}}\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\\left(a_{k}+1\\right)$ and putting $a_{k}=2014$, we get\n\n$$\n2^{k}=\\frac{2015}{a_{0}+1}+2015 \\cdot\\left(\\sum_{i=1}^{k} \\varepsilon_{i} \\cdot 2^{i-1}\\right)\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . Since $\\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,\n\n$$\n2^{k}-1=2015 \\cdot\\left(\\sum_{i=1}^{k} \\varepsilon_{i} \\cdot 2^{i-1}\\right)\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \\mid 2^{k}-1$. Since $2015=$ $5 \\cdot 13 \\cdot 31$, from the Fermat little theorem we obtain $5\\left|2^{4}-1,13\\right| 2^{12}-1$ and $31 \\mid 2^{30}-1$. We also have $\\operatorname{lcm}[4,12,30]=60$, hence $5\\left|2^{60}-1,13\\right| 2^{60}-1$ and $31 \\mid 2^{60}-1$, which gives $2015 \\mid 2^{60}-1$.\n\nBut $5 \\nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \\mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.\n\nAlternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\\frac{a_{i+1}-1}{2}$ or $a_{i}=\\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that\n\n$$\na_{i}=\\left\\{\\begin{array}{cl}\n\\frac{a_{i+1}-1}{2} & \\text { if } a_{i+1}>1 \\\\\n\\frac{2 a_{i+1}}{1-a_{i+1}} & \\text { if } a_{i+1}<1\n\\end{array}\\right.\n$$\n\nThus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.\n\n$$\n\\begin{aligned}\n& \\frac{2014}{1}, \\frac{2013}{2}, \\frac{2011}{4}, \\frac{2007}{8}, \\frac{1999}{16}, \\frac{1983}{32}, \\frac{1951}{64}, \\frac{1887}{128}, \\frac{1759}{256}, \\frac{1503}{512}, \\frac{991}{1024}, \\frac{1982}{33}, \\frac{1949}{66}, \\frac{1883}{132}, \\frac{1751}{264}, \\frac{1487}{528}, \\frac{959}{1056}, \\frac{1918}{97}, \\frac{1821}{194}, \\frac{1627}{388}, \\\\\n& \\frac{1239}{776}, \\frac{463}{1552}, \\frac{926}{1089}, \\frac{1852}{163}, \\frac{1689}{326}, \\frac{1363}{652}, \\frac{711}{1304}, \\frac{1422}{593}, \\frac{829}{1186}, \\frac{1658}{357}, \\frac{1301}{714}, \\frac{587}{1428}, \\frac{1174}{841}, \\frac{333}{1682}, \\frac{666}{1349}, \\frac{1332}{683}, \\frac{649}{1366}, \\frac{1298}{717}, \\frac{581}{1434}, \\frac{1162}{853}, \\\\\n& \\frac{309}{1706}, \\frac{618}{1397}, \\frac{1236}{779}, \\frac{457}{1558}, \\frac{914}{1101}, \\frac{1828}{187}, \\frac{1641}{374}, \\frac{1267}{748}, \\frac{519}{1496}, \\frac{1038}{977}, \\frac{61}{1954}, \\frac{122}{1893}, \\frac{244}{1771}, \\frac{488}{1527}, \\frac{976}{1039}, \\frac{1952}{63}, \\frac{1889}{126}, \\frac{1763}{252}, \\frac{1511}{504}, \\frac{1007}{1008}, \\frac{2014}{1}\n\\end{aligned}\n$$\n\nThere are 61 terms in the above list. Thus $k=60$.\nAlternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.\n\nAlternative solution 2. Start with $a_{k}=\\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\\frac{m_{i}}{n_{i}}$ for $i \\geq 0$ where\n\n$$\n\\left(m_{i+1}, n_{i+1}\\right)= \\begin{cases}\\left(m_{i}-n_{i}, 2 n_{i}\\right) & \\text { if } m_{i}>n_{i} \\\\ \\left(2 m_{i}, n_{i}-m_{i}\\right) & \\text { if } m_{i}<n_{i}\\end{cases}\n$$\n\nEasy inductions show that $m_{i}+n_{i}=2015,1 \\leq m_{i}, n_{i} \\leq 2014$ and $\\operatorname{gcd}\\left(m_{i}, n_{i}\\right)=1$ for $i \\geq 0$. Since $a_{0} \\in \\mathbb{N}^{+}$and $\\operatorname{gcd}\\left(m_{k}, n_{k}\\right)=1$, we require $n_{k}=1$. An easy induction shows that $\\left(m_{i}, n_{i}\\right) \\equiv\\left(-2^{i}, 2^{i}\\right)(\\bmod 2015)$ for $i=0,1, \\ldots, k$.\n\nThus $2^{k} \\equiv 1(\\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \\equiv 1(\\bmod 2015)$. But since $1 \\leq n_{k}, m_{k} \\leq 2014$, it follows that $a_{0}$ is an integer.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2015", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be a positive integer. Consider $2 n$ distinct lines on the plane, no two of which are parallel. Of the $2 n$ lines, $n$ are colored blue, the other $n$ are colored red. Let $\\mathcal{B}$ be the set of all points on the plane that lie on at least one blue line, and $\\mathcal{R}$ the set of all points on the plane that lie on at least one red line. Prove that there exists a circle that intersects $\\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\\mathcal{R}$ in exactly $2 n-1$ points.", "solution": "Consider a line $\\ell$ on the plane and a point $P$ on it such that $\\ell$ is not parallel to any of the $2 n$ lines. Rotate $\\ell$ about $P$ counterclockwise until it is parallel to one of the $2 n$ lines. Take note of that line and keep rotating until all the $2 n$ lines are met. The $2 n$ lines are now ordered according to which line is met before or after. Say the lines are in order $\\ell_{1}, \\ldots, \\ell_{2 n}$. Clearly there must be $k \\in\\{1, \\ldots, 2 n-1\\}$ such that $\\ell_{k}$ and $\\ell_{k+1}$ are of different colors.\n\nNow we set up a system of $X-$ and $Y$ - axes on the plane. Consider the two angular bisectors of $\\ell_{k}$ and $\\ell_{k+1}$. If we rotate $\\ell_{k+1}$ counterclockwise, the line will be parallel to one of the bisectors before the other. Let the bisector that is parallel to the rotation of $\\ell_{k+1}$ first be the $X$-axis, and the other the $Y$-axis. From now on, we will be using the directed angle notation: for lines $s$ and $s^{\\prime}$, we define $\\angle\\left(s, s^{\\prime}\\right)$ to be a real number in $[0, \\pi)$ denoting the angle in radians such that when $s$ is rotated counterclockwise by $\\angle\\left(s, s^{\\prime}\\right)$ radian, it becomes parallel to $s^{\\prime}$. Using this\nnotation, we notice that there is no $i=1, \\ldots, 2 n$ such that $\\angle\\left(X, l_{i}\\right)$ is between $\\angle\\left(X, \\ell_{k}\\right)$ and $\\angle\\left(X, \\ell_{k+1}\\right)$.\n\nBecause the $2 n$ lines are distinct, the set $S$ of all the intersections between $\\ell_{i}$ and $\\ell_{j}(i \\neq j)$ is a finite set of points. Consider a rectangle with two opposite vertices lying on $\\ell_{k}$ and the other two lying on $\\ell_{k+1}$. With respect to the origin (the intersection of $\\ell_{k}$ and $\\ell_{k+1}$ ), we can enlarge the rectangle as much as we want, while all the vertices remain on the lines. Thus, there is one of these rectangles $R$ which contains all the points in $S$ in its interior. Since each side of $R$ is parallel to either $X$ - or $Y$ - axis, $R$ is a part of the four lines $x= \\pm a, y= \\pm b$. where $a, b>0$.\n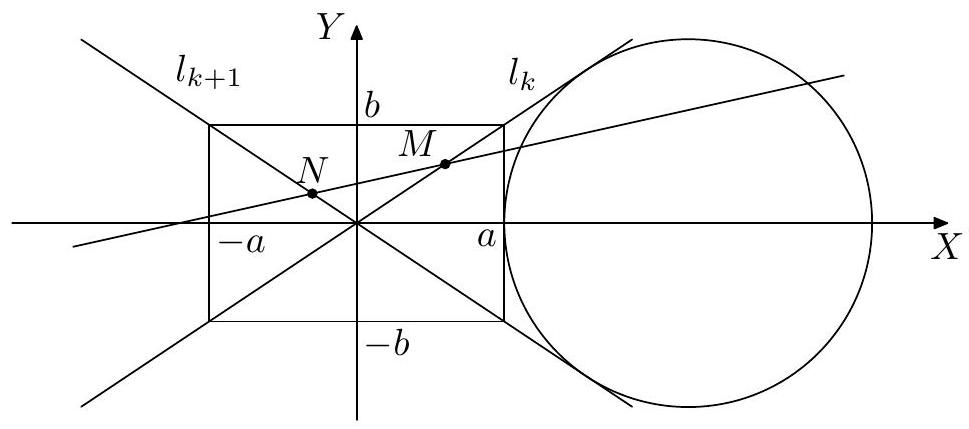\n\nConsider the circle $\\mathcal{C}$ tangent to the right of the $x=a$ side of the rectangle, and to both $\\ell_{k}$ and $\\ell_{k+1}$. We claim that this circle intersects $\\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\\mathcal{R}$ in exactly $2 n-1$ points. Since $\\mathcal{C}$ is tangent to both $\\ell_{k}$ and $\\ell_{k+1}$ and the two lines have different colors, it is enough to show that $\\mathcal{C}$ intersects with each of the other $2 n-2$ lines in exactly 2 points. Note that no two lines intersect on the circle because all the intersections between lines are in $S$ which is in the interior of $R$.\n\nConsider any line $L$ among these $2 n-2$ lines. Let $L$ intersect with $\\ell_{k}$ and $\\ell_{k+1}$ at the points $M$ and $N$, respectively ( $M$ and $N$ are not necessarily distinct). Notice that both $M$ and $N$ must be inside $R$. There are two cases:\n(i) $L$ intersects $R$ on the $x=-a$ side once and another time on $x=a$ side;\n(ii) $L$ intersects $y=-b$ and $y=b$ sides.\n\nHowever, if (ii) happens, $\\angle\\left(\\ell_{k}, L\\right)$ and $\\angle\\left(L, \\ell_{k+1}\\right)$ would be both positive, and then $\\angle(X, L)$ would be between $\\angle\\left(X, \\ell_{k}\\right)$ and $\\angle\\left(X, \\ell_{k+1}\\right)$, a contradiction. Thus, only (i) can happen. Then $L$ intersects $\\mathcal{C}$ in exactly two points, and we are done.\n\nAlternative solution. By rotating the diagram we can ensure that no line is vertical. Let $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2 n}$ be the lines listed in order of increasing gradient. Then there is a $k$ such that lines $\\ell_{k}$ and $\\ell_{k+1}$ are oppositely coloured. By rotating our coordinate system and cyclicly relabelling our lines we can ensure that $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2 n}$ are listed in order of increasing gradient, $\\ell_{1}$ and $\\ell_{2 n}$ are oppositely coloured, and no line is vertical.\n\nLet $\\mathcal{D}$ be a circle centred at the origin and of sufficiently large radius so that\n\n- All intersection points of all pairs of lines lie strictly inside $\\mathcal{D}$; and\n- Each line $\\ell_{i}$ intersects $\\mathcal{D}$ in two points $A_{i}$ and $B_{i}$ say, such that $A_{i}$ is on the right semicircle (the part of the circle in the positive $x$ half plane) and $B_{i}$ is on the left semicircle.\n\nNote that the anticlockwise order of the points $A_{i}, B_{i}$ around $\\mathcal{D}$ is $A_{1}, A_{2}, \\ldots, A_{n}, B_{1}, B_{2}, \\ldots, B_{n}$.\n(If $A_{i+1}$ occurred before $A_{i}$ then rays $r_{i}$ and $r_{i+1}$ (as defined below) would intersect outside $\\mathcal{D}$.)\n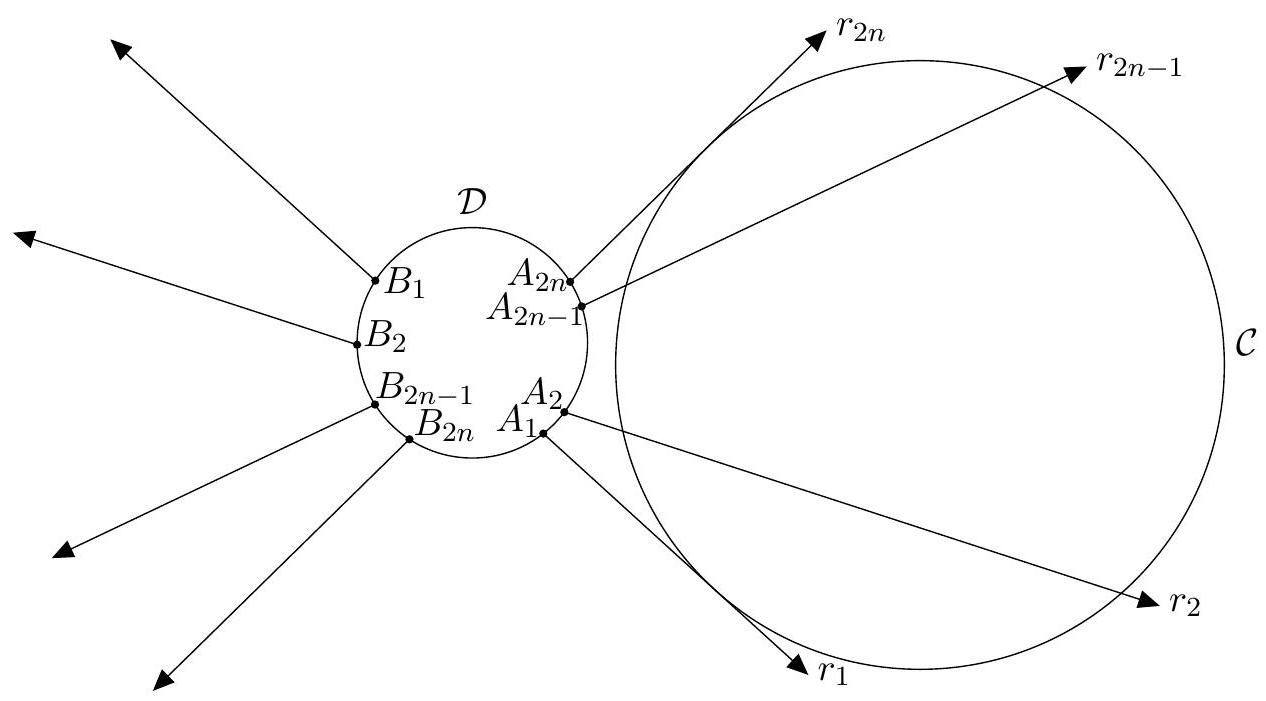\n\nFor each $i$, let $r_{i}$ be the ray that is the part of the line $\\ell_{i}$ starting from point $A_{i}$ and that extends to the right. Let $\\mathcal{C}$ be any circle tangent to $r_{1}$ and $r_{2 n}$, that lies entirely to the right of $\\mathcal{D}$. Then $\\mathcal{C}$ intersects each of $r_{2}, r_{3}, \\ldots, r_{2 n-1}$ twice and is tangent to $r_{1}$ and $r_{2 n}$. Thus $\\mathcal{C}$ has the required properties.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 5 |
-
{"year": "2015", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Determine all sequences $a_{0}, a_{1}, a_{2}, \\ldots$ of positive integers with $a_{0} \\geq 2015$ such that for all integers $n \\geq 1$ :\n(i) $a_{n+2}$ is divisible by $a_{n}$;\n(ii) $\\left|s_{n+1}-(n+1) a_{n}\\right|=1$, where $s_{n+1}=a_{n+1}-a_{n}+a_{n-1}-\\cdots+(-1)^{n+1} a_{0}$.\n\nAnswer: There are two families of answers:\n(a) $a_{n}=c(n+2) n$ ! for all $n \\geq 1$ and $a_{0}=c+1$ for some integer $c \\geq 2014$, and\n(b) $a_{n}=c(n+2) n$ ! for all $n \\geq 1$ and $a_{0}=c-1$ for some integer $c \\geq 2016$.", "solution": "Let $\\left\\{a_{n}\\right\\}_{n=0}^{\\infty}$ be a sequence of positive integers satisfying the given conditions. We can rewrite (ii) as $s_{n+1}=(n+1) a_{n}+h_{n}$, where $h_{n} \\in\\{-1,1\\}$. Substituting $n$ with $n-1$ yields $s_{n}=n a_{n-1}+h_{n-1}$, where $h_{n-1} \\in\\{-1,1\\}$. Note that $a_{n+1}=s_{n+1}+s_{n}$, therefore there exists $\\delta_{n} \\in\\{-2,0,2\\}$ such that\n\n$$\na_{n+1}=(n+1) a_{n}+n a_{n-1}+\\delta_{n}\n$$\n\nWe also have $\\left|s_{2}-2 a_{1}\\right|=1$, which yields $a_{0}=3 a_{1}-a_{2} \\pm 1 \\leq 3 a_{1}$, and therefore $a_{1} \\geq \\frac{a_{0}}{3} \\geq 671$. Substituting $n=2$ in (1), we find that $a_{3}=3 a_{2}+2 a_{1}+\\delta_{2}$. Since $a_{1} \\mid a_{3}$, we have $a_{1} \\mid 3 a_{2}+\\delta_{2}$, and therefore $a_{2} \\geq 223$. Using (1), we obtain that $a_{n} \\geq 223$ for all $n \\geq 0$.\n\nLemma 1: For $n \\geq 4$, we have $a_{n+2}=(n+1)(n+4) a_{n}$.\nProof. For $n \\geq 3$ we have\n\n$$\na_{n}=n a_{n-1}+(n-1) a_{n-2}+\\delta_{n-1}>n a_{n-1}+3 .\n$$\n\nBy applying (2) with $n$ substituted by $n-1$ we have for $n \\geq 4$,\n\n$$\na_{n}=n a_{n-1}+(n-1) a_{n-2}+\\delta_{n-1}<n a_{n-1}+\\left(a_{n-1}-3\\right)+\\delta_{n-1}<(n+1) a_{n-1}\n$$\n\nUsing (1) to write $a_{n+2}$ in terms of $a_{n}$ and $a_{n-1}$ along with (2), we obtain that for $n \\geq 3$,\n\n$$\n\\begin{aligned}\na_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \\delta_{n}+\\delta_{n+1} \\\\\n& <(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+3(n+2) \\\\\n& <\\left(n^{2}+5 n+5\\right) a_{n} .\n\\end{aligned}\n$$\n\nAlso for $n \\geq 4$,\n\n$$\n\\begin{aligned}\na_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \\delta_{n}+\\delta_{n+1} \\\\\n& >(n+3)(n+1) a_{n}+n a_{n} \\\\\n& =\\left(n^{2}+5 n+3\\right) a_{n} .\n\\end{aligned}\n$$\n\nSince $a_{n} \\mid a_{n+2}$, we obtain that $a_{n+2}=\\left(n^{2}+5 n+4\\right) a_{n}=(n+1)(n+4) a_{n}$, as desired.\nLemma 2: For $n \\geq 4$, we have $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$.\nProof. Using the recurrence $a_{n+3}=(n+3) a_{n+2}+(n+2) a_{n+1}+\\delta_{n+2}$ and writing $a_{n+3}$, $a_{n+2}$ in terms of $a_{n+1}, a_{n}$ according to Lemma 1 we obtain\n\n$$\n(n+2)(n+4) a_{n+1}=(n+3)(n+1)(n+4) a_{n}+\\delta_{n+2} .\n$$\n\nHence $n+4 \\mid \\delta_{n+2}$, which yields $\\delta_{n+2}=0$ and $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$, as desired.\nSuppose there exists $n \\geq 1$ such that $a_{n+1} \\neq \\frac{(n+1)(n+3)}{n+2} a_{n}$. By Lemma 2, there exist a greatest integer $1 \\leq m \\leq 3$ with this property. Then $a_{m+2}=\\frac{(m+2)(m+4)}{m+3} a_{m+1}$. If $\\delta_{m+1}=0$, we have $a_{m+1}=\\frac{(m+1)(m+3)}{m+2} a_{m}$, which contradicts our choice of $m$. Thus $\\delta_{m+1} \\neq 0$.\n\nClearly $m+3 \\mid a_{m+1}$. Write $a_{m+1}=(m+3) k$ and $a_{m+2}=(m+2)(m+4) k$. Then $(m+$ 1) $a_{m}+\\delta_{m+1}=a_{m+2}-(m+2) a_{m+1}=(m+2) k$. So, $a_{m} \\mid(m+2) k-\\delta_{m+1}$. But $a_{m}$ also divides $a_{m+2}=(m+2)(m+4) k$. Combining the two divisibility conditions, we obtain $a_{m} \\mid(m+4) \\delta_{m+1}$. Since $\\delta_{m+1} \\neq 0$, we have $a_{m} \\mid 2 m+8 \\leq 14$, which contradicts the previous result that $a_{n} \\geq 223$ for all nonnegative integers $n$.\n\nSo, $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$ for $n \\geq 1$. Substituting $n=1$ yields $3 \\mid a_{1}$. Letting $a_{1}=3 c$, we have by induction that $a_{n}=n!(n+2) c$ for $n \\geq 1$. Since $\\left|s_{2}-2 a_{1}\\right|=1$, we then get $a_{0}=c \\pm 1$, yielding the two families of solutions. By noting that $(n+2) n!=n!+(n+1)!$, we have $s_{n+1}=c(n+2)!+(-1)^{n}\\left(c-a_{0}\\right)$. Hence both families of solutions satisfy the given conditions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2015", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle, and let $D$ be a point on side $B C$. A line through $D$ intersects side $A B$ at $X$ and ray $A C$ at $Y$. The circumcircle of triangle $B X D$ intersects the circumcircle $\\omega$ of triangle $A B C$ again at point $Z \\neq B$. The lines $Z D$ and $Z Y$ intersect $\\omega$ again at $V$ and $W$, respectively. Prove that $A B=V W$.", "solution": "Suppose $X Y$ intersects $\\omega$ at points $P$ and $Q$, where $Q$ lies between $X$ and $Y$. We will show that $V$ and $W$ are the reflections of $A$ and $B$ with respect to the perpendicular bisector of $P Q$. From this, it follows that $A V W B$ is an isosceles trapezoid and hence $A B=V W$.\n\nFirst, note that\n\n$$\n\\angle B Z D=\\angle A X Y=\\angle A P Q+\\angle B A P=\\angle A P Q+\\angle B Z P,\n$$\n\nso $\\angle A P Q=\\angle P Z V=\\angle P Q V$, and hence $V$ is the reflection of $A$ with respect to the perpendicular bisector of $P Q$.\n\nNow, suppose $W^{\\prime}$ is the reflection of $B$ with respect to the perpendicular bisector of $P Q$, and let $Z^{\\prime}$ be the intersection of $Y W^{\\prime}$ and $\\omega$. It suffices to show that $B, X, D, Z^{\\prime}$ are concyclic. Note that\n\n$$\n\\angle Y D C=\\angle P D B=\\angle P C B+\\angle Q P C=\\angle W^{\\prime} P Q+\\angle Q P C=\\angle W^{\\prime} P C=\\angle Y Z^{\\prime} C .\n$$\n\nSo $D, C, Y, Z^{\\prime}$ are concyclic. Next, $\\angle B Z^{\\prime} D=\\angle C Z^{\\prime} B-\\angle C Z^{\\prime} D=180^{\\circ}-\\angle B X D$ and due to the previous concyclicity we are done.\n\nAlternative solution 1. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle Z D Y=\\angle Z B A=\\angle Z C Y$. So $Z D C Y$ is cyclic.\n\nUsing cyclic quadrilaterals $A B Z C$ and $Z D C Y$ in turn, we have $\\angle A Z B=\\angle A C B=\\angle W Z V$ (or $180^{\\circ}-\\angle W Z V$ if $Z$ lies between $W$ and $C$ ).\n\nSo $A B=V W$ because they subtend equal (or supplementary) angles in $\\omega$.\nAlternative solution 2. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle Z D Y=\\angle Z B A=\\angle Z C Y$. So $Z D C Y$ is cyclic.\n\nUsing cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\\angle D X A=\\angle V Z B=$ $180^{\\circ}-B A V$. So $X D \\| A V$.\n\nUsing cyclic quadrilaterals $Z D C Y$ and $B C W Z$ in turn, we have $\\angle Y D C=\\angle Y Z C=$ $\\angle W B C$. So $X D \\| B W$.\n\nHence $B W \\| A V$ which implies that $A V W B$ is an isosceles trapezium with $A B=V W$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2015", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $S=\\{2,3,4, \\ldots\\}$ denote the set of integers that are greater than or equal to 2 . Does there exist a function $f: S \\rightarrow S$ such that\n\n$$\nf(a) f(b)=f\\left(a^{2} b^{2}\\right) \\text { for all } a, b \\in S \\text { with } a \\neq b ?\n$$", "solution": "We prove that there is no such function. For arbitrary elements $a$ and $b$ of $S$, choose an integer $c$ that is greater than both of them. Since $b c>a$ and $c>b$, we have\n\n$$\nf\\left(a^{4} b^{4} c^{4}\\right)=f\\left(a^{2}\\right) f\\left(b^{2} c^{2}\\right)=f\\left(a^{2}\\right) f(b) f(c)\n$$\n\nFurthermore, since $a c>b$ and $c>a$, we have\n\n$$\nf\\left(a^{4} b^{4} c^{4}\\right)=f\\left(b^{2}\\right) f\\left(a^{2} c^{2}\\right)=f\\left(b^{2}\\right) f(a) f(c)\n$$\n\nComparing these two equations, we find that for all elements $a$ and $b$ of $S$,\n\n$$\nf\\left(a^{2}\\right) f(b)=f\\left(b^{2}\\right) f(a) \\quad \\Longrightarrow \\quad \\frac{f\\left(a^{2}\\right)}{f(a)}=\\frac{f\\left(b^{2}\\right)}{f(b)} .\n$$\n\nIt follows that there exists a positive rational number $k$ such that\n\n$$\nf\\left(a^{2}\\right)=k f(a), \\quad \\text { for all } a \\in S\n$$\n\nSubstituting this into the functional equation yields\n\n$$\nf(a b)=\\frac{f(a) f(b)}{k}, \\quad \\text { for all } a, b \\in S \\text { with } a \\neq b .\n$$\n\nNow combine the functional equation with equations (1) and (2) to obtain\n\n$$\nf(a) f\\left(a^{2}\\right)=f\\left(a^{6}\\right)=\\frac{f(a) f\\left(a^{5}\\right)}{k}=\\frac{f(a) f(a) f\\left(a^{4}\\right)}{k^{2}}=\\frac{f(a) f(a) f\\left(a^{2}\\right)}{k}, \\quad \\text { for all } a \\in S .\n$$\n\nIt follows that $f(a)=k$ for all $a \\in S$. Substituting $a=2$ and $b=3$ into the functional equation yields $k=1$, however $1 \\notin S$ and hence we have no solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2015", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "A sequence of real numbers $a_{0}, a_{1}, \\ldots$ is said to be good if the following three conditions hold.\n(i) The value of $a_{0}$ is a positive integer.\n(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\\frac{a_{i}}{a_{i}+2}$.\n(iii) There exists a positive integer $k$ such that $a_{k}=2014$.\n\nFind the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \\ldots$ of real numbers with the property that $a_{n}=2014$.\n\nAnswer: 60.", "solution": "Note that\n\n$$\na_{i+1}+1=2\\left(a_{i}+1\\right) \\text { or } a_{i+1}+1=\\frac{a_{i}+a_{i}+2}{a_{i}+2}=\\frac{2\\left(a_{i}+1\\right)}{a_{i}+2} .\n$$\n\nHence\n\n$$\n\\frac{1}{a_{i+1}+1}=\\frac{1}{2} \\cdot \\frac{1}{a_{i}+1} \\text { or } \\frac{1}{a_{i+1}+1}=\\frac{a_{i}+2}{2\\left(a_{i}+1\\right)}=\\frac{1}{2} \\cdot \\frac{1}{a_{i}+1}+\\frac{1}{2} .\n$$\n\nTherefore,\n\n$$\n\\frac{1}{a_{k}+1}=\\frac{1}{2^{k}} \\cdot \\frac{1}{a_{0}+1}+\\sum_{i=1}^{k} \\frac{\\varepsilon_{i}}{2^{k-i+1}}\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\\left(a_{k}+1\\right)$ and putting $a_{k}=2014$, we get\n\n$$\n2^{k}=\\frac{2015}{a_{0}+1}+2015 \\cdot\\left(\\sum_{i=1}^{k} \\varepsilon_{i} \\cdot 2^{i-1}\\right)\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . Since $\\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,\n\n$$\n2^{k}-1=2015 \\cdot\\left(\\sum_{i=1}^{k} \\varepsilon_{i} \\cdot 2^{i-1}\\right)\n$$\n\nwhere $\\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \\mid 2^{k}-1$. Since $2015=$ $5 \\cdot 13 \\cdot 31$, from the Fermat little theorem we obtain $5\\left|2^{4}-1,13\\right| 2^{12}-1$ and $31 \\mid 2^{30}-1$. We also have $\\operatorname{lcm}[4,12,30]=60$, hence $5\\left|2^{60}-1,13\\right| 2^{60}-1$ and $31 \\mid 2^{60}-1$, which gives $2015 \\mid 2^{60}-1$.\n\nBut $5 \\nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \\mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.\n\nAlternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\\frac{a_{i+1}-1}{2}$ or $a_{i}=\\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that\n\n$$\na_{i}=\\left\\{\\begin{array}{cl}\n\\frac{a_{i+1}-1}{2} & \\text { if } a_{i+1}>1 \\\\\n\\frac{2 a_{i+1}}{1-a_{i+1}} & \\text { if } a_{i+1}<1\n\\end{array}\\right.\n$$\n\nThus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.\n\n$$\n\\begin{aligned}\n& \\frac{2014}{1}, \\frac{2013}{2}, \\frac{2011}{4}, \\frac{2007}{8}, \\frac{1999}{16}, \\frac{1983}{32}, \\frac{1951}{64}, \\frac{1887}{128}, \\frac{1759}{256}, \\frac{1503}{512}, \\frac{991}{1024}, \\frac{1982}{33}, \\frac{1949}{66}, \\frac{1883}{132}, \\frac{1751}{264}, \\frac{1487}{528}, \\frac{959}{1056}, \\frac{1918}{97}, \\frac{1821}{194}, \\frac{1627}{388}, \\\\\n& \\frac{1239}{776}, \\frac{463}{1552}, \\frac{926}{1089}, \\frac{1852}{163}, \\frac{1689}{326}, \\frac{1363}{652}, \\frac{711}{1304}, \\frac{1422}{593}, \\frac{829}{1186}, \\frac{1658}{357}, \\frac{1301}{714}, \\frac{587}{1428}, \\frac{1174}{841}, \\frac{333}{1682}, \\frac{666}{1349}, \\frac{1332}{683}, \\frac{649}{1366}, \\frac{1298}{717}, \\frac{581}{1434}, \\frac{1162}{853}, \\\\\n& \\frac{309}{1706}, \\frac{618}{1397}, \\frac{1236}{779}, \\frac{457}{1558}, \\frac{914}{1101}, \\frac{1828}{187}, \\frac{1641}{374}, \\frac{1267}{748}, \\frac{519}{1496}, \\frac{1038}{977}, \\frac{61}{1954}, \\frac{122}{1893}, \\frac{244}{1771}, \\frac{488}{1527}, \\frac{976}{1039}, \\frac{1952}{63}, \\frac{1889}{126}, \\frac{1763}{252}, \\frac{1511}{504}, \\frac{1007}{1008}, \\frac{2014}{1}\n\\end{aligned}\n$$\n\nThere are 61 terms in the above list. Thus $k=60$.\nAlternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.\n\nAlternative solution 2. Start with $a_{k}=\\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\\frac{m_{i}}{n_{i}}$ for $i \\geq 0$ where\n\n$$\n\\left(m_{i+1}, n_{i+1}\\right)= \\begin{cases}\\left(m_{i}-n_{i}, 2 n_{i}\\right) & \\text { if } m_{i}>n_{i} \\\\ \\left(2 m_{i}, n_{i}-m_{i}\\right) & \\text { if } m_{i}<n_{i}\\end{cases}\n$$\n\nEasy inductions show that $m_{i}+n_{i}=2015,1 \\leq m_{i}, n_{i} \\leq 2014$ and $\\operatorname{gcd}\\left(m_{i}, n_{i}\\right)=1$ for $i \\geq 0$. Since $a_{0} \\in \\mathbb{N}^{+}$and $\\operatorname{gcd}\\left(m_{k}, n_{k}\\right)=1$, we require $n_{k}=1$. An easy induction shows that $\\left(m_{i}, n_{i}\\right) \\equiv\\left(-2^{i}, 2^{i}\\right)(\\bmod 2015)$ for $i=0,1, \\ldots, k$.\n\nThus $2^{k} \\equiv 1(\\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \\equiv 1(\\bmod 2015)$. But since $1 \\leq n_{k}, m_{k} \\leq 2014$, it follows that $a_{0}$ is an integer.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2015", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be a positive integer. Consider $2 n$ distinct lines on the plane, no two of which are parallel. Of the $2 n$ lines, $n$ are colored blue, the other $n$ are colored red. Let $\\mathcal{B}$ be the set of all points on the plane that lie on at least one blue line, and $\\mathcal{R}$ the set of all points on the plane that lie on at least one red line. Prove that there exists a circle that intersects $\\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\\mathcal{R}$ in exactly $2 n-1$ points.", "solution": "Consider a line $\\ell$ on the plane and a point $P$ on it such that $\\ell$ is not parallel to any of the $2 n$ lines. Rotate $\\ell$ about $P$ counterclockwise until it is parallel to one of the $2 n$ lines. Take note of that line and keep rotating until all the $2 n$ lines are met. The $2 n$ lines are now ordered according to which line is met before or after. Say the lines are in order $\\ell_{1}, \\ldots, \\ell_{2 n}$. Clearly there must be $k \\in\\{1, \\ldots, 2 n-1\\}$ such that $\\ell_{k}$ and $\\ell_{k+1}$ are of different colors.\n\nNow we set up a system of $X-$ and $Y$ - axes on the plane. Consider the two angular bisectors of $\\ell_{k}$ and $\\ell_{k+1}$. If we rotate $\\ell_{k+1}$ counterclockwise, the line will be parallel to one of the bisectors before the other. Let the bisector that is parallel to the rotation of $\\ell_{k+1}$ first be the $X$-axis, and the other the $Y$-axis. From now on, we will be using the directed angle notation: for lines $s$ and $s^{\\prime}$, we define $\\angle\\left(s, s^{\\prime}\\right)$ to be a real number in $[0, \\pi)$ denoting the angle in radians such that when $s$ is rotated counterclockwise by $\\angle\\left(s, s^{\\prime}\\right)$ radian, it becomes parallel to $s^{\\prime}$. Using this\nnotation, we notice that there is no $i=1, \\ldots, 2 n$ such that $\\angle\\left(X, l_{i}\\right)$ is between $\\angle\\left(X, \\ell_{k}\\right)$ and $\\angle\\left(X, \\ell_{k+1}\\right)$.\n\nBecause the $2 n$ lines are distinct, the set $S$ of all the intersections between $\\ell_{i}$ and $\\ell_{j}(i \\neq j)$ is a finite set of points. Consider a rectangle with two opposite vertices lying on $\\ell_{k}$ and the other two lying on $\\ell_{k+1}$. With respect to the origin (the intersection of $\\ell_{k}$ and $\\ell_{k+1}$ ), we can enlarge the rectangle as much as we want, while all the vertices remain on the lines. Thus, there is one of these rectangles $R$ which contains all the points in $S$ in its interior. Since each side of $R$ is parallel to either $X$ - or $Y$ - axis, $R$ is a part of the four lines $x= \\pm a, y= \\pm b$. where $a, b>0$.\n\n\nConsider the circle $\\mathcal{C}$ tangent to the right of the $x=a$ side of the rectangle, and to both $\\ell_{k}$ and $\\ell_{k+1}$. We claim that this circle intersects $\\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\\mathcal{R}$ in exactly $2 n-1$ points. Since $\\mathcal{C}$ is tangent to both $\\ell_{k}$ and $\\ell_{k+1}$ and the two lines have different colors, it is enough to show that $\\mathcal{C}$ intersects with each of the other $2 n-2$ lines in exactly 2 points. Note that no two lines intersect on the circle because all the intersections between lines are in $S$ which is in the interior of $R$.\n\nConsider any line $L$ among these $2 n-2$ lines. Let $L$ intersect with $\\ell_{k}$ and $\\ell_{k+1}$ at the points $M$ and $N$, respectively ( $M$ and $N$ are not necessarily distinct). Notice that both $M$ and $N$ must be inside $R$. There are two cases:\n(i) $L$ intersects $R$ on the $x=-a$ side once and another time on $x=a$ side;\n(ii) $L$ intersects $y=-b$ and $y=b$ sides.\n\nHowever, if (ii) happens, $\\angle\\left(\\ell_{k}, L\\right)$ and $\\angle\\left(L, \\ell_{k+1}\\right)$ would be both positive, and then $\\angle(X, L)$ would be between $\\angle\\left(X, \\ell_{k}\\right)$ and $\\angle\\left(X, \\ell_{k+1}\\right)$, a contradiction. Thus, only (i) can happen. Then $L$ intersects $\\mathcal{C}$ in exactly two points, and we are done.\n\nAlternative solution. By rotating the diagram we can ensure that no line is vertical. Let $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2 n}$ be the lines listed in order of increasing gradient. Then there is a $k$ such that lines $\\ell_{k}$ and $\\ell_{k+1}$ are oppositely coloured. By rotating our coordinate system and cyclicly relabelling our lines we can ensure that $\\ell_{1}, \\ell_{2}, \\ldots, \\ell_{2 n}$ are listed in order of increasing gradient, $\\ell_{1}$ and $\\ell_{2 n}$ are oppositely coloured, and no line is vertical.\n\nLet $\\mathcal{D}$ be a circle centred at the origin and of sufficiently large radius so that\n\n- All intersection points of all pairs of lines lie strictly inside $\\mathcal{D}$; and\n- Each line $\\ell_{i}$ intersects $\\mathcal{D}$ in two points $A_{i}$ and $B_{i}$ say, such that $A_{i}$ is on the right semicircle (the part of the circle in the positive $x$ half plane) and $B_{i}$ is on the left semicircle.\n\nNote that the anticlockwise order of the points $A_{i}, B_{i}$ around $\\mathcal{D}$ is $A_{1}, A_{2}, \\ldots, A_{n}, B_{1}, B_{2}, \\ldots, B_{n}$.\n(If $A_{i+1}$ occurred before $A_{i}$ then rays $r_{i}$ and $r_{i+1}$ (as defined below) would intersect outside $\\mathcal{D}$.)\n\n\nFor each $i$, let $r_{i}$ be the ray that is the part of the line $\\ell_{i}$ starting from point $A_{i}$ and that extends to the right. Let $\\mathcal{C}$ be any circle tangent to $r_{1}$ and $r_{2 n}$, that lies entirely to the right of $\\mathcal{D}$. Then $\\mathcal{C}$ intersects each of $r_{2}, r_{3}, \\ldots, r_{2 n-1}$ twice and is tangent to $r_{1}$ and $r_{2 n}$. Thus $\\mathcal{C}$ has the required properties.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 5 |
+
{"year": "2015", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Determine all sequences $a_{0}, a_{1}, a_{2}, \\ldots$ of positive integers with $a_{0} \\geq 2015$ such that for all integers $n \\geq 1$ :\n(i) $a_{n+2}$ is divisible by $a_{n}$;\n(ii) $\\left|s_{n+1}-(n+1) a_{n}\\right|=1$, where $s_{n+1}=a_{n+1}-a_{n}+a_{n-1}-\\cdots+(-1)^{n+1} a_{0}$.\n\nAnswer: There are two families of answers:\n(a) $a_{n}=c(n+2) n$ ! for all $n \\geq 1$ and $a_{0}=c+1$ for some integer $c \\geq 2014$, and\n(b) $a_{n}=c(n+2) n$ ! for all $n \\geq 1$ and $a_{0}=c-1$ for some integer $c \\geq 2016$.", "solution": "Let $\\left\\{a_{n}\\right\\}_{n=0}^{\\infty}$ be a sequence of positive integers satisfying the given conditions. We can rewrite (ii) as $s_{n+1}=(n+1) a_{n}+h_{n}$, where $h_{n} \\in\\{-1,1\\}$. Substituting $n$ with $n-1$ yields $s_{n}=n a_{n-1}+h_{n-1}$, where $h_{n-1} \\in\\{-1,1\\}$. Note that $a_{n+1}=s_{n+1}+s_{n}$, therefore there exists $\\delta_{n} \\in\\{-2,0,2\\}$ such that\n\n$$\na_{n+1}=(n+1) a_{n}+n a_{n-1}+\\delta_{n}\n$$\n\nWe also have $\\left|s_{2}-2 a_{1}\\right|=1$, which yields $a_{0}=3 a_{1}-a_{2} \\pm 1 \\leq 3 a_{1}$, and therefore $a_{1} \\geq \\frac{a_{0}}{3} \\geq 671$. Substituting $n=2$ in (1), we find that $a_{3}=3 a_{2}+2 a_{1}+\\delta_{2}$. Since $a_{1} \\mid a_{3}$, we have $a_{1} \\mid 3 a_{2}+\\delta_{2}$, and therefore $a_{2} \\geq 223$. Using (1), we obtain that $a_{n} \\geq 223$ for all $n \\geq 0$.\n\nLemma 1: For $n \\geq 4$, we have $a_{n+2}=(n+1)(n+4) a_{n}$.\nProof. For $n \\geq 3$ we have\n\n$$\na_{n}=n a_{n-1}+(n-1) a_{n-2}+\\delta_{n-1}>n a_{n-1}+3 .\n$$\n\nBy applying (2) with $n$ substituted by $n-1$ we have for $n \\geq 4$,\n\n$$\na_{n}=n a_{n-1}+(n-1) a_{n-2}+\\delta_{n-1}<n a_{n-1}+\\left(a_{n-1}-3\\right)+\\delta_{n-1}<(n+1) a_{n-1}\n$$\n\nUsing (1) to write $a_{n+2}$ in terms of $a_{n}$ and $a_{n-1}$ along with (2), we obtain that for $n \\geq 3$,\n\n$$\n\\begin{aligned}\na_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \\delta_{n}+\\delta_{n+1} \\\\\n& <(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+3(n+2) \\\\\n& <\\left(n^{2}+5 n+5\\right) a_{n} .\n\\end{aligned}\n$$\n\nAlso for $n \\geq 4$,\n\n$$\n\\begin{aligned}\na_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \\delta_{n}+\\delta_{n+1} \\\\\n& >(n+3)(n+1) a_{n}+n a_{n} \\\\\n& =\\left(n^{2}+5 n+3\\right) a_{n} .\n\\end{aligned}\n$$\n\nSince $a_{n} \\mid a_{n+2}$, we obtain that $a_{n+2}=\\left(n^{2}+5 n+4\\right) a_{n}=(n+1)(n+4) a_{n}$, as desired.\nLemma 2: For $n \\geq 4$, we have $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$.\nProof. Using the recurrence $a_{n+3}=(n+3) a_{n+2}+(n+2) a_{n+1}+\\delta_{n+2}$ and writing $a_{n+3}$, $a_{n+2}$ in terms of $a_{n+1}, a_{n}$ according to Lemma 1 we obtain\n\n$$\n(n+2)(n+4) a_{n+1}=(n+3)(n+1)(n+4) a_{n}+\\delta_{n+2} .\n$$\n\nHence $n+4 \\mid \\delta_{n+2}$, which yields $\\delta_{n+2}=0$ and $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$, as desired.\nSuppose there exists $n \\geq 1$ such that $a_{n+1} \\neq \\frac{(n+1)(n+3)}{n+2} a_{n}$. By Lemma 2, there exist a greatest integer $1 \\leq m \\leq 3$ with this property. Then $a_{m+2}=\\frac{(m+2)(m+4)}{m+3} a_{m+1}$. If $\\delta_{m+1}=0$, we have $a_{m+1}=\\frac{(m+1)(m+3)}{m+2} a_{m}$, which contradicts our choice of $m$. Thus $\\delta_{m+1} \\neq 0$.\n\nClearly $m+3 \\mid a_{m+1}$. Write $a_{m+1}=(m+3) k$ and $a_{m+2}=(m+2)(m+4) k$. Then $(m+$ 1) $a_{m}+\\delta_{m+1}=a_{m+2}-(m+2) a_{m+1}=(m+2) k$. So, $a_{m} \\mid(m+2) k-\\delta_{m+1}$. But $a_{m}$ also divides $a_{m+2}=(m+2)(m+4) k$. Combining the two divisibility conditions, we obtain $a_{m} \\mid(m+4) \\delta_{m+1}$. Since $\\delta_{m+1} \\neq 0$, we have $a_{m} \\mid 2 m+8 \\leq 14$, which contradicts the previous result that $a_{n} \\geq 223$ for all nonnegative integers $n$.\n\nSo, $a_{n+1}=\\frac{(n+1)(n+3)}{n+2} a_{n}$ for $n \\geq 1$. Substituting $n=1$ yields $3 \\mid a_{1}$. Letting $a_{1}=3 c$, we have by induction that $a_{n}=n!(n+2) c$ for $n \\geq 1$. Since $\\left|s_{2}-2 a_{1}\\right|=1$, we then get $a_{0}=c \\pm 1$, yielding the two families of solutions. By noting that $(n+2) n!=n!+(n+1)!$, we have $s_{n+1}=c(n+2)!+(-1)^{n}\\left(c-a_{0}\\right)$. Hence both families of solutions satisfy the given conditions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2016_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2016", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "We say that a triangle $A B C$ is great if the following holds: for any point $D$ on the side $B C$, if $P$ and $Q$ are the feet of the perpendiculars from $D$ to the lines $A B$ and $A C$, respectively, then the reflection of $D$ in the line $P Q$ lies on the circumcircle of the triangle $A B C$.\n\nProve that triangle $A B C$ is great if and only if $\\angle A=90^{\\circ}$ and $A B=A C$.", "solution": "For every point $D$ on the side $B C$, let $D^{\\prime}$ be the reflection of $D$ in the line $P Q$. We will first prove that if the triangle satisfies the condition then it is isosceles and right-angled at $A$.\n\nChoose $D$ to be the point where the angle bisector from $A$ meets $B C$. Note that $P$ and $Q$ lie on the rays $A B$ and $A C$ respectively. Furthermore, $P$ and $Q$ are reflections of each other in the line $A D$, from which it follows that $P Q \\perp A D$. Therefore, $D^{\\prime}$ lies on the line $A D$ and we may deduce that either $D^{\\prime}=A$ or $D^{\\prime}$ is the second point of the angle bisector at $A$ and the circumcircle of $A B C$. However, since $A P D Q$ is a cyclic quadrilateral, the segment $P Q$ intersects the segment $A D$. Therefore, $D^{\\prime}$ lies on the ray $D A$ and therefore $D^{\\prime}=A$. By angle chasing we obtain\n\n$$\n\\angle P D^{\\prime} Q=\\angle P D Q=180^{\\circ}-\\angle B A C\n$$\n\nand since $D^{\\prime}=A$ we also know $\\angle P D^{\\prime} Q=\\angle B A C$. This implies that $\\angle B A C=90^{\\circ}$.\nNow we choose $D$ to be the midpoint of $B C$. Since $\\angle B A C=90^{\\circ}$, we can deduce that $D Q P$ is the medial triangle of triangle $A B C$. Therefore, $P Q \\| B C$ from which it follows that $D D^{\\prime} \\perp B C$. But the distance from $D^{\\prime}$ to $B C$ is equal to both the circumradius of triangle $A B C$ and to the distance from $A$ to $B C$. This can only happen if $A=D^{\\prime}$. This implies that $A B C$ is isosceles and right-angled at $A$.\n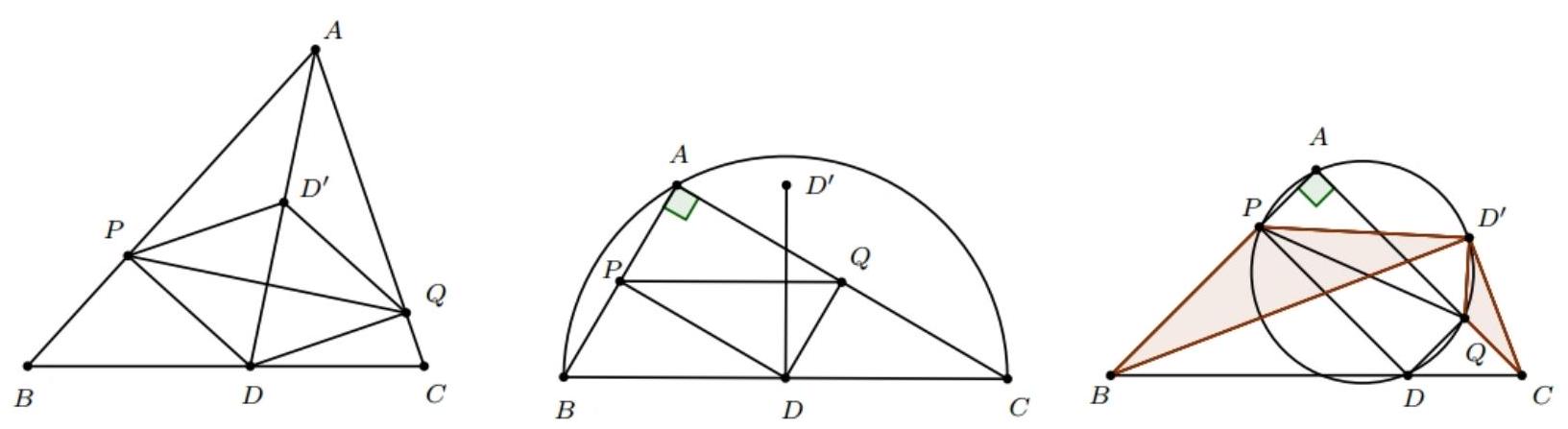\n\nWe will now prove that if $A B C$ is isosceles and right-angled at $A$ then the required property in the problem holds. Let $D$ be any point on side $B C$. Then $D^{\\prime} P=D P$ and we also have $D P=B P$. Hence, $D^{\\prime} P=B P$ and similarly $D^{\\prime} Q=C Q$. Note that $A P D Q D^{\\prime}$ is cyclic with diameter $P Q$. Therefore, $\\angle A P D^{\\prime}=\\angle A Q D^{\\prime}$, from which we obtain $\\angle B P D^{\\prime}=\\angle C Q D^{\\prime}$. So triangles $D^{\\prime} P B$ and $D^{\\prime} Q C$ are similar. It follows that $\\angle P D^{\\prime} Q=\\angle P D^{\\prime} C+\\angle C D^{\\prime} Q=$ $\\angle P D^{\\prime} C+\\angle B D^{\\prime} P=\\angle B D^{\\prime} C$ and $\\frac{D^{\\prime} P}{D^{\\prime} Q}=\\frac{D^{\\prime} B}{D^{\\prime} C}$. So we also obtain that triangles $D^{\\prime} P Q$ and $D^{\\prime} B C$ are similar. But since $D P Q$ and $D^{\\prime} P Q$ are congruent, we may deduce that $\\angle B D^{\\prime} C=$ $\\angle P D^{\\prime} Q=\\angle P D Q=90^{\\circ}$. Therefore, $D^{\\prime}$ lies on the circle with diameter $B C$, which is the circumcircle of triangle $A B C$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2016", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "A positive integer is called fancy if it can be expressed in the form\n\n$$\n2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{100}}\n$$\n\nwhere $a_{1}, a_{2}, \\ldots, a_{100}$ are non-negative integers that are not necessarily distinct.\nFind the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.\nAnswer: The answer is $n=2^{101}-1$.", "solution": "Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \\ldots, a_{r}$ such that $r \\leq 100$ and $k=2^{a_{1}}+\\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:\n\n$$\n\\begin{aligned}\n2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\\cdots+2^{a_{r-1}+s}+\\left(1+1+2+\\cdots+2^{s-1}\\right) 2^{a_{r}} \\\\\n& =2^{a_{1}+s}+2^{a_{2}+s}+\\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\\cdots+2^{a_{r}+s-1} .\n\\end{aligned}\n$$\n\nThis shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \\geq 0$, which shows that $k$ has a multiple that is a fancy number.\n\nWe will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .\n\nFor the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that\n\n$$\nc n=2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{r}}\n$$\n\nwhere $r \\leq 100$ and $a_{1}<a_{2}<\\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:\n\n- If $a_{r} \\geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.\n- If $a_{r} \\leq 100$, then $\\left\\{a_{1}, \\ldots, a_{r}\\right\\}$ is a proper subset of $\\{0,1, \\ldots, 100\\}$. Then\n\n$$\nn \\leq c n<2^{0}+2^{1}+\\cdots+2^{100}=n\n$$\n\nThis is also a contradiction.\nFrom these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "We present two approaches. The first one introduces an auxiliary point and studies similarities in the figure. The second one reduces the problem to computations involving a particular exradius of a triangle. The second approach has two variants.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": ".\n\n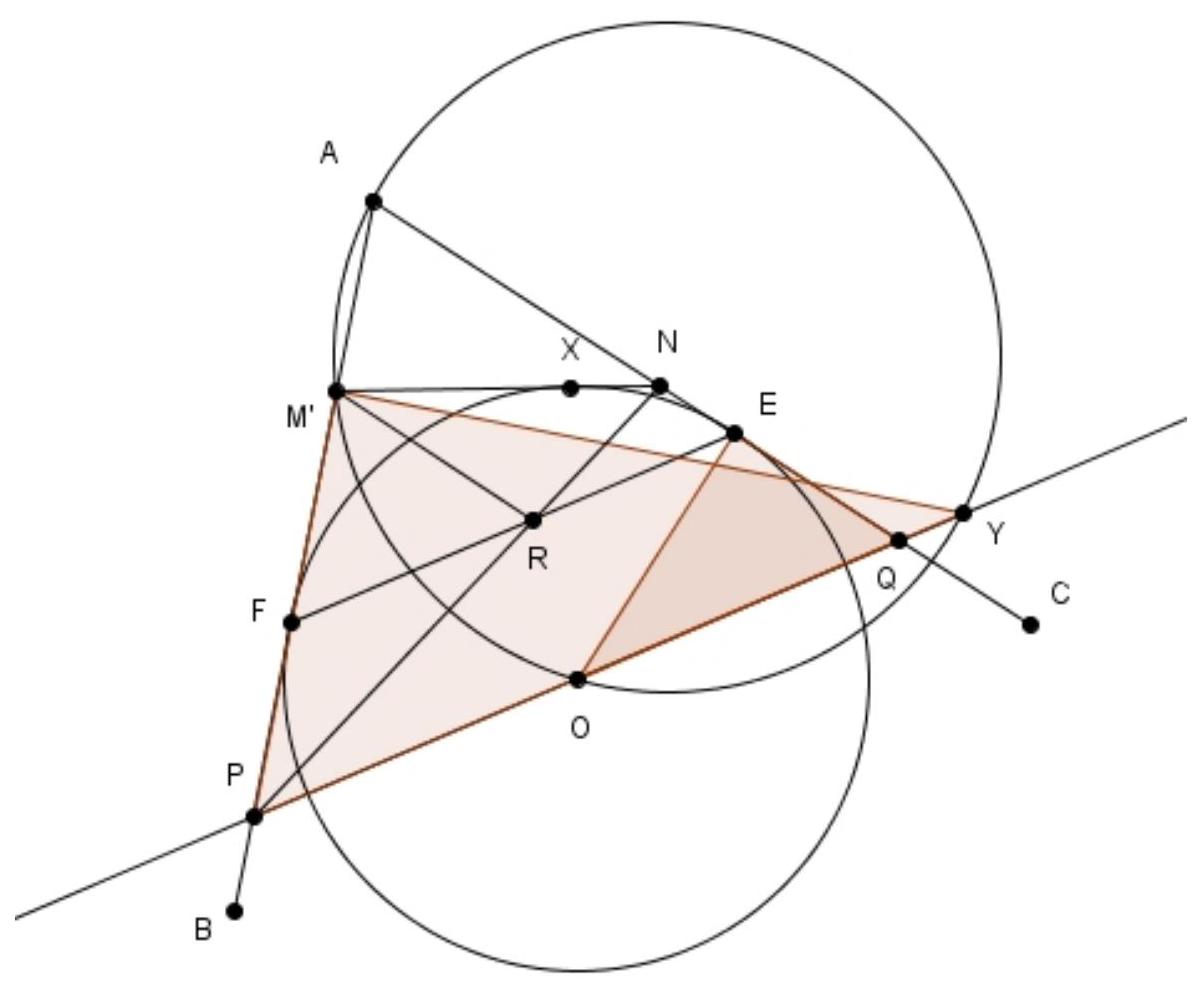\n\nLet the line through $N$ tangent to $\\omega$ at point $X \\neq E$ intersect $A B$ at point $M^{\\prime}$. It suffices to show that $M^{\\prime} R \\| A C$, since this would yield $M^{\\prime}=M$.\n\nSuppose that the line $P O$ intersects $A C$ at $Q$ and the circumcircle of $A M^{\\prime} O$ at $Y$, respectively. Then\n\n$$\n\\angle A Y M^{\\prime}=\\angle A O M^{\\prime}=90^{\\circ}-\\angle M^{\\prime} O P\n$$\n\nBy angle chasing we have $\\angle E O Q=\\angle F O P=90^{\\circ}-\\angle A O F=\\angle M^{\\prime} A O=\\angle M^{\\prime} Y P$ and by symmetry $\\angle E Q O=\\angle M^{\\prime} P Y$. Therefore $\\triangle M^{\\prime} Y P \\sim \\triangle E O Q$.\n\nOn the other hand, we have\n\n$$\n\\begin{aligned}\n\\angle M^{\\prime} O P & =\\angle M^{\\prime} O F+\\angle F O P=\\frac{1}{2}(\\angle F O X+\\angle F O P+\\angle E O Q)= \\\\\n& =\\frac{1}{2}\\left(\\frac{180^{\\circ}-\\angle X O E}{2}\\right)=90^{\\circ}-\\frac{\\angle X O E}{2} .\n\\end{aligned}\n$$\n\nSince we know that $\\angle A Y M^{\\prime}$ and $\\angle M^{\\prime} O P$ are complementary this implies\n\n$$\n\\angle A Y M^{\\prime}=\\frac{\\angle X O E}{2}=\\angle N O E\n$$\n\nTherefore, $\\angle A Y M^{\\prime}$ and $\\angle N O E$ are congruent angles, and this means that $A$ and $N$ are corresponding points in the similarity of triangles $\\triangle M^{\\prime} Y P$ and $\\triangle E O Q$. It follows that\n\n$$\n\\frac{A M^{\\prime}}{M^{\\prime} P}=\\frac{N E}{E Q}=\\frac{N R}{R P}\n$$\n\nWe conclude that $M^{\\prime} R \\| A C$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 1"}}
|
| 5 |
-
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "a.\n\nAs in Solution 1, we introduce point $M^{\\prime}$ and reduce the problem to proving $\\frac{P R}{R N}=\\frac{P M^{\\prime}}{M^{\\prime} A}$. Menelaus theorem in triangle $A N P$ with transversal line $F R E$ yields\n\n$$\n\\frac{P R}{R N} \\cdot \\frac{N E}{E A} \\cdot \\frac{A F}{F P}=1\n$$\n\nSince $A F=E A$, we have $\\frac{F P}{N E}=\\frac{P R}{R N}$, so that it suffices to prove\n\n$$\n\\frac{F P}{N E}=\\frac{P M^{\\prime}}{M^{\\prime} A}\n$$\n\nThis is a computation regarding the triangle $A M^{\\prime} N$ and its excircle opposite $A$. Indeed, setting $a=M^{\\prime} N, b=N A, c=M^{\\prime} A, s=\\frac{a+b+c}{2}, x=s-a, y=s-b$ and $z=s-c$, then $A E=A F=s, M^{\\prime} F=z$ and $N E=y$. From $\\triangle O F P \\sim \\triangle A F O$ we have $F P=\\frac{r_{a}^{2}}{s}$, where $r_{a}=O F$ is the exradius opposite $A$. Combining the following two standard formulas for the area of a triangle\n\n$$\n\\left|A M^{\\prime} N\\right|^{2}=x y z s \\quad \\text { (Heron's formula) and } \\quad\\left|A M^{\\prime} N\\right|=r_{a}(s-a),\n$$\n\nwe have $r_{a}^{2}=\\frac{y z s}{x}$. Therefore, $F P=\\frac{y z}{x}$. We can now write everything in (1) in terms of $x, y, z$. We conclude that we have to verify\n\n$$\n\\frac{\\frac{y z}{x}}{y}=\\frac{z+\\frac{y z}{x}}{x+y}\n$$\n\nwhich is easily seen to be true.\nNote: Antoher approach using Menalaus theorem is to construct the tangent from $M$ to create a point $N^{\\prime}$ in $A C$ and then prove, using the theorem, that $P, R$ and $N^{\\prime}$ are collinear. This also reduces to an algebraic identity.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 6 |
-
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "b.\n\nAs in Solution 1, we introduce point $M^{\\prime}$. Let the line through $M^{\\prime}$ and parallel to $A N$ intersect $E F$ at $R^{\\prime}$. Let $P^{\\prime}$ be the intersection of lines $N R^{\\prime}$ and $A M$. It suffices to show that $P^{\\prime} O \\| F E$, since this would yield $P=P^{\\prime}$, and then $R=R^{\\prime}$ and $M=M^{\\prime}$. Hence it is enough to prove that\n\n$$\n\\frac{A F}{F P^{\\prime}}=\\frac{A D}{D O}\n$$\n\nwhere $D$ is the intersection of $A O$ and $E F$. Once again, this reduces to a computation regarding the triangle $A M^{\\prime} N$ and its excircle opposite $A$.\n\nLet $u=P^{\\prime} F$ and $x, y, z, s$ as in Solution 2a. Note that since $A E=A F$ and $M^{\\prime} R^{\\prime} \\| A E$, we have $M^{\\prime} R^{\\prime}=M^{\\prime} F=z$. Since $M^{\\prime} R^{\\prime} \\| A N$, we have $\\frac{P^{\\prime} M^{\\prime}}{P^{\\prime} A}=\\frac{M^{\\prime} R^{\\prime}}{N A}$, that is,\n\n$$\n\\frac{u+z}{u+x+y+z}=\\frac{z}{x+z}\n$$\n\nFrom this last equation we obtain $u=\\frac{y z}{x}$. Hence $\\frac{A F}{F P^{\\prime}}=\\frac{x s}{y z}$. Also, as in Solution 2a, we have $r_{a}^{2}=\\frac{y z s}{x}$.\n\nFinally, using similar triangles $O D F, F D A$ and $O F A$, and the above equalities, we have\n\n$$\n\\frac{A D}{D O}=\\frac{A D}{D F} \\cdot \\frac{D F}{D O}=\\frac{A F}{O F} \\cdot \\frac{A F}{O F}=\\frac{s^{2}}{r_{a}^{2}}=\\frac{s^{2}}{\\frac{y z s}{x}}=\\frac{x s}{y z}=\\frac{A F}{F P^{\\prime}}\n$$\n\nas required.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "2016", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.\n\n## Answer: 57", "solution": "The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.\n\nWe first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.\n\nWe will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.\n\nLemma: Suppose we have a directed graph on $n \\geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.\n\nProof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 8 |
-
{"year": "2016", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Find all functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$such that\n\n$$\n(z+1) f(x+y)=f(x f(z)+y)+f(y f(z)+x)\n$$\n\nfor all positive real numbers $x, y, z$.\nAnswer: The only solution is $f(x)=x$ for all positive real numbers $x$.", "solution": "The identity function $f(x)=x$ clearly satisfies the functional equation. Now, let $f$ be a function satisfying the functional equation. Plugging $x=y=1$ into (3) we get $2 f(f(z)+1)=(z+1)(f(2))$ for all $z \\in \\mathbb{R}^{+}$. Hence, $f$ is not bounded above.\n\nLemma. Let $a, b, c$ be positive real numbers. If $c$ is greater than $1, a / b$ and $b / a$, then the system of linear equations\n\n$$\nc u+v=a \\quad u+c v=b\n$$\n\nhas a positive real solution $u, v$.\nProof. The solution is\n\n$$\nu=\\frac{c a-b}{c^{2}-1} \\quad v=\\frac{c b-a}{c^{2}-1} .\n$$\n\nThe numbers $u$ and $v$ are positive if the conditions on $c$ above are satisfied.\n\nWe will now prove that\n\n$$\nf(a)+f(b)=f(c)+f(d) \\quad \\text { for all } a, b, c, d \\in \\mathbb{R}^{+} \\text {with } a+b=c+d\n$$\n\nConsider $a, b, c, d \\in \\mathbb{R}^{+}$such that $a+b=c+d$. Since $f$ is not bounded above, we can choose a positive number $e$ such that $f(e)$ is greater than $1, a / b, b / a, c / d$ and $d / c$. Using the above lemma, we can find $u, v, w, t \\in \\mathbb{R}^{+}$satisfying\n\n$$\n\\begin{array}{ll}\nf(e) u+v=a, & u+f(e) v=b \\\\\nf(e) w+t=c, & w+f(e) t=d .\n\\end{array}\n$$\n\nNote that $u+v=w+t$ since $(u+v)(f(e)+1)=a+b$ and $(w+t)(f(e)+1)=c+d$. Plugging $x=u, y=v$ and $z=e$ into (3) yields $f(a)+f(b)=(e+1) f(u+v)$. Similarly, we have $f(c)+f(d)=(e+1) f(w+t)$. The claim follows immediately.\n\nWe then have\n\n$$\ny f(x)=f(x f(y)) \\quad \\text { for all } x, y \\in \\mathbb{R}^{+}\n$$\n\nsince by (3) and (4),\n\n$$\n(y+1) f(x)=f\\left(\\frac{x}{2} f(y)+\\frac{x}{2}\\right)+f\\left(\\frac{x}{2} f(y)+\\frac{x}{2}\\right)=f(x f(y))+f(x) .\n$$\n\nNow, let $a=f(1 / f(1))$. Plugging $x=1$ and $y=1 / f(1)$ into (5) yields $f(a)=1$. Hence $a=a f(a)$ and $f(a f(a))=f(a)=1$. Since $a f(a)=f(a f(a))$ by (5), we have $f(1)=a=1$. It follows from (5) that\n\n$$\nf(f(y))=y \\quad \\text { for all } y \\in \\mathbb{R}^{+} .\n$$\n\nUsing (4) we have for all $x, y \\in \\mathbb{R}^{+}$that\n\n$$\n\\begin{aligned}\n& f(x+y)+f(1)=f(x)+f(y+1), \\quad \\text { and } \\\\\n& f(y+1)+f(1)=f(y)+f(2)\n\\end{aligned}\n$$\n\nTherefore\n\n$$\nf(x+y)=f(x)+f(y)+b \\quad \\text { for all } x, y \\in \\mathbb{R}^{+},\n$$\n\nwhere $b=f(2)-2 f(1)=f(2)-2$. Using (5), (7) and (6), we get\n\n$$\n4+2 b=2 f(2)=f(2 f(2))=f(f(2)+f(2))=f(f(2))+f(f(2))+b=4+b\n$$\n\nThis shows that $b=0$ and thus\n\n$$\nf(x+y)=f(x)+f(y) \\quad \\text { for all } x, y \\in \\mathbb{R}^{+} .\n$$\n\nIn particular, $f$ is strictly increasing.\nWe conclude as follows. Take any positive real number $x$. If $f(x)>x$, then $f(f(x))>$ $f(x)>x=f(f(x))$, a contradiction. Similarly, it is not possible that $f(x)<x$. This shows that $f(x)=x$ for all positive real numbers $x$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2016", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "We say that a triangle $A B C$ is great if the following holds: for any point $D$ on the side $B C$, if $P$ and $Q$ are the feet of the perpendiculars from $D$ to the lines $A B$ and $A C$, respectively, then the reflection of $D$ in the line $P Q$ lies on the circumcircle of the triangle $A B C$.\n\nProve that triangle $A B C$ is great if and only if $\\angle A=90^{\\circ}$ and $A B=A C$.", "solution": "For every point $D$ on the side $B C$, let $D^{\\prime}$ be the reflection of $D$ in the line $P Q$. We will first prove that if the triangle satisfies the condition then it is isosceles and right-angled at $A$.\n\nChoose $D$ to be the point where the angle bisector from $A$ meets $B C$. Note that $P$ and $Q$ lie on the rays $A B$ and $A C$ respectively. Furthermore, $P$ and $Q$ are reflections of each other in the line $A D$, from which it follows that $P Q \\perp A D$. Therefore, $D^{\\prime}$ lies on the line $A D$ and we may deduce that either $D^{\\prime}=A$ or $D^{\\prime}$ is the second point of the angle bisector at $A$ and the circumcircle of $A B C$. However, since $A P D Q$ is a cyclic quadrilateral, the segment $P Q$ intersects the segment $A D$. Therefore, $D^{\\prime}$ lies on the ray $D A$ and therefore $D^{\\prime}=A$. By angle chasing we obtain\n\n$$\n\\angle P D^{\\prime} Q=\\angle P D Q=180^{\\circ}-\\angle B A C\n$$\n\nand since $D^{\\prime}=A$ we also know $\\angle P D^{\\prime} Q=\\angle B A C$. This implies that $\\angle B A C=90^{\\circ}$.\nNow we choose $D$ to be the midpoint of $B C$. Since $\\angle B A C=90^{\\circ}$, we can deduce that $D Q P$ is the medial triangle of triangle $A B C$. Therefore, $P Q \\| B C$ from which it follows that $D D^{\\prime} \\perp B C$. But the distance from $D^{\\prime}$ to $B C$ is equal to both the circumradius of triangle $A B C$ and to the distance from $A$ to $B C$. This can only happen if $A=D^{\\prime}$. This implies that $A B C$ is isosceles and right-angled at $A$.\n\n\nWe will now prove that if $A B C$ is isosceles and right-angled at $A$ then the required property in the problem holds. Let $D$ be any point on side $B C$. Then $D^{\\prime} P=D P$ and we also have $D P=B P$. Hence, $D^{\\prime} P=B P$ and similarly $D^{\\prime} Q=C Q$. Note that $A P D Q D^{\\prime}$ is cyclic with diameter $P Q$. Therefore, $\\angle A P D^{\\prime}=\\angle A Q D^{\\prime}$, from which we obtain $\\angle B P D^{\\prime}=\\angle C Q D^{\\prime}$. So triangles $D^{\\prime} P B$ and $D^{\\prime} Q C$ are similar. It follows that $\\angle P D^{\\prime} Q=\\angle P D^{\\prime} C+\\angle C D^{\\prime} Q=$ $\\angle P D^{\\prime} C+\\angle B D^{\\prime} P=\\angle B D^{\\prime} C$ and $\\frac{D^{\\prime} P}{D^{\\prime} Q}=\\frac{D^{\\prime} B}{D^{\\prime} C}$. So we also obtain that triangles $D^{\\prime} P Q$ and $D^{\\prime} B C$ are similar. But since $D P Q$ and $D^{\\prime} P Q$ are congruent, we may deduce that $\\angle B D^{\\prime} C=$ $\\angle P D^{\\prime} Q=\\angle P D Q=90^{\\circ}$. Therefore, $D^{\\prime}$ lies on the circle with diameter $B C$, which is the circumcircle of triangle $A B C$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2016", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "A positive integer is called fancy if it can be expressed in the form\n\n$$\n2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{100}}\n$$\n\nwhere $a_{1}, a_{2}, \\ldots, a_{100}$ are non-negative integers that are not necessarily distinct.\nFind the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.\nAnswer: The answer is $n=2^{101}-1$.", "solution": "Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \\ldots, a_{r}$ such that $r \\leq 100$ and $k=2^{a_{1}}+\\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:\n\n$$\n\\begin{aligned}\n2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\\cdots+2^{a_{r-1}+s}+\\left(1+1+2+\\cdots+2^{s-1}\\right) 2^{a_{r}} \\\\\n& =2^{a_{1}+s}+2^{a_{2}+s}+\\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\\cdots+2^{a_{r}+s-1} .\n\\end{aligned}\n$$\n\nThis shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \\geq 0$, which shows that $k$ has a multiple that is a fancy number.\n\nWe will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .\n\nFor the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that\n\n$$\nc n=2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{r}}\n$$\n\nwhere $r \\leq 100$ and $a_{1}<a_{2}<\\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:\n\n- If $a_{r} \\geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.\n- If $a_{r} \\leq 100$, then $\\left\\{a_{1}, \\ldots, a_{r}\\right\\}$ is a proper subset of $\\{0,1, \\ldots, 100\\}$. Then\n\n$$\nn \\leq c n<2^{0}+2^{1}+\\cdots+2^{100}=n\n$$\n\nThis is also a contradiction.\nFrom these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "We present two approaches. The first one introduces an auxiliary point and studies similarities in the figure. The second one reduces the problem to computations involving a particular exradius of a triangle. The second approach has two variants.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": ".\n\n\n\nLet the line through $N$ tangent to $\\omega$ at point $X \\neq E$ intersect $A B$ at point $M^{\\prime}$. It suffices to show that $M^{\\prime} R \\| A C$, since this would yield $M^{\\prime}=M$.\n\nSuppose that the line $P O$ intersects $A C$ at $Q$ and the circumcircle of $A M^{\\prime} O$ at $Y$, respectively. Then\n\n$$\n\\angle A Y M^{\\prime}=\\angle A O M^{\\prime}=90^{\\circ}-\\angle M^{\\prime} O P\n$$\n\nBy angle chasing we have $\\angle E O Q=\\angle F O P=90^{\\circ}-\\angle A O F=\\angle M^{\\prime} A O=\\angle M^{\\prime} Y P$ and by symmetry $\\angle E Q O=\\angle M^{\\prime} P Y$. Therefore $\\triangle M^{\\prime} Y P \\sim \\triangle E O Q$.\n\nOn the other hand, we have\n\n$$\n\\begin{aligned}\n\\angle M^{\\prime} O P & =\\angle M^{\\prime} O F+\\angle F O P=\\frac{1}{2}(\\angle F O X+\\angle F O P+\\angle E O Q)= \\\\\n& =\\frac{1}{2}\\left(\\frac{180^{\\circ}-\\angle X O E}{2}\\right)=90^{\\circ}-\\frac{\\angle X O E}{2} .\n\\end{aligned}\n$$\n\nSince we know that $\\angle A Y M^{\\prime}$ and $\\angle M^{\\prime} O P$ are complementary this implies\n\n$$\n\\angle A Y M^{\\prime}=\\frac{\\angle X O E}{2}=\\angle N O E\n$$\n\nTherefore, $\\angle A Y M^{\\prime}$ and $\\angle N O E$ are congruent angles, and this means that $A$ and $N$ are corresponding points in the similarity of triangles $\\triangle M^{\\prime} Y P$ and $\\triangle E O Q$. It follows that\n\n$$\n\\frac{A M^{\\prime}}{M^{\\prime} P}=\\frac{N E}{E Q}=\\frac{N R}{R P}\n$$\n\nWe conclude that $M^{\\prime} R \\| A C$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 1"}}
|
| 5 |
+
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "a.\n\nAs in Solution 1, we introduce point $M^{\\prime}$ and reduce the problem to proving $\\frac{P R}{R N}=\\frac{P M^{\\prime}}{M^{\\prime} A}$. Menelaus theorem in triangle $A N P$ with transversal line $F R E$ yields\n\n$$\n\\frac{P R}{R N} \\cdot \\frac{N E}{E A} \\cdot \\frac{A F}{F P}=1\n$$\n\nSince $A F=E A$, we have $\\frac{F P}{N E}=\\frac{P R}{R N}$, so that it suffices to prove\n\n$$\n\\frac{F P}{N E}=\\frac{P M^{\\prime}}{M^{\\prime} A}\n$$\n\nThis is a computation regarding the triangle $A M^{\\prime} N$ and its excircle opposite $A$. Indeed, setting $a=M^{\\prime} N, b=N A, c=M^{\\prime} A, s=\\frac{a+b+c}{2}, x=s-a, y=s-b$ and $z=s-c$, then $A E=A F=s, M^{\\prime} F=z$ and $N E=y$. From $\\triangle O F P \\sim \\triangle A F O$ we have $F P=\\frac{r_{a}^{2}}{s}$, where $r_{a}=O F$ is the exradius opposite $A$. Combining the following two standard formulas for the area of a triangle\n\n$$\n\\left|A M^{\\prime} N\\right|^{2}=x y z s \\quad \\text { (Heron's formula) and } \\quad\\left|A M^{\\prime} N\\right|=r_{a}(s-a),\n$$\n\nwe have $r_{a}^{2}=\\frac{y z s}{x}$. Therefore, $F P=\\frac{y z}{x}$. We can now write everything in (1) in terms of $x, y, z$. We conclude that we have to verify\n\n$$\n\\frac{\\frac{y z}{x}}{y}=\\frac{z+\\frac{y z}{x}}{x+y}\n$$\n\nwhich is easily seen to be true.\nNote: Antoher approach using Menalaus theorem is to construct the tangent from $M$ to create a point $N^{\\prime}$ in $A C$ and then prove, using the theorem, that $P, R$ and $N^{\\prime}$ are collinear. This also reduces to an algebraic identity.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 6 |
+
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\\omega$.", "solution": "b.\n\nAs in Solution 1, we introduce point $M^{\\prime}$. Let the line through $M^{\\prime}$ and parallel to $A N$ intersect $E F$ at $R^{\\prime}$. Let $P^{\\prime}$ be the intersection of lines $N R^{\\prime}$ and $A M$. It suffices to show that $P^{\\prime} O \\| F E$, since this would yield $P=P^{\\prime}$, and then $R=R^{\\prime}$ and $M=M^{\\prime}$. Hence it is enough to prove that\n\n$$\n\\frac{A F}{F P^{\\prime}}=\\frac{A D}{D O}\n$$\n\nwhere $D$ is the intersection of $A O$ and $E F$. Once again, this reduces to a computation regarding the triangle $A M^{\\prime} N$ and its excircle opposite $A$.\n\nLet $u=P^{\\prime} F$ and $x, y, z, s$ as in Solution 2a. Note that since $A E=A F$ and $M^{\\prime} R^{\\prime} \\| A E$, we have $M^{\\prime} R^{\\prime}=M^{\\prime} F=z$. Since $M^{\\prime} R^{\\prime} \\| A N$, we have $\\frac{P^{\\prime} M^{\\prime}}{P^{\\prime} A}=\\frac{M^{\\prime} R^{\\prime}}{N A}$, that is,\n\n$$\n\\frac{u+z}{u+x+y+z}=\\frac{z}{x+z}\n$$\n\nFrom this last equation we obtain $u=\\frac{y z}{x}$. Hence $\\frac{A F}{F P^{\\prime}}=\\frac{x s}{y z}$. Also, as in Solution 2a, we have $r_{a}^{2}=\\frac{y z s}{x}$.\n\nFinally, using similar triangles $O D F, F D A$ and $O F A$, and the above equalities, we have\n\n$$\n\\frac{A D}{D O}=\\frac{A D}{D F} \\cdot \\frac{D F}{D O}=\\frac{A F}{O F} \\cdot \\frac{A F}{O F}=\\frac{s^{2}}{r_{a}^{2}}=\\frac{s^{2}}{\\frac{y z s}{x}}=\\frac{x s}{y z}=\\frac{A F}{F P^{\\prime}}\n$$\n\nas required.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "2016", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.\n\n## Answer: 57", "solution": "The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.\n\nWe first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.\n\nWe will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.\n\nLemma: Suppose we have a directed graph on $n \\geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.\n\nProof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 8 |
+
{"year": "2016", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Find all functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$such that\n\n$$\n(z+1) f(x+y)=f(x f(z)+y)+f(y f(z)+x)\n$$\n\nfor all positive real numbers $x, y, z$.\nAnswer: The only solution is $f(x)=x$ for all positive real numbers $x$.", "solution": "The identity function $f(x)=x$ clearly satisfies the functional equation. Now, let $f$ be a function satisfying the functional equation. Plugging $x=y=1$ into (3) we get $2 f(f(z)+1)=(z+1)(f(2))$ for all $z \\in \\mathbb{R}^{+}$. Hence, $f$ is not bounded above.\n\nLemma. Let $a, b, c$ be positive real numbers. If $c$ is greater than $1, a / b$ and $b / a$, then the system of linear equations\n\n$$\nc u+v=a \\quad u+c v=b\n$$\n\nhas a positive real solution $u, v$.\nProof. The solution is\n\n$$\nu=\\frac{c a-b}{c^{2}-1} \\quad v=\\frac{c b-a}{c^{2}-1} .\n$$\n\nThe numbers $u$ and $v$ are positive if the conditions on $c$ above are satisfied.\n\nWe will now prove that\n\n$$\nf(a)+f(b)=f(c)+f(d) \\quad \\text { for all } a, b, c, d \\in \\mathbb{R}^{+} \\text {with } a+b=c+d\n$$\n\nConsider $a, b, c, d \\in \\mathbb{R}^{+}$such that $a+b=c+d$. Since $f$ is not bounded above, we can choose a positive number $e$ such that $f(e)$ is greater than $1, a / b, b / a, c / d$ and $d / c$. Using the above lemma, we can find $u, v, w, t \\in \\mathbb{R}^{+}$satisfying\n\n$$\n\\begin{array}{ll}\nf(e) u+v=a, & u+f(e) v=b \\\\\nf(e) w+t=c, & w+f(e) t=d .\n\\end{array}\n$$\n\nNote that $u+v=w+t$ since $(u+v)(f(e)+1)=a+b$ and $(w+t)(f(e)+1)=c+d$. Plugging $x=u, y=v$ and $z=e$ into (3) yields $f(a)+f(b)=(e+1) f(u+v)$. Similarly, we have $f(c)+f(d)=(e+1) f(w+t)$. The claim follows immediately.\n\nWe then have\n\n$$\ny f(x)=f(x f(y)) \\quad \\text { for all } x, y \\in \\mathbb{R}^{+}\n$$\n\nsince by (3) and (4),\n\n$$\n(y+1) f(x)=f\\left(\\frac{x}{2} f(y)+\\frac{x}{2}\\right)+f\\left(\\frac{x}{2} f(y)+\\frac{x}{2}\\right)=f(x f(y))+f(x) .\n$$\n\nNow, let $a=f(1 / f(1))$. Plugging $x=1$ and $y=1 / f(1)$ into (5) yields $f(a)=1$. Hence $a=a f(a)$ and $f(a f(a))=f(a)=1$. Since $a f(a)=f(a f(a))$ by (5), we have $f(1)=a=1$. It follows from (5) that\n\n$$\nf(f(y))=y \\quad \\text { for all } y \\in \\mathbb{R}^{+} .\n$$\n\nUsing (4) we have for all $x, y \\in \\mathbb{R}^{+}$that\n\n$$\n\\begin{aligned}\n& f(x+y)+f(1)=f(x)+f(y+1), \\quad \\text { and } \\\\\n& f(y+1)+f(1)=f(y)+f(2)\n\\end{aligned}\n$$\n\nTherefore\n\n$$\nf(x+y)=f(x)+f(y)+b \\quad \\text { for all } x, y \\in \\mathbb{R}^{+},\n$$\n\nwhere $b=f(2)-2 f(1)=f(2)-2$. Using (5), (7) and (6), we get\n\n$$\n4+2 b=2 f(2)=f(2 f(2))=f(f(2)+f(2))=f(f(2))+f(f(2))+b=4+b\n$$\n\nThis shows that $b=0$ and thus\n\n$$\nf(x+y)=f(x)+f(y) \\quad \\text { for all } x, y \\in \\mathbb{R}^{+} .\n$$\n\nIn particular, $f$ is strictly increasing.\nWe conclude as follows. Take any positive real number $x$. If $f(x)>x$, then $f(f(x))>$ $f(x)>x=f(f(x))$, a contradiction. Similarly, it is not possible that $f(x)<x$. This shows that $f(x)=x$ for all positive real numbers $x$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2017_sol.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "2017", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "We call a 5-tuple of integers arrangeable if its elements can be labeled $a$, $b, c, d, e$ in some order so that $a-b+c-d+e=29$. Determine all 2017-tuples of integers $n_{1}, n_{2}, \\ldots, n_{2017}$ such that if we place them in a circle in clockwise order, then any 5 -tuple of numbers in consecutive positions on the circle is arrangeable.\n\nAnswer: $n_{1}=\\cdots=n_{2017}=29$.", "solution": "A valid 2017-tuple is $n_{1}=\\cdots=n_{2017}=29$. We will show that it is the only solution.\n\nWe first replace each number $n_{i}$ in the circle by $m_{i}:=n_{i}-29$. Since the condition $a-b+$ $c-d+e=29$ can be rewritten as $(a-29)-(b-29)+(c-29)-(d-29)+(e-29)=0$, we have that any five consecutive replaced integers in the circle can be labeled $a, b, c, d, e$ in such a way that $a-b+c-d+e=0$. We claim that this is possible only when all of the $m_{i}$ 's are 0 (and thus all of the original $n_{i}$ 's are 29).\n\nWe work with indexes modulo 2017. Notice that for every $i, m_{i}$ and $m_{i+5}$ have the same parity. Indeed, this follows from $m_{i} \\equiv m_{i+1}+m_{i+2}+m_{i+3}+m_{i+4} \\equiv m_{i+5}(\\bmod 2)$. Since $\\operatorname{gcd}(5,2017)=1$, this implies that all $m_{i}$ 's are of the same parity. Since $m_{1}+m_{2}+m_{3}+m_{4}+m_{5}$ is even, all $m_{i}$ 's must be even as well.\n\nSuppose for the sake of contradiction that not all $m_{i}$ 's are zero. Then our condition still holds when we divide each number in the circle by 2 . However, by performing repeated divisions, we eventually reach a point where some $m_{i}$ is odd. This is a contradiction.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". Let $N$ be the midpoint of $A C$. Let $M$ be the intersection point of the circumcircle of triangle $A D Z$ and the segment $A B$. We will show that $M$ is the midpoint of $A B$. To do this, let $D^{\\prime}$ the reflection of $D$ with respect to $M$. It suffices to show that $A D B D^{\\prime}$ is a parallelogram.\n\nThe internal and external bisectors of an angle in a triangle are perpendicular. This implies that $Z D$ is a diameter of the circumcircle of $A Z D$ and thus $\\angle Z M D=90^{\\circ}$. This means that $Z M$ is the perpendicular bisector of $D^{\\prime} D$ and thus $Z D^{\\prime}=Z D$. By construction, $Z$ is in the perpendicular bisector of $A C$ and thus $Z A=Z C$.\n\nNow, let $\\alpha$ be the angle $\\angle B A D=\\angle D A C$. In the cyclic quadrilateral $A Z D M$ we get $\\angle M Z D=\\angle M A D=\\alpha$, and thus $\\angle D^{\\prime} Z D=2 \\alpha$. By angle chasing we get\n\n$$\n\\angle A Z N=90^{\\circ}-\\angle Z A N=\\angle D A C=\\alpha,\n$$\n\nwhich implies that $\\angle A Z C=2 \\alpha$. Therefore,\n\n$$\n\\angle D^{\\prime} Z A=\\angle D^{\\prime} Z D-\\angle A Z D=2 \\alpha-\\angle A Z D=\\angle A Z C-\\angle A Z D=\\angle D Z C .\n$$\n\nCombining $\\angle D^{\\prime} Z A=\\angle D Z C, Z D^{\\prime}=Z D$ and $Z A=Z C$, we obtain by the $S A S$ criterion that the triangles $D^{\\prime} Z A$ and $D Z C$ are congruent. In particular, $D^{\\prime} A=D C$ and $\\angle D^{\\prime} A Z=$ $\\angle D C Z$. From here $D B=D C=D^{\\prime} A$.\n\nFinally, let $\\beta=\\angle A B C=\\angle A D C$. We get the first of the following equalities by the sum of angles around point $A$ and the second one by the sum of internal angles of quadrilateral $A Z C D$\n\n$$\n\\begin{aligned}\n& 360^{\\circ}=\\angle D^{\\prime} A Z+\\angle Z A D+\\angle D A B+\\angle B A D^{\\prime}=\\angle D^{\\prime} A Z+90^{\\circ}+\\alpha+\\angle B A D^{\\prime} \\\\\n& 360^{\\circ}=\\angle D C Z+\\angle Z A D+\\angle C Z A+\\angle A D C=\\angle D C Z+90^{\\circ}+2 \\alpha+\\beta\n\\end{aligned}\n$$\n\nBy canceling equal terms we conclude that $\\angle B A D^{\\prime}=\\alpha+\\beta$. Also, $\\angle A B D=\\alpha+\\beta$. Therefore, the segments $D^{\\prime} A$ and $D B$ are parallel and have the same length. We conclude that $A D B D^{\\prime}$ is a parallelogram. As the diagonals of a parallelogram intersect at their midpoints, we obtain that $M$ is the midpoint of $A B$ as desired.\n\n\nVariant of solution. The solution above is indirect in the sense that it assumes that $M$ is in the circumcircle of $A Z D$ and then shows that $M$ is the midpoint of $A B$. We point out that the same ideas in the solution can be used to give a direct solution. Here we present a sketch on how to proceed in this manner.\n\nNow we know that $M$ is the midpoint of the side $A B$. We construct the point $D^{\\prime}$ in the same way. Now we have directly that $A D B D^{\\prime}$ is a parallelogram and thus $D^{\\prime} A=D B=D C$. By construction $Z A=Z C$. Also, the two sums of angles equal to $360^{\\circ}$ in the previous solution let us conclude that $\\angle D^{\\prime} A Z=\\angle D C Z$. Once again, we use (differently) the $S A S$ criterion and obtain that the triangles $D^{\\prime} A Z$ and $D C Z$ are congruent. Thus, $D^{\\prime} Z=D Z$.\n\nWe finish the problem by noting that $Z M$ is a median of the isosceles triangle $D^{\\prime} Z D$, so it is also a perpendicular bisector. This shows that $\\angle D M Z=90^{\\circ}=\\angle D A Z$, and therefore $M$ lies in the circumcircle of $D A Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 3 |
-
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". We proceed directly. As above, we name\n\n$$\n\\alpha=\\angle D A C=\\angle A Z N=\\angle C Z N=\\angle D C B .\n$$\n\nLet $L$ be the midpoint of the segment $B C$. Since $M$ and $N$ are midpoints of $A B$ and $A C$, we have that $M N=C L$ and that the segment $M N$ is parallel to $B C$. Thus, $\\angle A N M=\\angle A C B$.\n\nTherefore, $\\angle Z N M=\\angle A C B+90^{\\circ}$. Also, $\\angle D C Z=\\angle D C B+\\angle A C B+\\angle Z C A=\\angle A C B+90^{\\circ}$. We conclude that $\\angle Z N M=\\angle D C Z$.\n\nNow, the triangles $Z N C$ and $C L D$ are similar since $\\angle D C L=90^{\\circ}=\\angle C N Z$ and $\\angle D C L=$ $\\alpha=\\angle C Z N$. We use this fact to obtain the following chain of equalities\n\n$$\n\\frac{C D}{M N}=\\frac{C D}{C L}=\\frac{C Z}{Z N}\n$$\n\nWe combine the equality above with $\\angle Z N M=\\angle D C Z$ to conclude that the triangles $Z N M$ and $Z C D$ are similar. In particular, $\\angle M Z N=\\angle D Z C$ and $\\frac{Z M}{Z N}=\\frac{Z D}{Z C}$. Since we also have $\\angle M Z D=\\angle M Z N+\\angle N Z D=\\angle D Z C+\\angle N Z D=\\angle N Z C$, we conclude that the triangles $M Z D$ and $N Z C$ are similar. This yields that $\\angle Z M D=90^{\\circ}$ and therefore $M$ is in the circumcircle of triangle $D A Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 4 |
-
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". Let $m$ be the perpendicular bisector of $A D$; thus $m$ passes through the center $O$ of the circumcircle of triangle $A B C$. Since $A D$ is the internal angle bisector of $A$ and $O M$ and $O N$ are perpendicular to $A B$ and $A C$ respectively, we obtain that $O M$ and $O N$ form equal angles with $A D$. This implies that they are symmetric with respect to $M$.\n\nTherefore, the line $M O$ passes through the point $Z^{\\prime}$ symmetrical to $Z$ with respect to $m$. Since $\\angle D A Z=90^{\\circ}$, then also $\\angle A D Z^{\\prime}=90^{\\circ}$. Moreover, since $A Z=D Z^{\\prime}$, we have that $\\angle A Z Z^{\\prime}=\\angle D Z^{\\prime} Z=90^{\\circ}$, so $A Z Z^{\\prime} D$ is a rectangle. Since $\\angle A M Z^{\\prime}=\\angle A M O=90^{\\circ}$, we conclude that $M$ is in the circle with diameter $A Z^{\\prime}$, which is the circumcircle of the rectangle. Thus $M$ lies on the circumcircle of the triangle $A D Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 3"}}
|
| 5 |
-
{"year": "2017", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A(n)$ denote the number of sequences $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of positive integers for which $a_{1}+\\cdots+a_{k}=n$ and each $a_{i}+1$ is a power of two $(i=1,2, \\ldots, k)$. Let $B(n)$ denote the number of sequences $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$ of positive integers for which $b_{1}+\\cdots+b_{m}=n$ and each inequality $b_{j} \\geq 2 b_{j+1}$ holds $(j=1,2, \\ldots, m-1)$.\n\nProve that $A(n)=B(n)$ for every positive integer $n$.", "solution": "We say that a sequence $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of positive integers has type $A$ if $a_{i}+1$ is a power of two for $i=1,2, \\ldots, k$. We say that a sequence $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$ of positive integer has type $B$ if $b_{j} \\geq 2 b_{j+1}$ for $j=1,2, \\ldots, m-1$.\n\nRecall that the binary representation of a positive integer expresses it as a sum of distinct powers of two in a unique way. Furthermore, we have the following formula for every positive integer $N$\n\n$$\n2^{N}-1=2^{N-1}+2^{N-2}+\\cdots+2^{1}+2^{0}\n$$\n\nGiven a sequence $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of type $A$, use the preceding formula to express each term as a sum of powers of two. Write these powers of two in left-aligned rows, in decreasing order of size. By construction, $a_{i}$ is the sum of the numbers in the $i$ th row. For example, we obtain the following array when we start with the type A sequence $15,15,7,3,3,3,1$.\n\n| 8 | 4 | 2 | 1 |\n| :--- | :--- | :--- | :--- |\n| 8 | 4 | 2 | 1 |\n| 4 | 2 | 1 | |\n| 2 | 1 | | |\n| 2 | 1 | | |\n| 2 | 1 | | |\n| 1 | | | |\n| 27 | 13 | 5 | 2 |\n\nDefine the sequence $b_{1}, b_{2}, \\ldots, b_{n}$ by setting $b_{j}$ to be the sum of the numbers in the $j$ th column of the array. For example, we obtain the sequence $27,13,5,2$ from the array above. We now show that this new sequence has type B. This is clear from the fact that each column in the array contains at least as many entries as the column to the right of it and that each number larger than 1 in the array is twice the number to the right of it. Furthermore, it is clear that $a_{1}+a_{2}+\\cdots+a_{k}=b_{1}+b_{2}+\\cdots+b_{m}$, since both are equal to the sum of all the entries in the array.\n\nWe now show that we can do this operation backwards. Suppose that we are given a type B sequence $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$. We construct an array inductively as follows:\n\n- We fill $b_{m}$ left-aligned rows with the numbers $2^{m-1}, 2^{m-2}, \\ldots, 2^{1}, 2^{0}$.\n- Then we fill $b_{m-1}-2 b_{m}$ left aligned rows with the numbers $2^{m-2}, 2^{m-3}, \\ldots, 2^{1}, 2^{0}$.\n- Then we fill $b_{m-2}-2 b_{m-1}$ left aligned rows with the numbers $2^{m-3}, 2^{m-4}, \\ldots, 2^{1}, 2^{0}$, and so on.\n- In the last step we fill $b_{1}-2 b_{2}$ left-aligned rows with the number 1 .\n\nFor example, if we start with the type B sequence $27,13,5,2$, we obtain once again the array above. We define the sequence $a_{1}, a_{2}, \\ldots, a_{k}$ by setting $a_{i}$ to be the sum of the numbers in the $i$ th row of the array. By construction, this sequence has type A. Furthermore, it is clear that $a_{1}+\\cdots+a_{k}=b_{1}+\\cdots+b_{m}$, since once again both sums are equal to the sum of all the entries in the array.\n\nWe have defined an operation that starts with a sequence of type A , produces an array whose row sums are given by the sequence, and outputs a sequence of type B corresponding to the column sums. We have also defined an operation that starts with a sequence of type B, produces an array whose column sums are given by the sequence, and outputs a sequence of type A corresponding to the row sums. The arrays produced in both cases comprise leftaligned rows of the form $2^{N-1}, 2^{N-2}, \\ldots, 2^{1}, 2^{0}$, with non-increasing lengths. Let us refer to arrays obeying these properties as marvelous.\n\nTo show that these two operations are inverses of each other, it then suffices to prove that marvelous arrays are uniquely defined by either their row sums or their column sums. The former is obviously true and the latter arises from the observation that each step in the above inductive algorithm was forced in order to create a marvelous array with the prescribed column sums.\n\nThus, we have produced a bijection between the sequences of type A with sum $n$ and the sequences of type B with sum $n$. So we can conclude that $A(n)=B(n)$ for every positive integer $n$.\n\nRemark The solution above provides a bijection between type A and type B sequences via an algorithm. There are alternative ways to provide such a bijection. For example, given the numbers $a_{1} \\geq \\ldots \\geq a_{k}$ we may define the $b_{i}$ 's as\n\n$$\nb_{j}=\\sum_{i}\\left\\lfloor\\frac{a_{i}+1}{2^{j}}\\right\\rfloor .\n$$\n\nConversely, given the numbers $b_{1} \\geq \\ldots \\geq b_{m}$, one may define the $a_{i}$ 's by taking, as in the solution, $b_{m}$ numbers equal to $2^{m}-1, b_{m-1}-2 b_{m}$ numbers equal to $2^{m-1}-1, \\ldots$, and $b_{1}-2 b_{2}$ numbers equal to $2^{1}-1$. One now needs to verify that these maps are mutually inverse.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2017", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Call a rational number $r$ powerful if $r$ can be expressed in the form $\\frac{p^{k}}{q}$ for some relatively prime positive integers $p, q$ and some integer $k>1$. Let $a, b, c$ be positive\nrational numbers such that $a b c=1$. Suppose there exist positive integers $x, y, z$ such that $a^{x}+b^{y}+c^{z}$ is an integer. Prove that $a, b, c$ are all powerful.", "solution": "Let $a=\\frac{a_{1}}{b_{1}}, b=\\frac{a_{2}}{b_{2}}$, where $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=\\operatorname{gcd}\\left(a_{2}, b_{2}\\right)=1$. Then $c=\\frac{b_{1} b_{2}}{a_{1} a_{2}}$. The condition that $a^{x}+b^{y}+c^{z}$ is an integer becomes\n\n$$\n\\frac{a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}}{a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y}} \\in \\mathbb{Z}\n$$\n\nwhich can be restated as\n\n$$\na_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y} \\mid a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .\n$$\n\nIn particular, $a_{1}^{z}$ divides the right-hand side. Since it divides the first and second terms in the sum, we conclude that $a_{1}^{z} \\mid b_{1}^{x+z} b_{2}^{y+z}$. Since $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=1$, we have $a_{1}^{z} \\mid b_{2}^{y+z}$.\n\nLet $p$ be a prime that divides $a_{1}$. Let $m, n \\geq 1$ be integers such that $p^{n} \\| a_{1}$ (i.e. $p^{n} \\mid a_{1}$ but $\\left.p^{n+1} \\nmid a_{1}\\right)$ and $p^{m} \\| b_{2}$. The fact that $a_{1}^{z} \\mid b_{2}^{y+z}$ implies $n z \\leq m(y+z)$. Since $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=$ $\\operatorname{gcd}\\left(a_{2}, b_{2}\\right)=1$, we have $p$ does not divide $b_{1}$ and does not divide $a_{2}$. Thus\n\n$$\np^{n z} \\| a_{1}^{z} a_{2}^{y+z} b_{1}^{x} \\text { and } p^{m(y+z)} \\| b_{1}^{x+z} b_{2}^{y+z}\n$$\n\nOn the other hand, (1) implies that\n\n$$\np^{n z+m y} \\mid a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .\n$$\n\nIf $n z<m(y+z)$, then (2) gives $p^{n z} \\| a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}$, which contradicts (3). Thus $n z=m(y+z)$ so $n$ is divisible by $k:=\\frac{y+z}{\\operatorname{gcd}(z, y+z)}>1$. Thus each exponent in the prime decomposition of $a_{1}$ must be divisible by $k$. Hence $a_{1}$ is a perfect $k$-power which means $a$ is powerful. Similarly, $b$ and $c$ are also powerful.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 7 |
-
{"year": "2017", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $n$ be a positive integer. A pair of $n$-tuples $\\left(a_{1}, \\ldots, a_{n}\\right)$ and $\\left(b_{1}, \\ldots, b_{n}\\right)$ with integer entries is called an exquisite pair if\n\n$$\n\\left|a_{1} b_{1}+\\cdots+a_{n} b_{n}\\right| \\leq 1\n$$\n\nDetermine the maximum number of distinct $n$-tuples with integer entries such that any two of them form an exquisite pair.\n\nAnswer: The maximum is $n^{2}+n+1$.", "solution": "First, we construct an example with $n^{2}+n+1 n$-tuples, each two of them forming an exquisite pair. In the following list, $*$ represents any number of zeros as long as the total number of entries is $n$.\n\n- (*)\n- $(*, 1, *)$\n- $(*,-1, *)$\n- $(*, 1, *, 1, *)$\n- $(*, 1, *,-1, *)$\n\nFor example, for $n=2$ we have the tuples $(0,0),(0,1),(1,0),(0,-1),(-1,0),(1,1),(1,-1)$. The total number of such tuples is $1+n+n+\\binom{n}{2}+\\binom{n}{2}=n^{2}+n+1$. For any two of them, at most two of the products $a_{i} b_{i}$ are non-zero. The only case in which two of them are non-zero is when we take a sequence $(*, 1, *, 1, *)$ and a sequence $(*, 1, *,-1, *)$ with zero entries in the same places. But in this case one $a_{i} b_{i}$ is 1 and the other -1 . This shows that any two of these sequences form an exquisite pair.\n\nNext, we claim that among any $n^{2}+n+2$ tuples, some two of them do not form an exquisite pair. We begin with lemma.\n\nLemma. Given $2 n+1$ distinct non-zero $n$-tuples of real numbers, some two of them $\\left(a_{1}, \\ldots, a_{n}\\right)$ and $\\left(b_{1}, \\ldots, b_{n}\\right)$ satisfy $a_{1} b_{1}+\\cdots+a_{n} b_{n}>0$.\n\nProof of Lemma. We proceed by induction. The statement is easy for $n=1$ since for every three non-zero numbers there are two of them with the same sign. Assume that the statement is true for $n-1$ and consider $2 n+1$ tuples with $n$ entries. Since we are working with tuples of real numbers, we claim that we may assume that one of the tuples is $a=(0,0, \\ldots, 0,-1)$. Let us postpone the proof of this claim for the moment.\n\nIf one of the remaining tuples $b$ has a negative last entry, then $a$ and $b$ satisfy the desired condition. So we may assume all the remaining tuples has a non-negative last entry. Now, from each tuple remove the last number. If two $n$-tuples $b$ and $c$ yield the same $(n-1)$-tuple, then\n\n$$\nb_{1} c_{1}+\\cdots+b_{n-1} c_{n-1}+b_{n} c_{n}=b_{1}^{2}+\\cdots+b_{n-1}^{2}+b_{n} c_{n}>0\n$$\n\nand we are done. The remaining case is that all the $n$-tuples yield distinct ( $n-1$ )-tuples. Then at most one of them is the zero $(n-1)$-tuple, and thus we can use the inductive hypothesis on $2 n-1$ of them. So we find $b$ and $c$ for which\n\n$$\n\\left(b_{1} c_{1}+\\cdots+b_{n-1} c_{n-1}\\right)+b_{n} c_{n}>0+b_{n} c_{n}>0\n$$\n\nThe only thing that we are left to prove is that in the inductive step we may assume that one of the tuples is $a=(0,0, \\ldots, 0,-1)$. Fix one of the tuples $x=\\left(x_{1}, \\ldots, x_{n}\\right)$. Set a real number $\\varphi$ for which $\\tan \\varphi=\\frac{x_{1}}{x_{2}}$. Change each tuple $a=\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ (including $x$ ), to the tuple\n\n$$\n\\left(a_{1} \\cos \\varphi-a_{2} \\sin \\varphi, a_{1} \\sin \\varphi+a_{2} \\cos \\varphi, a_{3}, a_{4}, \\ldots, a_{n}\\right)\n$$\n\nA straightforward calculation shows that the first coordinate of the tuple $x$ becomes 0 , and that all the expressions of the form $a_{1} b_{1}+\\cdots+a_{n} b_{n}$ are preserved. We may iterate this process until all the entries of $x$ except for the last one are equal to 0 . We finish by multiplying all the entries in all the tuples by a suitable constant that makes the last entry of $x$ equal to -1 . This preserves the sign of all the expressions of the form $a_{1} b_{1}+\\cdots+a_{n} b_{n}$.\n\nWe proceed to the proof of our claim. Let $A$ be a set of non-zero tuples among which any two form an exquisite pair. It suffices to prove that $|A| \\leq n^{2}+n$. We can write $A$ as a disjoint union of subsets $A_{1} \\cup A_{2} \\cup \\ldots \\cup A_{n}$, where $A_{i}$ is the set of tuples in $A$ whose last non-zero entry appears in the $i$ th position. We will show that $\\left|A_{i}\\right| \\leq 2 i$, which will finish our proof since $2+4+\\cdots+2 n=n^{2}+n$.\n\nProceeding by contradiction, suppose that $\\left|A_{i}\\right| \\geq 2 i+1$. If $A_{i}$ has three or more tuples whose only non-zero entry is in the $i$ th position, then for two of them this entry has the same sign. Since the tuples are different and their entries are integers, this yields two tuples for which $\\left|\\sum a_{i} b_{i}\\right| \\geq 2$, a contradiction. So there are at most two such tuples. We remove them from $A_{i}$.\n\nNow, for each of the remaining tuples $a$, if it has a positive $i$ th coordinate, we keep $a$ as it is. If it has a negative $i$ th coordinate, we replace it with the opposite tuple $-a$ with entries with opposite signs. This does not changes the exquisite pairs condition.\n\nAfter making the necessary changes, we have two cases. The first case is that there are two tuples $a$ and $b$ that have the same first $i-1$ coordinates and thus\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1}=a_{1}^{2}+\\cdots+a_{i-1}^{2}>0\n$$\n\nand thus is at least 1 (the entries are integers). The second case is that no two tuples have the same first $i-1$ coordinates, but then by the Lemma we find two tuples $a$ and $b$ for which\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1} \\geq 1\n$$\n\nIn any case, we obtain\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1}+a_{i} b_{i} \\geq 2\n$$\n\nThis yields a final contradiction to the exquisite pair hypothesis.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2017", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "We call a 5-tuple of integers arrangeable if its elements can be labeled $a$, $b, c, d, e$ in some order so that $a-b+c-d+e=29$. Determine all 2017-tuples of integers $n_{1}, n_{2}, \\ldots, n_{2017}$ such that if we place them in a circle in clockwise order, then any 5 -tuple of numbers in consecutive positions on the circle is arrangeable.\n\nAnswer: $n_{1}=\\cdots=n_{2017}=29$.", "solution": "A valid 2017-tuple is $n_{1}=\\cdots=n_{2017}=29$. We will show that it is the only solution.\n\nWe first replace each number $n_{i}$ in the circle by $m_{i}:=n_{i}-29$. Since the condition $a-b+$ $c-d+e=29$ can be rewritten as $(a-29)-(b-29)+(c-29)-(d-29)+(e-29)=0$, we have that any five consecutive replaced integers in the circle can be labeled $a, b, c, d, e$ in such a way that $a-b+c-d+e=0$. We claim that this is possible only when all of the $m_{i}$ 's are 0 (and thus all of the original $n_{i}$ 's are 29).\n\nWe work with indexes modulo 2017. Notice that for every $i, m_{i}$ and $m_{i+5}$ have the same parity. Indeed, this follows from $m_{i} \\equiv m_{i+1}+m_{i+2}+m_{i+3}+m_{i+4} \\equiv m_{i+5}(\\bmod 2)$. Since $\\operatorname{gcd}(5,2017)=1$, this implies that all $m_{i}$ 's are of the same parity. Since $m_{1}+m_{2}+m_{3}+m_{4}+m_{5}$ is even, all $m_{i}$ 's must be even as well.\n\nSuppose for the sake of contradiction that not all $m_{i}$ 's are zero. Then our condition still holds when we divide each number in the circle by 2 . However, by performing repeated divisions, we eventually reach a point where some $m_{i}$ is odd. This is a contradiction.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". Let $N$ be the midpoint of $A C$. Let $M$ be the intersection point of the circumcircle of triangle $A D Z$ and the segment $A B$. We will show that $M$ is the midpoint of $A B$. To do this, let $D^{\\prime}$ the reflection of $D$ with respect to $M$. It suffices to show that $A D B D^{\\prime}$ is a parallelogram.\n\nThe internal and external bisectors of an angle in a triangle are perpendicular. This implies that $Z D$ is a diameter of the circumcircle of $A Z D$ and thus $\\angle Z M D=90^{\\circ}$. This means that $Z M$ is the perpendicular bisector of $D^{\\prime} D$ and thus $Z D^{\\prime}=Z D$. By construction, $Z$ is in the perpendicular bisector of $A C$ and thus $Z A=Z C$.\n\nNow, let $\\alpha$ be the angle $\\angle B A D=\\angle D A C$. In the cyclic quadrilateral $A Z D M$ we get $\\angle M Z D=\\angle M A D=\\alpha$, and thus $\\angle D^{\\prime} Z D=2 \\alpha$. By angle chasing we get\n\n$$\n\\angle A Z N=90^{\\circ}-\\angle Z A N=\\angle D A C=\\alpha,\n$$\n\nwhich implies that $\\angle A Z C=2 \\alpha$. Therefore,\n\n$$\n\\angle D^{\\prime} Z A=\\angle D^{\\prime} Z D-\\angle A Z D=2 \\alpha-\\angle A Z D=\\angle A Z C-\\angle A Z D=\\angle D Z C .\n$$\n\nCombining $\\angle D^{\\prime} Z A=\\angle D Z C, Z D^{\\prime}=Z D$ and $Z A=Z C$, we obtain by the $S A S$ criterion that the triangles $D^{\\prime} Z A$ and $D Z C$ are congruent. In particular, $D^{\\prime} A=D C$ and $\\angle D^{\\prime} A Z=$ $\\angle D C Z$. From here $D B=D C=D^{\\prime} A$.\n\nFinally, let $\\beta=\\angle A B C=\\angle A D C$. We get the first of the following equalities by the sum of angles around point $A$ and the second one by the sum of internal angles of quadrilateral $A Z C D$\n\n$$\n\\begin{aligned}\n& 360^{\\circ}=\\angle D^{\\prime} A Z+\\angle Z A D+\\angle D A B+\\angle B A D^{\\prime}=\\angle D^{\\prime} A Z+90^{\\circ}+\\alpha+\\angle B A D^{\\prime} \\\\\n& 360^{\\circ}=\\angle D C Z+\\angle Z A D+\\angle C Z A+\\angle A D C=\\angle D C Z+90^{\\circ}+2 \\alpha+\\beta\n\\end{aligned}\n$$\n\nBy canceling equal terms we conclude that $\\angle B A D^{\\prime}=\\alpha+\\beta$. Also, $\\angle A B D=\\alpha+\\beta$. Therefore, the segments $D^{\\prime} A$ and $D B$ are parallel and have the same length. We conclude that $A D B D^{\\prime}$ is a parallelogram. As the diagonals of a parallelogram intersect at their midpoints, we obtain that $M$ is the midpoint of $A B$ as desired.\n\n\nVariant of solution. The solution above is indirect in the sense that it assumes that $M$ is in the circumcircle of $A Z D$ and then shows that $M$ is the midpoint of $A B$. We point out that the same ideas in the solution can be used to give a direct solution. Here we present a sketch on how to proceed in this manner.\n\nNow we know that $M$ is the midpoint of the side $A B$. We construct the point $D^{\\prime}$ in the same way. Now we have directly that $A D B D^{\\prime}$ is a parallelogram and thus $D^{\\prime} A=D B=D C$. By construction $Z A=Z C$. Also, the two sums of angles equal to $360^{\\circ}$ in the previous solution let us conclude that $\\angle D^{\\prime} A Z=\\angle D C Z$. Once again, we use (differently) the $S A S$ criterion and obtain that the triangles $D^{\\prime} A Z$ and $D C Z$ are congruent. Thus, $D^{\\prime} Z=D Z$.\n\nWe finish the problem by noting that $Z M$ is a median of the isosceles triangle $D^{\\prime} Z D$, so it is also a perpendicular bisector. This shows that $\\angle D M Z=90^{\\circ}=\\angle D A Z$, and therefore $M$ lies in the circumcircle of $D A Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 3 |
+
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". We proceed directly. As above, we name\n\n$$\n\\alpha=\\angle D A C=\\angle A Z N=\\angle C Z N=\\angle D C B .\n$$\n\nLet $L$ be the midpoint of the segment $B C$. Since $M$ and $N$ are midpoints of $A B$ and $A C$, we have that $M N=C L$ and that the segment $M N$ is parallel to $B C$. Thus, $\\angle A N M=\\angle A C B$.\n\nTherefore, $\\angle Z N M=\\angle A C B+90^{\\circ}$. Also, $\\angle D C Z=\\angle D C B+\\angle A C B+\\angle Z C A=\\angle A C B+90^{\\circ}$. We conclude that $\\angle Z N M=\\angle D C Z$.\n\nNow, the triangles $Z N C$ and $C L D$ are similar since $\\angle D C L=90^{\\circ}=\\angle C N Z$ and $\\angle D C L=$ $\\alpha=\\angle C Z N$. We use this fact to obtain the following chain of equalities\n\n$$\n\\frac{C D}{M N}=\\frac{C D}{C L}=\\frac{C Z}{Z N}\n$$\n\nWe combine the equality above with $\\angle Z N M=\\angle D C Z$ to conclude that the triangles $Z N M$ and $Z C D$ are similar. In particular, $\\angle M Z N=\\angle D Z C$ and $\\frac{Z M}{Z N}=\\frac{Z D}{Z C}$. Since we also have $\\angle M Z D=\\angle M Z N+\\angle N Z D=\\angle D Z C+\\angle N Z D=\\angle N Z C$, we conclude that the triangles $M Z D$ and $N Z C$ are similar. This yields that $\\angle Z M D=90^{\\circ}$ and therefore $M$ is in the circumcircle of triangle $D A Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 4 |
+
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.", "solution": ". Let $m$ be the perpendicular bisector of $A D$; thus $m$ passes through the center $O$ of the circumcircle of triangle $A B C$. Since $A D$ is the internal angle bisector of $A$ and $O M$ and $O N$ are perpendicular to $A B$ and $A C$ respectively, we obtain that $O M$ and $O N$ form equal angles with $A D$. This implies that they are symmetric with respect to $M$.\n\nTherefore, the line $M O$ passes through the point $Z^{\\prime}$ symmetrical to $Z$ with respect to $m$. Since $\\angle D A Z=90^{\\circ}$, then also $\\angle A D Z^{\\prime}=90^{\\circ}$. Moreover, since $A Z=D Z^{\\prime}$, we have that $\\angle A Z Z^{\\prime}=\\angle D Z^{\\prime} Z=90^{\\circ}$, so $A Z Z^{\\prime} D$ is a rectangle. Since $\\angle A M Z^{\\prime}=\\angle A M O=90^{\\circ}$, we conclude that $M$ is in the circle with diameter $A Z^{\\prime}$, which is the circumcircle of the rectangle. Thus $M$ lies on the circumcircle of the triangle $A D Z$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 3"}}
|
| 5 |
+
{"year": "2017", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A(n)$ denote the number of sequences $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of positive integers for which $a_{1}+\\cdots+a_{k}=n$ and each $a_{i}+1$ is a power of two $(i=1,2, \\ldots, k)$. Let $B(n)$ denote the number of sequences $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$ of positive integers for which $b_{1}+\\cdots+b_{m}=n$ and each inequality $b_{j} \\geq 2 b_{j+1}$ holds $(j=1,2, \\ldots, m-1)$.\n\nProve that $A(n)=B(n)$ for every positive integer $n$.", "solution": "We say that a sequence $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of positive integers has type $A$ if $a_{i}+1$ is a power of two for $i=1,2, \\ldots, k$. We say that a sequence $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$ of positive integer has type $B$ if $b_{j} \\geq 2 b_{j+1}$ for $j=1,2, \\ldots, m-1$.\n\nRecall that the binary representation of a positive integer expresses it as a sum of distinct powers of two in a unique way. Furthermore, we have the following formula for every positive integer $N$\n\n$$\n2^{N}-1=2^{N-1}+2^{N-2}+\\cdots+2^{1}+2^{0}\n$$\n\nGiven a sequence $a_{1} \\geq a_{2} \\geq \\ldots \\geq a_{k}$ of type $A$, use the preceding formula to express each term as a sum of powers of two. Write these powers of two in left-aligned rows, in decreasing order of size. By construction, $a_{i}$ is the sum of the numbers in the $i$ th row. For example, we obtain the following array when we start with the type A sequence $15,15,7,3,3,3,1$.\n\n| 8 | 4 | 2 | 1 |\n| :--- | :--- | :--- | :--- |\n| 8 | 4 | 2 | 1 |\n| 4 | 2 | 1 | |\n| 2 | 1 | | |\n| 2 | 1 | | |\n| 2 | 1 | | |\n| 1 | | | |\n| 27 | 13 | 5 | 2 |\n\nDefine the sequence $b_{1}, b_{2}, \\ldots, b_{n}$ by setting $b_{j}$ to be the sum of the numbers in the $j$ th column of the array. For example, we obtain the sequence $27,13,5,2$ from the array above. We now show that this new sequence has type B. This is clear from the fact that each column in the array contains at least as many entries as the column to the right of it and that each number larger than 1 in the array is twice the number to the right of it. Furthermore, it is clear that $a_{1}+a_{2}+\\cdots+a_{k}=b_{1}+b_{2}+\\cdots+b_{m}$, since both are equal to the sum of all the entries in the array.\n\nWe now show that we can do this operation backwards. Suppose that we are given a type B sequence $b_{1} \\geq b_{2} \\geq \\ldots \\geq b_{m}$. We construct an array inductively as follows:\n\n- We fill $b_{m}$ left-aligned rows with the numbers $2^{m-1}, 2^{m-2}, \\ldots, 2^{1}, 2^{0}$.\n- Then we fill $b_{m-1}-2 b_{m}$ left aligned rows with the numbers $2^{m-2}, 2^{m-3}, \\ldots, 2^{1}, 2^{0}$.\n- Then we fill $b_{m-2}-2 b_{m-1}$ left aligned rows with the numbers $2^{m-3}, 2^{m-4}, \\ldots, 2^{1}, 2^{0}$, and so on.\n- In the last step we fill $b_{1}-2 b_{2}$ left-aligned rows with the number 1 .\n\nFor example, if we start with the type B sequence $27,13,5,2$, we obtain once again the array above. We define the sequence $a_{1}, a_{2}, \\ldots, a_{k}$ by setting $a_{i}$ to be the sum of the numbers in the $i$ th row of the array. By construction, this sequence has type A. Furthermore, it is clear that $a_{1}+\\cdots+a_{k}=b_{1}+\\cdots+b_{m}$, since once again both sums are equal to the sum of all the entries in the array.\n\nWe have defined an operation that starts with a sequence of type A , produces an array whose row sums are given by the sequence, and outputs a sequence of type B corresponding to the column sums. We have also defined an operation that starts with a sequence of type B, produces an array whose column sums are given by the sequence, and outputs a sequence of type A corresponding to the row sums. The arrays produced in both cases comprise leftaligned rows of the form $2^{N-1}, 2^{N-2}, \\ldots, 2^{1}, 2^{0}$, with non-increasing lengths. Let us refer to arrays obeying these properties as marvelous.\n\nTo show that these two operations are inverses of each other, it then suffices to prove that marvelous arrays are uniquely defined by either their row sums or their column sums. The former is obviously true and the latter arises from the observation that each step in the above inductive algorithm was forced in order to create a marvelous array with the prescribed column sums.\n\nThus, we have produced a bijection between the sequences of type A with sum $n$ and the sequences of type B with sum $n$. So we can conclude that $A(n)=B(n)$ for every positive integer $n$.\n\nRemark The solution above provides a bijection between type A and type B sequences via an algorithm. There are alternative ways to provide such a bijection. For example, given the numbers $a_{1} \\geq \\ldots \\geq a_{k}$ we may define the $b_{i}$ 's as\n\n$$\nb_{j}=\\sum_{i}\\left\\lfloor\\frac{a_{i}+1}{2^{j}}\\right\\rfloor .\n$$\n\nConversely, given the numbers $b_{1} \\geq \\ldots \\geq b_{m}$, one may define the $a_{i}$ 's by taking, as in the solution, $b_{m}$ numbers equal to $2^{m}-1, b_{m-1}-2 b_{m}$ numbers equal to $2^{m-1}-1, \\ldots$, and $b_{1}-2 b_{2}$ numbers equal to $2^{1}-1$. One now needs to verify that these maps are mutually inverse.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2017", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Call a rational number $r$ powerful if $r$ can be expressed in the form $\\frac{p^{k}}{q}$ for some relatively prime positive integers $p, q$ and some integer $k>1$. Let $a, b, c$ be positive\nrational numbers such that $a b c=1$. Suppose there exist positive integers $x, y, z$ such that $a^{x}+b^{y}+c^{z}$ is an integer. Prove that $a, b, c$ are all powerful.", "solution": "Let $a=\\frac{a_{1}}{b_{1}}, b=\\frac{a_{2}}{b_{2}}$, where $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=\\operatorname{gcd}\\left(a_{2}, b_{2}\\right)=1$. Then $c=\\frac{b_{1} b_{2}}{a_{1} a_{2}}$. The condition that $a^{x}+b^{y}+c^{z}$ is an integer becomes\n\n$$\n\\frac{a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}}{a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y}} \\in \\mathbb{Z}\n$$\n\nwhich can be restated as\n\n$$\na_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y} \\mid a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .\n$$\n\nIn particular, $a_{1}^{z}$ divides the right-hand side. Since it divides the first and second terms in the sum, we conclude that $a_{1}^{z} \\mid b_{1}^{x+z} b_{2}^{y+z}$. Since $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=1$, we have $a_{1}^{z} \\mid b_{2}^{y+z}$.\n\nLet $p$ be a prime that divides $a_{1}$. Let $m, n \\geq 1$ be integers such that $p^{n} \\| a_{1}$ (i.e. $p^{n} \\mid a_{1}$ but $\\left.p^{n+1} \\nmid a_{1}\\right)$ and $p^{m} \\| b_{2}$. The fact that $a_{1}^{z} \\mid b_{2}^{y+z}$ implies $n z \\leq m(y+z)$. Since $\\operatorname{gcd}\\left(a_{1}, b_{1}\\right)=$ $\\operatorname{gcd}\\left(a_{2}, b_{2}\\right)=1$, we have $p$ does not divide $b_{1}$ and does not divide $a_{2}$. Thus\n\n$$\np^{n z} \\| a_{1}^{z} a_{2}^{y+z} b_{1}^{x} \\text { and } p^{m(y+z)} \\| b_{1}^{x+z} b_{2}^{y+z}\n$$\n\nOn the other hand, (1) implies that\n\n$$\np^{n z+m y} \\mid a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .\n$$\n\nIf $n z<m(y+z)$, then (2) gives $p^{n z} \\| a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}$, which contradicts (3). Thus $n z=m(y+z)$ so $n$ is divisible by $k:=\\frac{y+z}{\\operatorname{gcd}(z, y+z)}>1$. Thus each exponent in the prime decomposition of $a_{1}$ must be divisible by $k$. Hence $a_{1}$ is a perfect $k$-power which means $a$ is powerful. Similarly, $b$ and $c$ are also powerful.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 7 |
+
{"year": "2017", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be a positive integer. A pair of $n$-tuples $\\left(a_{1}, \\ldots, a_{n}\\right)$ and $\\left(b_{1}, \\ldots, b_{n}\\right)$ with integer entries is called an exquisite pair if\n\n$$\n\\left|a_{1} b_{1}+\\cdots+a_{n} b_{n}\\right| \\leq 1\n$$\n\nDetermine the maximum number of distinct $n$-tuples with integer entries such that any two of them form an exquisite pair.\n\nAnswer: The maximum is $n^{2}+n+1$.", "solution": "First, we construct an example with $n^{2}+n+1 n$-tuples, each two of them forming an exquisite pair. In the following list, $*$ represents any number of zeros as long as the total number of entries is $n$.\n\n- (*)\n- $(*, 1, *)$\n- $(*,-1, *)$\n- $(*, 1, *, 1, *)$\n- $(*, 1, *,-1, *)$\n\nFor example, for $n=2$ we have the tuples $(0,0),(0,1),(1,0),(0,-1),(-1,0),(1,1),(1,-1)$. The total number of such tuples is $1+n+n+\\binom{n}{2}+\\binom{n}{2}=n^{2}+n+1$. For any two of them, at most two of the products $a_{i} b_{i}$ are non-zero. The only case in which two of them are non-zero is when we take a sequence $(*, 1, *, 1, *)$ and a sequence $(*, 1, *,-1, *)$ with zero entries in the same places. But in this case one $a_{i} b_{i}$ is 1 and the other -1 . This shows that any two of these sequences form an exquisite pair.\n\nNext, we claim that among any $n^{2}+n+2$ tuples, some two of them do not form an exquisite pair. We begin with lemma.\n\nLemma. Given $2 n+1$ distinct non-zero $n$-tuples of real numbers, some two of them $\\left(a_{1}, \\ldots, a_{n}\\right)$ and $\\left(b_{1}, \\ldots, b_{n}\\right)$ satisfy $a_{1} b_{1}+\\cdots+a_{n} b_{n}>0$.\n\nProof of Lemma. We proceed by induction. The statement is easy for $n=1$ since for every three non-zero numbers there are two of them with the same sign. Assume that the statement is true for $n-1$ and consider $2 n+1$ tuples with $n$ entries. Since we are working with tuples of real numbers, we claim that we may assume that one of the tuples is $a=(0,0, \\ldots, 0,-1)$. Let us postpone the proof of this claim for the moment.\n\nIf one of the remaining tuples $b$ has a negative last entry, then $a$ and $b$ satisfy the desired condition. So we may assume all the remaining tuples has a non-negative last entry. Now, from each tuple remove the last number. If two $n$-tuples $b$ and $c$ yield the same $(n-1)$-tuple, then\n\n$$\nb_{1} c_{1}+\\cdots+b_{n-1} c_{n-1}+b_{n} c_{n}=b_{1}^{2}+\\cdots+b_{n-1}^{2}+b_{n} c_{n}>0\n$$\n\nand we are done. The remaining case is that all the $n$-tuples yield distinct ( $n-1$ )-tuples. Then at most one of them is the zero $(n-1)$-tuple, and thus we can use the inductive hypothesis on $2 n-1$ of them. So we find $b$ and $c$ for which\n\n$$\n\\left(b_{1} c_{1}+\\cdots+b_{n-1} c_{n-1}\\right)+b_{n} c_{n}>0+b_{n} c_{n}>0\n$$\n\nThe only thing that we are left to prove is that in the inductive step we may assume that one of the tuples is $a=(0,0, \\ldots, 0,-1)$. Fix one of the tuples $x=\\left(x_{1}, \\ldots, x_{n}\\right)$. Set a real number $\\varphi$ for which $\\tan \\varphi=\\frac{x_{1}}{x_{2}}$. Change each tuple $a=\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)$ (including $x$ ), to the tuple\n\n$$\n\\left(a_{1} \\cos \\varphi-a_{2} \\sin \\varphi, a_{1} \\sin \\varphi+a_{2} \\cos \\varphi, a_{3}, a_{4}, \\ldots, a_{n}\\right)\n$$\n\nA straightforward calculation shows that the first coordinate of the tuple $x$ becomes 0 , and that all the expressions of the form $a_{1} b_{1}+\\cdots+a_{n} b_{n}$ are preserved. We may iterate this process until all the entries of $x$ except for the last one are equal to 0 . We finish by multiplying all the entries in all the tuples by a suitable constant that makes the last entry of $x$ equal to -1 . This preserves the sign of all the expressions of the form $a_{1} b_{1}+\\cdots+a_{n} b_{n}$.\n\nWe proceed to the proof of our claim. Let $A$ be a set of non-zero tuples among which any two form an exquisite pair. It suffices to prove that $|A| \\leq n^{2}+n$. We can write $A$ as a disjoint union of subsets $A_{1} \\cup A_{2} \\cup \\ldots \\cup A_{n}$, where $A_{i}$ is the set of tuples in $A$ whose last non-zero entry appears in the $i$ th position. We will show that $\\left|A_{i}\\right| \\leq 2 i$, which will finish our proof since $2+4+\\cdots+2 n=n^{2}+n$.\n\nProceeding by contradiction, suppose that $\\left|A_{i}\\right| \\geq 2 i+1$. If $A_{i}$ has three or more tuples whose only non-zero entry is in the $i$ th position, then for two of them this entry has the same sign. Since the tuples are different and their entries are integers, this yields two tuples for which $\\left|\\sum a_{i} b_{i}\\right| \\geq 2$, a contradiction. So there are at most two such tuples. We remove them from $A_{i}$.\n\nNow, for each of the remaining tuples $a$, if it has a positive $i$ th coordinate, we keep $a$ as it is. If it has a negative $i$ th coordinate, we replace it with the opposite tuple $-a$ with entries with opposite signs. This does not changes the exquisite pairs condition.\n\nAfter making the necessary changes, we have two cases. The first case is that there are two tuples $a$ and $b$ that have the same first $i-1$ coordinates and thus\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1}=a_{1}^{2}+\\cdots+a_{i-1}^{2}>0\n$$\n\nand thus is at least 1 (the entries are integers). The second case is that no two tuples have the same first $i-1$ coordinates, but then by the Lemma we find two tuples $a$ and $b$ for which\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1} \\geq 1\n$$\n\nIn any case, we obtain\n\n$$\na_{1} b_{1}+\\cdots+a_{i-1} b_{i-1}+a_{i} b_{i} \\geq 2\n$$\n\nThis yields a final contradiction to the exquisite pair hypothesis.", "metadata": {"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
APMO/segmented/en-apmo2018_sol.jsonl
CHANGED
|
@@ -1,9 +1,9 @@
|
|
| 1 |
-
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.", "solution": "Lemma 1. In a triangle $A B C$, let $D$ be the intersection of the interior angle bisector at $A$ with the circumcircle of $A B C$, and let $I$ be the incenter of $\\triangle A B C$. Then\n\n$$\nD I=D B=D C\n$$\n\n\n\nProof.\n\n$$\n\\angle D B I=\\frac{\\angle B A C}{2}+\\frac{\\widehat{B}}{2}=\\angle D I B \\quad \\Rightarrow \\quad D I=D B\n$$\n\nAnalogously $D I=D C$.\nWe start solving the problem. First we state some position considerations. Since there is an arc of the circumcircle of $B H M$ outside the triangle $A B C$, it must happen that $K$ and $N$ lie on opposite sides of $A M$. Similarly, $L$ and $M$ lie on opposite sides of $A N$. Also, $K$ and $L$ lie on the same side of $M N$, and opposite to $A$. Therefore, $F$ lies inside the triangle $A M N$.\n\nNow, since $H$ is the orthocenter of $\\triangle A B C$ and the circumcircles of $B M H$ and $C N H$ are tangent we have\n\n$$\n\\angle A B H=90^{\\circ}-\\angle B A C=\\angle A C H \\quad \\Rightarrow \\quad \\angle M H N=\\angle M B H+\\angle N C H=180^{\\circ}-2 \\angle B A C .\n$$\n\nSo $\\angle M B H=\\angle M K H=\\angle N C H=\\angle N L H=90^{\\circ}-\\angle B A C$ and, since $M N \\| K L$, we have\n\n$$\n\\angle F M N=\\angle F N M=90^{\\circ}-\\angle B A C \\Rightarrow \\angle M F N=2 \\angle B A C .\n$$\n\nThe relations (1) and (2) yield that the quadrilateral $M F N H$ is cyclic, with the vertices in this order around the circumference. Since $F M=F N, \\angle M F N=2 \\angle B A C$ and $F$ is the correct side of $M N$ we have that the point $F$ is the circumcenter of triangle $A M N$, and thus $F A=F M=F N$.\n\n\nSince the quadrilateral $M F N H$ is cyclic, $F M=F N$ and $H$ lies on the correct side of $M N$, we have that $H, J$ and $F$ are collinear. According to Lemma $1, F J=F M=F N$. So $F J=F A$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution."}}
|
| 2 |
-
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.", "solution": ": According to Solution 1, we have $\\angle M H N=180^{\\circ}-2 \\angle B A C$ and since the point $J$ is the incenter of $\\triangle M H N$, we have $\\angle M J N=90^{\\circ}+\\frac{1}{2} \\angle M H N=180^{\\circ}-\\angle B A C$. So the quadrilateral $A M J N$ is cyclic.\n\nAccording to Solution 1, the point $F$ is the circumcenter of $\\triangle A M N$. So $F J=F A$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "There are two cases: $2 n-1<x<2 n$ and $2 n<x<2 n+1$. Note that $f(2018-x)=-f(x)$ and $g(2018-x)=-g(x)$, that is, a half turn about the point $(1009,0)$ preserves the graphs of $f$ and $g$. So it suffices to consider only the case $2 n-1<x<2 n$.\n\nLet $d(x)=g(x)-f(x)$. We will show that $d(x)>2$ whenever $2 n-1<x<2 n$ and $n \\in\\{1,2, \\ldots, 1009\\}$.\n\nFor any non-integer $x$ with $0<x<2018$, we have\n\n$$\nd(x+2)-d(x)=\\left(\\frac{1}{x+1}-\\frac{1}{x+2}\\right)+\\left(\\frac{1}{x-2018}-\\frac{1}{x-2017}\\right)>0+0=0\n$$\n\nHence it suffices to prove $d(x)>2$ for $1<x<2$. Since $x<2$, it follows that $\\frac{1}{x-2 i-1}>$ $\\frac{1}{x-2 i}$ for $i=2,3, \\ldots, 1008$. We also have $\\frac{1}{x-2018}<0$. Hence it suffices to prove the following\nfor $1<x<2$.\n\n$$\n\\begin{aligned}\n& \\frac{1}{x-1}+\\frac{1}{x-3}-\\frac{1}{x}-\\frac{1}{x-2}>2 \\\\\n\\Leftrightarrow & \\left(\\frac{1}{x-1}+\\frac{1}{2-x}\\right)+\\left(\\frac{1}{x-3}-\\frac{1}{x}\\right)>2 \\\\\n\\Leftrightarrow & \\frac{1}{(x-1)(2-x)}+\\frac{3}{x(x-3)}>2 .\n\\end{aligned}\n$$\n\nBy the $G M-H M$ inequality (alternatively, by considering the maximum of the quadratic $(x-1)(2-x))$ we have\n\n$$\n\\frac{1}{x-1} \\cdot \\frac{1}{2-x}>\\left(\\frac{2}{(x-1)+(2-x)}\\right)^{2}=4\n$$\n\nTo find a lower bound for $\\frac{3}{x(x-3)}$, note that $x(x-3)<0$ for $1<x<2$. So we seek an upper bound for $x(x-3)$. From the shape of the quadratic, this occurs at $x=1$ or $x=2$, both of which yield $\\frac{3}{x(x-3)}>-\\frac{3}{2}$.\n\nIt follows that $d(x)>4-\\frac{3}{2}>2$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
-
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "As in Solution 1, we may assume $2 n-1<x<2 n$ for some $1 \\leq n \\leq 1009$. Let $d(x)=$ $f(x)-g(x)$, and note that\n\n$$\nd(x)=\\frac{1}{x}+\\sum_{m=1}^{1009} \\frac{1}{(x-2 m)(x-2 m+1)}\n$$\n\nWe split the sum into three parts: the terms before $m=n$, after $m=n$, and the term $m=n$. The first two are\n\n$$\n\\begin{aligned}\n0 & \\leq \\sum_{m=1}^{n-1} \\frac{1}{(x-2 m)(x-2 m+1)} \\\\\n& \\leq \\sum_{m=1}^{n-1} \\frac{1}{(2 n-1-2 m)(2 n-2 m)}=\\sum_{i=1}^{n-1} \\frac{1}{(2 i)(2 i-1)} \\leq \\sum_{i=1}^{1008} \\frac{1}{2 i-1}-\\frac{1}{2 i} \\\\\n0 & \\leq \\sum_{m=n+1}^{1009} \\frac{1}{(2 m-x)(2 m-1-x)} \\\\\n& \\leq \\sum_{m=n+1}^{1009} \\frac{1}{(2 m-2 n+1)(2 m-2 n)}=\\sum_{i=1}^{1009-n} \\frac{1}{(2 i+1)(2 i)} \\leq \\sum_{i=1}^{1008} \\frac{1}{2 i}-\\frac{1}{2 i+1} .\n\\end{aligned}\n$$\n\nWhen we add the two sums the terms telescope and we are left with\n\n$$\n0 \\leq \\sum_{1 \\leq m \\leq 1009, m \\neq n} \\frac{1}{(x-2 m)(x-2 m+1)} \\leq 1-\\frac{1}{2017}<1\n$$\n\nFor the term $m=n$, we write\n\n$$\n0<-(x-2 n)(x-2 n+1)=0.25-(x-2 n+0.5)^{2} \\leq 0.25\n$$\n\nwhence\n\n$$\n-4 \\geq \\frac{1}{(x-2 n)(x-2 n+1)}\n$$\n\nFinally, $\\frac{1}{x}<1$ since $x>2 n-1 \\geq 1$. Combining these we get\n\n$$\nd(x)=\\frac{1}{x}+\\sum_{m=1}^{1009} \\frac{1}{(x-2 m)(x-2 m+1)}<1+1-4<-2 .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
-
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "First notice that\n\n$$\nf(x)-g(x)=\\frac{1}{x}-\\frac{1}{x-1}+\\frac{1}{x-2}-\\cdots-\\frac{1}{x-2017}+\\frac{1}{x-2018} .\n$$\n\nAs in Solution 1, we may deal only with the case $2 n<x<2 n+1$. Then $x-2 k+1$ and $x-2 k$ never differ in sign for any integer $k$. Then\n\n$$\n\\begin{aligned}\n-\\frac{1}{x-2 k+1}+\\frac{1}{x-2 k} & =\\frac{1}{(x-2 k+1)(x-2 k)}>0 \\quad \\text { for } k=1,2, \\ldots, n-1, n+2, \\ldots, 1009 \\\\\n\\frac{1}{x-2 n}-\\frac{1}{x-2 n-1} & =\\frac{1}{(x-2 n)(2 n+1-x)} \\geq\\left(\\frac{2}{x-2 n+2 n+1-x}\\right)^{2}=4\n\\end{aligned}\n$$\n\nTherefore, summing all inequalities and collecting the remaining terms we find $f(x)-g(x)>$ $4+\\frac{1}{x-2}>4-1=3$ for $0<x<1$ and, for $n>0$,\n\n$$\n\\begin{aligned}\nf(x)-g(x) & >\\frac{1}{x}-\\frac{1}{x-2 n+1}+4+\\frac{1}{x-2 n-2} \\\\\n& =\\frac{1}{x}-\\frac{1}{x-2 n+1}+4-\\frac{1}{2 n+2-x} \\\\\n& >\\frac{1}{x}-\\frac{1}{2 n-2 n+1}+4-\\frac{1}{2 n+2-2 n-1} \\\\\n& =2+\\frac{1}{x}>2 .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 3"}}
|
| 6 |
-
{"year": "2018", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:\n(i) All the squares are congruent.\n(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.\n(iii) Each square touches exactly three other squares.\n\nHow many positive integers $n$ are there with $2018 \\leq n \\leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?\n\nAnswer: 501", "solution": "We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \\geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.\n\nFor any two different squares $A$ and $B$, let us write $A \\sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \\sim B$ is $3 n$. But $A \\sim B$ if and only if $B \\sim A$. Hence the total number of instances of $A \\sim B$ is even. Thus $3 n$ and hence also $n$ is even.\n\nWe now construct tri-connected collections for each even $n$ in the range. We show two\nConstruction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.\n\n\nPutting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \\geq 38$.\n\n\nConstruction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \\cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \\leq m \\leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \\geq 4$, this will be true. The picture for $n=24$ is as follows:\n\n\nTo treat the other cases, consider the following gadget\n\n\nTwo squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.\nThis gives us a valid configuration for $6 n+8$ squares, $n \\geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \\geq 4$, which finishes the proof for all even numbers at least 36 .", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 7 |
-
{"year": "2018", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $A B C$ be an equilateral triangle. From the vertex $A$ we draw a ray towards the interior of the triangle such that the ray reaches one of the sides of the triangle. When the ray reaches a side, it then bounces off following the law of reflection, that is, if it arrives with a directed angle $\\alpha$, it leaves with a directed angle $180^{\\circ}-\\alpha$. After $n$ bounces, the ray returns to $A$ without ever landing on any of the other two vertices. Find all possible values of $n$.\n\nAnswer: All $n \\equiv 1,5 \\bmod 6$ with the exception of 5 and 17", "solution": "Consider an equilateral triangle $A A_{1} A_{2}$ of side length $m$ and triangulate it with unitary triangles. See the figure. To each of the vertices that remain after the triangulation we can assign a pair of coordinates $(a, b)$ where $a, b$ are non-negative integers, $a$ is the number of edges we travel in the $A A_{1}$ direction and $b$ is the number of edges we travel in the $A A_{2}$ direction to arrive to the vertex, (we have $A=(0,0), A_{1}=(m, 0)$ and $A_{2}=(0, m)$ ). The unitary triangle with vertex $A$ will be our triangle $A B C,(B=(1,0), C=(0,1))$. We can obtain every unitary triangle by starting with $A B C$ and performing reflections with respect to a side (the vertex $(1,1)$ is the reflection of $A$ with respect to $B C$, the vertex $(0,2)$ is the reflection of $B=(1,0)$ with respect to the side formed by $C=(1,0)$ and $(1,1)$, and so on).\n\nWhen we reflect a vertex $(a, b)$ with respect to a side of one of the triangles, the congruence of $a-b$ is preserved modulo 3. Furthermore, an induction argument shows that any two vertices $(a, b)$ and $\\left(a^{\\prime}, b^{\\prime}\\right)$ with $a-b \\equiv a^{\\prime}-b^{\\prime}$ mod 3 can be obtained from each other by a series of such reflections. Therefore, the set of vertices $V$ that result from the reflections of $A$ will be those of the form $(a, b)$ satisfying $a \\equiv b \\bmod 3$. See the green vertices in the figure.\n\nNow, let $U$ be the set of vertices $u$ that satisfy that the line segment between $u$ and $A$ does not pass through any other vertex. A pair $(a, b)$ is in $U$ if and only if $\\operatorname{gcd}(a, b)=1$, since otherwise for $d=\\operatorname{gcd}(a, b)$ we have that the vertex $(a / d, b / d)$ also lies on the line segment between $u$ and $A$.\n\nObserve that the rays that come out from $A$ and eventually return to $A$ are those that come out towards a vertex in $V \\cap U$ (they would be in $V$ to be able to come back to $A$ and in $U$ so that they do not reach a vertex beforehand). In the diagram, a ray toward one such vertex $(a, b)$ will intersect exactly $(a-1)+(b-1)+(a+b-1)=2(a+b)-3$ lines: $a-1$ of them parallel to $A B, b-1$ parallel to $A C$ and $a+b-1$ parallel to $B C$. Therefore, in the triangle $A B C$ the ray will bounce $2(a+b)-3$ times before returning to $A$. So we want to find all\n\n$n=2(a+b)-3$ where $a \\equiv b \\bmod 3$ and $\\operatorname{gcd}(a, b)=1$.\nIf $a+b$ is a multiple of 3 then we cannot satisfy both conditions simultaneously, therefore $n$ is not a multiple of 3 . We also know that $n$ is odd. Therefore $n \\equiv 1,5,7,11 \\bmod 12$. Note that the pair $(1,3 k+1)$ satisfies the conditions and we can create $n=2(3 k+2)-3=6 k+1$ for all $k \\geq 0$ (this settles the question for $n \\equiv 1,7 \\bmod 12$ ). For $n \\equiv 5 \\bmod 12$ consider the pair $(3 k-1,3 k+5)$ when $k$ is even or $(3 k-4,3 k+8)$ when $k$ is odd. This gives us all the integers of the form $12 k+5$ for $k \\geq 2$. For $11 \\bmod 12$, take the pairs $(3 k-1,3 k+2)($ with $k \\geq 1)$, which yield all positive integers of the form $12 k-1$.\n\nFinally, to discard 5 and 17 note that the only pairs $(a, b)$ that are solutions to $2(a+b)-3=5$ or $2(a+b)-3=17$ with the same residue $\\bmod 3$ in this range are the non-relatively prime pairs $(2,2),(2,8)$ and $(5,5)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 8 |
-
{"year": "2018", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.\n\nAnswer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.", "solution": ": $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.\nNotice that if $P(x)$ is a solution, then so is $P(x)+k$ and $-P(x)+k$ for any integer $k$, so we may assume that the leading coefficient of $P(x)$ is positive and that $P(0)=0$, i.e., we can assume that $P(x)=\\sum_{i=1}^{n} a_{i} x^{i}$ with $a_{n}>0$. We are going to prove that $P(x)=x^{n}$ in this case.\n\nLet $p$ be a large prime such that $p>\\sum_{i=1}^{n}\\left|a_{i}\\right|$. Because $P$ has a positive leading coefficient and $p$ is large enough, we can find $t \\in \\mathbb{R}$ such that $P(t)=p$. Denote the greatest common divisor of the polynomial $P(x)-p$ and $P(2 x)-P(2 t)$ as $f(x)$, and $t$ is a root of it, so $f$ is a non-constant polynomial. Notice that $P(2 t)$ is an integer by using the hypothesis for $s=2$ and $t$. Since $P(x)-p$ and $P(2 x)-P(2 t)$ are polynomials with integer coefficients, $f$ can be chosen as a polynomial with rational coefficients.\n\nIn the following, we will prove that $f$ is the same as $P(x)-p$ up to a constant multiplier. Say $P(x)-p=f(x) g(x)$, where $f$ and $g$ are non-constant polynomials. By Gauss's lemma, we can get $f_{1}, g_{1}$ with $P(x)-p=f_{1}(x) g_{1}(x)$ where $f_{1}$ is a scalar multiple of $f$ and $g_{1}$ is a scalar multiple of $g$ and one of $f_{1}, g_{1}$ has constant term $\\pm 1$ (this is because $-p=P(0)-p=f(0) g(0)$ with $p$ prime). So $P(x)-p$ has at least one root $r$ with absolute value not greater than 1 (using\n\nVieta, the product of the roots of the polynomial with constant term $\\pm 1$ is $\\pm 1$ ), but\n\n$$\n|P(r)-p|=\\left|\\sum_{i=1}^{n} a_{i} r^{i}-p\\right|>p-\\sum_{i=1}^{n}\\left|a_{i}\\right|>0\n$$\n\nhence we get a contradiction!\nTherefore $f$ is a constant multiple of $P(x)-p$, so $P(2 x)-P(2 t)$ is a constant multiple of $P(x)-p$ because they both have the same degree. By comparing leading coefficients we get that $P(2 x)-P(2 t)=2^{n}(P(x)-p)$. Comparing the rest of the coefficients we get that $P(x)=a_{n} x^{n}$. If we let $a=b=\\left(1 / a_{n}\\right)^{1 / n}$, then $P(a)=P(b)=1$, so $P(a b)$ must also be an integer. But $P(a b)=\\frac{1}{a_{n}}$. Therefore $a_{n}=1$ and the proof is complete.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 1"}}
|
| 9 |
-
{"year": "2018", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.\n\nAnswer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.", "solution": ": Assume $P(x)=\\sum_{i=0}^{n} a_{i} x^{i}$. Consider the following system of equations\n\n$$\n\\begin{aligned}\n& a_{0}=P(0) \\\\\n& a_{n} t^{n}+a_{n-1} t^{n-1}+\\cdots+a_{0}=P(t) \\\\\n& 2^{n} a_{n} t^{n}+2^{n-1} a_{n-1} t^{n-1}+\\cdots+a_{0}=P(2 t) \\\\\n& \\vdots \\\\\n& n^{n} a_{n} t^{n}+n^{n-1} a_{n-1} t^{n-1}+\\cdots+a_{0}=P(n t)\n\\end{aligned}\n$$\n\nviewing $a_{k} t^{k}$ as variables. Note that if $P(t)$ is an integer, then by the hypothesis all the terms on the right hand side of the equations are integers as well. By using Cramer's rule, we can get that $a_{k} t^{k}=D / M$, where $D$ is an integer and $M$ is the following determinant\n\n$$\n\\left|\\begin{array}{ccccc}\n1 & 0 & 0 & \\cdots & 0 \\\\\n1 & 1 & 1 & \\cdots & 1 \\\\\n1 & 2 & 4 & \\cdots & 2^{n} \\\\\n\\vdots & \\vdots & \\vdots & & \\vdots \\\\\n1 & n & n^{2} & \\cdots & n^{n}\n\\end{array}\\right| \\neq 0\n$$\n\nThus, if we let $r$ be the smallest positive index such that $a_{r} \\neq 0$, we can express each $t \\in \\mathbb{R}$ with $P(t) \\in \\mathbb{Z}$ in the form $\\left(\\frac{m}{M^{\\prime}}\\right)^{1 / r}$ for some integer $m$, and where $M^{\\prime}=M \\times a_{r}$ is a constant.\n\nWe can choose $L$ large enough such that $\\left.P\\right|_{\\mathbb{R}_{\\geq L}}$ is injective, and for any larger $N$, the growth order of the number of values in the form $\\left(\\frac{m}{M^{\\prime}}\\right)^{1 / r}$ is $N^{r}$, while the growth order of the number of integers in $[P(L), P(N)]$ is $N^{n}$, so $r=n$. Therefore $P(x)$ is of the form $a_{n} x^{n}+k$. The problem can be finished as in Solution 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 2"}}
|
|
|
|
| 1 |
+
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.", "solution": "Lemma 1. In a triangle $A B C$, let $D$ be the intersection of the interior angle bisector at $A$ with the circumcircle of $A B C$, and let $I$ be the incenter of $\\triangle A B C$. Then\n\n$$\nD I=D B=D C\n$$\n\n\n\nProof.\n\n$$\n\\angle D B I=\\frac{\\angle B A C}{2}+\\frac{\\widehat{B}}{2}=\\angle D I B \\quad \\Rightarrow \\quad D I=D B\n$$\n\nAnalogously $D I=D C$.\nWe start solving the problem. First we state some position considerations. Since there is an arc of the circumcircle of $B H M$ outside the triangle $A B C$, it must happen that $K$ and $N$ lie on opposite sides of $A M$. Similarly, $L$ and $M$ lie on opposite sides of $A N$. Also, $K$ and $L$ lie on the same side of $M N$, and opposite to $A$. Therefore, $F$ lies inside the triangle $A M N$.\n\nNow, since $H$ is the orthocenter of $\\triangle A B C$ and the circumcircles of $B M H$ and $C N H$ are tangent we have\n\n$$\n\\angle A B H=90^{\\circ}-\\angle B A C=\\angle A C H \\quad \\Rightarrow \\quad \\angle M H N=\\angle M B H+\\angle N C H=180^{\\circ}-2 \\angle B A C .\n$$\n\nSo $\\angle M B H=\\angle M K H=\\angle N C H=\\angle N L H=90^{\\circ}-\\angle B A C$ and, since $M N \\| K L$, we have\n\n$$\n\\angle F M N=\\angle F N M=90^{\\circ}-\\angle B A C \\Rightarrow \\angle M F N=2 \\angle B A C .\n$$\n\nThe relations (1) and (2) yield that the quadrilateral $M F N H$ is cyclic, with the vertices in this order around the circumference. Since $F M=F N, \\angle M F N=2 \\angle B A C$ and $F$ is the correct side of $M N$ we have that the point $F$ is the circumcenter of triangle $A M N$, and thus $F A=F M=F N$.\n\n\nSince the quadrilateral $M F N H$ is cyclic, $F M=F N$ and $H$ lies on the correct side of $M N$, we have that $H, J$ and $F$ are collinear. According to Lemma $1, F J=F M=F N$. So $F J=F A$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution."}}
|
| 2 |
+
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.", "solution": ": According to Solution 1, we have $\\angle M H N=180^{\\circ}-2 \\angle B A C$ and since the point $J$ is the incenter of $\\triangle M H N$, we have $\\angle M J N=90^{\\circ}+\\frac{1}{2} \\angle M H N=180^{\\circ}-\\angle B A C$. So the quadrilateral $A M J N$ is cyclic.\n\nAccording to Solution 1, the point $F$ is the circumcenter of $\\triangle A M N$. So $F J=F A$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "There are two cases: $2 n-1<x<2 n$ and $2 n<x<2 n+1$. Note that $f(2018-x)=-f(x)$ and $g(2018-x)=-g(x)$, that is, a half turn about the point $(1009,0)$ preserves the graphs of $f$ and $g$. So it suffices to consider only the case $2 n-1<x<2 n$.\n\nLet $d(x)=g(x)-f(x)$. We will show that $d(x)>2$ whenever $2 n-1<x<2 n$ and $n \\in\\{1,2, \\ldots, 1009\\}$.\n\nFor any non-integer $x$ with $0<x<2018$, we have\n\n$$\nd(x+2)-d(x)=\\left(\\frac{1}{x+1}-\\frac{1}{x+2}\\right)+\\left(\\frac{1}{x-2018}-\\frac{1}{x-2017}\\right)>0+0=0\n$$\n\nHence it suffices to prove $d(x)>2$ for $1<x<2$. Since $x<2$, it follows that $\\frac{1}{x-2 i-1}>$ $\\frac{1}{x-2 i}$ for $i=2,3, \\ldots, 1008$. We also have $\\frac{1}{x-2018}<0$. Hence it suffices to prove the following\nfor $1<x<2$.\n\n$$\n\\begin{aligned}\n& \\frac{1}{x-1}+\\frac{1}{x-3}-\\frac{1}{x}-\\frac{1}{x-2}>2 \\\\\n\\Leftrightarrow & \\left(\\frac{1}{x-1}+\\frac{1}{2-x}\\right)+\\left(\\frac{1}{x-3}-\\frac{1}{x}\\right)>2 \\\\\n\\Leftrightarrow & \\frac{1}{(x-1)(2-x)}+\\frac{3}{x(x-3)}>2 .\n\\end{aligned}\n$$\n\nBy the $G M-H M$ inequality (alternatively, by considering the maximum of the quadratic $(x-1)(2-x))$ we have\n\n$$\n\\frac{1}{x-1} \\cdot \\frac{1}{2-x}>\\left(\\frac{2}{(x-1)+(2-x)}\\right)^{2}=4\n$$\n\nTo find a lower bound for $\\frac{3}{x(x-3)}$, note that $x(x-3)<0$ for $1<x<2$. So we seek an upper bound for $x(x-3)$. From the shape of the quadratic, this occurs at $x=1$ or $x=2$, both of which yield $\\frac{3}{x(x-3)}>-\\frac{3}{2}$.\n\nIt follows that $d(x)>4-\\frac{3}{2}>2$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
+
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "As in Solution 1, we may assume $2 n-1<x<2 n$ for some $1 \\leq n \\leq 1009$. Let $d(x)=$ $f(x)-g(x)$, and note that\n\n$$\nd(x)=\\frac{1}{x}+\\sum_{m=1}^{1009} \\frac{1}{(x-2 m)(x-2 m+1)}\n$$\n\nWe split the sum into three parts: the terms before $m=n$, after $m=n$, and the term $m=n$. The first two are\n\n$$\n\\begin{aligned}\n0 & \\leq \\sum_{m=1}^{n-1} \\frac{1}{(x-2 m)(x-2 m+1)} \\\\\n& \\leq \\sum_{m=1}^{n-1} \\frac{1}{(2 n-1-2 m)(2 n-2 m)}=\\sum_{i=1}^{n-1} \\frac{1}{(2 i)(2 i-1)} \\leq \\sum_{i=1}^{1008} \\frac{1}{2 i-1}-\\frac{1}{2 i} \\\\\n0 & \\leq \\sum_{m=n+1}^{1009} \\frac{1}{(2 m-x)(2 m-1-x)} \\\\\n& \\leq \\sum_{m=n+1}^{1009} \\frac{1}{(2 m-2 n+1)(2 m-2 n)}=\\sum_{i=1}^{1009-n} \\frac{1}{(2 i+1)(2 i)} \\leq \\sum_{i=1}^{1008} \\frac{1}{2 i}-\\frac{1}{2 i+1} .\n\\end{aligned}\n$$\n\nWhen we add the two sums the terms telescope and we are left with\n\n$$\n0 \\leq \\sum_{1 \\leq m \\leq 1009, m \\neq n} \\frac{1}{(x-2 m)(x-2 m+1)} \\leq 1-\\frac{1}{2017}<1\n$$\n\nFor the term $m=n$, we write\n\n$$\n0<-(x-2 n)(x-2 n+1)=0.25-(x-2 n+0.5)^{2} \\leq 0.25\n$$\n\nwhence\n\n$$\n-4 \\geq \\frac{1}{(x-2 n)(x-2 n+1)}\n$$\n\nFinally, $\\frac{1}{x}<1$ since $x>2 n-1 \\geq 1$. Combining these we get\n\n$$\nd(x)=\\frac{1}{x}+\\sum_{m=1}^{1009} \\frac{1}{(x-2 m)(x-2 m+1)}<1+1-4<-2 .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
+
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $f(x)$ and $g(x)$ be given by\n\n$$\nf(x)=\\frac{1}{x}+\\frac{1}{x-2}+\\frac{1}{x-4}+\\cdots+\\frac{1}{x-2018}\n$$\n\nand\n\n$$\ng(x)=\\frac{1}{x-1}+\\frac{1}{x-3}+\\frac{1}{x-5}+\\cdots+\\frac{1}{x-2017} .\n$$\n\nProve that\n\n$$\n|f(x)-g(x)|>2\n$$\n\nfor any non-integer real number $x$ satisfying $0<x<2018$.", "solution": "First notice that\n\n$$\nf(x)-g(x)=\\frac{1}{x}-\\frac{1}{x-1}+\\frac{1}{x-2}-\\cdots-\\frac{1}{x-2017}+\\frac{1}{x-2018} .\n$$\n\nAs in Solution 1, we may deal only with the case $2 n<x<2 n+1$. Then $x-2 k+1$ and $x-2 k$ never differ in sign for any integer $k$. Then\n\n$$\n\\begin{aligned}\n-\\frac{1}{x-2 k+1}+\\frac{1}{x-2 k} & =\\frac{1}{(x-2 k+1)(x-2 k)}>0 \\quad \\text { for } k=1,2, \\ldots, n-1, n+2, \\ldots, 1009 \\\\\n\\frac{1}{x-2 n}-\\frac{1}{x-2 n-1} & =\\frac{1}{(x-2 n)(2 n+1-x)} \\geq\\left(\\frac{2}{x-2 n+2 n+1-x}\\right)^{2}=4\n\\end{aligned}\n$$\n\nTherefore, summing all inequalities and collecting the remaining terms we find $f(x)-g(x)>$ $4+\\frac{1}{x-2}>4-1=3$ for $0<x<1$ and, for $n>0$,\n\n$$\n\\begin{aligned}\nf(x)-g(x) & >\\frac{1}{x}-\\frac{1}{x-2 n+1}+4+\\frac{1}{x-2 n-2} \\\\\n& =\\frac{1}{x}-\\frac{1}{x-2 n+1}+4-\\frac{1}{2 n+2-x} \\\\\n& >\\frac{1}{x}-\\frac{1}{2 n-2 n+1}+4-\\frac{1}{2 n+2-2 n-1} \\\\\n& =2+\\frac{1}{x}>2 .\n\\end{aligned}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 3"}}
|
| 6 |
+
{"year": "2018", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:\n(i) All the squares are congruent.\n(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.\n(iii) Each square touches exactly three other squares.\n\nHow many positive integers $n$ are there with $2018 \\leq n \\leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?\n\nAnswer: 501", "solution": "We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \\geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.\n\nFor any two different squares $A$ and $B$, let us write $A \\sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \\sim B$ is $3 n$. But $A \\sim B$ if and only if $B \\sim A$. Hence the total number of instances of $A \\sim B$ is even. Thus $3 n$ and hence also $n$ is even.\n\nWe now construct tri-connected collections for each even $n$ in the range. We show two\nConstruction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.\n\n\nPutting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \\geq 38$.\n\n\nConstruction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \\cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \\leq m \\leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \\geq 4$, this will be true. The picture for $n=24$ is as follows:\n\n\nTo treat the other cases, consider the following gadget\n\n\nTwo squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.\nThis gives us a valid configuration for $6 n+8$ squares, $n \\geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \\geq 4$, which finishes the proof for all even numbers at least 36 .", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 7 |
+
{"year": "2018", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an equilateral triangle. From the vertex $A$ we draw a ray towards the interior of the triangle such that the ray reaches one of the sides of the triangle. When the ray reaches a side, it then bounces off following the law of reflection, that is, if it arrives with a directed angle $\\alpha$, it leaves with a directed angle $180^{\\circ}-\\alpha$. After $n$ bounces, the ray returns to $A$ without ever landing on any of the other two vertices. Find all possible values of $n$.\n\nAnswer: All $n \\equiv 1,5 \\bmod 6$ with the exception of 5 and 17", "solution": "Consider an equilateral triangle $A A_{1} A_{2}$ of side length $m$ and triangulate it with unitary triangles. See the figure. To each of the vertices that remain after the triangulation we can assign a pair of coordinates $(a, b)$ where $a, b$ are non-negative integers, $a$ is the number of edges we travel in the $A A_{1}$ direction and $b$ is the number of edges we travel in the $A A_{2}$ direction to arrive to the vertex, (we have $A=(0,0), A_{1}=(m, 0)$ and $A_{2}=(0, m)$ ). The unitary triangle with vertex $A$ will be our triangle $A B C,(B=(1,0), C=(0,1))$. We can obtain every unitary triangle by starting with $A B C$ and performing reflections with respect to a side (the vertex $(1,1)$ is the reflection of $A$ with respect to $B C$, the vertex $(0,2)$ is the reflection of $B=(1,0)$ with respect to the side formed by $C=(1,0)$ and $(1,1)$, and so on).\n\nWhen we reflect a vertex $(a, b)$ with respect to a side of one of the triangles, the congruence of $a-b$ is preserved modulo 3. Furthermore, an induction argument shows that any two vertices $(a, b)$ and $\\left(a^{\\prime}, b^{\\prime}\\right)$ with $a-b \\equiv a^{\\prime}-b^{\\prime}$ mod 3 can be obtained from each other by a series of such reflections. Therefore, the set of vertices $V$ that result from the reflections of $A$ will be those of the form $(a, b)$ satisfying $a \\equiv b \\bmod 3$. See the green vertices in the figure.\n\nNow, let $U$ be the set of vertices $u$ that satisfy that the line segment between $u$ and $A$ does not pass through any other vertex. A pair $(a, b)$ is in $U$ if and only if $\\operatorname{gcd}(a, b)=1$, since otherwise for $d=\\operatorname{gcd}(a, b)$ we have that the vertex $(a / d, b / d)$ also lies on the line segment between $u$ and $A$.\n\nObserve that the rays that come out from $A$ and eventually return to $A$ are those that come out towards a vertex in $V \\cap U$ (they would be in $V$ to be able to come back to $A$ and in $U$ so that they do not reach a vertex beforehand). In the diagram, a ray toward one such vertex $(a, b)$ will intersect exactly $(a-1)+(b-1)+(a+b-1)=2(a+b)-3$ lines: $a-1$ of them parallel to $A B, b-1$ parallel to $A C$ and $a+b-1$ parallel to $B C$. Therefore, in the triangle $A B C$ the ray will bounce $2(a+b)-3$ times before returning to $A$. So we want to find all\n\n$n=2(a+b)-3$ where $a \\equiv b \\bmod 3$ and $\\operatorname{gcd}(a, b)=1$.\nIf $a+b$ is a multiple of 3 then we cannot satisfy both conditions simultaneously, therefore $n$ is not a multiple of 3 . We also know that $n$ is odd. Therefore $n \\equiv 1,5,7,11 \\bmod 12$. Note that the pair $(1,3 k+1)$ satisfies the conditions and we can create $n=2(3 k+2)-3=6 k+1$ for all $k \\geq 0$ (this settles the question for $n \\equiv 1,7 \\bmod 12$ ). For $n \\equiv 5 \\bmod 12$ consider the pair $(3 k-1,3 k+5)$ when $k$ is even or $(3 k-4,3 k+8)$ when $k$ is odd. This gives us all the integers of the form $12 k+5$ for $k \\geq 2$. For $11 \\bmod 12$, take the pairs $(3 k-1,3 k+2)($ with $k \\geq 1)$, which yield all positive integers of the form $12 k-1$.\n\nFinally, to discard 5 and 17 note that the only pairs $(a, b)$ that are solutions to $2(a+b)-3=5$ or $2(a+b)-3=17$ with the same residue $\\bmod 3$ in this range are the non-relatively prime pairs $(2,2),(2,8)$ and $(5,5)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 8 |
+
{"year": "2018", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.\n\nAnswer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.", "solution": ": $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.\nNotice that if $P(x)$ is a solution, then so is $P(x)+k$ and $-P(x)+k$ for any integer $k$, so we may assume that the leading coefficient of $P(x)$ is positive and that $P(0)=0$, i.e., we can assume that $P(x)=\\sum_{i=1}^{n} a_{i} x^{i}$ with $a_{n}>0$. We are going to prove that $P(x)=x^{n}$ in this case.\n\nLet $p$ be a large prime such that $p>\\sum_{i=1}^{n}\\left|a_{i}\\right|$. Because $P$ has a positive leading coefficient and $p$ is large enough, we can find $t \\in \\mathbb{R}$ such that $P(t)=p$. Denote the greatest common divisor of the polynomial $P(x)-p$ and $P(2 x)-P(2 t)$ as $f(x)$, and $t$ is a root of it, so $f$ is a non-constant polynomial. Notice that $P(2 t)$ is an integer by using the hypothesis for $s=2$ and $t$. Since $P(x)-p$ and $P(2 x)-P(2 t)$ are polynomials with integer coefficients, $f$ can be chosen as a polynomial with rational coefficients.\n\nIn the following, we will prove that $f$ is the same as $P(x)-p$ up to a constant multiplier. Say $P(x)-p=f(x) g(x)$, where $f$ and $g$ are non-constant polynomials. By Gauss's lemma, we can get $f_{1}, g_{1}$ with $P(x)-p=f_{1}(x) g_{1}(x)$ where $f_{1}$ is a scalar multiple of $f$ and $g_{1}$ is a scalar multiple of $g$ and one of $f_{1}, g_{1}$ has constant term $\\pm 1$ (this is because $-p=P(0)-p=f(0) g(0)$ with $p$ prime). So $P(x)-p$ has at least one root $r$ with absolute value not greater than 1 (using\n\nVieta, the product of the roots of the polynomial with constant term $\\pm 1$ is $\\pm 1$ ), but\n\n$$\n|P(r)-p|=\\left|\\sum_{i=1}^{n} a_{i} r^{i}-p\\right|>p-\\sum_{i=1}^{n}\\left|a_{i}\\right|>0\n$$\n\nhence we get a contradiction!\nTherefore $f$ is a constant multiple of $P(x)-p$, so $P(2 x)-P(2 t)$ is a constant multiple of $P(x)-p$ because they both have the same degree. By comparing leading coefficients we get that $P(2 x)-P(2 t)=2^{n}(P(x)-p)$. Comparing the rest of the coefficients we get that $P(x)=a_{n} x^{n}$. If we let $a=b=\\left(1 / a_{n}\\right)^{1 / n}$, then $P(a)=P(b)=1$, so $P(a b)$ must also be an integer. But $P(a b)=\\frac{1}{a_{n}}$. Therefore $a_{n}=1$ and the proof is complete.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 1"}}
|
| 9 |
+
{"year": "2018", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.\n\nAnswer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.", "solution": ": Assume $P(x)=\\sum_{i=0}^{n} a_{i} x^{i}$. Consider the following system of equations\n\n$$\n\\begin{aligned}\n& a_{0}=P(0) \\\\\n& a_{n} t^{n}+a_{n-1} t^{n-1}+\\cdots+a_{0}=P(t) \\\\\n& 2^{n} a_{n} t^{n}+2^{n-1} a_{n-1} t^{n-1}+\\cdots+a_{0}=P(2 t) \\\\\n& \\vdots \\\\\n& n^{n} a_{n} t^{n}+n^{n-1} a_{n-1} t^{n-1}+\\cdots+a_{0}=P(n t)\n\\end{aligned}\n$$\n\nviewing $a_{k} t^{k}$ as variables. Note that if $P(t)$ is an integer, then by the hypothesis all the terms on the right hand side of the equations are integers as well. By using Cramer's rule, we can get that $a_{k} t^{k}=D / M$, where $D$ is an integer and $M$ is the following determinant\n\n$$\n\\left|\\begin{array}{ccccc}\n1 & 0 & 0 & \\cdots & 0 \\\\\n1 & 1 & 1 & \\cdots & 1 \\\\\n1 & 2 & 4 & \\cdots & 2^{n} \\\\\n\\vdots & \\vdots & \\vdots & & \\vdots \\\\\n1 & n & n^{2} & \\cdots & n^{n}\n\\end{array}\\right| \\neq 0\n$$\n\nThus, if we let $r$ be the smallest positive index such that $a_{r} \\neq 0$, we can express each $t \\in \\mathbb{R}$ with $P(t) \\in \\mathbb{Z}$ in the form $\\left(\\frac{m}{M^{\\prime}}\\right)^{1 / r}$ for some integer $m$, and where $M^{\\prime}=M \\times a_{r}$ is a constant.\n\nWe can choose $L$ large enough such that $\\left.P\\right|_{\\mathbb{R}_{\\geq L}}$ is injective, and for any larger $N$, the growth order of the number of values in the form $\\left(\\frac{m}{M^{\\prime}}\\right)^{1 / r}$ is $N^{r}$, while the growth order of the number of integers in $[P(L), P(N)]$ is $N^{n}$, so $r=n$. Therefore $P(x)$ is of the form $a_{n} x^{n}+k$. The problem can be finished as in Solution 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 2"}}
|
APMO/segmented/en-apmo2019_sol.jsonl
CHANGED
|
@@ -1,10 +1,10 @@
|
|
| 1 |
-
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": "First we perform the following substitutions on the original relation:\n\n1. With $a=b=1$, we find that $f(1)+1 \\mid f(1)^{2}+1$, which implies $f(1)=1$.\n2. With $a=1$, we find that $b+1 \\mid f(b)+1$. In particular, $b \\leq f(b)$ for all $b \\in \\mathbb{Z}^{+}$.\n3. With $b=1$, we find that $f(a)+1 \\mid a^{2}+f(a)$, and thus $f(a)+1 \\mid a^{2}-1$. In particular, $f(a) \\leq a^{2}-2$ for all $a \\geq 2$.\n\nNow, let $p$ be any odd prime. Substituting $a=p$ and $b=f(p)$ in the original relation, we find that $2 f(p) \\mid p^{2}+f(p) f(f(p))$. Therefore, $f(p) \\mid p^{2}$. Hence the possible values of $f(p)$ are $1, p$ and $p^{2}$. By (2) above, $f(p) \\geq p$ and by (3) above $f(p) \\leq p^{2}-2$. So $f(p)=p$ for all primes $p$.\n\nSubstituting $a=p$ into the original relation, we find that $b+p \\mid p^{2}+p f(b)$. However, since $(b+p)(f(b)+p-b)=p^{2}-b^{2}+b f(b)+p f(b)$, we have $b+p \\mid b f(b)-b^{2}$. Thus, for any fixed $b$ this holds for arbitrarily large primes $p$ and therefore we must have $b f(b)-b^{2}=0$, or $f(b)=b$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": ": As above, we have relations (1)-(3). In (2) and (3), for $b=2$ we have $3 \\mid f(2)+1$ and $f(2)+1 \\mid 3$. These imply $f(2)=2$.\n\nNow, using $a=2$ we get $2+b \\mid 4+2 f(b)$. Let $f(b)=x$. We have\n\n$$\n\\begin{aligned}\n1+x & \\equiv 0 \\quad(\\bmod b+1) \\\\\n4+2 x & \\equiv 0 \\quad(\\bmod b+2)\n\\end{aligned}\n$$\n\nFrom the first equation $x \\equiv b(\\bmod b+1)$ so $x=b+(b+1) t$ for some integer $t \\geq 0$. Then\n\n$$\n0 \\equiv 4+2 x \\equiv 4+2(b+(b+1) t) \\equiv 4+2(-2-t) \\equiv-2 t \\quad(\\bmod b+2)\n$$\n\nAlso $t \\leq b-2$ because $1+x \\mid b^{2}-1$ by (3).\nIf $b+2$ is odd, then $t \\equiv 0(\\bmod b+2)$. Then $t=0$, which implies $f(b)=b$.\nIf $b+2$ is even, then $t \\equiv 0(\\bmod (b+2) / 2)$. Then $t=0$ or $t=(b+2) / 2$. But if $t \\neq 0$, then by definition $(b+4) / 2=(1+t)=(x+1) /(b+1)$ and since $x+1 \\mid b^{2}-1$, then $(b+4) / 2$ divides $b-1$. Therefore $b+4 \\mid 10$ and the only possibility is $b=6$. So for even $b, b \\neq 6$ we have $f(b)=b$.\n\nFinally, by (2) and (3), for $b=6$ we have $7 \\mid f(6)+1$ and $f(6)+1 \\mid 35$. This means $f(6)=6$ or $f(6)=34$. The later is discarded as, for $a=5, b=6$, we have by the original equation that $11 \\mid 5(5+f(6))$. Therefore $f(n)=n$ for every positive integer $n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": ": We proceed by induction. As in Solution 1, we have $f(1)=1$. Suppose that $f(n-1)=n-1$ for some integer $n \\geq 2$.\n\nWith the substitution $a=n$ and $b=n-1$ in the original relation we obtain that $f(n)+$ $n-1 \\mid n^{2}+f(n)(n-1)$. Since $f(n)+n-1 \\mid(n-1)(f(n)+n-1)$, then $f(n)+n-1 \\mid 2 n-1$.\n\nWith the substitution $a=n-1$ and $b=n$ in the original relation we obtain that $2 n-$ $1 \\mid(n-1)^{2}+(n-1) f(n)=(n-1)(n-1+f(n))$. Since $(2 n-1, n-1)=1$, we deduce that $2 n-1 \\mid f(n)+n-1$.\n\nTherefore, $f(n)+n-1=2 n-1$, which implies the desired $f(n)=n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 3"}}
|
| 4 |
-
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $m$ be a fixed positive integer. The infinite sequence $\\left\\{a_{n}\\right\\}_{n \\geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \\geq 1$ we have\n\n$$\na_{n+1}= \\begin{cases}a_{n}^{2}+2^{m} & \\text { if } a_{n}<2^{m} \\\\ a_{n} / 2 & \\text { if } a_{n} \\geq 2^{m}\\end{cases}\n$$\n\nFor each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.\n\nAnswer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$.", "solution": "Suppose that for integers $m$ and $a_{1}$ all the terms of the sequence are integers. For each $i \\geq 1$, write the $i$ th term of the sequence as $a_{i}=b_{i} 2^{c_{i}}$ where $b_{i}$ is the largest odd divisor of $a_{i}$ (the \"odd part\" of $a_{i}$ ) and $c_{i}$ is a nonnegative integer.\n\nLemma 1. The sequence $b_{1}, b_{2}, \\ldots$ is bounded above by $2^{m}$.\nProof. Suppose this is not the case and take an index $i$ for which $b_{i}>2^{m}$ and for which $c_{i}$ is minimal. Since $a_{i} \\geq b_{i}>2^{m}$, we are in the second case of the recursion. Therefore, $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}>2^{m}$ and $c_{i+1}=c_{i}-1<c_{i}$. This contradicts the minimality of $c_{i}$.\n\nLemma 2. The sequence $b_{1}, b_{2}, \\ldots$ is nondecreasing.\nProof. If $a_{i} \\geq 2^{m}$, then $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}$. On the other hand, if $a_{i}<2^{m}$, then\n\n$$\na_{i+1}=a_{i}^{2}+2^{m}=b_{i}^{2} 2^{2 c_{i}}+2^{m}\n$$\n\nand we have the following cases:\n\n- If $2 c_{i}>m$, then $a_{i+1}=2^{m}\\left(b_{i}^{2} 2^{2 c_{i}-m}+1\\right)$, so $b_{i+1}=b_{i}^{2} 2^{2 c_{i}-m}+1>b_{i}$.\n- If $2 c_{i}<m$, then $a_{i+1}=2^{2 c_{i}}\\left(b_{i}^{2}+2^{m-2 c_{i}}\\right)$, so $b_{i+1}=b_{i}^{2}+2^{m-2 c_{i}}>b_{i}$.\n- If $2 c_{i}=m$, then $a_{i+1}=2^{m+1} \\cdot \\frac{b_{i}^{2}+1}{2}$, so $b_{i+1}=\\left(b_{i}^{2}+1\\right) / 2 \\geq b_{i}$ since $b_{i}^{2}+1 \\equiv 2(\\bmod 4)$.\n\nBy combining these two lemmas we obtain that the sequence $b_{1}, b_{2}, \\ldots$ is eventually constant. Fix an index $j$ such that $b_{k}=b_{j}$ for all $k \\geq j$. Since $a_{n}$ descends to $a_{n} / 2$ whenever $a_{n} \\geq 2^{m}$, there are infinitely many terms which are smaller than $2^{m}$. Thus, we can choose an $i>j$ such that $a_{i}<2^{m}$. From the proof of Lemma $2, a_{i}<2^{m}$ and $b_{i+1}=b_{i}$ can happen simultaneously only when $2 c_{i}=m$ and $b_{i+1}=b_{i}=1$. By Lemma 2 , the sequence $b_{1}, b_{2}, \\ldots$ is constantly 1 and thus $a_{1}, a_{2}, \\ldots$ are all powers of two. Tracing the sequence starting from $a_{i}=2^{c_{i}}=2^{m / 2}<2^{m}$,\n\n$$\n2^{m / 2} \\rightarrow 2^{m+1} \\rightarrow 2^{m} \\rightarrow 2^{m-1} \\rightarrow 2^{2 m-2}+2^{m}\n$$\n\nNote that this last term is a power of two if and only if $2 m-2=m$. This implies that $m$ must be equal to 2 . When $m=2$ and $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$ the sequence eventually cycles through $2,8,4,2, \\ldots$. When $m=2$ and $a_{1}=1$ the sequence fails as the first terms are $1,5,5 / 2$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 5 |
-
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $m$ be a fixed positive integer. The infinite sequence $\\left\\{a_{n}\\right\\}_{n \\geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \\geq 1$ we have\n\n$$\na_{n+1}= \\begin{cases}a_{n}^{2}+2^{m} & \\text { if } a_{n}<2^{m} \\\\ a_{n} / 2 & \\text { if } a_{n} \\geq 2^{m}\\end{cases}\n$$\n\nFor each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.\n\nAnswer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$.", "solution": ": Let $m$ be a positive integer and suppose that $\\left\\{a_{n}\\right\\}$ consists only of positive integers. Call a number small if it is smaller than $2^{m}$ and large otherwise. By the recursion,\nafter a small number we have a large one and after a large one we successively divide by 2 until we get a small one.\n\nFirst, we note that $\\left\\{a_{n}\\right\\}$ is bounded. Indeed, $a_{1}$ turns into a small number after a finite number of steps. After this point, each small number is smaller than $2^{m}$, so each large number is smaller than $2^{2 m}+2^{m}$. Now, since $\\left\\{a_{n}\\right\\}$ is bounded and consists only of positive integers, it is eventually periodic. We focus only on the cycle.\n\nAny small number $a_{n}$ in the cycle can be writen as $a / 2$ for $a$ large, so $a_{n} \\geq 2^{m-1}$, then $a_{n+1} \\geq 2^{2 m-2}+2^{m}=2^{m-2}\\left(4+2^{m}\\right)$, so we have to divide $a_{n+1}$ at least $m-1$ times by 2 until we get a small number. This means that $a_{n+m}=\\left(a_{n}^{2}+2^{m}\\right) / 2^{m-1}$, so $2^{m-1} \\mid a_{n}^{2}$, and therefore $2^{\\lceil(m-1) / 2\\rceil} \\mid a_{n}$ for any small number $a_{n}$ in the cycle. On the other hand, $a_{n} \\leq 2^{m}-1$, so $a_{n+1} \\leq 2^{2 m}-2^{m+1}+1+2^{m} \\leq 2^{m}\\left(2^{m}-1\\right)$, so we have to divide $a_{n+1}$ at most $m$ times by two until we get a small number. This means that after $a_{n}$, the next small number is either $N=a_{m+n}=\\left(a_{n}^{2} / 2^{m-1}\\right)+2$ or $a_{m+n+1}=N / 2$. In any case, $2^{\\lceil(m-1) / 2\\rceil}$ divides $N$.\n\nIf $m$ is odd, then $x^{2} \\equiv-2\\left(\\bmod 2^{\\lceil(m-1) / 2\\rceil}\\right)$ has a solution $x=a_{n} / 2^{(m-1) / 2}$. If $(m-1) / 2 \\geq$ $2 \\Longleftrightarrow m \\geq 5$ then $x^{2} \\equiv-2(\\bmod 4)$, which has no solution. So if $m$ is odd, then $m \\leq 3$.\n\nIf $m$ is even, then $2^{m-1}\\left|a_{n}^{2} \\Longrightarrow 2^{\\lceil(m-1) / 2\\rceil}\\right| a_{n} \\Longleftrightarrow 2^{m / 2} \\mid a_{n}$. Then if $a_{n}=2^{m / 2} x$, $2 x^{2} \\equiv-2\\left(\\bmod 2^{m / 2}\\right) \\Longleftrightarrow x^{2} \\equiv-1\\left(\\bmod 2^{(m / 2)-1}\\right)$, which is not possible for $m \\geq 6$. So if $m$ is even, then $m \\leq 4$.\n\nThe cases $m=1,2,3,4$ are handed manually, checking the possible small numbers in the cycle, which have to be in the interval $\\left[2^{m-1}, 2^{m}\\right)$ and be divisible by $2^{\\lceil(m-1) / 2\\rceil}$ :\n\n- For $m=1$, the only small number is 1 , which leads to 5 , then $5 / 2$.\n- For $m=2$, the only eligible small number is 2 , which gives the cycle $(2,8,4)$. The only way to get to 2 is by dividing 4 by 2 , so the starting numbers greater than 2 are all numbers that lead to 4 , which are the powers of 2 .\n- For $m=3$, the eligible small numbers are 4 and 6 ; we then obtain $4,24,12,6,44,22,11,11 / 2$.\n- For $m=4$, the eligible small numbers are 8 and 12 ; we then obtain $8,80,40,20,10, \\ldots$ or $12,160,80,40,20,10, \\ldots$, but in either case 10 is not an elegible small number.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 6 |
-
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$\n\nbe a scalene triangle with circumcircle $\\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.", "solution": "Let $N$ be the radical center of the circumcircles of triangles $A B C, B M P$ and $C M P$. The pairwise radical axes of these circles are $B D, C E$ and $P M$, and hence they concur at $N$. Now, note that in directed angles:\n\n$$\n\\angle M C E=\\angle M P E=\\angle M P Y=\\angle M B Y .\n$$\n\n\n\nIt follows that $B Y$ is parallel to $C E$, and analogously that $C X$ is parallel to $B D$. Then, if $L$ is the intersection of $B Y$ and $C X$, it follows that $B N C L$ is a parallelogram. Since $B M=M C$ we deduce that $L$ is the reflection of $N$ with respect to $M$, and therefore $L \\in A M$. Using power of a point from $L$ to the circumcircles of triangles $B P M$ and $C P M$, we have\n\n$$\nL Y \\cdot L B=L P \\cdot L M=L X \\cdot L C\n$$\n\nHence, $B Y X C$ is cyclic. Using the cyclic quadrilateral we find in directed angles:\n\n$$\n\\angle L X Y=\\angle L B C=\\angle B C N=\\angle N D E .\n$$\n\nSince $C X \\| B N$, it follows that $X Y \\| D E$.\nLet $Q$ and $R$ be two points in $\\Gamma$ such that $C Q, B R$, and $A M$ are all parallel. Then in directed angles:\n\n$$\n\\angle Q D B=\\angle Q C B=\\angle A M B=\\angle P M B=\\angle P D B .\n$$\n\nThen $D, P, Q$ are collinear. Analogously $E, P, R$ are collinear. From here we get $\\angle P R Q=$ $\\angle P D E=\\angle P X Y$, since $X Y$ and $D E$ are parallel. Therefore $Q R Y X$ is cyclic. Let $S$ be the radical center of the circumcircle of triangle $A B C$ and the circles $B C Y X$ and $Q R Y X$. This point lies in the lines $B C, Q R$ and $X Y$ because these are the radical axes of the circles. Let $T$ be the second intersection of $A S$ with $\\Gamma$. By power of a point from $S$ to the circumcircle of $A B C$ and the circle $B C X Y$ we have\n\n$$\nS X \\cdot S Y=S B \\cdot S C=S T \\cdot S A\n$$\n\nTherefore $T$ is in the circumcircle of triangle $A X Y$. Since $Q$ and $R$ are fixed regardless of the choice of $P$, then $S$ is also fixed, since it is the intersection of $Q R$ and $B C$. This implies $T$ is also fixed, and therefore, the circumcircle of triangle $A X Y$ goes through $T \\neq A$ for any choice of $P$.\n\nNow we show an alternative way to prove that $B C X Y$ and $Q R X T$ are cyclic.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 7 |
-
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$\n\nbe a scalene triangle with circumcircle $\\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.", "solution": ". Let the lines $D P$ and $E P$ meet the circumcircle of $A B C$ again at $Q$ and $R$, respectively. Then $\\angle D Q C \\angle D B C=\\angle D P M$, so $Q C \\| P M$. Similarly, $R B \\| P M$.\n\n\nNow, $\\angle Q C B=\\angle P M B=\\angle P X C=\\angle(Q X, C X)$, which is half of the arc $Q C$ in the circumcircle $\\omega_{C}$ of $Q X C$. So $\\omega_{C}$ is tangent to $B S$; analogously, $\\omega_{B}$, the circumcicle of $R Y B$, is also tangent to $B C$. Since $B R \\| C Q$, the inscribed trapezoid $B R Q C$ is isosceles, and by symmetry $Q R$ is also tangent to both circles, and the common perpendicular bisector of $B R$ and $C Q$ passes through the centers of $\\omega_{B}$ and $\\omega_{C}$. Since $M B=M C$ and $P M\\|B R\\| C Q$, the line $P M$ is the radical axis of $\\omega_{B}$ and $\\omega_{C}$.\n\nHowever, $P M$ is also the radical axis of the circumcircles $\\gamma_{B}$ of $P M B$ and $\\gamma_{C}$ of $P M C$. Let $C X$ and $P M$ meet at $Z$. Let $p(K, \\omega)$ denote the power of a point $K$ with respect to a circumference $\\omega$. We have\n\n$$\np\\left(Z, \\gamma_{B}\\right)=p\\left(Z, \\gamma_{C}\\right)=Z X \\cdot Z C=p\\left(Z, \\omega_{B}\\right)=p\\left(Z, \\omega_{C}\\right)\n$$\n\nPoint $Z$ is thus the radical center of $\\gamma_{B}, \\gamma_{C}, \\omega_{B}, \\omega_{C}$. Thus, the radical axes $B Y, C X, P M$ meet at $Z$. From here,\n\n$$\n\\begin{aligned}\n& Z Y \\cdot Z B=Z C \\cdot Z X \\Rightarrow B C X Y \\text { cyclic } \\\\\n& P Y \\cdot P R=P X \\cdot P Q \\Rightarrow Q R X T \\text { cyclic. }\n\\end{aligned}\n$$\n\nWe may now finish as in Solution 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution 2"}}
|
| 8 |
-
{"year": "2019", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Consider a $2018 \\times 2019$ board with integers in each unit square. Two unit squares are said to be neighbours if they share a common edge. In each turn, you choose some unit squares. Then for each chosen unit square the average of all its neighbours is calculated. Finally, after these calculations are done, the number in each chosen unit square is replaced by the corresponding average. Is it always possible to make the numbers in all squares become the same after finitely many turns?\n\nAnswer: No", "solution": "Let $n$ be a positive integer relatively prime to 2 and 3 . We may study the whole process modulo $n$ by replacing divisions by $2,3,4$ with multiplications by the corresponding inverses modulo $n$. If at some point the original process makes all the numbers equal, then the process modulo $n$ will also have all the numbers equal. Our aim is to choose $n$ and an initial configuration modulo $n$ for which no process modulo $n$ reaches a board with all numbers equal modulo $n$. We split this goal into two lemmas.\n\nLemma 1. There is a $2 \\times 3$ board that stays constant modulo 5 and whose entries are not all equal.\n\nProof. Here is one such a board:\n\n\nThe fact that the board remains constant regardless of the choice of squares can be checked square by square.\n\nLemma 2. If there is an $r \\times s$ board with $r \\geq 2, s \\geq 2$, that stays constant modulo 5 , then there is also a $k r \\times l s$ board with the same property.\n\nProof. We prove by a case by case analysis that repeateadly reflecting the $r \\times s$ with respect to an edge preserves the property:\n\n- If a cell had 4 neighbors, after reflections it still has the same neighbors.\n- If a cell with $a$ had 3 neighbors $b, c, d$, we have by hypothesis that $a \\equiv 3^{-1}(b+c+d) \\equiv$ $2(b+c+d)(\\bmod 5)$. A reflection may add $a$ as a neighbor of the cell and now\n\n$$\n4^{-1}(a+b+c+d) \\equiv 4(a+b+c+d) \\equiv 4 a+2 a \\equiv a \\quad(\\bmod 5)\n$$\n\n- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \\equiv 2^{-1}(b+c) \\equiv 3(b+c)$ $(\\bmod 5)$. If the reflections add one $a$ as neighbor, now\n\n$$\n3^{-1}(a+b+c) \\equiv 2(3(b+c)+b+c) \\equiv 8(b+c) \\equiv 3(b+c) \\equiv a \\quad(\\bmod 5)\n$$\n\n- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \\equiv 2^{-1}(b+c)(\\bmod 5)$. If the reflections add two $a$ 's as neighbors, now\n\n$$\n4^{-1}(2 a+b+c) \\equiv\\left(2^{-1} a+2^{-1} a\\right) \\equiv a \\quad(\\bmod 5)\n$$\n\nIn the three cases, any cell is still preserved modulo 5 after an operation. Hence we can fill in the $k r \\times l s$ board by $k \\times l$ copies by reflection.\n\nSince 2|2018 and 3|2019, we can get through reflections the following board:\n\n\nBy the lemmas above, the board is invariant modulo 5, so the answer is no.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 9 |
-
{"year": "2019", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Determine all the functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf\\left(x^{2}+f(y)\\right)=f(f(x))+f\\left(y^{2}\\right)+2 f(x y)\n$$\n\nfor all real number $x$ and $y$.\nAnswer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.", "solution": "By substituting $x=y=0$ in the given equation of the problem, we obtain that $f(0)=0$. Also, by substituting $y=0$, we get $f\\left(x^{2}\\right)=f(f(x))$ for any $x$.\n\nFurthermore, by letting $y=1$ and simplifying, we get\n\n$$\n2 f(x)=f\\left(x^{2}+f(1)\\right)-f\\left(x^{2}\\right)-f(1)\n$$\n\nfrom which it follows that $f(-x)=f(x)$ must hold for every $x$.\nSuppose now that $f(a)=f(b)$ holds for some pair of numbers $a, b$. Then, by letting $y=a$ and $y=b$ in the given equation, comparing the two resulting identities and using the fact that $f\\left(a^{2}\\right)=f(f(a))=f(f(b))=f\\left(b^{2}\\right)$ also holds under the assumption, we get the fact that\n\n$$\nf(a)=f(b) \\Rightarrow f(a x)=f(b x) \\quad \\text { for any real number } x\n$$\n\nConsequently, if for some $a \\neq 0, f(a)=0$, then we see that, for any $x, f(x)=f\\left(a \\cdot \\frac{x}{a}\\right)=$ $f\\left(0 \\cdot \\frac{x}{a}\\right)=f(0)=0$, which gives a trivial solution to the problem.\n\nIn the sequel, we shall try to find a non-trivial solution for the problem. So, let us assume from now on that if $a \\neq 0$ then $f(a) \\neq 0$ must hold. We first note that since $f(f(x))=f\\left(x^{2}\\right)$ for all $x$, the right-hand side of the given equation equals $f\\left(x^{2}\\right)+f\\left(y^{2}\\right)+2 f(x y)$, which is invariant if we interchange $x$ and $y$. Therefore, we have\n\n$$\nf\\left(x^{2}\\right)+f\\left(y^{2}\\right)+2 f(x y)=f\\left(x^{2}+f(y)\\right)=f\\left(y^{2}+f(x)\\right) \\quad \\text { for every pair } x, y\n$$\n\nNext, let us show that for any $x, f(x) \\geq 0$ must hold. Suppose, on the contrary, $f(s)=-t^{2}$ holds for some pair $s, t$ of non-zero real numbers. By setting $x=s, y=t$ in the right hand side of (2), we get $f\\left(s^{2}+f(t)\\right)=f\\left(t^{2}+f(s)\\right)=f(0)=0$, so $f(t)=-s^{2}$. We also have $f\\left(t^{2}\\right)=f\\left(-t^{2}\\right)=f(f(s))=f\\left(s^{2}\\right)$. By applying (2) with $x=\\sqrt{s^{2}+t^{2}}$ and $y=s$, we obtain\n\n$$\nf\\left(s^{2}+t^{2}\\right)+2 f\\left(s \\cdot \\sqrt{s^{2}+t^{2}}\\right)=0\n$$\n\nand similarly, by applying (2) with $x=\\sqrt{s^{2}+t^{2}}$ and $y=t$, we obtain\n\n$$\nf\\left(s^{2}+t^{2}\\right)+2 f\\left(t \\cdot \\sqrt{s^{2}+t^{2}}\\right)=0\n$$\n\nConsequently, we obtain\n\n$$\nf\\left(s \\cdot \\sqrt{s^{2}+t^{2}}\\right)=f\\left(t \\cdot \\sqrt{s^{2}+t^{2}}\\right)\n$$\n\nBy applying (1) with $a=s \\sqrt{s^{2}+t^{2}}, b=t \\sqrt{s^{2}+t^{2}}$ and $x=1 / \\sqrt{s^{2}+t^{2}}$, we obtain $f(s)=$ $f(t)=-s^{2}$, from which it follows that\n\n$$\n0=f\\left(s^{2}+f(s)\\right)=f\\left(s^{2}\\right)+f\\left(s^{2}\\right)+2 f\\left(s^{2}\\right)=4 f\\left(s^{2}\\right)\n$$\n\na contradiction to the fact $s^{2}>0$. Thus we conclude that for all $x \\neq 0, f(x)>0$ must be satisfied.\n\nNow, we show the following fact\n\n$$\nk>0, f(k)=1 \\Leftrightarrow k=1\n$$\n\nLet $k>0$ for which $f(k)=1$. We have $f\\left(k^{2}\\right)=f(f(k))=f(1)$, so by $(1), f(1 / k)=f(k)=$ 1 , so we may assume $k \\geq 1$. By applying (2) with $x=\\sqrt{k^{2}-1}$ and $y=k$, and using $f(x) \\geq 0$, we get\n\n$$\nf\\left(k^{2}-1+f(k)\\right)=f\\left(k^{2}-1\\right)+f\\left(k^{2}\\right)+2 f\\left(k \\sqrt{k^{2}-1}\\right) \\geq f\\left(k^{2}-1\\right)+f\\left(k^{2}\\right) .\n$$\n\nThis simplifies to $0 \\geq f\\left(k^{2}-1\\right) \\geq 0$, so $k^{2}-1=0$ and thus $k=1$.\nNext we focus on showing $f(1)=1$. If $f(1)=m \\leq 1$, then we may proceed as above by setting $x=\\sqrt{1-m}$ and $y=1$ to get $m=1$. If $f(1)=m \\geq 1$, now we note that $f(m)=f(f(1))=f\\left(1^{2}\\right)=f(1)=m \\leq m^{2}$. We may then proceed as above with $x=\\sqrt{m^{2}-m}$ and $y=1$ to show $m^{2}=m$ and thus $m=1$.\n\nWe are now ready to finish. Let $x>0$ and $m=f(x)$. Since $f(f(x))=f\\left(x^{2}\\right)$, then $f\\left(x^{2}\\right)=$ $f(m)$. But by (1), $f\\left(m / x^{2}\\right)=1$. Therefore $m=x^{2}$. For $x<0$, we have $f(x)=f(-x)=f\\left(x^{2}\\right)$ as well. Therefore, for all $x, f(x)=x^{2}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
| 10 |
-
{"year": "2019", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Determine all the functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf\\left(x^{2}+f(y)\\right)=f(f(x))+f\\left(y^{2}\\right)+2 f(x y)\n$$\n\nfor all real number $x$ and $y$.\nAnswer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.", "solution": "After proving that $f(x)>0$ for $x \\neq 0$ as in the previous solution, we may also proceed as follows. We claim that $f$ is injective on the positive real numbers. Suppose that $a>b>0$ satisfy $f(a)=f(b)$. Then by setting $x=1 / b$ in (1) we have $f(a / b)=f(1)$. Now, by induction on $n$ and iteratively setting $x=a / b$ in (1) we get $f\\left((a / b)^{n}\\right)=1$ for any positive integer $n$.\n\nNow, let $m=f(1)$ and $n$ be a positive integer such that $(a / b)^{n}>m$. By setting $x=$ $\\sqrt{(a / b)^{n}-m}$ and $y=1$ in (2) we obtain that\n$f\\left((a / b)^{n}-m+f(1)\\right)=f\\left((a / b)^{n}-m\\right)+f\\left(1^{2}\\right)+2 f\\left(\\sqrt{\\left.(a / b)^{n}-m\\right)}\\right) \\geq f\\left((a / b)^{n}-m\\right)+f(1)$.\nSince $f\\left((a / b)^{n}\\right)=f(1)$, this last equation simplifies to $f\\left((a / b)^{n}-m\\right) \\leq 0$ and thus $m=$ $(a / b)^{n}$. But this is impossible since $m$ is constant and $a / b>1$. Thus, $f$ is injective on the positive real numbers. Since $f(f(x))=f\\left(x^{2}\\right)$, we obtain that $f(x)=x^{2}$ for any real value $x$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 2"}}
|
|
|
|
| 1 |
+
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": "First we perform the following substitutions on the original relation:\n\n1. With $a=b=1$, we find that $f(1)+1 \\mid f(1)^{2}+1$, which implies $f(1)=1$.\n2. With $a=1$, we find that $b+1 \\mid f(b)+1$. In particular, $b \\leq f(b)$ for all $b \\in \\mathbb{Z}^{+}$.\n3. With $b=1$, we find that $f(a)+1 \\mid a^{2}+f(a)$, and thus $f(a)+1 \\mid a^{2}-1$. In particular, $f(a) \\leq a^{2}-2$ for all $a \\geq 2$.\n\nNow, let $p$ be any odd prime. Substituting $a=p$ and $b=f(p)$ in the original relation, we find that $2 f(p) \\mid p^{2}+f(p) f(f(p))$. Therefore, $f(p) \\mid p^{2}$. Hence the possible values of $f(p)$ are $1, p$ and $p^{2}$. By (2) above, $f(p) \\geq p$ and by (3) above $f(p) \\leq p^{2}-2$. So $f(p)=p$ for all primes $p$.\n\nSubstituting $a=p$ into the original relation, we find that $b+p \\mid p^{2}+p f(b)$. However, since $(b+p)(f(b)+p-b)=p^{2}-b^{2}+b f(b)+p f(b)$, we have $b+p \\mid b f(b)-b^{2}$. Thus, for any fixed $b$ this holds for arbitrarily large primes $p$ and therefore we must have $b f(b)-b^{2}=0$, or $f(b)=b$, as desired.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": ": As above, we have relations (1)-(3). In (2) and (3), for $b=2$ we have $3 \\mid f(2)+1$ and $f(2)+1 \\mid 3$. These imply $f(2)=2$.\n\nNow, using $a=2$ we get $2+b \\mid 4+2 f(b)$. Let $f(b)=x$. We have\n\n$$\n\\begin{aligned}\n1+x & \\equiv 0 \\quad(\\bmod b+1) \\\\\n4+2 x & \\equiv 0 \\quad(\\bmod b+2)\n\\end{aligned}\n$$\n\nFrom the first equation $x \\equiv b(\\bmod b+1)$ so $x=b+(b+1) t$ for some integer $t \\geq 0$. Then\n\n$$\n0 \\equiv 4+2 x \\equiv 4+2(b+(b+1) t) \\equiv 4+2(-2-t) \\equiv-2 t \\quad(\\bmod b+2)\n$$\n\nAlso $t \\leq b-2$ because $1+x \\mid b^{2}-1$ by (3).\nIf $b+2$ is odd, then $t \\equiv 0(\\bmod b+2)$. Then $t=0$, which implies $f(b)=b$.\nIf $b+2$ is even, then $t \\equiv 0(\\bmod (b+2) / 2)$. Then $t=0$ or $t=(b+2) / 2$. But if $t \\neq 0$, then by definition $(b+4) / 2=(1+t)=(x+1) /(b+1)$ and since $x+1 \\mid b^{2}-1$, then $(b+4) / 2$ divides $b-1$. Therefore $b+4 \\mid 10$ and the only possibility is $b=6$. So for even $b, b \\neq 6$ we have $f(b)=b$.\n\nFinally, by (2) and (3), for $b=6$ we have $7 \\mid f(6)+1$ and $f(6)+1 \\mid 35$. This means $f(6)=6$ or $f(6)=34$. The later is discarded as, for $a=5, b=6$, we have by the original equation that $11 \\mid 5(5+f(6))$. Therefore $f(n)=n$ for every positive integer $n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $\\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.\n\nAnswer: The answer is $f(n)=n$ for all positive integers $n$.\nClearly, $f(n)=n$ for all $n \\in \\mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.", "solution": ": We proceed by induction. As in Solution 1, we have $f(1)=1$. Suppose that $f(n-1)=n-1$ for some integer $n \\geq 2$.\n\nWith the substitution $a=n$ and $b=n-1$ in the original relation we obtain that $f(n)+$ $n-1 \\mid n^{2}+f(n)(n-1)$. Since $f(n)+n-1 \\mid(n-1)(f(n)+n-1)$, then $f(n)+n-1 \\mid 2 n-1$.\n\nWith the substitution $a=n-1$ and $b=n$ in the original relation we obtain that $2 n-$ $1 \\mid(n-1)^{2}+(n-1) f(n)=(n-1)(n-1+f(n))$. Since $(2 n-1, n-1)=1$, we deduce that $2 n-1 \\mid f(n)+n-1$.\n\nTherefore, $f(n)+n-1=2 n-1$, which implies the desired $f(n)=n$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 3"}}
|
| 4 |
+
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $m$ be a fixed positive integer. The infinite sequence $\\left\\{a_{n}\\right\\}_{n \\geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \\geq 1$ we have\n\n$$\na_{n+1}= \\begin{cases}a_{n}^{2}+2^{m} & \\text { if } a_{n}<2^{m} \\\\ a_{n} / 2 & \\text { if } a_{n} \\geq 2^{m}\\end{cases}\n$$\n\nFor each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.\n\nAnswer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$.", "solution": "Suppose that for integers $m$ and $a_{1}$ all the terms of the sequence are integers. For each $i \\geq 1$, write the $i$ th term of the sequence as $a_{i}=b_{i} 2^{c_{i}}$ where $b_{i}$ is the largest odd divisor of $a_{i}$ (the \"odd part\" of $a_{i}$ ) and $c_{i}$ is a nonnegative integer.\n\nLemma 1. The sequence $b_{1}, b_{2}, \\ldots$ is bounded above by $2^{m}$.\nProof. Suppose this is not the case and take an index $i$ for which $b_{i}>2^{m}$ and for which $c_{i}$ is minimal. Since $a_{i} \\geq b_{i}>2^{m}$, we are in the second case of the recursion. Therefore, $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}>2^{m}$ and $c_{i+1}=c_{i}-1<c_{i}$. This contradicts the minimality of $c_{i}$.\n\nLemma 2. The sequence $b_{1}, b_{2}, \\ldots$ is nondecreasing.\nProof. If $a_{i} \\geq 2^{m}$, then $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}$. On the other hand, if $a_{i}<2^{m}$, then\n\n$$\na_{i+1}=a_{i}^{2}+2^{m}=b_{i}^{2} 2^{2 c_{i}}+2^{m}\n$$\n\nand we have the following cases:\n\n- If $2 c_{i}>m$, then $a_{i+1}=2^{m}\\left(b_{i}^{2} 2^{2 c_{i}-m}+1\\right)$, so $b_{i+1}=b_{i}^{2} 2^{2 c_{i}-m}+1>b_{i}$.\n- If $2 c_{i}<m$, then $a_{i+1}=2^{2 c_{i}}\\left(b_{i}^{2}+2^{m-2 c_{i}}\\right)$, so $b_{i+1}=b_{i}^{2}+2^{m-2 c_{i}}>b_{i}$.\n- If $2 c_{i}=m$, then $a_{i+1}=2^{m+1} \\cdot \\frac{b_{i}^{2}+1}{2}$, so $b_{i+1}=\\left(b_{i}^{2}+1\\right) / 2 \\geq b_{i}$ since $b_{i}^{2}+1 \\equiv 2(\\bmod 4)$.\n\nBy combining these two lemmas we obtain that the sequence $b_{1}, b_{2}, \\ldots$ is eventually constant. Fix an index $j$ such that $b_{k}=b_{j}$ for all $k \\geq j$. Since $a_{n}$ descends to $a_{n} / 2$ whenever $a_{n} \\geq 2^{m}$, there are infinitely many terms which are smaller than $2^{m}$. Thus, we can choose an $i>j$ such that $a_{i}<2^{m}$. From the proof of Lemma $2, a_{i}<2^{m}$ and $b_{i+1}=b_{i}$ can happen simultaneously only when $2 c_{i}=m$ and $b_{i+1}=b_{i}=1$. By Lemma 2 , the sequence $b_{1}, b_{2}, \\ldots$ is constantly 1 and thus $a_{1}, a_{2}, \\ldots$ are all powers of two. Tracing the sequence starting from $a_{i}=2^{c_{i}}=2^{m / 2}<2^{m}$,\n\n$$\n2^{m / 2} \\rightarrow 2^{m+1} \\rightarrow 2^{m} \\rightarrow 2^{m-1} \\rightarrow 2^{2 m-2}+2^{m}\n$$\n\nNote that this last term is a power of two if and only if $2 m-2=m$. This implies that $m$ must be equal to 2 . When $m=2$ and $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$ the sequence eventually cycles through $2,8,4,2, \\ldots$. When $m=2$ and $a_{1}=1$ the sequence fails as the first terms are $1,5,5 / 2$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 5 |
+
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $m$ be a fixed positive integer. The infinite sequence $\\left\\{a_{n}\\right\\}_{n \\geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \\geq 1$ we have\n\n$$\na_{n+1}= \\begin{cases}a_{n}^{2}+2^{m} & \\text { if } a_{n}<2^{m} \\\\ a_{n} / 2 & \\text { if } a_{n} \\geq 2^{m}\\end{cases}\n$$\n\nFor each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.\n\nAnswer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\\ell}$ for $\\ell \\geq 1$.", "solution": ": Let $m$ be a positive integer and suppose that $\\left\\{a_{n}\\right\\}$ consists only of positive integers. Call a number small if it is smaller than $2^{m}$ and large otherwise. By the recursion,\nafter a small number we have a large one and after a large one we successively divide by 2 until we get a small one.\n\nFirst, we note that $\\left\\{a_{n}\\right\\}$ is bounded. Indeed, $a_{1}$ turns into a small number after a finite number of steps. After this point, each small number is smaller than $2^{m}$, so each large number is smaller than $2^{2 m}+2^{m}$. Now, since $\\left\\{a_{n}\\right\\}$ is bounded and consists only of positive integers, it is eventually periodic. We focus only on the cycle.\n\nAny small number $a_{n}$ in the cycle can be writen as $a / 2$ for $a$ large, so $a_{n} \\geq 2^{m-1}$, then $a_{n+1} \\geq 2^{2 m-2}+2^{m}=2^{m-2}\\left(4+2^{m}\\right)$, so we have to divide $a_{n+1}$ at least $m-1$ times by 2 until we get a small number. This means that $a_{n+m}=\\left(a_{n}^{2}+2^{m}\\right) / 2^{m-1}$, so $2^{m-1} \\mid a_{n}^{2}$, and therefore $2^{\\lceil(m-1) / 2\\rceil} \\mid a_{n}$ for any small number $a_{n}$ in the cycle. On the other hand, $a_{n} \\leq 2^{m}-1$, so $a_{n+1} \\leq 2^{2 m}-2^{m+1}+1+2^{m} \\leq 2^{m}\\left(2^{m}-1\\right)$, so we have to divide $a_{n+1}$ at most $m$ times by two until we get a small number. This means that after $a_{n}$, the next small number is either $N=a_{m+n}=\\left(a_{n}^{2} / 2^{m-1}\\right)+2$ or $a_{m+n+1}=N / 2$. In any case, $2^{\\lceil(m-1) / 2\\rceil}$ divides $N$.\n\nIf $m$ is odd, then $x^{2} \\equiv-2\\left(\\bmod 2^{\\lceil(m-1) / 2\\rceil}\\right)$ has a solution $x=a_{n} / 2^{(m-1) / 2}$. If $(m-1) / 2 \\geq$ $2 \\Longleftrightarrow m \\geq 5$ then $x^{2} \\equiv-2(\\bmod 4)$, which has no solution. So if $m$ is odd, then $m \\leq 3$.\n\nIf $m$ is even, then $2^{m-1}\\left|a_{n}^{2} \\Longrightarrow 2^{\\lceil(m-1) / 2\\rceil}\\right| a_{n} \\Longleftrightarrow 2^{m / 2} \\mid a_{n}$. Then if $a_{n}=2^{m / 2} x$, $2 x^{2} \\equiv-2\\left(\\bmod 2^{m / 2}\\right) \\Longleftrightarrow x^{2} \\equiv-1\\left(\\bmod 2^{(m / 2)-1}\\right)$, which is not possible for $m \\geq 6$. So if $m$ is even, then $m \\leq 4$.\n\nThe cases $m=1,2,3,4$ are handed manually, checking the possible small numbers in the cycle, which have to be in the interval $\\left[2^{m-1}, 2^{m}\\right)$ and be divisible by $2^{\\lceil(m-1) / 2\\rceil}$ :\n\n- For $m=1$, the only small number is 1 , which leads to 5 , then $5 / 2$.\n- For $m=2$, the only eligible small number is 2 , which gives the cycle $(2,8,4)$. The only way to get to 2 is by dividing 4 by 2 , so the starting numbers greater than 2 are all numbers that lead to 4 , which are the powers of 2 .\n- For $m=3$, the eligible small numbers are 4 and 6 ; we then obtain $4,24,12,6,44,22,11,11 / 2$.\n- For $m=4$, the eligible small numbers are 8 and 12 ; we then obtain $8,80,40,20,10, \\ldots$ or $12,160,80,40,20,10, \\ldots$, but in either case 10 is not an elegible small number.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 6 |
+
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$\n\nbe a scalene triangle with circumcircle $\\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.", "solution": "Let $N$ be the radical center of the circumcircles of triangles $A B C, B M P$ and $C M P$. The pairwise radical axes of these circles are $B D, C E$ and $P M$, and hence they concur at $N$. Now, note that in directed angles:\n\n$$\n\\angle M C E=\\angle M P E=\\angle M P Y=\\angle M B Y .\n$$\n\n\n\nIt follows that $B Y$ is parallel to $C E$, and analogously that $C X$ is parallel to $B D$. Then, if $L$ is the intersection of $B Y$ and $C X$, it follows that $B N C L$ is a parallelogram. Since $B M=M C$ we deduce that $L$ is the reflection of $N$ with respect to $M$, and therefore $L \\in A M$. Using power of a point from $L$ to the circumcircles of triangles $B P M$ and $C P M$, we have\n\n$$\nL Y \\cdot L B=L P \\cdot L M=L X \\cdot L C\n$$\n\nHence, $B Y X C$ is cyclic. Using the cyclic quadrilateral we find in directed angles:\n\n$$\n\\angle L X Y=\\angle L B C=\\angle B C N=\\angle N D E .\n$$\n\nSince $C X \\| B N$, it follows that $X Y \\| D E$.\nLet $Q$ and $R$ be two points in $\\Gamma$ such that $C Q, B R$, and $A M$ are all parallel. Then in directed angles:\n\n$$\n\\angle Q D B=\\angle Q C B=\\angle A M B=\\angle P M B=\\angle P D B .\n$$\n\nThen $D, P, Q$ are collinear. Analogously $E, P, R$ are collinear. From here we get $\\angle P R Q=$ $\\angle P D E=\\angle P X Y$, since $X Y$ and $D E$ are parallel. Therefore $Q R Y X$ is cyclic. Let $S$ be the radical center of the circumcircle of triangle $A B C$ and the circles $B C Y X$ and $Q R Y X$. This point lies in the lines $B C, Q R$ and $X Y$ because these are the radical axes of the circles. Let $T$ be the second intersection of $A S$ with $\\Gamma$. By power of a point from $S$ to the circumcircle of $A B C$ and the circle $B C X Y$ we have\n\n$$\nS X \\cdot S Y=S B \\cdot S C=S T \\cdot S A\n$$\n\nTherefore $T$ is in the circumcircle of triangle $A X Y$. Since $Q$ and $R$ are fixed regardless of the choice of $P$, then $S$ is also fixed, since it is the intersection of $Q R$ and $B C$. This implies $T$ is also fixed, and therefore, the circumcircle of triangle $A X Y$ goes through $T \\neq A$ for any choice of $P$.\n\nNow we show an alternative way to prove that $B C X Y$ and $Q R X T$ are cyclic.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 7 |
+
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$\n\nbe a scalene triangle with circumcircle $\\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.", "solution": ". Let the lines $D P$ and $E P$ meet the circumcircle of $A B C$ again at $Q$ and $R$, respectively. Then $\\angle D Q C \\angle D B C=\\angle D P M$, so $Q C \\| P M$. Similarly, $R B \\| P M$.\n\n\nNow, $\\angle Q C B=\\angle P M B=\\angle P X C=\\angle(Q X, C X)$, which is half of the arc $Q C$ in the circumcircle $\\omega_{C}$ of $Q X C$. So $\\omega_{C}$ is tangent to $B S$; analogously, $\\omega_{B}$, the circumcicle of $R Y B$, is also tangent to $B C$. Since $B R \\| C Q$, the inscribed trapezoid $B R Q C$ is isosceles, and by symmetry $Q R$ is also tangent to both circles, and the common perpendicular bisector of $B R$ and $C Q$ passes through the centers of $\\omega_{B}$ and $\\omega_{C}$. Since $M B=M C$ and $P M\\|B R\\| C Q$, the line $P M$ is the radical axis of $\\omega_{B}$ and $\\omega_{C}$.\n\nHowever, $P M$ is also the radical axis of the circumcircles $\\gamma_{B}$ of $P M B$ and $\\gamma_{C}$ of $P M C$. Let $C X$ and $P M$ meet at $Z$. Let $p(K, \\omega)$ denote the power of a point $K$ with respect to a circumference $\\omega$. We have\n\n$$\np\\left(Z, \\gamma_{B}\\right)=p\\left(Z, \\gamma_{C}\\right)=Z X \\cdot Z C=p\\left(Z, \\omega_{B}\\right)=p\\left(Z, \\omega_{C}\\right)\n$$\n\nPoint $Z$ is thus the radical center of $\\gamma_{B}, \\gamma_{C}, \\omega_{B}, \\omega_{C}$. Thus, the radical axes $B Y, C X, P M$ meet at $Z$. From here,\n\n$$\n\\begin{aligned}\n& Z Y \\cdot Z B=Z C \\cdot Z X \\Rightarrow B C X Y \\text { cyclic } \\\\\n& P Y \\cdot P R=P X \\cdot P Q \\Rightarrow Q R X T \\text { cyclic. }\n\\end{aligned}\n$$\n\nWe may now finish as in Solution 1.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution 2"}}
|
| 8 |
+
{"year": "2019", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Consider a $2018 \\times 2019$ board with integers in each unit square. Two unit squares are said to be neighbours if they share a common edge. In each turn, you choose some unit squares. Then for each chosen unit square the average of all its neighbours is calculated. Finally, after these calculations are done, the number in each chosen unit square is replaced by the corresponding average. Is it always possible to make the numbers in all squares become the same after finitely many turns?\n\nAnswer: No", "solution": "Let $n$ be a positive integer relatively prime to 2 and 3 . We may study the whole process modulo $n$ by replacing divisions by $2,3,4$ with multiplications by the corresponding inverses modulo $n$. If at some point the original process makes all the numbers equal, then the process modulo $n$ will also have all the numbers equal. Our aim is to choose $n$ and an initial configuration modulo $n$ for which no process modulo $n$ reaches a board with all numbers equal modulo $n$. We split this goal into two lemmas.\n\nLemma 1. There is a $2 \\times 3$ board that stays constant modulo 5 and whose entries are not all equal.\n\nProof. Here is one such a board:\n\n\nThe fact that the board remains constant regardless of the choice of squares can be checked square by square.\n\nLemma 2. If there is an $r \\times s$ board with $r \\geq 2, s \\geq 2$, that stays constant modulo 5 , then there is also a $k r \\times l s$ board with the same property.\n\nProof. We prove by a case by case analysis that repeateadly reflecting the $r \\times s$ with respect to an edge preserves the property:\n\n- If a cell had 4 neighbors, after reflections it still has the same neighbors.\n- If a cell with $a$ had 3 neighbors $b, c, d$, we have by hypothesis that $a \\equiv 3^{-1}(b+c+d) \\equiv$ $2(b+c+d)(\\bmod 5)$. A reflection may add $a$ as a neighbor of the cell and now\n\n$$\n4^{-1}(a+b+c+d) \\equiv 4(a+b+c+d) \\equiv 4 a+2 a \\equiv a \\quad(\\bmod 5)\n$$\n\n- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \\equiv 2^{-1}(b+c) \\equiv 3(b+c)$ $(\\bmod 5)$. If the reflections add one $a$ as neighbor, now\n\n$$\n3^{-1}(a+b+c) \\equiv 2(3(b+c)+b+c) \\equiv 8(b+c) \\equiv 3(b+c) \\equiv a \\quad(\\bmod 5)\n$$\n\n- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \\equiv 2^{-1}(b+c)(\\bmod 5)$. If the reflections add two $a$ 's as neighbors, now\n\n$$\n4^{-1}(2 a+b+c) \\equiv\\left(2^{-1} a+2^{-1} a\\right) \\equiv a \\quad(\\bmod 5)\n$$\n\nIn the three cases, any cell is still preserved modulo 5 after an operation. Hence we can fill in the $k r \\times l s$ board by $k \\times l$ copies by reflection.\n\nSince 2|2018 and 3|2019, we can get through reflections the following board:\n\n\nBy the lemmas above, the board is invariant modulo 5, so the answer is no.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
| 9 |
+
{"year": "2019", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Determine all the functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf\\left(x^{2}+f(y)\\right)=f(f(x))+f\\left(y^{2}\\right)+2 f(x y)\n$$\n\nfor all real number $x$ and $y$.\nAnswer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.", "solution": "By substituting $x=y=0$ in the given equation of the problem, we obtain that $f(0)=0$. Also, by substituting $y=0$, we get $f\\left(x^{2}\\right)=f(f(x))$ for any $x$.\n\nFurthermore, by letting $y=1$ and simplifying, we get\n\n$$\n2 f(x)=f\\left(x^{2}+f(1)\\right)-f\\left(x^{2}\\right)-f(1)\n$$\n\nfrom which it follows that $f(-x)=f(x)$ must hold for every $x$.\nSuppose now that $f(a)=f(b)$ holds for some pair of numbers $a, b$. Then, by letting $y=a$ and $y=b$ in the given equation, comparing the two resulting identities and using the fact that $f\\left(a^{2}\\right)=f(f(a))=f(f(b))=f\\left(b^{2}\\right)$ also holds under the assumption, we get the fact that\n\n$$\nf(a)=f(b) \\Rightarrow f(a x)=f(b x) \\quad \\text { for any real number } x\n$$\n\nConsequently, if for some $a \\neq 0, f(a)=0$, then we see that, for any $x, f(x)=f\\left(a \\cdot \\frac{x}{a}\\right)=$ $f\\left(0 \\cdot \\frac{x}{a}\\right)=f(0)=0$, which gives a trivial solution to the problem.\n\nIn the sequel, we shall try to find a non-trivial solution for the problem. So, let us assume from now on that if $a \\neq 0$ then $f(a) \\neq 0$ must hold. We first note that since $f(f(x))=f\\left(x^{2}\\right)$ for all $x$, the right-hand side of the given equation equals $f\\left(x^{2}\\right)+f\\left(y^{2}\\right)+2 f(x y)$, which is invariant if we interchange $x$ and $y$. Therefore, we have\n\n$$\nf\\left(x^{2}\\right)+f\\left(y^{2}\\right)+2 f(x y)=f\\left(x^{2}+f(y)\\right)=f\\left(y^{2}+f(x)\\right) \\quad \\text { for every pair } x, y\n$$\n\nNext, let us show that for any $x, f(x) \\geq 0$ must hold. Suppose, on the contrary, $f(s)=-t^{2}$ holds for some pair $s, t$ of non-zero real numbers. By setting $x=s, y=t$ in the right hand side of (2), we get $f\\left(s^{2}+f(t)\\right)=f\\left(t^{2}+f(s)\\right)=f(0)=0$, so $f(t)=-s^{2}$. We also have $f\\left(t^{2}\\right)=f\\left(-t^{2}\\right)=f(f(s))=f\\left(s^{2}\\right)$. By applying (2) with $x=\\sqrt{s^{2}+t^{2}}$ and $y=s$, we obtain\n\n$$\nf\\left(s^{2}+t^{2}\\right)+2 f\\left(s \\cdot \\sqrt{s^{2}+t^{2}}\\right)=0\n$$\n\nand similarly, by applying (2) with $x=\\sqrt{s^{2}+t^{2}}$ and $y=t$, we obtain\n\n$$\nf\\left(s^{2}+t^{2}\\right)+2 f\\left(t \\cdot \\sqrt{s^{2}+t^{2}}\\right)=0\n$$\n\nConsequently, we obtain\n\n$$\nf\\left(s \\cdot \\sqrt{s^{2}+t^{2}}\\right)=f\\left(t \\cdot \\sqrt{s^{2}+t^{2}}\\right)\n$$\n\nBy applying (1) with $a=s \\sqrt{s^{2}+t^{2}}, b=t \\sqrt{s^{2}+t^{2}}$ and $x=1 / \\sqrt{s^{2}+t^{2}}$, we obtain $f(s)=$ $f(t)=-s^{2}$, from which it follows that\n\n$$\n0=f\\left(s^{2}+f(s)\\right)=f\\left(s^{2}\\right)+f\\left(s^{2}\\right)+2 f\\left(s^{2}\\right)=4 f\\left(s^{2}\\right)\n$$\n\na contradiction to the fact $s^{2}>0$. Thus we conclude that for all $x \\neq 0, f(x)>0$ must be satisfied.\n\nNow, we show the following fact\n\n$$\nk>0, f(k)=1 \\Leftrightarrow k=1\n$$\n\nLet $k>0$ for which $f(k)=1$. We have $f\\left(k^{2}\\right)=f(f(k))=f(1)$, so by $(1), f(1 / k)=f(k)=$ 1 , so we may assume $k \\geq 1$. By applying (2) with $x=\\sqrt{k^{2}-1}$ and $y=k$, and using $f(x) \\geq 0$, we get\n\n$$\nf\\left(k^{2}-1+f(k)\\right)=f\\left(k^{2}-1\\right)+f\\left(k^{2}\\right)+2 f\\left(k \\sqrt{k^{2}-1}\\right) \\geq f\\left(k^{2}-1\\right)+f\\left(k^{2}\\right) .\n$$\n\nThis simplifies to $0 \\geq f\\left(k^{2}-1\\right) \\geq 0$, so $k^{2}-1=0$ and thus $k=1$.\nNext we focus on showing $f(1)=1$. If $f(1)=m \\leq 1$, then we may proceed as above by setting $x=\\sqrt{1-m}$ and $y=1$ to get $m=1$. If $f(1)=m \\geq 1$, now we note that $f(m)=f(f(1))=f\\left(1^{2}\\right)=f(1)=m \\leq m^{2}$. We may then proceed as above with $x=\\sqrt{m^{2}-m}$ and $y=1$ to show $m^{2}=m$ and thus $m=1$.\n\nWe are now ready to finish. Let $x>0$ and $m=f(x)$. Since $f(f(x))=f\\left(x^{2}\\right)$, then $f\\left(x^{2}\\right)=$ $f(m)$. But by (1), $f\\left(m / x^{2}\\right)=1$. Therefore $m=x^{2}$. For $x<0$, we have $f(x)=f(-x)=f\\left(x^{2}\\right)$ as well. Therefore, for all $x, f(x)=x^{2}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution."}}
|
| 10 |
+
{"year": "2019", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Determine all the functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that\n\n$$\nf\\left(x^{2}+f(y)\\right)=f(f(x))+f\\left(y^{2}\\right)+2 f(x y)\n$$\n\nfor all real number $x$ and $y$.\nAnswer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.", "solution": "After proving that $f(x)>0$ for $x \\neq 0$ as in the previous solution, we may also proceed as follows. We claim that $f$ is injective on the positive real numbers. Suppose that $a>b>0$ satisfy $f(a)=f(b)$. Then by setting $x=1 / b$ in (1) we have $f(a / b)=f(1)$. Now, by induction on $n$ and iteratively setting $x=a / b$ in (1) we get $f\\left((a / b)^{n}\\right)=1$ for any positive integer $n$.\n\nNow, let $m=f(1)$ and $n$ be a positive integer such that $(a / b)^{n}>m$. By setting $x=$ $\\sqrt{(a / b)^{n}-m}$ and $y=1$ in (2) we obtain that\n$f\\left((a / b)^{n}-m+f(1)\\right)=f\\left((a / b)^{n}-m\\right)+f\\left(1^{2}\\right)+2 f\\left(\\sqrt{\\left.(a / b)^{n}-m\\right)}\\right) \\geq f\\left((a / b)^{n}-m\\right)+f(1)$.\nSince $f\\left((a / b)^{n}\\right)=f(1)$, this last equation simplifies to $f\\left((a / b)^{n}-m\\right) \\leq 0$ and thus $m=$ $(a / b)^{n}$. But this is impossible since $m$ is constant and $a / b>1$. Thus, $f$ is injective on the positive real numbers. Since $f(f(x))=f\\left(x^{2}\\right)$, we obtain that $f(x)=x^{2}$ for any real value $x$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "\nSolution 2"}}
|
APMO/segmented/en-apmo2020_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of $\\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.", "solution": "From the conditions, we have\n\n\nLet $P$ be the intersection of $A C$ and $B F$. Then we have\n\n$$\n\\angle P A E=\\angle C B A=\\angle B A C=\\angle B F C .\n$$\n\nThis implies $A, P, F, E$ are concyclic. It follows that\n\n$$\n\\angle F P E=\\angle F A E=\\angle F B A,\n$$\n\nand hence $A B$ and $E P$ are parallel. So $E, P, D$ are collinear, and the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 1"}}
|
| 2 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\Gamma$ be the circumcircle of $\\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.", "solution": "Let $E^{\\prime}$ be any point on the extension of $E A$. From $\\angle A E D=\\angle E^{\\prime} A B=\\angle A C D$, points $A, D, C, E$ are concyclic.\n\n\nLet $P$ be the intersection of $B F$ and $D E$. From $\\angle A F P=\\angle A C B=\\angle A E P$, the points $A, P, F, E$ are concyclic. In addition, from $\\angle E P A=\\angle E F A=\\angle D B A$, points $A, B, D, P$ are concyclic.\nBy considering the radical centre of $(B D F E),(A P F E)$ and $(B D P A)$, we find that the lines $B D, A P, E F$ are concurrent at $C$. The result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Show that $r=2$ is the largest real number $r$ which satisfies the following condition:\n\nIf a sequence $a_{1}, a_{2}, \\ldots$ of positive integers fulfills the inequalities\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+r a_{n+1}}\n$$\n\nfor every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \\geq M$.", "solution": ". First, let us assume that $r>2$, and take a positive integer $a \\geq 1 /(r-2)$.\nThen, if we let $a_{n}=a+\\lfloor n / 2\\rfloor$ for $n=1,2, \\ldots$, the sequence $a_{n}$ satisfies the inequalities\n\n$$\n\\sqrt{a_{n}^{2}+r a_{n+1}} \\geq \\sqrt{a_{n}^{2}+r a_{n}} \\geq \\sqrt{a_{n}^{2}+\\left(2+\\frac{1}{a}\\right) a_{n}} \\geq a_{n}+1=a_{n+2}\n$$\n\nbut since $a_{n+2}>a_{n}$ for any $n$, we see that $r$ does not satisfy the condition given in the problem.\nNow we show that $r=2$ does satisfy the condition of the problem. Suppose $a_{1}, a_{2}, \\ldots$ is a sequence of positive integers satisfying the inequalities given in the problem, and there exists a positive integer $m$ for which $a_{m+2}>a_{m}$ is satisfied.\nBy induction we prove the following assertion:\n\n$$\na_{m+2 k} \\leq a_{m+2 k-1}=a_{m+1} \\text { holds for every positive integer } k\n$$\n\nThe truth of $(\\dagger)$ for $k=1$ follows from the inequalities below\n\n$$\n2 a_{m+2}-1=a_{m+2}^{2}-\\left(a_{m+2}-1\\right)^{2} \\leq a_{m}^{2}+2 a_{m+1}-\\left(a_{m+2}-1\\right)^{2} \\leq 2 a_{m+1}\n$$\n\nLet us assume that $(\\dagger)$ holds for some positive integer $k$. From\n\n$$\na_{m+1}^{2} \\leq a_{m+2 k+1}^{2} \\leq a_{m+2 k-1}^{2}+2 a_{m+2 k} \\leq a_{m+1}^{2}+2 a_{m+1}<\\left(a_{m+1}+1\\right)^{2}\n$$\n\nit follows that $a_{m+2 k+1}=a_{m+1}$ must hold. Furthermore, since $a_{m+2 k} \\leq a_{m+1}$, we have\n\n$$\na_{m+2 k+2}^{2} \\leq a_{m+2 k}^{2}+2 a_{m+2 k+1} \\leq a_{m+1}^{2}+2 a_{m+1}<\\left(a_{m+1}+1\\right)^{2}\n$$\n\nfrom which it follows that $a_{m+2 k+2} \\leq a_{m+1}$, which proves the assertion $(\\dagger)$.\nWe can conclude that for the value of $m$ with which we started our argument above, $a_{m+2 k+1}=a_{m+1}$ holds for every positive integer $k$. Therefore, in order to finish the proof, it is enough to show that $a_{m+2 k}$ becomes constant after some value of $k$. Since every $a_{m+2 k}$ is a positive integer less than or equal to $a_{m+1}$, there exists $k=K$ for which $a_{m+2 K}$ takes the maximum value. By the monotonicity of $a_{m+2 k}$, it then follows that $a_{m+2 k}=a_{m+2 K}$ for all $k \\geq K$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
-
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Show that $r=2$ is the largest real number $r$ which satisfies the following condition:\n\nIf a sequence $a_{1}, a_{2}, \\ldots$ of positive integers fulfills the inequalities\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+r a_{n+1}}\n$$\n\nfor every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \\geq M$.", "solution": "We only give an alternative proof of the assertion $(\\dagger)$ in solution 1 . Let $\\left\\{a_{n}\\right\\}$ be a sequence satisfying the inequalities given in the problem. We will use the following key observations:\n(a) If $a_{n+1} \\leq a_{n}$ for some $n \\geq 1$, then\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+2 a_{n+1}}<\\sqrt{a_{n}^{2}+2 a_{n}+1}=a_{n}+1,\n$$\n\nhence $a_{n}=a_{n+2}$.\n(b) If $a_{n} \\leq a_{n+1}$ for some $n \\geq 1$, then\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+2 a_{n+1}}<\\sqrt{a_{n+1}^{2}+2 a_{n+1}+1}=a_{n+1}+1\n$$\n\nhence $a_{n} \\leq a_{n+2} \\leq a_{n+1}$.\nNow let $m$ be a positive integer such that $a_{m+2}>a_{m}$. By the observations above, we must have $a_{m}<a_{m+2} \\leq a_{m+1}$. Thus the assertion ( $\\dagger$ ) is true for $k=1$. Assume that the assertion holds for some positive integer $k$. Using observation (a), we get $a_{m+2 k+1}=a_{m+2 k-1}=a_{m+1}$. Thus $a_{m+2 k} \\leq a_{m+2 k+1}$, and then using observation (b), we get $a_{m+2 k+2} \\leq a_{m+2 k+1}=a_{m+1}$, which proves the assertion ( $\\dagger$ ).", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
-
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.", "solution": "We claim that $k=2^{a}$ for all $a \\geq 0$.\nLet $A=\\{1,2,4,8, \\ldots\\}$ and $B=\\mathbb{N} \\backslash A$. For any set $T$, let $s(T)$ denote the sum of the elements of $T$. (If $T$ is empty, we let $s(T)=0$.)\nWe first show that any positive integer $k=2^{a}$ satisfies the desired property. Let $B^{\\prime}$ be a subset of $B$ with $a$ elements, and let $S=A \\cup B^{\\prime}$. Recall that any nonnegative integer has a unique binary representation. Hence, for any integer $t>s\\left(B^{\\prime}\\right)$ and any subset $B^{\\prime \\prime} \\subseteq B^{\\prime}$, the number $t-s\\left(B^{\\prime \\prime}\\right)$ can be written as a sum of distinct elements of $A$ in a unique way. This means that $t$ can be written as a sum of distinct elements of $B^{\\prime}$ in exactly $2^{a}$ ways.\nNext, assume that some positive integer $k$ satisfies the desired property for a positive integer $m \\geq 2$ and a set $S$. Clearly, $S$ is infinite.\nLemma: For all sufficiently large $x \\in S$, the smallest element of $S$ larger than $x$ is $2 x$.\nProof of Lemma: Let $x \\in S$ with $x>3 m$, and let $x<y<2 x$. We will show that $y \\notin S$. Suppose first that $y>x+m$. Then $y-x$ can be written as a sum of distinct elements of $S$ not including $x$ in $k$ ways. If $y \\in S$, then $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Suppose now that $y \\leq x+m$. We consider $z \\in(2 x-m, 2 x)$. Similarly as before, $z-x$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$ in $k$ ways. If $y \\in S$, then since $m<z-y<x, z-y$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$. This means that $z$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction.\nWe now show that $2 x \\in S$; assume for contradiction that this is not the case. Observe that $2 x$ can be written as a sum of distinct elements of $S$ including $x$ in exactly $k-1$ ways. This means that $2 x$ can also be written as a sum of distinct elements of $S$ not including $x$. If this sum includes any number less than $x-m$, then removing this number, we can write some number $y \\in(x+m, 2 x)$ as a sum of distinct elements of $S$ not including $x$. Now if $y=y^{\\prime}+x$ where $y^{\\prime} \\in(m, x)$ then $y^{\\prime}$ can be written as\na sum of distinct elements of $S$ including $x$ in exactly $k$ ways. Therefore $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Hence the sum only includes numbers in the range $[x-m, x)$. Clearly two numbers do not suffice. On the other hand, three such numbers sum to at least $3(x-m)>2 x$, a contradiction.\nFrom the Lemma, we have that $S=T \\cup U$, where $T$ is finite and $U=\\{x, 2 x, 4 x, 8 x, \\ldots\\}$ for some positive integer $x$. Let $y$ be any positive integer greater than $s(T)$. For any subset $T^{\\prime} \\subseteq T$, if $y-s\\left(T^{\\prime}\\right) \\equiv 0(\\bmod x)$, then $y-s\\left(T^{\\prime}\\right)$ can be written as a sum of distinct elements of $U$ in a unique way; otherwise $y-s\\left(T^{\\prime}\\right)$ cannot be written as a sum of distinct elements of $U$. Hence the number of ways to write $y$ as a sum of distinct elements of $S$ is equal to the number of subsets $T^{\\prime} \\subseteq T$ such that $s\\left(T^{\\prime}\\right) \\equiv y(\\bmod x)$. Since this holds for all $y$, for any $0 \\leq a \\leq x-1$ there are exactly $k$ subsets $T^{\\prime} \\subseteq T$ such that $s\\left(T^{\\prime}\\right) \\equiv a(\\bmod x)$. This means that there are $k x$ subsets of $T$ in total. But the number of subsets of $T$ is a power of 2 , and therefore $k$ is a power of 2 , as claimed.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution:"}}
|
| 6 |
-
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.", "solution": ". We give an alternative proof of the first half of the lemma in the Solution 1 above.\nLet $s_{1}<s_{2}<\\cdots$ be the elements of $S$. For any positive integer $r$, define $A_{r}(x)=\\prod_{n=1}^{r}\\left(1+x^{s_{n}}\\right)$. For each $n$ such that $m \\leq n<s_{r+1}$, all $k$ ways of writing $n$ as a sum of elements of $S$ must only use $s_{1}, \\ldots, s_{r}$, so the coefficient of $x^{n}$ in $A_{r}(x)$ is $k$. Similarly the number of ways of writing $s_{r+1}$ as a sum of elements of $S$ without using $s_{r+1}$ is exactly $k-1$. Hence the coefficient of $x^{s_{r+1}}$ in $A_{r}(x)$ is $k-1$.\nFix a $t$ such that $s_{t}>2(m+1)$. Write\n\n$$\nA_{t-1}(x)=u(x)+k\\left(x^{m+1}+\\cdots+x^{s_{t}-1}\\right)+x^{s_{t}} v(x)\n$$\n\nfor some $u(x), v(x)$ where $u(x)$ is of degree at most $m$.\nNote that\n\n$$\nA_{t+1}(x)=A_{t-1}(x)+x^{s_{t}} A_{t-1}(x)+x^{s_{t+1}} A_{t-1}(x)+x^{s_{t}+s_{t+1}} A_{t-1}(x)\n$$\n\nIf $s_{t+1}+m+1<2 s_{t}$, we can find the term $x^{s_{t+1}+m+1}$ in $x^{s_{t}} A_{t-1}(x)$ and in $x^{s_{t+1}} A_{t-1}(x)$. Hence the coefficient of $x^{s_{t+1}+m+1}$ in $A_{t+1}(x)$ is at least $2 k$, which is impossible. So $s_{t+1} \\geq 2 s_{t}-(m+1)>$ $s_{t}+m+1$.\nNow\n\n$$\nA_{t}(x)=A_{t-1}(x)+x^{s_{t}} u(x)+k\\left(x^{s_{t}+m+1}+\\cdots x^{2 s_{t}-1}\\right)+x^{2 s_{t}} v(x)\n$$\n\nRecall that the coefficent of $x^{s_{t+1}}$ in $A_{t}(x)$ is $k-1$. But if $s_{t}+m+1<s_{t+1}<s_{2 t}$, then the coefficient of $x^{s_{t+1}}$ in $A_{t}(x)$ is at least $k$, which is a contradiction. Therefore $s_{t+1} \\geq 2 s_{t}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution 2"}}
|
| 7 |
-
{"year": "2020", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $\\mathbb{Z}$ denote the set of all integers. Find all polynomials $P(x)$ with integer coefficients that satisfy the following property:\nFor any infinite sequence $a_{1}, a_{2}, \\ldots$ of integers in which each integer in $\\mathbb{Z}$ appears exactly once, there exist indices $i<j$ and an integer $k$ such that $a_{i}+a_{i+1}+\\cdots+a_{j}=P(k)$.", "solution": "Part 1: All polynomials with $\\operatorname{deg} P=1$ satisfy the given property.\nSuppose $P(x)=c x+d$, and assume without loss of generality that $c>d \\geq 0$. Denote $s_{i}=a_{1}+a_{2}+$ $\\cdots+a_{i}(\\bmod c)$. It suffices to show that there exist indices $i$ and $j$ such that $j-i \\geq 2$ and $s_{j}-s_{i} \\equiv d$ $(\\bmod c)$.\nConsider $c+1$ indices $e_{1}, e_{2}, \\ldots, e_{c+1}>1$ such that $a_{e_{l}} \\equiv d(\\bmod c)$. By the pigeonhole principle, among the $n+1$ pairs $\\left(s_{e_{1}-1}, s_{e_{1}}\\right),\\left(s_{e_{2}-1}, s_{e_{2}}\\right), \\ldots,\\left(s_{e_{n+1}-1}, s_{e_{n+1}}\\right)$, some two are equal, say $\\left(s_{m-1}, s_{m}\\right)$ and $\\left(s_{n-1}, s_{n}\\right)$. We can then take $i=m-1$ and $j=n$.\nPart 2: All polynomials with $\\operatorname{deg} P \\neq 1$ do not satisfy the given property.\nLemma: If $\\operatorname{deg} P \\neq 1$, then for any positive integers $A, B$, and $C$, there exists an integer $y$ with $|y|>C$ such that no value in the range of $P$ falls within the interval $[y-A, y+B]$.\nProof of Lemma: The claim is immediate when $P$ is constant or when $\\operatorname{deg} P$ is even since $P$ is bounded from below. Let $P(x)=a_{n} x^{n}+\\cdots+a_{1} x+a_{0}$ be of odd degree greater than 1 , and assume without\nloss of generality that $a_{n}>0$. Since $P(x+1)-P(x)=a_{n} n x^{n-1}+\\ldots$, and $n-1>0$, the gap between $P(x)$ and $P(x+1)$ grows arbitrarily for large $x$. The claim follows.\nSuppose $\\operatorname{deg} P \\neq 1$. We will inductively construct a sequence $\\left\\{a_{i}\\right\\}$ such that for any indices $i<j$ and any integer $k$ it holds that $a_{i}+a_{i+1}+\\cdots+a_{j} \\neq P(k)$. Suppose that we have constructed the sequence up to $a_{i}$, and $m$ is an integer with smallest magnitude yet to appear in the sequence. We will add two more terms to the sequence. Take $a_{i+2}=m$. Consider all the new sums of at least two consecutive terms; each of them contains $a_{i+1}$. Hence all such sums are in the interval $\\left[a_{i+1}-A, a_{i+1}+B\\right]$ for fixed constants $A, B$. The lemma allows us to choose $a_{i+1}$ so that all such sums avoid the range of $P$.\nAlternate Solution for Part 1: Again, suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \\geq 0$. Let $S_{i}=\\left\\{a_{j}+a_{j+1}+\\cdots+a_{i}(\\bmod c) \\mid j=1,2, \\ldots, i\\right\\}$. Then $S_{i+1}=\\left\\{s_{i}+a_{i+1}\\right.$ $\\left.(\\bmod c) \\mid s_{i} \\in S_{i}\\right\\} \\cup\\left\\{a_{i+1}(\\bmod c)\\right\\}$. Hence $\\left|S_{i+1}\\right|=\\left|S_{i}\\right|$ or $S_{i+1}=\\left|S_{i}\\right|+1$, with the former occuring exactly when $0 \\in S_{i}$. Since $\\left|S_{i}\\right| \\leq c$, the latter can only occur finitely many times, so there exists $I$ such that $0 \\in S_{i}$ for all $i \\geq I$. Let $t>I$ be an index with $a_{t} \\equiv d(\\bmod c)$. Then we can find a sum of at least two consecutive terms ending at $a_{t}$ and congruent to $d(\\bmod c)$.\nAlternate Construction when $P(x)$ is constant or of even degree\nIf $P(x)$ is of even degree, then $P$ is bounded from below or from above. In case of $P$ is constant or bounded from above, then there exists a positive integer $c$ such that $P(x)<c$. Let $\\left\\{a_{i}\\right\\}$ be the sequence\n\n$$\n0,1,-1,2,3,-2,4,5,-3, \\cdots\n$$\n\nwhich is given by $a_{3 n+1}=2 n, a_{3 n+2}=2 n+1, a_{3 n+3}=-(n+1)$ for all $n \\geq 0$. Notice that for any $i<j$ we have $a_{i}+\\cdots+a_{j} \\geq 0$. Then for the sequence $\\left\\{b_{n}\\right\\}$ defined by $b_{n}=a_{n}+c$, clearly $b_{i}+\\cdots+b_{j} \\geq\\left(a_{i}+\\cdots+a_{j}\\right)+2 c>c$ which is out side the range of $P(x)$.\n\nNow if $P$ is bounded from below, there exist a positive integer $c$ such that $P(x)>-c$. In this case, take $b_{n}$ to be $b_{n}=-a_{n}-c$. Then for all $i<j$ we have $b_{i}+\\cdots+b_{j} \\leq-\\left(a_{1}+\\cdots a_{n}\\right)-2 c<-c$ which is again out side the range of $P(x)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution:"}}
|
| 8 |
-
{"year": "2020", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $n \\geq 3$ be a fixed integer. The number 1 is written $n$ times on a blackboard. Below the blackboard, there are two buckets that are initially empty. A move consists of erasing two of the numbers $a$ and $b$, replacing them with the numbers 1 and $a+b$, then adding one stone to the first bucket and $\\operatorname{gcd}(a, b)$ stones to the second bucket. After some finite number of moves, there are $s$ stones in the first bucket and $t$ stones in the second bucket, where $s$ and $t$ are positive integers. Find all possible values of the ratio $\\frac{t}{s}$.", "solution": "The answer is the set of all rational numbers in the interval $[1, n-1)$. First, we show that no other numbers are possible. Clearly the ratio is at least 1, since for every move, at least one stone is added to the second bucket. Note that the number $s$ of stones in the first bucket is always equal to $p-n$, where $p$ is the sum of the numbers on the blackboard. We will assume that the numbers are written in a row, and whenever two numbers $a$ and $b$ are erased, $a+b$ is written in the place of the number on the right. Let $a_{1}, a_{2}, \\ldots, a_{n}$ be the numbers on the blackboard from left to right, and let\n\n$$\nq=0 \\cdot a_{1}+1 \\cdot a_{2}+\\cdots+(n-1) a_{n}\n$$\n\nSince each number $a_{i}$ is at least 1 , we always have\n\n$$\nq \\leq(n-1) p-(1+\\cdots+(n-1))=(n-1) p-\\frac{n(n-1)}{2}=(n-1) s+\\frac{n(n-1)}{2}\n$$\n\nAlso, if a move changes $a_{i}$ and $a_{j}$ with $i<j$, then $t$ changes by $\\operatorname{gcd}\\left(a_{i}, a_{j}\\right) \\leq a_{i}$ and $q$ increases by\n\n$$\n(j-1) a_{i}-(i-1)\\left(a_{i}-1\\right) \\geq i a_{i}-(i-1)\\left(a_{i}-1\\right) \\geq a_{i}\n$$\n\nHence $q-t$ never decreases. We may assume without loss of generality that the first move involves the rightmost 1. Then immediately after this move, $q=0+1+\\cdots+(n-2)+(n-1) \\cdot 2=\\frac{(n+2)(n-1)}{2}$ and\n$t=1$. So after that move, we always have\n\n$$\n\\begin{aligned}\nt & \\leq q+1-\\frac{(n+2)(n-1)}{2} \\\\\n& \\leq(n-1) s+\\frac{n(n-1)}{2}-\\frac{(n+2)(n-1)}{2}+1 \\\\\n& =(n-1) s-(n-2)<(n-1) s\n\\end{aligned}\n$$\n\nHence, $\\frac{t}{s}<n-1$. So $\\frac{t}{s}$ must be a rational number in $[1, n-1)$.\n\nAfter a single move, we have $\\frac{t}{s}=1$, so it remains to prove that $\\frac{t}{s}$ can be any rational number in $(1, n-1)$. We will now show by induction on $n$ that for any positive integer $a$, it is possible to reach a situation where there are $n-1$ occurrences of 1 on the board and the number $a^{n-1}$, with $t$ and $s$ equal to $a^{n-2}(a-1)(n-1)$ and $a^{n-1}-1$, respectively. For $n=2$, this is clear as there is only one possible move at each step, so after $a-1$ moves $s$ and $t$ will both be equal to $a-1$. Now assume that the claim is true for $n-1$, where $n>2$. Call the algorithm which creates this situation using $n-1$ numbers algorithm $A$. Then to reach the situation for size $n$, we apply algorithm $A$, to create the number $a^{n-2}$. Next, apply algorithm $A$ again and then add the two large numbers, repeat until we get the number $a^{n-1}$. Then algorithm $A$ was applied $a$ times and the two larger numbers were added $a-1$ times. Each time the two larger numbers are added, $t$ increases by $a^{n-2}$ and each time algorithm $A$ is applied, $t$ increases by $a^{n-3}(a-1)(n-2)$. Hence, the final value of $t$ is\n\n$$\nt=(a-1) a^{n-2}+a \\cdot a^{n-3}(a-1)(n-2)=a^{n-2}(a-1)(n-1)\n$$\n\nThis completes the induction.\nNow we can choose 1 and the large number $b$ times for any positive integer $b$, and this will add $b$ stones to each bucket. At this point we have\n\n$$\n\\frac{t}{s}=\\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}\n$$\n\nSo we just need to show that for any rational number $\\frac{p}{q} \\in(1, n-1)$, there exist positive integers $a$ and $b$ such that\n\n$$\n\\frac{p}{q}=\\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}\n$$\n\nRearranging, we see that this happens if and only if\n\n$$\nb=\\frac{q a^{n-2}(a-1)(n-1)-p\\left(a^{n-1}-1\\right)}{p-q} .\n$$\n\nIf we choose $a \\equiv 1(\\bmod p-q)$, then this will be an integer, so we just need to check that the numerator is positive for sufficiently large $a$.\n\n$$\n\\begin{aligned}\nq a^{n-2}(a-1)(n-1)-p\\left(a^{n-1}-1\\right) & >q a^{n-2}(a-1)(n-1)-p a^{n-1} \\\\\n& =a^{n-2}(a(q(n-1)-p)-(n-1))\n\\end{aligned}\n$$\n\nwhich is positive for sufficiently large $a$ since $q(n-1)-p>0$.\n\nAlternative solution for the upper bound. Rather than starting with $n$ occurrences of 1 , we may start with infinitely many 1 s , but we are restricted to having at most $n-1$ numbers which are not equal to 1 on the board at any time. It is easy to see that this does not change the problem. Note also that we can ignore the 1 we write on the board each move, so the allowed move is to rub off two numbers and write their sum. We define the width and score of a number on the board as follows. Colour that number red, then reverse every move up to that point all the way back to the situation when the numbers are all 1 s . Whenever a red number is split, colour the two replacement numbers\nred. The width of the original number is equal to the maximum number of red integers greater than 1 which appear on the board at the same time. The score of the number is the number of stones which were removed from the second bucket during these splits. Then clearly the width of any number is at most $n-1$. Also, $t$ is equal to the sum of the scores of the final numbers. We claim that if a number $p>1$ has a width of at most $w$, then its score is at most $(p-1) w$. We will prove this by strong induction on $p$. If $p=1$, then clearly $p$ has a score of 0 , so the claim is true. If $p>1$, then $p$ was formed by adding two smaller numbers $a$ and $b$. Clearly $a$ and $b$ both have widths of at most $w$. Moreover, if $a$ has a width of $w$, then at some point in the reversed process there will be $w$ numbers in the set $\\{2,3,4, \\ldots\\}$ that have split from $a$, and hence there can be no such numbers at this point which have split from $b$. Between this point and the final situation, there must always be at least one number in the set $\\{2,3,4, \\ldots\\}$ that split from $a$, so the width of $b$ is at most $w-1$. Therefore, $a$ and $b$ cannot both have widths of $w$, so without loss of generality, $a$ has width at most $w$ and $b$ has width at most $w-1$. Then by the inductive hypothesis, $a$ has score at most $(a-1) w$ and $b$ has score at most $(b-1)(w-1)$. Hence, the score of $p$ is at most\n\n$$\n\\begin{aligned}\n(a-1) w+(b-1)(w-1)+\\operatorname{gcd}(a, b) & \\leq(a-1) w+(b-1)(w-1)+b \\\\\n& =(p-1) w+1-w \\\\\n& \\leq(p-1) w .\n\\end{aligned}\n$$\n\nThis completes the induction.\nNow, since each number $p$ in the final configuration has width at most $(n-1)$, it has score less than $(n-1)(p-1)$. Hence the number $t$ of stones in the second bucket is less than the sum over the values of $(n-1)(p-1)$, and $s$ is equal to the sum of the the values of $(p-1)$. Therefore, $\\frac{t}{s}<n-1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution:"}}
|
|
|
|
| 1 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $\\Gamma$ be the circumcircle of $\\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.", "solution": "From the conditions, we have\n\n\nLet $P$ be the intersection of $A C$ and $B F$. Then we have\n\n$$\n\\angle P A E=\\angle C B A=\\angle B A C=\\angle B F C .\n$$\n\nThis implies $A, P, F, E$ are concyclic. It follows that\n\n$$\n\\angle F P E=\\angle F A E=\\angle F B A,\n$$\n\nand hence $A B$ and $E P$ are parallel. So $E, P, D$ are collinear, and the result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 1"}}
|
| 2 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $\\Gamma$ be the circumcircle of $\\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.", "solution": "Let $E^{\\prime}$ be any point on the extension of $E A$. From $\\angle A E D=\\angle E^{\\prime} A B=\\angle A C D$, points $A, D, C, E$ are concyclic.\n\n\nLet $P$ be the intersection of $B F$ and $D E$. From $\\angle A F P=\\angle A C B=\\angle A E P$, the points $A, P, F, E$ are concyclic. In addition, from $\\angle E P A=\\angle E F A=\\angle D B A$, points $A, B, D, P$ are concyclic.\nBy considering the radical centre of $(B D F E),(A P F E)$ and $(B D P A)$, we find that the lines $B D, A P, E F$ are concurrent at $C$. The result follows.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Show that $r=2$ is the largest real number $r$ which satisfies the following condition:\n\nIf a sequence $a_{1}, a_{2}, \\ldots$ of positive integers fulfills the inequalities\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+r a_{n+1}}\n$$\n\nfor every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \\geq M$.", "solution": ". First, let us assume that $r>2$, and take a positive integer $a \\geq 1 /(r-2)$.\nThen, if we let $a_{n}=a+\\lfloor n / 2\\rfloor$ for $n=1,2, \\ldots$, the sequence $a_{n}$ satisfies the inequalities\n\n$$\n\\sqrt{a_{n}^{2}+r a_{n+1}} \\geq \\sqrt{a_{n}^{2}+r a_{n}} \\geq \\sqrt{a_{n}^{2}+\\left(2+\\frac{1}{a}\\right) a_{n}} \\geq a_{n}+1=a_{n+2}\n$$\n\nbut since $a_{n+2}>a_{n}$ for any $n$, we see that $r$ does not satisfy the condition given in the problem.\nNow we show that $r=2$ does satisfy the condition of the problem. Suppose $a_{1}, a_{2}, \\ldots$ is a sequence of positive integers satisfying the inequalities given in the problem, and there exists a positive integer $m$ for which $a_{m+2}>a_{m}$ is satisfied.\nBy induction we prove the following assertion:\n\n$$\na_{m+2 k} \\leq a_{m+2 k-1}=a_{m+1} \\text { holds for every positive integer } k\n$$\n\nThe truth of $(\\dagger)$ for $k=1$ follows from the inequalities below\n\n$$\n2 a_{m+2}-1=a_{m+2}^{2}-\\left(a_{m+2}-1\\right)^{2} \\leq a_{m}^{2}+2 a_{m+1}-\\left(a_{m+2}-1\\right)^{2} \\leq 2 a_{m+1}\n$$\n\nLet us assume that $(\\dagger)$ holds for some positive integer $k$. From\n\n$$\na_{m+1}^{2} \\leq a_{m+2 k+1}^{2} \\leq a_{m+2 k-1}^{2}+2 a_{m+2 k} \\leq a_{m+1}^{2}+2 a_{m+1}<\\left(a_{m+1}+1\\right)^{2}\n$$\n\nit follows that $a_{m+2 k+1}=a_{m+1}$ must hold. Furthermore, since $a_{m+2 k} \\leq a_{m+1}$, we have\n\n$$\na_{m+2 k+2}^{2} \\leq a_{m+2 k}^{2}+2 a_{m+2 k+1} \\leq a_{m+1}^{2}+2 a_{m+1}<\\left(a_{m+1}+1\\right)^{2}\n$$\n\nfrom which it follows that $a_{m+2 k+2} \\leq a_{m+1}$, which proves the assertion $(\\dagger)$.\nWe can conclude that for the value of $m$ with which we started our argument above, $a_{m+2 k+1}=a_{m+1}$ holds for every positive integer $k$. Therefore, in order to finish the proof, it is enough to show that $a_{m+2 k}$ becomes constant after some value of $k$. Since every $a_{m+2 k}$ is a positive integer less than or equal to $a_{m+1}$, there exists $k=K$ for which $a_{m+2 K}$ takes the maximum value. By the monotonicity of $a_{m+2 k}$, it then follows that $a_{m+2 k}=a_{m+2 K}$ for all $k \\geq K$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
+
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Show that $r=2$ is the largest real number $r$ which satisfies the following condition:\n\nIf a sequence $a_{1}, a_{2}, \\ldots$ of positive integers fulfills the inequalities\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+r a_{n+1}}\n$$\n\nfor every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \\geq M$.", "solution": "We only give an alternative proof of the assertion $(\\dagger)$ in solution 1 . Let $\\left\\{a_{n}\\right\\}$ be a sequence satisfying the inequalities given in the problem. We will use the following key observations:\n(a) If $a_{n+1} \\leq a_{n}$ for some $n \\geq 1$, then\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+2 a_{n+1}}<\\sqrt{a_{n}^{2}+2 a_{n}+1}=a_{n}+1,\n$$\n\nhence $a_{n}=a_{n+2}$.\n(b) If $a_{n} \\leq a_{n+1}$ for some $n \\geq 1$, then\n\n$$\na_{n} \\leq a_{n+2} \\leq \\sqrt{a_{n}^{2}+2 a_{n+1}}<\\sqrt{a_{n+1}^{2}+2 a_{n+1}+1}=a_{n+1}+1\n$$\n\nhence $a_{n} \\leq a_{n+2} \\leq a_{n+1}$.\nNow let $m$ be a positive integer such that $a_{m+2}>a_{m}$. By the observations above, we must have $a_{m}<a_{m+2} \\leq a_{m+1}$. Thus the assertion ( $\\dagger$ ) is true for $k=1$. Assume that the assertion holds for some positive integer $k$. Using observation (a), we get $a_{m+2 k+1}=a_{m+2 k-1}=a_{m+1}$. Thus $a_{m+2 k} \\leq a_{m+2 k+1}$, and then using observation (b), we get $a_{m+2 k+2} \\leq a_{m+2 k+1}=a_{m+1}$, which proves the assertion ( $\\dagger$ ).", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
+
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.", "solution": "We claim that $k=2^{a}$ for all $a \\geq 0$.\nLet $A=\\{1,2,4,8, \\ldots\\}$ and $B=\\mathbb{N} \\backslash A$. For any set $T$, let $s(T)$ denote the sum of the elements of $T$. (If $T$ is empty, we let $s(T)=0$.)\nWe first show that any positive integer $k=2^{a}$ satisfies the desired property. Let $B^{\\prime}$ be a subset of $B$ with $a$ elements, and let $S=A \\cup B^{\\prime}$. Recall that any nonnegative integer has a unique binary representation. Hence, for any integer $t>s\\left(B^{\\prime}\\right)$ and any subset $B^{\\prime \\prime} \\subseteq B^{\\prime}$, the number $t-s\\left(B^{\\prime \\prime}\\right)$ can be written as a sum of distinct elements of $A$ in a unique way. This means that $t$ can be written as a sum of distinct elements of $B^{\\prime}$ in exactly $2^{a}$ ways.\nNext, assume that some positive integer $k$ satisfies the desired property for a positive integer $m \\geq 2$ and a set $S$. Clearly, $S$ is infinite.\nLemma: For all sufficiently large $x \\in S$, the smallest element of $S$ larger than $x$ is $2 x$.\nProof of Lemma: Let $x \\in S$ with $x>3 m$, and let $x<y<2 x$. We will show that $y \\notin S$. Suppose first that $y>x+m$. Then $y-x$ can be written as a sum of distinct elements of $S$ not including $x$ in $k$ ways. If $y \\in S$, then $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Suppose now that $y \\leq x+m$. We consider $z \\in(2 x-m, 2 x)$. Similarly as before, $z-x$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$ in $k$ ways. If $y \\in S$, then since $m<z-y<x, z-y$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$. This means that $z$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction.\nWe now show that $2 x \\in S$; assume for contradiction that this is not the case. Observe that $2 x$ can be written as a sum of distinct elements of $S$ including $x$ in exactly $k-1$ ways. This means that $2 x$ can also be written as a sum of distinct elements of $S$ not including $x$. If this sum includes any number less than $x-m$, then removing this number, we can write some number $y \\in(x+m, 2 x)$ as a sum of distinct elements of $S$ not including $x$. Now if $y=y^{\\prime}+x$ where $y^{\\prime} \\in(m, x)$ then $y^{\\prime}$ can be written as\na sum of distinct elements of $S$ including $x$ in exactly $k$ ways. Therefore $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Hence the sum only includes numbers in the range $[x-m, x)$. Clearly two numbers do not suffice. On the other hand, three such numbers sum to at least $3(x-m)>2 x$, a contradiction.\nFrom the Lemma, we have that $S=T \\cup U$, where $T$ is finite and $U=\\{x, 2 x, 4 x, 8 x, \\ldots\\}$ for some positive integer $x$. Let $y$ be any positive integer greater than $s(T)$. For any subset $T^{\\prime} \\subseteq T$, if $y-s\\left(T^{\\prime}\\right) \\equiv 0(\\bmod x)$, then $y-s\\left(T^{\\prime}\\right)$ can be written as a sum of distinct elements of $U$ in a unique way; otherwise $y-s\\left(T^{\\prime}\\right)$ cannot be written as a sum of distinct elements of $U$. Hence the number of ways to write $y$ as a sum of distinct elements of $S$ is equal to the number of subsets $T^{\\prime} \\subseteq T$ such that $s\\left(T^{\\prime}\\right) \\equiv y(\\bmod x)$. Since this holds for all $y$, for any $0 \\leq a \\leq x-1$ there are exactly $k$ subsets $T^{\\prime} \\subseteq T$ such that $s\\left(T^{\\prime}\\right) \\equiv a(\\bmod x)$. This means that there are $k x$ subsets of $T$ in total. But the number of subsets of $T$ is a power of 2 , and therefore $k$ is a power of 2 , as claimed.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution:"}}
|
| 6 |
+
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.", "solution": ". We give an alternative proof of the first half of the lemma in the Solution 1 above.\nLet $s_{1}<s_{2}<\\cdots$ be the elements of $S$. For any positive integer $r$, define $A_{r}(x)=\\prod_{n=1}^{r}\\left(1+x^{s_{n}}\\right)$. For each $n$ such that $m \\leq n<s_{r+1}$, all $k$ ways of writing $n$ as a sum of elements of $S$ must only use $s_{1}, \\ldots, s_{r}$, so the coefficient of $x^{n}$ in $A_{r}(x)$ is $k$. Similarly the number of ways of writing $s_{r+1}$ as a sum of elements of $S$ without using $s_{r+1}$ is exactly $k-1$. Hence the coefficient of $x^{s_{r+1}}$ in $A_{r}(x)$ is $k-1$.\nFix a $t$ such that $s_{t}>2(m+1)$. Write\n\n$$\nA_{t-1}(x)=u(x)+k\\left(x^{m+1}+\\cdots+x^{s_{t}-1}\\right)+x^{s_{t}} v(x)\n$$\n\nfor some $u(x), v(x)$ where $u(x)$ is of degree at most $m$.\nNote that\n\n$$\nA_{t+1}(x)=A_{t-1}(x)+x^{s_{t}} A_{t-1}(x)+x^{s_{t+1}} A_{t-1}(x)+x^{s_{t}+s_{t+1}} A_{t-1}(x)\n$$\n\nIf $s_{t+1}+m+1<2 s_{t}$, we can find the term $x^{s_{t+1}+m+1}$ in $x^{s_{t}} A_{t-1}(x)$ and in $x^{s_{t+1}} A_{t-1}(x)$. Hence the coefficient of $x^{s_{t+1}+m+1}$ in $A_{t+1}(x)$ is at least $2 k$, which is impossible. So $s_{t+1} \\geq 2 s_{t}-(m+1)>$ $s_{t}+m+1$.\nNow\n\n$$\nA_{t}(x)=A_{t-1}(x)+x^{s_{t}} u(x)+k\\left(x^{s_{t}+m+1}+\\cdots x^{2 s_{t}-1}\\right)+x^{2 s_{t}} v(x)\n$$\n\nRecall that the coefficent of $x^{s_{t+1}}$ in $A_{t}(x)$ is $k-1$. But if $s_{t}+m+1<s_{t+1}<s_{2 t}$, then the coefficient of $x^{s_{t+1}}$ in $A_{t}(x)$ is at least $k$, which is a contradiction. Therefore $s_{t+1} \\geq 2 s_{t}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution 2"}}
|
| 7 |
+
{"year": "2020", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $\\mathbb{Z}$ denote the set of all integers. Find all polynomials $P(x)$ with integer coefficients that satisfy the following property:\nFor any infinite sequence $a_{1}, a_{2}, \\ldots$ of integers in which each integer in $\\mathbb{Z}$ appears exactly once, there exist indices $i<j$ and an integer $k$ such that $a_{i}+a_{i+1}+\\cdots+a_{j}=P(k)$.", "solution": "Part 1: All polynomials with $\\operatorname{deg} P=1$ satisfy the given property.\nSuppose $P(x)=c x+d$, and assume without loss of generality that $c>d \\geq 0$. Denote $s_{i}=a_{1}+a_{2}+$ $\\cdots+a_{i}(\\bmod c)$. It suffices to show that there exist indices $i$ and $j$ such that $j-i \\geq 2$ and $s_{j}-s_{i} \\equiv d$ $(\\bmod c)$.\nConsider $c+1$ indices $e_{1}, e_{2}, \\ldots, e_{c+1}>1$ such that $a_{e_{l}} \\equiv d(\\bmod c)$. By the pigeonhole principle, among the $n+1$ pairs $\\left(s_{e_{1}-1}, s_{e_{1}}\\right),\\left(s_{e_{2}-1}, s_{e_{2}}\\right), \\ldots,\\left(s_{e_{n+1}-1}, s_{e_{n+1}}\\right)$, some two are equal, say $\\left(s_{m-1}, s_{m}\\right)$ and $\\left(s_{n-1}, s_{n}\\right)$. We can then take $i=m-1$ and $j=n$.\nPart 2: All polynomials with $\\operatorname{deg} P \\neq 1$ do not satisfy the given property.\nLemma: If $\\operatorname{deg} P \\neq 1$, then for any positive integers $A, B$, and $C$, there exists an integer $y$ with $|y|>C$ such that no value in the range of $P$ falls within the interval $[y-A, y+B]$.\nProof of Lemma: The claim is immediate when $P$ is constant or when $\\operatorname{deg} P$ is even since $P$ is bounded from below. Let $P(x)=a_{n} x^{n}+\\cdots+a_{1} x+a_{0}$ be of odd degree greater than 1 , and assume without\nloss of generality that $a_{n}>0$. Since $P(x+1)-P(x)=a_{n} n x^{n-1}+\\ldots$, and $n-1>0$, the gap between $P(x)$ and $P(x+1)$ grows arbitrarily for large $x$. The claim follows.\nSuppose $\\operatorname{deg} P \\neq 1$. We will inductively construct a sequence $\\left\\{a_{i}\\right\\}$ such that for any indices $i<j$ and any integer $k$ it holds that $a_{i}+a_{i+1}+\\cdots+a_{j} \\neq P(k)$. Suppose that we have constructed the sequence up to $a_{i}$, and $m$ is an integer with smallest magnitude yet to appear in the sequence. We will add two more terms to the sequence. Take $a_{i+2}=m$. Consider all the new sums of at least two consecutive terms; each of them contains $a_{i+1}$. Hence all such sums are in the interval $\\left[a_{i+1}-A, a_{i+1}+B\\right]$ for fixed constants $A, B$. The lemma allows us to choose $a_{i+1}$ so that all such sums avoid the range of $P$.\nAlternate Solution for Part 1: Again, suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \\geq 0$. Let $S_{i}=\\left\\{a_{j}+a_{j+1}+\\cdots+a_{i}(\\bmod c) \\mid j=1,2, \\ldots, i\\right\\}$. Then $S_{i+1}=\\left\\{s_{i}+a_{i+1}\\right.$ $\\left.(\\bmod c) \\mid s_{i} \\in S_{i}\\right\\} \\cup\\left\\{a_{i+1}(\\bmod c)\\right\\}$. Hence $\\left|S_{i+1}\\right|=\\left|S_{i}\\right|$ or $S_{i+1}=\\left|S_{i}\\right|+1$, with the former occuring exactly when $0 \\in S_{i}$. Since $\\left|S_{i}\\right| \\leq c$, the latter can only occur finitely many times, so there exists $I$ such that $0 \\in S_{i}$ for all $i \\geq I$. Let $t>I$ be an index with $a_{t} \\equiv d(\\bmod c)$. Then we can find a sum of at least two consecutive terms ending at $a_{t}$ and congruent to $d(\\bmod c)$.\nAlternate Construction when $P(x)$ is constant or of even degree\nIf $P(x)$ is of even degree, then $P$ is bounded from below or from above. In case of $P$ is constant or bounded from above, then there exists a positive integer $c$ such that $P(x)<c$. Let $\\left\\{a_{i}\\right\\}$ be the sequence\n\n$$\n0,1,-1,2,3,-2,4,5,-3, \\cdots\n$$\n\nwhich is given by $a_{3 n+1}=2 n, a_{3 n+2}=2 n+1, a_{3 n+3}=-(n+1)$ for all $n \\geq 0$. Notice that for any $i<j$ we have $a_{i}+\\cdots+a_{j} \\geq 0$. Then for the sequence $\\left\\{b_{n}\\right\\}$ defined by $b_{n}=a_{n}+c$, clearly $b_{i}+\\cdots+b_{j} \\geq\\left(a_{i}+\\cdots+a_{j}\\right)+2 c>c$ which is out side the range of $P(x)$.\n\nNow if $P$ is bounded from below, there exist a positive integer $c$ such that $P(x)>-c$. In this case, take $b_{n}$ to be $b_{n}=-a_{n}-c$. Then for all $i<j$ we have $b_{i}+\\cdots+b_{j} \\leq-\\left(a_{1}+\\cdots a_{n}\\right)-2 c<-c$ which is again out side the range of $P(x)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution:"}}
|
| 8 |
+
{"year": "2020", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $n \\geq 3$ be a fixed integer. The number 1 is written $n$ times on a blackboard. Below the blackboard, there are two buckets that are initially empty. A move consists of erasing two of the numbers $a$ and $b$, replacing them with the numbers 1 and $a+b$, then adding one stone to the first bucket and $\\operatorname{gcd}(a, b)$ stones to the second bucket. After some finite number of moves, there are $s$ stones in the first bucket and $t$ stones in the second bucket, where $s$ and $t$ are positive integers. Find all possible values of the ratio $\\frac{t}{s}$.", "solution": "The answer is the set of all rational numbers in the interval $[1, n-1)$. First, we show that no other numbers are possible. Clearly the ratio is at least 1, since for every move, at least one stone is added to the second bucket. Note that the number $s$ of stones in the first bucket is always equal to $p-n$, where $p$ is the sum of the numbers on the blackboard. We will assume that the numbers are written in a row, and whenever two numbers $a$ and $b$ are erased, $a+b$ is written in the place of the number on the right. Let $a_{1}, a_{2}, \\ldots, a_{n}$ be the numbers on the blackboard from left to right, and let\n\n$$\nq=0 \\cdot a_{1}+1 \\cdot a_{2}+\\cdots+(n-1) a_{n}\n$$\n\nSince each number $a_{i}$ is at least 1 , we always have\n\n$$\nq \\leq(n-1) p-(1+\\cdots+(n-1))=(n-1) p-\\frac{n(n-1)}{2}=(n-1) s+\\frac{n(n-1)}{2}\n$$\n\nAlso, if a move changes $a_{i}$ and $a_{j}$ with $i<j$, then $t$ changes by $\\operatorname{gcd}\\left(a_{i}, a_{j}\\right) \\leq a_{i}$ and $q$ increases by\n\n$$\n(j-1) a_{i}-(i-1)\\left(a_{i}-1\\right) \\geq i a_{i}-(i-1)\\left(a_{i}-1\\right) \\geq a_{i}\n$$\n\nHence $q-t$ never decreases. We may assume without loss of generality that the first move involves the rightmost 1. Then immediately after this move, $q=0+1+\\cdots+(n-2)+(n-1) \\cdot 2=\\frac{(n+2)(n-1)}{2}$ and\n$t=1$. So after that move, we always have\n\n$$\n\\begin{aligned}\nt & \\leq q+1-\\frac{(n+2)(n-1)}{2} \\\\\n& \\leq(n-1) s+\\frac{n(n-1)}{2}-\\frac{(n+2)(n-1)}{2}+1 \\\\\n& =(n-1) s-(n-2)<(n-1) s\n\\end{aligned}\n$$\n\nHence, $\\frac{t}{s}<n-1$. So $\\frac{t}{s}$ must be a rational number in $[1, n-1)$.\n\nAfter a single move, we have $\\frac{t}{s}=1$, so it remains to prove that $\\frac{t}{s}$ can be any rational number in $(1, n-1)$. We will now show by induction on $n$ that for any positive integer $a$, it is possible to reach a situation where there are $n-1$ occurrences of 1 on the board and the number $a^{n-1}$, with $t$ and $s$ equal to $a^{n-2}(a-1)(n-1)$ and $a^{n-1}-1$, respectively. For $n=2$, this is clear as there is only one possible move at each step, so after $a-1$ moves $s$ and $t$ will both be equal to $a-1$. Now assume that the claim is true for $n-1$, where $n>2$. Call the algorithm which creates this situation using $n-1$ numbers algorithm $A$. Then to reach the situation for size $n$, we apply algorithm $A$, to create the number $a^{n-2}$. Next, apply algorithm $A$ again and then add the two large numbers, repeat until we get the number $a^{n-1}$. Then algorithm $A$ was applied $a$ times and the two larger numbers were added $a-1$ times. Each time the two larger numbers are added, $t$ increases by $a^{n-2}$ and each time algorithm $A$ is applied, $t$ increases by $a^{n-3}(a-1)(n-2)$. Hence, the final value of $t$ is\n\n$$\nt=(a-1) a^{n-2}+a \\cdot a^{n-3}(a-1)(n-2)=a^{n-2}(a-1)(n-1)\n$$\n\nThis completes the induction.\nNow we can choose 1 and the large number $b$ times for any positive integer $b$, and this will add $b$ stones to each bucket. At this point we have\n\n$$\n\\frac{t}{s}=\\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}\n$$\n\nSo we just need to show that for any rational number $\\frac{p}{q} \\in(1, n-1)$, there exist positive integers $a$ and $b$ such that\n\n$$\n\\frac{p}{q}=\\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}\n$$\n\nRearranging, we see that this happens if and only if\n\n$$\nb=\\frac{q a^{n-2}(a-1)(n-1)-p\\left(a^{n-1}-1\\right)}{p-q} .\n$$\n\nIf we choose $a \\equiv 1(\\bmod p-q)$, then this will be an integer, so we just need to check that the numerator is positive for sufficiently large $a$.\n\n$$\n\\begin{aligned}\nq a^{n-2}(a-1)(n-1)-p\\left(a^{n-1}-1\\right) & >q a^{n-2}(a-1)(n-1)-p a^{n-1} \\\\\n& =a^{n-2}(a(q(n-1)-p)-(n-1))\n\\end{aligned}\n$$\n\nwhich is positive for sufficiently large $a$ since $q(n-1)-p>0$.\n\nAlternative solution for the upper bound. Rather than starting with $n$ occurrences of 1 , we may start with infinitely many 1 s , but we are restricted to having at most $n-1$ numbers which are not equal to 1 on the board at any time. It is easy to see that this does not change the problem. Note also that we can ignore the 1 we write on the board each move, so the allowed move is to rub off two numbers and write their sum. We define the width and score of a number on the board as follows. Colour that number red, then reverse every move up to that point all the way back to the situation when the numbers are all 1 s . Whenever a red number is split, colour the two replacement numbers\nred. The width of the original number is equal to the maximum number of red integers greater than 1 which appear on the board at the same time. The score of the number is the number of stones which were removed from the second bucket during these splits. Then clearly the width of any number is at most $n-1$. Also, $t$ is equal to the sum of the scores of the final numbers. We claim that if a number $p>1$ has a width of at most $w$, then its score is at most $(p-1) w$. We will prove this by strong induction on $p$. If $p=1$, then clearly $p$ has a score of 0 , so the claim is true. If $p>1$, then $p$ was formed by adding two smaller numbers $a$ and $b$. Clearly $a$ and $b$ both have widths of at most $w$. Moreover, if $a$ has a width of $w$, then at some point in the reversed process there will be $w$ numbers in the set $\\{2,3,4, \\ldots\\}$ that have split from $a$, and hence there can be no such numbers at this point which have split from $b$. Between this point and the final situation, there must always be at least one number in the set $\\{2,3,4, \\ldots\\}$ that split from $a$, so the width of $b$ is at most $w-1$. Therefore, $a$ and $b$ cannot both have widths of $w$, so without loss of generality, $a$ has width at most $w$ and $b$ has width at most $w-1$. Then by the inductive hypothesis, $a$ has score at most $(a-1) w$ and $b$ has score at most $(b-1)(w-1)$. Hence, the score of $p$ is at most\n\n$$\n\\begin{aligned}\n(a-1) w+(b-1)(w-1)+\\operatorname{gcd}(a, b) & \\leq(a-1) w+(b-1)(w-1)+b \\\\\n& =(p-1) w+1-w \\\\\n& \\leq(p-1) w .\n\\end{aligned}\n$$\n\nThis completes the induction.\nNow, since each number $p$ in the final configuration has width at most $(n-1)$, it has score less than $(n-1)(p-1)$. Hence the number $t$ of stones in the second bucket is less than the sum over the values of $(n-1)(p-1)$, and $s$ is equal to the sum of the the values of $(p-1)$. Therefore, $\\frac{t}{s}<n-1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution:"}}
|
APMO/segmented/en-apmo2021_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Prove that for each real number $r>2$, there are exactly two or three positive real numbers $x$ satisfying the equation $x^{2}=r\\lfloor x\\rfloor$.\nNote: $\\lfloor x\\rfloor$ denotes the largest integer less than or equal to $x$", "solution": "Let $r>2$ be a real number. Let $x$ be a positive real number such that $x^{2}=r\\lfloor x\\rfloor$ with $\\lfloor x\\rfloor=k$. Since $x>0$ and $x^{2}=r k$, we also have $k>0$. From $k \\leq x<k+1$, we get $k^{2} \\leq x^{2}=r k<$ $k^{2}+2 k+1 \\leq k^{2}+3 k$, hence $k \\leq r<k+3$, or $r-3<k \\leq r$. There are at most three positive integers in the interval $(r-3, r]$. Thus there are at most three possible values for $k$. Consequently, there are at most three positive solutions to the given equation.\nNow suppose that $k$ is a positive integer in the interval $[r-2, r]$. There are at least two such positive integer. Observe that $k \\leq \\sqrt{r k} \\leq \\sqrt{(k+2) k}<k+1$ and so $r k=r\\lfloor\\sqrt{r k}\\rfloor$. We conclude that the equation $x^{2}=r\\lfloor x\\rfloor$ has at least two positive solutions, namely $x=\\sqrt{r k}$ with $k \\in[r-2, r]$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution "}}
|
| 2 |
-
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "There are two possible families of solutions:\n\n- $P(x)=x+d$, for some integer $d \\geq-2022$.\n- $P(x)=-x+d$, for some integer $d \\leq 2022$.\n\nSuppose $P$ satisfies the problem conditions. Clearly $P$ cannot be a constant polynomial. Notice that a polynomial $P$ satifies the conditions if and only if $-P$ also satisfies them. Hence, we may assume the leading coefficient of $P$ is positive. Then, there exists positive integer $M$ such that $P(x)>0$ for $x \\geq M$.\n\nLemma 1. For any positive integer $n$, the integers $P(1), P(2), \\ldots, P(n)$ leave pairwise distinct remainders upon division by $n$.\n\nProof. Assume for contradiction that this is not the case. Then, for some $1 \\leq y<z \\leq n$, there exists $0 \\leq r \\leq n-1$ such that $P(y) \\equiv P(z) \\equiv r(\\bmod n)$. Since $P(a n+b) \\equiv P(b)(\\bmod n)$ for all $a, b$ integers, we have $P(a n+y) \\equiv P(a n+z) \\equiv r(\\bmod n)$ for any integer $a$. Let $A$ be a positive integer such that $A n \\geq M$, and let $k$ be a positive integer such that $k>2 A+2021$. Each of the $2(k-A)$ integers $P(A n+y), P(A n+z), P((A+1) n+y), P((A+1) n+z), \\ldots, P((k-1) n+y), P((k-1) n+z)$ leaves one of the $k$ remainders\n\n$$\nr, n+r, 2 n+r, \\ldots,(k-1) n+r\n$$\n\nupon division by $k n$. This implies that at least $2(k-A)-k=k-2 A$ (possibly overlapping) pairs leave the same remainder upon division by $k n$. Since $k-2 A>2021$ and all of the $2(k-A)$ integers are positive, we find more than 2021 pairs $a, b$ with $a<b \\leq k n$ for which $|P(b)|-|P(a)|$ is divisible by $k n$-hence, $P_{k n}>2021$, a contradiction.\n\nNext, we show that $P$ is linear. Assume that this is not the case, i.e., $\\operatorname{deg} P \\geq 2$. Then we can find a positive integer $k$ such that $P(k)-P(1) \\geq k$. This means that among the integers $P(1), P(2), \\ldots, P(P(k)-P(1))$, two of them, namely $P(k)$ and $P(1)$, leave the same remainder upon division by $P(k)-P(1)$ - contradicting the lemma (by taking $n=P(k)-P(1)$ ). Hence, $P$ must be linear.\nWe can now write $P(x)=c x+d$ with $c>0$. We prove that $c=1$ by two ways.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution "}}
|
| 3 |
-
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "If $c \\geq 2$, then $P(1)$ and $P(2)$ leave the same remainder upon division by $c$, contradicting the Lemma. Hence $c=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
-
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "Suppose $c \\geq 2$. Let $n$ be a positive integer such that $n>2 c M, n\\left(1-\\frac{3}{2 c}\\right)>2022$ and $2 c \\mid n$. Notice that for any positive integers $i$ such that $\\frac{3 n}{2 c}+i<n, P\\left(\\frac{3 n}{2 c}+i\\right)-P\\left(\\frac{n}{2 c}+i\\right)=n$. Hence, $\\left(\\frac{n}{2 c}+i, \\frac{3 n}{2 c}+i\\right)$ satifies the condition in the question for all positive integers $i$ such that $\\frac{3 n}{2 c}+i<n$. Hence, $P_{n}>2021$, a contradiction. Then, $c=1$.\n\nIf $d \\leq-2023$, then there are at least 2022 pairs $a<b$ such that $P(a)=P(b)$, namely $(a, b)=$ $(1,-2 d-1),(2,-2 d-2), \\ldots,(-d-1,-d+1)$. This implies that $d \\geq-2022$.\nFinally, we verify that $P(x)=x+d$ satisfies the condition for any $d \\geq-2022$. Fix a positive integer $n$. Note that $\\| P(b)|-|P(a)||<n$ for all positive integers $a<b \\leq n$, so the only pairs $a, b$ for which $|P(b)|-|P(a)|$ could be divisible by $n$ are those for which $|P(a)|=|P(b)|$. When $d \\geq-2022$, there are indeed at most 2021 such pairs.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 5 |
-
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C D$ be a cyclic convex quadrilateral and $\\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.", "solution": "Let $L$ be the intersection of the bisectors of $\\angle A B C$ and $\\angle B C D$. Let $N$ be the $E$-excenter of $\\triangle B C E$. Let $\\angle B A C=\\angle B D C=\\alpha, \\angle D B C=\\beta$ and $\\angle A C B=\\gamma$.\nWe have the following:\n\n$$\n\\begin{array}{r}\n\\angle C B L=\\frac{1}{2} \\angle A B C=90^{\\circ}-\\frac{1}{2} \\alpha-\\frac{1}{2} \\gamma \\text { and } \\angle B C L=90^{\\circ}-\\frac{1}{2} \\alpha-\\frac{1}{2} \\beta, \\\\\n\\angle C B N=90^{\\circ}-\\frac{1}{2} \\beta \\text { and } \\angle B C N=90^{\\circ}-\\frac{1}{2} \\gamma, \\\\\n\\angle M B L=\\angle M B C+\\angle C B L=90^{\\circ}-\\frac{1}{2} \\gamma \\text { and } \\angle M C L=90^{\\circ}-\\frac{1}{2} \\beta, \\\\\n\\angle L C N=\\angle L B N=180^{\\circ}-\\frac{1}{2}(\\alpha+\\beta+\\gamma) .\n\\end{array}\n$$\n\nApplying the sine rule to $\\triangle M B L$ and $\\triangle M C L$ we obtain\n\n$$\n\\frac{M B}{M L}=\\frac{M C}{M L}=\\frac{\\sin \\angle B L M}{\\sin \\angle M B L}=\\frac{\\sin \\angle C L M}{\\sin \\angle M C L}\n$$\n\nIt follows that\n\n$$\n\\frac{\\sin \\angle B L M}{\\sin \\angle C L M}=\\frac{\\sin \\angle M B L}{\\sin \\angle M C L}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)}\n$$\n\nNow\n\n$$\n\\frac{\\sin \\angle B L M}{\\sin \\angle M L C} \\cdot \\frac{\\sin \\angle L C N}{\\sin \\angle N C B} \\cdot \\frac{\\sin \\angle N B C}{\\sin \\angle N B L}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)} \\cdot \\frac{\\sin \\left(90^{\\circ}-\\frac{1}{2} \\beta\\right)}{\\sin \\left(90^{\\circ}-\\frac{1}{2} \\gamma\\right)}=1\n$$\n\nHence $L M, B N, C N$ are concurrent and therefore $L, M, N$ are collinear.\n\n## Alternative proof\n\nWe proceed similarly as above until the equation (1).\nWe use the following lemma.\nLemma: If $\\pi>\\alpha, \\beta, \\gamma, \\delta>0, \\alpha+\\beta=\\gamma+\\delta<\\pi$, and $\\frac{\\sin \\alpha}{\\sin \\beta}=\\frac{\\sin \\gamma}{\\sin \\delta}$, then $\\alpha=\\gamma$ and $\\beta=\\delta$.\nProof of Lemma: Let $\\theta=\\alpha+\\beta=\\gamma+\\delta$. Then $\\frac{\\sin (\\theta-\\beta)}{\\sin \\beta}=\\frac{\\sin (\\theta-\\delta)}{\\sin \\delta}$.\n\n$$\n\\begin{gathered}\n\\Longleftrightarrow \\sin (\\theta-\\beta) \\sin \\delta=\\sin (\\theta-\\delta) \\sin \\beta \\\\\n\\Longleftrightarrow(\\sin \\theta \\cos \\beta-\\sin \\beta \\cos \\theta) \\sin \\delta=(\\sin \\theta \\cos \\delta-\\sin \\delta \\cos \\theta) \\sin \\beta \\\\\n\\Longleftrightarrow \\sin \\theta \\cos \\beta \\sin \\delta=\\sin \\theta \\cos \\delta \\sin \\beta \\\\\n\\Longleftrightarrow \\sin \\theta \\sin (\\beta-\\delta)=0\n\\end{gathered}\n$$\n\nSince $0<\\theta<\\pi$, then $\\sin \\theta \\neq 0$. Therefore, $\\sin (\\beta-\\delta)=0$, and we must have $\\beta=\\delta$.\nApplying the sine rule to $\\triangle N B L$ and $\\triangle N C L$ we obtain\n\n$$\n\\begin{aligned}\n& \\frac{N B}{N L}=\\frac{\\sin \\angle B L N}{\\sin \\angle L B N} \\\\\n& \\frac{N C}{N L}=\\frac{\\sin \\angle C L N}{\\sin \\angle L C N}\n\\end{aligned}\n$$\n\nSince $\\angle L B N=\\angle L C N$, it follows that\n\n$$\n\\frac{\\sin \\angle B L N}{\\sin \\angle C L N}=\\frac{N B}{N C}=\\frac{\\sin \\angle B C N}{\\sin \\angle C B N}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)}=\\frac{\\sin \\angle B L M}{\\sin \\angle C L M}\n$$\n\nBy the lemma, it is concluded that $\\angle B L M=\\angle B L N$ and $\\angle C L M=\\angle C L N$. Therefore, $L, M, N$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 1"}}
|
| 6 |
-
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C D$ be a cyclic convex quadrilateral and $\\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.", "solution": "Denote by $N$ the excenter of triangle $B C E$ opposite $E$. Since $B L$ bisects $\\angle A B C$, we have $\\angle C B L=$ $\\frac{\\angle A B C}{2}$. Since $M$ is the midpoint of arc $B C$, we have $\\angle M B C=\\frac{1}{2}(\\angle M B C+\\angle M C B)$ It follows by angle chasing that\n\n$$\n\\begin{aligned}\n\\angle M B L & =\\angle M B C+\\angle C B L=\\frac{1}{2}(\\angle M B C+\\angle M C B+\\angle A B C) \\\\\n& =\\frac{1}{2}(\\angle M B A+\\angle M C B)=90^{\\circ}-\\frac{\\angle B C E}{2}=\\angle B C N .\n\\end{aligned}\n$$\n\nDenote by $X$ and $Y$ the second intersections of lines $B M$ and $C M$ with the circumcircle of $B C L$, respectively. Since $\\angle M B C=\\angle M C B$, we have $B C \\| X Y$. It suffices to show that $B N \\| X L$ and $C N \\| Y L$. Indeed, from this it follows that $\\triangle B C N \\sim \\triangle X Y L$, and therefore a homothety with center $M$ that maps $B$ to $X$ and $C$ to $Y$ also maps $N$ to $L$, implying that $N$ lies on the line $L M$.\nBy symmetry, it suffices to show that $C N \\| Y L$, which is equivalent to showing that $\\angle B C N=\\angle X Y L$. But we have $\\angle B C N=\\angle M B L=\\angle X B L=\\angle X Y L$, completing the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Given a $32 \\times 32$ table, we put a mouse (facing up) at the bottom left cell and a piece of cheese at several other cells. The mouse then starts moving. It moves forward except that when it reaches a piece of cheese, it eats a part of it, turns right, and continues moving forward. We say that a subset of cells containing cheese is good if, during this process, the mouse tastes each piece of cheese exactly once and then falls off the table. Show that:\n(a) No good subset consists of 888 cells.\n(b) There exists a good subset consisting of at least 666 cells.", "solution": "(a) For the sake of contradiction, assume a good subset consisting of 888 cells exists. We call those cheese-cells and the other ones gap-cells. Observe that since each cheese-cell is visited once, each gap-cell is visited at most twice (once vertically and once horizontally). Define a finite sequence $s$ whose $i$-th element is $C$ if the $i$-th step of the mouse was onto a cheese-cell, and $G$ if it was onto a gap-cell. By assumption, $s$ contains $888 C$ 's. Note that $s$ does not contain a contiguous block of 4 (or more) $C$ 's. Hence $s$ contains at least $888 / 3=296$ such $C$-blocks and thus at least $295 G^{\\prime}$ 's. But since each gap-cell is traversed at most twice, this implies there are at least $\\lceil 295 / 2\\rceil=148$ gap-cells, for a total of $888+148=1036>32^{2}$ cells, a contradiction.\n(b) Let $L_{i}, X_{i}$ be two $2^{i} \\times 2^{i}$ tiles that allow the mouse to \"turn left\" and \"cross\", respectively. In detail, the \"turn left\" tiles allow the mouse to enter at its bottom left cell facing up and to leave at its bottom left cell facing left. The \"cross\" tiles allow the mouse to enter at its top right facing down and leave at its bottom left facing left, while also to enter at its bottom left facing up and leave at its top right facing right.\n(a) Basic tiles\n(b) Inductive construction\n(c) $16 \\times 16$\n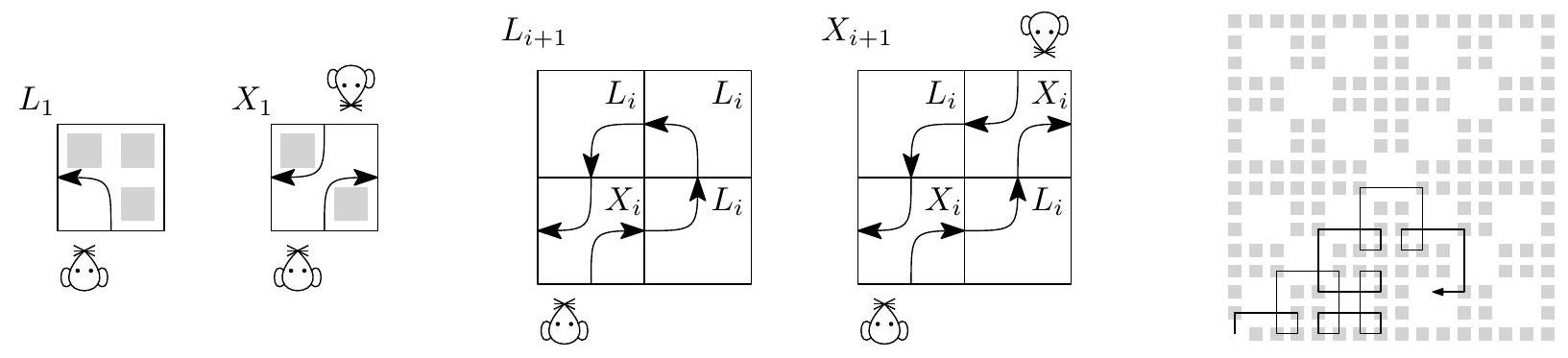\n\nNote that given two $2^{i} \\times 2^{i}$ tiles $L_{i}, X_{i}$ we can construct larger $2^{i+1} \\times 2^{i+1}$ tiles $L_{i+1}, X_{i+1}$ inductively as shown on in (b). The construction works because the path intersects itself (or the other path) only inside the smaller $X$-tiles where it works by induction.\nFor a tile $T$, let $|T|$ be the number of pieces of cheese in it. By straightforward induction, $\\left|L_{i}\\right|=\\left|X_{i}\\right|+1$ and $\\left|L_{i+1}\\right|=4 \\cdot\\left|L_{i}\\right|-1$. From the initial condition $\\left|L_{1}\\right|=3$. We now easily compute $\\left|L_{2}\\right|=11,\\left|L_{3}\\right|=43,\\left|L_{4}\\right|=171$, and $\\left|L_{5}\\right|=683$. Hence we get the desired subset.\n\n## Another proof of (a).\n\nLet $X_{N}$ be the largest possible density of cheese-cells in a good subset on an $N \\times N$ table. We will show that $X_{N} \\leq 4 / 5+o(1)$. Specifically, this gives $X_{32} \\leq 817 / 1024$. We look at the (discrete analogue) of the winding number of the trajectory of the mouse. Since the mouse enters and leaves the table, for every 4 right turns in its trajectory there has to be a self-crossing. But each self-crossing requires a different empty square, hence $X_{N} \\leq 4 / 5$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution."}}
|
| 8 |
-
{"year": "2021", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Determine all functions $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ such that $f(f(a)-b)+b f(2 a)$ is a perfect square for all integers $a$ and $b$.", "solution": ".\n\nThere are two families of functions which satisfy the condition:\n(1) $f(n)= \\begin{cases}0 & \\text { if } n \\text { is even, and } \\\\ \\text { any perfect square } & \\text { if } n \\text { is odd }\\end{cases}$\n(2) $f(n)=n^{2}$, for every integer $n$.\n\nIt is straightforward to verify that the two families of functions are indeed solutions. Now, suppose that f is any function which satisfies the condition that $f(f(a)-b)+b f(2 a)$ is a perfect square for every pair $(a, b)$ of integers. We denote this condition by $\\left(^{*}\\right)$. We will show that $f$ must belong to either Family (1) or Family (2).\nClaim 1. $f(0)=0$ and $f(n)$ is a perfect square for every integer $n$.\nProof. Plugging $(a, b) \\rightarrow(0, f(0))$ in $\\left(^{*}\\right)$ shows that $f(0)(f(0)+1)=z^{2}$ for some integer $z$. Thus, $(2 f(0)+1-2 z)(2 f(0)+1+2 z)=1$. Therefore, $f(0)$ is either -1 or 0.\nSuppose, for sake of contradiction, that $f(0)=-1$. For any integer $a$, plugging $(a, b) \\rightarrow(a, f(a))$ implies that $f(a) f(2 a)-1$ is a square. Thus, for each $a \\in \\mathbb{Z}$, there exists $x \\in \\mathbb{Z}$ such that $f(a) f(2 a)=x^{2}+1$ This implies that any prime divisor of $f(a)$ is either 2 or is congruent to $1(\\bmod 4)$, and that $4 \\nmid f(a)$, for every $a \\in \\mathbb{Z}$.\nPlugging $(a, b) \\rightarrow(0,3)$ in $\\left(^{*}\\right)$ shows that $f(-4)-3$ is a square. Thus, there is $y \\in \\mathbb{Z}$ such that $f(-4)=y^{2}+3$. Since $4 \\nmid f(-4)$, we note that $f(-4)$ is a positive integer congruent to $3(\\bmod 4)$, but any prime dividing $f(-4)$ is either 2 or is congruent to $1(\\bmod 4)$. This gives a contradiction. Therefore, $f(0)$ must be 0 .\nFor every integer $n$, plugging $(a, b) \\rightarrow(0,-n)$ in $\\left(^{*}\\right)$ shows that $f(n)$ is a square.\nReplacing $b$ with $f(a)-b$, we find that for all integers $a$ and $b$,\n\n$$\nf(b)+(f(a)-b) f(2 a) \\text { is a square. }\n$$\n\nNow, let $S$ be the set of all integers $n$ such that $f(n)=0$. We have two cases:\n\n- Case 1: $S$ is unbounded from above.\n\nWe claim that $f(2 n)=0$ for any integer $n$. Fix some integer $n$, and let $k \\in S$ with $k>f(n)$. Then, plugging $(a, b) \\mapsto(n, k)$ in $\\left({ }^{* *}\\right)$ gives us that $f(k)+(f(n)-k) f(2 n)=(f(n)-k) f(2 n)$ is a square. But $f(n)-k<0$ and $f(2 n)$ is a square by Claim 1. This is possible only if $f(2 n)=0$. In summary, $f(n)=0$ whenever $n$ is even and Claim 1 shows that $f(n)$ is a square whenever $n$ is odd.\n\n- Case 2: $S$ is bounded from above.\n\nLet $T$ be the set of all integers $n$ such that $f(n)=n^{2}$. We show that $T$ is unbounded from above. In fact, we show that $\\frac{p+1}{2} \\in T$ for all primes $p$ big enough.\nFix a prime number $p$ big enough, and let $n=\\frac{p+1}{2}$. Plugging $(a, b) \\mapsto(n, 2 n)$ in ( $\\left.{ }^{* *}\\right)$ shows us that $f(2 n)(f(n)-2 n+1)$ is a square for any integer $n$. For $p$ big enough, we have $2 n \\notin S$, so $f(2 n)$ is a non-zero square. As a result, when $p$ is big enough, $f(n)$ and $f(n)-2 n+1=f(n)-p$ are both squares. Writing $f(n)=k^{2}$ and $f(n)-p=m^{2}$ for some $k, m \\geq 0$, we have\n\n$$\n(k+m)(k-m)=k^{2}-m^{2}=p \\Longrightarrow k+m=p, k-m=1 \\Longrightarrow k=n, m=n-1\n$$\n\nThus, $f(n)=k^{2}=n^{2}$, giving us $n=\\frac{p+1}{2} \\in T$.\nNext, for all $k \\in T$ and $n \\in \\mathbb{Z}$, plugging $(a, b) \\mapsto(n, k)$ in $(* *)$ shows us that $k^{2}+(f(n)-k) f(2 n)$ is a square. But that means $(2 k-f(2 n))^{2}-\\left(f(2 n)^{2}-4 f(n) f(2 n)\\right)=4\\left(k^{2}+(f(n)-k) f(2 n)\\right)$ is also a square. When $k$ is large enough, we have $\\left|f(2 n)^{2}-4 f(n) f(2 n)\\right|+1<|2 k-f(2 n)|$. As a result, we must have $f(2 n)^{2}=4 f(n) f(2 n)$ and thus $f(2 n) \\in\\{0,4 f(n)\\}$ for all integers $n$.\nFinally, we prove that $f(n)=n^{2}$ for all integers $n$. Fix $n$, and take $k \\in T$ big enough such that $2 k \\notin S$. Then, we have $f(k)=k^{2}$ and $f(2 k)=4 f(k)=4 k^{2}$. Plugging $(a, b) \\mapsto(k, n)$ to $(* *)$ shows us that $f(n)+\\left(k^{2}-n\\right) 4 k^{2}=\\left(2 k^{2}-n\\right)^{2}+\\left(f(n)-n^{2}\\right)$ is a square. Since $T$ is unbounded from above, we can take $k \\in T$ such that $2 k \\notin S$ and also $\\left|2 k^{2}-n\\right|>\\left|f(n)-n^{2}\\right|$. This forces $f(n)=n^{2}$, giving us the second family of solution.\n\n## Another approach of Case 1.\n\nClaim 2. One of the following is true.\n(i) For every integer $n, f(2 n)=0$.\n(ii) There exists an integer $K>0$ such that for every integer $n \\geq K, f(n)>0$.\n\nProof. Suppose that there exists an integer $\\alpha \\neq 0$ such that $f(2 \\alpha)>0$. We claim that for every integer $n \\geq f(\\alpha)+1$, we have $f(n)>0$.\nFor every $n \\geq f(\\alpha)+1$, plugging $(a, b) \\rightarrow(\\alpha, f(\\alpha)-n)$ in $\\left(^{*}\\right)$ shows that $f(n)+(f(\\alpha)-n) f(2 \\alpha)$ is a square, and in particular, is non-negative. Hence, $f(n) \\geq(n-f(\\alpha)) f(2 \\alpha)>0$, as desired.\nIf $f$ belongs to Case (i), Claim 1 shows that $f$ belongs to Family (1).\nIf $f$ belongs to Case (ii), then $S$ is bounded from above. From Case 2 we get $f(n)=n^{2}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 1"}}
|
|
|
|
| 1 |
+
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Prove that for each real number $r>2$, there are exactly two or three positive real numbers $x$ satisfying the equation $x^{2}=r\\lfloor x\\rfloor$.\nNote: $\\lfloor x\\rfloor$ denotes the largest integer less than or equal to $x$", "solution": "Let $r>2$ be a real number. Let $x$ be a positive real number such that $x^{2}=r\\lfloor x\\rfloor$ with $\\lfloor x\\rfloor=k$. Since $x>0$ and $x^{2}=r k$, we also have $k>0$. From $k \\leq x<k+1$, we get $k^{2} \\leq x^{2}=r k<$ $k^{2}+2 k+1 \\leq k^{2}+3 k$, hence $k \\leq r<k+3$, or $r-3<k \\leq r$. There are at most three positive integers in the interval $(r-3, r]$. Thus there are at most three possible values for $k$. Consequently, there are at most three positive solutions to the given equation.\nNow suppose that $k$ is a positive integer in the interval $[r-2, r]$. There are at least two such positive integer. Observe that $k \\leq \\sqrt{r k} \\leq \\sqrt{(k+2) k}<k+1$ and so $r k=r\\lfloor\\sqrt{r k}\\rfloor$. We conclude that the equation $x^{2}=r\\lfloor x\\rfloor$ has at least two positive solutions, namely $x=\\sqrt{r k}$ with $k \\in[r-2, r]$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution "}}
|
| 2 |
+
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "There are two possible families of solutions:\n\n- $P(x)=x+d$, for some integer $d \\geq-2022$.\n- $P(x)=-x+d$, for some integer $d \\leq 2022$.\n\nSuppose $P$ satisfies the problem conditions. Clearly $P$ cannot be a constant polynomial. Notice that a polynomial $P$ satifies the conditions if and only if $-P$ also satisfies them. Hence, we may assume the leading coefficient of $P$ is positive. Then, there exists positive integer $M$ such that $P(x)>0$ for $x \\geq M$.\n\nLemma 1. For any positive integer $n$, the integers $P(1), P(2), \\ldots, P(n)$ leave pairwise distinct remainders upon division by $n$.\n\nProof. Assume for contradiction that this is not the case. Then, for some $1 \\leq y<z \\leq n$, there exists $0 \\leq r \\leq n-1$ such that $P(y) \\equiv P(z) \\equiv r(\\bmod n)$. Since $P(a n+b) \\equiv P(b)(\\bmod n)$ for all $a, b$ integers, we have $P(a n+y) \\equiv P(a n+z) \\equiv r(\\bmod n)$ for any integer $a$. Let $A$ be a positive integer such that $A n \\geq M$, and let $k$ be a positive integer such that $k>2 A+2021$. Each of the $2(k-A)$ integers $P(A n+y), P(A n+z), P((A+1) n+y), P((A+1) n+z), \\ldots, P((k-1) n+y), P((k-1) n+z)$ leaves one of the $k$ remainders\n\n$$\nr, n+r, 2 n+r, \\ldots,(k-1) n+r\n$$\n\nupon division by $k n$. This implies that at least $2(k-A)-k=k-2 A$ (possibly overlapping) pairs leave the same remainder upon division by $k n$. Since $k-2 A>2021$ and all of the $2(k-A)$ integers are positive, we find more than 2021 pairs $a, b$ with $a<b \\leq k n$ for which $|P(b)|-|P(a)|$ is divisible by $k n$-hence, $P_{k n}>2021$, a contradiction.\n\nNext, we show that $P$ is linear. Assume that this is not the case, i.e., $\\operatorname{deg} P \\geq 2$. Then we can find a positive integer $k$ such that $P(k)-P(1) \\geq k$. This means that among the integers $P(1), P(2), \\ldots, P(P(k)-P(1))$, two of them, namely $P(k)$ and $P(1)$, leave the same remainder upon division by $P(k)-P(1)$ - contradicting the lemma (by taking $n=P(k)-P(1)$ ). Hence, $P$ must be linear.\nWe can now write $P(x)=c x+d$ with $c>0$. We prove that $c=1$ by two ways.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution "}}
|
| 3 |
+
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "If $c \\geq 2$, then $P(1)$ and $P(2)$ leave the same remainder upon division by $c$, contradicting the Lemma. Hence $c=1$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 4 |
+
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \\leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.\nDetermine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \\leq 2021$.", "solution": "Suppose $c \\geq 2$. Let $n$ be a positive integer such that $n>2 c M, n\\left(1-\\frac{3}{2 c}\\right)>2022$ and $2 c \\mid n$. Notice that for any positive integers $i$ such that $\\frac{3 n}{2 c}+i<n, P\\left(\\frac{3 n}{2 c}+i\\right)-P\\left(\\frac{n}{2 c}+i\\right)=n$. Hence, $\\left(\\frac{n}{2 c}+i, \\frac{3 n}{2 c}+i\\right)$ satifies the condition in the question for all positive integers $i$ such that $\\frac{3 n}{2 c}+i<n$. Hence, $P_{n}>2021$, a contradiction. Then, $c=1$.\n\nIf $d \\leq-2023$, then there are at least 2022 pairs $a<b$ such that $P(a)=P(b)$, namely $(a, b)=$ $(1,-2 d-1),(2,-2 d-2), \\ldots,(-d-1,-d+1)$. This implies that $d \\geq-2022$.\nFinally, we verify that $P(x)=x+d$ satisfies the condition for any $d \\geq-2022$. Fix a positive integer $n$. Note that $\\| P(b)|-|P(a)||<n$ for all positive integers $a<b \\leq n$, so the only pairs $a, b$ for which $|P(b)|-|P(a)|$ could be divisible by $n$ are those for which $|P(a)|=|P(b)|$. When $d \\geq-2022$, there are indeed at most 2021 such pairs.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 2"}}
|
| 5 |
+
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C D$ be a cyclic convex quadrilateral and $\\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.", "solution": "Let $L$ be the intersection of the bisectors of $\\angle A B C$ and $\\angle B C D$. Let $N$ be the $E$-excenter of $\\triangle B C E$. Let $\\angle B A C=\\angle B D C=\\alpha, \\angle D B C=\\beta$ and $\\angle A C B=\\gamma$.\nWe have the following:\n\n$$\n\\begin{array}{r}\n\\angle C B L=\\frac{1}{2} \\angle A B C=90^{\\circ}-\\frac{1}{2} \\alpha-\\frac{1}{2} \\gamma \\text { and } \\angle B C L=90^{\\circ}-\\frac{1}{2} \\alpha-\\frac{1}{2} \\beta, \\\\\n\\angle C B N=90^{\\circ}-\\frac{1}{2} \\beta \\text { and } \\angle B C N=90^{\\circ}-\\frac{1}{2} \\gamma, \\\\\n\\angle M B L=\\angle M B C+\\angle C B L=90^{\\circ}-\\frac{1}{2} \\gamma \\text { and } \\angle M C L=90^{\\circ}-\\frac{1}{2} \\beta, \\\\\n\\angle L C N=\\angle L B N=180^{\\circ}-\\frac{1}{2}(\\alpha+\\beta+\\gamma) .\n\\end{array}\n$$\n\nApplying the sine rule to $\\triangle M B L$ and $\\triangle M C L$ we obtain\n\n$$\n\\frac{M B}{M L}=\\frac{M C}{M L}=\\frac{\\sin \\angle B L M}{\\sin \\angle M B L}=\\frac{\\sin \\angle C L M}{\\sin \\angle M C L}\n$$\n\nIt follows that\n\n$$\n\\frac{\\sin \\angle B L M}{\\sin \\angle C L M}=\\frac{\\sin \\angle M B L}{\\sin \\angle M C L}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)}\n$$\n\nNow\n\n$$\n\\frac{\\sin \\angle B L M}{\\sin \\angle M L C} \\cdot \\frac{\\sin \\angle L C N}{\\sin \\angle N C B} \\cdot \\frac{\\sin \\angle N B C}{\\sin \\angle N B L}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)} \\cdot \\frac{\\sin \\left(90^{\\circ}-\\frac{1}{2} \\beta\\right)}{\\sin \\left(90^{\\circ}-\\frac{1}{2} \\gamma\\right)}=1\n$$\n\nHence $L M, B N, C N$ are concurrent and therefore $L, M, N$ are collinear.\n\n## Alternative proof\n\nWe proceed similarly as above until the equation (1).\nWe use the following lemma.\nLemma: If $\\pi>\\alpha, \\beta, \\gamma, \\delta>0, \\alpha+\\beta=\\gamma+\\delta<\\pi$, and $\\frac{\\sin \\alpha}{\\sin \\beta}=\\frac{\\sin \\gamma}{\\sin \\delta}$, then $\\alpha=\\gamma$ and $\\beta=\\delta$.\nProof of Lemma: Let $\\theta=\\alpha+\\beta=\\gamma+\\delta$. Then $\\frac{\\sin (\\theta-\\beta)}{\\sin \\beta}=\\frac{\\sin (\\theta-\\delta)}{\\sin \\delta}$.\n\n$$\n\\begin{gathered}\n\\Longleftrightarrow \\sin (\\theta-\\beta) \\sin \\delta=\\sin (\\theta-\\delta) \\sin \\beta \\\\\n\\Longleftrightarrow(\\sin \\theta \\cos \\beta-\\sin \\beta \\cos \\theta) \\sin \\delta=(\\sin \\theta \\cos \\delta-\\sin \\delta \\cos \\theta) \\sin \\beta \\\\\n\\Longleftrightarrow \\sin \\theta \\cos \\beta \\sin \\delta=\\sin \\theta \\cos \\delta \\sin \\beta \\\\\n\\Longleftrightarrow \\sin \\theta \\sin (\\beta-\\delta)=0\n\\end{gathered}\n$$\n\nSince $0<\\theta<\\pi$, then $\\sin \\theta \\neq 0$. Therefore, $\\sin (\\beta-\\delta)=0$, and we must have $\\beta=\\delta$.\nApplying the sine rule to $\\triangle N B L$ and $\\triangle N C L$ we obtain\n\n$$\n\\begin{aligned}\n& \\frac{N B}{N L}=\\frac{\\sin \\angle B L N}{\\sin \\angle L B N} \\\\\n& \\frac{N C}{N L}=\\frac{\\sin \\angle C L N}{\\sin \\angle L C N}\n\\end{aligned}\n$$\n\nSince $\\angle L B N=\\angle L C N$, it follows that\n\n$$\n\\frac{\\sin \\angle B L N}{\\sin \\angle C L N}=\\frac{N B}{N C}=\\frac{\\sin \\angle B C N}{\\sin \\angle C B N}=\\frac{\\cos (\\gamma / 2)}{\\cos (\\beta / 2)}=\\frac{\\sin \\angle B L M}{\\sin \\angle C L M}\n$$\n\nBy the lemma, it is concluded that $\\angle B L M=\\angle B L N$ and $\\angle C L M=\\angle C L N$. Therefore, $L, M, N$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 1"}}
|
| 6 |
+
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C D$ be a cyclic convex quadrilateral and $\\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.", "solution": "Denote by $N$ the excenter of triangle $B C E$ opposite $E$. Since $B L$ bisects $\\angle A B C$, we have $\\angle C B L=$ $\\frac{\\angle A B C}{2}$. Since $M$ is the midpoint of arc $B C$, we have $\\angle M B C=\\frac{1}{2}(\\angle M B C+\\angle M C B)$ It follows by angle chasing that\n\n$$\n\\begin{aligned}\n\\angle M B L & =\\angle M B C+\\angle C B L=\\frac{1}{2}(\\angle M B C+\\angle M C B+\\angle A B C) \\\\\n& =\\frac{1}{2}(\\angle M B A+\\angle M C B)=90^{\\circ}-\\frac{\\angle B C E}{2}=\\angle B C N .\n\\end{aligned}\n$$\n\nDenote by $X$ and $Y$ the second intersections of lines $B M$ and $C M$ with the circumcircle of $B C L$, respectively. Since $\\angle M B C=\\angle M C B$, we have $B C \\| X Y$. It suffices to show that $B N \\| X L$ and $C N \\| Y L$. Indeed, from this it follows that $\\triangle B C N \\sim \\triangle X Y L$, and therefore a homothety with center $M$ that maps $B$ to $X$ and $C$ to $Y$ also maps $N$ to $L$, implying that $N$ lies on the line $L M$.\nBy symmetry, it suffices to show that $C N \\| Y L$, which is equivalent to showing that $\\angle B C N=\\angle X Y L$. But we have $\\angle B C N=\\angle M B L=\\angle X B L=\\angle X Y L$, completing the proof.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Given a $32 \\times 32$ table, we put a mouse (facing up) at the bottom left cell and a piece of cheese at several other cells. The mouse then starts moving. It moves forward except that when it reaches a piece of cheese, it eats a part of it, turns right, and continues moving forward. We say that a subset of cells containing cheese is good if, during this process, the mouse tastes each piece of cheese exactly once and then falls off the table. Show that:\n(a) No good subset consists of 888 cells.\n(b) There exists a good subset consisting of at least 666 cells.", "solution": "(a) For the sake of contradiction, assume a good subset consisting of 888 cells exists. We call those cheese-cells and the other ones gap-cells. Observe that since each cheese-cell is visited once, each gap-cell is visited at most twice (once vertically and once horizontally). Define a finite sequence $s$ whose $i$-th element is $C$ if the $i$-th step of the mouse was onto a cheese-cell, and $G$ if it was onto a gap-cell. By assumption, $s$ contains $888 C$ 's. Note that $s$ does not contain a contiguous block of 4 (or more) $C$ 's. Hence $s$ contains at least $888 / 3=296$ such $C$-blocks and thus at least $295 G^{\\prime}$ 's. But since each gap-cell is traversed at most twice, this implies there are at least $\\lceil 295 / 2\\rceil=148$ gap-cells, for a total of $888+148=1036>32^{2}$ cells, a contradiction.\n(b) Let $L_{i}, X_{i}$ be two $2^{i} \\times 2^{i}$ tiles that allow the mouse to \"turn left\" and \"cross\", respectively. In detail, the \"turn left\" tiles allow the mouse to enter at its bottom left cell facing up and to leave at its bottom left cell facing left. The \"cross\" tiles allow the mouse to enter at its top right facing down and leave at its bottom left facing left, while also to enter at its bottom left facing up and leave at its top right facing right.\n(a) Basic tiles\n(b) Inductive construction\n(c) $16 \\times 16$\n\n\nNote that given two $2^{i} \\times 2^{i}$ tiles $L_{i}, X_{i}$ we can construct larger $2^{i+1} \\times 2^{i+1}$ tiles $L_{i+1}, X_{i+1}$ inductively as shown on in (b). The construction works because the path intersects itself (or the other path) only inside the smaller $X$-tiles where it works by induction.\nFor a tile $T$, let $|T|$ be the number of pieces of cheese in it. By straightforward induction, $\\left|L_{i}\\right|=\\left|X_{i}\\right|+1$ and $\\left|L_{i+1}\\right|=4 \\cdot\\left|L_{i}\\right|-1$. From the initial condition $\\left|L_{1}\\right|=3$. We now easily compute $\\left|L_{2}\\right|=11,\\left|L_{3}\\right|=43,\\left|L_{4}\\right|=171$, and $\\left|L_{5}\\right|=683$. Hence we get the desired subset.\n\n## Another proof of (a).\n\nLet $X_{N}$ be the largest possible density of cheese-cells in a good subset on an $N \\times N$ table. We will show that $X_{N} \\leq 4 / 5+o(1)$. Specifically, this gives $X_{32} \\leq 817 / 1024$. We look at the (discrete analogue) of the winding number of the trajectory of the mouse. Since the mouse enters and leaves the table, for every 4 right turns in its trajectory there has to be a self-crossing. But each self-crossing requires a different empty square, hence $X_{N} \\leq 4 / 5$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution."}}
|
| 8 |
+
{"year": "2021", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Determine all functions $f: \\mathbb{Z} \\rightarrow \\mathbb{Z}$ such that $f(f(a)-b)+b f(2 a)$ is a perfect square for all integers $a$ and $b$.", "solution": ".\n\nThere are two families of functions which satisfy the condition:\n(1) $f(n)= \\begin{cases}0 & \\text { if } n \\text { is even, and } \\\\ \\text { any perfect square } & \\text { if } n \\text { is odd }\\end{cases}$\n(2) $f(n)=n^{2}$, for every integer $n$.\n\nIt is straightforward to verify that the two families of functions are indeed solutions. Now, suppose that f is any function which satisfies the condition that $f(f(a)-b)+b f(2 a)$ is a perfect square for every pair $(a, b)$ of integers. We denote this condition by $\\left(^{*}\\right)$. We will show that $f$ must belong to either Family (1) or Family (2).\nClaim 1. $f(0)=0$ and $f(n)$ is a perfect square for every integer $n$.\nProof. Plugging $(a, b) \\rightarrow(0, f(0))$ in $\\left(^{*}\\right)$ shows that $f(0)(f(0)+1)=z^{2}$ for some integer $z$. Thus, $(2 f(0)+1-2 z)(2 f(0)+1+2 z)=1$. Therefore, $f(0)$ is either -1 or 0.\nSuppose, for sake of contradiction, that $f(0)=-1$. For any integer $a$, plugging $(a, b) \\rightarrow(a, f(a))$ implies that $f(a) f(2 a)-1$ is a square. Thus, for each $a \\in \\mathbb{Z}$, there exists $x \\in \\mathbb{Z}$ such that $f(a) f(2 a)=x^{2}+1$ This implies that any prime divisor of $f(a)$ is either 2 or is congruent to $1(\\bmod 4)$, and that $4 \\nmid f(a)$, for every $a \\in \\mathbb{Z}$.\nPlugging $(a, b) \\rightarrow(0,3)$ in $\\left(^{*}\\right)$ shows that $f(-4)-3$ is a square. Thus, there is $y \\in \\mathbb{Z}$ such that $f(-4)=y^{2}+3$. Since $4 \\nmid f(-4)$, we note that $f(-4)$ is a positive integer congruent to $3(\\bmod 4)$, but any prime dividing $f(-4)$ is either 2 or is congruent to $1(\\bmod 4)$. This gives a contradiction. Therefore, $f(0)$ must be 0 .\nFor every integer $n$, plugging $(a, b) \\rightarrow(0,-n)$ in $\\left(^{*}\\right)$ shows that $f(n)$ is a square.\nReplacing $b$ with $f(a)-b$, we find that for all integers $a$ and $b$,\n\n$$\nf(b)+(f(a)-b) f(2 a) \\text { is a square. }\n$$\n\nNow, let $S$ be the set of all integers $n$ such that $f(n)=0$. We have two cases:\n\n- Case 1: $S$ is unbounded from above.\n\nWe claim that $f(2 n)=0$ for any integer $n$. Fix some integer $n$, and let $k \\in S$ with $k>f(n)$. Then, plugging $(a, b) \\mapsto(n, k)$ in $\\left({ }^{* *}\\right)$ gives us that $f(k)+(f(n)-k) f(2 n)=(f(n)-k) f(2 n)$ is a square. But $f(n)-k<0$ and $f(2 n)$ is a square by Claim 1. This is possible only if $f(2 n)=0$. In summary, $f(n)=0$ whenever $n$ is even and Claim 1 shows that $f(n)$ is a square whenever $n$ is odd.\n\n- Case 2: $S$ is bounded from above.\n\nLet $T$ be the set of all integers $n$ such that $f(n)=n^{2}$. We show that $T$ is unbounded from above. In fact, we show that $\\frac{p+1}{2} \\in T$ for all primes $p$ big enough.\nFix a prime number $p$ big enough, and let $n=\\frac{p+1}{2}$. Plugging $(a, b) \\mapsto(n, 2 n)$ in ( $\\left.{ }^{* *}\\right)$ shows us that $f(2 n)(f(n)-2 n+1)$ is a square for any integer $n$. For $p$ big enough, we have $2 n \\notin S$, so $f(2 n)$ is a non-zero square. As a result, when $p$ is big enough, $f(n)$ and $f(n)-2 n+1=f(n)-p$ are both squares. Writing $f(n)=k^{2}$ and $f(n)-p=m^{2}$ for some $k, m \\geq 0$, we have\n\n$$\n(k+m)(k-m)=k^{2}-m^{2}=p \\Longrightarrow k+m=p, k-m=1 \\Longrightarrow k=n, m=n-1\n$$\n\nThus, $f(n)=k^{2}=n^{2}$, giving us $n=\\frac{p+1}{2} \\in T$.\nNext, for all $k \\in T$ and $n \\in \\mathbb{Z}$, plugging $(a, b) \\mapsto(n, k)$ in $(* *)$ shows us that $k^{2}+(f(n)-k) f(2 n)$ is a square. But that means $(2 k-f(2 n))^{2}-\\left(f(2 n)^{2}-4 f(n) f(2 n)\\right)=4\\left(k^{2}+(f(n)-k) f(2 n)\\right)$ is also a square. When $k$ is large enough, we have $\\left|f(2 n)^{2}-4 f(n) f(2 n)\\right|+1<|2 k-f(2 n)|$. As a result, we must have $f(2 n)^{2}=4 f(n) f(2 n)$ and thus $f(2 n) \\in\\{0,4 f(n)\\}$ for all integers $n$.\nFinally, we prove that $f(n)=n^{2}$ for all integers $n$. Fix $n$, and take $k \\in T$ big enough such that $2 k \\notin S$. Then, we have $f(k)=k^{2}$ and $f(2 k)=4 f(k)=4 k^{2}$. Plugging $(a, b) \\mapsto(k, n)$ to $(* *)$ shows us that $f(n)+\\left(k^{2}-n\\right) 4 k^{2}=\\left(2 k^{2}-n\\right)^{2}+\\left(f(n)-n^{2}\\right)$ is a square. Since $T$ is unbounded from above, we can take $k \\in T$ such that $2 k \\notin S$ and also $\\left|2 k^{2}-n\\right|>\\left|f(n)-n^{2}\\right|$. This forces $f(n)=n^{2}$, giving us the second family of solution.\n\n## Another approach of Case 1.\n\nClaim 2. One of the following is true.\n(i) For every integer $n, f(2 n)=0$.\n(ii) There exists an integer $K>0$ such that for every integer $n \\geq K, f(n)>0$.\n\nProof. Suppose that there exists an integer $\\alpha \\neq 0$ such that $f(2 \\alpha)>0$. We claim that for every integer $n \\geq f(\\alpha)+1$, we have $f(n)>0$.\nFor every $n \\geq f(\\alpha)+1$, plugging $(a, b) \\rightarrow(\\alpha, f(\\alpha)-n)$ in $\\left(^{*}\\right)$ shows that $f(n)+(f(\\alpha)-n) f(2 \\alpha)$ is a square, and in particular, is non-negative. Hence, $f(n) \\geq(n-f(\\alpha)) f(2 \\alpha)>0$, as desired.\nIf $f$ belongs to Case (i), Claim 1 shows that $f$ belongs to Family (1).\nIf $f$ belongs to Case (ii), then $S$ is bounded from above. From Case 2 we get $f(n)=n^{2}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 1"}}
|
APMO/segmented/en-apmo2022_sol.jsonl
CHANGED
|
@@ -1,10 +1,10 @@
|
|
| 1 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".1\n\nBy inspection, we see that the pairs $(a, b)$ with $a=b$ are solutions, and so too are the pairs $(a, 1)$. We will see that these are the only solutions.\n\n- Case 1. Consider the case $b<a$. Since $b-1$ is a multiple of $a-1$, it follows that $b=1$. This yields the second set of solutions described above.\n- Case 2. This leaves the case $b \\geq a$. Since the positive integer $a^{3}$ is a multiple of $b^{2}$, there is a positive integer $c$ such that $a^{3}=b^{2} c$.\nNote that $a \\equiv b \\equiv 1$ modulo $a-1$. So we have\n\n$$\n1 \\equiv a^{3}=b^{2} c \\equiv c \\quad(\\bmod a-1) .\n$$\n\nIf $c<a$, then we must have $c=1$, hence, $a^{3}=b^{2}$. So there is a positive integer $d$ such that $a=d^{2}$ and $b=d^{3}$. Now $a-1 \\mid b-1$ yields $d^{2}-1 \\mid d^{3}-1$. This implies that $d+1 \\mid d(d+1)+1$, which is impossible.\nIf $c \\geq a$, then $b^{2} c \\geq b^{2} a \\geq a^{3}=b^{2} c$. So there's equality throughout, implying $a=c=b$. This yields the first set of solutions described above.\nTherefore, the solutions described above are the only solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 2 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".2\n\nWe will start by showing that there are positive integers $x, c, d$ such that $a=x^{2} c d$ and $b=x^{3} c$. Let $g=\\operatorname{gcd}(a, b)$ so that $a=g d$ and $b=g x$ for some coprime $d$ and $x$. Then, $b^{2} \\mid a^{3}$ is equivalent to $g^{2} x^{2} \\mid g^{3} d^{3}$, which is equivalent to $x^{2} \\mid g d^{3}$. Since $x$ and $d$ are coprime, this implies $x^{2} \\mid g$. Hence, $g=x^{2} c$ for some $c$, giving $a=x^{2} c d$ and $b=x^{3} c$ as required.\nNow, it remains to find all positive integers $x, c, d$ satisfying\n\n$$\nx^{2} c d-1 \\mid x^{3} c-1\n$$\n\nThat is, $x^{3} c \\equiv 1\\left(\\bmod x^{2} c d-1\\right)$. Assuming that this congruence holds, it follows that $d \\equiv x^{3} c d \\equiv x$ $\\left(\\bmod x^{2} c d-1\\right)$. Then, either $x=d$ or $x-d \\geq x^{2} c d-1$ or $d-x \\geq x^{2} c d-1$.\n\n- If $x=d$ then $b=a$.\n- If $x-d \\geq x^{2} c d-1$, then $x-d \\geq x^{2} c d-1 \\geq x-1 \\geq x-d$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=d=1$, which implies that $a=b=1$.\n- If $d-x \\geq x^{2} c d-1$, then $d-x \\geq x^{2} c d-1 \\geq d-1 \\geq d-x$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=1$, which implies that $b=1$.\nHence the only solutions are the pairs $(a, b)$ such that $a=b$ or $b=1$. These pairs can be checked to satisfy the given conditions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 3 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".3\n\nAll answers are $(n, n)$ and $(n, 1)$ where $n$ is any positive integer. They all clearly work.\nTo show that these are all solutions, note that we can easily eliminate the case $a=1$ or $b=1$. Thus, assume that $a, b \\neq 1$ and $a \\neq b$. By the second divisibility, we see that $a-1 \\mid b-a$. However, $\\operatorname{gcd}(a, b) \\mid b-a$ and $a-1$ is relatively prime to $\\operatorname{gcd}(a, b)$. This implies that $(a-1) \\operatorname{gcd}(a, b) \\mid b-a$, which implies $\\operatorname{gcd}(a, b) \\left\\lvert\\, \\frac{b-1}{a-1}-1\\right.$.\nThe last relation implies that $\\operatorname{gcd}(a, b)<\\frac{b-1}{a-1}$, since the right-hand side are positive. However, due to the first divisibility,\n\n$$\n\\operatorname{gcd}(a, b)^{3}=\\operatorname{gcd}\\left(a^{3}, b^{3}\\right) \\geq \\operatorname{gcd}\\left(b^{2}, b^{3}\\right)=b^{2} .\n$$\n\nCombining these two inequalities, we get that\n\n$$\nb^{\\frac{2}{3}}<\\frac{b-1}{a-1}<2 \\frac{b}{a}\n$$\n\nThis implies $a<2 b^{\\frac{1}{3}}$. However, $b^{2} \\mid a^{3}$ gives $b \\leq a^{\\frac{3}{2}}$. This forces\n\n$$\na<2\\left(a^{\\frac{3}{2}}\\right)^{\\frac{1}{3}}=2 \\sqrt{a} \\Longrightarrow a<4 .\n$$\n\nExtracting $a=2,3$ by hand yields no additional solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 4 |
-
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a right triangle with $\\angle B=90^{\\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\\triangle A C D$ and the circumcircle of $\\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.\n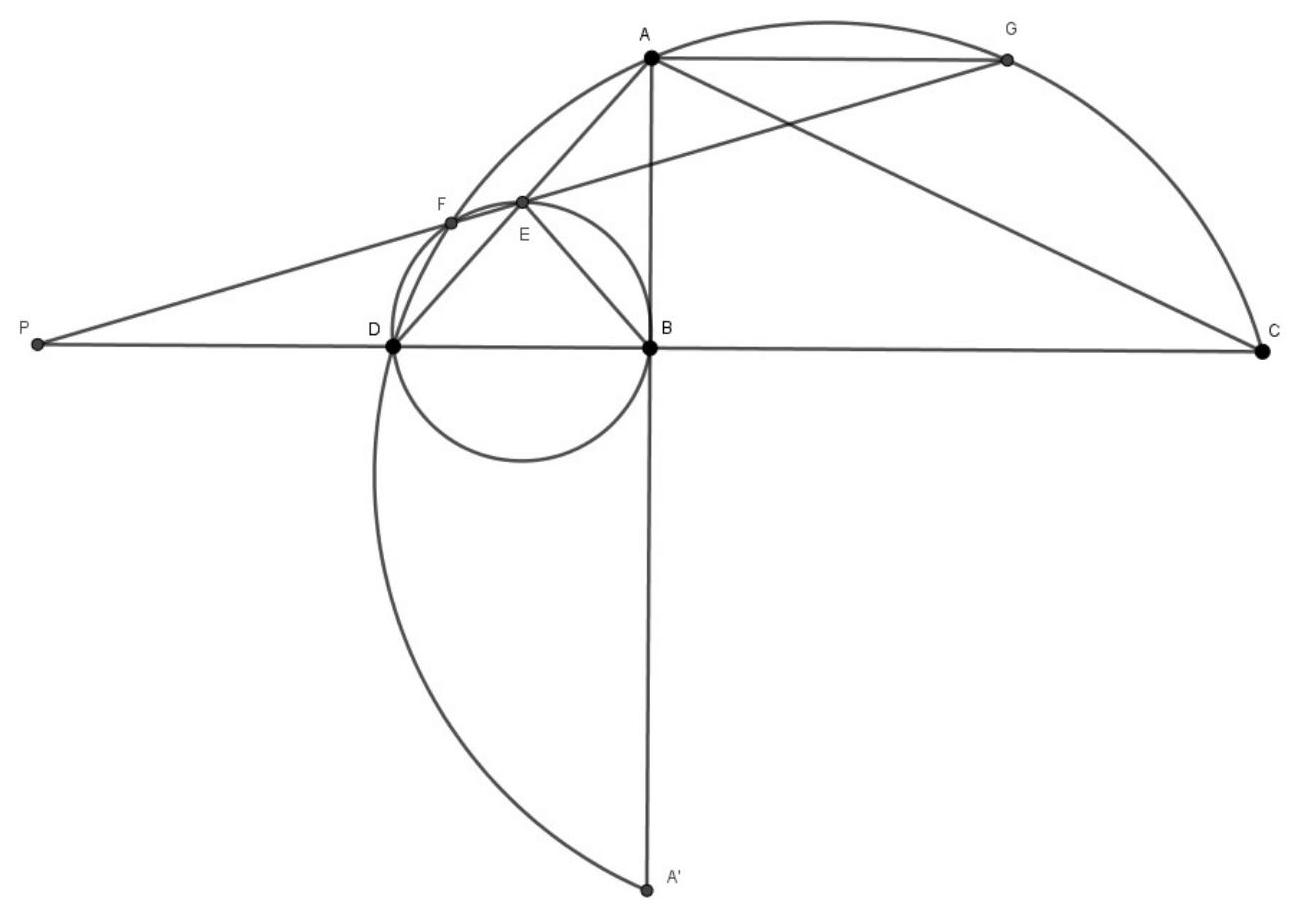", "solution": ".1\n\nLet the line $E F$ intersect the line $B C$ at $P$ and the circumcircle of $\\triangle A C D$ at $G$ distinct from $F$. We will prove that $P$ is the fixed point.\nFirst, notice that $\\triangle B E D$ is isosceles with $E B=E D$. This implies $\\angle E B C=\\angle E D P$.\nThen, $\\angle D A G=\\angle D F G=\\angle E B C=\\angle E D P$ which implies $A G \\| D C$. Hence, $A G C D$ is an isosceles trapezoid.\nAlso, $A G \\| D C$ and $A E=E D$. This implies $\\triangle A E G \\cong \\triangle D E P$ and $A G=D P$.\nSince $B$ is the foot of the perpendicular from $A$ onto the side $C D$ of the isosceles trapezoid $A G C D$, we have $P B=P D+D B=A G+D B=B C$, which does not depend on the choice of $D$. Hence, the initial statement is proven.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
-
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a right triangle with $\\angle B=90^{\\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\\triangle A C D$ and the circumcircle of $\\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.\n", "solution": ".2\n\nSet up a coordinate system where $B C$ is along the positive $x$-axis, $B A$ is along the positive $y$-axis, and $B$ is the origin. Take $A=(0, a), B=(0,0), C=(c, 0), D=(-d, 0)$ where $a, b, c, d>0$. Then $E=\\left(-\\frac{d}{2}, \\frac{a}{2}\\right)$. The general equation of a circle is\n\n$$\nx^{2}+y^{2}+2 f x+2 g y+h=0\n$$\n\nSubstituting the coordinates of $A, D, C$ into (1) and solving for $f, g, h$, we find that the equation of the circumcircle of $\\triangle A D C$ is\n\n$$\nx^{2}+y^{2}+(d-c) x+\\left(\\frac{c d}{a}-a\\right) y-c d=0\n$$\n\nSimilarly, the equation of the circumcircle of $\\triangle B D E$ is\n\n$$\nx^{2}+y^{2}+d x+\\left(\\frac{d^{2}}{2 a}-\\frac{a}{2}\\right) y=0\n$$\n\nThen (3)-(2) gives the equation of the line $D F$ which is\n\n$$\nc x+\\frac{a^{2}+d^{2}-2 c d}{2 a} y+c d=0\n$$\n\nSolving (3) and (4) simultaneously, we get\n\n$$\nF=\\left(\\frac{c\\left(d^{2}-a^{2}-2 c d\\right)}{a^{2}+(d-2 c)^{2}}, \\frac{2 a c(c-d)}{a^{2}+(d-2 c)^{2}}\\right)\n$$\n\nand the other solution $D=(-d, 0)$.\nFrom this we obtain the equation of the line $E F$ which is $a x+(d-2 c) y+a c=0$. It passes through $P(-c, 0)$ which is independent of $d$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 6 |
-
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Find all positive integers $k<202$ for which there exists a positive integer $n$ such that\n\n$$\n\\left\\{\\frac{n}{202}\\right\\}+\\left\\{\\frac{2 n}{202}\\right\\}+\\cdots+\\left\\{\\frac{k n}{202}\\right\\}=\\frac{k}{2}\n$$\n\nwhere $\\{x\\}$ denote the fractional part of $x$.\nNote: $\\{x\\}$ denotes the real number $k$ with $0 \\leq k<1$ such that $x-k$ is an integer.", "solution": "Denote the equation in the problem statement as $\\left(^{*}\\right)$, and note that it is equivalent to the condition that the average of the remainders when dividing $n, 2 n, \\ldots, k n$ by 202 is 101 . Since $\\left\\{\\frac{i n}{202}\\right\\}$ is invariant in each residue class modulo 202 for each $1 \\leq i \\leq k$, it suffices to consider $0 \\leq n<202$.\n\nIf $n=0$, so is $\\left\\{\\frac{i n}{202}\\right\\}$, meaning that $(*)$ does not hold for any $k$. If $n=101$, then it can be checked that $\\left(^{*}\\right)$ is satisfied if and only if $k=1$. From now on, we will assume that $101 \\nmid n$.\nFor each $1 \\leq i \\leq k$, let $a_{i}=\\left\\lfloor\\frac{i n}{202}\\right\\rfloor=\\frac{i n}{202}-\\left\\{\\frac{i n}{202}\\right\\}$. Rewriting $\\left(^{*}\\right)$ and multiplying the equation by 202, we find that\n\n$$\nn(1+2+\\ldots+k)-202\\left(a_{1}+a_{2}+\\ldots+a_{k}\\right)=101 k\n$$\n\nEquivalently, letting $z=a_{1}+a_{2}+\\ldots+a_{k}$,\n\n$$\nn k(k+1)-404 z=202 k\n$$\n\nSince $n$ is not divisible by 101 , which is prime, it follows that $101 \\mid k(k+1)$. In particular, $101 \\mid k$ or $101 \\mid k+1$. This means that $k \\in\\{100,101,201\\}$. We claim that all these values of $k$ work.\n\n- If $k=201$, we may choose $n=1$. The remainders when dividing $n, 2 n, \\ldots, k n$ by 202 are 1,2 , ..., 201, which have an average of 101 .\n- If $k=100$, we may choose $n=2$. The remainders when dividing $n, 2 n, \\ldots, k n$ by 202 are 2,4 , ..., 200, which have an average of 101.\n- If $k=101$, we may choose $n=51$. To see this, note that the first four remainders are $51,102,153$, 2 , which have an average of 77 . The next four remainders $(53,104,155,4)$ are shifted upwards from the first four remainders by 2 each, and so on, until the 25 th set of the remainders ( 99 , $150,201,50)$ which have an average of 125 . Hence, the first 100 remainders have an average of $\\frac{77+125}{2}=101$. The 101th remainder is also 101 , meaning that the average of all 101 remainders is 101 .\n\nIn conclusion, all values $k \\in\\{1,100,101,201\\}$ satisfy the initial condition.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution\n\n"}}
|
| 7 |
-
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $n$ and $k$ be positive integers. Cathy is playing the following game. There are $n$ marbles and $k$ boxes, with the marbles labelled 1 to $n$. Initially, all marbles are placed inside one box. Each turn, Cathy chooses a box and then moves the marbles with the smallest label, say $i$, to either any empty box or the box containing marble $i+1$. Cathy wins if at any point there is a box containing only marble $n$.\nDetermine all pairs of integers $(n, k)$ such that Cathy can win this game.", "solution": "We claim Cathy can win if and only if $n \\leq 2^{k-1}$.\n\nFirst, note that each non-empty box always contains a consecutive sequence of labeled marbles. This is true since Cathy is always either removing from or placing in the lowest marble in a box. As a consequence, every move made is reversible.\n\nNext, we prove by induction that Cathy can win if $n=2^{k-1}$. The base case of $n=k=1$ is trivial. Assume a victory can be obtained for $m$ boxes and $2^{m-1}$ marbles. Consider the case of $m+1$ boxes and $2^{m}$ marbles. Cathy can first perform a sequence of moves so that only marbles $2^{m-1}, \\ldots, 2^{m}$ are left in the starting box, while keeping one box, say $B$, empty. Now move the marble $2^{m-1}$ to box $B$, then reverse all of the initial moves while treating $B$ as the starting box. At the end of that, we will have marbles $2^{m-1}+1, \\ldots, 2^{m}$ in the starting box, marbles $1,2, \\ldots, 2^{m-1}$ in box $B$, and $m-1$ empty boxes. By repeating the original sequence of moves on marbles $2^{m-1}+1, \\ldots, 2^{m}$, using the $m$ boxes that are not box $B$, we can reach a state where only marble $2^{m}$ remains in the starting box. Therefore\na victory is possible if $n=2^{k-1}$ or smaller.\n\nWe now prove by induction that Cathy loses if $n=2^{k-1}+1$. The base case of $n=2$ and $k=1$ is trivial. Assume a victory is impossible for $m$ boxes and $2^{m-1}+1$ marbles. For the sake of contradiction, suppose that victory is possible for $m+1$ boxes and $2^{m}+1$ marbles. In a winning sequence of moves, consider the last time a marble $2^{m-1}+1$ leaves the starting box, call this move $X$. After $X$, there cannot be a time when marbles $1, \\ldots, 2^{m-1}+1$ are all in the same box. Otherwise, by reversing these moves after $X$ and deleting marbles greater than $2^{m-1}+1$, it gives us a winning sequence of moves for $2^{m-1}+1$ marbles and $m$ boxes (as the original starting box is not used here), contradicting the inductive hypothesis. Hence starting from $X$, marbles 1 will never be in the same box as any marbles greater than or equal to $2^{m-1}+1$.\n\nNow delete marbles $2, \\ldots, 2^{m-1}$ and consider the winning moves starting from $X$. Marble 1 would only move from one empty box to another, while blocking other marbles from entering its box. Thus we effectively have a sequence of moves for $2^{m-1}+1$ marbles, while only able to use $m$ boxes. This again contradicts the inductive hypothesis. Therefore, a victory is not possible if $n=2^{k-1}+1$ or greater.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution\n\n"}}
|
| 8 |
-
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": "The minimum value is $-\\frac{1}{8}$. There are eight equality cases in total. The first one is\n\n$$\n\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right) .\n$$\n\nCyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \\rightarrow$ $(-a,-b,-c,-d))$ all four entries in each of the four quadruples give four more equality cases.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution\n\n"}}
|
| 9 |
-
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": ".1\n\nSince the expression is cyclic, we could WLOG $a=\\max \\{a, b, c, d\\}$. Let\n\n$$\nS(a, b, c, d)=(a-b)(b-c)(c-d)(d-a)\n$$\n\nNote that we have given $(a, b, c, d)$ such that $S(a, b, c, d)=-\\frac{1}{8}$. Therefore, to prove that $S(a, b, c, d) \\geq$ $-\\frac{1}{8}$, we just need to consider the case where $S(a, b, c, d)<0$.\n\n- Exactly 1 of $a-b, b-c, c-d, d-a$ is negative.\n\nSince $a=\\max \\{a, b, c, d\\}$, then we must have $d-a<0$. This forces $a>b>c>d$. Now, let us write\n\n$$\nS(a, b, c, d)=-(a-b)(b-c)(c-d)(a-d)\n$$\n\nWrite $a-b=y, b-c=x, c-d=w$ for some positive reals $w, x, y>0$. Plugging to the original condition, we have\n\n$$\n(d+w+x+y)^{2}+(d+w+x)^{2}+(d+w)^{2}+d^{2}-1=0(*)\n$$\n\nand we want to prove that $w x y(w+x+y) \\leq \\frac{1}{8}$. Consider the expression $(*)$ as a quadratic in $d$ :\n\n$$\n4 d^{2}+d(6 w+4 x+2 y)+\\left((w+x+y)^{2}+(w+x)^{2}+w^{2}-1\\right)=0\n$$\n\nSince $d$ is a real number, then the discriminant of the given equation has to be non-negative, i.e. we must have\n\n$$\n\\begin{aligned}\n4 & \\geq 4\\left((w+x+y)^{2}+(w+x)^{2}+w^{2}\\right)-(3 w+2 x+y)^{2} \\\\\n& =\\left(3 w^{2}+2 w y+3 y^{2}\\right)+4 x(w+x+y) \\\\\n& \\geq 8 w y+4 x(w+x+y) \\\\\n& =4(x(w+x+y)+2 w y)\n\\end{aligned}\n$$\n\nHowever, AM-GM gives us\n\n$$\nw x y(w+x+y) \\leq \\frac{1}{2}\\left(\\frac{x(w+x+y)+2 w y}{2}\\right)^{2} \\leq \\frac{1}{8}\n$$\n\nThis proves $S(a, b, c, d) \\geq-\\frac{1}{8}$ for any $a, b, c, d \\in \\mathbb{R}$ such that $a>b>c>d$. Equality holds if and only if $w=y, x(w+x+y)=2 w y$ and $w x y(w+x+y)=\\frac{1}{8}$. Solving these equations gives us $w^{4}=\\frac{1}{16}$ which forces $w=\\frac{1}{2}$ since $w>0$. Solving for $x$ gives us $x(x+1)=\\frac{1}{2}$, and we will get $x=-\\frac{1}{2}+\\frac{\\sqrt{3}}{2}$ as $x>0$. Plugging back gives us $d=-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}$, and this gives us\n\n$$\n(a, b, c, d)=\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}\\right)\n$$\n\nThus, any cyclic permutation of the above solution will achieve the minimum equality.\n\n- Exactly 3 of $a-b, b-c, c-d, d-a$ are negative Since $a=\\max \\{a, b, c, d\\}$, then $a-b$ has to be positive. So we must have $b<c<d<a$. Now, note that\n\n$$\n\\begin{aligned}\nS(a, b, c, d) & =(a-b)(b-c)(c-d)(d-a) \\\\\n& =(a-d)(d-c)(c-b)(b-a) \\\\\n& =S(a, d, c, b)\n\\end{aligned}\n$$\n\nNow, note that $a>d>c>b$. By the previous case, $S(a, d, c, b) \\geq-\\frac{1}{8}$, which implies that\n\n$$\nS(a, b, c, d)=S(a, d, c, b) \\geq-\\frac{1}{8}\n$$\n\nas well. Equality holds if and only if\n\n$$\n(a, b, c, d)=\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right)\n$$\n\nand its cyclic permutation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 5"}}
|
| 10 |
-
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": ".2\n\nThe minimum value is $-\\frac{1}{8}$. There are eight equality cases in total. The first one is\n\n$$\n\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right) .\n$$\n\nCyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \\rightarrow$ $(-a,-b,-c,-d)$ ) all four entries in each of the four quadruples give four more equality cases. We then begin the proof by the following optimization:\n\nClaim 1. In order to get the minimum value, we must have $a+b+c+d=0$.\n\nProof. Assume not, let $\\delta=\\frac{a+b+c+d}{4}$ and note that\n\n$$\n(a-\\delta)^{2}+(b-\\delta)^{2}+(c-\\delta)^{2}+(d-\\delta)^{2}<a^{2}+b^{2}+c^{2}+d^{2}\n$$\n\nso by shifting by $\\delta$ and scaling, we get an even smaller value of $(a-b)(b-c)(c-d)(d-a)$.\n\nThe key idea is to substitute the variables\n\n$$\n\\begin{aligned}\n& x=a c+b d \\\\\n& y=a b+c d \\\\\n& z=a d+b c\n\\end{aligned}\n$$\n\nso that the original expression is just $(x-y)(x-z)$. We also have the conditions $x, y, z \\geq-0.5$ because of:\n\n$$\n2 x+\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)=(a+c)^{2}+(b+d)^{2} \\geq 0\n$$\n\nMoreover, notice that\n\n$$\n0=(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(x+y+z) \\Longrightarrow x+y+z=\\frac{-1}{2}\n$$\n\nNow, we reduce to the following optimization problem.\nClaim 2. Let $x, y, z \\geq-0.5$ such that $x+y+z=-0.5$. Then, the minimum value of\n\n$$\n(x-y)(x-z)\n$$\n\nis $-1 / 8$. Moreover, the equality case occurs when $x=-1 / 4$ and $\\{y, z\\}=\\{1 / 4,-1 / 2\\}$.\nProof. We notice that\n\n$$\n\\begin{aligned}\n(x-y)(x-z)+\\frac{1}{8} & =\\left(2 y+z+\\frac{1}{2}\\right)\\left(2 z+y+\\frac{1}{2}\\right)+\\frac{1}{8} \\\\\n& =\\frac{1}{8}(4 y+4 z+1)^{2}+\\left(y+\\frac{1}{2}\\right)\\left(z+\\frac{1}{2}\\right) \\geq 0\n\\end{aligned}\n$$\n\nThe last inequality is true since both $y+\\frac{1}{2}$ and $z+\\frac{1}{2}$ are not less than zero.\nThe equality in the last inequality is attained when either $y+\\frac{1}{2}=0$ or $z+\\frac{1}{2}=0$, and $4 y+4 z+1=0$. This system of equations give $(y, z)=(1 / 4,-1 / 2)$ or $(y, z)=(-1 / 2,1 / 4)$ as the desired equality cases.\n\nNote: We can also prove (the weakened) Claim 2 by using Lagrange Multiplier, as follows. We first prove that, in fact, $x, y, z \\in[-0.5,0.5]$. This can be proved by considering that\n\n$$\n-2 x+\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)=(a-c)^{2}+(b-d)^{2} \\geq 0\n$$\n\nWe will prove the Claim 2, only that in this case, $x, y, z \\in[-0.5,0.5]$. This is already sufficient to prove the original question. We already have the bounded domain $[-0.5,0.5]^{3}$, so the global minimum must occur somewhere. Thus, it suffices to consider two cases:\n\n- If the global minimum lies on the boundary of $[-0.5,0.5]^{3}$. Then, one of $x, y, z$ must be -0.5 or 0.5 . By symmetry between $y$ and $z$, we split to a few more cases.\n- If $x=0.5$, then $y=z=-0.5$, so $(x-y)(x-z)=1$, not the minimum.\n- If $x=-0.5$, then both $y$ and $z$ must be greater or equal to $x$, so $(x-y)(x-z) \\geq 0$, not the minimum.\n- If $y=0.5$, then $x=z=-0.5$, so $(x-y)(x-z)=0$, not the minimum.\n- If $y=-0.5$, then $z=-x$, so\n\n$$\n(x-y)(x-z)=2 x(x+0.5)\n$$\n\nwhich obtain the minimum at $x=-1 / 4$. This gives the desired equality case.\n\n- If the global minimum lies in the interior $(-0.5,0.5)^{3}$, then we apply Lagrange multiplier:\n\n$$\n\\begin{aligned}\n& \\frac{\\partial}{\\partial x}(x-y)(x-z)=\\lambda \\frac{\\partial}{\\partial x}(x+y+z) \\\\\n& \\frac{\\partial}{\\partial y}(x-y)(x-z)=\\lambda \\frac{\\partial}{\\partial y}(x+y+z) \\\\\n& \\frac{\\partial}{\\partial z}(x-y)(x-z) \\Longrightarrow z-x=\\lambda \\frac{\\partial}{\\partial z}(x+y+z) \\\\\n& \\Longrightarrow y-x=\\lambda .\n\\end{aligned}\n$$\n\nAdding the last two equations gives $\\lambda=0$, or $x=y=z$. This gives $(x-y)(x-z)=0$, not the minimum.\n\nHaving exhausted all cases, we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 5"}}
|
|
|
|
| 1 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".1\n\nBy inspection, we see that the pairs $(a, b)$ with $a=b$ are solutions, and so too are the pairs $(a, 1)$. We will see that these are the only solutions.\n\n- Case 1. Consider the case $b<a$. Since $b-1$ is a multiple of $a-1$, it follows that $b=1$. This yields the second set of solutions described above.\n- Case 2. This leaves the case $b \\geq a$. Since the positive integer $a^{3}$ is a multiple of $b^{2}$, there is a positive integer $c$ such that $a^{3}=b^{2} c$.\nNote that $a \\equiv b \\equiv 1$ modulo $a-1$. So we have\n\n$$\n1 \\equiv a^{3}=b^{2} c \\equiv c \\quad(\\bmod a-1) .\n$$\n\nIf $c<a$, then we must have $c=1$, hence, $a^{3}=b^{2}$. So there is a positive integer $d$ such that $a=d^{2}$ and $b=d^{3}$. Now $a-1 \\mid b-1$ yields $d^{2}-1 \\mid d^{3}-1$. This implies that $d+1 \\mid d(d+1)+1$, which is impossible.\nIf $c \\geq a$, then $b^{2} c \\geq b^{2} a \\geq a^{3}=b^{2} c$. So there's equality throughout, implying $a=c=b$. This yields the first set of solutions described above.\nTherefore, the solutions described above are the only solutions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 2 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".2\n\nWe will start by showing that there are positive integers $x, c, d$ such that $a=x^{2} c d$ and $b=x^{3} c$. Let $g=\\operatorname{gcd}(a, b)$ so that $a=g d$ and $b=g x$ for some coprime $d$ and $x$. Then, $b^{2} \\mid a^{3}$ is equivalent to $g^{2} x^{2} \\mid g^{3} d^{3}$, which is equivalent to $x^{2} \\mid g d^{3}$. Since $x$ and $d$ are coprime, this implies $x^{2} \\mid g$. Hence, $g=x^{2} c$ for some $c$, giving $a=x^{2} c d$ and $b=x^{3} c$ as required.\nNow, it remains to find all positive integers $x, c, d$ satisfying\n\n$$\nx^{2} c d-1 \\mid x^{3} c-1\n$$\n\nThat is, $x^{3} c \\equiv 1\\left(\\bmod x^{2} c d-1\\right)$. Assuming that this congruence holds, it follows that $d \\equiv x^{3} c d \\equiv x$ $\\left(\\bmod x^{2} c d-1\\right)$. Then, either $x=d$ or $x-d \\geq x^{2} c d-1$ or $d-x \\geq x^{2} c d-1$.\n\n- If $x=d$ then $b=a$.\n- If $x-d \\geq x^{2} c d-1$, then $x-d \\geq x^{2} c d-1 \\geq x-1 \\geq x-d$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=d=1$, which implies that $a=b=1$.\n- If $d-x \\geq x^{2} c d-1$, then $d-x \\geq x^{2} c d-1 \\geq d-1 \\geq d-x$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=1$, which implies that $b=1$.\nHence the only solutions are the pairs $(a, b)$ such that $a=b$ or $b=1$. These pairs can be checked to satisfy the given conditions.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 3 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.", "solution": ".3\n\nAll answers are $(n, n)$ and $(n, 1)$ where $n$ is any positive integer. They all clearly work.\nTo show that these are all solutions, note that we can easily eliminate the case $a=1$ or $b=1$. Thus, assume that $a, b \\neq 1$ and $a \\neq b$. By the second divisibility, we see that $a-1 \\mid b-a$. However, $\\operatorname{gcd}(a, b) \\mid b-a$ and $a-1$ is relatively prime to $\\operatorname{gcd}(a, b)$. This implies that $(a-1) \\operatorname{gcd}(a, b) \\mid b-a$, which implies $\\operatorname{gcd}(a, b) \\left\\lvert\\, \\frac{b-1}{a-1}-1\\right.$.\nThe last relation implies that $\\operatorname{gcd}(a, b)<\\frac{b-1}{a-1}$, since the right-hand side are positive. However, due to the first divisibility,\n\n$$\n\\operatorname{gcd}(a, b)^{3}=\\operatorname{gcd}\\left(a^{3}, b^{3}\\right) \\geq \\operatorname{gcd}\\left(b^{2}, b^{3}\\right)=b^{2} .\n$$\n\nCombining these two inequalities, we get that\n\n$$\nb^{\\frac{2}{3}}<\\frac{b-1}{a-1}<2 \\frac{b}{a}\n$$\n\nThis implies $a<2 b^{\\frac{1}{3}}$. However, $b^{2} \\mid a^{3}$ gives $b \\leq a^{\\frac{3}{2}}$. This forces\n\n$$\na<2\\left(a^{\\frac{3}{2}}\\right)^{\\frac{1}{3}}=2 \\sqrt{a} \\Longrightarrow a<4 .\n$$\n\nExtracting $a=2,3$ by hand yields no additional solution.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 1.", "solution_match": "# Solution 1"}}
|
| 4 |
+
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a right triangle with $\\angle B=90^{\\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\\triangle A C D$ and the circumcircle of $\\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.\n", "solution": ".1\n\nLet the line $E F$ intersect the line $B C$ at $P$ and the circumcircle of $\\triangle A C D$ at $G$ distinct from $F$. We will prove that $P$ is the fixed point.\nFirst, notice that $\\triangle B E D$ is isosceles with $E B=E D$. This implies $\\angle E B C=\\angle E D P$.\nThen, $\\angle D A G=\\angle D F G=\\angle E B C=\\angle E D P$ which implies $A G \\| D C$. Hence, $A G C D$ is an isosceles trapezoid.\nAlso, $A G \\| D C$ and $A E=E D$. This implies $\\triangle A E G \\cong \\triangle D E P$ and $A G=D P$.\nSince $B$ is the foot of the perpendicular from $A$ onto the side $C D$ of the isosceles trapezoid $A G C D$, we have $P B=P D+D B=A G+D B=B C$, which does not depend on the choice of $D$. Hence, the initial statement is proven.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 5 |
+
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be a right triangle with $\\angle B=90^{\\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\\triangle A C D$ and the circumcircle of $\\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.\n", "solution": ".2\n\nSet up a coordinate system where $B C$ is along the positive $x$-axis, $B A$ is along the positive $y$-axis, and $B$ is the origin. Take $A=(0, a), B=(0,0), C=(c, 0), D=(-d, 0)$ where $a, b, c, d>0$. Then $E=\\left(-\\frac{d}{2}, \\frac{a}{2}\\right)$. The general equation of a circle is\n\n$$\nx^{2}+y^{2}+2 f x+2 g y+h=0\n$$\n\nSubstituting the coordinates of $A, D, C$ into (1) and solving for $f, g, h$, we find that the equation of the circumcircle of $\\triangle A D C$ is\n\n$$\nx^{2}+y^{2}+(d-c) x+\\left(\\frac{c d}{a}-a\\right) y-c d=0\n$$\n\nSimilarly, the equation of the circumcircle of $\\triangle B D E$ is\n\n$$\nx^{2}+y^{2}+d x+\\left(\\frac{d^{2}}{2 a}-\\frac{a}{2}\\right) y=0\n$$\n\nThen (3)-(2) gives the equation of the line $D F$ which is\n\n$$\nc x+\\frac{a^{2}+d^{2}-2 c d}{2 a} y+c d=0\n$$\n\nSolving (3) and (4) simultaneously, we get\n\n$$\nF=\\left(\\frac{c\\left(d^{2}-a^{2}-2 c d\\right)}{a^{2}+(d-2 c)^{2}}, \\frac{2 a c(c-d)}{a^{2}+(d-2 c)^{2}}\\right)\n$$\n\nand the other solution $D=(-d, 0)$.\nFrom this we obtain the equation of the line $E F$ which is $a x+(d-2 c) y+a c=0$. It passes through $P(-c, 0)$ which is independent of $d$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 6 |
+
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Find all positive integers $k<202$ for which there exists a positive integer $n$ such that\n\n$$\n\\left\\{\\frac{n}{202}\\right\\}+\\left\\{\\frac{2 n}{202}\\right\\}+\\cdots+\\left\\{\\frac{k n}{202}\\right\\}=\\frac{k}{2}\n$$\n\nwhere $\\{x\\}$ denote the fractional part of $x$.\nNote: $\\{x\\}$ denotes the real number $k$ with $0 \\leq k<1$ such that $x-k$ is an integer.", "solution": "Denote the equation in the problem statement as $\\left(^{*}\\right)$, and note that it is equivalent to the condition that the average of the remainders when dividing $n, 2 n, \\ldots, k n$ by 202 is 101 . Since $\\left\\{\\frac{i n}{202}\\right\\}$ is invariant in each residue class modulo 202 for each $1 \\leq i \\leq k$, it suffices to consider $0 \\leq n<202$.\n\nIf $n=0$, so is $\\left\\{\\frac{i n}{202}\\right\\}$, meaning that $(*)$ does not hold for any $k$. If $n=101$, then it can be checked that $\\left(^{*}\\right)$ is satisfied if and only if $k=1$. From now on, we will assume that $101 \\nmid n$.\nFor each $1 \\leq i \\leq k$, let $a_{i}=\\left\\lfloor\\frac{i n}{202}\\right\\rfloor=\\frac{i n}{202}-\\left\\{\\frac{i n}{202}\\right\\}$. Rewriting $\\left(^{*}\\right)$ and multiplying the equation by 202, we find that\n\n$$\nn(1+2+\\ldots+k)-202\\left(a_{1}+a_{2}+\\ldots+a_{k}\\right)=101 k\n$$\n\nEquivalently, letting $z=a_{1}+a_{2}+\\ldots+a_{k}$,\n\n$$\nn k(k+1)-404 z=202 k\n$$\n\nSince $n$ is not divisible by 101 , which is prime, it follows that $101 \\mid k(k+1)$. In particular, $101 \\mid k$ or $101 \\mid k+1$. This means that $k \\in\\{100,101,201\\}$. We claim that all these values of $k$ work.\n\n- If $k=201$, we may choose $n=1$. The remainders when dividing $n, 2 n, \\ldots, k n$ by 202 are 1,2 , ..., 201, which have an average of 101 .\n- If $k=100$, we may choose $n=2$. The remainders when dividing $n, 2 n, \\ldots, k n$ by 202 are 2,4 , ..., 200, which have an average of 101.\n- If $k=101$, we may choose $n=51$. To see this, note that the first four remainders are $51,102,153$, 2 , which have an average of 77 . The next four remainders $(53,104,155,4)$ are shifted upwards from the first four remainders by 2 each, and so on, until the 25 th set of the remainders ( 99 , $150,201,50)$ which have an average of 125 . Hence, the first 100 remainders have an average of $\\frac{77+125}{2}=101$. The 101th remainder is also 101 , meaning that the average of all 101 remainders is 101 .\n\nIn conclusion, all values $k \\in\\{1,100,101,201\\}$ satisfy the initial condition.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 3.", "solution_match": "# Solution\n\n"}}
|
| 7 |
+
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $n$ and $k$ be positive integers. Cathy is playing the following game. There are $n$ marbles and $k$ boxes, with the marbles labelled 1 to $n$. Initially, all marbles are placed inside one box. Each turn, Cathy chooses a box and then moves the marbles with the smallest label, say $i$, to either any empty box or the box containing marble $i+1$. Cathy wins if at any point there is a box containing only marble $n$.\nDetermine all pairs of integers $(n, k)$ such that Cathy can win this game.", "solution": "We claim Cathy can win if and only if $n \\leq 2^{k-1}$.\n\nFirst, note that each non-empty box always contains a consecutive sequence of labeled marbles. This is true since Cathy is always either removing from or placing in the lowest marble in a box. As a consequence, every move made is reversible.\n\nNext, we prove by induction that Cathy can win if $n=2^{k-1}$. The base case of $n=k=1$ is trivial. Assume a victory can be obtained for $m$ boxes and $2^{m-1}$ marbles. Consider the case of $m+1$ boxes and $2^{m}$ marbles. Cathy can first perform a sequence of moves so that only marbles $2^{m-1}, \\ldots, 2^{m}$ are left in the starting box, while keeping one box, say $B$, empty. Now move the marble $2^{m-1}$ to box $B$, then reverse all of the initial moves while treating $B$ as the starting box. At the end of that, we will have marbles $2^{m-1}+1, \\ldots, 2^{m}$ in the starting box, marbles $1,2, \\ldots, 2^{m-1}$ in box $B$, and $m-1$ empty boxes. By repeating the original sequence of moves on marbles $2^{m-1}+1, \\ldots, 2^{m}$, using the $m$ boxes that are not box $B$, we can reach a state where only marble $2^{m}$ remains in the starting box. Therefore\na victory is possible if $n=2^{k-1}$ or smaller.\n\nWe now prove by induction that Cathy loses if $n=2^{k-1}+1$. The base case of $n=2$ and $k=1$ is trivial. Assume a victory is impossible for $m$ boxes and $2^{m-1}+1$ marbles. For the sake of contradiction, suppose that victory is possible for $m+1$ boxes and $2^{m}+1$ marbles. In a winning sequence of moves, consider the last time a marble $2^{m-1}+1$ leaves the starting box, call this move $X$. After $X$, there cannot be a time when marbles $1, \\ldots, 2^{m-1}+1$ are all in the same box. Otherwise, by reversing these moves after $X$ and deleting marbles greater than $2^{m-1}+1$, it gives us a winning sequence of moves for $2^{m-1}+1$ marbles and $m$ boxes (as the original starting box is not used here), contradicting the inductive hypothesis. Hence starting from $X$, marbles 1 will never be in the same box as any marbles greater than or equal to $2^{m-1}+1$.\n\nNow delete marbles $2, \\ldots, 2^{m-1}$ and consider the winning moves starting from $X$. Marble 1 would only move from one empty box to another, while blocking other marbles from entering its box. Thus we effectively have a sequence of moves for $2^{m-1}+1$ marbles, while only able to use $m$ boxes. This again contradicts the inductive hypothesis. Therefore, a victory is not possible if $n=2^{k-1}+1$ or greater.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 4.", "solution_match": "# Solution\n\n"}}
|
| 8 |
+
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": "The minimum value is $-\\frac{1}{8}$. There are eight equality cases in total. The first one is\n\n$$\n\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right) .\n$$\n\nCyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \\rightarrow$ $(-a,-b,-c,-d))$ all four entries in each of the four quadruples give four more equality cases.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution\n\n"}}
|
| 9 |
+
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": ".1\n\nSince the expression is cyclic, we could WLOG $a=\\max \\{a, b, c, d\\}$. Let\n\n$$\nS(a, b, c, d)=(a-b)(b-c)(c-d)(d-a)\n$$\n\nNote that we have given $(a, b, c, d)$ such that $S(a, b, c, d)=-\\frac{1}{8}$. Therefore, to prove that $S(a, b, c, d) \\geq$ $-\\frac{1}{8}$, we just need to consider the case where $S(a, b, c, d)<0$.\n\n- Exactly 1 of $a-b, b-c, c-d, d-a$ is negative.\n\nSince $a=\\max \\{a, b, c, d\\}$, then we must have $d-a<0$. This forces $a>b>c>d$. Now, let us write\n\n$$\nS(a, b, c, d)=-(a-b)(b-c)(c-d)(a-d)\n$$\n\nWrite $a-b=y, b-c=x, c-d=w$ for some positive reals $w, x, y>0$. Plugging to the original condition, we have\n\n$$\n(d+w+x+y)^{2}+(d+w+x)^{2}+(d+w)^{2}+d^{2}-1=0(*)\n$$\n\nand we want to prove that $w x y(w+x+y) \\leq \\frac{1}{8}$. Consider the expression $(*)$ as a quadratic in $d$ :\n\n$$\n4 d^{2}+d(6 w+4 x+2 y)+\\left((w+x+y)^{2}+(w+x)^{2}+w^{2}-1\\right)=0\n$$\n\nSince $d$ is a real number, then the discriminant of the given equation has to be non-negative, i.e. we must have\n\n$$\n\\begin{aligned}\n4 & \\geq 4\\left((w+x+y)^{2}+(w+x)^{2}+w^{2}\\right)-(3 w+2 x+y)^{2} \\\\\n& =\\left(3 w^{2}+2 w y+3 y^{2}\\right)+4 x(w+x+y) \\\\\n& \\geq 8 w y+4 x(w+x+y) \\\\\n& =4(x(w+x+y)+2 w y)\n\\end{aligned}\n$$\n\nHowever, AM-GM gives us\n\n$$\nw x y(w+x+y) \\leq \\frac{1}{2}\\left(\\frac{x(w+x+y)+2 w y}{2}\\right)^{2} \\leq \\frac{1}{8}\n$$\n\nThis proves $S(a, b, c, d) \\geq-\\frac{1}{8}$ for any $a, b, c, d \\in \\mathbb{R}$ such that $a>b>c>d$. Equality holds if and only if $w=y, x(w+x+y)=2 w y$ and $w x y(w+x+y)=\\frac{1}{8}$. Solving these equations gives us $w^{4}=\\frac{1}{16}$ which forces $w=\\frac{1}{2}$ since $w>0$. Solving for $x$ gives us $x(x+1)=\\frac{1}{2}$, and we will get $x=-\\frac{1}{2}+\\frac{\\sqrt{3}}{2}$ as $x>0$. Plugging back gives us $d=-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}$, and this gives us\n\n$$\n(a, b, c, d)=\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}\\right)\n$$\n\nThus, any cyclic permutation of the above solution will achieve the minimum equality.\n\n- Exactly 3 of $a-b, b-c, c-d, d-a$ are negative Since $a=\\max \\{a, b, c, d\\}$, then $a-b$ has to be positive. So we must have $b<c<d<a$. Now, note that\n\n$$\n\\begin{aligned}\nS(a, b, c, d) & =(a-b)(b-c)(c-d)(d-a) \\\\\n& =(a-d)(d-c)(c-b)(b-a) \\\\\n& =S(a, d, c, b)\n\\end{aligned}\n$$\n\nNow, note that $a>d>c>b$. By the previous case, $S(a, d, c, b) \\geq-\\frac{1}{8}$, which implies that\n\n$$\nS(a, b, c, d)=S(a, d, c, b) \\geq-\\frac{1}{8}\n$$\n\nas well. Equality holds if and only if\n\n$$\n(a, b, c, d)=\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right)\n$$\n\nand its cyclic permutation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 5"}}
|
| 10 |
+
{"year": "2022", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.", "solution": ".2\n\nThe minimum value is $-\\frac{1}{8}$. There are eight equality cases in total. The first one is\n\n$$\n\\left(\\frac{1}{4}+\\frac{\\sqrt{3}}{4},-\\frac{1}{4}-\\frac{\\sqrt{3}}{4}, \\frac{1}{4}-\\frac{\\sqrt{3}}{4},-\\frac{1}{4}+\\frac{\\sqrt{3}}{4}\\right) .\n$$\n\nCyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \\rightarrow$ $(-a,-b,-c,-d)$ ) all four entries in each of the four quadruples give four more equality cases. We then begin the proof by the following optimization:\n\nClaim 1. In order to get the minimum value, we must have $a+b+c+d=0$.\n\nProof. Assume not, let $\\delta=\\frac{a+b+c+d}{4}$ and note that\n\n$$\n(a-\\delta)^{2}+(b-\\delta)^{2}+(c-\\delta)^{2}+(d-\\delta)^{2}<a^{2}+b^{2}+c^{2}+d^{2}\n$$\n\nso by shifting by $\\delta$ and scaling, we get an even smaller value of $(a-b)(b-c)(c-d)(d-a)$.\n\nThe key idea is to substitute the variables\n\n$$\n\\begin{aligned}\n& x=a c+b d \\\\\n& y=a b+c d \\\\\n& z=a d+b c\n\\end{aligned}\n$$\n\nso that the original expression is just $(x-y)(x-z)$. We also have the conditions $x, y, z \\geq-0.5$ because of:\n\n$$\n2 x+\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)=(a+c)^{2}+(b+d)^{2} \\geq 0\n$$\n\nMoreover, notice that\n\n$$\n0=(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(x+y+z) \\Longrightarrow x+y+z=\\frac{-1}{2}\n$$\n\nNow, we reduce to the following optimization problem.\nClaim 2. Let $x, y, z \\geq-0.5$ such that $x+y+z=-0.5$. Then, the minimum value of\n\n$$\n(x-y)(x-z)\n$$\n\nis $-1 / 8$. Moreover, the equality case occurs when $x=-1 / 4$ and $\\{y, z\\}=\\{1 / 4,-1 / 2\\}$.\nProof. We notice that\n\n$$\n\\begin{aligned}\n(x-y)(x-z)+\\frac{1}{8} & =\\left(2 y+z+\\frac{1}{2}\\right)\\left(2 z+y+\\frac{1}{2}\\right)+\\frac{1}{8} \\\\\n& =\\frac{1}{8}(4 y+4 z+1)^{2}+\\left(y+\\frac{1}{2}\\right)\\left(z+\\frac{1}{2}\\right) \\geq 0\n\\end{aligned}\n$$\n\nThe last inequality is true since both $y+\\frac{1}{2}$ and $z+\\frac{1}{2}$ are not less than zero.\nThe equality in the last inequality is attained when either $y+\\frac{1}{2}=0$ or $z+\\frac{1}{2}=0$, and $4 y+4 z+1=0$. This system of equations give $(y, z)=(1 / 4,-1 / 2)$ or $(y, z)=(-1 / 2,1 / 4)$ as the desired equality cases.\n\nNote: We can also prove (the weakened) Claim 2 by using Lagrange Multiplier, as follows. We first prove that, in fact, $x, y, z \\in[-0.5,0.5]$. This can be proved by considering that\n\n$$\n-2 x+\\left(a^{2}+b^{2}+c^{2}+d^{2}\\right)=(a-c)^{2}+(b-d)^{2} \\geq 0\n$$\n\nWe will prove the Claim 2, only that in this case, $x, y, z \\in[-0.5,0.5]$. This is already sufficient to prove the original question. We already have the bounded domain $[-0.5,0.5]^{3}$, so the global minimum must occur somewhere. Thus, it suffices to consider two cases:\n\n- If the global minimum lies on the boundary of $[-0.5,0.5]^{3}$. Then, one of $x, y, z$ must be -0.5 or 0.5 . By symmetry between $y$ and $z$, we split to a few more cases.\n- If $x=0.5$, then $y=z=-0.5$, so $(x-y)(x-z)=1$, not the minimum.\n- If $x=-0.5$, then both $y$ and $z$ must be greater or equal to $x$, so $(x-y)(x-z) \\geq 0$, not the minimum.\n- If $y=0.5$, then $x=z=-0.5$, so $(x-y)(x-z)=0$, not the minimum.\n- If $y=-0.5$, then $z=-x$, so\n\n$$\n(x-y)(x-z)=2 x(x+0.5)\n$$\n\nwhich obtain the minimum at $x=-1 / 4$. This gives the desired equality case.\n\n- If the global minimum lies in the interior $(-0.5,0.5)^{3}$, then we apply Lagrange multiplier:\n\n$$\n\\begin{aligned}\n& \\frac{\\partial}{\\partial x}(x-y)(x-z)=\\lambda \\frac{\\partial}{\\partial x}(x+y+z) \\\\\n& \\frac{\\partial}{\\partial y}(x-y)(x-z)=\\lambda \\frac{\\partial}{\\partial y}(x+y+z) \\\\\n& \\frac{\\partial}{\\partial z}(x-y)(x-z) \\Longrightarrow z-x=\\lambda \\frac{\\partial}{\\partial z}(x+y+z) \\\\\n& \\Longrightarrow y-x=\\lambda .\n\\end{aligned}\n$$\n\nAdding the last two equations gives $\\lambda=0$, or $x=y=z$. This gives $(x-y)(x-z)=0$, not the minimum.\n\nHaving exhausted all cases, we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl", "problem_match": "\nProblem 5.", "solution_match": "# Solution 5"}}
|
APMO/segmented/en-apmo2023_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $n \\geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \\ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.\nShow that it is possible to arrange these squares in a way such that every square touches exactly two other squares.", "solution": "Set aside the squares with sidelengths $n-3, n-2, n-1$, and $n$ and suppose we can split the remaining squares into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$.\nString the squares of each set $A, B$ along two parallel diagonals, one for each diagonal. Now use the four largest squares along two perpendicular diagonals to finish the construction: one will have sidelengths $n$ and $n-3$, and the other, sidelengths $n-1$ and $n-2$. If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-1$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration, in which the $A$ and $B$-diagonals are represented by unit squares, and the sidelengths $a_{i}$ of squares from $A$ and $b_{j}$ of squares from $B$ are indicated within each square, follows:\n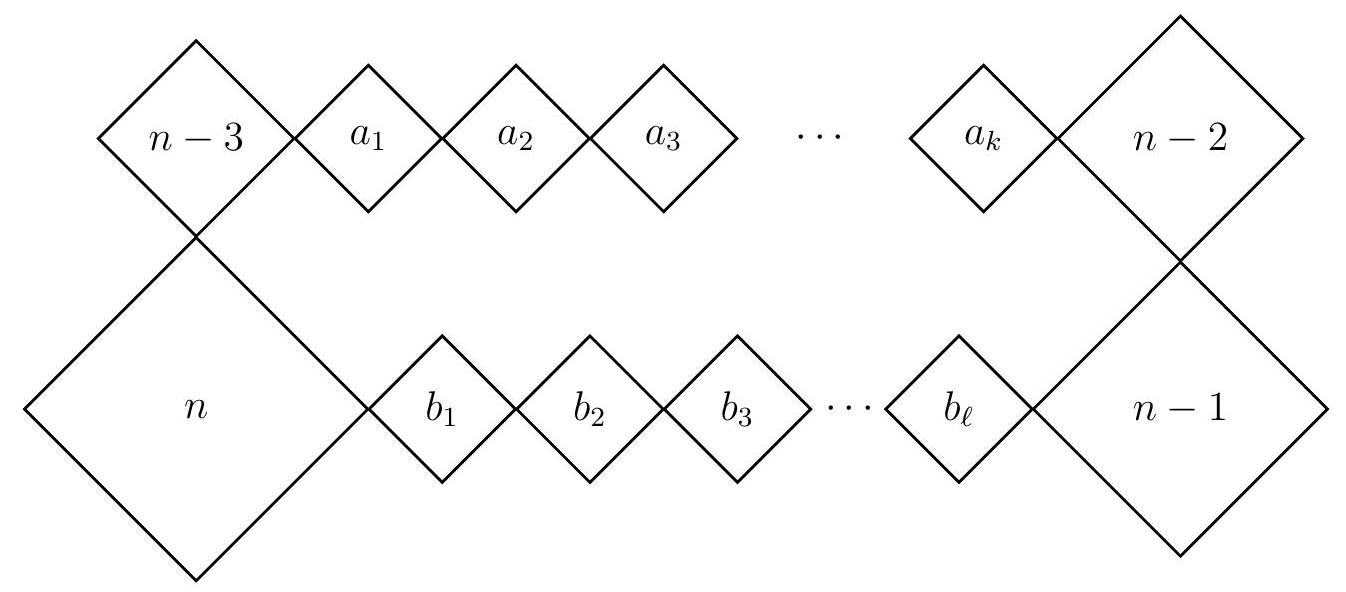\n\nSince $\\left(a_{1}+a_{2}+\\cdots+a_{k}\\right) \\sqrt{2}+\\frac{((n-3)+(n-2)) \\sqrt{2}}{2}=\\left(b_{1}+b_{2}+\\cdots+b_{\\ell}+2\\right) \\sqrt{2}+\\frac{(n+(n-1)) \\sqrt{2}}{2}$, this case is done.\nIf the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-2$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration follows:\n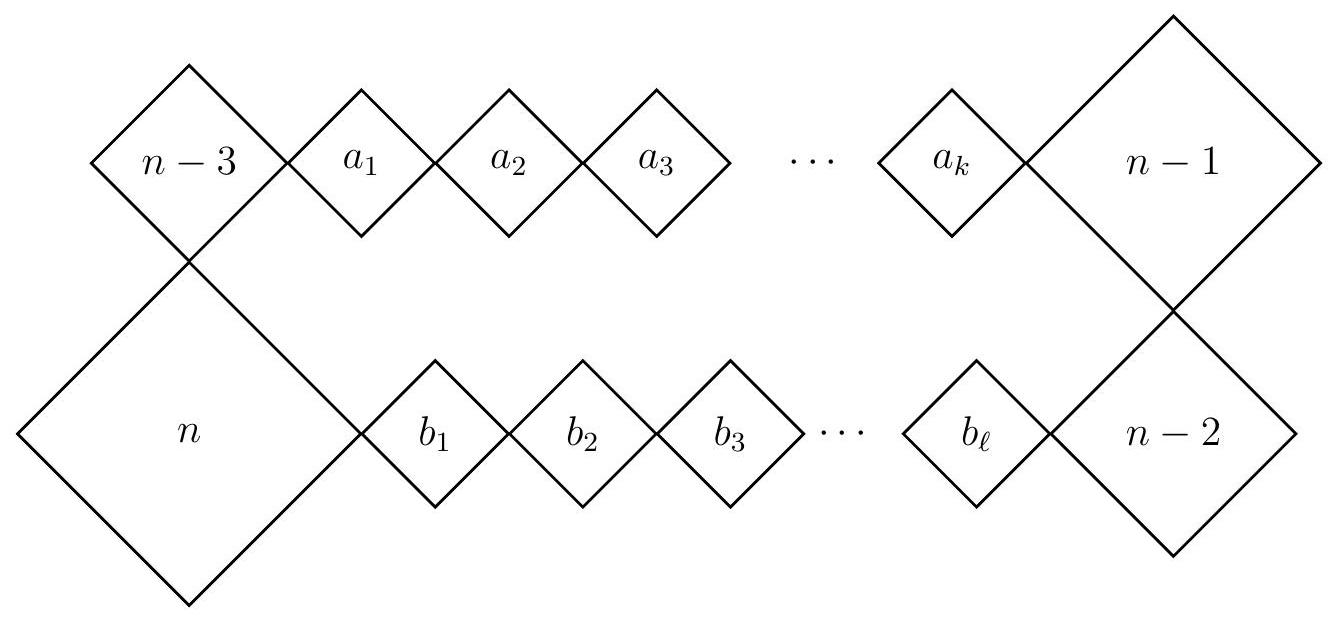\n\nSince $\\left(a_{1}+a_{2}+\\cdots+a_{k}\\right) \\sqrt{2}+\\frac{((n-3)+(n-1)) \\sqrt{2}}{2}=\\left(b_{1}+b_{2}+\\cdots+b_{\\ell}+1\\right) \\sqrt{2}+\\frac{(n+(n-2)) \\sqrt{2}}{2}$, this case is also done.\nIn both cases, the distance between the $A$-diagonal and the $B$-diagonal is $\\frac{((n-3)+n) \\sqrt{2}}{2}=\\frac{(2 n-3) \\sqrt{2}}{2}$. Since $a_{i}, b_{j} \\leq n-4, \\frac{\\left(a_{i}+b_{j}\\right) \\sqrt{2}}{2}<\\frac{(2 n-4) \\sqrt{2}}{2}<\\frac{(2 n-3) \\sqrt{2}}{2}$, and therefore the $A$ - and $B$-diagonals do not overlap.\nFinally, we prove that it is possible to split the squares of sidelengths 1 to $n-4$ into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$. One can do that in several ways; we present two possibilities:\n\n- Direct construction: Split the numbers from 1 to $n-4$ into several sets of four consecutive numbers $\\{t, t+1, t+2, t+3\\}$, beginning with the largest numbers; put squares of sidelengths $t$ and $t+3$ in $A$ and squares of sidelengths $t+1$ and $t+2$ in $B$. Notice that $t+(t+3)=$ $(t+1)+(t+2)$. In the end, at most four numbers remain.\n- If only 1 remains, put the corresponding square in $A$, so the sum of the sidelengths of the squares in $A$ is one unit larger that those in $B$;\n- If 1 and 2 remains, put the square of sidelength 2 in $A$ and the square of sidelength 1 in $B$ (the difference is 1 );\n- If 1,2 , and 3 remains, put the squares of sidelengths 1 and 3 in $A$, and the square of sidelength 2 in $B$ (the difference is 2 );\n- If $1,2,3$, and 4 remains, put the squares of sidelengths 2 and 4 in $A$, and the squares of sidelengths 1 and 3 in $B$ (the difference is 2 ).\n- Indirect construction: Starting with $A$ and $B$ as empty sets, add the squares of sidelengths $n-4, n-3, \\ldots, 2$ to either $A$ or $B$ in that order such that at each stage the difference between the sum of the sidelengths in $A$ and the sum of the sidelengths of B is minimized. By induction it is clear that after adding an integer $j$ to one of the sets, this difference is at most $j$. In particular, the difference is 0,1 or 2 at the end. Finally adding the final 1 to one of the sets can ensure that the final difference is 1 or 2 . If necessary, flip $A$ and $B$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
-
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $n \\geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \\ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.\nShow that it is possible to arrange these squares in a way such that every square touches exactly two other squares.", "solution": "Solve the problem by induction in $n$. Construct examples for $n=5,6,7,8,9,10$ (one can use the constructions from the previous solution, for instance). For $n>10$, set aside the six larger squares and arrange them in the following fashion:\n\n\nBy the induction hypothesis, one can arrange the remaining $n-6$ squares away from the six larger squares, so we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
-
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Find all integers $n$ satisfying $n \\geq 2$ and $\\frac{\\sigma(n)}{p(n)-1}=n$, in which $\\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.\n\nAnswer: $n=6$.", "solution": "Let $n=p_{1}^{\\alpha_{1}} \\cdot \\ldots \\cdot p_{k}^{\\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\\sigma(n)=\\left(1+p_{1}+\\cdots+p_{1}^{\\alpha_{1}}\\right) \\ldots\\left(1+p_{k}+\\cdots+p_{k}^{\\alpha_{k}}\\right)$. Hence\n$p_{k}-1=\\frac{\\sigma(n)}{n}=\\prod_{i=1}^{k}\\left(1+\\frac{1}{p_{i}}+\\cdots+\\frac{1}{p_{i}^{\\alpha_{i}}}\\right)<\\prod_{i=1}^{k} \\frac{1}{1-\\frac{1}{p_{i}}}=\\prod_{i=1}^{k}\\left(1+\\frac{1}{p_{i}-1}\\right) \\leq \\prod_{i=1}^{k}\\left(1+\\frac{1}{i}\\right)=k+1$,\nthat is, $p_{k}-1<k+1$, which is impossible for $k \\geq 3$, because in this case $p_{k}-1 \\geq 2 k-2 \\geq k+1$. Then $k \\leq 2$ and $p_{k}<k+2 \\leq 4$, which implies $p_{k} \\leq 3$.\nIf $k=1$ then $n=p^{\\alpha}$ and $\\sigma(n)=1+p+\\cdots+p^{\\alpha}$, and in this case $n \\nmid \\sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\\alpha} 3^{\\beta}$ with $\\alpha, \\beta>0$. If $\\alpha>1$ or $\\beta>1$,\n\n$$\n\\frac{\\sigma(n)}{n}>\\left(1+\\frac{1}{2}\\right)\\left(1+\\frac{1}{3}\\right)=2 .\n$$\n\nTherefore $\\alpha=\\beta=1$ and the only answer is $n=6$.\nComment: There are other ways to deal with the case $n=2^{\\alpha} 3^{\\beta}$. For instance, we have $2^{\\alpha+2} 3^{\\beta}=\\left(2^{\\alpha+1}-1\\right)\\left(3^{\\beta+1}-1\\right)$. Since $2^{\\alpha+1}-1$ is not divisible by 2 , and $3^{\\beta+1}-1$ is not divisible by 3 , we have\n\n$$\n\\left\\{\\begin{array} { l } \n{ 2 ^ { \\alpha + 1 } - 1 = 3 ^ { \\beta } } \\\\\n{ 3 ^ { \\beta + 1 } - 1 = 2 ^ { \\alpha + 2 } }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array} { c } \n{ 2 ^ { \\alpha + 1 } - 1 = 3 ^ { \\beta } } \\\\\n{ 3 \\cdot ( 2 ^ { \\alpha + 1 } - 1 ) - 1 = 2 \\cdot 2 ^ { \\alpha + 1 } }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array}{r}\n2^{\\alpha+1}=4 \\\\\n3^{\\beta}=3\n\\end{array}\\right.\\right.\\right.\n$$\n\nand $n=2^{\\alpha} 3^{\\beta}=6$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
-
{"year": "2023", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C D$ be a parallelogram. Let $W, X, Y$, and $Z$ be points on sides $A B, B C, C D$, and $D A$, respectively, such that the incenters of triangles $A W Z, B X W, C Y X$ and $D Z Y$ form a parallelogram. Prove that $W X Y Z$ is a parallelogram.", "solution": "Let the four incenters be $I_{1}, I_{2}, I_{3}$, and $I_{4}$ with inradii $r_{1}, r_{2}, r_{3}$, and $r_{4}$ respectively (in the order given in the question). Without loss of generality, let $I_{1}$ be closer to $A B$ than $I_{2}$. Let the acute angle between $I_{1} I_{2}$ and $A B$ (and hence also the angle between $I_{3} I_{4}$ and $C D$ ) be $\\theta$. Then\n\n$$\nr_{2}-r_{1}=I_{1} I_{2} \\sin \\theta=I_{3} I_{4} \\sin \\theta=r_{4}-r_{3}\n$$\n\nwhich implies $r_{1}+r_{4}=r_{2}+r_{3}$. Similar arguments show that $r_{1}+r_{2}=r_{3}+r_{4}$. Thus we obtain $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\n\n\nNow let's consider the possible positions of $W, X, Y, Z$. Suppose $A Z \\neq C X$. Without loss of generality assume $A Z>C X$. Since the incircles of $A W Z$ and $C Y X$ are symmetric about the centre of the parallelogram $A B C D$, this implies $C Y>A W$. Using similar arguments, we have\n\n$$\nC Y>A W \\Longrightarrow B W>D Y \\Longrightarrow D Z>B X \\Longrightarrow C X>A Z\n$$\n\nwhich is a contradiction. Therefore $A Z=C X \\Longrightarrow A W=C Y$ and $W X Y Z$ is a parallelogram.\nComment: There are several ways to prove that $r_{1}=r_{3}$ and $r_{2}=r_{4}$. The proposer shows the following three alternative approaches:\nUsing parallel lines: Let $O$ be the centre of parallelogram $A B C D$ and $P$ be the centre of parallelogram $I_{1} I_{2} I_{3} I_{4}$. Since $A I_{1}$ and $C I_{3}$ are angle bisectors, we must have $A I_{1} \\| C I_{3}$. Let $\\ell_{1}$ be the line through $O$ parallel to $A I_{1}$. Since $A O=O C, \\ell_{1}$ is halfway between $A I_{1}$ and $C I_{3}$. Hence $P$ must lie on $\\ell_{1}$.\nSimilarly, $P$ must also lie on $\\ell_{2}$, the line through $O$ parallel to $B I_{2}$. Thus $P$ is the intersection of $\\ell_{1}$ and $\\ell_{2}$, which must be $O$. So the four incentres and hence the four incircles must be symmetric about $O$, which implies $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\nUsing a rotation: Let the bisectors of $\\angle D A B$ and $\\angle A B C$ meet at $X$ and the bisectors of $\\angle B C D$ and $\\angle C D A$ meet at $Y$. Then $I_{1}$ is on $A X, I_{2}$ is on $B X, I_{3}$ is on $C Y$, and $I_{4}$ is on $D Y$. Let $O$ be the centre of $A B C D$. Then a 180 degree rotation about $O$ takes $\\triangle A X B$ to $\\triangle C Y D$. Under the same transformation $I_{1} I_{2}$ is mapped to a parallel segment $I_{1}^{\\prime} I_{2}^{\\prime}$ with $I_{1}^{\\prime}$ on $C Y$ and $I_{2}^{\\prime}$ on $D Y$. Since $I_{1} I_{2} I_{3} I_{4}$ is a parallelogram, $I_{3} I_{4}=I_{1} I_{2}$ and $I_{3} I_{4} \\| I_{1} I_{2}$. Hence $I_{1}^{\\prime} I_{2}^{\\prime}$ and $I_{3} I_{4}$ are parallel, equal length segments on sides $C Y, D Y$ and we conclude that $I_{1}^{\\prime}=I_{3}, I_{2}^{\\prime}=I_{4}$. Hence the centre of $I_{1} I_{2} I_{3} I_{4}$ is also $O$ and we establish that by rotational symmetry that $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\nUsing congruent triangles: Let $A I_{1}$ and $B I_{2}$ intersect at $E$ and let $C I_{3}$ and $D I_{4}$ intersect at $F$. Note that $\\triangle A B E$ and $\\triangle C D F$ are congruent, since $A B=C D$ and corresponding pairs of angles are equal (equal opposite angles parallelogram $A B C D$ are each bisected).\n\nSince $A I_{1} \\| C I_{3}$ and $I_{1} I_{2} \\| I_{4} I_{3}, \\angle I_{2} I_{1} E=\\angle I_{4} I_{3} F$. Similarly $\\angle I_{1} I_{2} E=\\angle I_{3} I_{4} F$. Furthermore $I_{1} I_{2}=I_{3} I_{4}$. Hence triangles $I_{2} I_{1} E$ and $I 4 I_{3} F$ are also congruent.\nHence $A B E I_{1} I_{2}$ and $D C F I_{3} I_{4}$ are congruent. Therefore, the perpendicular distance from $I_{1}$ to $A B$ equals the perpendicular distance from $I_{3}$ to $C D$, that is, $r_{1}=r_{3}$. Similarly $r_{2}=r_{4}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $c>0$ be a given positive real and $\\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ such that\n\n$$\nf((c+1) x+f(y))=f(x+2 y)+2 c x \\quad \\text { for all } x, y \\in \\mathbb{R}_{>0}\n$$\n\nAnswer: $f(x)=2 x$ for all $x>0$.", "solution": "We first prove that $f(x) \\geq 2 x$ for all $x>0$. Suppose, for the sake of contradiction, that $f(y)<2 y$ for some positive $y$. Choose $x$ such that $f((c+1) x+f(y))$ and $f(x+2 y)$ cancel out, that is,\n\n$$\n(c+1) x+f(y)=x+2 y \\Longleftrightarrow x=\\frac{2 y-f(y)}{c}\n$$\n\nNotice that $x>0$ because $2 y-f(y)>0$. Then $2 c x=0$, which is not possible. This contradiction yields $f(y) \\geq 2 y$ for all $y>0$.\nNow suppose, again for the sake of contradiction, that $f(y)>2 y$ for some $y>0$. Define the following sequence: $a_{0}$ is an arbitrary real greater than $2 y$, and $f\\left(a_{n}\\right)=f\\left(a_{n-1}\\right)+2 c x$, so that\n\n$$\n\\left\\{\\begin{array}{r}\n(c+1) x+f(y)=a_{n} \\\\\nx+2 y=a_{n-1}\n\\end{array} \\Longleftrightarrow x=a_{n-1}-2 y \\quad \\text { and } \\quad a_{n}=(c+1)\\left(a_{n-1}-2 y\\right)+f(y) .\\right.\n$$\n\nIf $x=a_{n-1}-2 y>0$ then $a_{n}>f(y)>2 y$, so inductively all the substitutions make sense.\nFor the sake of simplicity, let $b_{n}=a_{n}-2 y$, so $b_{n}=(c+1) b_{n-1}+f(y)-2 y \\quad(*)$. Notice that $x=b_{n-1}$ in the former equation, so $f\\left(a_{n}\\right)=f\\left(a_{n-1}\\right)+2 c b_{n-1}$. Telescoping yields\n\n$$\nf\\left(a_{n}\\right)=f\\left(a_{0}\\right)+2 c \\sum_{i=0}^{n-1} b_{i} .\n$$\n\nOne can find $b_{n}$ from the recurrence equation $(*): b_{n}=\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{n}-\\frac{f(y)-2 y}{c}$, and then\n\n$$\n\\begin{aligned}\nf\\left(a_{n}\\right) & =f\\left(a_{0}\\right)+2 c \\sum_{i=0}^{n-1}\\left(\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{i}-\\frac{f(y)-2 y}{c}\\right) \\\\\n& =f\\left(a_{0}\\right)+2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)\\left((c+1)^{n}-1\\right)-2 n(f(y)-2 y)\n\\end{aligned}\n$$\n\nSince $f\\left(a_{n}\\right) \\geq 2 a_{n}=2 b_{n}+4 y$,\n\n$$\n\\begin{aligned}\n& f\\left(a_{0}\\right)+2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)\\left((c+1)^{n}-1\\right)-2 n(f(y)-2 y) \\geq 2 b_{n}+4 y \\\\\n= & 2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{n}-2 \\frac{f(y)-2 y}{c}\n\\end{aligned}\n$$\n\nwhich implies\n\n$$\nf\\left(a_{0}\\right)+2 \\frac{f(y)-2 y}{c} \\geq 2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)+2 n(f(y)-2 y)\n$$\n\nwhich is not true for sufficiently large $n$.\nA contradiction is reached, and thus $f(y)=2 y$ for all $y>0$. It is immediate that this function satisfies the functional equation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
-
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $c>0$ be a given positive real and $\\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ such that\n\n$$\nf((c+1) x+f(y))=f(x+2 y)+2 c x \\quad \\text { for all } x, y \\in \\mathbb{R}_{>0}\n$$\n\nAnswer: $f(x)=2 x$ for all $x>0$.", "solution": "After proving that $f(y) \\geq 2 y$ for all $y>0$, one can define $g(x)=f(x)-2 x, g: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{\\geq 0}$, and our goal is proving that $g(x)=0$ for all $x>0$. The problem is now rewritten as\n\n$$\n\\begin{aligned}\n& g((c+1) x+g(y)+2 y)+2((c+1) x+g(y)+2 y)=g(x+2 y)+2(x+2 y)+2 c x \\\\\n\\Longleftrightarrow & g((c+1) x+g(y)+2 y)+2 g(y)=g(x+2 y) .\n\\end{aligned}\n$$\n\nThis readily implies that $g(x+2 y) \\geq 2 g(y)$, which can be interpreted as $z>2 y \\Longrightarrow g(z) \\geq$ $2 g(y)$, by plugging $z=x+2 y$.\nNow we prove by induction that $z>2 y \\Longrightarrow g(z) \\geq 2 m \\cdot g(y)$ for any positive integer $2 m$. In fact, since $(c+1) x+g(y)+2 y>2 y, g((c+1) x+g(y)+2 y) \\geq 2 m \\cdot g(y)$, and by (??),\n\n$$\ng(x+2 y) \\geq 2 m \\cdot g(y)+2 g(y)=2(m+1) g(y)\n$$\n\nand we are done by plugging $z=x+2 y$ again.\nThe problem now is done: if $g(y)>0$ for some $y>0$, choose a fixed $z>2 y$ arbitrarily and and integer $m$ such that $m>\\frac{g(z)}{2 g(y)}$. Then $g(z)<2 m \\cdot g(y)$, contradiction.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "2023", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:\nFirst, he chooses an endpoint of each segment as a \"sink\". Then he places the present at the endpoint of the segment he is at. The present moves as follows:\n\n- If it is on a line segment, it moves towards the sink.\n- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.\n\nIf the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.", "solution": "Draw a circle that encloses all the intersection points between line segments and extend all line segments until they meet the circle, and then move Tony and all his friends to the circle. Number the intersection points with the circle from 1 to $2 n$ anticlockwise, starting from Tony (Tony has number 1). We will prove that the friends eligible to receive presents are the ones on even-numbered intersection points.\nFirst part: at most $n$ friends can receive a present.\nThe solution relies on a well-known result: the $n$ lines determine regions inside the circle; then it is possible to paint the regions with two colors such that no regions with a common (line) boundary have the same color. The proof is an induction on $n$ : the fact immediately holds for $n=0$, and the induction step consists on taking away one line $\\ell$, painting the regions obtained with $n-1$ lines, drawing $\\ell$ again and flipping all colors on exactly one half plane determined by $\\ell$.\nNow consider the line starting on point 1. Color the regions in red and blue such that neighboring regions have different colors, and such that the two regions that have point 1 as a vertex are red on the right and blue on the left, from Tony's point of view. Finally, assign to each red region the clockwise direction and to each blue region the anticlockwise direction. Because of the coloring, every boundary will have two directions assigned, but the directions are the same since every boundary divides regions of different colors. Then the present will follow the directions assigned to the regions: it certainly does for both regions in the beginning, and when the present reaches an intersection it will keep bordering one of the two regions it was dividing. To finish this part of the problem, consider the regions that share a boundary with the circle. The directions alternate between outcoming and incoming, starting from 1 (outcoming), so all even-numbered vertices are directed as incoming and are the only ones able to receive presents. Second part: all even-numbered vertices can receive a present.\nFirst notice that, since every two chords intersect, every chord separates the endpoints of each of the other $n-1$ chords. Therefore, there are $n-1$ vertices on each side of every chord, and each chord connects vertices $k$ and $k+n, 1 \\leq k \\leq n$.\nWe prove a stronger result by induction in $n$ : let $k$ be an integer, $1 \\leq k \\leq n$. Direct each chord from $i$ to $i+n$ if $1 \\leq i \\leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \\ldots, k+n$. Now suppose that each chord sends a present, starting from the vertex opposite to each sink, and all presents move with the same rules. Then $k-i$ sends a present to $k+i+1, i=0,1, \\ldots, n-1$ (indices taken modulo $2 n$ ). In particular, for $i=k-1$, Tony, in vertex 1 , send a present to vertex $2 k$. Also, the $n$ paths the presents make do not cross (but they may touch.) More formally, for all $i, 1 \\leq i \\leq n$, if one path takes a present from $k-i$ to $k+i+1$, separating the circle into two regions, all paths taking a present from $k-j$ to $k+j+1, j<i$, are completely contained in one region, and all paths taking a present from\n$k-j$ to $k+j+1, j>i$, are completely contained in the other region. For instance, possible ${ }^{1}$ paths for $k=3$ and $n=5$ follow:\n\n\nThe result is true for $n=1$. Let $n>1$ and assume the result is true for less chords. Consider the chord that takes $k$ to $k+n$ and remove it. Apply the induction hypothesis to the remaining $n-1$ lines: after relabeling, presents would go from $k-i$ to $k+i+2,1 \\leq i \\leq n-1$ if the chord were not there.\nReintroduce the chord that takes $k$ to $k+n$. From the induction hypothesis, the chord intersects the paths of the presents in the following order: the $i$-th path the chord intersects is the the one that takes $k-i$ to $k+i, i=1,2, \\ldots, n-1$.\n\n\nPaths without chord $k \\rightarrow k+n$\n\n\nCorrected paths with chord $k \\rightarrow k+n$\n\nThen the presents cover the following new paths: the present from $k$ will leave its chord and take the path towards $k+1$; then, for $i=1,2, \\ldots, n-1$, the present from $k-i$ will meet the chord from $k$ to $k+n$, move towards the intersection with the path towards $k+i+1$ and go to $k+i+1$, as desired. Notice that the paths still do not cross. The induction (and the solution) is now complete.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 8 |
-
{"year": "2023", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:\nFirst, he chooses an endpoint of each segment as a \"sink\". Then he places the present at the endpoint of the segment he is at. The present moves as follows:\n\n- If it is on a line segment, it moves towards the sink.\n- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.\n\nIf the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.", "solution": "First part: at most n friends can receive a present.\nSimilarly to the first solution, consider a circle that encompasses all line segments, extend the lines, and use the endpoints of the chords instead of the line segments, and prove that each chord connects vertices $k$ and $k+n$. We also consider, even in the first part, $n$ presents leaving from $n$ outcoming vertices.\nFirst we prove that a present always goes to a sink. If it does not, then it loops; let it first enter the loop at point $P$ after turning from chord $a$ to chord $b$. Therefore after it loops once,\n\n[^0]it must turn to chord $b$ at $P$. But $P$ is the intersection of $a$ and $b$, so the present should turn from chord $a$ to chord $b$, which can only be done in one way - the same way it came in first. This means that some part of chord $a$ before the present enters the loop at $P$ is part of the loop, which contradicts the fact that $P$ is the first point in the loop. So no present enters a loop, and every present goes to a sink.\n\n\nThere are no loops\n\n\nNo two paths cross\n\nThe present paths also do not cross: in fact, every time two paths share a point $P$, intersection of chords $a$ and $b$, one path comes from $a$ to $b$ and the other path comes from $b$ to $a$, and they touch at $P$. This implies the following sequence of facts:\n\n- Every path divides the circle into two regions with paths connecting vertices within each region.\n- All $n$ presents will be delivered to $n$ different persons; that is, all sinks receive a present. This implies that every vertex is an endpoint of a path.\n- The number of chord endpoints inside each region is even, because they are connected within their own region.\n\nNow consider the path starting at vertex 1 , with Tony. It divides the circle into two regions with an even number of vertices in their interior. Then there is an even number of vertices between Tony and the recipient of his present, that is, their vertex is an even numbered one. Second part: all even-numbered vertices can receive a present.\nThe construction is the same as the in the previous solution: direct each chord from $i$ to $i+n$ if $1 \\leq i \\leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \\ldots, k+n$. Then, since the paths do not cross, $k$ will send a present to $k+1, k-1$ will send a present to $k+2$, and so on, until 1 sends a present to $(k+1)+(k-1)=2 k$.\n\n\n[^0]: ${ }^{1}$ The paths do not depend uniquely on $k$ and $n$; different chord configurations and vertex labelings may change the paths.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
|
|
|
| 1 |
+
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $n \\geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \\ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.\nShow that it is possible to arrange these squares in a way such that every square touches exactly two other squares.", "solution": "Set aside the squares with sidelengths $n-3, n-2, n-1$, and $n$ and suppose we can split the remaining squares into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$.\nString the squares of each set $A, B$ along two parallel diagonals, one for each diagonal. Now use the four largest squares along two perpendicular diagonals to finish the construction: one will have sidelengths $n$ and $n-3$, and the other, sidelengths $n-1$ and $n-2$. If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-1$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration, in which the $A$ and $B$-diagonals are represented by unit squares, and the sidelengths $a_{i}$ of squares from $A$ and $b_{j}$ of squares from $B$ are indicated within each square, follows:\n\n\nSince $\\left(a_{1}+a_{2}+\\cdots+a_{k}\\right) \\sqrt{2}+\\frac{((n-3)+(n-2)) \\sqrt{2}}{2}=\\left(b_{1}+b_{2}+\\cdots+b_{\\ell}+2\\right) \\sqrt{2}+\\frac{(n+(n-1)) \\sqrt{2}}{2}$, this case is done.\nIf the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-2$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration follows:\n\n\nSince $\\left(a_{1}+a_{2}+\\cdots+a_{k}\\right) \\sqrt{2}+\\frac{((n-3)+(n-1)) \\sqrt{2}}{2}=\\left(b_{1}+b_{2}+\\cdots+b_{\\ell}+1\\right) \\sqrt{2}+\\frac{(n+(n-2)) \\sqrt{2}}{2}$, this case is also done.\nIn both cases, the distance between the $A$-diagonal and the $B$-diagonal is $\\frac{((n-3)+n) \\sqrt{2}}{2}=\\frac{(2 n-3) \\sqrt{2}}{2}$. Since $a_{i}, b_{j} \\leq n-4, \\frac{\\left(a_{i}+b_{j}\\right) \\sqrt{2}}{2}<\\frac{(2 n-4) \\sqrt{2}}{2}<\\frac{(2 n-3) \\sqrt{2}}{2}$, and therefore the $A$ - and $B$-diagonals do not overlap.\nFinally, we prove that it is possible to split the squares of sidelengths 1 to $n-4$ into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$. One can do that in several ways; we present two possibilities:\n\n- Direct construction: Split the numbers from 1 to $n-4$ into several sets of four consecutive numbers $\\{t, t+1, t+2, t+3\\}$, beginning with the largest numbers; put squares of sidelengths $t$ and $t+3$ in $A$ and squares of sidelengths $t+1$ and $t+2$ in $B$. Notice that $t+(t+3)=$ $(t+1)+(t+2)$. In the end, at most four numbers remain.\n- If only 1 remains, put the corresponding square in $A$, so the sum of the sidelengths of the squares in $A$ is one unit larger that those in $B$;\n- If 1 and 2 remains, put the square of sidelength 2 in $A$ and the square of sidelength 1 in $B$ (the difference is 1 );\n- If 1,2 , and 3 remains, put the squares of sidelengths 1 and 3 in $A$, and the square of sidelength 2 in $B$ (the difference is 2 );\n- If $1,2,3$, and 4 remains, put the squares of sidelengths 2 and 4 in $A$, and the squares of sidelengths 1 and 3 in $B$ (the difference is 2 ).\n- Indirect construction: Starting with $A$ and $B$ as empty sets, add the squares of sidelengths $n-4, n-3, \\ldots, 2$ to either $A$ or $B$ in that order such that at each stage the difference between the sum of the sidelengths in $A$ and the sum of the sidelengths of B is minimized. By induction it is clear that after adding an integer $j$ to one of the sets, this difference is at most $j$. In particular, the difference is 0,1 or 2 at the end. Finally adding the final 1 to one of the sets can ensure that the final difference is 1 or 2 . If necessary, flip $A$ and $B$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
+
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $n \\geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \\ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.\nShow that it is possible to arrange these squares in a way such that every square touches exactly two other squares.", "solution": "Solve the problem by induction in $n$. Construct examples for $n=5,6,7,8,9,10$ (one can use the constructions from the previous solution, for instance). For $n>10$, set aside the six larger squares and arrange them in the following fashion:\n\n\nBy the induction hypothesis, one can arrange the remaining $n-6$ squares away from the six larger squares, so we are done.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
+
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Find all integers $n$ satisfying $n \\geq 2$ and $\\frac{\\sigma(n)}{p(n)-1}=n$, in which $\\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.\n\nAnswer: $n=6$.", "solution": "Let $n=p_{1}^{\\alpha_{1}} \\cdot \\ldots \\cdot p_{k}^{\\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\\sigma(n)=\\left(1+p_{1}+\\cdots+p_{1}^{\\alpha_{1}}\\right) \\ldots\\left(1+p_{k}+\\cdots+p_{k}^{\\alpha_{k}}\\right)$. Hence\n$p_{k}-1=\\frac{\\sigma(n)}{n}=\\prod_{i=1}^{k}\\left(1+\\frac{1}{p_{i}}+\\cdots+\\frac{1}{p_{i}^{\\alpha_{i}}}\\right)<\\prod_{i=1}^{k} \\frac{1}{1-\\frac{1}{p_{i}}}=\\prod_{i=1}^{k}\\left(1+\\frac{1}{p_{i}-1}\\right) \\leq \\prod_{i=1}^{k}\\left(1+\\frac{1}{i}\\right)=k+1$,\nthat is, $p_{k}-1<k+1$, which is impossible for $k \\geq 3$, because in this case $p_{k}-1 \\geq 2 k-2 \\geq k+1$. Then $k \\leq 2$ and $p_{k}<k+2 \\leq 4$, which implies $p_{k} \\leq 3$.\nIf $k=1$ then $n=p^{\\alpha}$ and $\\sigma(n)=1+p+\\cdots+p^{\\alpha}$, and in this case $n \\nmid \\sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\\alpha} 3^{\\beta}$ with $\\alpha, \\beta>0$. If $\\alpha>1$ or $\\beta>1$,\n\n$$\n\\frac{\\sigma(n)}{n}>\\left(1+\\frac{1}{2}\\right)\\left(1+\\frac{1}{3}\\right)=2 .\n$$\n\nTherefore $\\alpha=\\beta=1$ and the only answer is $n=6$.\nComment: There are other ways to deal with the case $n=2^{\\alpha} 3^{\\beta}$. For instance, we have $2^{\\alpha+2} 3^{\\beta}=\\left(2^{\\alpha+1}-1\\right)\\left(3^{\\beta+1}-1\\right)$. Since $2^{\\alpha+1}-1$ is not divisible by 2 , and $3^{\\beta+1}-1$ is not divisible by 3 , we have\n\n$$\n\\left\\{\\begin{array} { l } \n{ 2 ^ { \\alpha + 1 } - 1 = 3 ^ { \\beta } } \\\\\n{ 3 ^ { \\beta + 1 } - 1 = 2 ^ { \\alpha + 2 } }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array} { c } \n{ 2 ^ { \\alpha + 1 } - 1 = 3 ^ { \\beta } } \\\\\n{ 3 \\cdot ( 2 ^ { \\alpha + 1 } - 1 ) - 1 = 2 \\cdot 2 ^ { \\alpha + 1 } }\n\\end{array} \\Longleftrightarrow \\left\\{\\begin{array}{r}\n2^{\\alpha+1}=4 \\\\\n3^{\\beta}=3\n\\end{array}\\right.\\right.\\right.\n$$\n\nand $n=2^{\\alpha} 3^{\\beta}=6$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 4 |
+
{"year": "2023", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $A B C D$ be a parallelogram. Let $W, X, Y$, and $Z$ be points on sides $A B, B C, C D$, and $D A$, respectively, such that the incenters of triangles $A W Z, B X W, C Y X$ and $D Z Y$ form a parallelogram. Prove that $W X Y Z$ is a parallelogram.", "solution": "Let the four incenters be $I_{1}, I_{2}, I_{3}$, and $I_{4}$ with inradii $r_{1}, r_{2}, r_{3}$, and $r_{4}$ respectively (in the order given in the question). Without loss of generality, let $I_{1}$ be closer to $A B$ than $I_{2}$. Let the acute angle between $I_{1} I_{2}$ and $A B$ (and hence also the angle between $I_{3} I_{4}$ and $C D$ ) be $\\theta$. Then\n\n$$\nr_{2}-r_{1}=I_{1} I_{2} \\sin \\theta=I_{3} I_{4} \\sin \\theta=r_{4}-r_{3}\n$$\n\nwhich implies $r_{1}+r_{4}=r_{2}+r_{3}$. Similar arguments show that $r_{1}+r_{2}=r_{3}+r_{4}$. Thus we obtain $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\n\n\nNow let's consider the possible positions of $W, X, Y, Z$. Suppose $A Z \\neq C X$. Without loss of generality assume $A Z>C X$. Since the incircles of $A W Z$ and $C Y X$ are symmetric about the centre of the parallelogram $A B C D$, this implies $C Y>A W$. Using similar arguments, we have\n\n$$\nC Y>A W \\Longrightarrow B W>D Y \\Longrightarrow D Z>B X \\Longrightarrow C X>A Z\n$$\n\nwhich is a contradiction. Therefore $A Z=C X \\Longrightarrow A W=C Y$ and $W X Y Z$ is a parallelogram.\nComment: There are several ways to prove that $r_{1}=r_{3}$ and $r_{2}=r_{4}$. The proposer shows the following three alternative approaches:\nUsing parallel lines: Let $O$ be the centre of parallelogram $A B C D$ and $P$ be the centre of parallelogram $I_{1} I_{2} I_{3} I_{4}$. Since $A I_{1}$ and $C I_{3}$ are angle bisectors, we must have $A I_{1} \\| C I_{3}$. Let $\\ell_{1}$ be the line through $O$ parallel to $A I_{1}$. Since $A O=O C, \\ell_{1}$ is halfway between $A I_{1}$ and $C I_{3}$. Hence $P$ must lie on $\\ell_{1}$.\nSimilarly, $P$ must also lie on $\\ell_{2}$, the line through $O$ parallel to $B I_{2}$. Thus $P$ is the intersection of $\\ell_{1}$ and $\\ell_{2}$, which must be $O$. So the four incentres and hence the four incircles must be symmetric about $O$, which implies $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\nUsing a rotation: Let the bisectors of $\\angle D A B$ and $\\angle A B C$ meet at $X$ and the bisectors of $\\angle B C D$ and $\\angle C D A$ meet at $Y$. Then $I_{1}$ is on $A X, I_{2}$ is on $B X, I_{3}$ is on $C Y$, and $I_{4}$ is on $D Y$. Let $O$ be the centre of $A B C D$. Then a 180 degree rotation about $O$ takes $\\triangle A X B$ to $\\triangle C Y D$. Under the same transformation $I_{1} I_{2}$ is mapped to a parallel segment $I_{1}^{\\prime} I_{2}^{\\prime}$ with $I_{1}^{\\prime}$ on $C Y$ and $I_{2}^{\\prime}$ on $D Y$. Since $I_{1} I_{2} I_{3} I_{4}$ is a parallelogram, $I_{3} I_{4}=I_{1} I_{2}$ and $I_{3} I_{4} \\| I_{1} I_{2}$. Hence $I_{1}^{\\prime} I_{2}^{\\prime}$ and $I_{3} I_{4}$ are parallel, equal length segments on sides $C Y, D Y$ and we conclude that $I_{1}^{\\prime}=I_{3}, I_{2}^{\\prime}=I_{4}$. Hence the centre of $I_{1} I_{2} I_{3} I_{4}$ is also $O$ and we establish that by rotational symmetry that $r_{1}=r_{3}$ and $r_{2}=r_{4}$.\nUsing congruent triangles: Let $A I_{1}$ and $B I_{2}$ intersect at $E$ and let $C I_{3}$ and $D I_{4}$ intersect at $F$. Note that $\\triangle A B E$ and $\\triangle C D F$ are congruent, since $A B=C D$ and corresponding pairs of angles are equal (equal opposite angles parallelogram $A B C D$ are each bisected).\n\nSince $A I_{1} \\| C I_{3}$ and $I_{1} I_{2} \\| I_{4} I_{3}, \\angle I_{2} I_{1} E=\\angle I_{4} I_{3} F$. Similarly $\\angle I_{1} I_{2} E=\\angle I_{3} I_{4} F$. Furthermore $I_{1} I_{2}=I_{3} I_{4}$. Hence triangles $I_{2} I_{1} E$ and $I 4 I_{3} F$ are also congruent.\nHence $A B E I_{1} I_{2}$ and $D C F I_{3} I_{4}$ are congruent. Therefore, the perpendicular distance from $I_{1}$ to $A B$ equals the perpendicular distance from $I_{3}$ to $C D$, that is, $r_{1}=r_{3}$. Similarly $r_{2}=r_{4}$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $c>0$ be a given positive real and $\\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ such that\n\n$$\nf((c+1) x+f(y))=f(x+2 y)+2 c x \\quad \\text { for all } x, y \\in \\mathbb{R}_{>0}\n$$\n\nAnswer: $f(x)=2 x$ for all $x>0$.", "solution": "We first prove that $f(x) \\geq 2 x$ for all $x>0$. Suppose, for the sake of contradiction, that $f(y)<2 y$ for some positive $y$. Choose $x$ such that $f((c+1) x+f(y))$ and $f(x+2 y)$ cancel out, that is,\n\n$$\n(c+1) x+f(y)=x+2 y \\Longleftrightarrow x=\\frac{2 y-f(y)}{c}\n$$\n\nNotice that $x>0$ because $2 y-f(y)>0$. Then $2 c x=0$, which is not possible. This contradiction yields $f(y) \\geq 2 y$ for all $y>0$.\nNow suppose, again for the sake of contradiction, that $f(y)>2 y$ for some $y>0$. Define the following sequence: $a_{0}$ is an arbitrary real greater than $2 y$, and $f\\left(a_{n}\\right)=f\\left(a_{n-1}\\right)+2 c x$, so that\n\n$$\n\\left\\{\\begin{array}{r}\n(c+1) x+f(y)=a_{n} \\\\\nx+2 y=a_{n-1}\n\\end{array} \\Longleftrightarrow x=a_{n-1}-2 y \\quad \\text { and } \\quad a_{n}=(c+1)\\left(a_{n-1}-2 y\\right)+f(y) .\\right.\n$$\n\nIf $x=a_{n-1}-2 y>0$ then $a_{n}>f(y)>2 y$, so inductively all the substitutions make sense.\nFor the sake of simplicity, let $b_{n}=a_{n}-2 y$, so $b_{n}=(c+1) b_{n-1}+f(y)-2 y \\quad(*)$. Notice that $x=b_{n-1}$ in the former equation, so $f\\left(a_{n}\\right)=f\\left(a_{n-1}\\right)+2 c b_{n-1}$. Telescoping yields\n\n$$\nf\\left(a_{n}\\right)=f\\left(a_{0}\\right)+2 c \\sum_{i=0}^{n-1} b_{i} .\n$$\n\nOne can find $b_{n}$ from the recurrence equation $(*): b_{n}=\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{n}-\\frac{f(y)-2 y}{c}$, and then\n\n$$\n\\begin{aligned}\nf\\left(a_{n}\\right) & =f\\left(a_{0}\\right)+2 c \\sum_{i=0}^{n-1}\\left(\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{i}-\\frac{f(y)-2 y}{c}\\right) \\\\\n& =f\\left(a_{0}\\right)+2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)\\left((c+1)^{n}-1\\right)-2 n(f(y)-2 y)\n\\end{aligned}\n$$\n\nSince $f\\left(a_{n}\\right) \\geq 2 a_{n}=2 b_{n}+4 y$,\n\n$$\n\\begin{aligned}\n& f\\left(a_{0}\\right)+2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)\\left((c+1)^{n}-1\\right)-2 n(f(y)-2 y) \\geq 2 b_{n}+4 y \\\\\n= & 2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)(c+1)^{n}-2 \\frac{f(y)-2 y}{c}\n\\end{aligned}\n$$\n\nwhich implies\n\n$$\nf\\left(a_{0}\\right)+2 \\frac{f(y)-2 y}{c} \\geq 2\\left(b_{0}+\\frac{f(y)-2 y}{c}\\right)+2 n(f(y)-2 y)\n$$\n\nwhich is not true for sufficiently large $n$.\nA contradiction is reached, and thus $f(y)=2 y$ for all $y>0$. It is immediate that this function satisfies the functional equation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 1"}}
|
| 6 |
+
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Let $c>0$ be a given positive real and $\\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{>0}$ such that\n\n$$\nf((c+1) x+f(y))=f(x+2 y)+2 c x \\quad \\text { for all } x, y \\in \\mathbb{R}_{>0}\n$$\n\nAnswer: $f(x)=2 x$ for all $x>0$.", "solution": "After proving that $f(y) \\geq 2 y$ for all $y>0$, one can define $g(x)=f(x)-2 x, g: \\mathbb{R}_{>0} \\rightarrow \\mathbb{R}_{\\geq 0}$, and our goal is proving that $g(x)=0$ for all $x>0$. The problem is now rewritten as\n\n$$\n\\begin{aligned}\n& g((c+1) x+g(y)+2 y)+2((c+1) x+g(y)+2 y)=g(x+2 y)+2(x+2 y)+2 c x \\\\\n\\Longleftrightarrow & g((c+1) x+g(y)+2 y)+2 g(y)=g(x+2 y) .\n\\end{aligned}\n$$\n\nThis readily implies that $g(x+2 y) \\geq 2 g(y)$, which can be interpreted as $z>2 y \\Longrightarrow g(z) \\geq$ $2 g(y)$, by plugging $z=x+2 y$.\nNow we prove by induction that $z>2 y \\Longrightarrow g(z) \\geq 2 m \\cdot g(y)$ for any positive integer $2 m$. In fact, since $(c+1) x+g(y)+2 y>2 y, g((c+1) x+g(y)+2 y) \\geq 2 m \\cdot g(y)$, and by (??),\n\n$$\ng(x+2 y) \\geq 2 m \\cdot g(y)+2 g(y)=2(m+1) g(y)\n$$\n\nand we are done by plugging $z=x+2 y$ again.\nThe problem now is done: if $g(y)>0$ for some $y>0$, choose a fixed $z>2 y$ arbitrarily and and integer $m$ such that $m>\\frac{g(z)}{2 g(y)}$. Then $g(z)<2 m \\cdot g(y)$, contradiction.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "2023", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:\nFirst, he chooses an endpoint of each segment as a \"sink\". Then he places the present at the endpoint of the segment he is at. The present moves as follows:\n\n- If it is on a line segment, it moves towards the sink.\n- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.\n\nIf the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.", "solution": "Draw a circle that encloses all the intersection points between line segments and extend all line segments until they meet the circle, and then move Tony and all his friends to the circle. Number the intersection points with the circle from 1 to $2 n$ anticlockwise, starting from Tony (Tony has number 1). We will prove that the friends eligible to receive presents are the ones on even-numbered intersection points.\nFirst part: at most $n$ friends can receive a present.\nThe solution relies on a well-known result: the $n$ lines determine regions inside the circle; then it is possible to paint the regions with two colors such that no regions with a common (line) boundary have the same color. The proof is an induction on $n$ : the fact immediately holds for $n=0$, and the induction step consists on taking away one line $\\ell$, painting the regions obtained with $n-1$ lines, drawing $\\ell$ again and flipping all colors on exactly one half plane determined by $\\ell$.\nNow consider the line starting on point 1. Color the regions in red and blue such that neighboring regions have different colors, and such that the two regions that have point 1 as a vertex are red on the right and blue on the left, from Tony's point of view. Finally, assign to each red region the clockwise direction and to each blue region the anticlockwise direction. Because of the coloring, every boundary will have two directions assigned, but the directions are the same since every boundary divides regions of different colors. Then the present will follow the directions assigned to the regions: it certainly does for both regions in the beginning, and when the present reaches an intersection it will keep bordering one of the two regions it was dividing. To finish this part of the problem, consider the regions that share a boundary with the circle. The directions alternate between outcoming and incoming, starting from 1 (outcoming), so all even-numbered vertices are directed as incoming and are the only ones able to receive presents. Second part: all even-numbered vertices can receive a present.\nFirst notice that, since every two chords intersect, every chord separates the endpoints of each of the other $n-1$ chords. Therefore, there are $n-1$ vertices on each side of every chord, and each chord connects vertices $k$ and $k+n, 1 \\leq k \\leq n$.\nWe prove a stronger result by induction in $n$ : let $k$ be an integer, $1 \\leq k \\leq n$. Direct each chord from $i$ to $i+n$ if $1 \\leq i \\leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \\ldots, k+n$. Now suppose that each chord sends a present, starting from the vertex opposite to each sink, and all presents move with the same rules. Then $k-i$ sends a present to $k+i+1, i=0,1, \\ldots, n-1$ (indices taken modulo $2 n$ ). In particular, for $i=k-1$, Tony, in vertex 1 , send a present to vertex $2 k$. Also, the $n$ paths the presents make do not cross (but they may touch.) More formally, for all $i, 1 \\leq i \\leq n$, if one path takes a present from $k-i$ to $k+i+1$, separating the circle into two regions, all paths taking a present from $k-j$ to $k+j+1, j<i$, are completely contained in one region, and all paths taking a present from\n$k-j$ to $k+j+1, j>i$, are completely contained in the other region. For instance, possible ${ }^{1}$ paths for $k=3$ and $n=5$ follow:\n\n\nThe result is true for $n=1$. Let $n>1$ and assume the result is true for less chords. Consider the chord that takes $k$ to $k+n$ and remove it. Apply the induction hypothesis to the remaining $n-1$ lines: after relabeling, presents would go from $k-i$ to $k+i+2,1 \\leq i \\leq n-1$ if the chord were not there.\nReintroduce the chord that takes $k$ to $k+n$. From the induction hypothesis, the chord intersects the paths of the presents in the following order: the $i$-th path the chord intersects is the the one that takes $k-i$ to $k+i, i=1,2, \\ldots, n-1$.\n\n\nPaths without chord $k \\rightarrow k+n$\n\n\nCorrected paths with chord $k \\rightarrow k+n$\n\nThen the presents cover the following new paths: the present from $k$ will leave its chord and take the path towards $k+1$; then, for $i=1,2, \\ldots, n-1$, the present from $k-i$ will meet the chord from $k$ to $k+n$, move towards the intersection with the path towards $k+i+1$ and go to $k+i+1$, as desired. Notice that the paths still do not cross. The induction (and the solution) is now complete.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 8 |
+
{"year": "2023", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:\nFirst, he chooses an endpoint of each segment as a \"sink\". Then he places the present at the endpoint of the segment he is at. The present moves as follows:\n\n- If it is on a line segment, it moves towards the sink.\n- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.\n\nIf the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.", "solution": "First part: at most n friends can receive a present.\nSimilarly to the first solution, consider a circle that encompasses all line segments, extend the lines, and use the endpoints of the chords instead of the line segments, and prove that each chord connects vertices $k$ and $k+n$. We also consider, even in the first part, $n$ presents leaving from $n$ outcoming vertices.\nFirst we prove that a present always goes to a sink. If it does not, then it loops; let it first enter the loop at point $P$ after turning from chord $a$ to chord $b$. Therefore after it loops once,\n\n[^0]it must turn to chord $b$ at $P$. But $P$ is the intersection of $a$ and $b$, so the present should turn from chord $a$ to chord $b$, which can only be done in one way - the same way it came in first. This means that some part of chord $a$ before the present enters the loop at $P$ is part of the loop, which contradicts the fact that $P$ is the first point in the loop. So no present enters a loop, and every present goes to a sink.\n\n\nThere are no loops\n\n\nNo two paths cross\n\nThe present paths also do not cross: in fact, every time two paths share a point $P$, intersection of chords $a$ and $b$, one path comes from $a$ to $b$ and the other path comes from $b$ to $a$, and they touch at $P$. This implies the following sequence of facts:\n\n- Every path divides the circle into two regions with paths connecting vertices within each region.\n- All $n$ presents will be delivered to $n$ different persons; that is, all sinks receive a present. This implies that every vertex is an endpoint of a path.\n- The number of chord endpoints inside each region is even, because they are connected within their own region.\n\nNow consider the path starting at vertex 1 , with Tony. It divides the circle into two regions with an even number of vertices in their interior. Then there is an even number of vertices between Tony and the recipient of his present, that is, their vertex is an even numbered one. Second part: all even-numbered vertices can receive a present.\nThe construction is the same as the in the previous solution: direct each chord from $i$ to $i+n$ if $1 \\leq i \\leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \\ldots, k+n$. Then, since the paths do not cross, $k$ will send a present to $k+1, k-1$ will send a present to $k+2$, and so on, until 1 sends a present to $(k+1)+(k-1)=2 k$.\n\n\n[^0]: ${ }^{1}$ The paths do not depend uniquely on $k$ and $n$; different chord configurations and vertex labelings may change the paths.", "metadata": {"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
APMO/segmented/en-apmo2024_sol.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "\n\nLet $\\ell$ be the radical axis of circles $B Q X$ and $C P X$. Since $X$ and $Y$ are on $\\ell$, it is sufficient to show that $A$ is on $\\ell$. Let line $A X$ intersect segments $B C$ and $D E$ at $Z$ and $Z^{\\prime}$, respectively. Then it is sufficient to show that $Z$ is on $\\ell$. By $B C \\| D E$, we obtain\n\n$$\n\\frac{B Z}{Z C}=\\frac{D Z^{\\prime}}{Z^{\\prime} E}=\\frac{P Z}{Z Q},\n$$\n\nthus $B Z \\cdot Q Z=C Z \\cdot P Z$, which implies that $Z$ is on $\\ell$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
-
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "\n\nLet circle $B Q X$ intersect line $A B$ at a point $S$ which is different from $B$. Then $\\angle D E X=$ $\\angle X Q C=\\angle B S X$, thus $S$ is on circle $D E X$. Similarly, let circle $C P X$ intersect line $A C$ at a point $T$ which is different from $C$. Then $T$ is on circle $D E X$. The power of $A$ with respect to the circle $D E X$ is $A S \\cdot A D=A T \\cdot A E$. Since $\\frac{A D}{A B}=\\frac{A E}{A C}, A S \\cdot A B=A T \\cdot A C$. Then $A$ is in the radical axis of circles $B Q X$ and $C P X$, which implies that three points $A, X$ and $Y$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
-
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.\n\n\nThe homothety implies that $A, Y$, and $Y^{\\prime}$ are collinear, and that $\\angle D Y^{\\prime} E=\\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,\n$\\angle D Y^{\\prime} E=\\angle B Y C=\\angle B Y X+\\angle X Y C=\\angle X Q P+\\angle X P Q=180^{\\circ}-\\angle P X Q=180^{\\circ}-\\angle D X E$,\nwhich implies that $D Y^{\\prime} E X$ is cyclic. Therefore\n\n$$\n\\angle D Y^{\\prime} X=\\angle D E X=\\angle P Q X=\\angle B Y X\n$$\n\nwhich, combined with $D Y^{\\prime} \\| B Y$, implies $Y^{\\prime} X \\| Y X$. This proves that $X, Y$, and $Y^{\\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 3"}}
|
| 4 |
-
{"year": "2024", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Consider a $100 \\times 100$ table, and identify the cell in row $a$ and column $b, 1 \\leq a, b \\leq 100$, with the ordered pair $(a, b)$. Let $k$ be an integer such that $51 \\leq k \\leq 99$. A $k$-knight is a piece that moves one cell vertically or horizontally and $k$ cells to the other direction; that is, it moves from $(a, b)$ to $(c, d)$ such that $(|a-c|,|b-d|)$ is either $(1, k)$ or $(k, 1)$. The $k$-knight starts at cell $(1,1)$, and performs several moves. A sequence of moves is a sequence of cells $\\left(x_{0}, y_{0}\\right)=(1,1)$, $\\left(x_{1}, y_{1}\\right),\\left(x_{2}, y_{2}\\right), \\ldots,\\left(x_{n}, y_{n}\\right)$ such that, for all $i=1,2, \\ldots, n, 1 \\leq x_{i}, y_{i} \\leq 100$ and the $k$-knight can move from $\\left(x_{i-1}, y_{i-1}\\right)$ to $\\left(x_{i}, y_{i}\\right)$. In this case, each cell $\\left(x_{i}, y_{i}\\right)$ is said to be reachable. For each $k$, find $L(k)$, the number of reachable cells.\n\nAnswer: $L(k)=\\left\\{\\begin{array}{ll}100^{2}-(2 k-100)^{2} & \\text { if } k \\text { is even } \\\\ \\frac{100^{2}-(2 k-100)^{2}}{2} & \\text { if } k \\text { is odd }\\end{array}\\right.$.", "solution": "Cell $(x, y)$ is directly reachable from another cell if and only if $x-k \\geq 1$ or $x+k \\leq 100$ or $y-k \\geq 1$ or $y+k \\leq 100$, that is, $x \\geq k+1$ or $x \\leq 100-k$ or $y \\geq k+1$ or $y \\leq 100-k(*)$. Therefore the cells $(x, y)$ for which $101-k \\leq x \\leq k$ and $101-k \\leq y \\leq k$ are unreachable. Let $S$ be this set of unreachable cells in this square, namely the square of cells $(x, y), 101-k \\leq x, y \\leq k$. If condition $(*)$ is valid for both $(x, y)$ and $(x \\pm 2, y \\pm 2)$ then one can move from $(x, y)$ to $(x \\pm 2, y \\pm 2)$, if they are both in the table, with two moves: either $x \\leq 50$ or $x \\geq 51$; the same is true for $y$. In the first case, move $(x, y) \\rightarrow(x+k, y \\pm 1) \\rightarrow(x, y \\pm 2)$ or $(x, y) \\rightarrow$ $(x \\pm 1, y+k) \\rightarrow(x \\pm 2, y)$. In the second case, move $(x, y) \\rightarrow(x-k, y \\pm 1) \\rightarrow(x, y \\pm 2)$ or $(x, y) \\rightarrow(x \\pm 1, y-k) \\rightarrow(x \\pm 2, y)$.\nHence if the table is colored in two colors like a chessboard, if $k \\leq 50$, cells with the same color as $(1,1)$ are reachable. Moreover, if $k$ is even, every other move changes the color of the occupied cell, and all cells are potentially reachable; otherwise, only cells with the same color as $(1,1)$ can be visited. Therefore, if $k$ is even then the reachable cells consists of all cells except the center square defined by $101-k \\leq x \\leq k$ and $101-k \\leq y \\leq k$, that is, $L(k)=100^{2}-(2 k-100)^{2}$; if $k$ is odd, then only half of the cells are reachable: the ones with the same color as $(1,1)$, and $L(k)=\\frac{1}{2}\\left(100^{2}-(2 k-100)^{2}\\right)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 5 |
-
{"year": "2024", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be a positive integer and $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers. Prove that\n\n$$\n\\sum_{i=1}^{n} \\frac{1}{2^{i}}\\left(\\frac{2}{1+a_{i}}\\right)^{2^{i}} \\geq \\frac{2}{1+a_{1} a_{2} \\ldots a_{n}}-\\frac{1}{2^{n}}\n$$", "solution": "We first prove the following lemma:\nLemma 1. For $k$ positive integer and $x, y>0$,\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq 2\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n$$\n\nThe proof goes by induction. For $k=1$, we have\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2}+\\left(\\frac{2}{1+y}\\right)^{2} \\geq 2\\left(\\frac{2}{1+x y}\\right)\n$$\n\nwhich reduces to\n\n$$\nx y(x-y)^{2}+(x y-1)^{2} \\geq 0 .\n$$\n\nFor $k>1$, by the inequality $2\\left(A^{2}+B^{2}\\right) \\geq(A+B)^{2}$ applied at $A=\\left(\\frac{2}{1+x}\\right)^{2^{k-1}}$ and $B=\\left(\\frac{2}{1+y}\\right)^{2^{k-1}}$ followed by the induction hypothesis\n\n$$\n\\begin{aligned}\n2\\left(\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}}\\right) & \\geq\\left(\\left(\\frac{2}{1+x}\\right)^{2^{k-1}}+\\left(\\frac{2}{1+y}\\right)^{2^{k-1}}\\right)^{2} \\\\\n& \\geq\\left(2\\left(\\frac{2}{1+x y}\\right)^{2^{k-2}}\\right)^{2}=4\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n\\end{aligned}\n$$\n\nfrom which the lemma follows.\nThe problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:\n\n$$\n\\begin{aligned}\n\\frac{1}{2^{n}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+1}\\right)^{2^{n}} & \\geq \\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n} \\cdot 1}\\right)^{2^{n-1}} \\\\\n\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n-1}}\\right)^{2^{n-1}}+\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n-1}} & \\geq \\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-1} a_{n}}\\right)^{2^{n-2}} \\\\\n\\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-2}}\\right)^{2^{n-2}}+\\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-1} a_{n}}\\right)^{2^{n-2}} & \\geq \\frac{1}{2^{n-3}}\\left(\\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\\right)^{2^{n-3}} \\\\\n\\ldots & )^{2^{k}} \\\\\n\\frac{1}{2^{k}}\\left(\\frac{2}{1+a_{k}}\\right)^{2^{k}}+\\frac{1}{2^{k}}\\left(\\frac{2}{1+a_{k+1} \\ldots a_{n-1} a_{n}}\\right)^{2^{k-1}} & \\geq \\frac{1}{2^{k-1}}\\left(\\frac{2}{1+a_{k} \\ldots a_{n-2} a_{n-1} a_{n}}\\right)^{2} \\\\\n\\frac{1}{2}\\left(\\frac{2}{1+a_{1}}\\right)^{2}+\\frac{1}{2}\\left(\\frac{2}{1+a_{2} \\ldots a_{n-1} a_{n}}\\right)^{2} & \\geq \\frac{2}{1+a_{1} \\ldots a_{n-2} a_{n-1} a_{n}}\n\\end{aligned}\n$$\n\nComment: Equality occurs if and only if $a_{1}=a_{2}=\\cdots=a_{n}=1$.\n\nComment: The main motivation for the lemma is trying to \"telescope\" the sum\n\n$$\n\\frac{1}{2^{n}}+\\sum_{i=1}^{n} \\frac{1}{2^{i}}\\left(\\frac{2}{1+a_{i}}\\right)^{2^{i}}\n$$\n\nthat is,\n\n$$\n\\frac{1}{2}\\left(\\frac{2}{1+a_{1}}\\right)^{2}+\\cdots+\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n-1}}\\right)^{2^{n-1}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+1}\\right)^{2^{n}}\n$$\n\nto obtain an expression larger than or equal to\n\n$$\n\\frac{2}{1+a_{1} a_{2} \\ldots a_{n}}\n$$\n\nIt seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:\n\n$$\n\\frac{1}{2^{k}}\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\frac{1}{2^{k}}\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq \\frac{1}{2^{k-1}}\\left(\\frac{2}{1+x y}\\right)^{2^{i-1}}\n$$\n\nor\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq 2\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 6 |
-
{"year": "2024", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Prove that for every positive integer $t$ there is a unique permutation $a_{0}, a_{1}, \\ldots, a_{t-1}$ of $0,1, \\ldots, t-$ 1 such that, for every $0 \\leq i \\leq t-1$, the binomial coefficient $\\binom{t+i}{2 a_{i}}$ is odd and $2 a_{i} \\neq t+i$.", "solution": "We constantly make use of Kummer's theorem which, in particular, implies that $\\binom{n}{k}$ is odd if and only if $k$ and $n-k$ have ones in different positions in binary. In other words, if $S(x)$ is the set of positions of the digits 1 of $x$ in binary (in which the digit multiplied by $2^{i}$ is in position $i),\\binom{n}{k}$ is odd if and only if $S(k) \\subseteq S(n)$. Moreover, if we set $k<n, S(k)$ is a proper subset of $S(n)$, that is, $|S(k)|<|S(n)|$.\nWe start with a lemma that guides us how the permutation should be set.\n\n## Lemma 1.\n\n$$\n\\sum_{i=0}^{t-1}|S(t+i)|=t+\\sum_{i=0}^{t-1}|S(2 i)|\n$$\n\nThe proof is just realizing that $S(2 i)=\\{1+x, x \\in S(i)\\}$ and $S(2 i+1)=\\{0\\} \\cup\\{1+x, x \\in S(i)\\}$, because $2 i$ in binary is $i$ followed by a zero and $2 i+1$ in binary is $i$ followed by a one. Therefore\n\n$$\n\\begin{aligned}\n\\sum_{i=0}^{t-1}|S(t+i)| & =\\sum_{i=0}^{2 t-1}|S(i)|-\\sum_{i=0}^{t-1}|S(i)|=\\sum_{i=0}^{t-1}|S(2 i)|+\\sum_{i=0}^{t-1}|S(2 i+1)|-\\sum_{i=0}^{t-1}|S(i)| \\\\\n& =\\sum_{i=0}^{t-1}|S(i)|+\\sum_{i=0}^{t-1}(1+|S(i)|)-\\sum_{i=0}^{t-1}|S(i)|=t+\\sum_{i=0}^{t-1}|S(i)|=t+\\sum_{i=0}^{t-1}|S(2 i)|\n\\end{aligned}\n$$\n\nThe lemma has an immediate corollary: since $t+i>2 a_{i}$ and $\\binom{t+i}{2 a_{i}}$ is odd for all $i, 0 \\leq i \\leq t-1$, $S\\left(2 a_{i}\\right) \\subset S(t+i)$ with $\\left|S\\left(2 a_{i}\\right)\\right| \\leq|S(t+i)|-1$. Since the sum of $\\left|S\\left(2 a_{i}\\right)\\right|$ is $t$ less than the sum of $|S(t+i)|$, and there are $t$ values of $i$, equality must occur, that is, $\\left|S\\left(2 a_{i}\\right)\\right|=|S(t+i)|-1$, which in conjunction with $S\\left(2 a_{i}\\right) \\subset S(t+i)$ means that $t+i-2 a_{i}=2^{k_{i}}$ for every $i, 0 \\leq i \\leq t-1$, $k_{i} \\in S(t+i)$ (more precisely, $\\left\\{k_{i}\\right\\}=S(t+i) \\backslash S\\left(2 a_{i}\\right)$.)\nIn particular, for $t+i$ odd, this means that $t+i-2 a_{i}=1$, because the only odd power of 2 is 1. Then $a_{i}=\\frac{t+i-1}{2}$ for $t+i$ odd, which takes up all the numbers greater than or equal to $\\frac{t-1}{2}$. Now we need to distribute the numbers that are smaller than $\\frac{t-1}{2}$ (call these numbers small). If $t+i$ is even then by Lucas' Theorem $\\binom{t+i}{2 a_{i}} \\equiv\\binom{\\frac{t+i}{2}}{a_{i}}(\\bmod 2)$, so we pair numbers from $\\lceil t / 2\\rceil$ to $t-1$ (call these numbers big) with the small numbers.\nSay that a set $A$ is paired with another set $B$ whenever $|A|=|B|$ and there exists a bijection $\\pi: A \\rightarrow B$ such that $S(a) \\subset S(\\pi(a))$ and $|S(a)|=|S(\\pi(a))|-1$; we also say that $a$ and $\\pi(a)$ are paired. We prove by induction in $t$ that $A_{t}=\\{0,1,2, \\ldots,\\lfloor t / 2\\rfloor-1\\}$ (the set of small numbers) and $B_{t}=\\{\\lceil t / 2\\rceil, \\ldots, t-2, t-1\\}$ (the set of big numbers) can be uniquely paired.\nThe claim is immediate for $t=1$ and $t=2$. For $t>2$, there is exactly one power of two in $B_{t}$, since $t / 2 \\leq 2^{a}<t \\Longleftrightarrow a=\\left\\lceil\\log _{2}(t / 2)\\right\\rceil$. Let $2^{a}$ be this power of two. Then, since $2^{a} \\geq t / 2$, no number in $A_{t}$ has a one in position $a$ in binary. Since for every number $x, 2^{a} \\leq x<t, a \\in S(x)$ and $a \\notin S(y)$ for all $y \\in A_{t}, x$ can only be paired with $x-2^{a}$, since $S(x)$ needs to be stripped of exactly one position. This takes cares of $x \\in B_{t}, 2^{a} \\leq x<t$, and $y \\in A_{t}, 0 \\leq y<t-2^{a}$.\nNow we need to pair the numbers from $A^{\\prime}=\\left\\{t-2^{a}, t-2^{a}+1, \\ldots,\\lfloor t / 2\\rfloor-1\\right\\} \\subset A$ with the numbers from $B^{\\prime}=\\left\\{\\lceil t / 2\\rceil,\\lceil t / 2\\rceil+1, \\ldots, 2^{a}-1\\right\\} \\subset B$. In order to pair these $t-2\\left(t-2^{a}\\right)=$ $2^{a+1}-t<t$ numbers, we use the induction hypothesis and a bijection between $A^{\\prime} \\cup B^{\\prime}$ and $B_{2^{a+1}-t} \\cup A_{2^{a+1}-t}$. Let $S=S\\left(2^{a}-1\\right)=\\{0,1,2, \\ldots, a-1\\}$. Then take a pair $x, y, x \\in A_{2^{a+1}-t}$ and $y \\in B_{2^{a+1}-t}$ and biject it with $2^{a}-1-x \\in B^{\\prime}$ and $2^{a}-1-y \\in A^{\\prime}$. In fact,\n\n$$\n0 \\leq x \\leq\\left\\lfloor\\frac{2^{a+1}-t}{2}\\right\\rfloor-1=2^{a}-\\left\\lceil\\frac{t}{2}\\right\\rceil-1 \\Longleftrightarrow\\left\\lceil\\frac{t}{2}\\right\\rceil \\leq 2^{a}-1-x \\leq 2^{a}-1\n$$\n\nand\n\n$$\n\\left\\lceil\\frac{2^{a+1}-t}{2}\\right\\rceil=2^{a}-\\left\\lfloor\\frac{t}{2}\\right\\rfloor \\leq y \\leq 2^{a+1}-t-1 \\Longleftrightarrow t-2^{a} \\leq 2^{a}-1-y \\leq\\left\\lfloor\\frac{t}{2}\\right\\rfloor-1\n$$\n\nMoreover, $S\\left(2^{a}-1-x\\right)=S \\backslash S(x)$ and $S\\left(2^{a}-1-y\\right)=S \\backslash S(y)$ are complements with respect to $S$, and $S(x) \\subset S(y)$ and $|S(x)|=|S(y)|-1$ implies $S\\left(2^{a}-1-y\\right) \\subset S\\left(2^{a}-1-x\\right)$ and $\\left|S\\left(2^{a}-1-y\\right)\\right|=\\left|S\\left(2^{a}-1-x\\right)\\right|-1$. Therefore a pairing between $A^{\\prime}$ and $B^{\\prime}$ corresponds to a pairing between $A_{2^{a+1}-t}$ and $B_{2^{a+1}-t}$. Since the latter pairing is unique, the former pairing is also unique, and the result follows.\nWe illustrate the bijection by showing the case $t=23$ :\n\n$$\nA_{23}=\\{0,1,2, \\ldots, 10\\}, \\quad B_{23}=\\{12,13,14, \\ldots, 22\\}\n$$\n\nThe pairing is\n\n$$\n\\left(\\begin{array}{ccccccccccc}\n12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\\\\n8 & 9 & 10 & 7 & 0 & 1 & 2 & 3 & 4 & 5 & 6\n\\end{array}\\right)\n$$\n\nin which the bijection is between\n\n$$\n\\left(\\begin{array}{cccc}\n12 & 13 & 14 & 15 \\\\\n8 & 9 & 10 & 7\n\\end{array}\\right) \\quad \\text { and } \\quad\\left(\\begin{array}{llll}\n3 & 2 & 1 & 0 \\\\\n7 & 6 & 5 & 8\n\\end{array}\\right) \\rightarrow\\left(\\begin{array}{llll}\n5 & 6 & 7 & 8 \\\\\n1 & 2 & 3 & 0\n\\end{array}\\right) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 7 |
-
{"year": "2024", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Line $\\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \\neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \\neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.", "solution": "We start with the following lemma.\nLemma 1. Points $M, N, P, Q$ are concyclic.\nPoint $M$ is the Miquel point of lines $A P=A B, P S=\\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \\ell$, and $B C$, which is $L R S$.\nThen, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\\circ}$ )\n\n$$\n\\begin{aligned}\n\\measuredangle N M P & =\\measuredangle N M S+\\measuredangle S M P=\\measuredangle N R S+\\measuredangle S A P=\\measuredangle N R Q+\\measuredangle D A B=\\measuredangle N R Q+\\measuredangle D C B \\\\\n& =\\measuredangle N R Q+\\measuredangle Q C R=\\measuredangle N R Q+\\measuredangle Q N R=\\measuredangle N Q R=\\measuredangle N Q P,\n\\end{aligned}\n$$\n\nwhich implies that $M N Q P$ is a cyclic quadrilateral.\n\n\nLet $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \\neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,\n\n$$\n\\measuredangle T E M=\\measuredangle L E M=\\measuredangle L A M=\\measuredangle S A M=\\measuredangle S P M=\\measuredangle Q P M=\\measuredangle Q N M=\\measuredangle T N M,\n$$\n\nthat is, $T$ lies in the circumcircle $\\omega$ of $E M N$. If $T=E$, the same computation shows that $\\measuredangle L E M=\\measuredangle E N M$, which means that $t$ is tangent to $\\omega$.\n\nNow let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\\omega$ as well, and that if $V=E$ then $t$ is tangent to $\\omega$.\nTherefore, since $\\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \\neq E$ and $V \\neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 8 |
-
{"year": "2024", "tier": "T1", "problem_label": "5", "problem_type": null, "problem": "Line $\\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \\neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \\neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.", "solution": "Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.\n\nLemma 2. Denote by $\\operatorname{pow}_{\\omega} X$ the power of point $X$ with respect to circle $\\omega$. Let $\\Gamma_{1}$ and $\\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\\Gamma_{1}$ and $\\Gamma_{2}$ is given by\n\n$$\n\\left(\\operatorname{pow}_{\\Gamma_{1}} A-\\operatorname{pow}_{\\Gamma_{2}} A\\right) x+\\left(\\operatorname{pow}_{\\Gamma_{1}} B-\\operatorname{pow}_{\\Gamma_{2}} B\\right) y+\\left(\\operatorname{pow}_{\\Gamma_{1}} C-\\operatorname{pow}_{\\Gamma_{2}} C\\right) z=0\n$$\n\nProof: Let $\\Gamma_{i}$ have the equation $\\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\\left(r_{i} x+s_{i} y+t_{i} z\\right)$. Then $\\operatorname{pow}_{\\Gamma_{i}} P=\\Gamma_{i}(P)$. In particular, $\\operatorname{pow}_{\\Gamma_{i}} A=\\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\\operatorname{pow}_{\\Gamma_{i}} B=s_{i}$ and $\\operatorname{pow}_{\\Gamma_{i}} C=t_{i}$.\nFinally, the radical axis is\n\n$$\n\\begin{aligned}\n& \\operatorname{pow}_{\\Gamma_{1}} P=\\operatorname{pow}_{\\Gamma_{2}} P \\\\\n\\Longleftrightarrow & \\Gamma_{1}(x, y, z)=\\Gamma_{2}(x, y, z) \\\\\n\\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\\\\n\\Longleftrightarrow & \\left(\\operatorname{pow}_{\\Gamma_{1}} A-\\operatorname{pow}_{\\Gamma_{2}} A\\right) x+\\left(\\operatorname{pow}_{\\Gamma_{1}} B-\\operatorname{pow}_{\\Gamma_{2}} B\\right) y+\\left(\\operatorname{pow}_{\\Gamma_{1}} C-\\operatorname{pow}_{\\Gamma_{2}} C\\right) z=0 .\n\\end{aligned}\n$$\n\nWe still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :\n\n- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;\n- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;\n- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.\n\nLooking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.\n\n\nAssociate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are\n\n- MP: $(K A \\cdot K P-K B \\cdot K P) x+(Q S \\cdot Q P-Q R \\cdot Q P) y=0$\n- $N Q:(K C \\cdot K Q-K D \\cdot K Q) x+(P R \\cdot P Q-P S \\cdot P Q) z=0$\n- MP: $(-Q C \\cdot Q K+Q D \\cdot Q K) y+(P B \\cdot P K-P A \\cdot P K) z=0$\n\nThese equations simplify to\n\n- $M P:(A B \\cdot K P) x+(P Q \\cdot R S) y=0$\n- $N Q:(-C D \\cdot K Q) x+(P Q \\cdot R S) z=0$\n- $M P:(C D \\cdot K Q) y+(A B \\cdot K P) z=0$\n\nNow, if $u=A B \\cdot K P, v=P Q \\cdot R S$, and $w=C D \\cdot K Q$, it suffices to show that\n\n$$\n\\left|\\begin{array}{ccc}\nu & v & 0 \\\\\n-w & 0 & v \\\\\n0 & w & u\n\\end{array}\\right|=0\n$$\n\nwhich is a straightforward computation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
|
|
|
| 1 |
+
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "\n\nLet $\\ell$ be the radical axis of circles $B Q X$ and $C P X$. Since $X$ and $Y$ are on $\\ell$, it is sufficient to show that $A$ is on $\\ell$. Let line $A X$ intersect segments $B C$ and $D E$ at $Z$ and $Z^{\\prime}$, respectively. Then it is sufficient to show that $Z$ is on $\\ell$. By $B C \\| D E$, we obtain\n\n$$\n\\frac{B Z}{Z C}=\\frac{D Z^{\\prime}}{Z^{\\prime} E}=\\frac{P Z}{Z Q},\n$$\n\nthus $B Z \\cdot Q Z=C Z \\cdot P Z$, which implies that $Z$ is on $\\ell$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 1"}}
|
| 2 |
+
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "\n\nLet circle $B Q X$ intersect line $A B$ at a point $S$ which is different from $B$. Then $\\angle D E X=$ $\\angle X Q C=\\angle B S X$, thus $S$ is on circle $D E X$. Similarly, let circle $C P X$ intersect line $A C$ at a point $T$ which is different from $C$. Then $T$ is on circle $D E X$. The power of $A$ with respect to the circle $D E X$ is $A S \\cdot A D=A T \\cdot A E$. Since $\\frac{A D}{A B}=\\frac{A E}{A C}, A S \\cdot A B=A T \\cdot A C$. Then $A$ is in the radical axis of circles $B Q X$ and $C P X$, which implies that three points $A, X$ and $Y$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 2"}}
|
| 3 |
+
{"year": "2024", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "APMO", "problem": "Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \\neq X$. Prove that points $A, X$, and $Y$ are collinear.", "solution": "Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.\n\n\nThe homothety implies that $A, Y$, and $Y^{\\prime}$ are collinear, and that $\\angle D Y^{\\prime} E=\\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,\n$\\angle D Y^{\\prime} E=\\angle B Y C=\\angle B Y X+\\angle X Y C=\\angle X Q P+\\angle X P Q=180^{\\circ}-\\angle P X Q=180^{\\circ}-\\angle D X E$,\nwhich implies that $D Y^{\\prime} E X$ is cyclic. Therefore\n\n$$\n\\angle D Y^{\\prime} X=\\angle D E X=\\angle P Q X=\\angle B Y X\n$$\n\nwhich, combined with $D Y^{\\prime} \\| B Y$, implies $Y^{\\prime} X \\| Y X$. This proves that $X, Y$, and $Y^{\\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution 3"}}
|
| 4 |
+
{"year": "2024", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "APMO", "problem": "Consider a $100 \\times 100$ table, and identify the cell in row $a$ and column $b, 1 \\leq a, b \\leq 100$, with the ordered pair $(a, b)$. Let $k$ be an integer such that $51 \\leq k \\leq 99$. A $k$-knight is a piece that moves one cell vertically or horizontally and $k$ cells to the other direction; that is, it moves from $(a, b)$ to $(c, d)$ such that $(|a-c|,|b-d|)$ is either $(1, k)$ or $(k, 1)$. The $k$-knight starts at cell $(1,1)$, and performs several moves. A sequence of moves is a sequence of cells $\\left(x_{0}, y_{0}\\right)=(1,1)$, $\\left(x_{1}, y_{1}\\right),\\left(x_{2}, y_{2}\\right), \\ldots,\\left(x_{n}, y_{n}\\right)$ such that, for all $i=1,2, \\ldots, n, 1 \\leq x_{i}, y_{i} \\leq 100$ and the $k$-knight can move from $\\left(x_{i-1}, y_{i-1}\\right)$ to $\\left(x_{i}, y_{i}\\right)$. In this case, each cell $\\left(x_{i}, y_{i}\\right)$ is said to be reachable. For each $k$, find $L(k)$, the number of reachable cells.\n\nAnswer: $L(k)=\\left\\{\\begin{array}{ll}100^{2}-(2 k-100)^{2} & \\text { if } k \\text { is even } \\\\ \\frac{100^{2}-(2 k-100)^{2}}{2} & \\text { if } k \\text { is odd }\\end{array}\\right.$.", "solution": "Cell $(x, y)$ is directly reachable from another cell if and only if $x-k \\geq 1$ or $x+k \\leq 100$ or $y-k \\geq 1$ or $y+k \\leq 100$, that is, $x \\geq k+1$ or $x \\leq 100-k$ or $y \\geq k+1$ or $y \\leq 100-k(*)$. Therefore the cells $(x, y)$ for which $101-k \\leq x \\leq k$ and $101-k \\leq y \\leq k$ are unreachable. Let $S$ be this set of unreachable cells in this square, namely the square of cells $(x, y), 101-k \\leq x, y \\leq k$. If condition $(*)$ is valid for both $(x, y)$ and $(x \\pm 2, y \\pm 2)$ then one can move from $(x, y)$ to $(x \\pm 2, y \\pm 2)$, if they are both in the table, with two moves: either $x \\leq 50$ or $x \\geq 51$; the same is true for $y$. In the first case, move $(x, y) \\rightarrow(x+k, y \\pm 1) \\rightarrow(x, y \\pm 2)$ or $(x, y) \\rightarrow$ $(x \\pm 1, y+k) \\rightarrow(x \\pm 2, y)$. In the second case, move $(x, y) \\rightarrow(x-k, y \\pm 1) \\rightarrow(x, y \\pm 2)$ or $(x, y) \\rightarrow(x \\pm 1, y-k) \\rightarrow(x \\pm 2, y)$.\nHence if the table is colored in two colors like a chessboard, if $k \\leq 50$, cells with the same color as $(1,1)$ are reachable. Moreover, if $k$ is even, every other move changes the color of the occupied cell, and all cells are potentially reachable; otherwise, only cells with the same color as $(1,1)$ can be visited. Therefore, if $k$ is even then the reachable cells consists of all cells except the center square defined by $101-k \\leq x \\leq k$ and $101-k \\leq y \\leq k$, that is, $L(k)=100^{2}-(2 k-100)^{2}$; if $k$ is odd, then only half of the cells are reachable: the ones with the same color as $(1,1)$, and $L(k)=\\frac{1}{2}\\left(100^{2}-(2 k-100)^{2}\\right)$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution\n\n"}}
|
| 5 |
+
{"year": "2024", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "APMO", "problem": "Let $n$ be a positive integer and $a_{1}, a_{2}, \\ldots, a_{n}$ be positive real numbers. Prove that\n\n$$\n\\sum_{i=1}^{n} \\frac{1}{2^{i}}\\left(\\frac{2}{1+a_{i}}\\right)^{2^{i}} \\geq \\frac{2}{1+a_{1} a_{2} \\ldots a_{n}}-\\frac{1}{2^{n}}\n$$", "solution": "We first prove the following lemma:\nLemma 1. For $k$ positive integer and $x, y>0$,\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq 2\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n$$\n\nThe proof goes by induction. For $k=1$, we have\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2}+\\left(\\frac{2}{1+y}\\right)^{2} \\geq 2\\left(\\frac{2}{1+x y}\\right)\n$$\n\nwhich reduces to\n\n$$\nx y(x-y)^{2}+(x y-1)^{2} \\geq 0 .\n$$\n\nFor $k>1$, by the inequality $2\\left(A^{2}+B^{2}\\right) \\geq(A+B)^{2}$ applied at $A=\\left(\\frac{2}{1+x}\\right)^{2^{k-1}}$ and $B=\\left(\\frac{2}{1+y}\\right)^{2^{k-1}}$ followed by the induction hypothesis\n\n$$\n\\begin{aligned}\n2\\left(\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}}\\right) & \\geq\\left(\\left(\\frac{2}{1+x}\\right)^{2^{k-1}}+\\left(\\frac{2}{1+y}\\right)^{2^{k-1}}\\right)^{2} \\\\\n& \\geq\\left(2\\left(\\frac{2}{1+x y}\\right)^{2^{k-2}}\\right)^{2}=4\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n\\end{aligned}\n$$\n\nfrom which the lemma follows.\nThe problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:\n\n$$\n\\begin{aligned}\n\\frac{1}{2^{n}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+1}\\right)^{2^{n}} & \\geq \\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n} \\cdot 1}\\right)^{2^{n-1}} \\\\\n\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n-1}}\\right)^{2^{n-1}}+\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n-1}} & \\geq \\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-1} a_{n}}\\right)^{2^{n-2}} \\\\\n\\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-2}}\\right)^{2^{n-2}}+\\frac{1}{2^{n-2}}\\left(\\frac{2}{1+a_{n-1} a_{n}}\\right)^{2^{n-2}} & \\geq \\frac{1}{2^{n-3}}\\left(\\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\\right)^{2^{n-3}} \\\\\n\\ldots & )^{2^{k}} \\\\\n\\frac{1}{2^{k}}\\left(\\frac{2}{1+a_{k}}\\right)^{2^{k}}+\\frac{1}{2^{k}}\\left(\\frac{2}{1+a_{k+1} \\ldots a_{n-1} a_{n}}\\right)^{2^{k-1}} & \\geq \\frac{1}{2^{k-1}}\\left(\\frac{2}{1+a_{k} \\ldots a_{n-2} a_{n-1} a_{n}}\\right)^{2} \\\\\n\\frac{1}{2}\\left(\\frac{2}{1+a_{1}}\\right)^{2}+\\frac{1}{2}\\left(\\frac{2}{1+a_{2} \\ldots a_{n-1} a_{n}}\\right)^{2} & \\geq \\frac{2}{1+a_{1} \\ldots a_{n-2} a_{n-1} a_{n}}\n\\end{aligned}\n$$\n\nComment: Equality occurs if and only if $a_{1}=a_{2}=\\cdots=a_{n}=1$.\n\nComment: The main motivation for the lemma is trying to \"telescope\" the sum\n\n$$\n\\frac{1}{2^{n}}+\\sum_{i=1}^{n} \\frac{1}{2^{i}}\\left(\\frac{2}{1+a_{i}}\\right)^{2^{i}}\n$$\n\nthat is,\n\n$$\n\\frac{1}{2}\\left(\\frac{2}{1+a_{1}}\\right)^{2}+\\cdots+\\frac{1}{2^{n-1}}\\left(\\frac{2}{1+a_{n-1}}\\right)^{2^{n-1}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+a_{n}}\\right)^{2^{n}}+\\frac{1}{2^{n}}\\left(\\frac{2}{1+1}\\right)^{2^{n}}\n$$\n\nto obtain an expression larger than or equal to\n\n$$\n\\frac{2}{1+a_{1} a_{2} \\ldots a_{n}}\n$$\n\nIt seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:\n\n$$\n\\frac{1}{2^{k}}\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\frac{1}{2^{k}}\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq \\frac{1}{2^{k-1}}\\left(\\frac{2}{1+x y}\\right)^{2^{i-1}}\n$$\n\nor\n\n$$\n\\left(\\frac{2}{1+x}\\right)^{2^{k}}+\\left(\\frac{2}{1+y}\\right)^{2^{k}} \\geq 2\\left(\\frac{2}{1+x y}\\right)^{2^{k-1}}\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution\n\n"}}
|
| 6 |
+
{"year": "2024", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "APMO", "problem": "Prove that for every positive integer $t$ there is a unique permutation $a_{0}, a_{1}, \\ldots, a_{t-1}$ of $0,1, \\ldots, t-$ 1 such that, for every $0 \\leq i \\leq t-1$, the binomial coefficient $\\binom{t+i}{2 a_{i}}$ is odd and $2 a_{i} \\neq t+i$.", "solution": "We constantly make use of Kummer's theorem which, in particular, implies that $\\binom{n}{k}$ is odd if and only if $k$ and $n-k$ have ones in different positions in binary. In other words, if $S(x)$ is the set of positions of the digits 1 of $x$ in binary (in which the digit multiplied by $2^{i}$ is in position $i),\\binom{n}{k}$ is odd if and only if $S(k) \\subseteq S(n)$. Moreover, if we set $k<n, S(k)$ is a proper subset of $S(n)$, that is, $|S(k)|<|S(n)|$.\nWe start with a lemma that guides us how the permutation should be set.\n\n## Lemma 1.\n\n$$\n\\sum_{i=0}^{t-1}|S(t+i)|=t+\\sum_{i=0}^{t-1}|S(2 i)|\n$$\n\nThe proof is just realizing that $S(2 i)=\\{1+x, x \\in S(i)\\}$ and $S(2 i+1)=\\{0\\} \\cup\\{1+x, x \\in S(i)\\}$, because $2 i$ in binary is $i$ followed by a zero and $2 i+1$ in binary is $i$ followed by a one. Therefore\n\n$$\n\\begin{aligned}\n\\sum_{i=0}^{t-1}|S(t+i)| & =\\sum_{i=0}^{2 t-1}|S(i)|-\\sum_{i=0}^{t-1}|S(i)|=\\sum_{i=0}^{t-1}|S(2 i)|+\\sum_{i=0}^{t-1}|S(2 i+1)|-\\sum_{i=0}^{t-1}|S(i)| \\\\\n& =\\sum_{i=0}^{t-1}|S(i)|+\\sum_{i=0}^{t-1}(1+|S(i)|)-\\sum_{i=0}^{t-1}|S(i)|=t+\\sum_{i=0}^{t-1}|S(i)|=t+\\sum_{i=0}^{t-1}|S(2 i)|\n\\end{aligned}\n$$\n\nThe lemma has an immediate corollary: since $t+i>2 a_{i}$ and $\\binom{t+i}{2 a_{i}}$ is odd for all $i, 0 \\leq i \\leq t-1$, $S\\left(2 a_{i}\\right) \\subset S(t+i)$ with $\\left|S\\left(2 a_{i}\\right)\\right| \\leq|S(t+i)|-1$. Since the sum of $\\left|S\\left(2 a_{i}\\right)\\right|$ is $t$ less than the sum of $|S(t+i)|$, and there are $t$ values of $i$, equality must occur, that is, $\\left|S\\left(2 a_{i}\\right)\\right|=|S(t+i)|-1$, which in conjunction with $S\\left(2 a_{i}\\right) \\subset S(t+i)$ means that $t+i-2 a_{i}=2^{k_{i}}$ for every $i, 0 \\leq i \\leq t-1$, $k_{i} \\in S(t+i)$ (more precisely, $\\left\\{k_{i}\\right\\}=S(t+i) \\backslash S\\left(2 a_{i}\\right)$.)\nIn particular, for $t+i$ odd, this means that $t+i-2 a_{i}=1$, because the only odd power of 2 is 1. Then $a_{i}=\\frac{t+i-1}{2}$ for $t+i$ odd, which takes up all the numbers greater than or equal to $\\frac{t-1}{2}$. Now we need to distribute the numbers that are smaller than $\\frac{t-1}{2}$ (call these numbers small). If $t+i$ is even then by Lucas' Theorem $\\binom{t+i}{2 a_{i}} \\equiv\\binom{\\frac{t+i}{2}}{a_{i}}(\\bmod 2)$, so we pair numbers from $\\lceil t / 2\\rceil$ to $t-1$ (call these numbers big) with the small numbers.\nSay that a set $A$ is paired with another set $B$ whenever $|A|=|B|$ and there exists a bijection $\\pi: A \\rightarrow B$ such that $S(a) \\subset S(\\pi(a))$ and $|S(a)|=|S(\\pi(a))|-1$; we also say that $a$ and $\\pi(a)$ are paired. We prove by induction in $t$ that $A_{t}=\\{0,1,2, \\ldots,\\lfloor t / 2\\rfloor-1\\}$ (the set of small numbers) and $B_{t}=\\{\\lceil t / 2\\rceil, \\ldots, t-2, t-1\\}$ (the set of big numbers) can be uniquely paired.\nThe claim is immediate for $t=1$ and $t=2$. For $t>2$, there is exactly one power of two in $B_{t}$, since $t / 2 \\leq 2^{a}<t \\Longleftrightarrow a=\\left\\lceil\\log _{2}(t / 2)\\right\\rceil$. Let $2^{a}$ be this power of two. Then, since $2^{a} \\geq t / 2$, no number in $A_{t}$ has a one in position $a$ in binary. Since for every number $x, 2^{a} \\leq x<t, a \\in S(x)$ and $a \\notin S(y)$ for all $y \\in A_{t}, x$ can only be paired with $x-2^{a}$, since $S(x)$ needs to be stripped of exactly one position. This takes cares of $x \\in B_{t}, 2^{a} \\leq x<t$, and $y \\in A_{t}, 0 \\leq y<t-2^{a}$.\nNow we need to pair the numbers from $A^{\\prime}=\\left\\{t-2^{a}, t-2^{a}+1, \\ldots,\\lfloor t / 2\\rfloor-1\\right\\} \\subset A$ with the numbers from $B^{\\prime}=\\left\\{\\lceil t / 2\\rceil,\\lceil t / 2\\rceil+1, \\ldots, 2^{a}-1\\right\\} \\subset B$. In order to pair these $t-2\\left(t-2^{a}\\right)=$ $2^{a+1}-t<t$ numbers, we use the induction hypothesis and a bijection between $A^{\\prime} \\cup B^{\\prime}$ and $B_{2^{a+1}-t} \\cup A_{2^{a+1}-t}$. Let $S=S\\left(2^{a}-1\\right)=\\{0,1,2, \\ldots, a-1\\}$. Then take a pair $x, y, x \\in A_{2^{a+1}-t}$ and $y \\in B_{2^{a+1}-t}$ and biject it with $2^{a}-1-x \\in B^{\\prime}$ and $2^{a}-1-y \\in A^{\\prime}$. In fact,\n\n$$\n0 \\leq x \\leq\\left\\lfloor\\frac{2^{a+1}-t}{2}\\right\\rfloor-1=2^{a}-\\left\\lceil\\frac{t}{2}\\right\\rceil-1 \\Longleftrightarrow\\left\\lceil\\frac{t}{2}\\right\\rceil \\leq 2^{a}-1-x \\leq 2^{a}-1\n$$\n\nand\n\n$$\n\\left\\lceil\\frac{2^{a+1}-t}{2}\\right\\rceil=2^{a}-\\left\\lfloor\\frac{t}{2}\\right\\rfloor \\leq y \\leq 2^{a+1}-t-1 \\Longleftrightarrow t-2^{a} \\leq 2^{a}-1-y \\leq\\left\\lfloor\\frac{t}{2}\\right\\rfloor-1\n$$\n\nMoreover, $S\\left(2^{a}-1-x\\right)=S \\backslash S(x)$ and $S\\left(2^{a}-1-y\\right)=S \\backslash S(y)$ are complements with respect to $S$, and $S(x) \\subset S(y)$ and $|S(x)|=|S(y)|-1$ implies $S\\left(2^{a}-1-y\\right) \\subset S\\left(2^{a}-1-x\\right)$ and $\\left|S\\left(2^{a}-1-y\\right)\\right|=\\left|S\\left(2^{a}-1-x\\right)\\right|-1$. Therefore a pairing between $A^{\\prime}$ and $B^{\\prime}$ corresponds to a pairing between $A_{2^{a+1}-t}$ and $B_{2^{a+1}-t}$. Since the latter pairing is unique, the former pairing is also unique, and the result follows.\nWe illustrate the bijection by showing the case $t=23$ :\n\n$$\nA_{23}=\\{0,1,2, \\ldots, 10\\}, \\quad B_{23}=\\{12,13,14, \\ldots, 22\\}\n$$\n\nThe pairing is\n\n$$\n\\left(\\begin{array}{ccccccccccc}\n12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\\\\n8 & 9 & 10 & 7 & 0 & 1 & 2 & 3 & 4 & 5 & 6\n\\end{array}\\right)\n$$\n\nin which the bijection is between\n\n$$\n\\left(\\begin{array}{cccc}\n12 & 13 & 14 & 15 \\\\\n8 & 9 & 10 & 7\n\\end{array}\\right) \\quad \\text { and } \\quad\\left(\\begin{array}{llll}\n3 & 2 & 1 & 0 \\\\\n7 & 6 & 5 & 8\n\\end{array}\\right) \\rightarrow\\left(\\begin{array}{llll}\n5 & 6 & 7 & 8 \\\\\n1 & 2 & 3 & 0\n\\end{array}\\right) .\n$$", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution\n\n"}}
|
| 7 |
+
{"year": "2024", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Line $\\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \\neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \\neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.", "solution": "We start with the following lemma.\nLemma 1. Points $M, N, P, Q$ are concyclic.\nPoint $M$ is the Miquel point of lines $A P=A B, P S=\\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \\ell$, and $B C$, which is $L R S$.\nThen, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\\circ}$ )\n\n$$\n\\begin{aligned}\n\\measuredangle N M P & =\\measuredangle N M S+\\measuredangle S M P=\\measuredangle N R S+\\measuredangle S A P=\\measuredangle N R Q+\\measuredangle D A B=\\measuredangle N R Q+\\measuredangle D C B \\\\\n& =\\measuredangle N R Q+\\measuredangle Q C R=\\measuredangle N R Q+\\measuredangle Q N R=\\measuredangle N Q R=\\measuredangle N Q P,\n\\end{aligned}\n$$\n\nwhich implies that $M N Q P$ is a cyclic quadrilateral.\n\n\nLet $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \\neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,\n\n$$\n\\measuredangle T E M=\\measuredangle L E M=\\measuredangle L A M=\\measuredangle S A M=\\measuredangle S P M=\\measuredangle Q P M=\\measuredangle Q N M=\\measuredangle T N M,\n$$\n\nthat is, $T$ lies in the circumcircle $\\omega$ of $E M N$. If $T=E$, the same computation shows that $\\measuredangle L E M=\\measuredangle E N M$, which means that $t$ is tangent to $\\omega$.\n\nNow let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\\omega$ as well, and that if $V=E$ then $t$ is tangent to $\\omega$.\nTherefore, since $\\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \\neq E$ and $V \\neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 1"}}
|
| 8 |
+
{"year": "2024", "tier": "T1", "problem_label": "5", "problem_type": null, "exam": "APMO", "problem": "Line $\\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \\neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \\neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.", "solution": "Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.\n\nLemma 2. Denote by $\\operatorname{pow}_{\\omega} X$ the power of point $X$ with respect to circle $\\omega$. Let $\\Gamma_{1}$ and $\\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\\Gamma_{1}$ and $\\Gamma_{2}$ is given by\n\n$$\n\\left(\\operatorname{pow}_{\\Gamma_{1}} A-\\operatorname{pow}_{\\Gamma_{2}} A\\right) x+\\left(\\operatorname{pow}_{\\Gamma_{1}} B-\\operatorname{pow}_{\\Gamma_{2}} B\\right) y+\\left(\\operatorname{pow}_{\\Gamma_{1}} C-\\operatorname{pow}_{\\Gamma_{2}} C\\right) z=0\n$$\n\nProof: Let $\\Gamma_{i}$ have the equation $\\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\\left(r_{i} x+s_{i} y+t_{i} z\\right)$. Then $\\operatorname{pow}_{\\Gamma_{i}} P=\\Gamma_{i}(P)$. In particular, $\\operatorname{pow}_{\\Gamma_{i}} A=\\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\\operatorname{pow}_{\\Gamma_{i}} B=s_{i}$ and $\\operatorname{pow}_{\\Gamma_{i}} C=t_{i}$.\nFinally, the radical axis is\n\n$$\n\\begin{aligned}\n& \\operatorname{pow}_{\\Gamma_{1}} P=\\operatorname{pow}_{\\Gamma_{2}} P \\\\\n\\Longleftrightarrow & \\Gamma_{1}(x, y, z)=\\Gamma_{2}(x, y, z) \\\\\n\\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\\\\n\\Longleftrightarrow & \\left(\\operatorname{pow}_{\\Gamma_{1}} A-\\operatorname{pow}_{\\Gamma_{2}} A\\right) x+\\left(\\operatorname{pow}_{\\Gamma_{1}} B-\\operatorname{pow}_{\\Gamma_{2}} B\\right) y+\\left(\\operatorname{pow}_{\\Gamma_{1}} C-\\operatorname{pow}_{\\Gamma_{2}} C\\right) z=0 .\n\\end{aligned}\n$$\n\nWe still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :\n\n- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;\n- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;\n- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.\n\nLooking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.\n\n\nAssociate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are\n\n- MP: $(K A \\cdot K P-K B \\cdot K P) x+(Q S \\cdot Q P-Q R \\cdot Q P) y=0$\n- $N Q:(K C \\cdot K Q-K D \\cdot K Q) x+(P R \\cdot P Q-P S \\cdot P Q) z=0$\n- MP: $(-Q C \\cdot Q K+Q D \\cdot Q K) y+(P B \\cdot P K-P A \\cdot P K) z=0$\n\nThese equations simplify to\n\n- $M P:(A B \\cdot K P) x+(P Q \\cdot R S) y=0$\n- $N Q:(-C D \\cdot K Q) x+(P Q \\cdot R S) z=0$\n- $M P:(C D \\cdot K Q) y+(A B \\cdot K P) z=0$\n\nNow, if $u=A B \\cdot K P, v=P Q \\cdot R S$, and $w=C D \\cdot K Q$, it suffices to show that\n\n$$\n\\left|\\begin{array}{ccc}\nu & v & 0 \\\\\n-w & 0 & v \\\\\n0 & w & u\n\\end{array}\\right|=0\n$$\n\nwhich is a straightforward computation.", "metadata": {"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl", "problem_match": "# Problem 5", "solution_match": "# Solution 2"}}
|
Balkan_MO/segment_script/segment_type1 .py
CHANGED
|
@@ -79,6 +79,7 @@ def write_pairs(output_file: Path, pairs):
|
|
| 79 |
'tier': 'T1',
|
| 80 |
'problem_label': problem_label,
|
| 81 |
'problem_type': None,
|
|
|
|
| 82 |
'problem': problem,
|
| 83 |
'solution': solution,
|
| 84 |
'metadata': {
|
|
|
|
| 79 |
'tier': 'T1',
|
| 80 |
'problem_label': problem_label,
|
| 81 |
'problem_type': None,
|
| 82 |
+
'exam': 'Balkan_MO',
|
| 83 |
'problem': problem,
|
| 84 |
'solution': solution,
|
| 85 |
'metadata': {
|
Balkan_MO/segment_script/segment_type2.py
CHANGED
|
@@ -88,6 +88,7 @@ def write_pairs(output_file: Path, pairs):
|
|
| 88 |
'tier': 'T1',
|
| 89 |
'problem_label': problem_label,
|
| 90 |
'problem_type': None,
|
|
|
|
| 91 |
'problem': problem,
|
| 92 |
'solution': solution,
|
| 93 |
'metadata': {
|
|
|
|
| 88 |
'tier': 'T1',
|
| 89 |
'problem_label': problem_label,
|
| 90 |
'problem_type': None,
|
| 91 |
+
'exam': 'Balkan_MO',
|
| 92 |
'problem': problem,
|
| 93 |
'solution': solution,
|
| 94 |
'metadata': {
|
Balkan_MO/segment_script/segment_type3.py
CHANGED
|
@@ -78,6 +78,7 @@ def write_pairs(output_file: Path, pairs):
|
|
| 78 |
'tier': 'T1',
|
| 79 |
'problem_label': problem_label,
|
| 80 |
'problem_type': None,
|
|
|
|
| 81 |
'problem': problem,
|
| 82 |
'solution': solution,
|
| 83 |
'metadata': {
|
|
|
|
| 78 |
'tier': 'T1',
|
| 79 |
'problem_label': problem_label,
|
| 80 |
'problem_type': None,
|
| 81 |
+
'exam': 'Balkan_MO',
|
| 82 |
'problem': problem,
|
| 83 |
'solution': solution,
|
| 84 |
'metadata': {
|
Balkan_MO/segmented/en-2008-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2008", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "An acute-angled scalene triangle $A B C$ is given, with $A C>B C$. Let $O$ be its circumcentre, $H$ its orthocentre, and $F$ the foot of the altitude from $C$. Let $P$ be the point (other than $A$ ) on the line $A B$ such that $A F=P F$, and $M$ be the midpoint of $A C$. We denote the intersection of $P H$ and $B C$ by $X$, the intersection of $O M$ and $F X$ by $Y$, and the intersection of $O F$ and $A C$ by $Z$. Prove that the points $F, M, Y$ and $Z$ are concyclic.", "solution": "It is enough to show that $\\mathrm{O} F \\perp F X$.\nLet $\\mathrm{OE} \\perp \\mathrm{AB}$, then it is trivial that :\n\n$$\nC \\mathrm{H}=2 \\mathrm{OE} .\n$$\n\nSince from the hypothesis we have $\\mathrm{P} F=\\mathrm{A} F$ then we take $\\mathrm{PB}=\\mathrm{P} F-\\mathrm{B} F$ or\n\n$$\n\\mathrm{PB}=\\mathrm{A} F-\\mathrm{B} F\n$$\n\nAlso, $\\angle X P B=\\angle H A P$ and $\\angle H A P=\\angle H C X$ since AFGC in inscribable (where G is the foot of the altidude from A),\nso $\\angle X P B=\\angle H C X$ and since $\\angle B X P=\\angle H X C$, the triangles XHC and XBP are similar.\nIf XL and XD are respectively the heights of the triangles XHC and XBP we have:\n\n$$\n\\frac{X D}{X L}=\\frac{P B}{C H},\n$$\n\nand from (1) and (2) we get:\n\n$$\n\\frac{X D}{X L}=\\frac{A F-B F}{2 O E}=\\frac{F E}{O E} \\Rightarrow \\frac{X D}{F D}=\\frac{F E}{O E}\n$$\n\nTherefore the triangles XFD, OEF are similar and we get:\n$\\angle O F X=\\angle O F C+\\angle L F X=\\angle F O E+\\angle F X D=\\angle X F D+\\angle F X D=90^{\\circ}$, so $\\mathrm{O} F \\perp F X$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution:"}}
|
| 2 |
-
{"year": "2008", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Does there exist a sequence $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ of positive real numbers satisfying both of the following conditions:\n(i) $\\sum_{i=1}^{n} a_{i} \\leq n^{2}$, for every positive integer $n$;\n(ii) $\\sum_{i=1}^{n} \\frac{1}{a_{i}} \\leq 2008$, for every positive integer $n$ ?", "solution": "The answer is no.\nIt is enough to show that\nif $\\sum_{i=1}^{n} a_{i} \\leq n^{2}$ for any $n$, then $\\sum_{i=2}^{2^{n}} \\frac{1}{a_{i}}>\\frac{n}{4}$. (or any other precise estimate)\nFor this, we use that $\\sum_{i=2^{k}+1}^{2^{k+1}} a_{i} \\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}} \\geq 2^{2 k}$ for any $k \\geq 0$ by the arithmetic-harmonic mean inequality.\nSince $\\sum_{i=2^{k}+1}^{2^{k+1}} a_{i}<\\sum_{i=1}^{2^{k+1}} a_{i} \\leq 2^{2 k+2}$, it follows that $\\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}}>\\frac{1}{4}$ and hence $\\sum_{i=2}^{2^{n}} \\frac{1}{a^{i}}>\\sum_{k=0}^{n-1} \\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}}>\\frac{n}{4}$. (it can be stated in words)\n\n## Remark: no points for using some inequality, that doesn't lead to solution", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution."}}
|
| 3 |
-
{"year": "2008", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be a positive integer. The rectangle $A B C D$ with side lengths $A B=90 n+1$ and $B C=90 n+5$ is partitioned into unit squares with sides parallel to the sides of $A B C D$. Let $S$ be the set of all points which are vertices of these unit squares. Prove that the number of lines which pass through at least two points from $S$ is divisible by 4.", "solution": "Denote $90 n+1=m$. We investigate the number of the lines modulo 4 consecutively reducing different types of lines.\nThe vertical and horizontal lines are\n$(m+5)+(m+1)=2(m+3)$ which is divisible to 4.\nMoreover, every line which makes an acute angle to the axe $O x$ (i.e. that line has a positive angular coefficient) corresponds to unique line with an obtuse angle (consider the symmetry with respect to the line through the midpoints of $A B$ and $C D$ ). Therefore it is enough to prove that the lines with acute angles are an even number.\nEvery line which does not pass through the center $O$ of the rectangle corresponds to another line with the same angular coefficent(consider the symmetry with respect to $O$ ). Therefore it is enough to consider the lines through $O$.\nEvery line through $O$ has an angular coefficient $\\frac{p}{q}$, where $(p, q)=1, p$ and $q$ are odd positive integers. (To see this, consider the two nearest, from the two sides, to $O$ points of the line).\nIf $p \\neq 1, q \\neq 1, \\quad p \\leq m$ and $q \\leq m$, the line with angular coefficient $\\frac{p}{q}$, uniquely corresponds to the line with angular coefficient $\\frac{q}{p}$. It remains to prove that the number of the remaining lines is even.\n\nThe last number is\n\n$$\n1+\\frac{\\varphi(m+2)}{2}+\\frac{\\varphi(m+4)}{2}-1=\\frac{\\varphi(m+2)+\\varphi(m+4)}{2}\n$$\n\nbecause we have:\n\n1) one line with $p=q=1$;\n2) $\\frac{\\varphi(m+2)}{2}$ lines with angular coefficient $\\frac{p}{m+2}, p \\leq m$ is odd and $(p, m+2)=1$;\n3) $\\frac{\\varphi(m+4)}{2}-1$ lines with angular coefficient $\\frac{p}{m+4}, p \\leq m$ is odd and $(p, m+4)=1$.\nNow the assertion follows from the fact that the number $\\varphi(m+2)+\\varphi(m+4)=\\varphi(90 n+3)+\\varphi(90 n+5)$ is divisible to 4.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution."}}
|
| 4 |
-
{"year": "2008", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $c$ be a positive integer. The sequence $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ is defined by $a_{1}=c$, and $a_{n+1}=a_{n}^{2}+a_{n}+c^{3}$, for every positive integer $n$. Find all values of $c$ for which there exist some integers $k \\geq 1$ and $m \\geq 2$, such that $a_{k}^{2}+c^{3}$ is the $m^{\\text {th }}$ power of some positive integer.", "solution": "First, notice:\n\n$$\na_{n+1}^{2}+c^{3}=\\left(a_{n}^{2}+a_{n}+c^{3}\\right)^{2}+c^{3}=\\left(a_{n}^{2}+c^{3}\\right)\\left(a_{n}^{2}+2 a_{n}+1+c^{3}\\right)\n$$\n\nWe first prove that $a_{n}^{2}+c^{3}$ and $a_{n}^{2}+2 a_{n}+1+c^{3}$ are coprime.\nWe prove by induction that $4 c^{3}+1$ is coprime with $2 a_{n}+1$, for every $n \\geq 1$.\nLet $n=1$ and $p$ be a prime divisor of $4 c^{3}+1$ and $2 a_{1}+1=2 c+1$. Then $p$ divides $2\\left(4 c^{3}+1\\right)=(2 c+1)\\left(4 c^{2}-2 c+1\\right)+1$, hence $p$ divides 1 , a contradiction. Assume now that $\\left(4 c^{3}+1,2 a_{n}+1\\right)=1$ for some $n \\geq 1$ and the prime $p$ divides $4 c^{3}+1$ and $2 a_{n+1}+1$. Then $p$ divides $4 a_{n+1}+2=\\left(2 a_{n}+1\\right)^{2}+4 c^{3}+1$, which gives a contradiction.\n\nAssume that for some $n \\geq 1$ the number\n\n$$\na_{n+1}^{2}+c^{3}=\\left(a_{n}^{2}+a_{n}+c^{3}\\right)^{2}+c^{3}=\\left(a_{n}^{2}+c^{3}\\right)\\left(a_{n}^{2}+2 a_{n}+1+c^{3}\\right)\n$$\n\nis a power. Since $a_{n}^{2}+c^{3}$ and $a_{n}^{2}+2 a_{n}+1+c^{3}$ are coprime, than $a_{n}^{2}+c^{3}$ is a power as well.\nThe same argument can be further applied giving that $a_{1}^{2}+c^{3}=c^{2}+c^{3}=c^{2}(c+1)$ is a power.\nIf $a^{2}(a+1)=t^{m}$ with odd $m \\geq 3$, then $a=t_{1}^{m}$ and $a+1=t_{2}^{m}$, which is impossible. If $a^{2}(a+1)=t^{2 m_{1}}$ with $m_{1} \\geq 2$, then $a=t_{1}^{m_{1}}$ and $a+1=t_{2}^{m_{1}}$, which is impossible.\n\nTherefore $a^{2}(a+1)=t^{2}$ whence we obtain the solutions $a=s^{2}-1, s \\geq 2, s \\in \\mathbb{N}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution."}}
|
|
|
|
| 1 |
+
{"year": "2008", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "An acute-angled scalene triangle $A B C$ is given, with $A C>B C$. Let $O$ be its circumcentre, $H$ its orthocentre, and $F$ the foot of the altitude from $C$. Let $P$ be the point (other than $A$ ) on the line $A B$ such that $A F=P F$, and $M$ be the midpoint of $A C$. We denote the intersection of $P H$ and $B C$ by $X$, the intersection of $O M$ and $F X$ by $Y$, and the intersection of $O F$ and $A C$ by $Z$. Prove that the points $F, M, Y$ and $Z$ are concyclic.", "solution": "It is enough to show that $\\mathrm{O} F \\perp F X$.\nLet $\\mathrm{OE} \\perp \\mathrm{AB}$, then it is trivial that :\n\n$$\nC \\mathrm{H}=2 \\mathrm{OE} .\n$$\n\nSince from the hypothesis we have $\\mathrm{P} F=\\mathrm{A} F$ then we take $\\mathrm{PB}=\\mathrm{P} F-\\mathrm{B} F$ or\n\n$$\n\\mathrm{PB}=\\mathrm{A} F-\\mathrm{B} F\n$$\n\nAlso, $\\angle X P B=\\angle H A P$ and $\\angle H A P=\\angle H C X$ since AFGC in inscribable (where G is the foot of the altidude from A),\nso $\\angle X P B=\\angle H C X$ and since $\\angle B X P=\\angle H X C$, the triangles XHC and XBP are similar.\nIf XL and XD are respectively the heights of the triangles XHC and XBP we have:\n\n$$\n\\frac{X D}{X L}=\\frac{P B}{C H},\n$$\n\nand from (1) and (2) we get:\n\n$$\n\\frac{X D}{X L}=\\frac{A F-B F}{2 O E}=\\frac{F E}{O E} \\Rightarrow \\frac{X D}{F D}=\\frac{F E}{O E}\n$$\n\nTherefore the triangles XFD, OEF are similar and we get:\n$\\angle O F X=\\angle O F C+\\angle L F X=\\angle F O E+\\angle F X D=\\angle X F D+\\angle F X D=90^{\\circ}$, so $\\mathrm{O} F \\perp F X$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "# Solution:"}}
|
| 2 |
+
{"year": "2008", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Does there exist a sequence $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ of positive real numbers satisfying both of the following conditions:\n(i) $\\sum_{i=1}^{n} a_{i} \\leq n^{2}$, for every positive integer $n$;\n(ii) $\\sum_{i=1}^{n} \\frac{1}{a_{i}} \\leq 2008$, for every positive integer $n$ ?", "solution": "The answer is no.\nIt is enough to show that\nif $\\sum_{i=1}^{n} a_{i} \\leq n^{2}$ for any $n$, then $\\sum_{i=2}^{2^{n}} \\frac{1}{a_{i}}>\\frac{n}{4}$. (or any other precise estimate)\nFor this, we use that $\\sum_{i=2^{k}+1}^{2^{k+1}} a_{i} \\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}} \\geq 2^{2 k}$ for any $k \\geq 0$ by the arithmetic-harmonic mean inequality.\nSince $\\sum_{i=2^{k}+1}^{2^{k+1}} a_{i}<\\sum_{i=1}^{2^{k+1}} a_{i} \\leq 2^{2 k+2}$, it follows that $\\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}}>\\frac{1}{4}$ and hence $\\sum_{i=2}^{2^{n}} \\frac{1}{a^{i}}>\\sum_{k=0}^{n-1} \\sum_{i=2^{k}+1}^{2^{k+1}} \\frac{1}{a_{i}}>\\frac{n}{4}$. (it can be stated in words)\n\n## Remark: no points for using some inequality, that doesn't lead to solution", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 2", "solution_match": "# Solution."}}
|
| 3 |
+
{"year": "2008", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $n$ be a positive integer. The rectangle $A B C D$ with side lengths $A B=90 n+1$ and $B C=90 n+5$ is partitioned into unit squares with sides parallel to the sides of $A B C D$. Let $S$ be the set of all points which are vertices of these unit squares. Prove that the number of lines which pass through at least two points from $S$ is divisible by 4.", "solution": "Denote $90 n+1=m$. We investigate the number of the lines modulo 4 consecutively reducing different types of lines.\nThe vertical and horizontal lines are\n$(m+5)+(m+1)=2(m+3)$ which is divisible to 4.\nMoreover, every line which makes an acute angle to the axe $O x$ (i.e. that line has a positive angular coefficient) corresponds to unique line with an obtuse angle (consider the symmetry with respect to the line through the midpoints of $A B$ and $C D$ ). Therefore it is enough to prove that the lines with acute angles are an even number.\nEvery line which does not pass through the center $O$ of the rectangle corresponds to another line with the same angular coefficent(consider the symmetry with respect to $O$ ). Therefore it is enough to consider the lines through $O$.\nEvery line through $O$ has an angular coefficient $\\frac{p}{q}$, where $(p, q)=1, p$ and $q$ are odd positive integers. (To see this, consider the two nearest, from the two sides, to $O$ points of the line).\nIf $p \\neq 1, q \\neq 1, \\quad p \\leq m$ and $q \\leq m$, the line with angular coefficient $\\frac{p}{q}$, uniquely corresponds to the line with angular coefficient $\\frac{q}{p}$. It remains to prove that the number of the remaining lines is even.\n\nThe last number is\n\n$$\n1+\\frac{\\varphi(m+2)}{2}+\\frac{\\varphi(m+4)}{2}-1=\\frac{\\varphi(m+2)+\\varphi(m+4)}{2}\n$$\n\nbecause we have:\n\n1) one line with $p=q=1$;\n2) $\\frac{\\varphi(m+2)}{2}$ lines with angular coefficient $\\frac{p}{m+2}, p \\leq m$ is odd and $(p, m+2)=1$;\n3) $\\frac{\\varphi(m+4)}{2}-1$ lines with angular coefficient $\\frac{p}{m+4}, p \\leq m$ is odd and $(p, m+4)=1$.\nNow the assertion follows from the fact that the number $\\varphi(m+2)+\\varphi(m+4)=\\varphi(90 n+3)+\\varphi(90 n+5)$ is divisible to 4.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "# Solution."}}
|
| 4 |
+
{"year": "2008", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $c$ be a positive integer. The sequence $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ is defined by $a_{1}=c$, and $a_{n+1}=a_{n}^{2}+a_{n}+c^{3}$, for every positive integer $n$. Find all values of $c$ for which there exist some integers $k \\geq 1$ and $m \\geq 2$, such that $a_{k}^{2}+c^{3}$ is the $m^{\\text {th }}$ power of some positive integer.", "solution": "First, notice:\n\n$$\na_{n+1}^{2}+c^{3}=\\left(a_{n}^{2}+a_{n}+c^{3}\\right)^{2}+c^{3}=\\left(a_{n}^{2}+c^{3}\\right)\\left(a_{n}^{2}+2 a_{n}+1+c^{3}\\right)\n$$\n\nWe first prove that $a_{n}^{2}+c^{3}$ and $a_{n}^{2}+2 a_{n}+1+c^{3}$ are coprime.\nWe prove by induction that $4 c^{3}+1$ is coprime with $2 a_{n}+1$, for every $n \\geq 1$.\nLet $n=1$ and $p$ be a prime divisor of $4 c^{3}+1$ and $2 a_{1}+1=2 c+1$. Then $p$ divides $2\\left(4 c^{3}+1\\right)=(2 c+1)\\left(4 c^{2}-2 c+1\\right)+1$, hence $p$ divides 1 , a contradiction. Assume now that $\\left(4 c^{3}+1,2 a_{n}+1\\right)=1$ for some $n \\geq 1$ and the prime $p$ divides $4 c^{3}+1$ and $2 a_{n+1}+1$. Then $p$ divides $4 a_{n+1}+2=\\left(2 a_{n}+1\\right)^{2}+4 c^{3}+1$, which gives a contradiction.\n\nAssume that for some $n \\geq 1$ the number\n\n$$\na_{n+1}^{2}+c^{3}=\\left(a_{n}^{2}+a_{n}+c^{3}\\right)^{2}+c^{3}=\\left(a_{n}^{2}+c^{3}\\right)\\left(a_{n}^{2}+2 a_{n}+1+c^{3}\\right)\n$$\n\nis a power. Since $a_{n}^{2}+c^{3}$ and $a_{n}^{2}+2 a_{n}+1+c^{3}$ are coprime, than $a_{n}^{2}+c^{3}$ is a power as well.\nThe same argument can be further applied giving that $a_{1}^{2}+c^{3}=c^{2}+c^{3}=c^{2}(c+1)$ is a power.\nIf $a^{2}(a+1)=t^{m}$ with odd $m \\geq 3$, then $a=t_{1}^{m}$ and $a+1=t_{2}^{m}$, which is impossible. If $a^{2}(a+1)=t^{2 m_{1}}$ with $m_{1} \\geq 2$, then $a=t_{1}^{m_{1}}$ and $a+1=t_{2}^{m_{1}}$, which is impossible.\n\nTherefore $a^{2}(a+1)=t^{2}$ whence we obtain the solutions $a=s^{2}-1, s \\geq 2, s \\in \\mathbb{N}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "# Solution."}}
|
Balkan_MO/segmented/en-2009-BMO-type2.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2009", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "We start by observing that $z$ must be even, so $z^{2}=3^{x}-5^{y} \\equiv(-1)^{x}-1(\\bmod 4)$ is divisible by 4 , which implies that $x$ is even, say $x=2 t$. Then our equation can be rewritten as $\\left(3^{t}-z\\right)\\left(3^{t}+z\\right)=5^{y}$, which means that both $3^{t}-z=5^{k}$ and $3^{t}+z=5^{y-k}$ for some nonnegative integer $k$. Since $5^{k}+5^{y-k}=2 \\cdot 3^{t}$ is not divisible by 5 , it follows that $k=0$ and\n\n$$\n2 \\cdot 3^{t}=5^{y}+1\n$$\n\nSuppose that $t \\geq 2$. Then $5^{y}+1$ is divisible by 9 , which is only possible if $y \\equiv 3$ $(\\bmod 6)$. However, in this case $5^{y}+1 \\equiv 5^{3}+1 \\equiv 0(\\bmod 7)$, so $5^{y}+1$ is also divisible by 7 , which is impossible.\nTherefore we must have $t \\leq 1$, which yields a (unique) solution $(x, y, z)=(2,1,2)$.", "solution": "We start by observing that $f$ is injective. From the known identity\n\n$$\n\\left(a^{2}+2 b^{2}\\right)\\left(c^{2}+2 d^{2}\\right)=(a c \\pm 2 b d)^{2}+2(a d \\mp b c)^{2}\n$$\n\nwe obtain $f(a c+2 b d)^{2}+2 f(a d-b c)^{2}=f(a c-2 b d)^{2}+2 f(a d+b c)^{2}$, assuming that the arguments are positive integers. Specially, for $b=c=d=1$ and $a \\geq 3$ we have $f(a+2)^{2}+2 f(a-1)^{2}=f(a-2)^{2}+2 f(a+1)^{2}$. Denoting $g(n)=f(n)^{2}$ we get a recurrent relation $g(a+2)-2 g(a+1)+2 g(a-1)-g(a-2)=0$ whose characteristic polynomial is $(x+1)(x-1)^{3}$, which leads to\n\n$$\ng(n)=A(-1)^{n}+B+C n+D n^{2} .\n$$\n\nSubstituting $m=n$ in the original equation yields $g(3 g(n))=9 n^{4}$, which together with $(\\dagger)$ gives us\n\n$$\n\\begin{aligned}\nL=9 n^{4} & =A(-1)^{3\\left(A(-1)^{n}+B+C n+D n^{2}\\right)}+B+\\underbrace{3 C\\left[A(-1)^{n}+B+C n+D n^{2}\\right]} \\\\\n& +9 D\\left[A(-1)^{n}+B+C n+D n^{2}\\right]^{2}=R .\n\\end{aligned}\n$$\n\nSince $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{4}}=9 D^{3}-9$, we have $D^{3}=1$ (so $D \\neq 0$ ); similarly, $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{3}}=18 D^{2} C$, so $C=0$. Moreover, for $n=2 k$ and $n=2 k+1$\nrespectively we obtain $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k)^{2}}=18 D^{2}(A+B)$ and $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k+1)^{2}}=$ $18 D^{2}(-A+B)$, implying $A+B=-A+B=0$; hence $A=B=0$.\nFinally, $g(n)=D n^{2}, D^{3}=1$ and $g: \\mathbb{N} \\rightarrow \\mathbb{N}$ gives us $D=1$, i.e. $f(n)=n$. It is directly verified that this function satisfies the conditions of the problem.\n\nRemark. Using limits can be avoided. Since the rigth-hand side in ( $\\dagger$ ) takes only integer values, it follows that $A, B, C, D$ are rational, so taking suitable multiples of integers for $n$ eliminates the powers of -1 and leaves a polynomial equality.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
-
{"year": "2009", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "In a triangle $A B C$, points $M$ and $N$ on the sides $A B$ and $A C$ respectively are such that $M N \\| B C$. Let $B N$ and $C M$ intersect at point $P$. The circumcircles of triangles $B M P$ and $C N P$ intersect at two distinct points $P$ and $Q$. Prove that $\\angle B A Q=\\angle C A P$.\n(Moldova)", "solution": "Since the quadrilaterals $B M P Q$ and $C N P Q$ are cyclic, we have $\\angle B Q N=\\angle B Q P+$ $\\angle P Q N=\\angle A M C+\\angle M C A=180^{\\circ}-$ $\\angle C A B$, so $A B Q N$ is cyclic as well. Hence $\\frac{\\sin \\angle B A Q}{\\sin \\angle N A Q}=\\frac{B Q}{N Q}$. Moreover, triangles $M B Q$ and $C N Q$ are similar, so\n\n$$\n\\frac{\\sin \\angle B A Q}{\\sin \\angle C A Q}=\\frac{B Q}{N Q}=\\frac{B M}{C N}=\\frac{A B}{A C}\n$$\n\nOn the other hand, if $A P$ meets $B C$ at $A_{1}$, then by the Cheva theorem $\\frac{B A_{1}}{A_{1} C}=$\n\n$\\frac{B M}{M A} \\cdot \\frac{A N}{N C}=1$, so $A_{1}$ is the midpoint of $B C$ and\n\n$$\n\\frac{\\sin \\angle C A P}{\\sin \\angle B A P}=\\frac{A B}{A C} \\cdot \\frac{A C \\cdot A A_{1} \\sin \\angle C A P}{A B \\cdot A A_{1} \\sin \\angle B A P}=\\frac{A B}{A C} \\cdot \\frac{S_{\\triangle C A A_{1}}}{S_{\\triangle B A A_{1}}}=\\frac{A B}{A C}\n$$\n\nTherefore, if we denote $\\angle C A P=\\varphi, \\angle B A Q=\\psi$ and $\\angle B A C=\\alpha$, we have $\\frac{\\sin \\psi}{\\sin (\\alpha-\\psi)}=\\frac{\\sin \\varphi}{\\sin (\\alpha-\\varphi)}$, which is equivalent to $\\sin \\psi \\sin (\\alpha-\\varphi)=\\sin \\varphi \\sin (\\alpha-\\psi)$. The addition formulas reduce the last equality to $0=\\sin \\alpha(\\sin \\varphi \\cos \\psi-\\sin \\psi \\cos \\varphi)=$ $\\sin \\alpha \\sin (\\varphi-\\psi)$, from which we conclude that $\\psi=\\varphi$, as desired.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
-
{"year": "2009", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "A $9 \\times 12$ rectangle is divided into unit squares. The centers of all the unit squares, except the four corner squares and the eight squares adjacent (by side) to them, are colored red. Is it possible to numerate the red centers by $C_{1}, C_{2}, \\ldots, C_{96}$ so that the following two conditions are fulfilled:\n$1^{\\circ}$ All segments $C_{1} C_{2}, C_{2} C_{3}, \\ldots C_{95} C_{96}, C_{96} C_{1}$ have the length $\\sqrt{13}$;\n$2^{\\circ}$ The poligonal line $C_{1} C_{2} \\ldots C_{96} C_{1}$ is centrally symmetric?\n(Bulgaria)", "solution": "Place the given rectangle into the coordinate plane so that the center of the square at the intersection of $i$-th column and $j$-th row has the coordinates $(i, j)$. Suppose that a desired numeration of the red points exists; it corresponds to a path, i.e. a closed poligonal line consisting of 96 segments of length $\\sqrt{13}$, passing through each red point exactly once. Note that points $(i, j)$ and $(k, l)$ are adjacent in the path if and only if $\\{|i-k|,|j-l|\\}=\\{2,3\\}$.\n\nThe center of symmetry must be at point $C\\left(5 \\frac{1}{2}, 5\\right)$. Consider the points $A(2,2)$, $B(11,8)$. These two points are symmetric with respect to $C$ and divide the path into two parts $\\gamma_{1}$ and $\\gamma_{2}$. Note that, if the rectangular board is colored alternately white and black (like a chessboard), $A$ and $B$ are of different colors, and each segment connects two squares of different colors. It follows that each of $\\gamma_{1}, \\gamma_{2}$ consists of an odd number of segments. Thus these two parts are of different lengths and cannot be symmetric to each other. Therefore each\n\nof $\\gamma_{1}, \\gamma_{2}$ is centrally symmetric itself.\nBeing of an odd length, each of the parts $\\gamma_{1}, \\gamma_{2}$ must contain a segment which is centrally symmetric with respect to $C$. There are only two such segments one connecting $(5,4)$ and $(8,6)$, and one connecting $(5,6)$ and $(8,4)$, so these two segments must be parts of our path. Moreover, point $(2,2)$ is connected with only two points, namely $(4,5)$ and $(5,4)$, so these three points are directly connected. Analogous conclusions can be made about points $(2,8),(11,2)$ and $(11,8)$, so the closed path $(5,4)-(2,2)-(4,5)-(2,8)-(5,6)-(8,4)-(11,2)-(9,5)-(11,8)-$ $(8,6)-(5,4)$ is entirely contained in our path, which is clearly a contradiction.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
-
{"year": "2009", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Determine all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ satisfying\n\n$$\nf\\left(f(m)^{2}+2 f(n)^{2}\\right)=m^{2}+2 n^{2} \\quad \\text { for all } m, n \\in \\mathbb{N} . \\quad \\text { (Bulgaria) }\n$$\n\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "We start by observing that $f$ is injective. From the known identity\n\n$$\n\\left(a^{2}+2 b^{2}\\right)\\left(c^{2}+2 d^{2}\\right)=(a c \\pm 2 b d)^{2}+2(a d \\mp b c)^{2}\n$$\n\nwe obtain $f(a c+2 b d)^{2}+2 f(a d-b c)^{2}=f(a c-2 b d)^{2}+2 f(a d+b c)^{2}$, assuming that the arguments are positive integers. Specially, for $b=c=d=1$ and $a \\geq 3$ we have $f(a+2)^{2}+2 f(a-1)^{2}=f(a-2)^{2}+2 f(a+1)^{2}$. Denoting $g(n)=f(n)^{2}$ we get a recurrent relation $g(a+2)-2 g(a+1)+2 g(a-1)-g(a-2)=0$ whose characteristic polynomial is $(x+1)(x-1)^{3}$, which leads to\n\n$$\ng(n)=A(-1)^{n}+B+C n+D n^{2} .\n$$\n\nSubstituting $m=n$ in the original equation yields $g(3 g(n))=9 n^{4}$, which together with $(\\dagger)$ gives us\n\n$$\n\\begin{aligned}\nL=9 n^{4} & =A(-1)^{3\\left(A(-1)^{n}+B+C n+D n^{2}\\right)}+B+\\underbrace{3 C\\left[A(-1)^{n}+B+C n+D n^{2}\\right]} \\\\\n& +9 D\\left[A(-1)^{n}+B+C n+D n^{2}\\right]^{2}=R .\n\\end{aligned}\n$$\n\nSince $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{4}}=9 D^{3}-9$, we have $D^{3}=1$ (so $D \\neq 0$ ); similarly, $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{3}}=18 D^{2} C$, so $C=0$. Moreover, for $n=2 k$ and $n=2 k+1$\nrespectively we obtain $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k)^{2}}=18 D^{2}(A+B)$ and $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k+1)^{2}}=$ $18 D^{2}(-A+B)$, implying $A+B=-A+B=0$; hence $A=B=0$.\nFinally, $g(n)=D n^{2}, D^{3}=1$ and $g: \\mathbb{N} \\rightarrow \\mathbb{N}$ gives us $D=1$, i.e. $f(n)=n$. It is directly verified that this function satisfies the conditions of the problem.\n\nRemark. Using limits can be avoided. Since the rigth-hand side in ( $\\dagger$ ) takes only integer values, it follows that $A, B, C, D$ are rational, so taking suitable multiples of integers for $n$ eliminates the powers of -1 and leaves a polynomial equality.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
|
|
|
| 1 |
+
{"year": "2009", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "We start by observing that $z$ must be even, so $z^{2}=3^{x}-5^{y} \\equiv(-1)^{x}-1(\\bmod 4)$ is divisible by 4 , which implies that $x$ is even, say $x=2 t$. Then our equation can be rewritten as $\\left(3^{t}-z\\right)\\left(3^{t}+z\\right)=5^{y}$, which means that both $3^{t}-z=5^{k}$ and $3^{t}+z=5^{y-k}$ for some nonnegative integer $k$. Since $5^{k}+5^{y-k}=2 \\cdot 3^{t}$ is not divisible by 5 , it follows that $k=0$ and\n\n$$\n2 \\cdot 3^{t}=5^{y}+1\n$$\n\nSuppose that $t \\geq 2$. Then $5^{y}+1$ is divisible by 9 , which is only possible if $y \\equiv 3$ $(\\bmod 6)$. However, in this case $5^{y}+1 \\equiv 5^{3}+1 \\equiv 0(\\bmod 7)$, so $5^{y}+1$ is also divisible by 7 , which is impossible.\nTherefore we must have $t \\leq 1$, which yields a (unique) solution $(x, y, z)=(2,1,2)$.", "solution": "We start by observing that $f$ is injective. From the known identity\n\n$$\n\\left(a^{2}+2 b^{2}\\right)\\left(c^{2}+2 d^{2}\\right)=(a c \\pm 2 b d)^{2}+2(a d \\mp b c)^{2}\n$$\n\nwe obtain $f(a c+2 b d)^{2}+2 f(a d-b c)^{2}=f(a c-2 b d)^{2}+2 f(a d+b c)^{2}$, assuming that the arguments are positive integers. Specially, for $b=c=d=1$ and $a \\geq 3$ we have $f(a+2)^{2}+2 f(a-1)^{2}=f(a-2)^{2}+2 f(a+1)^{2}$. Denoting $g(n)=f(n)^{2}$ we get a recurrent relation $g(a+2)-2 g(a+1)+2 g(a-1)-g(a-2)=0$ whose characteristic polynomial is $(x+1)(x-1)^{3}$, which leads to\n\n$$\ng(n)=A(-1)^{n}+B+C n+D n^{2} .\n$$\n\nSubstituting $m=n$ in the original equation yields $g(3 g(n))=9 n^{4}$, which together with $(\\dagger)$ gives us\n\n$$\n\\begin{aligned}\nL=9 n^{4} & =A(-1)^{3\\left(A(-1)^{n}+B+C n+D n^{2}\\right)}+B+\\underbrace{3 C\\left[A(-1)^{n}+B+C n+D n^{2}\\right]} \\\\\n& +9 D\\left[A(-1)^{n}+B+C n+D n^{2}\\right]^{2}=R .\n\\end{aligned}\n$$\n\nSince $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{4}}=9 D^{3}-9$, we have $D^{3}=1$ (so $D \\neq 0$ ); similarly, $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{3}}=18 D^{2} C$, so $C=0$. Moreover, for $n=2 k$ and $n=2 k+1$\nrespectively we obtain $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k)^{2}}=18 D^{2}(A+B)$ and $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k+1)^{2}}=$ $18 D^{2}(-A+B)$, implying $A+B=-A+B=0$; hence $A=B=0$.\nFinally, $g(n)=D n^{2}, D^{3}=1$ and $g: \\mathbb{N} \\rightarrow \\mathbb{N}$ gives us $D=1$, i.e. $f(n)=n$. It is directly verified that this function satisfies the conditions of the problem.\n\nRemark. Using limits can be avoided. Since the rigth-hand side in ( $\\dagger$ ) takes only integer values, it follows that $A, B, C, D$ are rational, so taking suitable multiples of integers for $n$ eliminates the powers of -1 and leaves a polynomial equality.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
+
{"year": "2009", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "In a triangle $A B C$, points $M$ and $N$ on the sides $A B$ and $A C$ respectively are such that $M N \\| B C$. Let $B N$ and $C M$ intersect at point $P$. The circumcircles of triangles $B M P$ and $C N P$ intersect at two distinct points $P$ and $Q$. Prove that $\\angle B A Q=\\angle C A P$.\n(Moldova)", "solution": "Since the quadrilaterals $B M P Q$ and $C N P Q$ are cyclic, we have $\\angle B Q N=\\angle B Q P+$ $\\angle P Q N=\\angle A M C+\\angle M C A=180^{\\circ}-$ $\\angle C A B$, so $A B Q N$ is cyclic as well. Hence $\\frac{\\sin \\angle B A Q}{\\sin \\angle N A Q}=\\frac{B Q}{N Q}$. Moreover, triangles $M B Q$ and $C N Q$ are similar, so\n\n$$\n\\frac{\\sin \\angle B A Q}{\\sin \\angle C A Q}=\\frac{B Q}{N Q}=\\frac{B M}{C N}=\\frac{A B}{A C}\n$$\n\nOn the other hand, if $A P$ meets $B C$ at $A_{1}$, then by the Cheva theorem $\\frac{B A_{1}}{A_{1} C}=$\n\n$\\frac{B M}{M A} \\cdot \\frac{A N}{N C}=1$, so $A_{1}$ is the midpoint of $B C$ and\n\n$$\n\\frac{\\sin \\angle C A P}{\\sin \\angle B A P}=\\frac{A B}{A C} \\cdot \\frac{A C \\cdot A A_{1} \\sin \\angle C A P}{A B \\cdot A A_{1} \\sin \\angle B A P}=\\frac{A B}{A C} \\cdot \\frac{S_{\\triangle C A A_{1}}}{S_{\\triangle B A A_{1}}}=\\frac{A B}{A C}\n$$\n\nTherefore, if we denote $\\angle C A P=\\varphi, \\angle B A Q=\\psi$ and $\\angle B A C=\\alpha$, we have $\\frac{\\sin \\psi}{\\sin (\\alpha-\\psi)}=\\frac{\\sin \\varphi}{\\sin (\\alpha-\\varphi)}$, which is equivalent to $\\sin \\psi \\sin (\\alpha-\\varphi)=\\sin \\varphi \\sin (\\alpha-\\psi)$. The addition formulas reduce the last equality to $0=\\sin \\alpha(\\sin \\varphi \\cos \\psi-\\sin \\psi \\cos \\varphi)=$ $\\sin \\alpha \\sin (\\varphi-\\psi)$, from which we conclude that $\\psi=\\varphi$, as desired.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
+
{"year": "2009", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "A $9 \\times 12$ rectangle is divided into unit squares. The centers of all the unit squares, except the four corner squares and the eight squares adjacent (by side) to them, are colored red. Is it possible to numerate the red centers by $C_{1}, C_{2}, \\ldots, C_{96}$ so that the following two conditions are fulfilled:\n$1^{\\circ}$ All segments $C_{1} C_{2}, C_{2} C_{3}, \\ldots C_{95} C_{96}, C_{96} C_{1}$ have the length $\\sqrt{13}$;\n$2^{\\circ}$ The poligonal line $C_{1} C_{2} \\ldots C_{96} C_{1}$ is centrally symmetric?\n(Bulgaria)", "solution": "Place the given rectangle into the coordinate plane so that the center of the square at the intersection of $i$-th column and $j$-th row has the coordinates $(i, j)$. Suppose that a desired numeration of the red points exists; it corresponds to a path, i.e. a closed poligonal line consisting of 96 segments of length $\\sqrt{13}$, passing through each red point exactly once. Note that points $(i, j)$ and $(k, l)$ are adjacent in the path if and only if $\\{|i-k|,|j-l|\\}=\\{2,3\\}$.\n\nThe center of symmetry must be at point $C\\left(5 \\frac{1}{2}, 5\\right)$. Consider the points $A(2,2)$, $B(11,8)$. These two points are symmetric with respect to $C$ and divide the path into two parts $\\gamma_{1}$ and $\\gamma_{2}$. Note that, if the rectangular board is colored alternately white and black (like a chessboard), $A$ and $B$ are of different colors, and each segment connects two squares of different colors. It follows that each of $\\gamma_{1}, \\gamma_{2}$ consists of an odd number of segments. Thus these two parts are of different lengths and cannot be symmetric to each other. Therefore each\n\nof $\\gamma_{1}, \\gamma_{2}$ is centrally symmetric itself.\nBeing of an odd length, each of the parts $\\gamma_{1}, \\gamma_{2}$ must contain a segment which is centrally symmetric with respect to $C$. There are only two such segments one connecting $(5,4)$ and $(8,6)$, and one connecting $(5,6)$ and $(8,4)$, so these two segments must be parts of our path. Moreover, point $(2,2)$ is connected with only two points, namely $(4,5)$ and $(5,4)$, so these three points are directly connected. Analogous conclusions can be made about points $(2,8),(11,2)$ and $(11,8)$, so the closed path $(5,4)-(2,2)-(4,5)-(2,8)-(5,6)-(8,4)-(11,2)-(9,5)-(11,8)-$ $(8,6)-(5,4)$ is entirely contained in our path, which is clearly a contradiction.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
+
{"year": "2009", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Determine all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ satisfying\n\n$$\nf\\left(f(m)^{2}+2 f(n)^{2}\\right)=m^{2}+2 n^{2} \\quad \\text { for all } m, n \\in \\mathbb{N} . \\quad \\text { (Bulgaria) }\n$$\n\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "We start by observing that $f$ is injective. From the known identity\n\n$$\n\\left(a^{2}+2 b^{2}\\right)\\left(c^{2}+2 d^{2}\\right)=(a c \\pm 2 b d)^{2}+2(a d \\mp b c)^{2}\n$$\n\nwe obtain $f(a c+2 b d)^{2}+2 f(a d-b c)^{2}=f(a c-2 b d)^{2}+2 f(a d+b c)^{2}$, assuming that the arguments are positive integers. Specially, for $b=c=d=1$ and $a \\geq 3$ we have $f(a+2)^{2}+2 f(a-1)^{2}=f(a-2)^{2}+2 f(a+1)^{2}$. Denoting $g(n)=f(n)^{2}$ we get a recurrent relation $g(a+2)-2 g(a+1)+2 g(a-1)-g(a-2)=0$ whose characteristic polynomial is $(x+1)(x-1)^{3}$, which leads to\n\n$$\ng(n)=A(-1)^{n}+B+C n+D n^{2} .\n$$\n\nSubstituting $m=n$ in the original equation yields $g(3 g(n))=9 n^{4}$, which together with $(\\dagger)$ gives us\n\n$$\n\\begin{aligned}\nL=9 n^{4} & =A(-1)^{3\\left(A(-1)^{n}+B+C n+D n^{2}\\right)}+B+\\underbrace{3 C\\left[A(-1)^{n}+B+C n+D n^{2}\\right]} \\\\\n& +9 D\\left[A(-1)^{n}+B+C n+D n^{2}\\right]^{2}=R .\n\\end{aligned}\n$$\n\nSince $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{4}}=9 D^{3}-9$, we have $D^{3}=1$ (so $D \\neq 0$ ); similarly, $0=\\lim _{n \\rightarrow \\infty} \\frac{R-L}{n^{3}}=18 D^{2} C$, so $C=0$. Moreover, for $n=2 k$ and $n=2 k+1$\nrespectively we obtain $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k)^{2}}=18 D^{2}(A+B)$ and $0=\\lim _{k \\rightarrow \\infty} \\frac{R-L}{(2 k+1)^{2}}=$ $18 D^{2}(-A+B)$, implying $A+B=-A+B=0$; hence $A=B=0$.\nFinally, $g(n)=D n^{2}, D^{3}=1$ and $g: \\mathbb{N} \\rightarrow \\mathbb{N}$ gives us $D=1$, i.e. $f(n)=n$. It is directly verified that this function satisfies the conditions of the problem.\n\nRemark. Using limits can be avoided. Since the rigth-hand side in ( $\\dagger$ ) takes only integer values, it follows that $A, B, C, D$ are rational, so taking suitable multiples of integers for $n$ eliminates the powers of -1 and leaves a polynomial equality.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
Balkan_MO/segmented/en-2010-BMO-type2.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2010", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "The left-hand side is equal to\n\n$$\n\\frac{a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}-a^{3} b^{2} c-b^{3} c^{2} a-c^{3} a^{2} b}{(a+b)(b+c)(c+a)}\n$$\n\nso it is enough to show that $a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3} \\geq a^{3} b^{2} c+b^{3} c^{2} a+c^{3} a^{2} b$. The AM-GM inequality gives us $a^{3} b^{3}+a^{3} b^{3}+a^{3} c^{3} \\geq 3 \\sqrt[3]{a^{3} b^{3} \\cdot a^{3} b^{3} \\cdot a^{3} c^{3}}=3 a^{3} b^{2} c$; summing this inequality and its cyclic analogs yields the desired inequality. Equality holds if and only if $a=b=c$.", "solution": "There are $n+1-\\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\\frac{1}{2} n(n+1-\\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \\in \\mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\\varphi(k p))=(k+1)(k p+p+$ $1-\\varphi(k p+p)$ ), so\n\n$$\nk p+1-\\varphi(k p)=(k+1) x \\quad \\text { and } \\quad k p+p+1-\\varphi(k p+p)=k x\n$$\n\nfor some $x \\in \\mathbb{N}, x<p$. Subtraction gives us $x=\\varphi(k p+p)-\\varphi(k p)-p$. Since $\\varphi(k p)$ and $\\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\\varphi(n)$ ), we obtain $x \\equiv-1(\\bmod p-1)$.\nIf $p=2$ then $x=1$ and $\\varphi(2 k+2)=k+3$, which is impossible because $\\varphi(2 k+2) \\leq$ $k+1$. If $p=3$ then $x=1$ and $\\varphi(3 k+3)=2 k+4$, again impossible because $\\varphi(3 k+3) \\leq 2 k+2$. Therefore $p \\geq 5$, so $x \\equiv-1(\\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to\n\n$$\n\\varphi(k p)=2 k+3-p \\quad \\text { and } \\quad \\varphi(k p+p)=2 k+1+p\n$$\n\nIf $k$ is divisible by $p$, then $\\varphi(k p)$ is also divisible by $p$, so $p \\mid 2 k+3$ and hence $p \\mid 3$, a contradiction. Similarly, $p \\nmid k+1$. It follows that $\\varphi(k p)=(p-1) \\varphi(k)$ and $\\varphi(k p+p)=(p-1) \\varphi(k+1)$ which together with (1) yields\n\n$$\n\\varphi(k)=\\frac{2 k+2}{p-1}-1 \\quad \\text { and } \\quad \\varphi(k+1)=\\frac{2 k+2}{p-1}+1\n$$\n\nFrom here we see that $\\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \\in \\mathbb{N}$, or $t \\in\\{1,2,4\\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \\varphi\\left(q^{i}\\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\\frac{2}{3}\\left(2 q^{i}+2\\right)$. The other three cases are similarly shown to be impossible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
-
{"year": "2010", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be an acute-angled triangle with orthocenter $H$ and let $M$ be the midpoint of $A C$. The foot of the altitude from $C$ is $C_{1}$. Point $H_{1}$ is symmetric to $H$ in $A B$. The projections of $C_{1}$ on lines $A H_{1}, A C$ and $B C$ are $P, Q$ and $R$ respectively. If $M_{1}$ is the circumcenter of triangle $P Q R$, prove that the point symmetric to $M$ with respect to $M_{1}$ lies on line $B H_{1}$.\n(Serbia)", "solution": "We shall use the following simple statement.\n\nLemma. Let $A_{1} A_{2} A_{3} A_{4}$ be a convex cyclic quadrilateral whose diagonals are orthogonal and meet at $X$. If $B_{i}$ is the midpoint of side $A_{i} A_{i+1}$ and $X_{i}$ the projection of $X$ on this side $\\left(A_{5}=A_{1}\\right)$, then the eight points $B_{i}, X_{i}$ $(i=1,2,3,4)$ lie on a circle.\n\nProof. Quadrilateral $B_{1} B_{2} B_{3} B_{4}$ is a rectangle because $B_{1} B_{2}\\left\\|B_{3} B_{4}\\right\\| A_{1} A_{3}$ and $B_{2} B_{3}\\left\\|B_{4} B_{1}\\right\\| A_{2} A_{4}$. Denote by $k$ the circumcircle of $B_{1} B_{2} B_{3} B_{4}$. Since $\\angle B_{3} X A_{3}=\\angle A_{4} A_{3} A_{1}=\\angle A_{4} A_{2} A_{1}=\\angle A_{1} X X_{1}$, points $B_{3}, X, X_{1}$ are collinear, so $X_{1}$ lies on the circle with diameter $B_{1} B_{3}$, i.e. $k$. Similarly, $X_{2}, X_{3}, X_{4}$ lie on $k$.\n\nIt is known that $H_{1}$ lies on the circumcircle of $A B C$. By the lemma, points $P, Q, R$ all lie on the circle with diameter $M N$, where $N$ is the midpoint of $B H_{1}$. Therefore $N$ is symmetric to $M$ with respect to $M_{1}$ and lies on $B H_{1}$ as desired.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
-
{"year": "2010", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "We define a $w$-strip as the set of all points in the plane that are between or on two parallel lines on a mutual distance $w$. Let $S$ be a set of $n$ points in the plane such that any three points from $S$ can be covered by a 1 -strip. Show that the entire set $S$ can be covered by a 2 -strip.\n(Romania)", "solution": "Of all triangles with the vertices in $S$, consider one with a maximum area, say $\\triangle A B C$. Let $A^{\\prime}, B^{\\prime}, C^{\\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$, respectively. We claim that all points from $S$ must lie inside or on the boundary of $\\triangle A^{\\prime} B^{\\prime} C^{\\prime}$. Indeed, if $X \\in S$ is outside $\\triangle A^{\\prime} B^{\\prime} C^{\\prime}$, we can assume without loss of generality that $X$ and $B C$ are on different sides of $B^{\\prime} C^{\\prime}$, and then $\\triangle B C X$ has an area greater than $\\triangle A B C$, a contradiction.\nThe triangle $A B C$ can be covered by a 1-strip, so the triangle $A^{\\prime} B^{\\prime} C^{\\prime}$, being similar to $A B C$ with ratio 2 , can be covered by a 2 -strip, also covering all of $S$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
-
{"year": "2010", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "For every integer $n \\geq 2$, denote by $f(n)$ the sum of positive integers not exceeding $n$ that are not coprime to $n$. Prove that $f(n+p) \\neq f(n)$ for any such $n$ and any prime number $p$.\n(Turkey)\n\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "There are $n+1-\\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\\frac{1}{2} n(n+1-\\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \\in \\mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\\varphi(k p))=(k+1)(k p+p+$ $1-\\varphi(k p+p)$ ), so\n\n$$\nk p+1-\\varphi(k p)=(k+1) x \\quad \\text { and } \\quad k p+p+1-\\varphi(k p+p)=k x\n$$\n\nfor some $x \\in \\mathbb{N}, x<p$. Subtraction gives us $x=\\varphi(k p+p)-\\varphi(k p)-p$. Since $\\varphi(k p)$ and $\\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\\varphi(n)$ ), we obtain $x \\equiv-1(\\bmod p-1)$.\nIf $p=2$ then $x=1$ and $\\varphi(2 k+2)=k+3$, which is impossible because $\\varphi(2 k+2) \\leq$ $k+1$. If $p=3$ then $x=1$ and $\\varphi(3 k+3)=2 k+4$, again impossible because $\\varphi(3 k+3) \\leq 2 k+2$. Therefore $p \\geq 5$, so $x \\equiv-1(\\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to\n\n$$\n\\varphi(k p)=2 k+3-p \\quad \\text { and } \\quad \\varphi(k p+p)=2 k+1+p\n$$\n\nIf $k$ is divisible by $p$, then $\\varphi(k p)$ is also divisible by $p$, so $p \\mid 2 k+3$ and hence $p \\mid 3$, a contradiction. Similarly, $p \\nmid k+1$. It follows that $\\varphi(k p)=(p-1) \\varphi(k)$ and $\\varphi(k p+p)=(p-1) \\varphi(k+1)$ which together with (1) yields\n\n$$\n\\varphi(k)=\\frac{2 k+2}{p-1}-1 \\quad \\text { and } \\quad \\varphi(k+1)=\\frac{2 k+2}{p-1}+1\n$$\n\nFrom here we see that $\\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \\in \\mathbb{N}$, or $t \\in\\{1,2,4\\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \\varphi\\left(q^{i}\\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\\frac{2}{3}\\left(2 q^{i}+2\\right)$. The other three cases are similarly shown to be impossible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
|
|
|
| 1 |
+
{"year": "2010", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "The left-hand side is equal to\n\n$$\n\\frac{a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}-a^{3} b^{2} c-b^{3} c^{2} a-c^{3} a^{2} b}{(a+b)(b+c)(c+a)}\n$$\n\nso it is enough to show that $a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3} \\geq a^{3} b^{2} c+b^{3} c^{2} a+c^{3} a^{2} b$. The AM-GM inequality gives us $a^{3} b^{3}+a^{3} b^{3}+a^{3} c^{3} \\geq 3 \\sqrt[3]{a^{3} b^{3} \\cdot a^{3} b^{3} \\cdot a^{3} c^{3}}=3 a^{3} b^{2} c$; summing this inequality and its cyclic analogs yields the desired inequality. Equality holds if and only if $a=b=c$.", "solution": "There are $n+1-\\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\\frac{1}{2} n(n+1-\\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \\in \\mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\\varphi(k p))=(k+1)(k p+p+$ $1-\\varphi(k p+p)$ ), so\n\n$$\nk p+1-\\varphi(k p)=(k+1) x \\quad \\text { and } \\quad k p+p+1-\\varphi(k p+p)=k x\n$$\n\nfor some $x \\in \\mathbb{N}, x<p$. Subtraction gives us $x=\\varphi(k p+p)-\\varphi(k p)-p$. Since $\\varphi(k p)$ and $\\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\\varphi(n)$ ), we obtain $x \\equiv-1(\\bmod p-1)$.\nIf $p=2$ then $x=1$ and $\\varphi(2 k+2)=k+3$, which is impossible because $\\varphi(2 k+2) \\leq$ $k+1$. If $p=3$ then $x=1$ and $\\varphi(3 k+3)=2 k+4$, again impossible because $\\varphi(3 k+3) \\leq 2 k+2$. Therefore $p \\geq 5$, so $x \\equiv-1(\\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to\n\n$$\n\\varphi(k p)=2 k+3-p \\quad \\text { and } \\quad \\varphi(k p+p)=2 k+1+p\n$$\n\nIf $k$ is divisible by $p$, then $\\varphi(k p)$ is also divisible by $p$, so $p \\mid 2 k+3$ and hence $p \\mid 3$, a contradiction. Similarly, $p \\nmid k+1$. It follows that $\\varphi(k p)=(p-1) \\varphi(k)$ and $\\varphi(k p+p)=(p-1) \\varphi(k+1)$ which together with (1) yields\n\n$$\n\\varphi(k)=\\frac{2 k+2}{p-1}-1 \\quad \\text { and } \\quad \\varphi(k+1)=\\frac{2 k+2}{p-1}+1\n$$\n\nFrom here we see that $\\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \\in \\mathbb{N}$, or $t \\in\\{1,2,4\\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \\varphi\\left(q^{i}\\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\\frac{2}{3}\\left(2 q^{i}+2\\right)$. The other three cases are similarly shown to be impossible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
+
{"year": "2010", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute-angled triangle with orthocenter $H$ and let $M$ be the midpoint of $A C$. The foot of the altitude from $C$ is $C_{1}$. Point $H_{1}$ is symmetric to $H$ in $A B$. The projections of $C_{1}$ on lines $A H_{1}, A C$ and $B C$ are $P, Q$ and $R$ respectively. If $M_{1}$ is the circumcenter of triangle $P Q R$, prove that the point symmetric to $M$ with respect to $M_{1}$ lies on line $B H_{1}$.\n(Serbia)", "solution": "We shall use the following simple statement.\n\nLemma. Let $A_{1} A_{2} A_{3} A_{4}$ be a convex cyclic quadrilateral whose diagonals are orthogonal and meet at $X$. If $B_{i}$ is the midpoint of side $A_{i} A_{i+1}$ and $X_{i}$ the projection of $X$ on this side $\\left(A_{5}=A_{1}\\right)$, then the eight points $B_{i}, X_{i}$ $(i=1,2,3,4)$ lie on a circle.\n\nProof. Quadrilateral $B_{1} B_{2} B_{3} B_{4}$ is a rectangle because $B_{1} B_{2}\\left\\|B_{3} B_{4}\\right\\| A_{1} A_{3}$ and $B_{2} B_{3}\\left\\|B_{4} B_{1}\\right\\| A_{2} A_{4}$. Denote by $k$ the circumcircle of $B_{1} B_{2} B_{3} B_{4}$. Since $\\angle B_{3} X A_{3}=\\angle A_{4} A_{3} A_{1}=\\angle A_{4} A_{2} A_{1}=\\angle A_{1} X X_{1}$, points $B_{3}, X, X_{1}$ are collinear, so $X_{1}$ lies on the circle with diameter $B_{1} B_{3}$, i.e. $k$. Similarly, $X_{2}, X_{3}, X_{4}$ lie on $k$.\n\nIt is known that $H_{1}$ lies on the circumcircle of $A B C$. By the lemma, points $P, Q, R$ all lie on the circle with diameter $M N$, where $N$ is the midpoint of $B H_{1}$. Therefore $N$ is symmetric to $M$ with respect to $M_{1}$ and lies on $B H_{1}$ as desired.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
+
{"year": "2010", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "We define a $w$-strip as the set of all points in the plane that are between or on two parallel lines on a mutual distance $w$. Let $S$ be a set of $n$ points in the plane such that any three points from $S$ can be covered by a 1 -strip. Show that the entire set $S$ can be covered by a 2 -strip.\n(Romania)", "solution": "Of all triangles with the vertices in $S$, consider one with a maximum area, say $\\triangle A B C$. Let $A^{\\prime}, B^{\\prime}, C^{\\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$, respectively. We claim that all points from $S$ must lie inside or on the boundary of $\\triangle A^{\\prime} B^{\\prime} C^{\\prime}$. Indeed, if $X \\in S$ is outside $\\triangle A^{\\prime} B^{\\prime} C^{\\prime}$, we can assume without loss of generality that $X$ and $B C$ are on different sides of $B^{\\prime} C^{\\prime}$, and then $\\triangle B C X$ has an area greater than $\\triangle A B C$, a contradiction.\nThe triangle $A B C$ can be covered by a 1-strip, so the triangle $A^{\\prime} B^{\\prime} C^{\\prime}$, being similar to $A B C$ with ratio 2 , can be covered by a 2 -strip, also covering all of $S$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
+
{"year": "2010", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "For every integer $n \\geq 2$, denote by $f(n)$ the sum of positive integers not exceeding $n$ that are not coprime to $n$. Prove that $f(n+p) \\neq f(n)$ for any such $n$ and any prime number $p$.\n(Turkey)\n\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "There are $n+1-\\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\\frac{1}{2} n(n+1-\\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \\in \\mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\\varphi(k p))=(k+1)(k p+p+$ $1-\\varphi(k p+p)$ ), so\n\n$$\nk p+1-\\varphi(k p)=(k+1) x \\quad \\text { and } \\quad k p+p+1-\\varphi(k p+p)=k x\n$$\n\nfor some $x \\in \\mathbb{N}, x<p$. Subtraction gives us $x=\\varphi(k p+p)-\\varphi(k p)-p$. Since $\\varphi(k p)$ and $\\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\\varphi(n)$ ), we obtain $x \\equiv-1(\\bmod p-1)$.\nIf $p=2$ then $x=1$ and $\\varphi(2 k+2)=k+3$, which is impossible because $\\varphi(2 k+2) \\leq$ $k+1$. If $p=3$ then $x=1$ and $\\varphi(3 k+3)=2 k+4$, again impossible because $\\varphi(3 k+3) \\leq 2 k+2$. Therefore $p \\geq 5$, so $x \\equiv-1(\\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to\n\n$$\n\\varphi(k p)=2 k+3-p \\quad \\text { and } \\quad \\varphi(k p+p)=2 k+1+p\n$$\n\nIf $k$ is divisible by $p$, then $\\varphi(k p)$ is also divisible by $p$, so $p \\mid 2 k+3$ and hence $p \\mid 3$, a contradiction. Similarly, $p \\nmid k+1$. It follows that $\\varphi(k p)=(p-1) \\varphi(k)$ and $\\varphi(k p+p)=(p-1) \\varphi(k+1)$ which together with (1) yields\n\n$$\n\\varphi(k)=\\frac{2 k+2}{p-1}-1 \\quad \\text { and } \\quad \\varphi(k+1)=\\frac{2 k+2}{p-1}+1\n$$\n\nFrom here we see that $\\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \\in \\mathbb{N}$, or $t \\in\\{1,2,4\\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \\varphi\\left(q^{i}\\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\\frac{2}{3}\\left(2 q^{i}+2\\right)$. The other three cases are similarly shown to be impossible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
Balkan_MO/segmented/en-2011-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2011", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C D$ be a cyclic quadrilateral which is not a trapezoid and whose diagonals meet at $E$. The midpoints of $A B$ and $C D$ are $F$ and $G$ respectively, and $\\ell$ is the line through $G$ parallel to $A B$. The feet of the perpendiculars from $E$ onto the lines $\\ell$ and $C D$ are $H$ and $K$, respectively. Prove that the lines $E F$ and $H K$ are perpendicular.", "solution": "The points $E, K, H, G$ are on the circle of diameter $G E$, so\n\n$$\n\\angle E H K=\\angle E G K\n$$\n\nAlso, from $\\angle D C A=\\angle D B A$ and $\\frac{C E}{C D}=\\frac{B E}{B A}$ it follows\n\n$$\n\\frac{C E}{C G}=\\frac{2 C E}{C D}=\\frac{2 B E}{B A}=\\frac{B E}{B F},\n$$\n\ntherefore $\\triangle C G E \\sim \\triangle B F E$. In particular, $\\angle E G C=\\angle B F E$, so by $(\\dagger)$\n\n$$\n\\angle E H K=\\angle B F E .\n$$\n\nBut $H E \\perp F B$ and so, since $F E$ and $H K$ are obtained by rotations of these lines by the same (directed) angle, $F E \\perp H K$.\n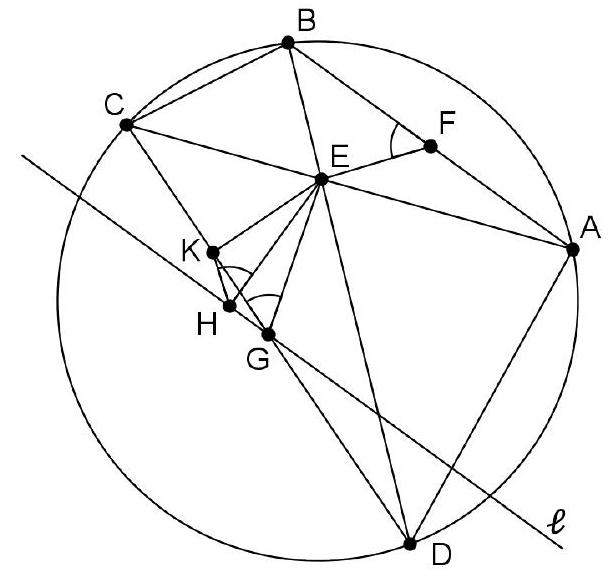\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 1", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2011", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Given real numbers $x, y, z$ such that $x+y+z=0$, show that\n\n$$\n\\frac{x(x+2)}{2 x^{2}+1}+\\frac{y(y+2)}{2 y^{2}+1}+\\frac{z(z+2)}{2 z^{2}+1} \\geq 0 .\n$$\n\nWhen does equality hold?", "solution": "The inequality is clear if $x y z=0$, in which case equality holds if and only if $x=y=z=0$.\n\nHenceforth assume $x y z \\neq 0$ and rewrite the inequality as\n\n$$\n\\frac{(2 x+1)^{2}}{2 x^{2}+1}+\\frac{(2 y+1)^{2}}{2 y^{2}+1}+\\frac{(2 z+1)^{2}}{2 z^{2}+1} \\geq 3 .\n$$\n\nNotice that (exactly) one of the products $x y, y z, z x$ is positive, say $y z>0$, to get\n\n$$\n\\begin{array}{rlr}\n\\frac{(2 y+1)^{2}}{2 y^{2}+1}+\\frac{(2 z+1)^{2}}{2 z^{2}+1} & \\geq \\frac{2(y+z+1)^{2}}{y^{2}+z^{2}+1} & \\text { (by Jensen) } \\\\\n& =\\frac{2(x-1)^{2}}{x^{2}-2 y z+1} & (\\text { for } x+y+z=0) \\\\\n& \\geq \\frac{2(x-1)^{2}}{x^{2}+1} . & (\\text { for } y z>0)\n\\end{array}\n$$\n\nHere equality holds if and only if $x=1$ and $y=z=-1 / 2$. Finally, since\n\n$$\n\\frac{(2 x+1)^{2}}{2 x^{2}+1}+\\frac{2(x-1)^{2}}{x^{2}+1}-3=\\frac{2 x^{2}(x-1)^{2}}{\\left(2 x^{2}+1\\right)\\left(x^{2}+1\\right)} \\geq 0, \\quad x \\in \\mathbb{R},\n$$\n\nthe conclusion follows. Clearly, equality holds if and only if $x=1$, so $y=z=-1 / 2$. Therefore, if $x y z \\neq 0$, equality holds if and only if one of the numbers is 1 , and the other two are $-1 / 2$.\n\nMarking Scheme. Proving the inequality and identifying the equality case when one of the variables vanishes\n\n\nApplying Jensen or Cauchy-Schwarz inequality to the fractions involving the pair of numbers of the same sign 3p\nProducing the corresponding lower bound in the third variable ................... 3p\n\n\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 2", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2011", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $S$ be a finite set of positive integers which has the following property: if $x$ is a member of $S$, then so are all positive divisors of $x$. A non-empty subset $T$ of $S$ is good if whenever $x, y \\in T$ and $x<y$, the ratio $y / x$ is a power of a prime number. A non-empty subset $T$ of $S$ is bad if whenever $x, y \\in T$ and $x<y$, the ratio $y / x$ is not a power of a prime number. We agree that a singleton subset of $S$ is both good and bad. Let $k$ be the largest possible size of a good subset of $S$. Prove that $k$ is also the smallest number of pairwise-disjoint bad subsets whose union is $S$.", "solution": "Notice first that a bad subset of $S$ contains at most one element from a good one, to deduce that a partition of $S$ into bad subsets has at least as many members as a maximal good subset.\n\nNotice further that the elements of a good subset of $S$ must be among the terms of a geometric sequence whose ratio is a prime: if $x<y<z$ are elements of a good subset of $S$, then $y=x p^{\\alpha}$ and $z=y q^{\\beta}=x p^{\\alpha} q^{\\beta}$ for some primes $p$ and $q$ and some positive integers $\\alpha$ and $\\beta$, so $p=q$ for $z / x$ to be a power of a prime.\nNext, let $P=\\{2,3,5,7,11, \\cdots\\}$ denote the set of all primes, let\n\n$$\nm=\\max \\left\\{\\exp _{p} x: x \\in S \\text { and } p \\in P\\right\\}\n$$\n\nwhere $\\exp _{p} x$ is the exponent of the prime $p$ in the canonical decomposition of $x$, and notice that a maximal good subset of $S$ must be of the form $\\left\\{a, a p, \\cdots, a p^{m}\\right\\}$ for some prime $p$ and some positive integer $a$ which is not divisible by $p$. Consequently, a maximal good subset of $S$ has $m+1$ elements, so a partition of $S$ into bad subsets has at least $m+1$ members.\n\nFinally, notice by maximality of $m$ that the sets\n\n$$\nS_{k}=\\left\\{x: x \\in S \\text { and } \\sum_{p \\in P} \\exp _{p} x \\equiv k(\\bmod m+1)\\right\\}, \\quad k=0,1, \\cdots, m\n$$\n\nform a partition of $S$ into $m+1$ bad subsets. The conclusion follows.\n Considering the maximal exponent $m$ of a prime and deriving $k=m+1 \\ldots \\ldots \\mathbf{1 p}$ Noticing that the intersection of a bad set and a good set contains at most one element and infering that a partition of $S$ into bad sets has at least $k$ members.....2p\n\nProducing a partition of $S$ into $k$ bad subsets . . . . . . . . . . . . . . . . . . . . . . .\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 3", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2011", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $A B C D E F$ be a convex hexagon of area 1 , whose opposite sides are parallel. The lines $A B, C D$ and $E F$ meet in pairs to determine the vertices of a triangle. Similarly, the lines $B C, D E$ and $F A$ meet in pairs to determine the vertices of another triangle. Show that the area of at least one of these two triangles is at least $3 / 2$.", "solution": "Unless otherwise stated, throughout the proof indices take on values from 0 to 5 and are reduced modulo 6 . Label the vertices of the hexagon in circular order, $A_{0}, A_{1}, \\cdots, A_{5}$, and let the lines of support of the alternate sides $A_{i} A_{i+1}$ and $A_{i+2} A_{i+3}$ meet at $B_{i}$. To show that the area of at least one of the triangles $B_{0} B_{2} B_{4}, B_{1} B_{3} B_{5}$ is greater than or equal to $3 / 2$, it is sufficient to prove that the total area of the six triangles $A_{i+1} B_{i} A_{i+2}$ is at least 1:\n\n$$\n\\sum_{i=0}^{5} \\operatorname{area} A_{i+1} B_{i} A_{i+2} \\geq 1\n$$\n\nTo begin with, reflect each $B_{i}$ through the midpoint of the segment $A_{i+1} A_{i+2}$ to get the points $B_{i}^{\\prime}$. We shall prove that the six triangles $A_{i+1} B_{i}^{\\prime} A_{i+2}$ cover the hexagon. To this end, reflect $A_{2 i+1}$ through the midpoint of the segment $A_{2 i} A_{2 i+2}$ to get the points $A_{2 i+1}^{\\prime}$, $i=0,1,2$. The hexagon splits into three parallelograms, $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\\prime}, i=0,1,2$, and a (possibly degenerate) triangle, $A_{1}^{\\prime} A_{3}^{\\prime} A_{5}^{\\prime}$. Notice first that each parallelogram $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\\prime}$ is covered by the pair of triangles $\\left(A_{2 i} B_{2 i+5}^{\\prime} A_{2 i+1}, A_{2 i+1} B_{2 i}^{\\prime} A_{2 i+2}\\right)$, $i=0,1,2$. The proof is completed by showing that at least one of these pairs contains a triangle that covers the triangle $A_{1}^{\\prime} A_{3}^{\\prime} A_{5}^{\\prime}$. To this end, it is sufficient to prove that $A_{2 i} B_{2 i+5}^{\\prime} \\geq A_{2 i} A_{2 i+5}^{\\prime}$ and $A_{2 j+2} B_{2 j}^{\\prime} \\geq A_{2 j+2} A_{2 j+3}^{\\prime}$ for some indices $i, j \\in\\{0,1,2\\}$. To establish the first inequality, notice that\n\n$$\n\\begin{gathered}\nA_{2 i} B_{2 i+5}^{\\prime}=A_{2 i+1} B_{2 i+5}, \\quad A_{2 i} A_{2 i+5}^{\\prime}=A_{2 i+4} A_{2 i+5}, \\quad i=0,1,2, \\\\\n\\\\\n\\frac{A_{1} B_{5}}{A_{4} A_{5}}=\\frac{A_{0} B_{5}}{A_{5} B_{3}} \\quad \\text { and } \\quad \\frac{A_{3} B_{1}}{A_{0} A_{1}}=\\frac{A_{2} A_{3}}{A_{0} B_{5}},\n\\end{gathered}\n$$\n\nto get\n\n$$\n\\prod_{i=0}^{2} \\frac{A_{2 i} B_{2 i+5}^{\\prime}}{A_{2 i} A_{2 i+5}^{\\prime}}=1\n$$\n\nSimilarly,\n\n$$\n\\prod_{j=0}^{2} \\frac{A_{2 j+2} B_{2 j}^{\\prime}}{A_{2 j+2} A_{2 j+3}^{\\prime}}=1\n$$\n\nwhence the conclusion.\n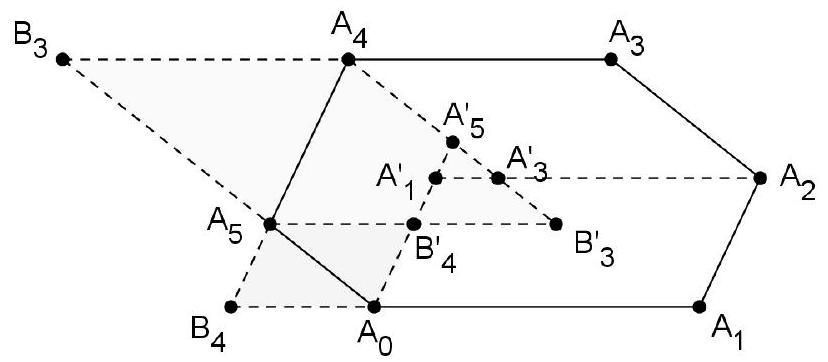\n\nMarking Scheme. Stating that the total area of the small triangles $\\geq 1 \\ldots \\ldots . . \\mathbf{1 p}$\n\nDecomposition of the hexagon into three adequate parallelograms and a triangle $\\mathbf{1 p}$\nProving that each pair of triangles adjacent to a parallelogram covers that parallelogram\n\nProving the central triangle also covered 5p\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 4", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2011", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C D$ be a cyclic quadrilateral which is not a trapezoid and whose diagonals meet at $E$. The midpoints of $A B$ and $C D$ are $F$ and $G$ respectively, and $\\ell$ is the line through $G$ parallel to $A B$. The feet of the perpendiculars from $E$ onto the lines $\\ell$ and $C D$ are $H$ and $K$, respectively. Prove that the lines $E F$ and $H K$ are perpendicular.", "solution": "The points $E, K, H, G$ are on the circle of diameter $G E$, so\n\n$$\n\\angle E H K=\\angle E G K\n$$\n\nAlso, from $\\angle D C A=\\angle D B A$ and $\\frac{C E}{C D}=\\frac{B E}{B A}$ it follows\n\n$$\n\\frac{C E}{C G}=\\frac{2 C E}{C D}=\\frac{2 B E}{B A}=\\frac{B E}{B F},\n$$\n\ntherefore $\\triangle C G E \\sim \\triangle B F E$. In particular, $\\angle E G C=\\angle B F E$, so by $(\\dagger)$\n\n$$\n\\angle E H K=\\angle B F E .\n$$\n\nBut $H E \\perp F B$ and so, since $F E$ and $H K$ are obtained by rotations of these lines by the same (directed) angle, $F E \\perp H K$.\n\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 1", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2011", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Given real numbers $x, y, z$ such that $x+y+z=0$, show that\n\n$$\n\\frac{x(x+2)}{2 x^{2}+1}+\\frac{y(y+2)}{2 y^{2}+1}+\\frac{z(z+2)}{2 z^{2}+1} \\geq 0 .\n$$\n\nWhen does equality hold?", "solution": "The inequality is clear if $x y z=0$, in which case equality holds if and only if $x=y=z=0$.\n\nHenceforth assume $x y z \\neq 0$ and rewrite the inequality as\n\n$$\n\\frac{(2 x+1)^{2}}{2 x^{2}+1}+\\frac{(2 y+1)^{2}}{2 y^{2}+1}+\\frac{(2 z+1)^{2}}{2 z^{2}+1} \\geq 3 .\n$$\n\nNotice that (exactly) one of the products $x y, y z, z x$ is positive, say $y z>0$, to get\n\n$$\n\\begin{array}{rlr}\n\\frac{(2 y+1)^{2}}{2 y^{2}+1}+\\frac{(2 z+1)^{2}}{2 z^{2}+1} & \\geq \\frac{2(y+z+1)^{2}}{y^{2}+z^{2}+1} & \\text { (by Jensen) } \\\\\n& =\\frac{2(x-1)^{2}}{x^{2}-2 y z+1} & (\\text { for } x+y+z=0) \\\\\n& \\geq \\frac{2(x-1)^{2}}{x^{2}+1} . & (\\text { for } y z>0)\n\\end{array}\n$$\n\nHere equality holds if and only if $x=1$ and $y=z=-1 / 2$. Finally, since\n\n$$\n\\frac{(2 x+1)^{2}}{2 x^{2}+1}+\\frac{2(x-1)^{2}}{x^{2}+1}-3=\\frac{2 x^{2}(x-1)^{2}}{\\left(2 x^{2}+1\\right)\\left(x^{2}+1\\right)} \\geq 0, \\quad x \\in \\mathbb{R},\n$$\n\nthe conclusion follows. Clearly, equality holds if and only if $x=1$, so $y=z=-1 / 2$. Therefore, if $x y z \\neq 0$, equality holds if and only if one of the numbers is 1 , and the other two are $-1 / 2$.\n\nMarking Scheme. Proving the inequality and identifying the equality case when one of the variables vanishes\n\n\nApplying Jensen or Cauchy-Schwarz inequality to the fractions involving the pair of numbers of the same sign 3p\nProducing the corresponding lower bound in the third variable ................... 3p\n\n\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 2", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2011", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $S$ be a finite set of positive integers which has the following property: if $x$ is a member of $S$, then so are all positive divisors of $x$. A non-empty subset $T$ of $S$ is good if whenever $x, y \\in T$ and $x<y$, the ratio $y / x$ is a power of a prime number. A non-empty subset $T$ of $S$ is bad if whenever $x, y \\in T$ and $x<y$, the ratio $y / x$ is not a power of a prime number. We agree that a singleton subset of $S$ is both good and bad. Let $k$ be the largest possible size of a good subset of $S$. Prove that $k$ is also the smallest number of pairwise-disjoint bad subsets whose union is $S$.", "solution": "Notice first that a bad subset of $S$ contains at most one element from a good one, to deduce that a partition of $S$ into bad subsets has at least as many members as a maximal good subset.\n\nNotice further that the elements of a good subset of $S$ must be among the terms of a geometric sequence whose ratio is a prime: if $x<y<z$ are elements of a good subset of $S$, then $y=x p^{\\alpha}$ and $z=y q^{\\beta}=x p^{\\alpha} q^{\\beta}$ for some primes $p$ and $q$ and some positive integers $\\alpha$ and $\\beta$, so $p=q$ for $z / x$ to be a power of a prime.\nNext, let $P=\\{2,3,5,7,11, \\cdots\\}$ denote the set of all primes, let\n\n$$\nm=\\max \\left\\{\\exp _{p} x: x \\in S \\text { and } p \\in P\\right\\}\n$$\n\nwhere $\\exp _{p} x$ is the exponent of the prime $p$ in the canonical decomposition of $x$, and notice that a maximal good subset of $S$ must be of the form $\\left\\{a, a p, \\cdots, a p^{m}\\right\\}$ for some prime $p$ and some positive integer $a$ which is not divisible by $p$. Consequently, a maximal good subset of $S$ has $m+1$ elements, so a partition of $S$ into bad subsets has at least $m+1$ members.\n\nFinally, notice by maximality of $m$ that the sets\n\n$$\nS_{k}=\\left\\{x: x \\in S \\text { and } \\sum_{p \\in P} \\exp _{p} x \\equiv k(\\bmod m+1)\\right\\}, \\quad k=0,1, \\cdots, m\n$$\n\nform a partition of $S$ into $m+1$ bad subsets. The conclusion follows.\n Considering the maximal exponent $m$ of a prime and deriving $k=m+1 \\ldots \\ldots \\mathbf{1 p}$ Noticing that the intersection of a bad set and a good set contains at most one element and infering that a partition of $S$ into bad sets has at least $k$ members.....2p\n\nProducing a partition of $S$ into $k$ bad subsets . . . . . . . . . . . . . . . . . . . . . . .\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 3", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2011", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C D E F$ be a convex hexagon of area 1 , whose opposite sides are parallel. The lines $A B, C D$ and $E F$ meet in pairs to determine the vertices of a triangle. Similarly, the lines $B C, D E$ and $F A$ meet in pairs to determine the vertices of another triangle. Show that the area of at least one of these two triangles is at least $3 / 2$.", "solution": "Unless otherwise stated, throughout the proof indices take on values from 0 to 5 and are reduced modulo 6 . Label the vertices of the hexagon in circular order, $A_{0}, A_{1}, \\cdots, A_{5}$, and let the lines of support of the alternate sides $A_{i} A_{i+1}$ and $A_{i+2} A_{i+3}$ meet at $B_{i}$. To show that the area of at least one of the triangles $B_{0} B_{2} B_{4}, B_{1} B_{3} B_{5}$ is greater than or equal to $3 / 2$, it is sufficient to prove that the total area of the six triangles $A_{i+1} B_{i} A_{i+2}$ is at least 1:\n\n$$\n\\sum_{i=0}^{5} \\operatorname{area} A_{i+1} B_{i} A_{i+2} \\geq 1\n$$\n\nTo begin with, reflect each $B_{i}$ through the midpoint of the segment $A_{i+1} A_{i+2}$ to get the points $B_{i}^{\\prime}$. We shall prove that the six triangles $A_{i+1} B_{i}^{\\prime} A_{i+2}$ cover the hexagon. To this end, reflect $A_{2 i+1}$ through the midpoint of the segment $A_{2 i} A_{2 i+2}$ to get the points $A_{2 i+1}^{\\prime}$, $i=0,1,2$. The hexagon splits into three parallelograms, $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\\prime}, i=0,1,2$, and a (possibly degenerate) triangle, $A_{1}^{\\prime} A_{3}^{\\prime} A_{5}^{\\prime}$. Notice first that each parallelogram $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\\prime}$ is covered by the pair of triangles $\\left(A_{2 i} B_{2 i+5}^{\\prime} A_{2 i+1}, A_{2 i+1} B_{2 i}^{\\prime} A_{2 i+2}\\right)$, $i=0,1,2$. The proof is completed by showing that at least one of these pairs contains a triangle that covers the triangle $A_{1}^{\\prime} A_{3}^{\\prime} A_{5}^{\\prime}$. To this end, it is sufficient to prove that $A_{2 i} B_{2 i+5}^{\\prime} \\geq A_{2 i} A_{2 i+5}^{\\prime}$ and $A_{2 j+2} B_{2 j}^{\\prime} \\geq A_{2 j+2} A_{2 j+3}^{\\prime}$ for some indices $i, j \\in\\{0,1,2\\}$. To establish the first inequality, notice that\n\n$$\n\\begin{gathered}\nA_{2 i} B_{2 i+5}^{\\prime}=A_{2 i+1} B_{2 i+5}, \\quad A_{2 i} A_{2 i+5}^{\\prime}=A_{2 i+4} A_{2 i+5}, \\quad i=0,1,2, \\\\\n\\\\\n\\frac{A_{1} B_{5}}{A_{4} A_{5}}=\\frac{A_{0} B_{5}}{A_{5} B_{3}} \\quad \\text { and } \\quad \\frac{A_{3} B_{1}}{A_{0} A_{1}}=\\frac{A_{2} A_{3}}{A_{0} B_{5}},\n\\end{gathered}\n$$\n\nto get\n\n$$\n\\prod_{i=0}^{2} \\frac{A_{2 i} B_{2 i+5}^{\\prime}}{A_{2 i} A_{2 i+5}^{\\prime}}=1\n$$\n\nSimilarly,\n\n$$\n\\prod_{j=0}^{2} \\frac{A_{2 j+2} B_{2 j}^{\\prime}}{A_{2 j+2} A_{2 j+3}^{\\prime}}=1\n$$\n\nwhence the conclusion.\n\n\nMarking Scheme. Stating that the total area of the small triangles $\\geq 1 \\ldots \\ldots . . \\mathbf{1 p}$\n\nDecomposition of the hexagon into three adequate parallelograms and a triangle $\\mathbf{1 p}$\nProving that each pair of triangles adjacent to a parallelogram covers that parallelogram\n\nProving the central triangle also covered 5p\nRemark. Any partial or equivalent approach should be marked accordingly.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl", "problem_match": "# PROBLEM 4", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2012-BMO-type3.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "2012", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "\\quad$ Let $A, B$ and $C$ be points lying on a circle $\\Gamma$ with centre $O$. Assume that $\\angle A B C>90$. Let $D$ be the point of intersection of the line $A B$ with the line perpendicular to $A C$ at $C$. Let $l$ be the line through $D$ which is perpendicular to $A O$. Let $E$ be the point of intersection of $l$ with the line $A C$, and let $F$ be the point of intersection of $\\Gamma$ with $l$ that lies between $D$ and $E$.\nProve that the circumcircles of triangles $B F E$ and $C F D$ are tangent at $F$.", "solution": "Let $\\ell \\cap A O=\\{K\\}$ and $G$ be the other end point of the diameter of $\\Gamma$ through $A$. Then $D, C, G$ are collinear. Moreover, $E$ is the orthocenter of triangle $A D G$. Therefore $G E \\perp A D$ and $G, E, B$ are collinear.\n\n\nAs $\\angle C D F=\\angle G D K=\\angle G A C=\\angle G F C, F G$ is tangent to the circumcircle of triangle $C F D$ at $F$. As $\\angle F B E=\\angle F B G=\\angle F A G=\\angle G F K=\\angle G F E, F G$ is also tangent to the circumcircle of $B F E$ at $F$. Hence the circumcircles of the triangles $C F D$ and $B F E$ are tangent at $F$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2012", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Prove that\n\n$$\n\\sum_{c y c}(x+y) \\sqrt{(z+x)(z+y)} \\geq 4(x y+y z+z x),\n$$\n\nfor all positive real numbers $x, y$ and $z$.", "solution": "We will obtain the inequality by adding the inequalities\n\n$$\n(x+y) \\sqrt{(z+x)(z+y)} \\geq 2 x y+y z+z x\n$$\n\nfor cyclic permutation of $x, y, z$.\nSquaring both sides of this inequality we obtain\n\n$$\n(x+y)^{2}(z+x)(z+y) \\geq 4 x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}+4 x y^{2} z+4 x^{2} y z+2 x y z^{2}\n$$\n\nwhich is equivalent to\n\n$$\nx^{3} y+x y^{3}+z\\left(x^{3}+y^{3}\\right) \\geq 2 x^{2} y^{2}+x y z(x+y)\n$$\n\nwhich can be rearranged to\n\n$$\n(x y+y z+z x)(x-y)^{2} \\geq 0\n$$\n\nwhich is clearly true.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
-
{"year": "2012", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Prove that\n\n$$\n\\sum_{c y c}(x+y) \\sqrt{(z+x)(z+y)} \\geq 4(x y+y z+z x),\n$$\n\nfor all positive real numbers $x, y$ and $z$.", "solution": "For positive real numbers $x, y, z$ there exists a triangle with the side lengths $\\sqrt{x+y}, \\sqrt{y+z}, \\sqrt{z+x}$ and the area $K=\\sqrt{x y+y z+z x} / 2$.\n\nThe existence of the triangle is clear by simple checking of the triangle inequality. To prove the area formula, we have\n\n$$\nK=\\frac{1}{2} \\sqrt{x+y} \\sqrt{z+x} \\sin \\alpha\n$$\n\nwhere $\\alpha$ is the angle between the sides of length $\\sqrt{x+y}$ and $\\sqrt{z+x}$. On the other hand, from the law of cosines we have\n\n$$\n\\cos \\alpha=\\frac{x+y+z+x-y-z}{2 \\sqrt{(x+y)(z+x)}}=\\frac{x}{\\sqrt{(x+y)(z+x)}}\n$$\n\nand\n\n$$\n\\sin \\alpha=\\sqrt{1-\\cos ^{2} \\alpha}=\\frac{\\sqrt{x y+y z+z x}}{\\sqrt{(x+y)(z+x)}}\n$$\n\nNow the inequality is equivalent to\n\n$$\n\\sqrt{x+y} \\sqrt{y+z} \\sqrt{z+x} \\sum_{c y c} \\sqrt{x+y} \\geq 16 K^{2}\n$$\n\nThis can be rewritten as\n\n$$\n\\frac{\\sqrt{x+y} \\sqrt{y+z} \\sqrt{z+x}}{4 K} \\geq 2 \\frac{K}{\\sum_{c y c} \\sqrt{x+y} / 2}\n$$\n\nto become the Euler inequality $R \\geq 2 r$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 2."}}
|
| 4 |
-
{"year": "2012", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be a positive integer. Let $P_{n}=\\left\\{2^{n}, 2^{n-1} \\cdot 3,2^{n-2} \\cdot 3^{2}, \\ldots, 3^{n}\\right\\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\\emptyset}=0$ where $\\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \\leq y \\leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \\leq y-S_{Y}<2^{n}$", "solution": "Let $\\alpha=3 / 2$ so $1+\\alpha>\\alpha^{2}$.\nGiven $y$, we construct $Y$ algorithmically. Let $Y=\\varnothing$ and of course $S_{\\varnothing}=0$. For $i=0$ to $m$, perform the following operation:\n\n$$\n\\text { If } S_{Y}+2^{i} 3^{m-i} \\leq y \\text {, then replace } Y \\text { by } Y \\cup\\left\\{2^{i} 3^{m-i}\\right\\}\n$$\n\nWhen this process is finished, we have a subset $Y$ of $P_{m}$ such that $S_{Y} \\leq y$.\nNotice that the elements of $P_{m}$ are in ascending order of size as given, and may alternatively be described as $2^{m}, 2^{m} \\alpha, 2^{m} \\alpha^{2}, \\ldots, 2^{m} \\alpha^{m}$. If any member of this list is not in $Y$, then no two consecutive members of the list to the left of the omitted member can both be in $Y$. This is because $1+\\alpha>\\alpha^{2}$, and the greedy nature of the process used to construct $Y$.\n\nTherefore either $Y=P_{m}$, in which case $y=3^{m+1}-2^{m+1}$ and all is well, or at least one of the two leftmost elements of the list is omitted from $Y$.\n\nIf $2^{m}$ is not omitted from $Y$, then the algorithmic process ensures that $\\left(S_{Y}-2^{m}\\right)+2^{m-1} 3>y$, and so $y-S_{Y}<2^{m}$. On the other hand, if $2^{m}$ is omitted from $Y$, then $y-S_{Y}<2^{m}$ ).", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution 1."}}
|
| 5 |
-
{"year": "2012", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $n$ be a positive integer. Let $P_{n}=\\left\\{2^{n}, 2^{n-1} \\cdot 3,2^{n-2} \\cdot 3^{2}, \\ldots, 3^{n}\\right\\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\\emptyset}=0$ where $\\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \\leq y \\leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \\leq y-S_{Y}<2^{n}$", "solution": "Note that $3^{m+1}-2^{m+1}=(3-2)\\left(3^{m}+3^{m-1} \\cdot 2+\\cdots+3 \\cdot 2^{m-1}+2^{m}\\right)=S_{P_{m}}$. Dividing every element of $P_{m}$ by $2^{m}$ gives us the following equivalent problem:\n\nLet $m$ be a positive integer, $a=3 / 2$, and $Q_{m}=\\left\\{1, a, a^{2}, \\ldots, a^{m}\\right\\}$. Show that for any real number $x$ satisfying $0 \\leq x \\leq 1+a+a^{2}+\\cdots+a^{m}$, there exists a subset $X$ of $Q_{m}$ such that $0 \\leq x-S_{X}<1$.\n\nWe will prove this problem by induction on $m$. When $m=1, S_{\\varnothing}=0, S_{\\{1\\}}=1, S_{\\{a\\}}=3 / 2$, $S_{\\{1, a\\}}=5 / 2$. Since the difference between any two consecutive of them is at most 1, the claim is true.\n\nSuppose that the statement is true for positive integer $m$. Let $x$ be a real number with $0 \\leq$ $x \\leq 1+a+a^{2}+\\cdots+a^{m+1}$. If $0 \\leq x \\leq 1+a+a^{2}+\\cdots+a^{m}$, then by the induction hypothesis there exists a subset $X$ of $Q_{m} \\subset Q_{m+1}$ such that $0 \\leq x-S_{X}<1$.\nIf $\\frac{a^{m+1}-1}{a-1}=1+a+a^{2}+\\cdots+a^{m}<x$, then $x>a^{m+1}$ as\n\n$$\n\\frac{a^{m+1}-1}{a-1}=2\\left(a^{m+1}-1\\right)=a^{m+1}+\\left(a^{m+1}-2\\right) \\geq a^{m+1}+a^{2}-2=a^{m+1}+\\frac{1}{4} .\n$$\n\nTherefore $0<\\left(x-a^{m+1}\\right) \\leq 1+a+a^{2}+\\cdots+a^{m}$. Again by the induction hypothesis, there exists a subset $X$ of $Q_{m}$ satisfying $0 \\leq\\left(x-a^{m+1}\\right)-S_{X}<1$. Hence $0 \\leq x-S_{X^{\\prime}}<1$ where $X^{\\prime}=X \\cup\\left\\{a^{m+1}\\right\\} \\subset Q_{m+1}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution 2."}}
|
| 6 |
-
{"year": "2012", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "\\quad$ Let $\\mathbb{Z}^{+}$be the set of positive integers. Find all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$such that the following conditions both hold:\n(i) $f(n!)=f(n)$ ! for every positive integer $n$,\n(ii) $m-n$ divides $f(m)-f(n)$ whenever $m$ and $n$ are different positive integers.", "solution": "There are three such functions: the constant functions 1, 2 and the identity function $\\mathrm{id}_{\\mathbf{Z}^{+}}$. These functions clearly satisfy the conditions in the hypothesis. Let us prove that there are only ones.\n\nConsider such a function $f$ and suppose that it has a fixed point $a \\geq 3$, that is $f(a)=a$. Then $a!,(a!)!, \\cdots$ are all fixed points of $f$, hence the function $f$ has a strictly increasing sequence $a_{1}<a_{2}<\\cdots<a_{k}<\\cdots$ of fixed points. For a positive integer $n$, $a_{k}-n$ divides $a_{k}-f(n)=$ $f\\left(a_{k}\\right)-f(n)$ for every $k \\in \\mathbf{Z}^{+}$. Also $a_{k}-n$ divides $a_{k}-n$, so it divides $a_{k}-f(n)-\\left(a_{k}-n\\right)=$ $n-f(n)$. This is possible only if $f(n)=n$, hence in this case we get $f=\\mathrm{id}_{\\mathbf{Z}^{+}}$.\n\nNow suppose that $f$ has no fixed points greater than 2 . Let $p \\geq 5$ be a prime and notice that by Wilson's Theorem we have $(p-2)!\\equiv 1(\\bmod p)$. Therefore $p$ divides $(p-2)!-1$. But $(p-2)!-1$ divides $f((p-2)!)-f(1)$, hence $p$ divides $f((p-2)!)-f(1)=(f(p-2))!-f(1)$. Clearly we have $f(1)=1$ or $f(1)=2$. As $p \\geq 5$, the fact that $p$ divides $(f(p-2))!-f(1)$ implies that $f(p-2)<p$. It is easy to check, again by Wilson's Theorem, that $p$ does not divide $(p-1)!-1$ and $(p-1)!-2$, hence we deduce that $f(p-2) \\leq p-2$. On the other hand, $p-3=(p-2)-1$ divides $f(p-2)-f(1) \\leq(p-2)-1$. Thus either $f(p-2)=f(1)$ or $f(p-2)=p-2$. As $p-2 \\geq 3$, the last case is excluded, since the function $f$ has no fixed points greater than 2 . It follows $f(p-2)=f(1)$ and this property holds for all primes $p \\geq 5$. Taking $n$ any positive integer, we deduce that $p-2-n$ divides $f(p-2)-f(n)=f(1)-f(n)$ for all primes $p \\geq 5$. Thus $f(n)=f(1)$, hence $f$ is the constant function 1 or 2 .", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 1."}}
|
| 7 |
-
{"year": "2012", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "\\quad$ Let $\\mathbb{Z}^{+}$be the set of positive integers. Find all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$such that the following conditions both hold:\n(i) $f(n!)=f(n)$ ! for every positive integer $n$,\n(ii) $m-n$ divides $f(m)-f(n)$ whenever $m$ and $n$ are different positive integers.", "solution": "Note first that if $f\\left(n_{0}\\right)=n_{0}$, then $m-n_{0} \\mid f(m)-m$ for all $m \\in \\mathbf{Z}^{+}$. If $f\\left(n_{0}\\right)=n_{0}$ for infinitely many $n_{0} \\in \\mathbf{Z}^{+}$, then $f(m)-m$ has infinitely many divisors, hence $f(m)=m$ for all $m \\in \\mathbf{Z}^{+}$. On the other hand, if $f\\left(n_{0}\\right)=n_{0}$ for some $n_{0} \\geq 3$, then $f$ fixes each term of the sequence $\\left(n_{k}\\right)_{k=0}^{\\infty}$, which is recursively defined by $n_{k}=n_{k-1}!$. Hence if $f(3)=3$, then $f(n)=n$ for all $n \\in \\mathbf{Z}^{+}$.\n\nWe may assume that $f(3) \\neq 3$. Since $f(1)=f(1)!$, and $f(2)=f(2)!, f(1), f(2) \\in\\{1,2\\}$. We have $4=3!-2 \\mid f(3)!-f(2)$. This together with $f(3) \\neq 3$ implies that $f(3) \\in\\{1,2\\}$. Let $n>3$, then $n!-3 \\mid f(n)!-f(3)$ and $3 \\nmid f(n)!$, i.e. $f(n)!\\in\\{1,2\\}$. Hence we conclude that $f(n) \\in\\{1,2\\}$ for all $n \\in \\mathbf{Z}^{+}$.\n\nIf $f$ is not constant, then there exist positive integers $m, n$ with $\\{f(n), f(m)\\}=\\{1,2\\}$. Let $k=2+\\max \\{m, n\\}$. If $f(k) \\neq f(m)$, then $k-m \\mid f(k)-f(m)$. This is a contradiction as $|f(k)-f(m)|=1$ and $k-m \\geq 2$.\n\nTherefore the functions satisfying the conditions are $f \\equiv 1, f \\equiv 2, f=\\mathrm{id}_{\\mathbf{z}^{+}}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 2."}}
|
|
|
|
| 1 |
+
{"year": "2012", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "\\quad$ Let $A, B$ and $C$ be points lying on a circle $\\Gamma$ with centre $O$. Assume that $\\angle A B C>90$. Let $D$ be the point of intersection of the line $A B$ with the line perpendicular to $A C$ at $C$. Let $l$ be the line through $D$ which is perpendicular to $A O$. Let $E$ be the point of intersection of $l$ with the line $A C$, and let $F$ be the point of intersection of $\\Gamma$ with $l$ that lies between $D$ and $E$.\nProve that the circumcircles of triangles $B F E$ and $C F D$ are tangent at $F$.", "solution": "Let $\\ell \\cap A O=\\{K\\}$ and $G$ be the other end point of the diameter of $\\Gamma$ through $A$. Then $D, C, G$ are collinear. Moreover, $E$ is the orthocenter of triangle $A D G$. Therefore $G E \\perp A D$ and $G, E, B$ are collinear.\n\n\nAs $\\angle C D F=\\angle G D K=\\angle G A C=\\angle G F C, F G$ is tangent to the circumcircle of triangle $C F D$ at $F$. As $\\angle F B E=\\angle F B G=\\angle F A G=\\angle G F K=\\angle G F E, F G$ is also tangent to the circumcircle of $B F E$ at $F$. Hence the circumcircles of the triangles $C F D$ and $B F E$ are tangent at $F$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2012", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Prove that\n\n$$\n\\sum_{c y c}(x+y) \\sqrt{(z+x)(z+y)} \\geq 4(x y+y z+z x),\n$$\n\nfor all positive real numbers $x, y$ and $z$.", "solution": "We will obtain the inequality by adding the inequalities\n\n$$\n(x+y) \\sqrt{(z+x)(z+y)} \\geq 2 x y+y z+z x\n$$\n\nfor cyclic permutation of $x, y, z$.\nSquaring both sides of this inequality we obtain\n\n$$\n(x+y)^{2}(z+x)(z+y) \\geq 4 x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}+4 x y^{2} z+4 x^{2} y z+2 x y z^{2}\n$$\n\nwhich is equivalent to\n\n$$\nx^{3} y+x y^{3}+z\\left(x^{3}+y^{3}\\right) \\geq 2 x^{2} y^{2}+x y z(x+y)\n$$\n\nwhich can be rearranged to\n\n$$\n(x y+y z+z x)(x-y)^{2} \\geq 0\n$$\n\nwhich is clearly true.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
+
{"year": "2012", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Prove that\n\n$$\n\\sum_{c y c}(x+y) \\sqrt{(z+x)(z+y)} \\geq 4(x y+y z+z x),\n$$\n\nfor all positive real numbers $x, y$ and $z$.", "solution": "For positive real numbers $x, y, z$ there exists a triangle with the side lengths $\\sqrt{x+y}, \\sqrt{y+z}, \\sqrt{z+x}$ and the area $K=\\sqrt{x y+y z+z x} / 2$.\n\nThe existence of the triangle is clear by simple checking of the triangle inequality. To prove the area formula, we have\n\n$$\nK=\\frac{1}{2} \\sqrt{x+y} \\sqrt{z+x} \\sin \\alpha\n$$\n\nwhere $\\alpha$ is the angle between the sides of length $\\sqrt{x+y}$ and $\\sqrt{z+x}$. On the other hand, from the law of cosines we have\n\n$$\n\\cos \\alpha=\\frac{x+y+z+x-y-z}{2 \\sqrt{(x+y)(z+x)}}=\\frac{x}{\\sqrt{(x+y)(z+x)}}\n$$\n\nand\n\n$$\n\\sin \\alpha=\\sqrt{1-\\cos ^{2} \\alpha}=\\frac{\\sqrt{x y+y z+z x}}{\\sqrt{(x+y)(z+x)}}\n$$\n\nNow the inequality is equivalent to\n\n$$\n\\sqrt{x+y} \\sqrt{y+z} \\sqrt{z+x} \\sum_{c y c} \\sqrt{x+y} \\geq 16 K^{2}\n$$\n\nThis can be rewritten as\n\n$$\n\\frac{\\sqrt{x+y} \\sqrt{y+z} \\sqrt{z+x}}{4 K} \\geq 2 \\frac{K}{\\sum_{c y c} \\sqrt{x+y} / 2}\n$$\n\nto become the Euler inequality $R \\geq 2 r$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 2."}}
|
| 4 |
+
{"year": "2012", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $n$ be a positive integer. Let $P_{n}=\\left\\{2^{n}, 2^{n-1} \\cdot 3,2^{n-2} \\cdot 3^{2}, \\ldots, 3^{n}\\right\\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\\emptyset}=0$ where $\\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \\leq y \\leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \\leq y-S_{Y}<2^{n}$", "solution": "Let $\\alpha=3 / 2$ so $1+\\alpha>\\alpha^{2}$.\nGiven $y$, we construct $Y$ algorithmically. Let $Y=\\varnothing$ and of course $S_{\\varnothing}=0$. For $i=0$ to $m$, perform the following operation:\n\n$$\n\\text { If } S_{Y}+2^{i} 3^{m-i} \\leq y \\text {, then replace } Y \\text { by } Y \\cup\\left\\{2^{i} 3^{m-i}\\right\\}\n$$\n\nWhen this process is finished, we have a subset $Y$ of $P_{m}$ such that $S_{Y} \\leq y$.\nNotice that the elements of $P_{m}$ are in ascending order of size as given, and may alternatively be described as $2^{m}, 2^{m} \\alpha, 2^{m} \\alpha^{2}, \\ldots, 2^{m} \\alpha^{m}$. If any member of this list is not in $Y$, then no two consecutive members of the list to the left of the omitted member can both be in $Y$. This is because $1+\\alpha>\\alpha^{2}$, and the greedy nature of the process used to construct $Y$.\n\nTherefore either $Y=P_{m}$, in which case $y=3^{m+1}-2^{m+1}$ and all is well, or at least one of the two leftmost elements of the list is omitted from $Y$.\n\nIf $2^{m}$ is not omitted from $Y$, then the algorithmic process ensures that $\\left(S_{Y}-2^{m}\\right)+2^{m-1} 3>y$, and so $y-S_{Y}<2^{m}$. On the other hand, if $2^{m}$ is omitted from $Y$, then $y-S_{Y}<2^{m}$ ).", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution 1."}}
|
| 5 |
+
{"year": "2012", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $n$ be a positive integer. Let $P_{n}=\\left\\{2^{n}, 2^{n-1} \\cdot 3,2^{n-2} \\cdot 3^{2}, \\ldots, 3^{n}\\right\\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\\emptyset}=0$ where $\\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \\leq y \\leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \\leq y-S_{Y}<2^{n}$", "solution": "Note that $3^{m+1}-2^{m+1}=(3-2)\\left(3^{m}+3^{m-1} \\cdot 2+\\cdots+3 \\cdot 2^{m-1}+2^{m}\\right)=S_{P_{m}}$. Dividing every element of $P_{m}$ by $2^{m}$ gives us the following equivalent problem:\n\nLet $m$ be a positive integer, $a=3 / 2$, and $Q_{m}=\\left\\{1, a, a^{2}, \\ldots, a^{m}\\right\\}$. Show that for any real number $x$ satisfying $0 \\leq x \\leq 1+a+a^{2}+\\cdots+a^{m}$, there exists a subset $X$ of $Q_{m}$ such that $0 \\leq x-S_{X}<1$.\n\nWe will prove this problem by induction on $m$. When $m=1, S_{\\varnothing}=0, S_{\\{1\\}}=1, S_{\\{a\\}}=3 / 2$, $S_{\\{1, a\\}}=5 / 2$. Since the difference between any two consecutive of them is at most 1, the claim is true.\n\nSuppose that the statement is true for positive integer $m$. Let $x$ be a real number with $0 \\leq$ $x \\leq 1+a+a^{2}+\\cdots+a^{m+1}$. If $0 \\leq x \\leq 1+a+a^{2}+\\cdots+a^{m}$, then by the induction hypothesis there exists a subset $X$ of $Q_{m} \\subset Q_{m+1}$ such that $0 \\leq x-S_{X}<1$.\nIf $\\frac{a^{m+1}-1}{a-1}=1+a+a^{2}+\\cdots+a^{m}<x$, then $x>a^{m+1}$ as\n\n$$\n\\frac{a^{m+1}-1}{a-1}=2\\left(a^{m+1}-1\\right)=a^{m+1}+\\left(a^{m+1}-2\\right) \\geq a^{m+1}+a^{2}-2=a^{m+1}+\\frac{1}{4} .\n$$\n\nTherefore $0<\\left(x-a^{m+1}\\right) \\leq 1+a+a^{2}+\\cdots+a^{m}$. Again by the induction hypothesis, there exists a subset $X$ of $Q_{m}$ satisfying $0 \\leq\\left(x-a^{m+1}\\right)-S_{X}<1$. Hence $0 \\leq x-S_{X^{\\prime}}<1$ where $X^{\\prime}=X \\cup\\left\\{a^{m+1}\\right\\} \\subset Q_{m+1}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution 2."}}
|
| 6 |
+
{"year": "2012", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "\\quad$ Let $\\mathbb{Z}^{+}$be the set of positive integers. Find all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$such that the following conditions both hold:\n(i) $f(n!)=f(n)$ ! for every positive integer $n$,\n(ii) $m-n$ divides $f(m)-f(n)$ whenever $m$ and $n$ are different positive integers.", "solution": "There are three such functions: the constant functions 1, 2 and the identity function $\\mathrm{id}_{\\mathbf{Z}^{+}}$. These functions clearly satisfy the conditions in the hypothesis. Let us prove that there are only ones.\n\nConsider such a function $f$ and suppose that it has a fixed point $a \\geq 3$, that is $f(a)=a$. Then $a!,(a!)!, \\cdots$ are all fixed points of $f$, hence the function $f$ has a strictly increasing sequence $a_{1}<a_{2}<\\cdots<a_{k}<\\cdots$ of fixed points. For a positive integer $n$, $a_{k}-n$ divides $a_{k}-f(n)=$ $f\\left(a_{k}\\right)-f(n)$ for every $k \\in \\mathbf{Z}^{+}$. Also $a_{k}-n$ divides $a_{k}-n$, so it divides $a_{k}-f(n)-\\left(a_{k}-n\\right)=$ $n-f(n)$. This is possible only if $f(n)=n$, hence in this case we get $f=\\mathrm{id}_{\\mathbf{Z}^{+}}$.\n\nNow suppose that $f$ has no fixed points greater than 2 . Let $p \\geq 5$ be a prime and notice that by Wilson's Theorem we have $(p-2)!\\equiv 1(\\bmod p)$. Therefore $p$ divides $(p-2)!-1$. But $(p-2)!-1$ divides $f((p-2)!)-f(1)$, hence $p$ divides $f((p-2)!)-f(1)=(f(p-2))!-f(1)$. Clearly we have $f(1)=1$ or $f(1)=2$. As $p \\geq 5$, the fact that $p$ divides $(f(p-2))!-f(1)$ implies that $f(p-2)<p$. It is easy to check, again by Wilson's Theorem, that $p$ does not divide $(p-1)!-1$ and $(p-1)!-2$, hence we deduce that $f(p-2) \\leq p-2$. On the other hand, $p-3=(p-2)-1$ divides $f(p-2)-f(1) \\leq(p-2)-1$. Thus either $f(p-2)=f(1)$ or $f(p-2)=p-2$. As $p-2 \\geq 3$, the last case is excluded, since the function $f$ has no fixed points greater than 2 . It follows $f(p-2)=f(1)$ and this property holds for all primes $p \\geq 5$. Taking $n$ any positive integer, we deduce that $p-2-n$ divides $f(p-2)-f(n)=f(1)-f(n)$ for all primes $p \\geq 5$. Thus $f(n)=f(1)$, hence $f$ is the constant function 1 or 2 .", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 1."}}
|
| 7 |
+
{"year": "2012", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "\\quad$ Let $\\mathbb{Z}^{+}$be the set of positive integers. Find all functions $f: \\mathbb{Z}^{+} \\rightarrow \\mathbb{Z}^{+}$such that the following conditions both hold:\n(i) $f(n!)=f(n)$ ! for every positive integer $n$,\n(ii) $m-n$ divides $f(m)-f(n)$ whenever $m$ and $n$ are different positive integers.", "solution": "Note first that if $f\\left(n_{0}\\right)=n_{0}$, then $m-n_{0} \\mid f(m)-m$ for all $m \\in \\mathbf{Z}^{+}$. If $f\\left(n_{0}\\right)=n_{0}$ for infinitely many $n_{0} \\in \\mathbf{Z}^{+}$, then $f(m)-m$ has infinitely many divisors, hence $f(m)=m$ for all $m \\in \\mathbf{Z}^{+}$. On the other hand, if $f\\left(n_{0}\\right)=n_{0}$ for some $n_{0} \\geq 3$, then $f$ fixes each term of the sequence $\\left(n_{k}\\right)_{k=0}^{\\infty}$, which is recursively defined by $n_{k}=n_{k-1}!$. Hence if $f(3)=3$, then $f(n)=n$ for all $n \\in \\mathbf{Z}^{+}$.\n\nWe may assume that $f(3) \\neq 3$. Since $f(1)=f(1)!$, and $f(2)=f(2)!, f(1), f(2) \\in\\{1,2\\}$. We have $4=3!-2 \\mid f(3)!-f(2)$. This together with $f(3) \\neq 3$ implies that $f(3) \\in\\{1,2\\}$. Let $n>3$, then $n!-3 \\mid f(n)!-f(3)$ and $3 \\nmid f(n)!$, i.e. $f(n)!\\in\\{1,2\\}$. Hence we conclude that $f(n) \\in\\{1,2\\}$ for all $n \\in \\mathbf{Z}^{+}$.\n\nIf $f$ is not constant, then there exist positive integers $m, n$ with $\\{f(n), f(m)\\}=\\{1,2\\}$. Let $k=2+\\max \\{m, n\\}$. If $f(k) \\neq f(m)$, then $k-m \\mid f(k)-f(m)$. This is a contradiction as $|f(k)-f(m)|=1$ and $k-m \\geq 2$.\n\nTherefore the functions satisfying the conditions are $f \\equiv 1, f \\equiv 2, f=\\mathrm{id}_{\\mathbf{z}^{+}}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution 2."}}
|
Balkan_MO/segmented/en-2013-BMO-type2.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2013", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "We denote the angles of the triangle by $\\alpha, \\beta$ and $\\gamma$ as usual. Since $\\angle K M P=90^{\\circ}-\\frac{\\beta}{2}$, it suffices to prove that $\\angle K L P=90^{\\circ}+\\frac{\\beta}{2}$, which is equivalent to $\\angle K L C=\\frac{\\beta}{2}$.\nLet $I$ be the incenter of triangle $A B C$ and let $D$ be the tangency point of the incircle with $A B$. Since $C K \\| I B$ and $C L \\| I A$, it holds that $\\angle K C L=\\angle A I B$. Moreover, from $C N=A D=\\frac{b+c-a}{2}$ and $\\angle K C N=\\frac{\\beta}{2}$ we obtain $C K=C N \\cos \\frac{\\beta}{2}=$ $A D \\cos \\frac{\\beta}{2}=A I \\cos \\frac{\\alpha}{2} \\cos \\frac{\\beta}{2}$ and analogously $C L=B I \\cos \\frac{\\alpha}{2} \\cos \\frac{\\beta}{2}$, which imply $\\frac{C K}{C L}=\\frac{A I}{B I}$. Hence the triangles $K C L$ and $A I B$ are similar, and thus $\\angle K L C=$ $\\angle A B I=\\frac{\\beta}{2}$.", "solution": "Consider the graph $\\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.\n\nLemma. There is a vertex in graph $\\mathcal{G}$ with degree at most 2 .\nProof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \\ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \\geq j$. Then $u_{0}, u_{1}, \\ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.\n\nWe now prove the problem statement by induction on the number $n$ of vertices in $\\mathcal{G}$. For $n \\leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\\mathcal{G}$ of degree at most two. Graph $\\mathcal{G}^{\\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
-
{"year": "2013", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Determine all positive integers $x, y$ and $z$ such that\n\n$$\nx^{5}+4^{y}=2013^{z}\n$$", "solution": "Reducing modulo 11 yields $x^{5}+4^{y} \\equiv 0(\\bmod 11)$, where $x^{5} \\equiv \\pm 1(\\bmod 11)$, so we also have $4^{y} \\equiv \\pm 1(\\bmod 11)$. Congruence $4^{y} \\equiv-1(\\bmod 11)$ does not hold for any $y$, whereas $4^{y} \\equiv 1(\\bmod 11)$ holds if and only if $5 \\mid y$.\nSetting $t=4^{y / 5}$, the equation becomes $x^{5}+t^{5}=A \\cdot B=2013^{z}$, where $(x, t)=1$ and $A=x+t, B=x^{4}-x^{3} t+x^{2} t^{2}-x t^{3}+t^{4}$. Furthermore, from $B=A\\left(x^{3}-\\right.$ $\\left.2 x^{2} t+3 x t^{2}-4 t^{3}\\right)+5 t^{4}$ we deduce $(A, B)=\\left(A, 5 t^{4}\\right) \\mid 5$, but $5 \\nmid 2013^{z}$, so we must have $(A, B)=1$. Therefore $A=a^{z}$ and $B=b^{z}$ for some positive integers $a$ and $b$ with $a \\cdot b=2013$.\nOn the other hand, from $\\frac{1}{16} A^{4} \\leq B \\leq A^{4}$ (which is a simple consequence of the mean inequality) we obtain $\\frac{1}{16} a^{4} \\leq b \\leq a^{4}$, i.e. $\\frac{1}{16} a^{5} \\leq a b=2013 \\leq a^{5}$. Therefore $5 \\leq a \\leq 8$, which is impossible because 2013 has no divisors in the interval [5,8].", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
-
{"year": "2013", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $S$ be the set of positive real numbers. Find all functions $f: S^{3} \\rightarrow S$ such that, for all positive real numbers $x, y, z$ and $k$, the following three conditions are satisfied:\n(i) $x f(x, y, z)=z f(z, y, x)$;\n(ii) $f\\left(x, k y, k^{2} z\\right)=k f(x, y, z)$;\n(iii) $f(1, k, k+1)=k+1$.\n(United Kingdom)", "solution": "It follows from the properties of function $f$ that, for all $x, y, z, a, b>0$, $f\\left(a^{2} x, a b y, b^{2} z\\right)=b f\\left(a^{2} x, a y, z\\right)=b \\cdot \\frac{z}{a^{2} x} f\\left(z, a y, a^{2} x\\right)=\\frac{b z}{a x} f(z, y, x)=\\frac{b}{a} f(x, y, z)$.\n\nWe shall choose $a$ and $b$ in such a way that the triple $\\left(a^{2} x, a b y, b^{2} z\\right)$ is of the form $(1, k, k+1)$ for some $k$ : namely, we take $a=\\frac{1}{\\sqrt{x}}$ and $b$ satisfying $b^{2} z-a b y=1$, which upon solving the quadratic equation yields $b=\\frac{y+\\sqrt{y^{2}+4 x z}}{2 z \\sqrt{x}}$ and $k=\\frac{y\\left(y+\\sqrt{y^{2}+4 x z}\\right)}{2 x z}$. Now we easily obtain\n\n$$\nf(x, y, z)=\\frac{a}{b} f\\left(a^{2} x, a b y, b^{2} z\\right)=\\frac{a}{b} f(1, k, k+1)=\\frac{a}{b}(k+1)=\\frac{y+\\sqrt{y^{2}+4 x z}}{2 x} .\n$$\n\nIt is directly verified that $f$ satisfies the problem conditions.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
-
{"year": "2013", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "In a mathematical competition some competitors are friends; friendship is always mutual, that is to say that when $A$ is a friend of $B$, then also $B$ is a friend of $A$. We say that $n \\geq 3$ different competitors $A_{1}, A_{2}, \\ldots, A_{n}$ form a weakly-friendly cycle if $A_{i}$ is not a friend of $A_{i+1}$ for $1 \\leq i \\leq n\\left(A_{n+1}=A_{1}\\right)$, and there are no other pairs of non-friends among the components of this cycle.\nThe following property is satisfied:\nfor every competitor $C$, and every weakly-friendly cycle $\\mathscr{S}$ of competitors not including $C$, the set of competitors $D$ in $\\mathscr{S}$ which are not friends of $C$ has at most one element.\n\nProve that all competitors of this mathematical competition can be arranged into three rooms, such that every two competitors that are in the same room are friends.\n(Serbia)\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "Consider the graph $\\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.\n\nLemma. There is a vertex in graph $\\mathcal{G}$ with degree at most 2 .\nProof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \\ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \\geq j$. Then $u_{0}, u_{1}, \\ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.\n\nWe now prove the problem statement by induction on the number $n$ of vertices in $\\mathcal{G}$. For $n \\leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\\mathcal{G}$ of degree at most two. Graph $\\mathcal{G}^{\\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
|
|
|
| 1 |
+
{"year": "2013", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "We denote the angles of the triangle by $\\alpha, \\beta$ and $\\gamma$ as usual. Since $\\angle K M P=90^{\\circ}-\\frac{\\beta}{2}$, it suffices to prove that $\\angle K L P=90^{\\circ}+\\frac{\\beta}{2}$, which is equivalent to $\\angle K L C=\\frac{\\beta}{2}$.\nLet $I$ be the incenter of triangle $A B C$ and let $D$ be the tangency point of the incircle with $A B$. Since $C K \\| I B$ and $C L \\| I A$, it holds that $\\angle K C L=\\angle A I B$. Moreover, from $C N=A D=\\frac{b+c-a}{2}$ and $\\angle K C N=\\frac{\\beta}{2}$ we obtain $C K=C N \\cos \\frac{\\beta}{2}=$ $A D \\cos \\frac{\\beta}{2}=A I \\cos \\frac{\\alpha}{2} \\cos \\frac{\\beta}{2}$ and analogously $C L=B I \\cos \\frac{\\alpha}{2} \\cos \\frac{\\beta}{2}$, which imply $\\frac{C K}{C L}=\\frac{A I}{B I}$. Hence the triangles $K C L$ and $A I B$ are similar, and thus $\\angle K L C=$ $\\angle A B I=\\frac{\\beta}{2}$.", "solution": "Consider the graph $\\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.\n\nLemma. There is a vertex in graph $\\mathcal{G}$ with degree at most 2 .\nProof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \\ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \\geq j$. Then $u_{0}, u_{1}, \\ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.\n\nWe now prove the problem statement by induction on the number $n$ of vertices in $\\mathcal{G}$. For $n \\leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\\mathcal{G}$ of degree at most two. Graph $\\mathcal{G}^{\\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n1.", "solution_match": "\n4."}}
|
| 2 |
+
{"year": "2013", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Determine all positive integers $x, y$ and $z$ such that\n\n$$\nx^{5}+4^{y}=2013^{z}\n$$", "solution": "Reducing modulo 11 yields $x^{5}+4^{y} \\equiv 0(\\bmod 11)$, where $x^{5} \\equiv \\pm 1(\\bmod 11)$, so we also have $4^{y} \\equiv \\pm 1(\\bmod 11)$. Congruence $4^{y} \\equiv-1(\\bmod 11)$ does not hold for any $y$, whereas $4^{y} \\equiv 1(\\bmod 11)$ holds if and only if $5 \\mid y$.\nSetting $t=4^{y / 5}$, the equation becomes $x^{5}+t^{5}=A \\cdot B=2013^{z}$, where $(x, t)=1$ and $A=x+t, B=x^{4}-x^{3} t+x^{2} t^{2}-x t^{3}+t^{4}$. Furthermore, from $B=A\\left(x^{3}-\\right.$ $\\left.2 x^{2} t+3 x t^{2}-4 t^{3}\\right)+5 t^{4}$ we deduce $(A, B)=\\left(A, 5 t^{4}\\right) \\mid 5$, but $5 \\nmid 2013^{z}$, so we must have $(A, B)=1$. Therefore $A=a^{z}$ and $B=b^{z}$ for some positive integers $a$ and $b$ with $a \\cdot b=2013$.\nOn the other hand, from $\\frac{1}{16} A^{4} \\leq B \\leq A^{4}$ (which is a simple consequence of the mean inequality) we obtain $\\frac{1}{16} a^{4} \\leq b \\leq a^{4}$, i.e. $\\frac{1}{16} a^{5} \\leq a b=2013 \\leq a^{5}$. Therefore $5 \\leq a \\leq 8$, which is impossible because 2013 has no divisors in the interval [5,8].", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n2.", "solution_match": "\n2."}}
|
| 3 |
+
{"year": "2013", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $S$ be the set of positive real numbers. Find all functions $f: S^{3} \\rightarrow S$ such that, for all positive real numbers $x, y, z$ and $k$, the following three conditions are satisfied:\n(i) $x f(x, y, z)=z f(z, y, x)$;\n(ii) $f\\left(x, k y, k^{2} z\\right)=k f(x, y, z)$;\n(iii) $f(1, k, k+1)=k+1$.\n(United Kingdom)", "solution": "It follows from the properties of function $f$ that, for all $x, y, z, a, b>0$, $f\\left(a^{2} x, a b y, b^{2} z\\right)=b f\\left(a^{2} x, a y, z\\right)=b \\cdot \\frac{z}{a^{2} x} f\\left(z, a y, a^{2} x\\right)=\\frac{b z}{a x} f(z, y, x)=\\frac{b}{a} f(x, y, z)$.\n\nWe shall choose $a$ and $b$ in such a way that the triple $\\left(a^{2} x, a b y, b^{2} z\\right)$ is of the form $(1, k, k+1)$ for some $k$ : namely, we take $a=\\frac{1}{\\sqrt{x}}$ and $b$ satisfying $b^{2} z-a b y=1$, which upon solving the quadratic equation yields $b=\\frac{y+\\sqrt{y^{2}+4 x z}}{2 z \\sqrt{x}}$ and $k=\\frac{y\\left(y+\\sqrt{y^{2}+4 x z}\\right)}{2 x z}$. Now we easily obtain\n\n$$\nf(x, y, z)=\\frac{a}{b} f\\left(a^{2} x, a b y, b^{2} z\\right)=\\frac{a}{b} f(1, k, k+1)=\\frac{a}{b}(k+1)=\\frac{y+\\sqrt{y^{2}+4 x z}}{2 x} .\n$$\n\nIt is directly verified that $f$ satisfies the problem conditions.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n3.", "solution_match": "\n3."}}
|
| 4 |
+
{"year": "2013", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "In a mathematical competition some competitors are friends; friendship is always mutual, that is to say that when $A$ is a friend of $B$, then also $B$ is a friend of $A$. We say that $n \\geq 3$ different competitors $A_{1}, A_{2}, \\ldots, A_{n}$ form a weakly-friendly cycle if $A_{i}$ is not a friend of $A_{i+1}$ for $1 \\leq i \\leq n\\left(A_{n+1}=A_{1}\\right)$, and there are no other pairs of non-friends among the components of this cycle.\nThe following property is satisfied:\nfor every competitor $C$, and every weakly-friendly cycle $\\mathscr{S}$ of competitors not including $C$, the set of competitors $D$ in $\\mathscr{S}$ which are not friends of $C$ has at most one element.\n\nProve that all competitors of this mathematical competition can be arranged into three rooms, such that every two competitors that are in the same room are friends.\n(Serbia)\nTime allowed: 270 minutes.\nEach problem is worth 10 points.\n\n## SOLUTIONS", "solution": "Consider the graph $\\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.\n\nLemma. There is a vertex in graph $\\mathcal{G}$ with degree at most 2 .\nProof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \\ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \\geq j$. Then $u_{0}, u_{1}, \\ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.\n\nWe now prove the problem statement by induction on the number $n$ of vertices in $\\mathcal{G}$. For $n \\leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\\mathcal{G}$ of degree at most two. Graph $\\mathcal{G}^{\\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl", "problem_match": "\n4.", "solution_match": "\n4."}}
|
Balkan_MO/segmented/en-2014-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2014", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $x, y$ and $z$ be positive real numbers such that $x y+y z+z x=3 x y z$. Prove that\n\n$$\nx^{2} y+y^{2} z+z^{2} x \\geq 2(x+y+z)-3\n$$\n\nand determine when equality holds.", "solution": "The given condition can be rearranged to $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=3$. Using this, we obtain:\n\n$$\n\\begin{aligned}\nx^{2} y+y^{2} z+z^{2} x-2(x+y+z)+3 & =x^{2} y-2 x+\\frac{1}{y}+y^{2} z-2 y+\\frac{1}{z}+z^{2} x-2 x+\\frac{1}{x}= \\\\\n& =y\\left(x-\\frac{1}{y}\\right)^{2}+z\\left(y-\\frac{1}{z}\\right)^{2}+x\\left(z-\\frac{1}{z}\\right)^{2} \\geq 0\n\\end{aligned}\n$$\n\nEquality holds if and only if we have $x y=y z=z x=1$, or, in other words, $x=y=z=1$.\nAlternative solution. It follows from $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=3$ and Cauchy-Schwarz inequality that\n\n$$\n\\begin{aligned}\n3\\left(x^{2} y+y^{2} z+z^{2} x\\right) & =\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)\\left(x^{2} y+y^{2} z+z^{2} x\\right) \\\\\n& \\left.=\\left(\\left(\\frac{1}{\\sqrt{y}}\\right)^{2}+\\left(\\frac{1}{\\sqrt{z}}\\right)^{2}+\\left(\\frac{1}{\\sqrt{x}}\\right)^{2}\\right)\\left((x \\sqrt{y})^{2}\\right)+(y \\sqrt{z})^{2}+(z \\sqrt{x})^{2}\\right) \\\\\n& \\geq(x+y+z)^{2}\n\\end{aligned}\n$$\n\nTherefore, $x^{2} y+y^{2} z+z^{2} x \\geq \\frac{(x+y+z)^{2}}{3}$ and if $x+y+z=t$ it suffices to show that $\\frac{t^{2}}{3} \\geq 2 t-3$. The latter is equivalent to $(t-3)^{2} \\geq 0$. Equality holds when\n\n$$\nx \\sqrt{y} \\sqrt{y}=y \\sqrt{z} \\sqrt{z}=z \\sqrt{x} \\sqrt{x},\n$$\n\ni.e. $x y=y z=z x$ and $t=x+y+z=3$. Hence, $x=y=z=1$.\n\nComment. The inequality is true with the condition $x y+y z+z x \\leq 3 x y z$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2014", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "A special number is a positive integer $n$ for which there exist positive integers $a, b, c$ and $d$ with\n\n$$\nn=\\frac{a^{3}+2 b^{3}}{c^{3}+2 d^{3}}\n$$\n\nProve that:\n(a) there are infinitely many special numbers;\n(b) 2014 is not a special number.", "solution": "(a) Every perfect cube $k^{3}$ of a positive integer is special because we can write\n\n$$\nk^{3}=k^{3} \\frac{a^{3}+2 b^{3}}{a^{3}+2 b^{3}}=\\frac{(k a)^{3}+2(k b)^{3}}{a^{3}+2 b^{3}}\n$$\n\nfor some positive integers $a, b$.\n(b) Observe that $2014=2.19 .53$. If 2014 is special, then we have,\n\n$$\nx^{3}+2 y^{3}=2014\\left(u^{3}+2 v^{3}\\right)\n$$\n\nfor some positive integers $x, y, u, v$. We may assume that $x^{3}+2 y^{3}$ is minimal with this property. Now, we will use the fact that if 19 divides $x^{3}+2 y^{3}$, then it divides both $x$ and $y$. Indeed, if 19 does not divide $x$, then it does not divide $y$ too. The relation $x^{3} \\equiv-2 y^{3}(\\bmod 19)$ implies $\\left(x^{3}\\right)^{6} \\equiv\\left(-2 y^{3}\\right)^{6}(\\bmod 19)$. The latter congruence is equivalent to $x^{18} \\equiv 2^{6} y^{18}(\\bmod 19)$. Now, according to the Fermat's Little Theorem, we obtain $1 \\equiv 2^{6}(\\bmod 19)$, that is 19 divides 63 , not possible.\nIt follows $x=19 x_{1}, y=19 y_{1}$, for some positive integers $x_{1}$ and $y_{1}$. Replacing in (1) we get\n\n$$\n19^{2}\\left(x_{1}^{3}+2 y_{1}^{3}\\right)=2.53\\left(u^{3}+2 v^{3}\\right)\n$$\n\ni.e. $19 \\mid u^{3}+2 v^{3}$. It follows $u=19 u_{1}$ and $v=19 v_{1}$, and replacing in (2) we get\n\n$$\nx_{1}^{3}+2 y_{1}^{3}=2014\\left(u_{1}^{3}+2 v_{1}^{3}\\right) .\n$$\n\nClearly, $x_{1}^{3}+2 y_{1}^{3}<x^{3}+2 y^{3}$, contradicting the minimality of $x^{3}+2 y^{3}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2014", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C D$ be a trapezium inscribed in a circle $\\Gamma$ with diameter $A B$. Let $E$ be the intersection point of the diagonals $A C$ and $B D$. The circle with center $B$ and radius $B E$ meets $\\Gamma$ at the points $K$ and $L$, where $K$ is on the same side of $A B$ as $C$. The line perpendicular to $B D$ at $E$ intersects $C D$ at $M$.\n\nProve that $K M$ is perpendicular to $D L$.", "solution": "Since $A B \\| C D$, we have that $A B C D$ is isosceles trapezium. Let $O$ be the center of $k$ and $E M$ meets $A B$ at point $Q$. Then, from the right angled triangle $B E Q$, we have $B E^{2}=B O \\cdot B Q$. Since $B E=B K$, we get $B K^{2}=B O \\cdot B Q$ (1). Suppose that $K L$ meets $A B$ at $P$. Then, from the right angled triangle $B A K$, we have $B K^{2}=B P . B A$ (2)\n\n\nFrom (1) and (2) we get $\\frac{B P}{B Q}=\\frac{B O}{B A}=\\frac{1}{2}$, and therefore $P$ is the midpoint of $B Q$ (3). However, $D M \\| A Q$ and $M Q \\| A D$ (both are perpendicular to $D B$ ). Hence, $A Q M D$ is parallelogram and thus $M Q=A D=B C$. We conclude that $Q B C M$ is isosceles trapezium. It follows from (3) that $K L$ is the perpendicular bisector of $B Q$ and $C M$, that is, $M$ is symmetric to $C$ with respect to $K L$. Finally, we get that $M$ is the orthocenter\nof the triangle $D L K$ by using the well-known result that the reflection of the orthocenter of a triangle to every side belongs to the circumcircle of the triangle and vise versa.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2014", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $n$ be a positive integer. A regular hexagon with side length $n$ is divided into equilateral triangles with side length 1 by lines parallel to its sides.\nFind the number of regular hexagons all of whose vertices are among the vertices of the equilateral triangles.", "solution": "By a lattice hexagon we will mean a regular hexagon whose sides run along edges of the lattice. Given any regular hexagon $H$, we construct a lattice hexagon whose edges pass through the vertices of $H$, as shown in the figure, which we will call the enveloping lattice hexagon of $H$. Given a lattice hexagon $G$ of side length $m$, the number of regular hexagons whose enveloping lattice hexagon is $G$ is exactly $m$.\n\nYet also there are precisely $3(n-m)(n-m+1)+1$ lattice hexagons of side length $m$ in our lattice: they are those with centres lying at most $n-m$ steps from the centre of the lattice. In particular, the total number of regular hexagons equals\n\n$N=\\sum_{m=1}^{n}(3(n-m)(n-m+1)+1) m=\\left(3 n^{2}+3 n\\right) \\sum_{m=1}^{n} m-3(2 m+1) \\sum_{m=1}^{n} m^{2}+3 \\sum_{m=1}^{n} m^{3}$.\nSince $\\sum_{m=1}^{n} m=\\frac{n(n+1)}{2}, \\sum_{m=1}^{n} m^{2}=\\frac{n(n+1)(2 n+1)}{6}$ and $\\sum_{m=1}^{n} m^{3}=\\left(\\frac{n(n+1)}{2}\\right)^{2}$ it is easily checked that $N=\\left(\\frac{n(n+1)}{2}\\right)^{2}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2014", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $x, y$ and $z$ be positive real numbers such that $x y+y z+z x=3 x y z$. Prove that\n\n$$\nx^{2} y+y^{2} z+z^{2} x \\geq 2(x+y+z)-3\n$$\n\nand determine when equality holds.", "solution": "The given condition can be rearranged to $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=3$. Using this, we obtain:\n\n$$\n\\begin{aligned}\nx^{2} y+y^{2} z+z^{2} x-2(x+y+z)+3 & =x^{2} y-2 x+\\frac{1}{y}+y^{2} z-2 y+\\frac{1}{z}+z^{2} x-2 x+\\frac{1}{x}= \\\\\n& =y\\left(x-\\frac{1}{y}\\right)^{2}+z\\left(y-\\frac{1}{z}\\right)^{2}+x\\left(z-\\frac{1}{z}\\right)^{2} \\geq 0\n\\end{aligned}\n$$\n\nEquality holds if and only if we have $x y=y z=z x=1$, or, in other words, $x=y=z=1$.\nAlternative solution. It follows from $\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}=3$ and Cauchy-Schwarz inequality that\n\n$$\n\\begin{aligned}\n3\\left(x^{2} y+y^{2} z+z^{2} x\\right) & =\\left(\\frac{1}{x}+\\frac{1}{y}+\\frac{1}{z}\\right)\\left(x^{2} y+y^{2} z+z^{2} x\\right) \\\\\n& \\left.=\\left(\\left(\\frac{1}{\\sqrt{y}}\\right)^{2}+\\left(\\frac{1}{\\sqrt{z}}\\right)^{2}+\\left(\\frac{1}{\\sqrt{x}}\\right)^{2}\\right)\\left((x \\sqrt{y})^{2}\\right)+(y \\sqrt{z})^{2}+(z \\sqrt{x})^{2}\\right) \\\\\n& \\geq(x+y+z)^{2}\n\\end{aligned}\n$$\n\nTherefore, $x^{2} y+y^{2} z+z^{2} x \\geq \\frac{(x+y+z)^{2}}{3}$ and if $x+y+z=t$ it suffices to show that $\\frac{t^{2}}{3} \\geq 2 t-3$. The latter is equivalent to $(t-3)^{2} \\geq 0$. Equality holds when\n\n$$\nx \\sqrt{y} \\sqrt{y}=y \\sqrt{z} \\sqrt{z}=z \\sqrt{x} \\sqrt{x},\n$$\n\ni.e. $x y=y z=z x$ and $t=x+y+z=3$. Hence, $x=y=z=1$.\n\nComment. The inequality is true with the condition $x y+y z+z x \\leq 3 x y z$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2014", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "A special number is a positive integer $n$ for which there exist positive integers $a, b, c$ and $d$ with\n\n$$\nn=\\frac{a^{3}+2 b^{3}}{c^{3}+2 d^{3}}\n$$\n\nProve that:\n(a) there are infinitely many special numbers;\n(b) 2014 is not a special number.", "solution": "(a) Every perfect cube $k^{3}$ of a positive integer is special because we can write\n\n$$\nk^{3}=k^{3} \\frac{a^{3}+2 b^{3}}{a^{3}+2 b^{3}}=\\frac{(k a)^{3}+2(k b)^{3}}{a^{3}+2 b^{3}}\n$$\n\nfor some positive integers $a, b$.\n(b) Observe that $2014=2.19 .53$. If 2014 is special, then we have,\n\n$$\nx^{3}+2 y^{3}=2014\\left(u^{3}+2 v^{3}\\right)\n$$\n\nfor some positive integers $x, y, u, v$. We may assume that $x^{3}+2 y^{3}$ is minimal with this property. Now, we will use the fact that if 19 divides $x^{3}+2 y^{3}$, then it divides both $x$ and $y$. Indeed, if 19 does not divide $x$, then it does not divide $y$ too. The relation $x^{3} \\equiv-2 y^{3}(\\bmod 19)$ implies $\\left(x^{3}\\right)^{6} \\equiv\\left(-2 y^{3}\\right)^{6}(\\bmod 19)$. The latter congruence is equivalent to $x^{18} \\equiv 2^{6} y^{18}(\\bmod 19)$. Now, according to the Fermat's Little Theorem, we obtain $1 \\equiv 2^{6}(\\bmod 19)$, that is 19 divides 63 , not possible.\nIt follows $x=19 x_{1}, y=19 y_{1}$, for some positive integers $x_{1}$ and $y_{1}$. Replacing in (1) we get\n\n$$\n19^{2}\\left(x_{1}^{3}+2 y_{1}^{3}\\right)=2.53\\left(u^{3}+2 v^{3}\\right)\n$$\n\ni.e. $19 \\mid u^{3}+2 v^{3}$. It follows $u=19 u_{1}$ and $v=19 v_{1}$, and replacing in (2) we get\n\n$$\nx_{1}^{3}+2 y_{1}^{3}=2014\\left(u_{1}^{3}+2 v_{1}^{3}\\right) .\n$$\n\nClearly, $x_{1}^{3}+2 y_{1}^{3}<x^{3}+2 y^{3}$, contradicting the minimality of $x^{3}+2 y^{3}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2014", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C D$ be a trapezium inscribed in a circle $\\Gamma$ with diameter $A B$. Let $E$ be the intersection point of the diagonals $A C$ and $B D$. The circle with center $B$ and radius $B E$ meets $\\Gamma$ at the points $K$ and $L$, where $K$ is on the same side of $A B$ as $C$. The line perpendicular to $B D$ at $E$ intersects $C D$ at $M$.\n\nProve that $K M$ is perpendicular to $D L$.", "solution": "Since $A B \\| C D$, we have that $A B C D$ is isosceles trapezium. Let $O$ be the center of $k$ and $E M$ meets $A B$ at point $Q$. Then, from the right angled triangle $B E Q$, we have $B E^{2}=B O \\cdot B Q$. Since $B E=B K$, we get $B K^{2}=B O \\cdot B Q$ (1). Suppose that $K L$ meets $A B$ at $P$. Then, from the right angled triangle $B A K$, we have $B K^{2}=B P . B A$ (2)\n\n\nFrom (1) and (2) we get $\\frac{B P}{B Q}=\\frac{B O}{B A}=\\frac{1}{2}$, and therefore $P$ is the midpoint of $B Q$ (3). However, $D M \\| A Q$ and $M Q \\| A D$ (both are perpendicular to $D B$ ). Hence, $A Q M D$ is parallelogram and thus $M Q=A D=B C$. We conclude that $Q B C M$ is isosceles trapezium. It follows from (3) that $K L$ is the perpendicular bisector of $B Q$ and $C M$, that is, $M$ is symmetric to $C$ with respect to $K L$. Finally, we get that $M$ is the orthocenter\nof the triangle $D L K$ by using the well-known result that the reflection of the orthocenter of a triangle to every side belongs to the circumcircle of the triangle and vise versa.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2014", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $n$ be a positive integer. A regular hexagon with side length $n$ is divided into equilateral triangles with side length 1 by lines parallel to its sides.\nFind the number of regular hexagons all of whose vertices are among the vertices of the equilateral triangles.", "solution": "By a lattice hexagon we will mean a regular hexagon whose sides run along edges of the lattice. Given any regular hexagon $H$, we construct a lattice hexagon whose edges pass through the vertices of $H$, as shown in the figure, which we will call the enveloping lattice hexagon of $H$. Given a lattice hexagon $G$ of side length $m$, the number of regular hexagons whose enveloping lattice hexagon is $G$ is exactly $m$.\n\nYet also there are precisely $3(n-m)(n-m+1)+1$ lattice hexagons of side length $m$ in our lattice: they are those with centres lying at most $n-m$ steps from the centre of the lattice. In particular, the total number of regular hexagons equals\n\n$N=\\sum_{m=1}^{n}(3(n-m)(n-m+1)+1) m=\\left(3 n^{2}+3 n\\right) \\sum_{m=1}^{n} m-3(2 m+1) \\sum_{m=1}^{n} m^{2}+3 \\sum_{m=1}^{n} m^{3}$.\nSince $\\sum_{m=1}^{n} m=\\frac{n(n+1)}{2}, \\sum_{m=1}^{n} m^{2}=\\frac{n(n+1)(2 n+1)}{6}$ and $\\sum_{m=1}^{n} m^{3}=\\left(\\frac{n(n+1)}{2}\\right)^{2}$ it is easily checked that $N=\\left(\\frac{n(n+1)}{2}\\right)^{2}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2015-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2015", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $a, b$ and $c$ be positive real numbers. Prove that\n\n$$\na^{3} b^{6}+b^{3} c^{6}+c^{3} a^{6}+3 a^{3} b^{3} c^{3} \\geq a b c\\left(a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}\\right)+a^{2} b^{2} c^{2}\\left(a^{3}+b^{3}+c^{3}\\right)\n$$", "solution": "After dividing both sides of the given inequality by $a^{3} b^{3} c^{3}$ it becomes\n\n$$\n\\left(\\frac{b}{c}\\right)^{3}+\\left(\\frac{c}{a}\\right)^{3}+\\left(\\frac{a}{b}\\right)^{3}+3 \\geq\\left(\\frac{a}{c} \\cdot \\frac{b}{c}+\\frac{b}{a} \\cdot \\frac{c}{a}+\\frac{c}{b} \\cdot \\frac{a}{b}\\right)+\\left(\\frac{a}{b} \\cdot \\frac{a}{c}+\\frac{b}{a} \\cdot \\frac{b}{c}+\\frac{c}{a} \\cdot \\frac{c}{b}\\right) .\n$$\n\nSet\n\n$$\n\\frac{b}{a}=\\frac{1}{x}, \\quad \\frac{c}{b}=\\frac{1}{y}, \\quad \\frac{a}{c}=\\frac{1}{z} .\n$$\n\nThen we have that $x y z=1$ and by substituting (2) into (1), we find that\n\n$$\nx^{3}+y^{3}+z^{3}+3 \\geq\\left(\\frac{y}{z}+\\frac{z}{x}+\\frac{x}{y}\\right)+\\left(\\frac{x}{z}+\\frac{y}{x}+\\frac{z}{y}\\right) .\n$$\n\nMultiplying the inequality (3) by $x y z$, and using the fact that $x y z=1$, the inequality is equivalent to\n\n$$\nx^{3}+y^{3}+z^{3}+3 x y z-x y^{2}-y z^{2}-z x^{2}-y x^{2}-z y^{2}-x z^{2} \\geq 0 .\n$$\n\nFinally, notice that by the special case of Schur's inequality\n\n$$\nx^{r}(x-y)(x-z)+y^{r}(y-x)(y-z)+z^{r}(z-y)(z-x) \\geq 0, \\quad x, y, z \\geq 0, r>0,\n$$\n\nwith $r=1$ there holds\n\n$$\nx(x-y)(x-z)+y(y-x)(y-z)+z(z-y)(z-x) \\geq 0\n$$\n\nwhich after expansion actually coincides with the congruence (4).\nRemark 1. The inequality (5) immediately follows by supposing (without loss of generality) that $x \\geq y \\geq z$, and then writing the left hand side of the inequality (5) in the form\n\n$$\n(x-y)(x(x-z)-y(y-z))+z(y-z)(x-z)\n$$\n\nwhich is obviously $\\geq 0$.\nRemark 2. One can obtain the relation (4) using also the substitution $x=a b^{2}, y=b c^{2}$ and $z=c a^{2}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2015", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be a scalene triangle with incentre $I$ and circumcircle ( $\\omega$ ). The lines $A I, B I, C I$ intersect $(\\omega)$ for the second time at the points $D, E, F$, respectively. The lines through $I$ parallel to the sides $B C, A C, A B$ intersect the lines $E F, D F, D E$ at the points $K, L, M$, respectively. Prove that the points $K, L, M$ are collinear.", "solution": "First we will prove that $K A$ is tangent to $(\\omega)$.\nIndeed, it is a well-known fact that $F A=F B=F I$ and $E A=E C=E I$, so $F E$ is the perpendicular bisector of $A I$. It follows that $K A=K I$ and\n\n$$\n\\angle K A F=\\angle K I F=\\angle F C B=\\angle F E B=\\angle F E A,\n$$\n\nso $K A$ is tangent to $(\\omega)$. Similarly we can prove that $L B, M C$ are tangent to $(\\omega)$ as well.\n\n\nLet $A^{\\prime}, B^{\\prime}, C^{\\prime}$ the intersections of $A I, B I, C I$ with $B C, C A, A B$ respectively. From Pascal's Theorem on the cyclic hexagon $A A C D E B$ we get $K, C^{\\prime}, B^{\\prime}$ collinear. Similarly $L, C^{\\prime}, A^{\\prime}$ collinear and $M, B^{\\prime}, A^{\\prime}$ collinear.\n\nThen from Desargues' Theorem for $\\triangle D E F, \\triangle A^{\\prime} B^{\\prime} C^{\\prime}$ which are perspective from the point $I$, we get that points $K, L, M$ of the intersection of their corresponding sides are collinear as wanted.\nRemark (P.S.C.). After proving that $K A, L B, M C$ are tangent to ( $\\omega$ ), we can argue as follows:\nIt readily follows that $\\triangle K A F \\sim \\triangle K A E$ and so $\\frac{K A}{K E}=\\frac{K F}{K A}=\\frac{A F}{A E}$, thus $\\frac{K F}{K E}=\\left(\\frac{A F}{A E}\\right)^{2}$. In a similar way we can find that $\\frac{M E}{M D}=\\left(\\frac{C E}{C D}\\right)^{2}$ and $\\frac{L D}{L F}=\\left(\\frac{B D}{B F}\\right)^{2}$. Multiplying we obtain $\\frac{K F}{K E} \\cdot \\frac{M E}{M D} \\cdot \\frac{L D}{L F}=1$, so by the converse of Menelaus theorem applied in the triangle $D E F$ we get that the points $K, L, M$ are collinear.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2015", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "A jury of 3366 film critics are judging the Oscars. Each critic makes a single vote for his favourite actor, and a single vote for his favourite actress. It turns out that for every integer $n \\in\\{1,2, \\ldots, 100\\}$ there is an actor or actress who has been voted for exactly $n$ times. Show that there are two critics who voted for the same actor and for the same actress.", "solution": "Let us assume that every critic votes for a different pair of actor and actress. We'll arrive at a contradiction proving the required result. Indeed:\n\nCall the vote of each critic, i.e his choice for the pair of an actor and an actress, as a double-vote, and call as a single-vote each one of the two choices he makes, i.e. the one for an actor and the other one for an actress. In this terminology, a double-vote corresponds to two single-votes.\n\nFor each $n=34,35, \\ldots, 100$ let us pick out one actor or one actress who has been voted by exactly $n$ critics (i.e. appears in exactly $n$ single-votes) and call $S$ the set of these movie stars. Calling $a, b$ the number of men and women in $S$, we have $a+b=67$.\n\nNow let $S_{1}$ be the set of double-votes, each having exactly one of its two corresponding singlevotes in $S$, and let $S_{2}$ be the set of double-votes with both its single-votes in $S$. If $s_{1}, s_{2}$ are the number of elements in $S_{1}, S_{2}$ respectively, we have that the number of all double-votes with at least one single-vote in $S$ is $s_{1}+s_{2}$, whereas the number of all double-votes with both single-votes in $S$ is $s_{2} \\leq a b$.\n\nSince all double-votes are distinct, there must exist at least $s_{1}+s_{2}$ critics. But the number of all single-votes in $S$ is $s_{1}+2 s_{2}=34+35+\\cdots+100=4489$, and moreover $s \\leq a b$. So there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \\geq 4489-a b$ critics.\n\nNow notice that as $a+b=67$, the maximum value of $a b$ with $a, b$ integers is obtained for $\\{a, b\\}=$ $\\{33,34\\}$, so $a b \\leq 33 \\cdot 34=1122$. A quick proof of this is the following: $a b=\\frac{(a+b)^{2}-(a-b)^{2}}{4}=$ $\\frac{67^{2}-(a-b)^{2}}{4}$ which is maximized (for not equal integers $a, b$ as $a+b=67$ ) whenever $|a-b|=1$, thus for $\\{a, b\\}=\\{33,34\\}$.\n\nThus there exist at least $4489-1122=3367$ critics which is a contradiction and we are done.\nRemark. We are going here to give some motivation about the choice of number 34, used in the above solution.\nLet us assume that every critic votes for a different pair of actor and actress. One can again start by picking out one actor or one actress who has been voted by exactly $n$ critics for $n=k, k+1, \\ldots, 100$. Then $a+b=100-k+1=101-k$ and the number of all single-votes is $s_{1}+2 s_{2}=k+k+1+\\cdots+100=$ $5050-\\frac{k(k-1)}{2}$, so there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \\geq 5050-\\frac{k(k-1)}{2}-a b$ and\n\n$$\na b=\\frac{(a+b)^{2}-(a-b)^{2}}{4}=\\frac{(101-k)^{2}-(a-b)^{2}}{4} \\leq \\frac{(101-k)^{2}-1}{4} .\n$$\n\nAfter all, the number of critics is at least\n\n$$\n5050-\\frac{k(k-1)}{2}-\\frac{(101-k)^{2}-1}{4}\n$$\n\nIn order to arrive at a contradiction we have to choose $k$ such that\n\n$$\n5050-\\frac{k(k-1)}{2}-\\frac{(101-k)^{2}-1}{4} \\geq 3367\n$$\n\nand solving the inequality with respect to $k$, the only value that makes the last one true is $k=34$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2015", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Prove that among any 20 consecutive positive integers there exists an integer $d$ such that for each positive integer $n$ we have the inequality\n\n$$\nn \\sqrt{d}\\{n \\sqrt{d}\\}>\\frac{5}{2}\n$$\n\nwhere $\\{x\\}$ denotes the fractional part of the real number $x$. The fractional part of a real number $x$ is $x$ minus the greatest integer less than or equal to $x$.", "solution": "Among the given numbers there is a number of the form $20 k+15=5(4 k+3)$. We shall prove that $d=5(4 k+3)$ satisfies the statement's condition. Since $d \\equiv-1(\\bmod 4)$, it follows that $d$ is not a perfect square, and thus for any $n \\in \\mathbb{N}$ there exists $a \\in \\mathbb{N}$ such that $a+1>n \\sqrt{d}>a$, that is, $(a+1)^{2}>n^{2} d>a^{2}$. Actually, we are going to prove that $n^{2} d \\geq a^{2}+5$. Indeed:\n\nIt is known that each positive integer of the form $4 s+3$ has a prime divisor of the same form. Let $p \\mid 4 k+3$ and $p \\equiv-1(\\bmod 4)$. Because of the form of $p$, the numbers $a^{2}+1^{2}$ and $a^{2}+2^{2}$ are not divisible by $p$, and since $p \\mid n^{2} d$, it follows that $n^{2} d \\neq a^{2}+1, a^{2}+4$. On the other hand, $5 \\mid n^{2} d$, and since $5 \\nmid a^{2}+2, a^{2}+3$, we conclude $n^{2} d \\neq a^{2}+2, a^{2}+3$. Since $n^{2} d>a^{2}$ we must have $n^{2} d \\geq a^{2}+5$ as claimed. Therefore,\n\n$$\nn \\sqrt{d}\\{n \\sqrt{d}\\}=n \\sqrt{d}(n \\sqrt{d}-a) \\geq a^{2}+5-a \\sqrt{a^{2}+5}>a^{2}+5-\\frac{a^{2}+\\left(a^{2}+5\\right)}{2}=\\frac{5}{2},\n$$\n\nwhich was to be proved.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2015", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $a, b$ and $c$ be positive real numbers. Prove that\n\n$$\na^{3} b^{6}+b^{3} c^{6}+c^{3} a^{6}+3 a^{3} b^{3} c^{3} \\geq a b c\\left(a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}\\right)+a^{2} b^{2} c^{2}\\left(a^{3}+b^{3}+c^{3}\\right)\n$$", "solution": "After dividing both sides of the given inequality by $a^{3} b^{3} c^{3}$ it becomes\n\n$$\n\\left(\\frac{b}{c}\\right)^{3}+\\left(\\frac{c}{a}\\right)^{3}+\\left(\\frac{a}{b}\\right)^{3}+3 \\geq\\left(\\frac{a}{c} \\cdot \\frac{b}{c}+\\frac{b}{a} \\cdot \\frac{c}{a}+\\frac{c}{b} \\cdot \\frac{a}{b}\\right)+\\left(\\frac{a}{b} \\cdot \\frac{a}{c}+\\frac{b}{a} \\cdot \\frac{b}{c}+\\frac{c}{a} \\cdot \\frac{c}{b}\\right) .\n$$\n\nSet\n\n$$\n\\frac{b}{a}=\\frac{1}{x}, \\quad \\frac{c}{b}=\\frac{1}{y}, \\quad \\frac{a}{c}=\\frac{1}{z} .\n$$\n\nThen we have that $x y z=1$ and by substituting (2) into (1), we find that\n\n$$\nx^{3}+y^{3}+z^{3}+3 \\geq\\left(\\frac{y}{z}+\\frac{z}{x}+\\frac{x}{y}\\right)+\\left(\\frac{x}{z}+\\frac{y}{x}+\\frac{z}{y}\\right) .\n$$\n\nMultiplying the inequality (3) by $x y z$, and using the fact that $x y z=1$, the inequality is equivalent to\n\n$$\nx^{3}+y^{3}+z^{3}+3 x y z-x y^{2}-y z^{2}-z x^{2}-y x^{2}-z y^{2}-x z^{2} \\geq 0 .\n$$\n\nFinally, notice that by the special case of Schur's inequality\n\n$$\nx^{r}(x-y)(x-z)+y^{r}(y-x)(y-z)+z^{r}(z-y)(z-x) \\geq 0, \\quad x, y, z \\geq 0, r>0,\n$$\n\nwith $r=1$ there holds\n\n$$\nx(x-y)(x-z)+y(y-x)(y-z)+z(z-y)(z-x) \\geq 0\n$$\n\nwhich after expansion actually coincides with the congruence (4).\nRemark 1. The inequality (5) immediately follows by supposing (without loss of generality) that $x \\geq y \\geq z$, and then writing the left hand side of the inequality (5) in the form\n\n$$\n(x-y)(x(x-z)-y(y-z))+z(y-z)(x-z)\n$$\n\nwhich is obviously $\\geq 0$.\nRemark 2. One can obtain the relation (4) using also the substitution $x=a b^{2}, y=b c^{2}$ and $z=c a^{2}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2015", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be a scalene triangle with incentre $I$ and circumcircle ( $\\omega$ ). The lines $A I, B I, C I$ intersect $(\\omega)$ for the second time at the points $D, E, F$, respectively. The lines through $I$ parallel to the sides $B C, A C, A B$ intersect the lines $E F, D F, D E$ at the points $K, L, M$, respectively. Prove that the points $K, L, M$ are collinear.", "solution": "First we will prove that $K A$ is tangent to $(\\omega)$.\nIndeed, it is a well-known fact that $F A=F B=F I$ and $E A=E C=E I$, so $F E$ is the perpendicular bisector of $A I$. It follows that $K A=K I$ and\n\n$$\n\\angle K A F=\\angle K I F=\\angle F C B=\\angle F E B=\\angle F E A,\n$$\n\nso $K A$ is tangent to $(\\omega)$. Similarly we can prove that $L B, M C$ are tangent to $(\\omega)$ as well.\n\n\nLet $A^{\\prime}, B^{\\prime}, C^{\\prime}$ the intersections of $A I, B I, C I$ with $B C, C A, A B$ respectively. From Pascal's Theorem on the cyclic hexagon $A A C D E B$ we get $K, C^{\\prime}, B^{\\prime}$ collinear. Similarly $L, C^{\\prime}, A^{\\prime}$ collinear and $M, B^{\\prime}, A^{\\prime}$ collinear.\n\nThen from Desargues' Theorem for $\\triangle D E F, \\triangle A^{\\prime} B^{\\prime} C^{\\prime}$ which are perspective from the point $I$, we get that points $K, L, M$ of the intersection of their corresponding sides are collinear as wanted.\nRemark (P.S.C.). After proving that $K A, L B, M C$ are tangent to ( $\\omega$ ), we can argue as follows:\nIt readily follows that $\\triangle K A F \\sim \\triangle K A E$ and so $\\frac{K A}{K E}=\\frac{K F}{K A}=\\frac{A F}{A E}$, thus $\\frac{K F}{K E}=\\left(\\frac{A F}{A E}\\right)^{2}$. In a similar way we can find that $\\frac{M E}{M D}=\\left(\\frac{C E}{C D}\\right)^{2}$ and $\\frac{L D}{L F}=\\left(\\frac{B D}{B F}\\right)^{2}$. Multiplying we obtain $\\frac{K F}{K E} \\cdot \\frac{M E}{M D} \\cdot \\frac{L D}{L F}=1$, so by the converse of Menelaus theorem applied in the triangle $D E F$ we get that the points $K, L, M$ are collinear.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2015", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "A jury of 3366 film critics are judging the Oscars. Each critic makes a single vote for his favourite actor, and a single vote for his favourite actress. It turns out that for every integer $n \\in\\{1,2, \\ldots, 100\\}$ there is an actor or actress who has been voted for exactly $n$ times. Show that there are two critics who voted for the same actor and for the same actress.", "solution": "Let us assume that every critic votes for a different pair of actor and actress. We'll arrive at a contradiction proving the required result. Indeed:\n\nCall the vote of each critic, i.e his choice for the pair of an actor and an actress, as a double-vote, and call as a single-vote each one of the two choices he makes, i.e. the one for an actor and the other one for an actress. In this terminology, a double-vote corresponds to two single-votes.\n\nFor each $n=34,35, \\ldots, 100$ let us pick out one actor or one actress who has been voted by exactly $n$ critics (i.e. appears in exactly $n$ single-votes) and call $S$ the set of these movie stars. Calling $a, b$ the number of men and women in $S$, we have $a+b=67$.\n\nNow let $S_{1}$ be the set of double-votes, each having exactly one of its two corresponding singlevotes in $S$, and let $S_{2}$ be the set of double-votes with both its single-votes in $S$. If $s_{1}, s_{2}$ are the number of elements in $S_{1}, S_{2}$ respectively, we have that the number of all double-votes with at least one single-vote in $S$ is $s_{1}+s_{2}$, whereas the number of all double-votes with both single-votes in $S$ is $s_{2} \\leq a b$.\n\nSince all double-votes are distinct, there must exist at least $s_{1}+s_{2}$ critics. But the number of all single-votes in $S$ is $s_{1}+2 s_{2}=34+35+\\cdots+100=4489$, and moreover $s \\leq a b$. So there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \\geq 4489-a b$ critics.\n\nNow notice that as $a+b=67$, the maximum value of $a b$ with $a, b$ integers is obtained for $\\{a, b\\}=$ $\\{33,34\\}$, so $a b \\leq 33 \\cdot 34=1122$. A quick proof of this is the following: $a b=\\frac{(a+b)^{2}-(a-b)^{2}}{4}=$ $\\frac{67^{2}-(a-b)^{2}}{4}$ which is maximized (for not equal integers $a, b$ as $a+b=67$ ) whenever $|a-b|=1$, thus for $\\{a, b\\}=\\{33,34\\}$.\n\nThus there exist at least $4489-1122=3367$ critics which is a contradiction and we are done.\nRemark. We are going here to give some motivation about the choice of number 34, used in the above solution.\nLet us assume that every critic votes for a different pair of actor and actress. One can again start by picking out one actor or one actress who has been voted by exactly $n$ critics for $n=k, k+1, \\ldots, 100$. Then $a+b=100-k+1=101-k$ and the number of all single-votes is $s_{1}+2 s_{2}=k+k+1+\\cdots+100=$ $5050-\\frac{k(k-1)}{2}$, so there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \\geq 5050-\\frac{k(k-1)}{2}-a b$ and\n\n$$\na b=\\frac{(a+b)^{2}-(a-b)^{2}}{4}=\\frac{(101-k)^{2}-(a-b)^{2}}{4} \\leq \\frac{(101-k)^{2}-1}{4} .\n$$\n\nAfter all, the number of critics is at least\n\n$$\n5050-\\frac{k(k-1)}{2}-\\frac{(101-k)^{2}-1}{4}\n$$\n\nIn order to arrive at a contradiction we have to choose $k$ such that\n\n$$\n5050-\\frac{k(k-1)}{2}-\\frac{(101-k)^{2}-1}{4} \\geq 3367\n$$\n\nand solving the inequality with respect to $k$, the only value that makes the last one true is $k=34$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2015", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Prove that among any 20 consecutive positive integers there exists an integer $d$ such that for each positive integer $n$ we have the inequality\n\n$$\nn \\sqrt{d}\\{n \\sqrt{d}\\}>\\frac{5}{2}\n$$\n\nwhere $\\{x\\}$ denotes the fractional part of the real number $x$. The fractional part of a real number $x$ is $x$ minus the greatest integer less than or equal to $x$.", "solution": "Among the given numbers there is a number of the form $20 k+15=5(4 k+3)$. We shall prove that $d=5(4 k+3)$ satisfies the statement's condition. Since $d \\equiv-1(\\bmod 4)$, it follows that $d$ is not a perfect square, and thus for any $n \\in \\mathbb{N}$ there exists $a \\in \\mathbb{N}$ such that $a+1>n \\sqrt{d}>a$, that is, $(a+1)^{2}>n^{2} d>a^{2}$. Actually, we are going to prove that $n^{2} d \\geq a^{2}+5$. Indeed:\n\nIt is known that each positive integer of the form $4 s+3$ has a prime divisor of the same form. Let $p \\mid 4 k+3$ and $p \\equiv-1(\\bmod 4)$. Because of the form of $p$, the numbers $a^{2}+1^{2}$ and $a^{2}+2^{2}$ are not divisible by $p$, and since $p \\mid n^{2} d$, it follows that $n^{2} d \\neq a^{2}+1, a^{2}+4$. On the other hand, $5 \\mid n^{2} d$, and since $5 \\nmid a^{2}+2, a^{2}+3$, we conclude $n^{2} d \\neq a^{2}+2, a^{2}+3$. Since $n^{2} d>a^{2}$ we must have $n^{2} d \\geq a^{2}+5$ as claimed. Therefore,\n\n$$\nn \\sqrt{d}\\{n \\sqrt{d}\\}=n \\sqrt{d}(n \\sqrt{d}-a) \\geq a^{2}+5-a \\sqrt{a^{2}+5}>a^{2}+5-\\frac{a^{2}+\\left(a^{2}+5\\right)}{2}=\\frac{5}{2},\n$$\n\nwhich was to be proved.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2016-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2016", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all injective functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that for every real number $x$ and every positive integer $n$,\n\n$$\n\\left|\\sum_{i=1}^{n} i(f(x+i+1)-f(f(x+i)))\\right|<2016\n$$", "solution": "From the condition of the problem we get\n\n$$\n\\left|\\sum_{i=1}^{n-1} i(f(x+i+1)-f(f(x+i)))\\right|<2016\n$$\n\nThen\n\n$$\n\\begin{aligned}\n& |n(f(x+n+1)-f(f(x+n)))| \\\\\n= & \\left|\\sum_{i=1}^{n} i(f(x+i+1)-f(f(x+i)))-\\sum_{i=1}^{n-1} i(f(x+i+1)-f(f(x+i)))\\right| \\\\\n< & 2 \\cdot 2016=4032\n\\end{aligned}\n$$\n\nimplying\n\n$$\n|f(x+n+1)-f(f(x+n))|<\\frac{4032}{n}\n$$\n\nfor every real number $x$ and every positive integer $n$.\nLet $y \\in \\mathbb{R}$ be arbitrary. Then there exists $x$ such that $y=x+n$. We obtain\n\n$$\n|f(y+1)-f(f(y))|<\\frac{4032}{n}\n$$\n\nfor every real number $y$ and every positive integer $n$. The last inequality holds for every positive integer $n$ from where $f(y+1)=f(f(y))$ for every $y \\in \\mathbb{R}$ and since the function $f$ is an injection, then $f(y)=y+1$. The function $f(y)=y+1$ satisfies the required condition.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2016", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C D$ be a cyclic quadrilateral with $A B<C D$. The diagonals intersect at the point $F$ and lines $A D$ and $B C$ intersect at the point $E$. Let $K$ and $L$ be the orthogonal projections of $F$ onto lines $A D$ and $B C$ respectively, and let $M, S$ and $T$ be the midpoints of $E F, C F$ and $D F$ respectively. Prove that the second intersection point of the circumcircles of triangles $M K T$ and $M L S$ lies on the segment $C D$.", "solution": "Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T$ and $M L S$ pass through $N$. (1)\nFirst will prove that the circumcircle of $M L S$ passes through $N$.\nLet $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle (2) of the triangle $E F C$, so it passes also through $Q .\\left({ }^{*}\\right)(3)$\n\n\nWe will prove that\n\n$$\n\\angle S L Q=\\angle Q N S \\quad \\text { or } \\quad \\angle S L Q+\\angle Q N S=180^{\\circ}\n$$\n\nIndeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and\n\n$$\n\\angle S L C=\\angle S C L=\\angle A C B\n$$\n\nIn addition, since $N$ and $S$ are the midpoints of $D C$ and $F C$ we have that $S N \\| F D$ and similarly, since $Q$ and $N$ are the midpoints of $E C$ and $C D$, so $Q N \\| E D$.\nIt follows that the angles $\\angle E D B$ and $\\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that\n\n$$\n\\angle E D B=\\angle Q N S \\quad \\text { or } \\quad \\angle E D B+\\angle Q N S=180^{\\circ}\n$$\n\nBut, from the cyclic quadrilateral $A B C D$, we get that\n\n$$\n\\angle E D B=\\angle A C B\n$$\n\nNow, from (2),(3) and (4) we obtain immediately (1), so the quadrilateral $L N S Q$ is cyclic. Since from $\\left(^{*}\\right)$, its circumcircle passes also through $M$, we get that the points $M, L, Q, S, N$ are cocylic and this means that the circumcircle of $M L S$ passes through $N$.\nSimilarly, the circumcircle of $M K T$ passes also through $N$ and we have the desired.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Find all monic polynomials $f$ with integer coefficients satisfying the following condition: there exists a positive integer $N$ such that $p$ divides $2(f(p)!)+1$ for every prime $p>N$ for which $f(p)$ is a positive integer.\nNote: A monic polynomial has leading coefficient equal to 1.", "solution": "If $f$ is a constant polynomial then it's obvious that the condition cannot hold for\n\n$$\np \\geq 5 \\text { since } f(p)=1\n$$\n\nFrom the divisibility relation $p \\mid 2(f(p))$ ! +1 we conclude that:\n\n$$\nf(p)<p, \\text { for all primes } p>N \\quad(*)\n$$\n\nIn fact, if for some prime number $p$ we have $f(p) \\geq p$, then $p \\mid(f(p))$ ! and then $p \\mid 1$, which is absurd.\nNow suppose that $\\operatorname{deg} f=m>1$. Then $f(x)=x^{m}+Q(x), \\operatorname{deg} Q(x) \\leq m-1$ and so $f(p)=$ $p^{m}+Q(p)$. Hence for some large enough prime number $p$ holds that $f(p)>p$, which contradicts $\\left.{ }^{*}\\right)$. Therefore we must have $\\operatorname{deg} f(x)=1$ and $f(x)=x-a$, for some positive integer $a$. (3)\nThus the given condition becomes:\n\n$$\np \\mid 2(p-a)!+1\n$$\n\nBut we have (using Wilsons theorem)\n\n$$\n\\begin{gathered}\n2(p-3)!\\equiv-(p-3)!(p-2) \\equiv-(p-2)!\\equiv-1(\\bmod p) \\\\\n\\Rightarrow p \\mid 2(p-3)!+1\n\\end{gathered}\n$$\n\nFrom (1) and (2) we get\n\n$$\n\\begin{aligned}\n& (p-3)!\\equiv(p-a)!(\\bmod p) \\\\\n& (p-3)!(-1)^{a}(a-1)!\\equiv(p-a)!(-1)^{a}(a-1)!(\\bmod p) \\\\\n& (p-3)!(-1)^{a}(a-1)!\\equiv 1(\\bmod p)\n\\end{aligned}\n$$\n\nSince $-2(p-3)!\\equiv 1(\\bmod p)$, it follows that\n\n$$\n(-1)^{a}(a-1)!\\equiv-2(\\bmod p)\n$$\n\nTaking $p>(a-1)$ !, we conclude that $a=3$ and so $f(x)=x-3$, for all $x$.\nThe function $f(x)=x-3$ satisfies the required condition.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2016", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "The plane is divided into unit squares by two sets of parallel lines, forming an infinite grid. Each unit square is coloured with one of 1201 colours so that no rectangle with perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \\times 1201$ or $1201 \\times 1$ contains two squares of the same colour.\nNote: Any rectangle is assumed here to have sides contained in the lines of the grid.", "solution": "Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.\nConsider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \\leq 24$. Any integer translate of $D$ is called a diamond.\nSince any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100 , a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.\n\nChoose one colour, say, green, and let $a_{1}, a_{2}, \\ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.\nIndeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.\n\nLet, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.\n\nTherefore, $P_{1}, P_{2}, \\ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)\n\n\nFigure 1:\nWithout loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \\times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.\n\n\nFigure 2:", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2016", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all injective functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that for every real number $x$ and every positive integer $n$,\n\n$$\n\\left|\\sum_{i=1}^{n} i(f(x+i+1)-f(f(x+i)))\\right|<2016\n$$", "solution": "From the condition of the problem we get\n\n$$\n\\left|\\sum_{i=1}^{n-1} i(f(x+i+1)-f(f(x+i)))\\right|<2016\n$$\n\nThen\n\n$$\n\\begin{aligned}\n& |n(f(x+n+1)-f(f(x+n)))| \\\\\n= & \\left|\\sum_{i=1}^{n} i(f(x+i+1)-f(f(x+i)))-\\sum_{i=1}^{n-1} i(f(x+i+1)-f(f(x+i)))\\right| \\\\\n< & 2 \\cdot 2016=4032\n\\end{aligned}\n$$\n\nimplying\n\n$$\n|f(x+n+1)-f(f(x+n))|<\\frac{4032}{n}\n$$\n\nfor every real number $x$ and every positive integer $n$.\nLet $y \\in \\mathbb{R}$ be arbitrary. Then there exists $x$ such that $y=x+n$. We obtain\n\n$$\n|f(y+1)-f(f(y))|<\\frac{4032}{n}\n$$\n\nfor every real number $y$ and every positive integer $n$. The last inequality holds for every positive integer $n$ from where $f(y+1)=f(f(y))$ for every $y \\in \\mathbb{R}$ and since the function $f$ is an injection, then $f(y)=y+1$. The function $f(y)=y+1$ satisfies the required condition.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2016", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C D$ be a cyclic quadrilateral with $A B<C D$. The diagonals intersect at the point $F$ and lines $A D$ and $B C$ intersect at the point $E$. Let $K$ and $L$ be the orthogonal projections of $F$ onto lines $A D$ and $B C$ respectively, and let $M, S$ and $T$ be the midpoints of $E F, C F$ and $D F$ respectively. Prove that the second intersection point of the circumcircles of triangles $M K T$ and $M L S$ lies on the segment $C D$.", "solution": "Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T$ and $M L S$ pass through $N$. (1)\nFirst will prove that the circumcircle of $M L S$ passes through $N$.\nLet $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle (2) of the triangle $E F C$, so it passes also through $Q .\\left({ }^{*}\\right)(3)$\n\n\nWe will prove that\n\n$$\n\\angle S L Q=\\angle Q N S \\quad \\text { or } \\quad \\angle S L Q+\\angle Q N S=180^{\\circ}\n$$\n\nIndeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and\n\n$$\n\\angle S L C=\\angle S C L=\\angle A C B\n$$\n\nIn addition, since $N$ and $S$ are the midpoints of $D C$ and $F C$ we have that $S N \\| F D$ and similarly, since $Q$ and $N$ are the midpoints of $E C$ and $C D$, so $Q N \\| E D$.\nIt follows that the angles $\\angle E D B$ and $\\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that\n\n$$\n\\angle E D B=\\angle Q N S \\quad \\text { or } \\quad \\angle E D B+\\angle Q N S=180^{\\circ}\n$$\n\nBut, from the cyclic quadrilateral $A B C D$, we get that\n\n$$\n\\angle E D B=\\angle A C B\n$$\n\nNow, from (2),(3) and (4) we obtain immediately (1), so the quadrilateral $L N S Q$ is cyclic. Since from $\\left(^{*}\\right)$, its circumcircle passes also through $M$, we get that the points $M, L, Q, S, N$ are cocylic and this means that the circumcircle of $M L S$ passes through $N$.\nSimilarly, the circumcircle of $M K T$ passes also through $N$ and we have the desired.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2016", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all monic polynomials $f$ with integer coefficients satisfying the following condition: there exists a positive integer $N$ such that $p$ divides $2(f(p)!)+1$ for every prime $p>N$ for which $f(p)$ is a positive integer.\nNote: A monic polynomial has leading coefficient equal to 1.", "solution": "If $f$ is a constant polynomial then it's obvious that the condition cannot hold for\n\n$$\np \\geq 5 \\text { since } f(p)=1\n$$\n\nFrom the divisibility relation $p \\mid 2(f(p))$ ! +1 we conclude that:\n\n$$\nf(p)<p, \\text { for all primes } p>N \\quad(*)\n$$\n\nIn fact, if for some prime number $p$ we have $f(p) \\geq p$, then $p \\mid(f(p))$ ! and then $p \\mid 1$, which is absurd.\nNow suppose that $\\operatorname{deg} f=m>1$. Then $f(x)=x^{m}+Q(x), \\operatorname{deg} Q(x) \\leq m-1$ and so $f(p)=$ $p^{m}+Q(p)$. Hence for some large enough prime number $p$ holds that $f(p)>p$, which contradicts $\\left.{ }^{*}\\right)$. Therefore we must have $\\operatorname{deg} f(x)=1$ and $f(x)=x-a$, for some positive integer $a$. (3)\nThus the given condition becomes:\n\n$$\np \\mid 2(p-a)!+1\n$$\n\nBut we have (using Wilsons theorem)\n\n$$\n\\begin{gathered}\n2(p-3)!\\equiv-(p-3)!(p-2) \\equiv-(p-2)!\\equiv-1(\\bmod p) \\\\\n\\Rightarrow p \\mid 2(p-3)!+1\n\\end{gathered}\n$$\n\nFrom (1) and (2) we get\n\n$$\n\\begin{aligned}\n& (p-3)!\\equiv(p-a)!(\\bmod p) \\\\\n& (p-3)!(-1)^{a}(a-1)!\\equiv(p-a)!(-1)^{a}(a-1)!(\\bmod p) \\\\\n& (p-3)!(-1)^{a}(a-1)!\\equiv 1(\\bmod p)\n\\end{aligned}\n$$\n\nSince $-2(p-3)!\\equiv 1(\\bmod p)$, it follows that\n\n$$\n(-1)^{a}(a-1)!\\equiv-2(\\bmod p)\n$$\n\nTaking $p>(a-1)$ !, we conclude that $a=3$ and so $f(x)=x-3$, for all $x$.\nThe function $f(x)=x-3$ satisfies the required condition.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2016", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "The plane is divided into unit squares by two sets of parallel lines, forming an infinite grid. Each unit square is coloured with one of 1201 colours so that no rectangle with perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \\times 1201$ or $1201 \\times 1$ contains two squares of the same colour.\nNote: Any rectangle is assumed here to have sides contained in the lines of the grid.", "solution": "Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.\nConsider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \\leq 24$. Any integer translate of $D$ is called a diamond.\nSince any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100 , a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.\n\nChoose one colour, say, green, and let $a_{1}, a_{2}, \\ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.\nIndeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.\n\nLet, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.\n\nTherefore, $P_{1}, P_{2}, \\ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)\n\n\nFigure 1:\nWithout loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \\times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.\n\n\nFigure 2:", "metadata": {"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2017-BMO-type3.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2017", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all ordered pairs $(x, y)$ of positive integers such that:\n\n$$\nx^{3}+y^{3}=x^{2}+42 x y+y^{2} \\text {. }\n$$", "solution": "Possible initial thoughts about this equation might include:\n(i) I can factorise the sum of cubes on the left.\n(ii) How can I use the 42?\n(iii) The left is cubic and the right is quadratic, so if $x$ or $y$ is very large there will be no solutions.\n\nThe first two might lead us to rewrite the equation as $(x+y)\\left(x^{2}-x y+y^{2}\\right)=x^{2}-x y+y^{2}+43 x y$. The number $43=42+1$ is prime which is good news since we have $(x+y-1)\\left(x^{2}-x y+y^{2}\\right)=43 x y$.\n\nNow we can employ some wishful thinking: if $x$ and $y$ happen to be coprime, then $\\left(x^{2}-x y+y^{2}\\right)$ has no factors in common with $x$ or $y$ so it must divide 43 . This feels like a significant step except for the fact that $x$ and $y$ may not be coprime.\n\nThis suggests writing $x=d X$ and $y=d Y$ where $d$ is the highest common factor of $x$ and $y$.\nWe end up with $(d X+d Y-1)\\left(X^{2}-X Y+Y^{2}\\right)=43 X Y$ so $X^{2}-X Y+Y^{2}$ equals 1 or 43.\nThe first of these readily gives $X=Y=1$. A neat way to deal with the second is to assume $Y \\leq X$ so $43=X^{2}-X Y+Y^{2} \\geq Y^{2}$. This gives six cases for $Y$ which can be checked in turn. Alternatively you can solve $X^{2}-X Y+Y^{2}=43$ for $X$ and fuss about the discriminant.\n\nIn the end the only solutions turn out to be $(x, y)=(22,22),(1,7)$ or $(7,1)$.\nAnother reasonable initial plan is to bound $x+y$ (using observation (iii) above) and then use modular arithmetic to eliminate cases until only the correct solutions remain. Working modulo 7 is particularly appealing since $7 \\mid 42$ and the only cubes modulo 7 are 0,1 and -1 .\n\nWe have $x^{3}+y^{3}=(x+y)^{3}-3 x y(x+y)$ and also $x^{2}+42 x y+y^{2}=(x+y)^{2}+40 x y$ so the equation becomes $(x+y)^{3}=(x+y)^{2}+x y(3 x y+40)$. Now using $x y \\leq\\left(\\frac{x+y}{2}\\right)^{2}$ leads to $x+y \\leq 44$.\n\nThis leaves a mere 484 cases to check! The modulo 7 magic is not really enough to cut this down to an attractive number, and although the approach can obviously be made to work, to call it laborious is an understatement.\n\nOther possible approaches, such as substituting $u=x+y, v=x-y$, seem to lie somewhere between the two described above in terms of the amount of fortitude needed to pull them off.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with with $A B<A C$ and let $\\Gamma$ be its circumcircle. Let the tangents to $\\Gamma$ at $B$ and $C$ be $t_{B}$ and $t_{C}$ respectively and let their point of intersection be $L$. The line through $B$ parallel to $A C$ intersects $t_{C}$ at $D$. The line through $C$ parallel to $A B$ intersects $t_{B}$ at $E$. The circumcircle of triangle $B D C$ meets the side $A C$ at $T$ where $T$ lies between $A$ and $C$. The circumcircle of triangle $B E C$ meets the line $A B$ at $S$ where $B$ lies between $A$ and $S$.\nProve that the lines $S T, B C$ and $A L$ are concurrent.", "solution": "How we attack this problem depends on how much triangle geometry we can effortlessly recall - a good knowledge of some standard results helps a great deal.\n\nWe might instantly note that $A L$ is a symmedian of $A B C$, and so divides the line $B C$ in the ratio $c^{2}: b^{2}$. Now the plan is to show that $S T$ also divides $B C$ in this ratio.\n\nSince we are working with ratios of distances, Menelaus' theorem may prove useful.\n\n\nA key step is to notice (based on a careful diagram) that $A C$ is tangent to circle $C B S$. Once spotted this is easy to prove. The parallels give us $\\angle B=\\angle B C E$, and, since $B E$ is tangent to circle $A B C$, we have $\\angle E B C=\\angle A$ by the alternate segment theorem. Now angles in a triangle give $\\angle C=\\angle C E B$, and we have the converse to the alternate segment theorem. We obtain $A B$ is tangent to circle $C B D$ in the same way.\n\nNow we have some tangencies and want some ratios.\nTangent-secant yields $A T . b=c^{2}$ and $c . A S=b^{2}$ or, equivalently, $b . C T=b^{2}-c^{2}$ and $c . B S=b^{2}-c^{2}$.\nBy Menelaus we know that $S T$ divides $B C$ in the ratio $A T . B S: A S . C T$ and it's all over bar the shouting.\n\nIf we are not lucky enough to have the stuff about the symmedian at our fingertips, we can still get essentially the same solution with a bit more work. We begin with the second half of the proof above, and establish that $S T$ divides $B C$ in the ratio $c^{2}: b^{2}$. Now we need to prove that $A L$ divides $B C$ in the same ratio.\n\nThe next (non-obvious!) step is to draw a parallel to $B C$ through $A$ as shown.\n\n\nNow $\\triangle A B C \\sim \\triangle B^{\\prime} A B \\sim \\triangle C C^{\\prime} A$ and the ratio $B^{\\prime} A: A C^{\\prime}$ which equals $B X: X C$ drops out as $c^{2}: b^{2}$ as required.\n\nClearly knowing the standard symmedian configuration and corresponding ratio is an enormous advantage.\n\nFinally it is worth noting that, to the right sort of mind, the problem screams out for areal coordinates. These turn out to kill it fairly easily, not least because all three circles pass through at least two vertices of $\\triangle A B C$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2017", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $\\mathbb{N}$ be the set of positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that:\n\n$$\nn+f(m) \\text { divides } f(n)+n f(m)\n$$", "solution": "The striking thing about this problem is that the relation concerns divisibility rather than equality. How can we exploit this? We are given that $n+f(m) \\mid f(n)+n f(m)$ but we can certainly add or subtract multiples of the left hand side from the right hand side and preserve the divisibility. This leads to a key idea:\n'Eliminate one of the variables from the right hand side.'\nClearly $n+f(m) \\mid f(n)+n f(m)-n(n+f(m))$ so for any $n, m$ we have\n\n$$\nn+f(m) \\mid f(n)-n^{2}\n$$\n\nThis feels like a strong condition: if we fix $n$ and let $f(m)$ go to infinity, then $f(n)-n^{2}$ will have arbitrarily large factors, which implies it must be zero.\n\nWe must be careful: this argument is fine, so long as the function $f$ takes arbitrarily large values. (We also need to check that $f(n)=n^{2}$ satisfies the original statement which it does.)\n\nWe are left with the case where $f$ takes only finitely many values.\nIn this case $f$ must take the same value infinitely often, so it is natural to focus on an infinite set $S \\subset \\mathbb{N}$ such that $f(s)=k$ for all $s \\in S$. If $n, m \\in S$ then the original statement gives $n+k \\mid k+n k$ where $k$ is fixed and $n$ can be as large as we like.\n\nNow we recycle our key idea and eliminate $n$ from the right.\n$n+k \\mid k+n k-k(n+k)$ so $n+k \\mid k-k^{2}$ for arbitrarily large $n$. This means that $k-k^{2}=0$ so $k=1$, since it must be positive.\n\nAt this point we suspect that $f(n)=1$ for all $n$ is the only bounded solution, so we pick some $t$ such that $f(t)=L>1$ and try to get a contradiction.\n\nIn the original statement we can set $m=t$ and get $n+L \\mid f(n)+n L$. Eliminating $L$ from the right gives us nothing new, so how can we proceed? Well, we have an infinite set $S$ such that $f$ is constantly 1 on $S$ so we can take $n \\in S$ to obtain $n+L \\mid 1+n L$\n\nUsing our key idea one more time and eliminating $n$ from the right, we get $n+L \\mid 1-L^{2}$ for arbitrarily large $n$ which is impossible if $L>1$.\n\nA rather different solution can be found by playing around with small values of $m$ and $n$.\nAs before it helps to establish $(\\star)$ but now $(n, m)=(1,1)$ gives $1+f(1) \\mid f(1)-1$.\nThe left is bigger than the right, so the right must be zero $-f(1)=1$.\nNow try $(n, m)=(2,1)$ and obtain $2+f(2) \\mid f(2)-4$. Subtracting the left from the right gives $2+f(2) \\mid-6$. Since $f(2) \\in \\mathbb{N}$ the left is a factor of -6 which is bigger than 2 . This gives $f(2)=1$ or $f(2)=4$.\n\nIn the first case we can plug this back into the orginal statement to get $2+f(m) \\mid 1+2 f(m)$. Now taking two copies of the left away from the right we have $2+f(m) \\mid-3$.\n\nThus $2+f(m)$ must a factor of -3 which is bigger than 2 , so $f(m)=1$ for any $m$.\nBefore proceeding with the case $f(2)=4$ we take another look at our strong result $(\\star)$. Setting $n=m$ gives $n+f(n) \\mid f(n)-n^{2}$ so taking $f(n)-n^{2}$ away from $n+f(n)$ shows that\n\n$$\nn+f(n) \\mid n+n^{2}\n$$\n\nLet see if we can use $(\\star)$ and $(\\dagger)$ to pin down the value of $f(3)$, using $f(2)=4$.\nFrom $(\\star)$ we have $3+4 \\mid f(3)-9$ and from $(\\dagger)$ we have $3+f(3) \\mid 12$. The second of these shows $f(3)$ is 1,3 or 9 , but 1 and 3 are too small to work in the first relation.\n\nSimilarly, setting $(n, m)=(4,3)$ in $(\\star)$ gives $4+9 \\mid f(4)-16$ while $n=4$ in $(\\dagger)$ gives $4+f(4) \\mid 20$. The latter shows $f(4) \\leq 16$ so $13 \\mid 16-f(4)$. The only possible multiples of 13 are 0 and 13 , of which only the first one works. Thus $f(4)=16$.\n\nNow we are ready to try induction. Assume $f(n-1)=(n-1)^{2}$ and use $(\\star)$ and $(\\dagger)$ to obtain $n+(n-1)^{2} \\mid f(n)-n^{2}$ and $n+f(n) \\mid n+n^{2}$. The latter implies $f(n) \\leq n^{2}$ so the former becomes $n^{2}-n+1 \\mid n^{2}-f(n)$. If $f(n) \\neq n^{2}$ then $n^{2}-f(n)=1 \\times\\left(n^{2}-n+1\\right)$ since any other multiple would be too large. However, putting $f(n)=n-1$ into $n+f(n) \\mid n+n^{2}$ implies $2 n-1 \\mid n(1+n)$. This is a contradiction since $2 n-1$ is coprime to $n$ and clearly cannot divide $1+n$.\n\nfor all $m, n \\in \\mathbb{N}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2017", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "There are $n>2$ students sitting at a round table. Initially each student has exactly one candy. At each step, each student chooses one of the following operations:\n(a) Pass one candy to the student on their left or the student on their right.\n(b) Divide all their candies into two, possibly empty, sets and pass one set to the student on their left and the other to the student on their right.\n\nAt each step the students perform their chosen operations simultaneously.\nAn arrangement of candies is legal if it can be obtained in a finite number of steps.\nFind the number of legal arrangements.\n(Two arrangements are different if there is a student who has different numbers of candies in each one.)", "solution": "One possible initial reaction to this problem is that there is rather too much movement of caramels ${ }^{2}$ at each step to keep track of easily. This leads to the question: 'How little can I do in, say, two steps?' If every student passes all their caramels left on one step using (b), and all their caramels right on the next step, then no caramels move. (This is rather too little movement.) Let us see what a small change to this sequence can accomplish. We choose a student with at least one caramel. At the first step, she passes one caramel to the right and any others she has to the left. Every one else passes everything left. At the next step everybody passes everything right. The effect of this is that exactly one caramel has moved exactly two places to the right. Similarly, there is a double step which moves exactly one caramel to places to the left.\n\nIf we have not already done so, now is the time to start working through some small values of $n$.\nThe case $n=3$ yields a useful observation. Going two places (let's call this a double jump) to the left on a triangle is the same as going one place to the right. Indeed if $n$ is odd, say $2 k+1$, then $k$ double jumps to the left moves the caramel one place to the right and vice versa.\n\nIt is now clear that, if $n$ is odd, any arrangement of caramels is possible. We simply move them into position one at a time.\n\nIn the case $n=4$ it seems hard to get all the caramels into one place. Indeed, if we limit ourselves to double jumps, then we can only get $(1,1,1,1),(1,2,1,0),(2,2,0,0)$ and rotations of these arrangements. What can we say about these? Well it seems that students one and three always hold two candies between them. Having noticed this, it is not too hard to make a more general observation: if $n$ is even then a double jump cannot change the total number of caramels held by the odd numbered students. However, double jumps are not the only moves available to us. For example, it is possible to go from $(2,2,0,0)$ to $(3,1,0,0)$. A double jump now gives $(2,1,1,0)$ as well.\n\nTo squeeze maximum value out of the $n=4$ case, it is worth looking at the arrangements we have not yet managed to get to. They are (rotations of) $(4,0,0,0),(3,0,1,0)$ and $(2,0,2,0)$. What do these have in common? They are precisely the arrangements where the even numbered students hold all the caramels. Can we prove that these are illegal? Well, what can we say about an arrangement which precedes one of these elusive ones? This question leads to the last big idea in the solution to this problem. If after some step the even numbered students have all the caramels, they cannot have had any at all before the step, else they would have passed at least one caramel to an odd numbered student.\n\nTurning this around gives a crucial lemma for even values of $n$. Let's call a caramel held by an odd numbered student an odd caramel and define even caramels similarly. Let's call an arrangement with at least one odd caramel and at least one even caramel balanced. If the arrangement is balanced before some step, then it will be balanced after the step. The initial position is balanced, so every legal position is balanced.\n\nFinally we are on the home straight. We claim that every balanced position is legal. Using double jumps we can move to $\\left(\\ldots, \\frac{n}{2}, \\frac{n}{2}, 0, \\ldots\\right)$. Now we need to tinker with the numbers of odd and even caramels. There are lots of usable sequences. For example:\n\n$$\n\\begin{gathered}\n(\\ldots, a, b, 0, \\ldots) \\\\\n(\\ldots, a-1,1, b, \\ldots) \\\\\n(\\ldots, a-1, b+1,0, \\ldots)\n\\end{gathered}\n$$\n\ncan be used to change the number of odd caramels provided $a-1 \\geq 1$.\nOnce we have the correct number of odd and even caramels, they can be moved into place using double jumps.\n\nIt remains to observe that there are $\\binom{2 n-1}{n}$ possible arrangements of caramels, and that if $n$ is even, then $2\\left(\\frac{\\frac{3 n}{2}-1}{n}\\right)$ of these are not balanced.\n\nAnother sensible approach is to think about which steps are reversible. It turns out that many are, including all those where the students all use option (b).\n\nIt is possible to argue that if $n$ is odd, then we can start with any position, move to $(\\ldots, n, \\ldots)$ reversibly, then move to the initial position reversibly. Playing the whole tape backwards shows all positions are legal.\n\nIf $n$ is even it is possible to start from any balanced position and reversibly move to $(\\ldots, n-1,1, \\ldots)$ and thence to the initial position so we are done.\n\n[^0]\n[^0]: ${ }^{2}$ The word 'candy' was a little too grating for my delicate British ears. I am grateful to the Italians for suggesting the more elegant alternative.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2017", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all ordered pairs $(x, y)$ of positive integers such that:\n\n$$\nx^{3}+y^{3}=x^{2}+42 x y+y^{2} \\text {. }\n$$", "solution": "Possible initial thoughts about this equation might include:\n(i) I can factorise the sum of cubes on the left.\n(ii) How can I use the 42?\n(iii) The left is cubic and the right is quadratic, so if $x$ or $y$ is very large there will be no solutions.\n\nThe first two might lead us to rewrite the equation as $(x+y)\\left(x^{2}-x y+y^{2}\\right)=x^{2}-x y+y^{2}+43 x y$. The number $43=42+1$ is prime which is good news since we have $(x+y-1)\\left(x^{2}-x y+y^{2}\\right)=43 x y$.\n\nNow we can employ some wishful thinking: if $x$ and $y$ happen to be coprime, then $\\left(x^{2}-x y+y^{2}\\right)$ has no factors in common with $x$ or $y$ so it must divide 43 . This feels like a significant step except for the fact that $x$ and $y$ may not be coprime.\n\nThis suggests writing $x=d X$ and $y=d Y$ where $d$ is the highest common factor of $x$ and $y$.\nWe end up with $(d X+d Y-1)\\left(X^{2}-X Y+Y^{2}\\right)=43 X Y$ so $X^{2}-X Y+Y^{2}$ equals 1 or 43.\nThe first of these readily gives $X=Y=1$. A neat way to deal with the second is to assume $Y \\leq X$ so $43=X^{2}-X Y+Y^{2} \\geq Y^{2}$. This gives six cases for $Y$ which can be checked in turn. Alternatively you can solve $X^{2}-X Y+Y^{2}=43$ for $X$ and fuss about the discriminant.\n\nIn the end the only solutions turn out to be $(x, y)=(22,22),(1,7)$ or $(7,1)$.\nAnother reasonable initial plan is to bound $x+y$ (using observation (iii) above) and then use modular arithmetic to eliminate cases until only the correct solutions remain. Working modulo 7 is particularly appealing since $7 \\mid 42$ and the only cubes modulo 7 are 0,1 and -1 .\n\nWe have $x^{3}+y^{3}=(x+y)^{3}-3 x y(x+y)$ and also $x^{2}+42 x y+y^{2}=(x+y)^{2}+40 x y$ so the equation becomes $(x+y)^{3}=(x+y)^{2}+x y(3 x y+40)$. Now using $x y \\leq\\left(\\frac{x+y}{2}\\right)^{2}$ leads to $x+y \\leq 44$.\n\nThis leaves a mere 484 cases to check! The modulo 7 magic is not really enough to cut this down to an attractive number, and although the approach can obviously be made to work, to call it laborious is an understatement.\n\nOther possible approaches, such as substituting $u=x+y, v=x-y$, seem to lie somewhere between the two described above in terms of the amount of fortitude needed to pull them off.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2017", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute triangle with with $A B<A C$ and let $\\Gamma$ be its circumcircle. Let the tangents to $\\Gamma$ at $B$ and $C$ be $t_{B}$ and $t_{C}$ respectively and let their point of intersection be $L$. The line through $B$ parallel to $A C$ intersects $t_{C}$ at $D$. The line through $C$ parallel to $A B$ intersects $t_{B}$ at $E$. The circumcircle of triangle $B D C$ meets the side $A C$ at $T$ where $T$ lies between $A$ and $C$. The circumcircle of triangle $B E C$ meets the line $A B$ at $S$ where $B$ lies between $A$ and $S$.\nProve that the lines $S T, B C$ and $A L$ are concurrent.", "solution": "How we attack this problem depends on how much triangle geometry we can effortlessly recall - a good knowledge of some standard results helps a great deal.\n\nWe might instantly note that $A L$ is a symmedian of $A B C$, and so divides the line $B C$ in the ratio $c^{2}: b^{2}$. Now the plan is to show that $S T$ also divides $B C$ in this ratio.\n\nSince we are working with ratios of distances, Menelaus' theorem may prove useful.\n\n\nA key step is to notice (based on a careful diagram) that $A C$ is tangent to circle $C B S$. Once spotted this is easy to prove. The parallels give us $\\angle B=\\angle B C E$, and, since $B E$ is tangent to circle $A B C$, we have $\\angle E B C=\\angle A$ by the alternate segment theorem. Now angles in a triangle give $\\angle C=\\angle C E B$, and we have the converse to the alternate segment theorem. We obtain $A B$ is tangent to circle $C B D$ in the same way.\n\nNow we have some tangencies and want some ratios.\nTangent-secant yields $A T . b=c^{2}$ and $c . A S=b^{2}$ or, equivalently, $b . C T=b^{2}-c^{2}$ and $c . B S=b^{2}-c^{2}$.\nBy Menelaus we know that $S T$ divides $B C$ in the ratio $A T . B S: A S . C T$ and it's all over bar the shouting.\n\nIf we are not lucky enough to have the stuff about the symmedian at our fingertips, we can still get essentially the same solution with a bit more work. We begin with the second half of the proof above, and establish that $S T$ divides $B C$ in the ratio $c^{2}: b^{2}$. Now we need to prove that $A L$ divides $B C$ in the same ratio.\n\nThe next (non-obvious!) step is to draw a parallel to $B C$ through $A$ as shown.\n\n\nNow $\\triangle A B C \\sim \\triangle B^{\\prime} A B \\sim \\triangle C C^{\\prime} A$ and the ratio $B^{\\prime} A: A C^{\\prime}$ which equals $B X: X C$ drops out as $c^{2}: b^{2}$ as required.\n\nClearly knowing the standard symmedian configuration and corresponding ratio is an enormous advantage.\n\nFinally it is worth noting that, to the right sort of mind, the problem screams out for areal coordinates. These turn out to kill it fairly easily, not least because all three circles pass through at least two vertices of $\\triangle A B C$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2017", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $\\mathbb{N}$ be the set of positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that:\n\n$$\nn+f(m) \\text { divides } f(n)+n f(m)\n$$", "solution": "The striking thing about this problem is that the relation concerns divisibility rather than equality. How can we exploit this? We are given that $n+f(m) \\mid f(n)+n f(m)$ but we can certainly add or subtract multiples of the left hand side from the right hand side and preserve the divisibility. This leads to a key idea:\n'Eliminate one of the variables from the right hand side.'\nClearly $n+f(m) \\mid f(n)+n f(m)-n(n+f(m))$ so for any $n, m$ we have\n\n$$\nn+f(m) \\mid f(n)-n^{2}\n$$\n\nThis feels like a strong condition: if we fix $n$ and let $f(m)$ go to infinity, then $f(n)-n^{2}$ will have arbitrarily large factors, which implies it must be zero.\n\nWe must be careful: this argument is fine, so long as the function $f$ takes arbitrarily large values. (We also need to check that $f(n)=n^{2}$ satisfies the original statement which it does.)\n\nWe are left with the case where $f$ takes only finitely many values.\nIn this case $f$ must take the same value infinitely often, so it is natural to focus on an infinite set $S \\subset \\mathbb{N}$ such that $f(s)=k$ for all $s \\in S$. If $n, m \\in S$ then the original statement gives $n+k \\mid k+n k$ where $k$ is fixed and $n$ can be as large as we like.\n\nNow we recycle our key idea and eliminate $n$ from the right.\n$n+k \\mid k+n k-k(n+k)$ so $n+k \\mid k-k^{2}$ for arbitrarily large $n$. This means that $k-k^{2}=0$ so $k=1$, since it must be positive.\n\nAt this point we suspect that $f(n)=1$ for all $n$ is the only bounded solution, so we pick some $t$ such that $f(t)=L>1$ and try to get a contradiction.\n\nIn the original statement we can set $m=t$ and get $n+L \\mid f(n)+n L$. Eliminating $L$ from the right gives us nothing new, so how can we proceed? Well, we have an infinite set $S$ such that $f$ is constantly 1 on $S$ so we can take $n \\in S$ to obtain $n+L \\mid 1+n L$\n\nUsing our key idea one more time and eliminating $n$ from the right, we get $n+L \\mid 1-L^{2}$ for arbitrarily large $n$ which is impossible if $L>1$.\n\nA rather different solution can be found by playing around with small values of $m$ and $n$.\nAs before it helps to establish $(\\star)$ but now $(n, m)=(1,1)$ gives $1+f(1) \\mid f(1)-1$.\nThe left is bigger than the right, so the right must be zero $-f(1)=1$.\nNow try $(n, m)=(2,1)$ and obtain $2+f(2) \\mid f(2)-4$. Subtracting the left from the right gives $2+f(2) \\mid-6$. Since $f(2) \\in \\mathbb{N}$ the left is a factor of -6 which is bigger than 2 . This gives $f(2)=1$ or $f(2)=4$.\n\nIn the first case we can plug this back into the orginal statement to get $2+f(m) \\mid 1+2 f(m)$. Now taking two copies of the left away from the right we have $2+f(m) \\mid-3$.\n\nThus $2+f(m)$ must a factor of -3 which is bigger than 2 , so $f(m)=1$ for any $m$.\nBefore proceeding with the case $f(2)=4$ we take another look at our strong result $(\\star)$. Setting $n=m$ gives $n+f(n) \\mid f(n)-n^{2}$ so taking $f(n)-n^{2}$ away from $n+f(n)$ shows that\n\n$$\nn+f(n) \\mid n+n^{2}\n$$\n\nLet see if we can use $(\\star)$ and $(\\dagger)$ to pin down the value of $f(3)$, using $f(2)=4$.\nFrom $(\\star)$ we have $3+4 \\mid f(3)-9$ and from $(\\dagger)$ we have $3+f(3) \\mid 12$. The second of these shows $f(3)$ is 1,3 or 9 , but 1 and 3 are too small to work in the first relation.\n\nSimilarly, setting $(n, m)=(4,3)$ in $(\\star)$ gives $4+9 \\mid f(4)-16$ while $n=4$ in $(\\dagger)$ gives $4+f(4) \\mid 20$. The latter shows $f(4) \\leq 16$ so $13 \\mid 16-f(4)$. The only possible multiples of 13 are 0 and 13 , of which only the first one works. Thus $f(4)=16$.\n\nNow we are ready to try induction. Assume $f(n-1)=(n-1)^{2}$ and use $(\\star)$ and $(\\dagger)$ to obtain $n+(n-1)^{2} \\mid f(n)-n^{2}$ and $n+f(n) \\mid n+n^{2}$. The latter implies $f(n) \\leq n^{2}$ so the former becomes $n^{2}-n+1 \\mid n^{2}-f(n)$. If $f(n) \\neq n^{2}$ then $n^{2}-f(n)=1 \\times\\left(n^{2}-n+1\\right)$ since any other multiple would be too large. However, putting $f(n)=n-1$ into $n+f(n) \\mid n+n^{2}$ implies $2 n-1 \\mid n(1+n)$. This is a contradiction since $2 n-1$ is coprime to $n$ and clearly cannot divide $1+n$.\n\nfor all $m, n \\in \\mathbb{N}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2017", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "There are $n>2$ students sitting at a round table. Initially each student has exactly one candy. At each step, each student chooses one of the following operations:\n(a) Pass one candy to the student on their left or the student on their right.\n(b) Divide all their candies into two, possibly empty, sets and pass one set to the student on their left and the other to the student on their right.\n\nAt each step the students perform their chosen operations simultaneously.\nAn arrangement of candies is legal if it can be obtained in a finite number of steps.\nFind the number of legal arrangements.\n(Two arrangements are different if there is a student who has different numbers of candies in each one.)", "solution": "One possible initial reaction to this problem is that there is rather too much movement of caramels ${ }^{2}$ at each step to keep track of easily. This leads to the question: 'How little can I do in, say, two steps?' If every student passes all their caramels left on one step using (b), and all their caramels right on the next step, then no caramels move. (This is rather too little movement.) Let us see what a small change to this sequence can accomplish. We choose a student with at least one caramel. At the first step, she passes one caramel to the right and any others she has to the left. Every one else passes everything left. At the next step everybody passes everything right. The effect of this is that exactly one caramel has moved exactly two places to the right. Similarly, there is a double step which moves exactly one caramel to places to the left.\n\nIf we have not already done so, now is the time to start working through some small values of $n$.\nThe case $n=3$ yields a useful observation. Going two places (let's call this a double jump) to the left on a triangle is the same as going one place to the right. Indeed if $n$ is odd, say $2 k+1$, then $k$ double jumps to the left moves the caramel one place to the right and vice versa.\n\nIt is now clear that, if $n$ is odd, any arrangement of caramels is possible. We simply move them into position one at a time.\n\nIn the case $n=4$ it seems hard to get all the caramels into one place. Indeed, if we limit ourselves to double jumps, then we can only get $(1,1,1,1),(1,2,1,0),(2,2,0,0)$ and rotations of these arrangements. What can we say about these? Well it seems that students one and three always hold two candies between them. Having noticed this, it is not too hard to make a more general observation: if $n$ is even then a double jump cannot change the total number of caramels held by the odd numbered students. However, double jumps are not the only moves available to us. For example, it is possible to go from $(2,2,0,0)$ to $(3,1,0,0)$. A double jump now gives $(2,1,1,0)$ as well.\n\nTo squeeze maximum value out of the $n=4$ case, it is worth looking at the arrangements we have not yet managed to get to. They are (rotations of) $(4,0,0,0),(3,0,1,0)$ and $(2,0,2,0)$. What do these have in common? They are precisely the arrangements where the even numbered students hold all the caramels. Can we prove that these are illegal? Well, what can we say about an arrangement which precedes one of these elusive ones? This question leads to the last big idea in the solution to this problem. If after some step the even numbered students have all the caramels, they cannot have had any at all before the step, else they would have passed at least one caramel to an odd numbered student.\n\nTurning this around gives a crucial lemma for even values of $n$. Let's call a caramel held by an odd numbered student an odd caramel and define even caramels similarly. Let's call an arrangement with at least one odd caramel and at least one even caramel balanced. If the arrangement is balanced before some step, then it will be balanced after the step. The initial position is balanced, so every legal position is balanced.\n\nFinally we are on the home straight. We claim that every balanced position is legal. Using double jumps we can move to $\\left(\\ldots, \\frac{n}{2}, \\frac{n}{2}, 0, \\ldots\\right)$. Now we need to tinker with the numbers of odd and even caramels. There are lots of usable sequences. For example:\n\n$$\n\\begin{gathered}\n(\\ldots, a, b, 0, \\ldots) \\\\\n(\\ldots, a-1,1, b, \\ldots) \\\\\n(\\ldots, a-1, b+1,0, \\ldots)\n\\end{gathered}\n$$\n\ncan be used to change the number of odd caramels provided $a-1 \\geq 1$.\nOnce we have the correct number of odd and even caramels, they can be moved into place using double jumps.\n\nIt remains to observe that there are $\\binom{2 n-1}{n}$ possible arrangements of caramels, and that if $n$ is even, then $2\\left(\\frac{\\frac{3 n}{2}-1}{n}\\right)$ of these are not balanced.\n\nAnother sensible approach is to think about which steps are reversible. It turns out that many are, including all those where the students all use option (b).\n\nIt is possible to argue that if $n$ is odd, then we can start with any position, move to $(\\ldots, n, \\ldots)$ reversibly, then move to the initial position reversibly. Playing the whole tape backwards shows all positions are legal.\n\nIf $n$ is even it is possible to start from any balanced position and reversibly move to $(\\ldots, n-1,1, \\ldots)$ and thence to the initial position so we are done.\n\n[^0]\n[^0]: ${ }^{2}$ The word 'candy' was a little too grating for my delicate British ears. I am grateful to the Italians for suggesting the more elegant alternative.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2018-BMO-type3.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and the perpendicular from $M$ to $A B$ intersects the segment $A B$ at the point $E$. If $E M$ bisects the angle $C E D$, prove that $A B$ is a diameter of the circle $k$.", "solution": "Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from\n\n$$\n\\frac{M P}{B H}=\\frac{D M}{D B}=\\frac{K M}{A B} \\quad \\text { and } \\quad \\frac{M Q}{A H}=\\frac{C M}{C A}=\\frac{M L}{A B}\n$$\n\nwe obtain $A H / H B=K M / M L$.\nLet the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\\prime}$. Then $A H^{\\prime} / H^{\\prime} B=K M / M L=A H / H B$, so $H^{\\prime} \\equiv H$, i.e. $S$ lies on the line $M H$.\nThe quadrilateral $A B C D$ is not a trapezoid, so $A H \\neq B H$. Consider the point $A^{\\prime}$ on the ray $H B$ such that $H A^{\\prime}=H A$. Since $\\varangle S A^{\\prime} M=\\varangle S A M=\\varangle S B M$, quadrilateral $A^{\\prime} B S M$ is cyclic and therefore $\\varangle A B C=\\varangle A^{\\prime} B S=\\varangle A^{\\prime} M H=\\varangle A M H=90^{\\circ}-\\varangle B A C$, which implies that $\\varangle A C B=90^{\\circ}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $q$ be a positive rational number. Two ants are initially at the same point $X$ in the plane. In the $n$-th minute $(n=1,2, \\ldots)$ each of them chooses whether to walk due north, east, south or west and then walks the distance of $q^{n}$ metres. After a whole number of minutes, they are at the same point in the plane (not necessarily $X$ ), but have not taken exactly the same route within that time. Determine all possible values of $q$.", "solution": "Answer: $q=1$.\nLet $x_{A}^{(n)}$ (resp. $x_{B}^{(n)}$ ) be the $x$-coordinates of the first (resp. second) ant's position after $n$ minutes. Then $x_{A}^{(n)}-x_{A}^{(n-1)} \\in\\left\\{q^{n},-q^{n}, 0\\right\\}$, and so $x_{A}^{(n)}, x_{B}^{(n)}$ are given by polynomials in $q$ with coefficients in $\\{-1,0,1\\}$. So if the ants meet after $n$ minutes, then\n\n$$\n0=x_{A}^{(n)}-x_{B}^{(n)}=P(q),\n$$\n\nwhere $P$ is a polynomial with degree at most $n$ and coefficients in $\\{-2,-, 1,0,1,2\\}$. Thus if $q=\\frac{a}{b}(a, b \\in \\mathbb{N})$, we have $a \\mid 2$ and $b \\mid 2$, i.e. $q \\in\\left\\{\\frac{1}{2}, 1,2\\right\\}$.\nIt is clearly possible when $q=1$.\n\nWe argue that $q=\\frac{1}{2}$ is not possible. Assume that the ants diverge for the first time after the $k$ th minute, for $k \\geqslant 0$. Then\n\n$$\n\\left|x_{B}^{(k+1)}-x_{A}^{(k+1)}\\right|+\\left|y_{B}^{(k+1)}-y_{A}^{(k+1)}\\right|=2 q^{k} .\n$$\n\nBut also $\\left|x_{A}^{(\\ell+1)}-x_{A}^{(\\ell)}\\right|+\\left|y_{A}^{(\\ell+1)}-y_{A}^{(\\ell)}\\right|=q^{\\ell}$ for each $l \\geqslant k+1$, and so\n\n$$\n\\left|x_{A}^{(n)}-x_{A}^{(k+1)}\\right|+\\left|y_{A}^{(n)}-y_{A}^{(k+1)}\\right| \\leqslant q^{k+1}+q^{k+2}+\\ldots+q^{n-1}\n$$\n\nand similarly for the second ant. Combining (1) and (2) with the triangle inequality, we obtain for any $n \\geqslant k+1$\n\n$$\n\\left|x_{B}^{(n)}-x_{A}^{(n)}\\right|+\\left|y_{B}^{(n)}-y_{A}^{(n)}\\right| \\geqslant 2 q^{k}-2\\left(q^{k+1}+q^{k+2}+\\ldots+q^{n-1}\\right),\n$$\n\nwhich is strictly positive for $q=\\frac{1}{2}$. So for any $n \\geqslant k+1$, the ants cannot meet after $n$ minutes. Thus $q \\neq \\frac{1}{2}$.\nFinally, we show that $q=2$ is also not possible. Suppose to the contrary that there is a pair of routes for $q=2$, meeting after $n$ minutes. Now consider rescaling the plane by a factor $2^{-n}$, and looking at the routes in the opposite direction. This would then be an example for $q=1 / 2$ and we have just shown that this is not possible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
-
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $q$ be a positive rational number. Two ants are initially at the same point $X$ in the plane. In the $n$-th minute $(n=1,2, \\ldots)$ each of them chooses whether to walk due north, east, south or west and then walks the distance of $q^{n}$ metres. After a whole number of minutes, they are at the same point in the plane (not necessarily $X$ ), but have not taken exactly the same route within that time. Determine all possible values of $q$.", "solution": "Consider the ants' positions $\\alpha_{k}$ and $\\beta_{k}$ after $k$ steps in the complex plane, assuming that their initial positions are at the origin and that all steps are parallel to one of the axes. We have $\\alpha_{k+1}-\\alpha_{k}=a_{k} q^{k}$ and $\\beta_{k+1}-\\beta_{k}=b_{k} q^{k}$ with $a_{k}, b_{k} \\in\\{1,-1, i,-i\\}$.\nIf $\\alpha_{n}=\\beta_{n}$ for some $n>0$, then\n\n$$\n\\sum_{k=0}^{n-1}\\left(a_{k}-b_{k}\\right) q^{k}=0, \\quad \\text { where } \\quad a_{k}-b_{k} \\in\\{0, \\pm 1 \\pm i, \\pm 2, \\pm 2 i\\}\n$$\n\nNote that the coefficient $a_{k}-b_{k}$ is always divisible by $1+i$ in Gaussian integers: indeed,\n\n$$\nc_{k}=\\frac{a_{k}-b_{k}}{1+i} \\in\\{0, \\pm 1, \\pm i, \\pm 1 \\pm i\\}\n$$\n\nCanceling $1+i$, we obtain $c_{0}+c_{1} q+\\cdots+c_{n-1} q^{n-1}=0$. Therefore if $q=\\frac{a}{b}(a, b \\in \\mathbb{N})$, we have $a \\mid c_{0}$ and $b \\mid c_{n-1}$ in Gaussian integers, which is only possible if $a=b=1$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 2."}}
|
| 4 |
-
{"year": "2018", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Alice and Bob play the following game: They start with two non-empty piles of coins. Taking turns, with Alice playing first, each player chooses a pile with an even number of coins and moves half of the coins of this pile to the other pile. The game ends if a player cannot move, in which case the other player wins.\nDetermine all pairs $(a, b)$ of positive integers such that if initially the two piles have $a$ and $b$ coins respectively, then Bob has a winning strategy.", "solution": "By $v_{2}(n)$ we denote the largest nonnegative integer $r$ such that $2^{r} \\mid n$.\nA position $(a, b)$ (i.e. two piles of sizes $a$ and $b$ ) is said to be $k$-happy if $v_{2}(a)=v_{2}(b)=k$ for some integer $k \\geqslant 0$, and $k$-unhappy if $\\min \\left\\{v_{2}(a), v_{2}(b)\\right\\}=k<\\max \\left\\{v_{2}(a), v_{2}(b)\\right\\}$. We shall prove that Bob has a winning strategy if and only if the initial position is $k$-happy for some even $k$.\n\n- Given a 0-happy position, the player in turn is unable to play and loses.\n- Given a $k$-happy position $(a, b)$ with $k \\geqslant 1$, the player in turn will transform it into one of the positions $\\left(a+\\frac{1}{2} b, \\frac{1}{2} b\\right)$ and $\\left(b+\\frac{1}{2} a, \\frac{1}{2} a\\right)$, both of which are ( $\\left.k-1\\right)$-happy because $v_{2}\\left(a+\\frac{1}{2} b\\right)=v_{2}\\left(\\frac{1}{2} b\\right)=v_{2}\\left(b+\\frac{1}{2} a\\right)=v_{2}\\left(\\frac{1}{2} a\\right)=k-1$.\n\nTherefore, if the starting position is $k$-happy, after $k$ moves they will get stuck at a 0 -happy position, so Bob will win if and only if $k$ is even.\n\n- Given a $k$-unhappy position $(a, b)$ with $k$ odd and $v_{2}(a)=k<v_{2}(b)=\\ell$, Alice can move to position $\\left(\\frac{1}{2} a, b+\\frac{1}{2} a\\right)$. Since $v_{2}\\left(\\frac{1}{2} a\\right)=v_{2}\\left(b+\\frac{1}{2} a\\right)=k-1$, this position is ( $k-1$ )-happy with $2 \\mid k-1$, so Alice will win.\n- Given a $k$-unhappy position $(a, b)$ with $k$ even and $v_{2}(a)=k<v_{2}(b)=\\ell$, Alice must not play to position $\\left(\\frac{1}{2} a, b+\\frac{1}{2} a\\right)$, because the new position is ( $\\left.k-1\\right)$-happy and will lead to Bob's victory. Thus she must play to position $\\left(a+\\frac{1}{2} b, \\frac{1}{2} b\\right)$. We claim that this position is also $k$-unhappy. Indeed, if $\\ell>k+1$, then $v_{2}\\left(a+\\frac{1}{2} b\\right)=$ $k<v_{2}\\left(\\frac{1}{2} b\\right)=\\ell-1$, whereas if $\\ell=k+1$, then $v_{2}\\left(a+\\frac{1}{2} b\\right)>v_{2}\\left(\\frac{1}{2} b\\right)=k$.\n\nTherefore a $k$-unhappy position is winning for Alice if $k$ is odd, and drawing if $k$ is even.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 5 |
-
{"year": "2018", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Find all primes $p$ and $q$ such that $3 p^{q-1}+1$ divides $11^{p}+17^{p}$.\n\nTime allowed: 4 hours and 30 minutes.\nEach problem is worth 10 points.", "solution": "Answer: $(p, q)=(3,3)$.\nFor $p=2$ it is directly checked that there are no solutions. Assume that $p>2$.\nObserve that $N=11^{p}+17^{p} \\equiv 4(\\bmod 8)$, so $8 \\nmid 3 p^{q-1}+1>4$. Consider an odd prime divisor $r$ of $3 p^{q-1}+1$. Obviously, $r \\notin\\{3,11,17\\}$. There exists $b$ such that $17 b \\equiv 1$ $(\\bmod r)$. Then $r \\mid b^{p} N \\equiv a^{p}+1(\\bmod r)$, where $a=11 b$. Thus $r \\mid a^{2 p}-1$, but $r \\nmid a^{p}-1$, which means that $\\operatorname{ord}_{r}(a) \\mid 2 p$ and $\\operatorname{ord}_{r}(a) \\nmid p$, i.e. $\\operatorname{ord}_{r}(a) \\in\\{2,2 p\\}$.\nNote that if $\\operatorname{ord}_{r}(a)=2$, then $r \\mid a^{2}-1 \\equiv\\left(11^{2}-17^{2}\\right) b^{2}(\\bmod r)$, which gives $r=7$ as the only possibility. On the other hand, $\\operatorname{ord}_{r}(a)=2 p$ implies $2 p \\mid r-1$. Thus, all prime divisors of $3 p^{q-1}+1$ other than 2 or 7 are congruent to 1 modulo $2 p$, i.e.\n\n$$\n3 p^{q-1}+1=2^{\\alpha} 7^{\\beta} p_{1}^{\\gamma_{1}} \\cdots p_{k}^{\\gamma_{k}}\n$$\n\nwhere $p_{i} \\notin\\{2,7\\}$ are prime divisors with $p_{i} \\equiv 1(\\bmod 2 p)$.\nWe already know that $\\alpha \\leqslant 2$. Also, note that\n\n$$\n\\frac{11^{p}+17^{p}}{28}=11^{p-1}-11^{p-2} 17+11^{p-3} 17^{2}-\\cdots+17^{p-1} \\equiv p \\cdot 4^{p-1} \\quad(\\bmod 7)\n$$\n\nso $11^{p}+17^{p}$ is not divisible by $7^{2}$ and hence $\\beta \\leqslant 1$.\nIf $q=2$, then $(*)$ becomes $3 p+1=2^{\\alpha} 7^{\\beta} p_{1}^{\\gamma_{1}} \\cdots p_{k}^{\\gamma_{k}}$, but $p_{i} \\geqslant 2 p+1$, which is only possible if $\\gamma_{i}=0$ for all $i$, i.e. $3 p+1=2^{\\alpha} 7^{\\beta} \\in\\{2,4,14,28\\}$, which gives us no solutions.\nThus $q>2$, which implies $4 \\mid 3 p^{q-1}+1$, i.e. $\\alpha=2$. Now the right hand side of $(*)$ is congruent to 4 or 28 modulo $p$, which gives us $p=3$. Consequently $3^{q}+1 \\mid 6244$, which is only possible for $q=3$. The pair $(p, q)=(3,3)$ is indeed a solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2018", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and the perpendicular from $M$ to $A B$ intersects the segment $A B$ at the point $E$. If $E M$ bisects the angle $C E D$, prove that $A B$ is a diameter of the circle $k$.", "solution": "Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from\n\n$$\n\\frac{M P}{B H}=\\frac{D M}{D B}=\\frac{K M}{A B} \\quad \\text { and } \\quad \\frac{M Q}{A H}=\\frac{C M}{C A}=\\frac{M L}{A B}\n$$\n\nwe obtain $A H / H B=K M / M L$.\nLet the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\\prime}$. Then $A H^{\\prime} / H^{\\prime} B=K M / M L=A H / H B$, so $H^{\\prime} \\equiv H$, i.e. $S$ lies on the line $M H$.\nThe quadrilateral $A B C D$ is not a trapezoid, so $A H \\neq B H$. Consider the point $A^{\\prime}$ on the ray $H B$ such that $H A^{\\prime}=H A$. Since $\\varangle S A^{\\prime} M=\\varangle S A M=\\varangle S B M$, quadrilateral $A^{\\prime} B S M$ is cyclic and therefore $\\varangle A B C=\\varangle A^{\\prime} B S=\\varangle A^{\\prime} M H=\\varangle A M H=90^{\\circ}-\\varangle B A C$, which implies that $\\varangle A C B=90^{\\circ}$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n1. ", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $q$ be a positive rational number. Two ants are initially at the same point $X$ in the plane. In the $n$-th minute $(n=1,2, \\ldots)$ each of them chooses whether to walk due north, east, south or west and then walks the distance of $q^{n}$ metres. After a whole number of minutes, they are at the same point in the plane (not necessarily $X$ ), but have not taken exactly the same route within that time. Determine all possible values of $q$.", "solution": "Answer: $q=1$.\nLet $x_{A}^{(n)}$ (resp. $x_{B}^{(n)}$ ) be the $x$-coordinates of the first (resp. second) ant's position after $n$ minutes. Then $x_{A}^{(n)}-x_{A}^{(n-1)} \\in\\left\\{q^{n},-q^{n}, 0\\right\\}$, and so $x_{A}^{(n)}, x_{B}^{(n)}$ are given by polynomials in $q$ with coefficients in $\\{-1,0,1\\}$. So if the ants meet after $n$ minutes, then\n\n$$\n0=x_{A}^{(n)}-x_{B}^{(n)}=P(q),\n$$\n\nwhere $P$ is a polynomial with degree at most $n$ and coefficients in $\\{-2,-, 1,0,1,2\\}$. Thus if $q=\\frac{a}{b}(a, b \\in \\mathbb{N})$, we have $a \\mid 2$ and $b \\mid 2$, i.e. $q \\in\\left\\{\\frac{1}{2}, 1,2\\right\\}$.\nIt is clearly possible when $q=1$.\n\nWe argue that $q=\\frac{1}{2}$ is not possible. Assume that the ants diverge for the first time after the $k$ th minute, for $k \\geqslant 0$. Then\n\n$$\n\\left|x_{B}^{(k+1)}-x_{A}^{(k+1)}\\right|+\\left|y_{B}^{(k+1)}-y_{A}^{(k+1)}\\right|=2 q^{k} .\n$$\n\nBut also $\\left|x_{A}^{(\\ell+1)}-x_{A}^{(\\ell)}\\right|+\\left|y_{A}^{(\\ell+1)}-y_{A}^{(\\ell)}\\right|=q^{\\ell}$ for each $l \\geqslant k+1$, and so\n\n$$\n\\left|x_{A}^{(n)}-x_{A}^{(k+1)}\\right|+\\left|y_{A}^{(n)}-y_{A}^{(k+1)}\\right| \\leqslant q^{k+1}+q^{k+2}+\\ldots+q^{n-1}\n$$\n\nand similarly for the second ant. Combining (1) and (2) with the triangle inequality, we obtain for any $n \\geqslant k+1$\n\n$$\n\\left|x_{B}^{(n)}-x_{A}^{(n)}\\right|+\\left|y_{B}^{(n)}-y_{A}^{(n)}\\right| \\geqslant 2 q^{k}-2\\left(q^{k+1}+q^{k+2}+\\ldots+q^{n-1}\\right),\n$$\n\nwhich is strictly positive for $q=\\frac{1}{2}$. So for any $n \\geqslant k+1$, the ants cannot meet after $n$ minutes. Thus $q \\neq \\frac{1}{2}$.\nFinally, we show that $q=2$ is also not possible. Suppose to the contrary that there is a pair of routes for $q=2$, meeting after $n$ minutes. Now consider rescaling the plane by a factor $2^{-n}$, and looking at the routes in the opposite direction. This would then be an example for $q=1 / 2$ and we have just shown that this is not possible.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 1."}}
|
| 3 |
+
{"year": "2018", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $q$ be a positive rational number. Two ants are initially at the same point $X$ in the plane. In the $n$-th minute $(n=1,2, \\ldots)$ each of them chooses whether to walk due north, east, south or west and then walks the distance of $q^{n}$ metres. After a whole number of minutes, they are at the same point in the plane (not necessarily $X$ ), but have not taken exactly the same route within that time. Determine all possible values of $q$.", "solution": "Consider the ants' positions $\\alpha_{k}$ and $\\beta_{k}$ after $k$ steps in the complex plane, assuming that their initial positions are at the origin and that all steps are parallel to one of the axes. We have $\\alpha_{k+1}-\\alpha_{k}=a_{k} q^{k}$ and $\\beta_{k+1}-\\beta_{k}=b_{k} q^{k}$ with $a_{k}, b_{k} \\in\\{1,-1, i,-i\\}$.\nIf $\\alpha_{n}=\\beta_{n}$ for some $n>0$, then\n\n$$\n\\sum_{k=0}^{n-1}\\left(a_{k}-b_{k}\\right) q^{k}=0, \\quad \\text { where } \\quad a_{k}-b_{k} \\in\\{0, \\pm 1 \\pm i, \\pm 2, \\pm 2 i\\}\n$$\n\nNote that the coefficient $a_{k}-b_{k}$ is always divisible by $1+i$ in Gaussian integers: indeed,\n\n$$\nc_{k}=\\frac{a_{k}-b_{k}}{1+i} \\in\\{0, \\pm 1, \\pm i, \\pm 1 \\pm i\\}\n$$\n\nCanceling $1+i$, we obtain $c_{0}+c_{1} q+\\cdots+c_{n-1} q^{n-1}=0$. Therefore if $q=\\frac{a}{b}(a, b \\in \\mathbb{N})$, we have $a \\mid c_{0}$ and $b \\mid c_{n-1}$ in Gaussian integers, which is only possible if $a=b=1$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n2. ", "solution_match": "\nSolution 2."}}
|
| 4 |
+
{"year": "2018", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Alice and Bob play the following game: They start with two non-empty piles of coins. Taking turns, with Alice playing first, each player chooses a pile with an even number of coins and moves half of the coins of this pile to the other pile. The game ends if a player cannot move, in which case the other player wins.\nDetermine all pairs $(a, b)$ of positive integers such that if initially the two piles have $a$ and $b$ coins respectively, then Bob has a winning strategy.", "solution": "By $v_{2}(n)$ we denote the largest nonnegative integer $r$ such that $2^{r} \\mid n$.\nA position $(a, b)$ (i.e. two piles of sizes $a$ and $b$ ) is said to be $k$-happy if $v_{2}(a)=v_{2}(b)=k$ for some integer $k \\geqslant 0$, and $k$-unhappy if $\\min \\left\\{v_{2}(a), v_{2}(b)\\right\\}=k<\\max \\left\\{v_{2}(a), v_{2}(b)\\right\\}$. We shall prove that Bob has a winning strategy if and only if the initial position is $k$-happy for some even $k$.\n\n- Given a 0-happy position, the player in turn is unable to play and loses.\n- Given a $k$-happy position $(a, b)$ with $k \\geqslant 1$, the player in turn will transform it into one of the positions $\\left(a+\\frac{1}{2} b, \\frac{1}{2} b\\right)$ and $\\left(b+\\frac{1}{2} a, \\frac{1}{2} a\\right)$, both of which are ( $\\left.k-1\\right)$-happy because $v_{2}\\left(a+\\frac{1}{2} b\\right)=v_{2}\\left(\\frac{1}{2} b\\right)=v_{2}\\left(b+\\frac{1}{2} a\\right)=v_{2}\\left(\\frac{1}{2} a\\right)=k-1$.\n\nTherefore, if the starting position is $k$-happy, after $k$ moves they will get stuck at a 0 -happy position, so Bob will win if and only if $k$ is even.\n\n- Given a $k$-unhappy position $(a, b)$ with $k$ odd and $v_{2}(a)=k<v_{2}(b)=\\ell$, Alice can move to position $\\left(\\frac{1}{2} a, b+\\frac{1}{2} a\\right)$. Since $v_{2}\\left(\\frac{1}{2} a\\right)=v_{2}\\left(b+\\frac{1}{2} a\\right)=k-1$, this position is ( $k-1$ )-happy with $2 \\mid k-1$, so Alice will win.\n- Given a $k$-unhappy position $(a, b)$ with $k$ even and $v_{2}(a)=k<v_{2}(b)=\\ell$, Alice must not play to position $\\left(\\frac{1}{2} a, b+\\frac{1}{2} a\\right)$, because the new position is ( $\\left.k-1\\right)$-happy and will lead to Bob's victory. Thus she must play to position $\\left(a+\\frac{1}{2} b, \\frac{1}{2} b\\right)$. We claim that this position is also $k$-unhappy. Indeed, if $\\ell>k+1$, then $v_{2}\\left(a+\\frac{1}{2} b\\right)=$ $k<v_{2}\\left(\\frac{1}{2} b\\right)=\\ell-1$, whereas if $\\ell=k+1$, then $v_{2}\\left(a+\\frac{1}{2} b\\right)>v_{2}\\left(\\frac{1}{2} b\\right)=k$.\n\nTherefore a $k$-unhappy position is winning for Alice if $k$ is odd, and drawing if $k$ is even.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n3. ", "solution_match": "\nSolution."}}
|
| 5 |
+
{"year": "2018", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all primes $p$ and $q$ such that $3 p^{q-1}+1$ divides $11^{p}+17^{p}$.\n\nTime allowed: 4 hours and 30 minutes.\nEach problem is worth 10 points.", "solution": "Answer: $(p, q)=(3,3)$.\nFor $p=2$ it is directly checked that there are no solutions. Assume that $p>2$.\nObserve that $N=11^{p}+17^{p} \\equiv 4(\\bmod 8)$, so $8 \\nmid 3 p^{q-1}+1>4$. Consider an odd prime divisor $r$ of $3 p^{q-1}+1$. Obviously, $r \\notin\\{3,11,17\\}$. There exists $b$ such that $17 b \\equiv 1$ $(\\bmod r)$. Then $r \\mid b^{p} N \\equiv a^{p}+1(\\bmod r)$, where $a=11 b$. Thus $r \\mid a^{2 p}-1$, but $r \\nmid a^{p}-1$, which means that $\\operatorname{ord}_{r}(a) \\mid 2 p$ and $\\operatorname{ord}_{r}(a) \\nmid p$, i.e. $\\operatorname{ord}_{r}(a) \\in\\{2,2 p\\}$.\nNote that if $\\operatorname{ord}_{r}(a)=2$, then $r \\mid a^{2}-1 \\equiv\\left(11^{2}-17^{2}\\right) b^{2}(\\bmod r)$, which gives $r=7$ as the only possibility. On the other hand, $\\operatorname{ord}_{r}(a)=2 p$ implies $2 p \\mid r-1$. Thus, all prime divisors of $3 p^{q-1}+1$ other than 2 or 7 are congruent to 1 modulo $2 p$, i.e.\n\n$$\n3 p^{q-1}+1=2^{\\alpha} 7^{\\beta} p_{1}^{\\gamma_{1}} \\cdots p_{k}^{\\gamma_{k}}\n$$\n\nwhere $p_{i} \\notin\\{2,7\\}$ are prime divisors with $p_{i} \\equiv 1(\\bmod 2 p)$.\nWe already know that $\\alpha \\leqslant 2$. Also, note that\n\n$$\n\\frac{11^{p}+17^{p}}{28}=11^{p-1}-11^{p-2} 17+11^{p-3} 17^{2}-\\cdots+17^{p-1} \\equiv p \\cdot 4^{p-1} \\quad(\\bmod 7)\n$$\n\nso $11^{p}+17^{p}$ is not divisible by $7^{2}$ and hence $\\beta \\leqslant 1$.\nIf $q=2$, then $(*)$ becomes $3 p+1=2^{\\alpha} 7^{\\beta} p_{1}^{\\gamma_{1}} \\cdots p_{k}^{\\gamma_{k}}$, but $p_{i} \\geqslant 2 p+1$, which is only possible if $\\gamma_{i}=0$ for all $i$, i.e. $3 p+1=2^{\\alpha} 7^{\\beta} \\in\\{2,4,14,28\\}$, which gives us no solutions.\nThus $q>2$, which implies $4 \\mid 3 p^{q-1}+1$, i.e. $\\alpha=2$. Now the right hand side of $(*)$ is congruent to 4 or 28 modulo $p$, which gives us $p=3$. Consequently $3^{q}+1 \\mid 6244$, which is only possible for $q=3$. The pair $(p, q)=(3,3)$ is indeed a solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl", "problem_match": "\n4. ", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2019-BMO-type1.jsonl
CHANGED
|
@@ -1,4 +1,4 @@
|
|
| 1 |
-
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $\\mathbb{P}$ be the set of all prime numbers. Find all functions $f: \\mathbb{P} \\rightarrow \\mathbb{P}$ such that\n\n$$\nf(p)^{f(q)}+q^{p}=f(q)^{f(p)}+p^{q}\n$$\n\nholds for all $p, q \\in \\mathbb{P}$.\nProposed by Albania", "solution": "Obviously, the identical function $f(p)=p$ for all $p \\in \\mathbb{P}$ is a solution. We will show that this is the only one.\n\nFirst we will show that $f(2)=2$. Taking $q=2$ and $p$ any odd prime number, we have\n\n$$\nf(p)^{f(2)}+2^{p}=f(2)^{f(p)}+p^{2}\n$$\n\nAssume that $f(2) \\neq 2$. It follows that $f(2)$ is odd and so $f(p)=2$ for any odd prime number $p$.\n\nTaking any two different odd prime numbers $p, q$ we have\n\n$$\n2^{2}+q^{p}=2^{2}+p^{q} \\Rightarrow p^{q}=q^{p} \\Rightarrow p=q,\n$$\n\ncontradiction. Hence, $f(2)=2$.\nSo for any odd prime number $p$ we have\n\n$$\nf(p)^{2}+2^{p}=2^{f(p)}+p^{2} .\n$$\n\nCopy this relation as\n\n$$\n2^{p}-p^{2}=2^{f(p)}-f(p)^{2}\n$$\n\nLet $T$ be the set of all positive integers greater than 2 , i.e. $T=\\{3,4,5, \\ldots\\}$. The function $g: T \\rightarrow \\mathbb{Z}, g(n)=2^{n}-n^{2}$, is strictly increasing, i.e.\n\n$$\ng(n+1)-g(n)=2^{n}-2 n-1>0\n$$\n\nfor all $n \\in T$. We show this by induction. Indeed, for $n=3$ it is true, $2^{3}-2 \\cdot 3-1>0$. Assume that $2^{k}-2 k-1>0$. It follows that for $n=k+1$ we have\n\n$$\n2^{k+1}-2(k+1)-1=\\left(2^{k}-2 k-1\\right)+\\left(2^{k}-2\\right)>0\n$$\n\nfor any $k \\geq 3$. Therefore, (2) is true for all $n \\in T$.\nAs consequence, (1) holds if and only if $f(p)=p$ for all odd prime numbers $p$, as well as for $p=2$.\n\nTherefore, the only function that satisfies the given relation is $f(p)=p$, for all $p \\in \\mathbb{P}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Let $a, b, c$ be real numbers, such that $0 \\leq a \\leq b \\leq c$ and $a+b+c=a b+b c+c a>0$. Prove that $\\sqrt{b c}(a+1) \\geq 2$. Find all triples $(a, b, c)$ for which equality holds.\n\n## Proposed by Romania", "solution": "Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \\geq 3(a b+b c+c a)$, we get that $k^{2} \\geq 3 k$. Since $k>0$, we obtain that $k \\geq 3$.\n\nWe have $b c \\geq c a \\geq a b$, so from the above relation we deduce that $b c \\geq 1$.\nBy AM-GM, $b+c \\geq 2 \\sqrt{b c}$ and consequently $b+c \\geq 2$. The equality holds iff $b=c$.\nThe constraint gives us\n\n$$\na=\\frac{b+c-b c}{b+c-1}=1-\\frac{b c-1}{b+c-1} \\geq 1-\\frac{b c-1}{2 \\sqrt{b c}-1}=\\frac{\\sqrt{b c}(2-\\sqrt{b c})}{2 \\sqrt{b c}-1}\n$$\n\nFor $\\sqrt{b c}=2$ condition $a \\geq 0$ gives $\\sqrt{b c}(a+1) \\geq 2$ with equality iff $a=0$ and $b=c=2$. For $\\sqrt{b c}<2$, taking into account the estimation for $a$, we get\n\n$$\na \\sqrt{b c} \\geq \\frac{b c(2-\\sqrt{b c})}{2 \\sqrt{b c}-1}=\\frac{b c}{2 \\sqrt{b c}-1}(2-\\sqrt{b c}) .\n$$\n\nSince $\\frac{b c}{2 \\sqrt{b c}-1} \\geq 1$, with equality for $b c=1$, we get $\\sqrt{b c}(a+1) \\geq 2$ with equality iff $a=b=c=1$.\n\nFor $\\sqrt{b c}>2$ we have $\\sqrt{b c}(a+1)>2(a+1) \\geq 2$.\nThe proof is complete.\nThe equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution."}}
|
| 3 |
-
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $A B C$ be an acute scalene triangle. Let $X$ and $Y$ be two distinct interior points of the segment $B C$ such that $\\angle C A X=\\angle Y A B$. Suppose that:\n\n1) $K$ and $S$ are the feet of perpendiculars from $B$ to the lines $A X$ and $A Y$ respectively;\n2) $T$ and $L$ are the feet of perpendiculars from $C$ to the lines $A X$ and $A Y$ respectively. Prove that $K L$ and $S T$ intersect on the line $B C$.\n\n## Proposed by Greece", "solution": "Denote $\\phi=\\widehat{X A B}=\\widehat{Y A C}, \\alpha=\\widehat{C A X}=\\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have\n\n$$\n\\widehat{B S K}+\\widehat{B A K}=180^{\\circ}=\\widehat{B S K}+\\phi=\\widehat{L A C}+\\widehat{L T C}=\\widehat{L T C}+\\phi\n$$\n\nso, due to the 90-degree angles formed, we have $\\widehat{K S L}=\\widehat{K T L}$. Thus, KLST is cyclic.\n\n\nFigure 1: G6\n\nConsider $M$ to be the midpoint of $B C$ and $K^{\\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\\prime}$ is a parallelogram, and so $B K \\| C K^{\\prime}$. But $B K \\| C T$, because they are both perpendicular to $A X$. So, $K^{\\prime}$ lies on $C T$ and, as $\\widehat{K T K^{\\prime}}=90$ and $M$ is the midpoint of $K K^{\\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.\n\nConsider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and $(A C L T)$. So,\n\n$$\n\\widehat{A D T}+\\widehat{A C T}=180^{\\circ}=\\widehat{A B S}+\\widehat{A D S}=\\widehat{A D T}+90^{\\circ}-\\alpha=\\widehat{A D S}+90^{\\circ}-\\alpha\n$$\n\nand $A D$ is the bisector of $\\widehat{S D T}$.\nBecause $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.\n\nSo, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 4 |
-
{"year": "2019", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "A grid consists of all points of the form $(m, n)$ where $m$ and $n$ are integers with $|m| \\leqslant 2019$, $|n| \\leqslant 2019$ and $|m|+|n|<4038$. We call the points $(m, n)$ of the grid with either $|m|=2019$ or $|n|=2019$ the boundary points. The four lines $x= \\pm 2019$ and $y= \\pm 2019$ are called boundary lines. Two points in the grid are called neighbours if the distance between them is equal to 1 .\n\nAnna and Bob play a game on this grid.\nAnna starts with a token at the point $(0,0)$. They take turns, with Bob playing first.\n\n1) On each of his turns, Bob deletes at most two boundary points on each boundary line.\n2) On each of her turns, Anna makes exactly three steps, where a step consists of moving her token from its current point to any neighbouring point which has not been deleted.\n\nAs soon as Anna places her token on some boundary point which has not been deleted, the game is over and Anna wins.\n\nDoes Anna have a winning strategy?\nProposed by Cyprus", "solution": "Anna does not have a winning strategy. We will provide a winning strategy for Bob. It is enough to describe his strategy for the deletions on the line $y=2019$.\n\nBob starts by deleting $(0,2019)$ and $(-1,2019)$. Once Anna completes her turn, he deletes the next two available points on the left if Anna decreased her $x$-coordinate, the next two available points on the right if Anna increased her $x$-coordinate, and the next available point to the left and the next available point to the right if Anna did not change her $x$-coordinate. The only exception to the above rule is on the very first time Anna decreases $x$ by exactly 1 . In that turn, Bob deletes the next available point to the left and the next available point to the right.\n\nBob's strategy guarantees the following: If Anna makes a sequence of steps reaching $(-x, y)$ with $x>0$ and the exact opposite sequence of steps in the horizontal direction reaching $(x, y)$, then Bob deletes at least as many points to the left of $(0,2019)$ in the first sequence than points to the right of $(0,2019)$ in the second sequence.\n\nSo we may assume for contradiction that Anna wins by placing her token at $(k, 2019)$ for some $k>0$.\n\nDefine $\\Delta=3 m-(2 x+y)$, where $m$ is the total number of points deleted by Bob to the right of $(0,2019)$, and $(x, y)$ is the position of Anna's token.\n\nFor each sequence of steps performed first by Anna and then by Bob, $\\Delta$ does not decrease. This can be seen by looking at the following table exhibiting the changes in 3 m and $2 x+y$. We have excluded the cases where $2 x+y<0$.\n\n| Turn | $(0,3)$ | $(1,2)$ | $(-1,2)$ | $(2,1)$ | $(0,1)$ | $(3,0)$ | $(1,0)$ | $(2,-1)$ | $(1,-2)$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $m$ | 1 | 2 | 0 (or 1$)$ | 2 | 1 | 2 | 2 | 2 | 2 |\n| $3 m$ | 3 | 6 | 0 (or 3$)$ | 6 | 3 | 6 | 6 | 6 | 6 |\n| $2 x+y$ | 3 | 4 | 0 | 5 | 1 | 6 | 2 | 3 | 0 |\n\nThe table also shows that, if in this sequence of turns Anna changes $y$ by +1 or -2 , then $\\Delta$ is increased by 1 . Also, if Anna changes $y$ by +2 or -1 , then the first time this happens $\\Delta$ is increased by 2 . (This also holds if her turn is $(0,-1)$ or $(-2,-1)$, which are not shown in the table.)\n\nSince Anna wins by placing her token at $(k, 2019)$ we must have $m \\leqslant k-1$ and $k \\leqslant 2018$. So at that exact moment we have:\n\n$$\n\\Delta=3 m-(2 k+2019)=k-2022 \\leqslant-4 .\n$$\n\nSo in her last turn she must have decreased $\\Delta$ by at least 4 . So her last turn must have been $(1,2)$ or $(2,1)$, which give a decrease of 4 and 5 respectively. (It could not be $(3,0)$ because then she must have already won. Also she could not have done just one or two steps in her last turn since this is not enough for the required decrease in $\\Delta$.)\n\nIf her last turn was $(1,2)$, then just before doing it we had $y=2017$ and $\\Delta=0$. This means that in one of her turns the total change in $y$ was not $0 \\bmod 3$. However, in that case we have seen that $\\Delta>0$, a contradiction.\n\nIf her last turn was $(2,1)$, then just before doing it we had $y=2018$ and $\\Delta=0$ or $\\Delta=1$. So she must have made at least two turns with the change of $y$ being +1 or -2 or at least one step with the change of $y$ being +2 or -1 . In both cases, consulting the table, we get an increase of at least 2 in $\\Delta$, a contradiction.\n\nNote 1: If Anna is allowed to make at most three steps at each turn, then she actually has a winning strategy.\n\nNote 2: If 2019 is replaced by $N>1$, then Bob has a winning strategy if and only if $3 \\mid N$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2019", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $\\mathbb{P}$ be the set of all prime numbers. Find all functions $f: \\mathbb{P} \\rightarrow \\mathbb{P}$ such that\n\n$$\nf(p)^{f(q)}+q^{p}=f(q)^{f(p)}+p^{q}\n$$\n\nholds for all $p, q \\in \\mathbb{P}$.\nProposed by Albania", "solution": "Obviously, the identical function $f(p)=p$ for all $p \\in \\mathbb{P}$ is a solution. We will show that this is the only one.\n\nFirst we will show that $f(2)=2$. Taking $q=2$ and $p$ any odd prime number, we have\n\n$$\nf(p)^{f(2)}+2^{p}=f(2)^{f(p)}+p^{2}\n$$\n\nAssume that $f(2) \\neq 2$. It follows that $f(2)$ is odd and so $f(p)=2$ for any odd prime number $p$.\n\nTaking any two different odd prime numbers $p, q$ we have\n\n$$\n2^{2}+q^{p}=2^{2}+p^{q} \\Rightarrow p^{q}=q^{p} \\Rightarrow p=q,\n$$\n\ncontradiction. Hence, $f(2)=2$.\nSo for any odd prime number $p$ we have\n\n$$\nf(p)^{2}+2^{p}=2^{f(p)}+p^{2} .\n$$\n\nCopy this relation as\n\n$$\n2^{p}-p^{2}=2^{f(p)}-f(p)^{2}\n$$\n\nLet $T$ be the set of all positive integers greater than 2 , i.e. $T=\\{3,4,5, \\ldots\\}$. The function $g: T \\rightarrow \\mathbb{Z}, g(n)=2^{n}-n^{2}$, is strictly increasing, i.e.\n\n$$\ng(n+1)-g(n)=2^{n}-2 n-1>0\n$$\n\nfor all $n \\in T$. We show this by induction. Indeed, for $n=3$ it is true, $2^{3}-2 \\cdot 3-1>0$. Assume that $2^{k}-2 k-1>0$. It follows that for $n=k+1$ we have\n\n$$\n2^{k+1}-2(k+1)-1=\\left(2^{k}-2 k-1\\right)+\\left(2^{k}-2\\right)>0\n$$\n\nfor any $k \\geq 3$. Therefore, (2) is true for all $n \\in T$.\nAs consequence, (1) holds if and only if $f(p)=p$ for all odd prime numbers $p$, as well as for $p=2$.\n\nTherefore, the only function that satisfies the given relation is $f(p)=p$, for all $p \\in \\mathbb{P}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2019", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $a, b, c$ be real numbers, such that $0 \\leq a \\leq b \\leq c$ and $a+b+c=a b+b c+c a>0$. Prove that $\\sqrt{b c}(a+1) \\geq 2$. Find all triples $(a, b, c)$ for which equality holds.\n\n## Proposed by Romania", "solution": "Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \\geq 3(a b+b c+c a)$, we get that $k^{2} \\geq 3 k$. Since $k>0$, we obtain that $k \\geq 3$.\n\nWe have $b c \\geq c a \\geq a b$, so from the above relation we deduce that $b c \\geq 1$.\nBy AM-GM, $b+c \\geq 2 \\sqrt{b c}$ and consequently $b+c \\geq 2$. The equality holds iff $b=c$.\nThe constraint gives us\n\n$$\na=\\frac{b+c-b c}{b+c-1}=1-\\frac{b c-1}{b+c-1} \\geq 1-\\frac{b c-1}{2 \\sqrt{b c}-1}=\\frac{\\sqrt{b c}(2-\\sqrt{b c})}{2 \\sqrt{b c}-1}\n$$\n\nFor $\\sqrt{b c}=2$ condition $a \\geq 0$ gives $\\sqrt{b c}(a+1) \\geq 2$ with equality iff $a=0$ and $b=c=2$. For $\\sqrt{b c}<2$, taking into account the estimation for $a$, we get\n\n$$\na \\sqrt{b c} \\geq \\frac{b c(2-\\sqrt{b c})}{2 \\sqrt{b c}-1}=\\frac{b c}{2 \\sqrt{b c}-1}(2-\\sqrt{b c}) .\n$$\n\nSince $\\frac{b c}{2 \\sqrt{b c}-1} \\geq 1$, with equality for $b c=1$, we get $\\sqrt{b c}(a+1) \\geq 2$ with equality iff $a=b=c=1$.\n\nFor $\\sqrt{b c}>2$ we have $\\sqrt{b c}(a+1)>2(a+1) \\geq 2$.\nThe proof is complete.\nThe equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution."}}
|
| 3 |
+
{"year": "2019", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute scalene triangle. Let $X$ and $Y$ be two distinct interior points of the segment $B C$ such that $\\angle C A X=\\angle Y A B$. Suppose that:\n\n1) $K$ and $S$ are the feet of perpendiculars from $B$ to the lines $A X$ and $A Y$ respectively;\n2) $T$ and $L$ are the feet of perpendiculars from $C$ to the lines $A X$ and $A Y$ respectively. Prove that $K L$ and $S T$ intersect on the line $B C$.\n\n## Proposed by Greece", "solution": "Denote $\\phi=\\widehat{X A B}=\\widehat{Y A C}, \\alpha=\\widehat{C A X}=\\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have\n\n$$\n\\widehat{B S K}+\\widehat{B A K}=180^{\\circ}=\\widehat{B S K}+\\phi=\\widehat{L A C}+\\widehat{L T C}=\\widehat{L T C}+\\phi\n$$\n\nso, due to the 90-degree angles formed, we have $\\widehat{K S L}=\\widehat{K T L}$. Thus, KLST is cyclic.\n\n\nFigure 1: G6\n\nConsider $M$ to be the midpoint of $B C$ and $K^{\\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\\prime}$ is a parallelogram, and so $B K \\| C K^{\\prime}$. But $B K \\| C T$, because they are both perpendicular to $A X$. So, $K^{\\prime}$ lies on $C T$ and, as $\\widehat{K T K^{\\prime}}=90$ and $M$ is the midpoint of $K K^{\\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.\n\nConsider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and $(A C L T)$. So,\n\n$$\n\\widehat{A D T}+\\widehat{A C T}=180^{\\circ}=\\widehat{A B S}+\\widehat{A D S}=\\widehat{A D T}+90^{\\circ}-\\alpha=\\widehat{A D S}+90^{\\circ}-\\alpha\n$$\n\nand $A D$ is the bisector of $\\widehat{S D T}$.\nBecause $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.\n\nSo, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}}
|
| 4 |
+
{"year": "2019", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "A grid consists of all points of the form $(m, n)$ where $m$ and $n$ are integers with $|m| \\leqslant 2019$, $|n| \\leqslant 2019$ and $|m|+|n|<4038$. We call the points $(m, n)$ of the grid with either $|m|=2019$ or $|n|=2019$ the boundary points. The four lines $x= \\pm 2019$ and $y= \\pm 2019$ are called boundary lines. Two points in the grid are called neighbours if the distance between them is equal to 1 .\n\nAnna and Bob play a game on this grid.\nAnna starts with a token at the point $(0,0)$. They take turns, with Bob playing first.\n\n1) On each of his turns, Bob deletes at most two boundary points on each boundary line.\n2) On each of her turns, Anna makes exactly three steps, where a step consists of moving her token from its current point to any neighbouring point which has not been deleted.\n\nAs soon as Anna places her token on some boundary point which has not been deleted, the game is over and Anna wins.\n\nDoes Anna have a winning strategy?\nProposed by Cyprus", "solution": "Anna does not have a winning strategy. We will provide a winning strategy for Bob. It is enough to describe his strategy for the deletions on the line $y=2019$.\n\nBob starts by deleting $(0,2019)$ and $(-1,2019)$. Once Anna completes her turn, he deletes the next two available points on the left if Anna decreased her $x$-coordinate, the next two available points on the right if Anna increased her $x$-coordinate, and the next available point to the left and the next available point to the right if Anna did not change her $x$-coordinate. The only exception to the above rule is on the very first time Anna decreases $x$ by exactly 1 . In that turn, Bob deletes the next available point to the left and the next available point to the right.\n\nBob's strategy guarantees the following: If Anna makes a sequence of steps reaching $(-x, y)$ with $x>0$ and the exact opposite sequence of steps in the horizontal direction reaching $(x, y)$, then Bob deletes at least as many points to the left of $(0,2019)$ in the first sequence than points to the right of $(0,2019)$ in the second sequence.\n\nSo we may assume for contradiction that Anna wins by placing her token at $(k, 2019)$ for some $k>0$.\n\nDefine $\\Delta=3 m-(2 x+y)$, where $m$ is the total number of points deleted by Bob to the right of $(0,2019)$, and $(x, y)$ is the position of Anna's token.\n\nFor each sequence of steps performed first by Anna and then by Bob, $\\Delta$ does not decrease. This can be seen by looking at the following table exhibiting the changes in 3 m and $2 x+y$. We have excluded the cases where $2 x+y<0$.\n\n| Turn | $(0,3)$ | $(1,2)$ | $(-1,2)$ | $(2,1)$ | $(0,1)$ | $(3,0)$ | $(1,0)$ | $(2,-1)$ | $(1,-2)$ |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| $m$ | 1 | 2 | 0 (or 1$)$ | 2 | 1 | 2 | 2 | 2 | 2 |\n| $3 m$ | 3 | 6 | 0 (or 3$)$ | 6 | 3 | 6 | 6 | 6 | 6 |\n| $2 x+y$ | 3 | 4 | 0 | 5 | 1 | 6 | 2 | 3 | 0 |\n\nThe table also shows that, if in this sequence of turns Anna changes $y$ by +1 or -2 , then $\\Delta$ is increased by 1 . Also, if Anna changes $y$ by +2 or -1 , then the first time this happens $\\Delta$ is increased by 2 . (This also holds if her turn is $(0,-1)$ or $(-2,-1)$, which are not shown in the table.)\n\nSince Anna wins by placing her token at $(k, 2019)$ we must have $m \\leqslant k-1$ and $k \\leqslant 2018$. So at that exact moment we have:\n\n$$\n\\Delta=3 m-(2 k+2019)=k-2022 \\leqslant-4 .\n$$\n\nSo in her last turn she must have decreased $\\Delta$ by at least 4 . So her last turn must have been $(1,2)$ or $(2,1)$, which give a decrease of 4 and 5 respectively. (It could not be $(3,0)$ because then she must have already won. Also she could not have done just one or two steps in her last turn since this is not enough for the required decrease in $\\Delta$.)\n\nIf her last turn was $(1,2)$, then just before doing it we had $y=2017$ and $\\Delta=0$. This means that in one of her turns the total change in $y$ was not $0 \\bmod 3$. However, in that case we have seen that $\\Delta>0$, a contradiction.\n\nIf her last turn was $(2,1)$, then just before doing it we had $y=2018$ and $\\Delta=0$ or $\\Delta=1$. So she must have made at least two turns with the change of $y$ being +1 or -2 or at least one step with the change of $y$ being +2 or -1 . In both cases, consulting the table, we get an increase of at least 2 in $\\Delta$, a contradiction.\n\nNote 1: If Anna is allowed to make at most three steps at each turn, then she actually has a winning strategy.\n\nNote 2: If 2019 is replaced by $N>1$, then Bob has a winning strategy if and only if $3 \\mid N$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2020-BMO-type1.jsonl
CHANGED
|
@@ -1,8 +1,8 @@
|
|
| 1 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". We will first prove that $C$ is the midpoint of the segment $B E$. From the angle equalities\n\n- $\\angle B C D=\\angle A C B=\\angle C B A=\\angle E B A$\n- $\\angle B D C=\\angle B A D+\\angle D B A=\\angle B A D+\\angle D A E=\\angle B A E$\nwe can conclude that the triangles $\\triangle A B E$ and $\\triangle D C B$ are similar.\nThus, $B E / B C=A B / C D=2$, which implies that $C$ is indeed the midpoint of the segment $B E$.\nWe will now prove that $A E$ is tangent to the circle $A C O$. From the angle equalities\n- $\\angle O A E=90^{\\circ}-\\angle E B A$\n- $\\angle O C A=\\angle O C B-\\angle A C B=90^{\\circ}-\\angle C B A=90^{\\circ}-\\angle E B A$\nwe can conclude that $\\angle O A E=\\angle O C A$, which implies that $A E$ is indeed tangent to the circle $A C O$.\nFinally, let $\\Gamma$ be the image of $\\gamma$ under the homothethy of center $A$ and factor 2 . Clearly, $\\Gamma$ is also tangent to $A E$ at $A$ and passes through $C$, so $\\Gamma$ must coincide with the circle $A C O$, which obviously passes through $O$. Thus, $\\gamma$ passes through the midpoint of the segment $A O$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 1"}}
|
| 2 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solution, we will first prove that $C$ is the midpoint of the segment $B E$. Let $F$ be the midpoint of the segment $A B$. Because $\\angle E A C=\\angle A B D=\\angle F C D$, we have that $C F \\| A E$. This implies that $C F$ is a midline in triangle $\\triangle B A E$, so $C$ is indeed the midpoint of the segment $B E$.\n\nLet $L$ be the midpoint of the segment $A O$. Because $L D$ is a midline in triangle $\\triangle A O C$, so $L D \\| O C$, which means that $\\angle A L D=\\angle A O C$. From the angle equalities\n\n- $\\angle A L D=\\angle A O C=\\angle B O C+\\angle A O B=\\angle B A E+2 \\angle B E A$\n- $\\angle A B D=\\angle C E A=\\angle B C A-\\angle B E A=\\angle A B E-\\angle B E A$\n- $\\angle A L D+\\angle A B D=\\angle B A E+2 \\angle B E A+\\angle A B E-\\angle B E A=180^{\\circ}$\nwe obtain that the quadrilateral $A B D L$ is cyclic, thus $L$ lies on $\\gamma$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.\nLet $S$ be the intersection between $B D$ and $A E$. We will first show that $S$ also lies on $C O$. Because\n\n$$\n\\angle B D C=\\angle B A D+\\angle D B A=\\angle B A D+\\angle D A E=\\angle B A E\n$$\n\n(just like in solution 1), we obtain that the triangle $\\triangle S B E$ is isosceles, so $C O$ passes through $S$, because it is the perpendicular bisector of the segment $B E$.\n\nBecause $\\angle B O C=\\angle B A S$, we obtain that the quadrilateral $A S O B$ is cyclic, so $\\angle B A L=\\angle B S O$. Denote by $L$ the intersection between $A O$ and $\\gamma$, then $\\angle L D S=\\angle B A L$. Combining these two equalities leads to $\\angle B S O=\\angle L D S$, so $L D \\| S O$.\n\nThis means that $L D$ is midline in triangle $\\triangle A O C$, so $L$, which lies on $\\gamma$, is the midpoint of the segment $A O$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 3"}}
|
| 4 |
-
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.\nLet $F$ be the midpoint of the segment $A B$. Then both $F$ and $C$ lie on the circle of diameter $B O$. Because the quadrilateral $B F D C$ is cyclic, it means that $D$ also lies on that circle.\n\nLet $K$ be the midpoint of $B O$. Then, $A K$ must be the perpendicular bisector of the segment $B C$, so $A K \\| O C$, which implies that $\\angle K A D=\\angle D C O$. However, $\\angle D C O=\\angle K B D$, because $D B C O$ is cyclic. From the two equalities we obtain that $\\angle K A D=\\angle K B D$, so $K$ lies on $\\gamma$. Furthermore, $A K$ is the bisector of $\\angle B A D$, so $K$ is in fact the midpoint of the $\\operatorname{arc} B D$.\n\nNow consider a reflection across $O F$. Clearly, $B$ maps to $A$. Because $O F$ is the perpendicular bisector of the segment $A B, \\gamma$ maps to itself through this reflection. Thus, $K$, the intersection between $O B$ and $\\gamma$, will map to $L$, the intersection between $O A$ and $\\gamma$. This implies that $L$ is the midpoint of the segment $A O$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 4"}}
|
| 5 |
-
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Denote $\\mathbb{Z}_{>0}=\\{1,2,3, \\ldots\\}$ the set of all positive integers. Determine all functions $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ such that, for each positive integer $n$,\ni) $\\sum_{k=1}^{n} f(k)$ is a perfect square, and\nii) $f(n)$ divides $n^{3}$.", "solution": "Induct on $n$ to show that $f(n)=n^{3}$ for all positive integers $n$. It is readily checked that this $f$ satisfies the conditions in the statement. The base case, $n=1$, is clear.\n\nLet $n \\geqslant 2$ and assume that $f(m)=m^{3}$ for all positive integers $m<n$. Then $\\sum_{k=1}^{n-1} f(k)=\\frac{n^{2}(n-1)^{2}}{4}$, and reference to the first condition in the statement yields\n$f(n)=\\sum_{k=1}^{n} f(k)-\\sum_{k=1}^{n-1} f(k)=\\left(\\frac{n(n-1)}{2}+k\\right)^{2}-\\frac{n^{2}(n-1)^{2}}{4}=k\\left(n^{2}-n+k\\right)$,\nfor some positive integer $k$.\nThe divisibility condition in the statement implies $k\\left(n^{2}-n+k\\right) \\leqslant n^{3}$, which is equivalent to $(n-k)\\left(n^{2}+k\\right) \\geqslant 0$, showing that $k \\leqslant n$.\n\nOn the other hand, $n^{2}-n+k$ must also divide $n^{3}$. But, if $k<n$, then\n\n$$\nn<\\frac{n^{3}}{n^{2}-1} \\leqslant \\frac{n^{3}}{n^{2}-n+k} \\leqslant \\frac{n^{3}}{n^{2}-n+1}<\\frac{n^{3}+1}{n^{2}-n+1}=n+1\n$$\n\ntherefore $\\frac{n^{3}}{n^{2}-n+k}$ cannot be an integer.\nConsequently, $k=n$, so $f(n)=n^{3}$. This completes induction and concludes the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 2", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "", "solution": "Let $F(n)=f(1)+f(2)+\\ldots+f(n)$. We use the following two observations:\nLemma $1 F(n) \\leq\\left(\\frac{n(n+1)}{2}\\right)^{2}$\nProof: Since $f(i) \\mid i^{3}$, for all $i$ we have $f(i) \\leq i^{3}$, and adding all up we get\n\n$$\nf(1)+f(2)+\\ldots+f(n) \\leq 1^{3}+2^{3}+\\ldots+n^{3}=\\left(\\frac{n(n+1)}{2}\\right)^{2}\n$$\n\nLemma $2 F(n) \\geq n^{2}$\nProof: Note that $F(n)$ is injective and increasing since $f(i)>0, \\forall i$. Since $F(n)$ is a perfect square for all $n$ the desired result is obtained.\n\nLemma $3 f(p)=p^{3}$ for all $p$ prime.\nProof: Since $f(p) \\mid p^{3}$, the only possible values for $f(p)$ are $1, p, p^{2}, p^{3}$. We show that $f(p)$ can not be 1 or $p$ or $p^{2}$.\nCase 1: Suppose $f(p)=1$. This implies $F(p-1)$ and $F(p)$ are two consecutive numbers, grater than 1 and perfect squares. This is impossible, contradiction.\nCase 2: Suppose $f(p)=p$. Let $F(p-1)=a^{2}$ and $F(p)=b^{2}$. Hence we have $p=(a-b)(a+b)$, so $a^{2}$ has to be $\\left(\\frac{(p-1)}{2}\\right)^{2}$ and $b^{2}$ has to be $\\left(\\frac{(p+1)}{2}\\right)^{2}$. But by Lemma 2 we know $F(p-1)=a^{2} \\geq(p-1)^{2}$, contradiction.\nCase 3: Suppose $f(p)=p^{2}$. Again we have $p^{2}=(a-b)(a+b)$ and since $a, b>0$ we have to have $a-b=1$ and $a+b=p^{2}$. This gives $F(p-1)=\\left(\\frac{p^{2}-1}{2}\\right)^{2}$. But from Lemma 2, we know $F(p-1) \\leq\\left(\\frac{p^{2}-p}{2}\\right)^{2}$, hence we get a contradiction again and $f(p)$ can not be $p^{2}$.\n\nTo finish the proof, we need to show that $f(n)=n^{3}$ for all nonprime values as well. Let $p>n$ be a prime. We know $f(p)=p^{3}$ and $f(p)=F(p)-F(p-1)=(a-b)(a+b)$. By a reasoning similar to Case 2 above, we can not have $a-b=1$ and $a+b=p^{3}$ so we have to have $a-b=p$ and $a+b=p^{2}$. This gives us $F(p-1)=f(1)+f(2)+\\ldots+f(p-1)=\\left(\\frac{p^{2}-p}{2}\\right)$, so we have equality in Lemma 1 . We know this only happens if $f(i)=i^{3}$ for all $i \\leq p-1$. This concludes the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 2", "solution_match": "# Solution 2"}}
|
| 7 |
-
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $k$ be a positive integer. Determine the least integer $n \\geqslant k+1$ for which the game below can be played indefinitely:\n\nConsider $n$ boxes, labelled $b_{1}, b_{2}, \\ldots, b_{n}$. For each index $i$, box $b_{i}$ contains initially exactly $i$ coins. At each step, the following three substeps are performed in order:\n(1) Choose $k+1$ boxes;\n(2) Of these $k+1$ boxes, choose $k$ and remove at least half of the coins from each, and add to the remaining box, if labelled $b_{i}$, a number of $i$ coins.\n(3) If one of the boxes is left empty, the game ends; otherwise, go to the next step.", "solution": "The required minimum is $n=2^{k}+k-1$.\nIn this case the game can be played indefinitely by choosing the last $k+1$ boxes, $b_{2^{k}-1}, b_{2^{k}}, \\ldots, b_{2^{k}+k-1}$, at each step: At step $r$, if box $b_{2^{k}+i-1}$ has exactly $m_{i}$ coins, then $\\left\\lceil m_{i} / 2\\right\\rceil$ coins are removed from that box, unless $i \\equiv r-1(\\bmod k+1)$, in which case $2^{k}+i-1$ coins are added. Thus, after step $r$ has been performed, box $b_{2^{k}+i-1}$ contains exactly $\\left\\lfloor m_{i} / 2\\right\\rfloor$ coins, unless $i \\equiv r-1(\\bmod k+1)$, in which case it contains exactly $m_{i}+2^{k}+i-1$ coins. This game goes on indefinitely, since each time a box is supplied, at least $2^{k}-1$ coins are added, so it will then contain at least $2^{k}$ coins, good enough to survive the $k$ steps to its next supply.\n\nWe now show that no smaller value of $n$ works. So, let $n \\leqslant 2^{k}+k-2$ and suppose, if possible, that a game can be played indefinitely. Notice that a box currently containing exactly $m$ coins survives at most $w=\\left\\lfloor\\log _{2} m\\right\\rfloor$ withdrawals; this $w$ will be referred to as the weight of that box. The sum of the weigths of all boxes will referred to as the total weight. The argument hinges on the lemma below, proved at the end of the solution.\n\nLemma. Performing a step does not increase the total weight. Moreover, supplying one of the first $2^{k}-2$ boxes strictly decreases the total weight.\n\nSince the total weight cannot strictly decrease indefinitely, $n>2^{k}-2$, and from some stage on none of the first $2^{k}-2$ boxes is ever supplied. Recall that each step involves a $(k+1)$-box choice. Since $n \\leqslant 2^{k}+k-2$, from that stage on, each step involves a withdrawal from at least one of the first $2^{k}-2$ boxes. This cannot go on indefinitely, so the game must eventually come to an end, contradicting the assumption.\n\nConsequently, a game that can be played indefinitely requires $n \\geqslant 2^{k}+$ $k-1$.\n\nProof of the Lemma. Since a withdrawal from a box decreases its weight by at least 1 , it is sufficient to show that supplying a box increases its weight by at most $k$; and if the latter is amongst the first $2^{k}-2$ boxes, then its weight increases by at most $k-1$. Let the box to be supplied be $b_{i}$ and let it currently contain exactly $m_{i}$ coins, to proceed by case analysis:\n\nIf $m_{i}=1$, the weight increases by $\\left\\lfloor\\log _{2}(i+1)\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}+k-1\\right)\\right\\rfloor \\leqslant$ $\\left\\lfloor\\log _{2}\\left(2^{k+1}-2\\right)\\right\\rfloor \\leqslant k$; and if, in addition, $i \\leqslant 2^{k}-2$, then the weight increases by $\\left\\lfloor\\log _{2}(i+1)\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}-1\\right)\\right\\rfloor=k-1$.\n\nIf $m_{i}=2$, then the weight increases by $\\left\\lfloor\\log _{2}(i+2)\\right\\rfloor-\\left\\lfloor\\log _{2} 2\\right\\rfloor \\leqslant$ $\\left\\lfloor\\log _{2}\\left(2^{k}+k\\right)\\right\\rfloor-1 \\leqslant k-1$.\n\nIf $m_{i} \\geqslant 3$, then the weight increases by\n\n$$\n\\begin{aligned}\n\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)\\right\\rfloor-\\left\\lfloor\\log _{2} m_{i}\\right\\rfloor & \\leqslant\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)-\\log _{2} m_{i}\\right\\rfloor+1 \\\\\n& \\leqslant\\left\\lfloor\\log _{2}\\left(1+\\frac{2^{k}+k-2}{3}\\right)\\right\\rfloor+1 \\leqslant k,\n\\end{aligned}\n$$\n\nsince $1+\\frac{1}{3}\\left(2^{k}+k-2\\right)=\\frac{1}{3}\\left(2^{k}+k+1\\right)<\\frac{1}{3}\\left(2^{k}+2^{k+1}\\right)=2^{k}$.\nFinally, let $i \\leqslant 2^{k}-2$ to consider the subcases $m_{i}=3$ and $m_{i} \\geqslant 4$. In the former subcase, the weight increases by\n\n$$\n\\left\\lfloor\\log _{2}(i+3)\\right\\rfloor-\\left\\lfloor\\log _{2} 3\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}+1\\right)\\right\\rfloor-1=k-1,\n$$\n\nand in the latter by\n\n$$\n\\begin{aligned}\n\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)\\right\\rfloor-\\left\\lfloor\\log _{2} m_{i}\\right\\rfloor & \\leqslant\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)-\\log _{2} m_{i}\\right\\rfloor+1 \\\\\n& \\leqslant\\left\\lfloor\\log _{2}\\left(1+\\frac{2^{k}-2}{4}\\right)\\right\\rfloor+1 \\leqslant k-1,\n\\end{aligned}\n$$\n\nsince $1+\\frac{1}{4}\\left(2^{k}-2\\right)=\\frac{1}{4}\\left(2^{k}+2\\right)<2^{k-2}+1$. This ends the proof and completes the solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 3", "solution_match": "\nSolution."}}
|
| 8 |
-
{"year": "2020", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Let $a_{1}=2$ and, for every positive integer $n$, let $a_{n+1}$ be the smallest integer strictly greater than $a_{n}$ that has more positive divisors than $a_{n}$. Prove that $2 a_{n+1}=3 a_{n}$ only for finitely many indices $n$.", "solution": "Begin with a mere remark on the terms of the sequence under consideration.\n\nLemma 1. Each $a_{n}$ is minimal amongst all positive integers having the same number of positive divisors as $a_{n}$.\nProof. Suppose, if possible, that for some $n$, some positive integer $b<a_{n}$ has as many positive divisors as $a_{n}$. Then $a_{m}<b \\leqslant a_{m+1}$ for some $m<n$, and the definition of the sequence forces $b=a_{m+1}$. Since $b<a_{n}$, it follows that $m+1<n$, which is a contradiction, as $a_{m+1}$ should have less positive divisors than $a_{n}$.\n\nLet $p_{1}<p_{2}<\\cdots<p_{n}<\\cdots$ be the strictly increasing sequence of prime numbers, and write canonical factorisations into primes in the form $N=\\prod_{i \\geqslant 1} p_{i}^{e_{i}}$, where $e_{i} \\geqslant 0$ for all $i$, and $e_{i}=0$ for all but finitely many indices $i$; in this notation, the number of positive divisors of $N$ is $\\tau(N)=$ $\\prod_{i \\geqslant 1}\\left(e_{i}+1\\right)$.\nLemma 2. The exponents in the canonical factorisation of each $a_{n}$ into primes form a non-strictly decreasing sequence.\nProof. Indeed, if $e_{i}<e_{j}$ for some $i<j$ in the canonical decomposition of $a_{n}$ into primes, then swapping the two exponents yields a smaller integer with the same number of positive divisors, contradicting Lemma 1.\n\nWe are now in a position to prove the required result. For convenience, a term $a_{n}$ satisfying $3 a_{n}=2 a_{n+1}$ will be referred to as a special term of the sequence.\n\nSuppose now, if possible, that the sequence has infinitely many special terms, so the latter form a strictly increasing, and hence unbounded, subsequence. To reach a contradiction, it is sufficient to show that:\n(1) The exponents of the primes in the factorisation of special terms have a common upper bound $e$; and\n(2) For all large enough primes $p$, no special term is divisible by $p$.\n\nRefer to Lemma 2 to write $a_{n}=\\prod_{i \\geqslant 1} p_{i}^{e_{i}(n)}$, where $e_{i}(n) \\geqslant e_{i+1}(n)$ for all $i$.\n\nStatement (2) is a straightforward consequence of (1) and Lemma 1. Suppose, if possible, that some special term $a_{n}$ is divisible by a prime $p_{i}>2^{e+1}$, where $e$ is the integer provided by (1). Then $e \\geqslant e_{i}(n)>0$, so $2^{e_{1}(n) e_{i}(n)+e_{i}(n)} a_{n} / p_{i}^{e_{i}(n)}$ is a positive integer with the same number of positive divisors as $a_{n}$, but smaller than $a_{n}$. This contradicts Lemma 1. Consequently, no special term is divisible by a prime exceeding $2^{e+1}$.\n\nTo prove (1), it is sufficient to show that, as $a_{n}$ runs through the special terms, the exponents $e_{1}(n)$ are bounded from above. Then, Lemma 2 shows that such an upper bound $e$ suits all primes.\n\nConsider a large enough special $a_{n}$. The condition $\\tau\\left(a_{n}\\right)<\\tau\\left(a_{n+1}\\right)$ is then equivalent to $\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right)<e_{1}(n)\\left(e_{2}(n)+2\\right)$. Alternatively, but equivalently, $e_{1}(n) \\geqslant e_{2}(n)+2$. The latter implies that $a_{n}$ is divisible by 8 , for either $e_{1}(n) \\geqslant 3$ or $a_{n}$ is a large enough power of 2 .\n\nNext, note that $9 a_{n} / 8$ is an integer strictly between $a_{n}$ and $a_{n+1}$, so $\\tau\\left(9 a_{n} / 8\\right) \\leqslant \\tau\\left(a_{n}\\right)$, which is equivalent to\n\n$$\n\\left(e_{1}(n)-2\\right)\\left(e_{2}(n)+3\\right) \\leqslant\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right),\n$$\n\nso $2 e_{1}(n) \\leqslant 3 e_{2}(n)+7$. This shows that $a_{n}$ is divisible by 3 , for otherwise, letting $a_{n}$ run through the special terms, 3 would be an upper bound for all but finitely many $e_{1}(n)$, and the special terms would therefore form a bounded sequence.\n\nThus, $4 a_{n} / 3$ is another integer strictly between $a_{n}$ and $a_{n+1}$. As before, $\\tau\\left(4 a_{n} / 3\\right) \\leqslant \\tau\\left(a_{n}\\right)$. Alternatively, but equivalently,\n\n$$\n\\left(e_{1}(n)+3\\right) e_{2}(n) \\leqslant\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right),\n$$\n\nso $2 e_{2}(n)-1 \\leqslant e_{1}(n)$. Combine this with the inequality in the previous paragraph to write $4 e_{2}(n)-2 \\leqslant 2 e_{1}(n) \\leqslant 3 e_{2}(n)+7$ and infer that $e_{2}(n) \\leqslant 9$. Consequently, $2 e_{1}(n) \\leqslant 3 e_{2}(n)+7 \\leqslant 34$, showing that $e=17$ is suitable for (1) to hold. This establishes (1) and completes the solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 4", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". We will first prove that $C$ is the midpoint of the segment $B E$. From the angle equalities\n\n- $\\angle B C D=\\angle A C B=\\angle C B A=\\angle E B A$\n- $\\angle B D C=\\angle B A D+\\angle D B A=\\angle B A D+\\angle D A E=\\angle B A E$\nwe can conclude that the triangles $\\triangle A B E$ and $\\triangle D C B$ are similar.\nThus, $B E / B C=A B / C D=2$, which implies that $C$ is indeed the midpoint of the segment $B E$.\nWe will now prove that $A E$ is tangent to the circle $A C O$. From the angle equalities\n- $\\angle O A E=90^{\\circ}-\\angle E B A$\n- $\\angle O C A=\\angle O C B-\\angle A C B=90^{\\circ}-\\angle C B A=90^{\\circ}-\\angle E B A$\nwe can conclude that $\\angle O A E=\\angle O C A$, which implies that $A E$ is indeed tangent to the circle $A C O$.\nFinally, let $\\Gamma$ be the image of $\\gamma$ under the homothethy of center $A$ and factor 2 . Clearly, $\\Gamma$ is also tangent to $A E$ at $A$ and passes through $C$, so $\\Gamma$ must coincide with the circle $A C O$, which obviously passes through $O$. Thus, $\\gamma$ passes through the midpoint of the segment $A O$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 1"}}
|
| 2 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solution, we will first prove that $C$ is the midpoint of the segment $B E$. Let $F$ be the midpoint of the segment $A B$. Because $\\angle E A C=\\angle A B D=\\angle F C D$, we have that $C F \\| A E$. This implies that $C F$ is a midline in triangle $\\triangle B A E$, so $C$ is indeed the midpoint of the segment $B E$.\n\nLet $L$ be the midpoint of the segment $A O$. Because $L D$ is a midline in triangle $\\triangle A O C$, so $L D \\| O C$, which means that $\\angle A L D=\\angle A O C$. From the angle equalities\n\n- $\\angle A L D=\\angle A O C=\\angle B O C+\\angle A O B=\\angle B A E+2 \\angle B E A$\n- $\\angle A B D=\\angle C E A=\\angle B C A-\\angle B E A=\\angle A B E-\\angle B E A$\n- $\\angle A L D+\\angle A B D=\\angle B A E+2 \\angle B E A+\\angle A B E-\\angle B E A=180^{\\circ}$\nwe obtain that the quadrilateral $A B D L$ is cyclic, thus $L$ lies on $\\gamma$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.\nLet $S$ be the intersection between $B D$ and $A E$. We will first show that $S$ also lies on $C O$. Because\n\n$$\n\\angle B D C=\\angle B A D+\\angle D B A=\\angle B A D+\\angle D A E=\\angle B A E\n$$\n\n(just like in solution 1), we obtain that the triangle $\\triangle S B E$ is isosceles, so $C O$ passes through $S$, because it is the perpendicular bisector of the segment $B E$.\n\nBecause $\\angle B O C=\\angle B A S$, we obtain that the quadrilateral $A S O B$ is cyclic, so $\\angle B A L=\\angle B S O$. Denote by $L$ the intersection between $A O$ and $\\gamma$, then $\\angle L D S=\\angle B A L$. Combining these two equalities leads to $\\angle B S O=\\angle L D S$, so $L D \\| S O$.\n\nThis means that $L D$ is midline in triangle $\\triangle A O C$, so $L$, which lies on $\\gamma$, is the midpoint of the segment $A O$.\n", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 3"}}
|
| 4 |
+
{"year": "2020", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\\gamma$.\n", "solution": ". Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.\nLet $F$ be the midpoint of the segment $A B$. Then both $F$ and $C$ lie on the circle of diameter $B O$. Because the quadrilateral $B F D C$ is cyclic, it means that $D$ also lies on that circle.\n\nLet $K$ be the midpoint of $B O$. Then, $A K$ must be the perpendicular bisector of the segment $B C$, so $A K \\| O C$, which implies that $\\angle K A D=\\angle D C O$. However, $\\angle D C O=\\angle K B D$, because $D B C O$ is cyclic. From the two equalities we obtain that $\\angle K A D=\\angle K B D$, so $K$ lies on $\\gamma$. Furthermore, $A K$ is the bisector of $\\angle B A D$, so $K$ is in fact the midpoint of the $\\operatorname{arc} B D$.\n\nNow consider a reflection across $O F$. Clearly, $B$ maps to $A$. Because $O F$ is the perpendicular bisector of the segment $A B, \\gamma$ maps to itself through this reflection. Thus, $K$, the intersection between $O B$ and $\\gamma$, will map to $L$, the intersection between $O A$ and $\\gamma$. This implies that $L$ is the midpoint of the segment $A O$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution 4"}}
|
| 5 |
+
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Denote $\\mathbb{Z}_{>0}=\\{1,2,3, \\ldots\\}$ the set of all positive integers. Determine all functions $f: \\mathbb{Z}_{>0} \\rightarrow \\mathbb{Z}_{>0}$ such that, for each positive integer $n$,\ni) $\\sum_{k=1}^{n} f(k)$ is a perfect square, and\nii) $f(n)$ divides $n^{3}$.", "solution": "Induct on $n$ to show that $f(n)=n^{3}$ for all positive integers $n$. It is readily checked that this $f$ satisfies the conditions in the statement. The base case, $n=1$, is clear.\n\nLet $n \\geqslant 2$ and assume that $f(m)=m^{3}$ for all positive integers $m<n$. Then $\\sum_{k=1}^{n-1} f(k)=\\frac{n^{2}(n-1)^{2}}{4}$, and reference to the first condition in the statement yields\n$f(n)=\\sum_{k=1}^{n} f(k)-\\sum_{k=1}^{n-1} f(k)=\\left(\\frac{n(n-1)}{2}+k\\right)^{2}-\\frac{n^{2}(n-1)^{2}}{4}=k\\left(n^{2}-n+k\\right)$,\nfor some positive integer $k$.\nThe divisibility condition in the statement implies $k\\left(n^{2}-n+k\\right) \\leqslant n^{3}$, which is equivalent to $(n-k)\\left(n^{2}+k\\right) \\geqslant 0$, showing that $k \\leqslant n$.\n\nOn the other hand, $n^{2}-n+k$ must also divide $n^{3}$. But, if $k<n$, then\n\n$$\nn<\\frac{n^{3}}{n^{2}-1} \\leqslant \\frac{n^{3}}{n^{2}-n+k} \\leqslant \\frac{n^{3}}{n^{2}-n+1}<\\frac{n^{3}+1}{n^{2}-n+1}=n+1\n$$\n\ntherefore $\\frac{n^{3}}{n^{2}-n+k}$ cannot be an integer.\nConsequently, $k=n$, so $f(n)=n^{3}$. This completes induction and concludes the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 2", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2020", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "", "solution": "Let $F(n)=f(1)+f(2)+\\ldots+f(n)$. We use the following two observations:\nLemma $1 F(n) \\leq\\left(\\frac{n(n+1)}{2}\\right)^{2}$\nProof: Since $f(i) \\mid i^{3}$, for all $i$ we have $f(i) \\leq i^{3}$, and adding all up we get\n\n$$\nf(1)+f(2)+\\ldots+f(n) \\leq 1^{3}+2^{3}+\\ldots+n^{3}=\\left(\\frac{n(n+1)}{2}\\right)^{2}\n$$\n\nLemma $2 F(n) \\geq n^{2}$\nProof: Note that $F(n)$ is injective and increasing since $f(i)>0, \\forall i$. Since $F(n)$ is a perfect square for all $n$ the desired result is obtained.\n\nLemma $3 f(p)=p^{3}$ for all $p$ prime.\nProof: Since $f(p) \\mid p^{3}$, the only possible values for $f(p)$ are $1, p, p^{2}, p^{3}$. We show that $f(p)$ can not be 1 or $p$ or $p^{2}$.\nCase 1: Suppose $f(p)=1$. This implies $F(p-1)$ and $F(p)$ are two consecutive numbers, grater than 1 and perfect squares. This is impossible, contradiction.\nCase 2: Suppose $f(p)=p$. Let $F(p-1)=a^{2}$ and $F(p)=b^{2}$. Hence we have $p=(a-b)(a+b)$, so $a^{2}$ has to be $\\left(\\frac{(p-1)}{2}\\right)^{2}$ and $b^{2}$ has to be $\\left(\\frac{(p+1)}{2}\\right)^{2}$. But by Lemma 2 we know $F(p-1)=a^{2} \\geq(p-1)^{2}$, contradiction.\nCase 3: Suppose $f(p)=p^{2}$. Again we have $p^{2}=(a-b)(a+b)$ and since $a, b>0$ we have to have $a-b=1$ and $a+b=p^{2}$. This gives $F(p-1)=\\left(\\frac{p^{2}-1}{2}\\right)^{2}$. But from Lemma 2, we know $F(p-1) \\leq\\left(\\frac{p^{2}-p}{2}\\right)^{2}$, hence we get a contradiction again and $f(p)$ can not be $p^{2}$.\n\nTo finish the proof, we need to show that $f(n)=n^{3}$ for all nonprime values as well. Let $p>n$ be a prime. We know $f(p)=p^{3}$ and $f(p)=F(p)-F(p-1)=(a-b)(a+b)$. By a reasoning similar to Case 2 above, we can not have $a-b=1$ and $a+b=p^{3}$ so we have to have $a-b=p$ and $a+b=p^{2}$. This gives us $F(p-1)=f(1)+f(2)+\\ldots+f(p-1)=\\left(\\frac{p^{2}-p}{2}\\right)$, so we have equality in Lemma 1 . We know this only happens if $f(i)=i^{3}$ for all $i \\leq p-1$. This concludes the proof.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 2", "solution_match": "# Solution 2"}}
|
| 7 |
+
{"year": "2020", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $k$ be a positive integer. Determine the least integer $n \\geqslant k+1$ for which the game below can be played indefinitely:\n\nConsider $n$ boxes, labelled $b_{1}, b_{2}, \\ldots, b_{n}$. For each index $i$, box $b_{i}$ contains initially exactly $i$ coins. At each step, the following three substeps are performed in order:\n(1) Choose $k+1$ boxes;\n(2) Of these $k+1$ boxes, choose $k$ and remove at least half of the coins from each, and add to the remaining box, if labelled $b_{i}$, a number of $i$ coins.\n(3) If one of the boxes is left empty, the game ends; otherwise, go to the next step.", "solution": "The required minimum is $n=2^{k}+k-1$.\nIn this case the game can be played indefinitely by choosing the last $k+1$ boxes, $b_{2^{k}-1}, b_{2^{k}}, \\ldots, b_{2^{k}+k-1}$, at each step: At step $r$, if box $b_{2^{k}+i-1}$ has exactly $m_{i}$ coins, then $\\left\\lceil m_{i} / 2\\right\\rceil$ coins are removed from that box, unless $i \\equiv r-1(\\bmod k+1)$, in which case $2^{k}+i-1$ coins are added. Thus, after step $r$ has been performed, box $b_{2^{k}+i-1}$ contains exactly $\\left\\lfloor m_{i} / 2\\right\\rfloor$ coins, unless $i \\equiv r-1(\\bmod k+1)$, in which case it contains exactly $m_{i}+2^{k}+i-1$ coins. This game goes on indefinitely, since each time a box is supplied, at least $2^{k}-1$ coins are added, so it will then contain at least $2^{k}$ coins, good enough to survive the $k$ steps to its next supply.\n\nWe now show that no smaller value of $n$ works. So, let $n \\leqslant 2^{k}+k-2$ and suppose, if possible, that a game can be played indefinitely. Notice that a box currently containing exactly $m$ coins survives at most $w=\\left\\lfloor\\log _{2} m\\right\\rfloor$ withdrawals; this $w$ will be referred to as the weight of that box. The sum of the weigths of all boxes will referred to as the total weight. The argument hinges on the lemma below, proved at the end of the solution.\n\nLemma. Performing a step does not increase the total weight. Moreover, supplying one of the first $2^{k}-2$ boxes strictly decreases the total weight.\n\nSince the total weight cannot strictly decrease indefinitely, $n>2^{k}-2$, and from some stage on none of the first $2^{k}-2$ boxes is ever supplied. Recall that each step involves a $(k+1)$-box choice. Since $n \\leqslant 2^{k}+k-2$, from that stage on, each step involves a withdrawal from at least one of the first $2^{k}-2$ boxes. This cannot go on indefinitely, so the game must eventually come to an end, contradicting the assumption.\n\nConsequently, a game that can be played indefinitely requires $n \\geqslant 2^{k}+$ $k-1$.\n\nProof of the Lemma. Since a withdrawal from a box decreases its weight by at least 1 , it is sufficient to show that supplying a box increases its weight by at most $k$; and if the latter is amongst the first $2^{k}-2$ boxes, then its weight increases by at most $k-1$. Let the box to be supplied be $b_{i}$ and let it currently contain exactly $m_{i}$ coins, to proceed by case analysis:\n\nIf $m_{i}=1$, the weight increases by $\\left\\lfloor\\log _{2}(i+1)\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}+k-1\\right)\\right\\rfloor \\leqslant$ $\\left\\lfloor\\log _{2}\\left(2^{k+1}-2\\right)\\right\\rfloor \\leqslant k$; and if, in addition, $i \\leqslant 2^{k}-2$, then the weight increases by $\\left\\lfloor\\log _{2}(i+1)\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}-1\\right)\\right\\rfloor=k-1$.\n\nIf $m_{i}=2$, then the weight increases by $\\left\\lfloor\\log _{2}(i+2)\\right\\rfloor-\\left\\lfloor\\log _{2} 2\\right\\rfloor \\leqslant$ $\\left\\lfloor\\log _{2}\\left(2^{k}+k\\right)\\right\\rfloor-1 \\leqslant k-1$.\n\nIf $m_{i} \\geqslant 3$, then the weight increases by\n\n$$\n\\begin{aligned}\n\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)\\right\\rfloor-\\left\\lfloor\\log _{2} m_{i}\\right\\rfloor & \\leqslant\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)-\\log _{2} m_{i}\\right\\rfloor+1 \\\\\n& \\leqslant\\left\\lfloor\\log _{2}\\left(1+\\frac{2^{k}+k-2}{3}\\right)\\right\\rfloor+1 \\leqslant k,\n\\end{aligned}\n$$\n\nsince $1+\\frac{1}{3}\\left(2^{k}+k-2\\right)=\\frac{1}{3}\\left(2^{k}+k+1\\right)<\\frac{1}{3}\\left(2^{k}+2^{k+1}\\right)=2^{k}$.\nFinally, let $i \\leqslant 2^{k}-2$ to consider the subcases $m_{i}=3$ and $m_{i} \\geqslant 4$. In the former subcase, the weight increases by\n\n$$\n\\left\\lfloor\\log _{2}(i+3)\\right\\rfloor-\\left\\lfloor\\log _{2} 3\\right\\rfloor \\leqslant\\left\\lfloor\\log _{2}\\left(2^{k}+1\\right)\\right\\rfloor-1=k-1,\n$$\n\nand in the latter by\n\n$$\n\\begin{aligned}\n\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)\\right\\rfloor-\\left\\lfloor\\log _{2} m_{i}\\right\\rfloor & \\leqslant\\left\\lfloor\\log _{2}\\left(i+m_{i}\\right)-\\log _{2} m_{i}\\right\\rfloor+1 \\\\\n& \\leqslant\\left\\lfloor\\log _{2}\\left(1+\\frac{2^{k}-2}{4}\\right)\\right\\rfloor+1 \\leqslant k-1,\n\\end{aligned}\n$$\n\nsince $1+\\frac{1}{4}\\left(2^{k}-2\\right)=\\frac{1}{4}\\left(2^{k}+2\\right)<2^{k-2}+1$. This ends the proof and completes the solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 3", "solution_match": "\nSolution."}}
|
| 8 |
+
{"year": "2020", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $a_{1}=2$ and, for every positive integer $n$, let $a_{n+1}$ be the smallest integer strictly greater than $a_{n}$ that has more positive divisors than $a_{n}$. Prove that $2 a_{n+1}=3 a_{n}$ only for finitely many indices $n$.", "solution": "Begin with a mere remark on the terms of the sequence under consideration.\n\nLemma 1. Each $a_{n}$ is minimal amongst all positive integers having the same number of positive divisors as $a_{n}$.\nProof. Suppose, if possible, that for some $n$, some positive integer $b<a_{n}$ has as many positive divisors as $a_{n}$. Then $a_{m}<b \\leqslant a_{m+1}$ for some $m<n$, and the definition of the sequence forces $b=a_{m+1}$. Since $b<a_{n}$, it follows that $m+1<n$, which is a contradiction, as $a_{m+1}$ should have less positive divisors than $a_{n}$.\n\nLet $p_{1}<p_{2}<\\cdots<p_{n}<\\cdots$ be the strictly increasing sequence of prime numbers, and write canonical factorisations into primes in the form $N=\\prod_{i \\geqslant 1} p_{i}^{e_{i}}$, where $e_{i} \\geqslant 0$ for all $i$, and $e_{i}=0$ for all but finitely many indices $i$; in this notation, the number of positive divisors of $N$ is $\\tau(N)=$ $\\prod_{i \\geqslant 1}\\left(e_{i}+1\\right)$.\nLemma 2. The exponents in the canonical factorisation of each $a_{n}$ into primes form a non-strictly decreasing sequence.\nProof. Indeed, if $e_{i}<e_{j}$ for some $i<j$ in the canonical decomposition of $a_{n}$ into primes, then swapping the two exponents yields a smaller integer with the same number of positive divisors, contradicting Lemma 1.\n\nWe are now in a position to prove the required result. For convenience, a term $a_{n}$ satisfying $3 a_{n}=2 a_{n+1}$ will be referred to as a special term of the sequence.\n\nSuppose now, if possible, that the sequence has infinitely many special terms, so the latter form a strictly increasing, and hence unbounded, subsequence. To reach a contradiction, it is sufficient to show that:\n(1) The exponents of the primes in the factorisation of special terms have a common upper bound $e$; and\n(2) For all large enough primes $p$, no special term is divisible by $p$.\n\nRefer to Lemma 2 to write $a_{n}=\\prod_{i \\geqslant 1} p_{i}^{e_{i}(n)}$, where $e_{i}(n) \\geqslant e_{i+1}(n)$ for all $i$.\n\nStatement (2) is a straightforward consequence of (1) and Lemma 1. Suppose, if possible, that some special term $a_{n}$ is divisible by a prime $p_{i}>2^{e+1}$, where $e$ is the integer provided by (1). Then $e \\geqslant e_{i}(n)>0$, so $2^{e_{1}(n) e_{i}(n)+e_{i}(n)} a_{n} / p_{i}^{e_{i}(n)}$ is a positive integer with the same number of positive divisors as $a_{n}$, but smaller than $a_{n}$. This contradicts Lemma 1. Consequently, no special term is divisible by a prime exceeding $2^{e+1}$.\n\nTo prove (1), it is sufficient to show that, as $a_{n}$ runs through the special terms, the exponents $e_{1}(n)$ are bounded from above. Then, Lemma 2 shows that such an upper bound $e$ suits all primes.\n\nConsider a large enough special $a_{n}$. The condition $\\tau\\left(a_{n}\\right)<\\tau\\left(a_{n+1}\\right)$ is then equivalent to $\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right)<e_{1}(n)\\left(e_{2}(n)+2\\right)$. Alternatively, but equivalently, $e_{1}(n) \\geqslant e_{2}(n)+2$. The latter implies that $a_{n}$ is divisible by 8 , for either $e_{1}(n) \\geqslant 3$ or $a_{n}$ is a large enough power of 2 .\n\nNext, note that $9 a_{n} / 8$ is an integer strictly between $a_{n}$ and $a_{n+1}$, so $\\tau\\left(9 a_{n} / 8\\right) \\leqslant \\tau\\left(a_{n}\\right)$, which is equivalent to\n\n$$\n\\left(e_{1}(n)-2\\right)\\left(e_{2}(n)+3\\right) \\leqslant\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right),\n$$\n\nso $2 e_{1}(n) \\leqslant 3 e_{2}(n)+7$. This shows that $a_{n}$ is divisible by 3 , for otherwise, letting $a_{n}$ run through the special terms, 3 would be an upper bound for all but finitely many $e_{1}(n)$, and the special terms would therefore form a bounded sequence.\n\nThus, $4 a_{n} / 3$ is another integer strictly between $a_{n}$ and $a_{n+1}$. As before, $\\tau\\left(4 a_{n} / 3\\right) \\leqslant \\tau\\left(a_{n}\\right)$. Alternatively, but equivalently,\n\n$$\n\\left(e_{1}(n)+3\\right) e_{2}(n) \\leqslant\\left(e_{1}(n)+1\\right)\\left(e_{2}(n)+1\\right),\n$$\n\nso $2 e_{2}(n)-1 \\leqslant e_{1}(n)$. Combine this with the inequality in the previous paragraph to write $4 e_{2}(n)-2 \\leqslant 2 e_{1}(n) \\leqslant 3 e_{2}(n)+7$ and infer that $e_{2}(n) \\leqslant 9$. Consequently, $2 e_{1}(n) \\leqslant 3 e_{2}(n)+7 \\leqslant 34$, showing that $e=17$ is suitable for (1) to hold. This establishes (1) and completes the solution.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl", "problem_match": "## 2020 BMO, Problem 4", "solution_match": "\nSolution."}}
|
Balkan_MO/segmented/en-2021-BMO-type1.jsonl
CHANGED
|
@@ -1,7 +1,7 @@
|
|
| 1 |
-
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $\\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\\omega$. Suppose $X, Y$ lie on $\\omega$ such that $\\angle B X A=\\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.\n\nShow that, as $X, Y$ vary on $\\omega$, the line $X Y$ passes through a fixed point.", "solution": ". Extend $X A$ and $Y A$ to meet $\\omega$ again at $X^{\\prime}$ and $Y^{\\prime}$ respectively. We then have that:\n\n$$\n\\angle Y^{\\prime} Y C=\\angle A Y C=\\angle B X A=\\angle B X X^{\\prime} .\n$$\n\nso $B C X^{\\prime} Y^{\\prime}$ is an isosceles trapezium and hence $X^{\\prime} Y^{\\prime} \\| B C$.\n\n\nLet $\\ell$ be the line through $A$ parallel to $B C$ and let $\\ell$ intersect $\\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\\prime} Y^{\\prime}\\|B C\\| P Q$ then\n\n$$\n\\angle X A P=\\angle X X^{\\prime} Y^{\\prime}=\\angle X Y Y^{\\prime}=\\angle X Y A\n$$\n\nwhich shows that $\\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that\n\n$$\nZ A^{2}=Z X \\cdot Z Y=Z P \\cdot Z Q\n$$\n\nAs $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 1", "solution_match": "\nSolution 1"}}
|
| 2 |
-
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $\\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\\omega$. Suppose $X, Y$ lie on $\\omega$ such that $\\angle B X A=\\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.\n\nShow that, as $X, Y$ vary on $\\omega$, the line $X Y$ passes through a fixed point.", "solution": ". Let $B^{\\prime}$ and $C^{\\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\\omega$ respectively and let $\\omega_{1}$ be the circumcircle of the triangle $A B^{\\prime} C^{\\prime}$. Let $\\varepsilon$ be the tangent to $\\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\\prime} C^{\\prime}$ and $\\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.\n\n\nWe have\n\n$$\n\\angle Z A C^{\\prime}=\\angle C^{\\prime} B^{\\prime} A=\\angle C^{\\prime} B^{\\prime} B=\\angle C^{\\prime} C B .\n$$\n\nTherefore, $\\varepsilon \\| B C$.\nLet $X^{\\prime}, Y^{\\prime}$ be the points of intersection of the lines $X A, Y A$ with $\\omega$ respecively. From the hypothesis we have $\\angle B X X^{\\prime}=\\angle Y^{\\prime} Y C$. Therefore\n\n$$\n\\widehat{B X^{\\prime}}=\\widehat{Y^{\\prime} C} \\Longrightarrow \\widehat{B C}+\\widehat{C X^{\\prime}}=\\widehat{Y^{\\prime} B}+\\widehat{B C} \\Longrightarrow \\widehat{C X^{\\prime}}=\\widehat{Y^{\\prime} B}\n$$\n\nand so $X^{\\prime} Y^{\\prime}\\|B C\\| \\varepsilon$. Thus\n\n$$\n\\angle X A Z=\\angle X X^{\\prime} Y^{\\prime}=\\angle X Y Y^{\\prime}=\\angle X Y A .\n$$\n\nFrom the last equality we have that $\\varepsilon$ is also tangent to the circmucircle $\\omega_{2}$ of the triangle $X A Y$.\n\nConsider now the radical centre of the circles $\\omega, \\omega_{1}, \\omega_{2}$. This is the point of intersection of the radical axes $B^{\\prime} C^{\\prime}\\left(\\right.$ of $\\omega$ and $\\left.\\omega_{1}\\right), \\varepsilon\\left(\\right.$ of $\\omega_{1}$ and $\\left.\\omega_{2}\\right)$ and $X Y$ (of $\\omega$ and $\\omega_{2}$ ).\nThis must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 1", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Find all functions $f:(0,+\\infty) \\rightarrow(0,+\\infty)$ such that\n\n$$\nf(x+f(x)+f(y))=2 f(x)+y\n$$\n\nholds for all $x, y \\in(0,+\\infty)$.", "solution": ". We will show that $f(x)=x$ for every $x \\in \\mathbb{R}^{+}$. It is easy to check that this function satisfies the equation.\n\nWe write $P(x, y)$ for the assertion that $f(x+f(x)+f(y))=2 f(x)+y$.\nWe first show that $f$ is injective. So assume $f(a)=f(b)$. Now $P(1, a)$ and $P(1, b)$ show that\n\n$$\n2 f(1)+a=f(1+f(1)+f(a))=f(1+f(1)+f(b))=2 f(1)+b\n$$\n\nand therefore $a=b$.\nLet $A=\\left\\{x \\in \\mathbb{R}^{+}: f(x)=x\\right\\}$. It is enough to show that $A=\\mathbb{R}^{+}$.\n$P(x, x)$ shows that $x+2 f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. Now $P(x, x+2 f(x))$ gives that\n\n$$\nf(2 x+3 f(x))=x+4 f(x)\n$$\n\nfor every $x \\in \\mathbb{R}^{+}$. Therefore $P(x, 2 x+3 f(x))$ gives that $2 x+5 f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. Suppose $x, y \\in \\mathbb{R}^{+}$such that $x, 2 x+y \\in A$. Then $P(x, y)$ gives that\n\n$$\nf(2 x+f(y))=f(x+f(x)+f(y))=2 f(x)+y=2 x+y=f(2 x+y)\n$$\n\nand by the injectivity of $f$ we have that $2 x+f(y)=2 x+y$. We conlude that $y \\in A$ as well. Now since $x+2 f(x) \\in A$ and $2 x+5 f(x)=2(x+2 f(x))+f(x) \\in A$ we deduce that $f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. I.e. $f(f(x))=f(x)$ for every $x \\in \\mathbb{R}^{+}$.\nBy injectivity of $f$ we now conclude that $f(x)=x$ for every $x \\in \\mathbb{R}^{+}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 2", "solution_match": "\nSolution 1"}}
|
| 4 |
-
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Find all functions $f:(0,+\\infty) \\rightarrow(0,+\\infty)$ such that\n\n$$\nf(x+f(x)+f(y))=2 f(x)+y\n$$\n\nholds for all $x, y \\in(0,+\\infty)$.", "solution": ". As in Solution 1, $f$ is injective. Furthermore, letting $m=2 f(1)$ we have that the image of $f$ contains $(m, \\infty)$. Indeed, if $t>m$, say $t=m+y$ for some $y>0$, then $P(1, y)$ shows that $f(1+f(1)+f(y))=t$.\n\nLet $a, b \\in \\mathbb{R}$. We will show that $f(a)-a=f(b)-b$. Define $c=2 f(a)-2 f(b)$ and $d=a+f(a)-b-f(b)$. It is enough to show that $c=d$. By interchanging the roles of $a$ and $b$ in necessary, we may assume that $d \\geqslant 0$.\n\nFrom $P(a, y)$ and $P(b, y)$, after subtraction, we get\n\n$$\nf(a+f(a)+f(y))-f(b+f(b)+f(y))=2 f(a)-2 f(b)=c .\n$$\n\nso for any $t>m$ (picking $y$ such that $f(y)=t$ in (1)) we get\n\n$$\nf(a+f(a)+t)-f(b+f(b)+t)=2 f(a)-2 f(b)=c .\n$$\n\nNow for any $z>m+b+f(b)$, taking $t=z-b-f(b)$ in (2) we get\n\n$$\nf(z+d)-f(z)=c\n$$\n\nNow for any $x>m+b+f(b)$ from (3) we get that\n\n$$\n2 f(x+d)+y=2 f(x)+y+2 c\n$$\n\nAlso, for any $x$ large enough, $(x>\\max \\{m+b+f(b), m+b+f(b)+c-d\\}$ will do), by repeated application of (3), we have\n\n$$\n\\begin{aligned}\nf(x+d+f(x+d)+f(y)) & =f(x+f(x+d)+y)+c \\\\\n& =f(x+f(x)+y+c)+c \\\\\n& =f(x+f(x)+y+c-d)+2 c .\n\\end{aligned}\n$$\n\n(In the first equality we applied (3) with $z=x+f(x+d)+y>x>m+b+f(b)$, in the second with $z=x>m+b+f(b)$ and in the third with $z=x+f(x)+y-c+d>x+c-d>m+b+f(b)$.\n\nIn particular, now $P(x+d, y)$ implies that\n\n$$\nf(x+f(x)+y+c-d)=2 f(x)+y=f(x+f(x)+y)\n$$\n\nfor every large enough $x$. By injectivity of $f$ we deduce that $x+f(x)+y+c-d=x+f(x)+y$ and therefore $c=d$ as required.\n\nIt now follows that $f(x)=x+k$ for every $x \\in \\mathbb{R}^{+}$and some fixed constant $k$. Substituting in the initial equation we get $k=0$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 2", "solution_match": "\nSolution 2"}}
|
| 5 |
-
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Let $a, b$ and $c$ be positive integers satisfying the equation\n\n$$\n(a, b)+[a, b]=2021^{c} .\n$$\n\nIf $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.\nHere, $(a, b)$ denotes the greatest common divisor of $a$ and $b$, and $[a, b]$ denotes the least common multiple of $a$ and $b$.", "solution": "We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.\n\nSince $(a, b) \\mid[a, b]$, we have that $(a, b) \\mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \\in\\{1,43,47\\}$. We will consider all 3 cases separately:\n(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore\n\n$$\nq=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \\cdot 2021^{c} .\n$$\n\n(a) Suppose $c$ is even. Since $q \\equiv 1 \\bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \\mid q$ a contradiction.\n(b) If $c$ is odd then $a b=2021^{c}-1 \\equiv 1 \\bmod 3$. Thus $a \\equiv b \\bmod 3$ implying that $p=|a-b| \\equiv 0 \\bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so\n\n$$\n(2 a+3)^{2}=4 a^{2}+12 a+9=4 \\cdot 2021^{c}+5\n$$\n\nSo 5 is a quadratic residue modulo 47, a contradiction as\n\n$$\n\\left(\\frac{5}{47}\\right)=\\left(\\frac{47}{5}\\right)=\\left(\\frac{2}{5}\\right)=-1 .\n$$\n\n(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \\in \\mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that\n\n$$\n(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \\cdot 43^{c-1} \\cdot 47-3 .\n$$\n\nSo -3 is a quadratic residue modulo 47 , a contradiction as\n\n$$\n\\left(\\frac{-3}{47}\\right)=\\left(\\frac{-1}{47}\\right)\\left(\\frac{3}{47}\\right)=\\left(\\frac{47}{3}\\right)=\\left(\\frac{2}{3}\\right)=-1\n$$\n\n(3) If $(a, b)=47$ then analogously there is a $k \\in \\mathbb{N}$ such that\n\n$$\n(2 k+1)^{2}=4 \\cdot 43^{c} \\cdot 47^{c-1}-3 .\n$$\n\nIf $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \\cdot 6+47 \\cdot 7=47 \\cdot 13 \\equiv 1 \\bmod 5$. Thus $q=(a+b)^{2}+4 \\equiv 0 \\bmod 5$, a contradiction.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 3", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Angel has a warehouse, which initially contains 100 piles of 100 pieces of rubbish each. Each morning, Angel performs exactly one of the following moves:\n(a) He clears every piece of rubbish from a single pile.\n(b) He clears one piece of rubbish from each pile.\n\nHowever, every evening, a demon sneaks into the warehouse and performs exactly one of the following moves:\n(a) He adds one piece of rubbish to each non-empty pile.\n(b) He creates a new pile with one piece of rubbish.\n\nWhat is the first morning when Angel can guarantee to have cleared all the rubbish from the warehouse?", "solution": ". We will show that he can do so by the morning of day 199 but not earlier.If we have $n$ piles with at least two pieces of rubbish and $m$ piles with exactly one piece of rubbish, then we define the value of the pile to be\n\n$$\nV= \\begin{cases}n & m=0 \\\\ n+\\frac{1}{2} & m=1 \\\\ n+1 & m \\geqslant 2\\end{cases}\n$$\n\nWe also denote this position by $(n, m)$. Implicitly we will also write $k$ for the number of piles with exactly two pieces of rubbish.\n\nAngel's strategy is the following:\n(i) From position $(0, m)$ remove one piece from each pile to go position $(0,0)$. The game ends.\n(ii) From position $(n, 0)$, where $n \\geqslant 1$, remove one pile to go to position $(n-1,0)$. Either the game ends, or the demon can move to position $(n-1,0)$ or $(n-1,1)$. In any case $V$ reduces by at least $1 / 2$.\n(iii) From position $(n, 1)$, where $n \\geqslant 1$, remove one pile with at least two pieces to go to position $(n-1,1)$. The demon can move to position $(n, 0)$ or $(n-1,2)$. In any case $V$ reduces by (at least) $1 / 2$.\n(iv) From position $(n, m)$, where $n \\geqslant 1$ and $m \\geqslant 2$, remove one piece from each pile to go to position $(n-k, k)$. The demon can move to position $(n, 0)$ or $(n-k, k+1)$. In any case $V$ reduces by at least $1 / 2$. (The value of position $(n-k, k+1)$ is $n+\\frac{1}{2}$ if $k=0$, and $n-k+1 \\leqslant n$ if $k \\geqslant 1$.)\nSo during every day if the game does not end then $V$ is decreased by at least $1 / 2$. So after 198 days if the game did not already end we will have $V \\leqslant 1$ and we will be in one of positions $(0, m),(1,0)$. The game can then end on the morning of day 199.\nWe will now provide a strategy for demon which guarantees that at the end of each day $V$ has decreased by at most $1 / 2$ and furthermore at the end of the day $m \\leqslant 1$.\n(i) If Angel moves from $(n, 0)$ to $(n-1,0)$ (by removing a pile) then create a new pile with one piece to move to $(n-1,1)$. Then $V$ decreases by $1 / 2$ and and $m=1 \\leqslant 1$\n(ii) If Angel moves from $(n, 0)$ to $(n-k, k)$ (by removing one piece from each pile) then add one piece back to each pile to move to $(n, 0)$. Then $V$ stays the same and $m=0 \\leqslant 1$.\n(iii) If Angels moves from $(n, 1)$ to $(n-1,1)$ or $(n, 0)$ (by removing a pile) then add one piece to each pile to move to $(n, 0)$. Then $V$ decreases by $1 / 2$ and $m=0 \\leqslant 1$.\n(iv) If Angel moves from $(n, 1)$ to $(n-k, k)$ (by removing a piece from each pile) then add one piece to each pile to move to $(n, 0)$. Then $V$ decreases by $1 / 2$ and $m=0 \\leqslant 1$.\nSince after every move of demon we have $m \\leqslant 1$, in order for Angel to finish the game in the next morning we must have $n=1, m=0$ or $n=0, m=1$ and therefore we must have $V \\leqslant 1$. But now inductively the demon can guarantee that by the end of day $N$, where $N \\leqslant 198$ the game has not yet finished and that $V \\geqslant 100-N / 2$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 4", "solution_match": "\nSolution 1"}}
|
| 7 |
-
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Angel has a warehouse, which initially contains 100 piles of 100 pieces of rubbish each. Each morning, Angel performs exactly one of the following moves:\n(a) He clears every piece of rubbish from a single pile.\n(b) He clears one piece of rubbish from each pile.\n\nHowever, every evening, a demon sneaks into the warehouse and performs exactly one of the following moves:\n(a) He adds one piece of rubbish to each non-empty pile.\n(b) He creates a new pile with one piece of rubbish.\n\nWhat is the first morning when Angel can guarantee to have cleared all the rubbish from the warehouse?", "solution": ".\n\nDefine Angel's score $S_{A}$ to be $S_{A}=2 n+m-1$. The Angel can clear the rubbish in at most $\\max \\left\\{S_{A}, 1\\right\\}$ days. The proof is by induction on $(n, m)$ in lexicographic order.\n\nAngel's strategy is the same as in Solution 1 and in each of cases (ii)-(iv) one needs to check that $S_{A}$ reduces by at least 1 in each day. (Case (i) is trivial as the game ends in one day.)\n\nNow define demon's score $S_{D}$ to be $S_{D}=2 n-1$ if $m=0$ and $S_{D}=2 n$ if $m \\geqslant 1$. The claim is the if $(n, m) \\neq(0,0)$, then the demon can ensure that Angel requires $S_{D}$ days to clear the rubbish.\n\nAgain, demon's strategy is the same as in the Solution by PSC and in each of cases (i)-(iv) one needs to check that $S_{D}$ reduced by at most 1 in each day.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 4", "solution_match": "# Solution 2"}}
|
|
|
|
| 1 |
+
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $\\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\\omega$. Suppose $X, Y$ lie on $\\omega$ such that $\\angle B X A=\\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.\n\nShow that, as $X, Y$ vary on $\\omega$, the line $X Y$ passes through a fixed point.", "solution": ". Extend $X A$ and $Y A$ to meet $\\omega$ again at $X^{\\prime}$ and $Y^{\\prime}$ respectively. We then have that:\n\n$$\n\\angle Y^{\\prime} Y C=\\angle A Y C=\\angle B X A=\\angle B X X^{\\prime} .\n$$\n\nso $B C X^{\\prime} Y^{\\prime}$ is an isosceles trapezium and hence $X^{\\prime} Y^{\\prime} \\| B C$.\n\n\nLet $\\ell$ be the line through $A$ parallel to $B C$ and let $\\ell$ intersect $\\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\\prime} Y^{\\prime}\\|B C\\| P Q$ then\n\n$$\n\\angle X A P=\\angle X X^{\\prime} Y^{\\prime}=\\angle X Y Y^{\\prime}=\\angle X Y A\n$$\n\nwhich shows that $\\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that\n\n$$\nZ A^{2}=Z X \\cdot Z Y=Z P \\cdot Z Q\n$$\n\nAs $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 1", "solution_match": "\nSolution 1"}}
|
| 2 |
+
{"year": "2021", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $A B C$ be a triangle with $A B<A C$. Let $\\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\\omega$. Suppose $X, Y$ lie on $\\omega$ such that $\\angle B X A=\\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.\n\nShow that, as $X, Y$ vary on $\\omega$, the line $X Y$ passes through a fixed point.", "solution": ". Let $B^{\\prime}$ and $C^{\\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\\omega$ respectively and let $\\omega_{1}$ be the circumcircle of the triangle $A B^{\\prime} C^{\\prime}$. Let $\\varepsilon$ be the tangent to $\\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\\prime} C^{\\prime}$ and $\\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.\n\n\nWe have\n\n$$\n\\angle Z A C^{\\prime}=\\angle C^{\\prime} B^{\\prime} A=\\angle C^{\\prime} B^{\\prime} B=\\angle C^{\\prime} C B .\n$$\n\nTherefore, $\\varepsilon \\| B C$.\nLet $X^{\\prime}, Y^{\\prime}$ be the points of intersection of the lines $X A, Y A$ with $\\omega$ respecively. From the hypothesis we have $\\angle B X X^{\\prime}=\\angle Y^{\\prime} Y C$. Therefore\n\n$$\n\\widehat{B X^{\\prime}}=\\widehat{Y^{\\prime} C} \\Longrightarrow \\widehat{B C}+\\widehat{C X^{\\prime}}=\\widehat{Y^{\\prime} B}+\\widehat{B C} \\Longrightarrow \\widehat{C X^{\\prime}}=\\widehat{Y^{\\prime} B}\n$$\n\nand so $X^{\\prime} Y^{\\prime}\\|B C\\| \\varepsilon$. Thus\n\n$$\n\\angle X A Z=\\angle X X^{\\prime} Y^{\\prime}=\\angle X Y Y^{\\prime}=\\angle X Y A .\n$$\n\nFrom the last equality we have that $\\varepsilon$ is also tangent to the circmucircle $\\omega_{2}$ of the triangle $X A Y$.\n\nConsider now the radical centre of the circles $\\omega, \\omega_{1}, \\omega_{2}$. This is the point of intersection of the radical axes $B^{\\prime} C^{\\prime}\\left(\\right.$ of $\\omega$ and $\\left.\\omega_{1}\\right), \\varepsilon\\left(\\right.$ of $\\omega_{1}$ and $\\left.\\omega_{2}\\right)$ and $X Y$ (of $\\omega$ and $\\omega_{2}$ ).\nThis must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 1", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all functions $f:(0,+\\infty) \\rightarrow(0,+\\infty)$ such that\n\n$$\nf(x+f(x)+f(y))=2 f(x)+y\n$$\n\nholds for all $x, y \\in(0,+\\infty)$.", "solution": ". We will show that $f(x)=x$ for every $x \\in \\mathbb{R}^{+}$. It is easy to check that this function satisfies the equation.\n\nWe write $P(x, y)$ for the assertion that $f(x+f(x)+f(y))=2 f(x)+y$.\nWe first show that $f$ is injective. So assume $f(a)=f(b)$. Now $P(1, a)$ and $P(1, b)$ show that\n\n$$\n2 f(1)+a=f(1+f(1)+f(a))=f(1+f(1)+f(b))=2 f(1)+b\n$$\n\nand therefore $a=b$.\nLet $A=\\left\\{x \\in \\mathbb{R}^{+}: f(x)=x\\right\\}$. It is enough to show that $A=\\mathbb{R}^{+}$.\n$P(x, x)$ shows that $x+2 f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. Now $P(x, x+2 f(x))$ gives that\n\n$$\nf(2 x+3 f(x))=x+4 f(x)\n$$\n\nfor every $x \\in \\mathbb{R}^{+}$. Therefore $P(x, 2 x+3 f(x))$ gives that $2 x+5 f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. Suppose $x, y \\in \\mathbb{R}^{+}$such that $x, 2 x+y \\in A$. Then $P(x, y)$ gives that\n\n$$\nf(2 x+f(y))=f(x+f(x)+f(y))=2 f(x)+y=2 x+y=f(2 x+y)\n$$\n\nand by the injectivity of $f$ we have that $2 x+f(y)=2 x+y$. We conlude that $y \\in A$ as well. Now since $x+2 f(x) \\in A$ and $2 x+5 f(x)=2(x+2 f(x))+f(x) \\in A$ we deduce that $f(x) \\in A$ for every $x \\in \\mathbb{R}^{+}$. I.e. $f(f(x))=f(x)$ for every $x \\in \\mathbb{R}^{+}$.\nBy injectivity of $f$ we now conclude that $f(x)=x$ for every $x \\in \\mathbb{R}^{+}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 2", "solution_match": "\nSolution 1"}}
|
| 4 |
+
{"year": "2021", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all functions $f:(0,+\\infty) \\rightarrow(0,+\\infty)$ such that\n\n$$\nf(x+f(x)+f(y))=2 f(x)+y\n$$\n\nholds for all $x, y \\in(0,+\\infty)$.", "solution": ". As in Solution 1, $f$ is injective. Furthermore, letting $m=2 f(1)$ we have that the image of $f$ contains $(m, \\infty)$. Indeed, if $t>m$, say $t=m+y$ for some $y>0$, then $P(1, y)$ shows that $f(1+f(1)+f(y))=t$.\n\nLet $a, b \\in \\mathbb{R}$. We will show that $f(a)-a=f(b)-b$. Define $c=2 f(a)-2 f(b)$ and $d=a+f(a)-b-f(b)$. It is enough to show that $c=d$. By interchanging the roles of $a$ and $b$ in necessary, we may assume that $d \\geqslant 0$.\n\nFrom $P(a, y)$ and $P(b, y)$, after subtraction, we get\n\n$$\nf(a+f(a)+f(y))-f(b+f(b)+f(y))=2 f(a)-2 f(b)=c .\n$$\n\nso for any $t>m$ (picking $y$ such that $f(y)=t$ in (1)) we get\n\n$$\nf(a+f(a)+t)-f(b+f(b)+t)=2 f(a)-2 f(b)=c .\n$$\n\nNow for any $z>m+b+f(b)$, taking $t=z-b-f(b)$ in (2) we get\n\n$$\nf(z+d)-f(z)=c\n$$\n\nNow for any $x>m+b+f(b)$ from (3) we get that\n\n$$\n2 f(x+d)+y=2 f(x)+y+2 c\n$$\n\nAlso, for any $x$ large enough, $(x>\\max \\{m+b+f(b), m+b+f(b)+c-d\\}$ will do), by repeated application of (3), we have\n\n$$\n\\begin{aligned}\nf(x+d+f(x+d)+f(y)) & =f(x+f(x+d)+y)+c \\\\\n& =f(x+f(x)+y+c)+c \\\\\n& =f(x+f(x)+y+c-d)+2 c .\n\\end{aligned}\n$$\n\n(In the first equality we applied (3) with $z=x+f(x+d)+y>x>m+b+f(b)$, in the second with $z=x>m+b+f(b)$ and in the third with $z=x+f(x)+y-c+d>x+c-d>m+b+f(b)$.\n\nIn particular, now $P(x+d, y)$ implies that\n\n$$\nf(x+f(x)+y+c-d)=2 f(x)+y=f(x+f(x)+y)\n$$\n\nfor every large enough $x$. By injectivity of $f$ we deduce that $x+f(x)+y+c-d=x+f(x)+y$ and therefore $c=d$ as required.\n\nIt now follows that $f(x)=x+k$ for every $x \\in \\mathbb{R}^{+}$and some fixed constant $k$. Substituting in the initial equation we get $k=0$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 2", "solution_match": "\nSolution 2"}}
|
| 5 |
+
{"year": "2021", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Let $a, b$ and $c$ be positive integers satisfying the equation\n\n$$\n(a, b)+[a, b]=2021^{c} .\n$$\n\nIf $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.\nHere, $(a, b)$ denotes the greatest common divisor of $a$ and $b$, and $[a, b]$ denotes the least common multiple of $a$ and $b$.", "solution": "We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.\n\nSince $(a, b) \\mid[a, b]$, we have that $(a, b) \\mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \\in\\{1,43,47\\}$. We will consider all 3 cases separately:\n(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore\n\n$$\nq=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \\cdot 2021^{c} .\n$$\n\n(a) Suppose $c$ is even. Since $q \\equiv 1 \\bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \\mid q$ a contradiction.\n(b) If $c$ is odd then $a b=2021^{c}-1 \\equiv 1 \\bmod 3$. Thus $a \\equiv b \\bmod 3$ implying that $p=|a-b| \\equiv 0 \\bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so\n\n$$\n(2 a+3)^{2}=4 a^{2}+12 a+9=4 \\cdot 2021^{c}+5\n$$\n\nSo 5 is a quadratic residue modulo 47, a contradiction as\n\n$$\n\\left(\\frac{5}{47}\\right)=\\left(\\frac{47}{5}\\right)=\\left(\\frac{2}{5}\\right)=-1 .\n$$\n\n(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \\in \\mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that\n\n$$\n(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \\cdot 43^{c-1} \\cdot 47-3 .\n$$\n\nSo -3 is a quadratic residue modulo 47 , a contradiction as\n\n$$\n\\left(\\frac{-3}{47}\\right)=\\left(\\frac{-1}{47}\\right)\\left(\\frac{3}{47}\\right)=\\left(\\frac{47}{3}\\right)=\\left(\\frac{2}{3}\\right)=-1\n$$\n\n(3) If $(a, b)=47$ then analogously there is a $k \\in \\mathbb{N}$ such that\n\n$$\n(2 k+1)^{2}=4 \\cdot 43^{c} \\cdot 47^{c-1}-3 .\n$$\n\nIf $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \\cdot 6+47 \\cdot 7=47 \\cdot 13 \\equiv 1 \\bmod 5$. Thus $q=(a+b)^{2}+4 \\equiv 0 \\bmod 5$, a contradiction.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 3", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Angel has a warehouse, which initially contains 100 piles of 100 pieces of rubbish each. Each morning, Angel performs exactly one of the following moves:\n(a) He clears every piece of rubbish from a single pile.\n(b) He clears one piece of rubbish from each pile.\n\nHowever, every evening, a demon sneaks into the warehouse and performs exactly one of the following moves:\n(a) He adds one piece of rubbish to each non-empty pile.\n(b) He creates a new pile with one piece of rubbish.\n\nWhat is the first morning when Angel can guarantee to have cleared all the rubbish from the warehouse?", "solution": ". We will show that he can do so by the morning of day 199 but not earlier.If we have $n$ piles with at least two pieces of rubbish and $m$ piles with exactly one piece of rubbish, then we define the value of the pile to be\n\n$$\nV= \\begin{cases}n & m=0 \\\\ n+\\frac{1}{2} & m=1 \\\\ n+1 & m \\geqslant 2\\end{cases}\n$$\n\nWe also denote this position by $(n, m)$. Implicitly we will also write $k$ for the number of piles with exactly two pieces of rubbish.\n\nAngel's strategy is the following:\n(i) From position $(0, m)$ remove one piece from each pile to go position $(0,0)$. The game ends.\n(ii) From position $(n, 0)$, where $n \\geqslant 1$, remove one pile to go to position $(n-1,0)$. Either the game ends, or the demon can move to position $(n-1,0)$ or $(n-1,1)$. In any case $V$ reduces by at least $1 / 2$.\n(iii) From position $(n, 1)$, where $n \\geqslant 1$, remove one pile with at least two pieces to go to position $(n-1,1)$. The demon can move to position $(n, 0)$ or $(n-1,2)$. In any case $V$ reduces by (at least) $1 / 2$.\n(iv) From position $(n, m)$, where $n \\geqslant 1$ and $m \\geqslant 2$, remove one piece from each pile to go to position $(n-k, k)$. The demon can move to position $(n, 0)$ or $(n-k, k+1)$. In any case $V$ reduces by at least $1 / 2$. (The value of position $(n-k, k+1)$ is $n+\\frac{1}{2}$ if $k=0$, and $n-k+1 \\leqslant n$ if $k \\geqslant 1$.)\nSo during every day if the game does not end then $V$ is decreased by at least $1 / 2$. So after 198 days if the game did not already end we will have $V \\leqslant 1$ and we will be in one of positions $(0, m),(1,0)$. The game can then end on the morning of day 199.\nWe will now provide a strategy for demon which guarantees that at the end of each day $V$ has decreased by at most $1 / 2$ and furthermore at the end of the day $m \\leqslant 1$.\n(i) If Angel moves from $(n, 0)$ to $(n-1,0)$ (by removing a pile) then create a new pile with one piece to move to $(n-1,1)$. Then $V$ decreases by $1 / 2$ and and $m=1 \\leqslant 1$\n(ii) If Angel moves from $(n, 0)$ to $(n-k, k)$ (by removing one piece from each pile) then add one piece back to each pile to move to $(n, 0)$. Then $V$ stays the same and $m=0 \\leqslant 1$.\n(iii) If Angels moves from $(n, 1)$ to $(n-1,1)$ or $(n, 0)$ (by removing a pile) then add one piece to each pile to move to $(n, 0)$. Then $V$ decreases by $1 / 2$ and $m=0 \\leqslant 1$.\n(iv) If Angel moves from $(n, 1)$ to $(n-k, k)$ (by removing a piece from each pile) then add one piece to each pile to move to $(n, 0)$. Then $V$ decreases by $1 / 2$ and $m=0 \\leqslant 1$.\nSince after every move of demon we have $m \\leqslant 1$, in order for Angel to finish the game in the next morning we must have $n=1, m=0$ or $n=0, m=1$ and therefore we must have $V \\leqslant 1$. But now inductively the demon can guarantee that by the end of day $N$, where $N \\leqslant 198$ the game has not yet finished and that $V \\geqslant 100-N / 2$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 4", "solution_match": "\nSolution 1"}}
|
| 7 |
+
{"year": "2021", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Angel has a warehouse, which initially contains 100 piles of 100 pieces of rubbish each. Each morning, Angel performs exactly one of the following moves:\n(a) He clears every piece of rubbish from a single pile.\n(b) He clears one piece of rubbish from each pile.\n\nHowever, every evening, a demon sneaks into the warehouse and performs exactly one of the following moves:\n(a) He adds one piece of rubbish to each non-empty pile.\n(b) He creates a new pile with one piece of rubbish.\n\nWhat is the first morning when Angel can guarantee to have cleared all the rubbish from the warehouse?", "solution": ".\n\nDefine Angel's score $S_{A}$ to be $S_{A}=2 n+m-1$. The Angel can clear the rubbish in at most $\\max \\left\\{S_{A}, 1\\right\\}$ days. The proof is by induction on $(n, m)$ in lexicographic order.\n\nAngel's strategy is the same as in Solution 1 and in each of cases (ii)-(iv) one needs to check that $S_{A}$ reduces by at least 1 in each day. (Case (i) is trivial as the game ends in one day.)\n\nNow define demon's score $S_{D}$ to be $S_{D}=2 n-1$ if $m=0$ and $S_{D}=2 n$ if $m \\geqslant 1$. The claim is the if $(n, m) \\neq(0,0)$, then the demon can ensure that Angel requires $S_{D}$ days to clear the rubbish.\n\nAgain, demon's strategy is the same as in the Solution by PSC and in each of cases (i)-(iv) one needs to check that $S_{D}$ reduced by at most 1 in each day.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl", "problem_match": "## BMO 2021 - Problem 4", "solution_match": "# Solution 2"}}
|
Balkan_MO/segmented/en-2022-BMO-type1.jsonl
CHANGED
|
@@ -1,9 +1,9 @@
|
|
| 1 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Firstly observe that $O A X B$ is cyclic, with diameter $O X$, and $Y$ also lies on this circle since $O Y \\perp X C$. Hence:\n\n$$\n\\angle A Z C=\\angle X A B=\\angle A B X=\\angle A Y X\n$$\n\nand so $C Y A Z$ is cyclic.\n\n\nLet $M$ be the intersection of $Y Z$ and $A C$ and let $C Y$ intersect $\\omega$ again at $W$. Using the new cyclic relation we get $\\angle C Y Z=\\angle C A Z$ and then using that $Z A$ is tangent to $\\omega$ we get $\\angle C A Z=\\angle C W A$, so $\\angle C Y M=\\angle C W A$. Therefore the triangles $C W A$ and $C Y M$ are similar. But $C W$ is a chord of $\\omega$, and $Y$ is the foot of the perpendicular from $O$, hence $Y$ is the midpoint of $C W$. It follows from the similarity relation that $M$ is the midpoint of $A C$, as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 1"}}
|
| 2 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Let $M$ be the midpoint of $A C$. We have $\\angle C A Z=\\angle C B A$ and $\\angle Z C A=$ $\\angle B A C$ so the triangles $C A Z$ and $A B C$ are similar. The line $C Y X$ is the $C$-symmedian of triangle $A B C$, and $Z M$ is the corresponding median in triangle $C A Z$, hence by isogonality $\\angle A Z M=\\angle A C Y$. So\n\n$$\n\\angle Z M A=180^{\\circ}-\\angle A Z M-\\angle M A Z=180^{\\circ}-\\angle A C Y-\\angle C B A\n$$\n\nNow observe $\\angle O M C=\\angle O Y C=90^{\\circ}$, so $C M Y O$ is cyclic. Thus:\n\n$$\n\\angle C Y M=\\angle C O M=\\frac{1}{2} \\angle C O A=\\angle C B A\n$$\n\nThis shows that\n\n$$\n\\angle Y M C=180^{\\circ}-\\angle M C Y-\\angle C Y M=180^{\\circ}-\\angle A C Y-\\angle C B A\n$$\n\nCombining this with (1) we get that $\\angle Y M C=\\angle Z M A$ and as $A, C, M$ are collinear, it follows that $Z, M, Y$ are collinear as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 2"}}
|
| 3 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". As in Solution 2 we have that $C X$ is the $A$-symmedian of triangle $A B C$ and that triangle $A B C$ is similar to triangle $C A Z$.\n\nLet $f$ be the spiral similarity which maps $A C$ onto $A B$ and let $g$ be the reflection on the perpendicular bisector of $A B$. Note that $f$ is a rotation about $A$ by an angle of $\\angle C A B$ (clockwise in our figure) followed by a homothety centered at $A$ by a factor of $A B / A C$. By the similarity of triangles $A B C$ and $C A Z$ we have that $g(f(Z))=C$, so actually $f(Z)$ is the other point of intersection, say $C^{\\prime}$, of $C Z$ with $\\omega$.\n\nAs in Solution 1 we have that $C Y A Z$ is cyclic. Therefore, letting $W$ be the other point of intersection of $C Y$ with $\\omega$, we have $\\angle W A B=\\angle W C B=\\angle C A Y$. We also have $\\angle A C Y=$ $\\angle A B W$. It follows that $f(Y)=W$.\n\nLet $W^{\\prime}=g(W)$. Then $W^{\\prime} \\in \\omega$ and since $C W$ is the $A$-symmedian, then $C W^{\\prime}$ passes through the midpoint $N$ of $A B$. Now $C W^{\\prime}$ and $C^{\\prime} W$ intersect on the perpendicular bisector of $A B$ and therefore they intersect on $N$. It follows that $N=A B \\cap C^{\\prime} W=A f(C) \\cap f(Z) f(Y)$ is the image of $M=A C \\cap Z Y$ under $f$. Since $N$ is the midpoint of $A B$, then $M$ is the midpoint of $A C$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 3"}}
|
| 4 |
-
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Let $E=A B \\cap C X$ and $F=A W \\cap C Z$. We have $(C, W ; X, E)=-1$. Projecting from the line $C X$ onto the line $C Z$ from $A$ we get that $(C, F ; Z, \\infty)=-1$. Thus $Z$ is the midpoint of $C F$. Since also $Y$ is the midpoint of $C W$, we get that $Z Y$ bisects $C A$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 4"}}
|
| 5 |
-
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "Problem. Let $a, b$ and $n$ be positive integers with $a>b$ such that all of the following hold:\n(i) $a^{2021}$ divides $n$,\n(ii) $b^{2021}$ divides $n$,\n(iii) 2022 divides $a-b$.\n\nProve that there is a subset $T$ of the set of positive divisors of the number $n$ such that the sum of the elements of $T$ is divisible by 2022 but not divisible by $2022^{2}$.", "solution": "If $1011 \\mid a$, then $1011^{2021} \\mid n$ and we can take $T=\\left\\{1011,1011^{2}\\right\\}$. So we can assume that $3 \\nmid a$ or $337 \\nmid a$.\n\nWe continue with the following claim:\nClaim. If $k$ is a positive integer, then $a^{k} b^{2021-k} \\mid n$.\nProof of the Claim. We have that $n^{2021}=n^{k} \\cdot n^{2021-k}$ is divisible by $a^{2021 k} \\cdot b^{2021(2021-k)}$ and taking the 2021-root we get the desired result.\nBack to the problem, we will prove that the set $T=\\left\\{a^{k} b^{2021-k}: k \\geqslant 0\\right\\}$ consisting of 2022 divisors of $n$, has the desired property. The sum of its elements is equal to\n\n$$\nS=\\sum_{k=0}^{2021} a^{k} b^{2021-k} \\equiv \\sum_{k=0}^{2021} a^{2021} \\equiv 0 \\bmod 2022\n$$\n\nOn the other hand, the last sum is equal to $\\frac{a^{2022}-b^{2022}}{a-b}$.\nIf $3 \\nmid a$, we will prove that $S$ is not divisible by 9 . Indeed if $3 \\nmid a$ then we also have $3 \\nmid b$. So if $3^{t} \\| a-b$ then, since $3^{1} \\| 2022$, by the Lifting the Exponent Lemma, we have that $3^{t+1} \\| a^{2022}-b^{2022}$. This implies that $S$ is not divisible by 9 , therefore, $2022^{2}$ doesn't divide $S$.\n\nIf $3 \\mid a$, then we have $337 \\nmid a$ and a similar argument shows that $337^{2} \\nmid S$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 2", "solution_match": "\nSolution."}}
|
| 6 |
-
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Problem. Find all functions $f:(0, \\infty) \\rightarrow(0, \\infty)$ such that\n\n$$\nf\\left(y(f(x))^{3}+x\\right)=x^{3} f(y)+f(x)\n$$\n\nfor all $x, y>0$.", "solution": ". Setting $y=\\frac{t}{f(x)^{3}}$ we get\n\n$$\nf(x+t)=x^{3} f\\left(\\frac{t}{f(x)^{3}}\\right)+f(x)\n$$\n\nfor every $x, t>0$.\nFrom (1) it is immediate that $f$ is increasing.\nClaim. $f(1)=1$\nProof of Claim. Let $c=f(1)$. If $c<1$, taking $x=1$ and $y=\\frac{1}{1-c^{3}}$ we have $y-y c^{3}=1$, so $y f(1)^{3}+1=y$ and $f\\left(y f(1)^{3}+1\\right)=f(y)=1^{3} f(y)$. Thus $f(1)=0$, a contradiction. Assume now for contradiction that $c>1$. We claim that\n\n$$\nf\\left(1+c^{3}+\\cdots+c^{3 n}\\right)=(n+1) c\n$$\n\nfor every $n \\in \\mathbb{N}$. We proceed by induction, the case $n=0$ being trivial. The inductive step follows easily by taking $x=1, t=c^{3}+c^{6}+\\cdots+c^{3(k+1)}$ in (1).\n\nNow taking $x=1+c^{3}+\\cdots+c^{3 n-3}, t=c^{3 n}$ in (1) we get\n\n$$\n(n+1) c=f\\left(1+c^{3}+\\cdots+c^{3 n}\\right)=\\left(1+c^{3}+\\cdots+c^{3 n-3}\\right)^{3} f\\left(\\frac{c^{3 n}}{(c n)^{3}}\\right)+n c\n$$\n\ngiving\n\n$$\nf\\left(\\frac{c^{3 n-3}}{n^{3}}\\right)=\\frac{c}{\\left(1+c^{3}+\\cdots+c^{3 n}\\right)^{3}}<c=f(1) \\Longrightarrow \\frac{c^{3 n-3}}{n^{3}}<1 .\n$$\n\nBut this leads to a contradiction if $n$ is large enough.\nNow for $x=1$ we get $f(y+1)=f(y)+1$ and since $f(1)=1$ inductively we get $f(n)=n$ for every $n \\in \\mathbb{N}$. For $m, n \\in \\mathbb{N}$, setting $x=n, y=q=m / n$ we get\n\n$$\nm n^{2}+n=f\\left(q n^{3}+n\\right)=f\\left(y f(x)^{3}+x\\right)=x^{3} f(y)+f(x)=n^{3} f(q)+n \\Longrightarrow f(q)=q .\n$$\n\nSince $f$ is strictly increasing with $f(q)=q$ for every $q \\in \\mathbb{Q}^{>0}$ we deduce that $f(x)=x$ for every $x>0$. It is easily checked that this satisfies the functional equation.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution 1"}}
|
| 7 |
-
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "Problem. Find all functions $f:(0, \\infty) \\rightarrow(0, \\infty)$ such that\n\n$$\nf\\left(y(f(x))^{3}+x\\right)=x^{3} f(y)+f(x)\n$$\n\nfor all $x, y>0$.", "solution": ". We can also derive a contradiction in the case $c>1$ as follows:\nSince $f$ is strictly increasing then\n\n$$\nf(y)+f(1)=f\\left(y f(1)^{3}+1\\right)>f\\left(y f(1)^{3}\\right) \\Longrightarrow f\\left(c^{3} y\\right)<f(y)+c\n$$\n\nfor every $y>0$. So by induction we get $f\\left(c^{3 n}\\right)<(n+1) c$ for every $n \\in \\mathbb{N}$. Setting $x=c^{3 n}$ and $t=c^{3 n+3}-c^{3 n}$ in (1) we get\n\n$$\n(n+2) c>f\\left(c^{3 n+3}\\right)>f\\left(c^{3 n+3}\\right)-f\\left(c^{3 n}\\right)=c^{9 n} f\\left(\\frac{c^{3 n+3}-c^{3 n}}{f\\left(c^{3 n}\\right)^{3}}\\right)>c^{9 n} f\\left(\\frac{c^{3 n+3}-c^{3 n}}{c^{3}(n+1)^{3}}\\right)\n$$\n\nBut\n\n$$\n\\frac{c^{3 n+3}-c^{3 n}}{c^{3}(n+1)^{3}}=\\frac{c^{3 n}}{(n+1)^{3}} \\cdot \\frac{c^{3}-1}{c^{3}}>1\n$$\n\nfor $c$ large enough. So $(n+2) c>c^{9 n+1}$ which leads to a contradiction if $n$ is large enough.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution 2"}}
|
| 8 |
-
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Problem. Consider an $n \\times n$ grid consisting of $n^{2}$ unit cells, where $n \\geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.\n\nNote. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.", "solution": ". Let $G$ be the graph whose vertices are all $(n+1)^{2}$ vertices of the grid and where two vertices are adjacent if and only if they are adjacent in the grid and moreover the two cells in either side of the corresponding edge have different colours.\n\nThe connnected components of $G$, excluding the isolated vertices, are precisely the boundaries between pairs of monochromatic regions each of which can be covered by a single frog. Each time we add one of these components in the grid, it creates exactly one new monochromatic region. So the number of frogs required is one more than the number of such components of $G$.\n\nIt is easy to check that every corner vertex of the grid has degree 0 , every boundary vertex of the grid has degree 0 or 1 and every 'internal' vertex of the grid has degree 0,2 or 4 . It is also easy to see that every component of $G$ which is not an isolated vertex must contain at least four vertices unless it is the boundary of a single corner of the grid, in which case it contains only three vertices.\n\nWriting $N$ for the number of components which are not isolated vertices, we see that in total they contain at least $4 N-4$ vertices. (As at most four of them contain 3 vertices and all others contain 4 vertices.) Since we also have at least 4 components which are isolated vertices, then $4 N=(4 N-4)+4 \\leqslant(n+1)^{2}$. Thus $N \\leqslant \\frac{(n+1)^{2}}{4}$ and therefore the minimal number of frogs required is $\\frac{(n+1)^{2}}{4}+1$.\n\n\nThis bound for $n=2 m+1$ is achieved by putting coordinates $(x, y)$ with $x, y \\in\\{0,1, \\ldots, 2 m\\}$ in the cells and colouring red all cells both of whose coordinates are even, and blue all other cells. An example for $n=9$ is shown above.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "\nSolution 1"}}
|
| 9 |
-
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Problem. Consider an $n \\times n$ grid consisting of $n^{2}$ unit cells, where $n \\geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.\n\nNote. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.", "solution": ". Consider an $n \\times m$ grid with $n, m \\geqslant 3$ being odd. We say that a column is of 'Type A' if, when partitioned into its monochromatic pieces, the first and last piece have the same colour with each one containing at least two cells. Otherwise we say that that it is of 'Type B'.\n\nIt is enough to show that the number $F$ of frogs required satisfies the inequality\n\n$$\nF \\leqslant \\frac{(m+1)(n+1)}{4}+1-C\n$$\n\nwhere $C$ is the number of boundary columns of Type $A$.\nWe will proceed by induction but we first need a preliminary result.\nClaim. Consider two neighbouring columns of height $n$ which when taken alone need $k$ and $\\ell$ frogs respectively. Let $k+t$ be the number of frogs required when both columns are taken together. (It is allowed for $t$ to be negative.) Then the maximum value of $t$ is given by the following table according to the types of the two columns:\n\n| Column 1 | Column 2 | $t$ |\n| :---: | :---: | :---: |\n| $A$ | $A$ | $\\min \\left\\{\\frac{\\ell+1}{2}, \\frac{n-k}{2}\\right\\}$ |\n| $A$ | $B$ | $\\min \\left\\{\\frac{\\ell+1}{2}, \\frac{n-k+2}{2}\\right\\}$ |\n| $B$ | $A$ | $\\min \\left\\{\\frac{\\ell-1}{2}, \\frac{n-k}{2}\\right\\}$ |\n| $B$ | $B$ | $\\min \\left\\{\\frac{\\ell}{2}, \\frac{n-k+1}{2}\\right\\}$ |\n\nProof of Claim. Note that for every two consecutive monochromatic regions of the second column, one can be covered by a frog from the first column. This is because there is a cell in the first column which neighbours both of them and a from can jump from it to the region of the corresponding colour. So the new frogs needed is at most $\\frac{\\ell+1}{2}$. Furthermore, if we have equality, then $\\ell$ must be odd so its top and bottom cell have the same colour. Furthermore the neighbouring cells in the first column must be of opposite colour, so the first column is of Type $A$. If the first column is of Type $B$ and the second column is of Type $A$, then even $\\frac{\\ell}{2}$ cannot be achieved. If it could, then $\\ell$ ought to be even but this contradicts the fact that the second column is of type $A$.\nWe draw the $k-1$ horizontal lines separating the first column into monochromatics regions and suppose that those they have heights $h_{1}, h_{2}, \\ldots, h_{k}$. Note that the cells touching these lines in the second column do not need any frog as a frog from the first column can jump to them. So the remaining cells are partitioned in columns of heights $h_{1}-1, h_{2}-2, \\ldots, h_{k-1}-$ $2, h_{k}-1$ all of whose cells to the left are the same colour. Now in each one of them we will need at most $\\frac{h_{1}}{2}, \\frac{h_{2}-1}{2}, \\ldots, \\frac{h_{k-1}-1}{2}, \\frac{h_{k}}{2}$ frogs. Their sum is $\\frac{n-k+2}{2}$ so we need at most that many frogs. Equality holds only if $h_{1}, h_{k}$ are even and the other $h_{i}$ 's are odd. In that case,\nsince their sum is equal to $n$ which is odd we must have that $k$ is odd. So the first column must be of Type $A$. Furthermore, if the second column is of Type $A$, then the first and last monochromatic regions need at most $\\frac{h_{1}-1}{2}$ and $\\frac{h_{k}-1}{2}$ new frogs respectively. So the total number of new frogs needed is at most $\\frac{n-k}{2}$.\n\nSuppose now that $m=3$ and the middle column needs $k$ frogs. So depending on the type of the three columns we need at most the following number of frogs:\n\n| Column 1 | Column 2 | Column 3 | Number of Frogs |\n| :---: | :---: | :---: | :---: |\n| $A$ | $A$ | $A$ | $k+\\frac{n-k}{2}+\\frac{n-k}{2}=n$ |\n| $A$ | $A$ | $B$ | $k+\\frac{n-k}{2}+\\frac{n-k+2}{2}=n+1$ |\n| $A$ | $B$ | $A$ | $k+\\frac{n-k}{2}+\\frac{n-k}{2}=n$ |\n| $A$ | $B$ | $B$ | $k+\\frac{n-k}{2}+\\frac{n-k+1}{2}=n-\\frac{1}{2}$ |\n| $B$ | $A$ | $A$ | $k+\\frac{n-k+2}{2}+\\frac{n-k}{2}=n+1$ |\n| $B$ | $A$ | $B$ | $k+\\frac{n-k+2}{2}+\\frac{n-k+2}{2}=n+2$ |\n| $B$ | $B$ | $A$ | $k+\\frac{n-k+1}{2}+\\frac{n-k}{2}=n+\\frac{1}{2}$ |\n| $B$ | $B$ | $B$ | $k+\\frac{n-k+1}{2}+\\frac{n-k+1}{2}=n+1$ |\n\nThis proves (1) for the case $m=3$ as the claim is $F \\leqslant n+2-C$ and it can be checked that this is satisfied in all cases.\n\nSuppose now by induction that the result is true for $m$ and we are trying to prove it for $m+2$. We attach two columns at the end of the table. We need to show that we need additionally at most $\\frac{n+1}{2}+C_{\\text {old }}-C_{\\text {new }}$ number of frogs.\nSuppose they need $k$ and $\\ell$ frogs respectively. So depending on the type of these two columns with the previous one we need at most the following additional number of frogs:\n\n| Column 1 | Column 2 | Column 3 | Number of Frogs |\n| :---: | :---: | :---: | :---: |\n| $A$ | $A$ | $A$ | $\\frac{k+1}{2}+\\frac{n-k}{2}=\\frac{n+1}{2}$ |\n| $A$ | $A$ | $B$ | $\\frac{k+1}{2}+\\frac{n-k+2}{2}=\\frac{n+3}{2}$ |\n| $A$ | $B$ | $A$ | $\\frac{k+1}{2}+\\frac{n-k}{2}=\\frac{n+1}{2}$ |\n| $A$ | $B$ | $B$ | $\\frac{k+1}{2}+\\frac{n-k+1}{2}=\\frac{n+2}{2}$ |\n| $B$ | $A$ | $A$ | $\\frac{k-1}{2}+\\frac{n-k}{2}=\\frac{n-1}{2}$ |\n| $B$ | $A$ | $B$ | $\\frac{k-1}{2}+\\frac{n-k+2}{2}=\\frac{n+1}{2}$ |\n| $B$ | $B$ | $A$ | $\\frac{k}{2}+\\frac{n-k}{2}=\\frac{n}{2}$ |\n| $B$ | $B$ | $B$ | $\\frac{k}{2}+\\frac{n-k+1}{2}=\\frac{n+1}{2}$ |\n\nIt can now be checked (using also that $n$ is odd) that this completes the inductive step.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "\nSolution 2"}}
|
|
|
|
| 1 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Firstly observe that $O A X B$ is cyclic, with diameter $O X$, and $Y$ also lies on this circle since $O Y \\perp X C$. Hence:\n\n$$\n\\angle A Z C=\\angle X A B=\\angle A B X=\\angle A Y X\n$$\n\nand so $C Y A Z$ is cyclic.\n\n\nLet $M$ be the intersection of $Y Z$ and $A C$ and let $C Y$ intersect $\\omega$ again at $W$. Using the new cyclic relation we get $\\angle C Y Z=\\angle C A Z$ and then using that $Z A$ is tangent to $\\omega$ we get $\\angle C A Z=\\angle C W A$, so $\\angle C Y M=\\angle C W A$. Therefore the triangles $C W A$ and $C Y M$ are similar. But $C W$ is a chord of $\\omega$, and $Y$ is the foot of the perpendicular from $O$, hence $Y$ is the midpoint of $C W$. It follows from the similarity relation that $M$ is the midpoint of $A C$, as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 1"}}
|
| 2 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Let $M$ be the midpoint of $A C$. We have $\\angle C A Z=\\angle C B A$ and $\\angle Z C A=$ $\\angle B A C$ so the triangles $C A Z$ and $A B C$ are similar. The line $C Y X$ is the $C$-symmedian of triangle $A B C$, and $Z M$ is the corresponding median in triangle $C A Z$, hence by isogonality $\\angle A Z M=\\angle A C Y$. So\n\n$$\n\\angle Z M A=180^{\\circ}-\\angle A Z M-\\angle M A Z=180^{\\circ}-\\angle A C Y-\\angle C B A\n$$\n\nNow observe $\\angle O M C=\\angle O Y C=90^{\\circ}$, so $C M Y O$ is cyclic. Thus:\n\n$$\n\\angle C Y M=\\angle C O M=\\frac{1}{2} \\angle C O A=\\angle C B A\n$$\n\nThis shows that\n\n$$\n\\angle Y M C=180^{\\circ}-\\angle M C Y-\\angle C Y M=180^{\\circ}-\\angle A C Y-\\angle C B A\n$$\n\nCombining this with (1) we get that $\\angle Y M C=\\angle Z M A$ and as $A, C, M$ are collinear, it follows that $Z, M, Y$ are collinear as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 2"}}
|
| 3 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". As in Solution 2 we have that $C X$ is the $A$-symmedian of triangle $A B C$ and that triangle $A B C$ is similar to triangle $C A Z$.\n\nLet $f$ be the spiral similarity which maps $A C$ onto $A B$ and let $g$ be the reflection on the perpendicular bisector of $A B$. Note that $f$ is a rotation about $A$ by an angle of $\\angle C A B$ (clockwise in our figure) followed by a homothety centered at $A$ by a factor of $A B / A C$. By the similarity of triangles $A B C$ and $C A Z$ we have that $g(f(Z))=C$, so actually $f(Z)$ is the other point of intersection, say $C^{\\prime}$, of $C Z$ with $\\omega$.\n\nAs in Solution 1 we have that $C Y A Z$ is cyclic. Therefore, letting $W$ be the other point of intersection of $C Y$ with $\\omega$, we have $\\angle W A B=\\angle W C B=\\angle C A Y$. We also have $\\angle A C Y=$ $\\angle A B W$. It follows that $f(Y)=W$.\n\nLet $W^{\\prime}=g(W)$. Then $W^{\\prime} \\in \\omega$ and since $C W$ is the $A$-symmedian, then $C W^{\\prime}$ passes through the midpoint $N$ of $A B$. Now $C W^{\\prime}$ and $C^{\\prime} W$ intersect on the perpendicular bisector of $A B$ and therefore they intersect on $N$. It follows that $N=A B \\cap C^{\\prime} W=A f(C) \\cap f(Z) f(Y)$ is the image of $M=A C \\cap Z Y$ under $f$. Since $N$ is the midpoint of $A B$, then $M$ is the midpoint of $A C$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 3"}}
|
| 4 |
+
{"year": "2022", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Let $A B C$ be an acute triangle such that $C A \\neq C B$ with circumcircle $\\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.", "solution": ". Let $E=A B \\cap C X$ and $F=A W \\cap C Z$. We have $(C, W ; X, E)=-1$. Projecting from the line $C X$ onto the line $C Z$ from $A$ we get that $(C, F ; Z, \\infty)=-1$. Thus $Z$ is the midpoint of $C F$. Since also $Y$ is the midpoint of $C W$, we get that $Z Y$ bisects $C A$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 1", "solution_match": "\nSolution 4"}}
|
| 5 |
+
{"year": "2022", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Let $a, b$ and $n$ be positive integers with $a>b$ such that all of the following hold:\n(i) $a^{2021}$ divides $n$,\n(ii) $b^{2021}$ divides $n$,\n(iii) 2022 divides $a-b$.\n\nProve that there is a subset $T$ of the set of positive divisors of the number $n$ such that the sum of the elements of $T$ is divisible by 2022 but not divisible by $2022^{2}$.", "solution": "If $1011 \\mid a$, then $1011^{2021} \\mid n$ and we can take $T=\\left\\{1011,1011^{2}\\right\\}$. So we can assume that $3 \\nmid a$ or $337 \\nmid a$.\n\nWe continue with the following claim:\nClaim. If $k$ is a positive integer, then $a^{k} b^{2021-k} \\mid n$.\nProof of the Claim. We have that $n^{2021}=n^{k} \\cdot n^{2021-k}$ is divisible by $a^{2021 k} \\cdot b^{2021(2021-k)}$ and taking the 2021-root we get the desired result.\nBack to the problem, we will prove that the set $T=\\left\\{a^{k} b^{2021-k}: k \\geqslant 0\\right\\}$ consisting of 2022 divisors of $n$, has the desired property. The sum of its elements is equal to\n\n$$\nS=\\sum_{k=0}^{2021} a^{k} b^{2021-k} \\equiv \\sum_{k=0}^{2021} a^{2021} \\equiv 0 \\bmod 2022\n$$\n\nOn the other hand, the last sum is equal to $\\frac{a^{2022}-b^{2022}}{a-b}$.\nIf $3 \\nmid a$, we will prove that $S$ is not divisible by 9 . Indeed if $3 \\nmid a$ then we also have $3 \\nmid b$. So if $3^{t} \\| a-b$ then, since $3^{1} \\| 2022$, by the Lifting the Exponent Lemma, we have that $3^{t+1} \\| a^{2022}-b^{2022}$. This implies that $S$ is not divisible by 9 , therefore, $2022^{2}$ doesn't divide $S$.\n\nIf $3 \\mid a$, then we have $337 \\nmid a$ and a similar argument shows that $337^{2} \\nmid S$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 2", "solution_match": "\nSolution."}}
|
| 6 |
+
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Find all functions $f:(0, \\infty) \\rightarrow(0, \\infty)$ such that\n\n$$\nf\\left(y(f(x))^{3}+x\\right)=x^{3} f(y)+f(x)\n$$\n\nfor all $x, y>0$.", "solution": ". Setting $y=\\frac{t}{f(x)^{3}}$ we get\n\n$$\nf(x+t)=x^{3} f\\left(\\frac{t}{f(x)^{3}}\\right)+f(x)\n$$\n\nfor every $x, t>0$.\nFrom (1) it is immediate that $f$ is increasing.\nClaim. $f(1)=1$\nProof of Claim. Let $c=f(1)$. If $c<1$, taking $x=1$ and $y=\\frac{1}{1-c^{3}}$ we have $y-y c^{3}=1$, so $y f(1)^{3}+1=y$ and $f\\left(y f(1)^{3}+1\\right)=f(y)=1^{3} f(y)$. Thus $f(1)=0$, a contradiction. Assume now for contradiction that $c>1$. We claim that\n\n$$\nf\\left(1+c^{3}+\\cdots+c^{3 n}\\right)=(n+1) c\n$$\n\nfor every $n \\in \\mathbb{N}$. We proceed by induction, the case $n=0$ being trivial. The inductive step follows easily by taking $x=1, t=c^{3}+c^{6}+\\cdots+c^{3(k+1)}$ in (1).\n\nNow taking $x=1+c^{3}+\\cdots+c^{3 n-3}, t=c^{3 n}$ in (1) we get\n\n$$\n(n+1) c=f\\left(1+c^{3}+\\cdots+c^{3 n}\\right)=\\left(1+c^{3}+\\cdots+c^{3 n-3}\\right)^{3} f\\left(\\frac{c^{3 n}}{(c n)^{3}}\\right)+n c\n$$\n\ngiving\n\n$$\nf\\left(\\frac{c^{3 n-3}}{n^{3}}\\right)=\\frac{c}{\\left(1+c^{3}+\\cdots+c^{3 n}\\right)^{3}}<c=f(1) \\Longrightarrow \\frac{c^{3 n-3}}{n^{3}}<1 .\n$$\n\nBut this leads to a contradiction if $n$ is large enough.\nNow for $x=1$ we get $f(y+1)=f(y)+1$ and since $f(1)=1$ inductively we get $f(n)=n$ for every $n \\in \\mathbb{N}$. For $m, n \\in \\mathbb{N}$, setting $x=n, y=q=m / n$ we get\n\n$$\nm n^{2}+n=f\\left(q n^{3}+n\\right)=f\\left(y f(x)^{3}+x\\right)=x^{3} f(y)+f(x)=n^{3} f(q)+n \\Longrightarrow f(q)=q .\n$$\n\nSince $f$ is strictly increasing with $f(q)=q$ for every $q \\in \\mathbb{Q}^{>0}$ we deduce that $f(x)=x$ for every $x>0$. It is easily checked that this satisfies the functional equation.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution 1"}}
|
| 7 |
+
{"year": "2022", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Find all functions $f:(0, \\infty) \\rightarrow(0, \\infty)$ such that\n\n$$\nf\\left(y(f(x))^{3}+x\\right)=x^{3} f(y)+f(x)\n$$\n\nfor all $x, y>0$.", "solution": ". We can also derive a contradiction in the case $c>1$ as follows:\nSince $f$ is strictly increasing then\n\n$$\nf(y)+f(1)=f\\left(y f(1)^{3}+1\\right)>f\\left(y f(1)^{3}\\right) \\Longrightarrow f\\left(c^{3} y\\right)<f(y)+c\n$$\n\nfor every $y>0$. So by induction we get $f\\left(c^{3 n}\\right)<(n+1) c$ for every $n \\in \\mathbb{N}$. Setting $x=c^{3 n}$ and $t=c^{3 n+3}-c^{3 n}$ in (1) we get\n\n$$\n(n+2) c>f\\left(c^{3 n+3}\\right)>f\\left(c^{3 n+3}\\right)-f\\left(c^{3 n}\\right)=c^{9 n} f\\left(\\frac{c^{3 n+3}-c^{3 n}}{f\\left(c^{3 n}\\right)^{3}}\\right)>c^{9 n} f\\left(\\frac{c^{3 n+3}-c^{3 n}}{c^{3}(n+1)^{3}}\\right)\n$$\n\nBut\n\n$$\n\\frac{c^{3 n+3}-c^{3 n}}{c^{3}(n+1)^{3}}=\\frac{c^{3 n}}{(n+1)^{3}} \\cdot \\frac{c^{3}-1}{c^{3}}>1\n$$\n\nfor $c$ large enough. So $(n+2) c>c^{9 n+1}$ which leads to a contradiction if $n$ is large enough.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 3", "solution_match": "\nSolution 2"}}
|
| 8 |
+
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Consider an $n \\times n$ grid consisting of $n^{2}$ unit cells, where $n \\geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.\n\nNote. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.", "solution": ". Let $G$ be the graph whose vertices are all $(n+1)^{2}$ vertices of the grid and where two vertices are adjacent if and only if they are adjacent in the grid and moreover the two cells in either side of the corresponding edge have different colours.\n\nThe connnected components of $G$, excluding the isolated vertices, are precisely the boundaries between pairs of monochromatic regions each of which can be covered by a single frog. Each time we add one of these components in the grid, it creates exactly one new monochromatic region. So the number of frogs required is one more than the number of such components of $G$.\n\nIt is easy to check that every corner vertex of the grid has degree 0 , every boundary vertex of the grid has degree 0 or 1 and every 'internal' vertex of the grid has degree 0,2 or 4 . It is also easy to see that every component of $G$ which is not an isolated vertex must contain at least four vertices unless it is the boundary of a single corner of the grid, in which case it contains only three vertices.\n\nWriting $N$ for the number of components which are not isolated vertices, we see that in total they contain at least $4 N-4$ vertices. (As at most four of them contain 3 vertices and all others contain 4 vertices.) Since we also have at least 4 components which are isolated vertices, then $4 N=(4 N-4)+4 \\leqslant(n+1)^{2}$. Thus $N \\leqslant \\frac{(n+1)^{2}}{4}$ and therefore the minimal number of frogs required is $\\frac{(n+1)^{2}}{4}+1$.\n\n\nThis bound for $n=2 m+1$ is achieved by putting coordinates $(x, y)$ with $x, y \\in\\{0,1, \\ldots, 2 m\\}$ in the cells and colouring red all cells both of whose coordinates are even, and blue all other cells. An example for $n=9$ is shown above.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "\nSolution 1"}}
|
| 9 |
+
{"year": "2022", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Problem. Consider an $n \\times n$ grid consisting of $n^{2}$ unit cells, where $n \\geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.\n\nNote. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.", "solution": ". Consider an $n \\times m$ grid with $n, m \\geqslant 3$ being odd. We say that a column is of 'Type A' if, when partitioned into its monochromatic pieces, the first and last piece have the same colour with each one containing at least two cells. Otherwise we say that that it is of 'Type B'.\n\nIt is enough to show that the number $F$ of frogs required satisfies the inequality\n\n$$\nF \\leqslant \\frac{(m+1)(n+1)}{4}+1-C\n$$\n\nwhere $C$ is the number of boundary columns of Type $A$.\nWe will proceed by induction but we first need a preliminary result.\nClaim. Consider two neighbouring columns of height $n$ which when taken alone need $k$ and $\\ell$ frogs respectively. Let $k+t$ be the number of frogs required when both columns are taken together. (It is allowed for $t$ to be negative.) Then the maximum value of $t$ is given by the following table according to the types of the two columns:\n\n| Column 1 | Column 2 | $t$ |\n| :---: | :---: | :---: |\n| $A$ | $A$ | $\\min \\left\\{\\frac{\\ell+1}{2}, \\frac{n-k}{2}\\right\\}$ |\n| $A$ | $B$ | $\\min \\left\\{\\frac{\\ell+1}{2}, \\frac{n-k+2}{2}\\right\\}$ |\n| $B$ | $A$ | $\\min \\left\\{\\frac{\\ell-1}{2}, \\frac{n-k}{2}\\right\\}$ |\n| $B$ | $B$ | $\\min \\left\\{\\frac{\\ell}{2}, \\frac{n-k+1}{2}\\right\\}$ |\n\nProof of Claim. Note that for every two consecutive monochromatic regions of the second column, one can be covered by a frog from the first column. This is because there is a cell in the first column which neighbours both of them and a from can jump from it to the region of the corresponding colour. So the new frogs needed is at most $\\frac{\\ell+1}{2}$. Furthermore, if we have equality, then $\\ell$ must be odd so its top and bottom cell have the same colour. Furthermore the neighbouring cells in the first column must be of opposite colour, so the first column is of Type $A$. If the first column is of Type $B$ and the second column is of Type $A$, then even $\\frac{\\ell}{2}$ cannot be achieved. If it could, then $\\ell$ ought to be even but this contradicts the fact that the second column is of type $A$.\nWe draw the $k-1$ horizontal lines separating the first column into monochromatics regions and suppose that those they have heights $h_{1}, h_{2}, \\ldots, h_{k}$. Note that the cells touching these lines in the second column do not need any frog as a frog from the first column can jump to them. So the remaining cells are partitioned in columns of heights $h_{1}-1, h_{2}-2, \\ldots, h_{k-1}-$ $2, h_{k}-1$ all of whose cells to the left are the same colour. Now in each one of them we will need at most $\\frac{h_{1}}{2}, \\frac{h_{2}-1}{2}, \\ldots, \\frac{h_{k-1}-1}{2}, \\frac{h_{k}}{2}$ frogs. Their sum is $\\frac{n-k+2}{2}$ so we need at most that many frogs. Equality holds only if $h_{1}, h_{k}$ are even and the other $h_{i}$ 's are odd. In that case,\nsince their sum is equal to $n$ which is odd we must have that $k$ is odd. So the first column must be of Type $A$. Furthermore, if the second column is of Type $A$, then the first and last monochromatic regions need at most $\\frac{h_{1}-1}{2}$ and $\\frac{h_{k}-1}{2}$ new frogs respectively. So the total number of new frogs needed is at most $\\frac{n-k}{2}$.\n\nSuppose now that $m=3$ and the middle column needs $k$ frogs. So depending on the type of the three columns we need at most the following number of frogs:\n\n| Column 1 | Column 2 | Column 3 | Number of Frogs |\n| :---: | :---: | :---: | :---: |\n| $A$ | $A$ | $A$ | $k+\\frac{n-k}{2}+\\frac{n-k}{2}=n$ |\n| $A$ | $A$ | $B$ | $k+\\frac{n-k}{2}+\\frac{n-k+2}{2}=n+1$ |\n| $A$ | $B$ | $A$ | $k+\\frac{n-k}{2}+\\frac{n-k}{2}=n$ |\n| $A$ | $B$ | $B$ | $k+\\frac{n-k}{2}+\\frac{n-k+1}{2}=n-\\frac{1}{2}$ |\n| $B$ | $A$ | $A$ | $k+\\frac{n-k+2}{2}+\\frac{n-k}{2}=n+1$ |\n| $B$ | $A$ | $B$ | $k+\\frac{n-k+2}{2}+\\frac{n-k+2}{2}=n+2$ |\n| $B$ | $B$ | $A$ | $k+\\frac{n-k+1}{2}+\\frac{n-k}{2}=n+\\frac{1}{2}$ |\n| $B$ | $B$ | $B$ | $k+\\frac{n-k+1}{2}+\\frac{n-k+1}{2}=n+1$ |\n\nThis proves (1) for the case $m=3$ as the claim is $F \\leqslant n+2-C$ and it can be checked that this is satisfied in all cases.\n\nSuppose now by induction that the result is true for $m$ and we are trying to prove it for $m+2$. We attach two columns at the end of the table. We need to show that we need additionally at most $\\frac{n+1}{2}+C_{\\text {old }}-C_{\\text {new }}$ number of frogs.\nSuppose they need $k$ and $\\ell$ frogs respectively. So depending on the type of these two columns with the previous one we need at most the following additional number of frogs:\n\n| Column 1 | Column 2 | Column 3 | Number of Frogs |\n| :---: | :---: | :---: | :---: |\n| $A$ | $A$ | $A$ | $\\frac{k+1}{2}+\\frac{n-k}{2}=\\frac{n+1}{2}$ |\n| $A$ | $A$ | $B$ | $\\frac{k+1}{2}+\\frac{n-k+2}{2}=\\frac{n+3}{2}$ |\n| $A$ | $B$ | $A$ | $\\frac{k+1}{2}+\\frac{n-k}{2}=\\frac{n+1}{2}$ |\n| $A$ | $B$ | $B$ | $\\frac{k+1}{2}+\\frac{n-k+1}{2}=\\frac{n+2}{2}$ |\n| $B$ | $A$ | $A$ | $\\frac{k-1}{2}+\\frac{n-k}{2}=\\frac{n-1}{2}$ |\n| $B$ | $A$ | $B$ | $\\frac{k-1}{2}+\\frac{n-k+2}{2}=\\frac{n+1}{2}$ |\n| $B$ | $B$ | $A$ | $\\frac{k}{2}+\\frac{n-k}{2}=\\frac{n}{2}$ |\n| $B$ | $B$ | $B$ | $\\frac{k}{2}+\\frac{n-k+1}{2}=\\frac{n+1}{2}$ |\n\nIt can now be checked (using also that $n$ is odd) that this completes the inductive step.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl", "problem_match": "# Problem 4", "solution_match": "\nSolution 2"}}
|
Balkan_MO/segmented/en-2023-BMO-type1.jsonl
CHANGED
|
@@ -1,5 +1,5 @@
|
|
| 1 |
-
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "problem": "Find all functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that for all $x, y \\in \\mathbb{R}$,\n\n$$\nx f(x+f(y))=(y-x) f(f(x))\n$$", "solution": "Answer: For any real $c, f(x)=c-x$ for all $x \\in \\mathbb{R}$ and $f(x)=0$ for all $x \\in \\mathbb{R}$.\n\nLet $P(x, y)$ denote the proposition that $x$ and $y$ satisfy the given equation. $P(0,1)$ gives us $f(f(0))=0$.\n\nFrom $P(x, x)$ we get that $x f(x+f(x))=0$ for all $x \\in \\mathbb{R}$, which together with $f(f(0))=$ 0 gives us $f(x+f(x))=0$ for all $x$.\n\nNow let $t$ be any real number such that $f(t)=0$. If $y$ is any number, we have from $P(t-f(y), y)$ the equality\n\n$$\n(y+f(y)-t) f(f(t-f(y)))=0\n$$\n\nfor all $y$ and all $t$ such that $f(t)=0$. So, by taking $y=f(0)$ we obtain\n\n$$\n(f(0)-t) f(f(t))=0 \\quad \\text { and hence } \\quad(f(0)-t) f(0)=0\n$$\n\nRecall that as $t$ with $f(t)=0$ we can take $x+f(x)$ for any real number $x$. If for all reals $x$ we have $x+f(x)=f(0)$, then $f(x)$ must be of the form $f(x)=c-x$ for some real $c$. It is straightforward that all functions of this form are indeed solutions.\n\nOtherwise we can find some $a \\neq 0$ so that $a+f(a) \\neq f(0)$. If $t=a+f(a)$ in (A1-1), then $f(0)$ must be equal to 0 . Now $P(x, 0)$ gives us $f(f(x))=-f(x)$ for all real $x$. From here $P(x, x+f(x))$ gives us $x f(x)=-f(x)^{2}$ for all real $x$, which means for every $x$ either $f(x)=0$ or $f(x)=-x$.\n\nLet us assume that in this case there is some $b \\neq 0$ so that $f(b)=-b$. For any $y$ we get from $P(b, y)$ and $f(f(b))=-f(b)=b$ the equality $b f(b+f(y))=(y-b) b$, which gives us $f(b+f(y))=y-b$ for all $y$. If $y \\neq b$, then the right hand side in the previous equality is not zero, so we must have $f(b+f(y))=-b-f(y)$, which means that $-b-f(y)=y-b$, or that $f(y)=-y$ for all real $y$. But we already covered this solution (take $c=0$ above). If there is no such $b$, then $f(x)=0$ for all $x$, which gives us the final solution.\n\nThus, all such functions are of the form $c-x$ for real $c$ or the zero function.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
-
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that\n\n$$\n\\angle X B C=\\angle X C B=45^{\\circ} .\n$$\n\nLet $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.", "solution": ". We first state a well-known lemma.\nLemma: In triangle $A B C$, let $D, E, F$ be the points of tangency of the incircle to the sides $B C, C A, A B$ and let $I$ be the incenter. Then the intersection of $E F$ and $B I$ lies on the circle of diameter $B C$.\n\nProof: Let $S$ be the intersection of $E F$ and $B I . \\angle B I C=\\angle E F C$, hence $S$ lies on the circumcircle of $F I C$ in which $I C$ is a diameter. Thus $\\angle I S C=90^{\\circ}$, hence $\\angle B S C=90^{\\circ}$.\n\nReturning to the problem, let $I$ be the incenter. The lemma implies that the two intersection points of $E F$ with the circle of diameter $B C$ are precisely the intersection points of $E F$ with $B I$ and $C I$. We have $\\angle B X C=90^{\\circ}$, therefore either $B X$ or $C X$ is an internal angle bisector, which means either $\\angle B=90^{\\circ}$ or $\\angle C=90^{\\circ}$.\n\nAssume, without loss of generality, that $\\angle B=90^{\\circ}$. Then we have $\\angle A M C=90^{\\circ}$, so $M$ is the second intersection point of $A I$ with the circle of diameter $A C$, thus the lemma implies that $M$ lies on $D F$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 3 |
-
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "problem": "In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that\n\n$$\n\\angle X B C=\\angle X C B=45^{\\circ} .\n$$\n\nLet $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.", "solution": ".\n\nLet $I$ be the incenter of $\\triangle A B C$ and let $K$ be the foot of the perpendicular from $D$ to $E F$. We begin by proving that $B K X C$ is cyclic, which can be done in two ways:\n\nFirst Way. Note that $\\angle K F D=90^{\\circ}-\\frac{\\angle C}{2}$ and $\\angle K E D=90^{\\circ}-\\frac{\\angle B}{2}$, so by using $K D \\perp E F$, we have $\\frac{F K}{E D}=\\frac{\\tan \\frac{\\angle C}{2}}{\\tan \\frac{\\angle B}{2}}$. Similarly, since $\\angle I B D=\\frac{\\angle B}{2}$ and $\\angle I C D=\\frac{\\angle C}{2}$, by using $I D \\perp B C$, we have $\\frac{B F}{E C}=\\frac{B D}{D C}=\\frac{\\tan \\frac{\\angle C}{2}}{\\tan \\frac{\\angle B}{2}}$. Then, since $\\angle B F K=90^{\\circ}+\\frac{\\angle A}{2}=$ $\\angle K E C$, we conclude that $\\triangle B F K$ and $\\triangle C E K$ are similar, so $\\angle F K B=\\angle C K E$ which shows line $E F$ is the external-angle bisector of $\\angle B K C$. Therefore, $X$ lies on both the perpendicular bisector of the segment $B C$ and the external angle bisector of $\\angle B K C$ (and these lines are distinct) thus it lies on the circumcirle of $\\triangle B K C$ (in particular the midpoint of arc $B K C$ ).\n\nSecond Way. Let $T$ be the intersection of $E F$ and $B C$, and $N$ be the midpoint of the segment $B C$. It is well-known that $(T, D ; B, C)$ is harmonic and $T B \\cdot T C=T D \\cdot T N$. On the other hand, since $X B=X C$, we have $\\angle X N D=90^{\\circ}=\\angle X K D$, so $X K D N$ is cyclic and $T D \\cdot T N=T K \\cdot T X$. Therefore, we have $T K \\cdot T X=T B \\cdot T C$, which implies $B K X C$ is cyclic.\n\nNow we will show that either $\\angle B=90^{\\circ}$ or $\\angle C=90^{\\circ}$. Note that $\\angle B K C=\\angle B X C=$ $90^{\\circ}=\\angle F K D=\\angle E K D$ and $\\angle F K B=\\angle E K C$. Then we have\n\n$$\n\\angle F K B=\\angle B K D=\\angle D K C=\\angle C K E=45^{\\circ} .\n$$\n\nHence $B K$ bisects $\\angle F K D$, but $B$ also lies on the perpendicular bisector of $D F$. Therefore, either $F K D B$ is cyclic or $K F=K D$ while the former implies that $\\angle B=180^{\\circ}-\\angle F K D=$ $90^{\\circ}$. In the latter case, we have $K B \\perp F D$, which gives $90^{\\circ}-\\frac{\\angle C}{2}=\\angle K F D=90^{\\circ}-$ $\\angle F K B=45^{\\circ}$ and so $\\angle C=90^{\\circ}$ as desired.\n\nWe consider, without loss of generality, the case where $\\angle B=90^{\\circ}$. Observing that $A, I, M$ are collinear we get:\n\n$$\n\\angle C D I=90^{\\circ}=\\angle C B A=\\angle C M A=\\angle C M I\n$$\n\nHence $M D I C$ is cyclic so:\n\n$$\n\\angle M D C=\\angle M I C=180^{\\circ}-\\angle C I A=180^{\\circ}-\\left(90^{\\circ}+\\frac{\\angle B}{2}\\right)=45^{\\circ}\n$$\n\nWe also have $\\angle F D B=90^{\\circ}-\\frac{\\angle B}{2}=45^{\\circ}$ so $\\angle F D B=\\angle M D C$ and thus $M, D, F$ are collinear as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 4 |
-
{"year": "2023", "tier": "T1", "problem_label": "3", "problem_type": null, "problem": "For each positive integer $n$, denote by $\\omega(n)$ the number of distinct prime divisors of $n$ (for example, $\\omega(1)=0$ and $\\omega(12)=2$ ). Find all polynomials $P(x)$ with integer coefficients, such that whenever $n$ is a positive integer satisfying $\\omega(n)>2023^{2023}$, then $P(n)$ is also a positive integer with\n\n$$\n\\omega(n) \\geq \\omega(P(n)) .\n$$", "solution": "Answer: All polynomials of the form $f(x)=x^{m}$ for some $m \\in \\mathbb{Z}^{+}$and $f(x)=c$ for some $c \\in \\mathbb{Z}^{+}$with $\\omega(c) \\leq 2023^{2023}+1$.\n\nFirst of all we prove the following (well-known) Lemma. Lemma: Let $f(x)$ be a nonconstant polynomial with integer coefficients. Then, the number of primes $p$ such that $p \\mid f(n)$ for some $n$ is infinite.\n\nProof: If $f(0)=0$, then the Lemma is obvious. Otherwise, define the polynomial\n\n$$\ng(x)=\\frac{f(x f(0))}{f(0)}\n$$\n\nwhich has integer coefficients. Observe that $g(0)=1$ and if $g$ satisfies the property of the Lemma, then so does $f$. So, we need to prove that there are infinitely many primes $p$ such that $p \\mid g(n)$ for some $n$. Suppose, for the sake of contradiction that the number of such primes is finite, and let those be $p_{1}, \\ldots, p_{k}$. Then, set $n=N p_{1} \\cdots p_{k}$ for some large $N$, such that $|g(n)|>1$. It is evident that $g(n)$ has a prime divisor, but it is none of the $p_{i}$ 's. This is a contradiction and therefore the result follows.\n\nLet $M=2023{ }^{2023}+1$. Observe that constant polynomials $f(x)=c$ with $c \\in \\mathbb{N}$ such that $\\omega(c) \\leq M$ satisfy the conditions of the problem. On the other hand, if $f(x)=c$ with $\\omega(c)>M$, we can choose some $n$ such that $\\omega(n)=M$ to see that the condition of the problem is not satisfied. Next, we look for non-constant polynomials that satisfy the conditions of the problem. Let $f(x)=x^{m} g(x)$, where $m \\geq 0$ and $g(x)$ is a polynomial with $g(0) \\neq 0$. We claim that $g$ is a constant polynomial. Indeed, if it is not, then (due to the Lemma) there exist pairwise distinct primes $q_{1}, \\ldots, q_{M+1}$ and non-zero integers $n_{1}, \\ldots, n_{M+1}$ such that $q_{i}>|g(0)|$ and $q_{i} \\mid g\\left(n_{i}\\right)$ for $i=1,2, \\ldots, M+1$. Set $n=p_{1} p_{2} \\cdots p_{M}$, where $p_{1}, \\ldots, p_{M}$ are distinct primes such that\n\n$$\np_{1} \\equiv n_{i} \\quad\\left(\\bmod q_{i}\\right), \\forall i=1,2, \\ldots, M+1\n$$\n\nand\n\n$$\np_{j} \\equiv 1 \\quad\\left(\\bmod q_{i}\\right), \\forall i=1,2, \\ldots, M+1, \\forall j=2,3, \\ldots, M\n$$\n\nObserve that since $q_{i}>|g(0)|$, it is impossible to have $q_{i} \\mid n_{i}$, so the existence of such primes is guaranteed by the Chinese Remainder Theorem and the Dirichlet's Theorem. Now, for every $i=1,2, \\ldots, M+1$ we can see that $n=p_{1} \\cdots p_{M} \\equiv n_{i}\\left(\\bmod q_{i}\\right)$, which means that\n\n$$\ng(n) \\equiv g\\left(n_{i}\\right) \\equiv 0 \\quad\\left(\\bmod q_{i}\\right) \\forall i=1,2, \\ldots, M+1\n$$\n\nThus, $\\omega(f(n)) \\geq \\omega(g(n)) \\geq M+1>M=\\omega(n)$, which gives the desired contradiction. Therefore, $f(x)=c x^{m}$, for some $m \\geq 1$ (since $f$ was non-constant). If $c<0$, take some $n$ with $\\omega(n)=M$ to see that $f(n)$ is negative and so, does not satisfy the conditions of the problem. If $c>1$, choose some $n$ with $\\omega(n)=M$ and $\\operatorname{gcd}(n, c)=1$ to observe that $f$ cannot satisfy the conditions of the problem. This means that $f(x)=x^{m}$ (which is for sure a solution to the problem) for some $m \\geq 1$ and $f(x)=c$ for some $c \\in \\mathbb{Z}^{+}$with $\\omega(c) \\leq M$ are the only polynomials that satisfy the conditions of the problem.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 5 |
-
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "problem": "Find the greatest integer $k \\leq 2023$ for which the following holds: whenever Alice colours exactly $k$ numbers of the set $\\{1,2, \\ldots, 2023\\}$ in red, Bob can colour some of the remaining uncoloured numbers in blue, such that the sum of the red numbers is the same as the sum of the blue numbers.", "solution": "Answer: 592.\nFor $k \\geq 593$, Alice can color the greatest 593 numbers $1431,1432, \\ldots, 2023$ and any other $(k-593)$ numbers so that their sum $s$ would satisfy\n\n$$\ns \\geq \\frac{2023 \\cdot 2024}{2}-\\frac{1430 \\cdot 1431}{2}>\\frac{1}{2} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right),\n$$\n\nthus anyhow Bob chooses his numbers, the sum of his numbers will be less than Alice's numbers' sum.\n\nWe now show that $k=592$ satisfies the condition. Let $s$ be the sum of Alice's 592 numbers; note that $s<\\frac{1}{2} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)$. Below is a strategy for Bob to find some of the remaining 1431 numbers so that their sum is\n\n$$\ns_{0}=\\min \\left\\{s, \\frac{2023.2024}{2}-2 s\\right\\} \\leqslant \\frac{1}{3} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)\n$$\n\n(Clearly, if Bob finds some numbers whose sum is $\\frac{2023.2024}{2}-2 s$, then the sum of remaining numbers will be $s$ ).\n\nCase 1. $s_{0} \\geq 2024$. Let $s_{0}=2024 a+b$, where $0 \\leqslant b \\leqslant 2023$. Bob finds two of the remaining numbers with sum $b$ or $2024+b$, then he finds $a$ (or $a-1$ ) pairs among the remaining numbers with sum 2024 . Note that $a \\leq 337$ since $s_{0} \\leq \\frac{1}{3} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)$.\n\nThe $\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor$ pairs\n\n$$\n(1, b-1),(2, b-2), \\ldots,\\left(\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor, b-\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor\\right),\n$$\n\nhave sum of their components equal to $b$ and the $\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor-b$ pairs\n\n$$\n(2023, b+1),(2022, b+2), \\ldots,\\left(2024+b-\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor,\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor\\right)\n$$\n\nhave sum of their components equal to $2024+b$. The total number of these pairs is\n\n$$\n\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor-b+\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor \\geq \\frac{2022+b}{2}+\\frac{b-2}{2}-b=\\frac{2020}{2}=1010>592\n$$\n\nhence some of these pairs have no red-colored components, so Bob can choose one of these pairs and color those two numbers in blue. Thus 594 numbers are colored so far.\n\nFurther, the 1011 pairs\n\n$$\n(1,2023),(2,2022), \\ldots,(1011,1013)\n$$\n\nhave sum of the components equal to 2024. Among these, at least $1011-594=417>$ $337 \\geq a$ pairs have no components colored, so Bob can choose $a$ (or $a-1$ ) uncolored pairs and color them all blue to achieve a collection of blue numbers with their sum equal to $s_{0}$.\n\nCase 2. $s_{0} \\leq 2023$. Note that $s \\geq 1+2+\\ldots+592>2023$, thus we have $s_{0}=$ $\\frac{2023 \\cdot 2024}{2}-2 s$, i.e. $s=\\frac{2023 \\cdot 2024}{4}-\\frac{s_{0}}{2}$.\n\nIf $s_{0}>2 \\cdot 593$, at least one of the 593 pairs\n\n$$\n\\left(1, s_{0}-1\\right),\\left(2, s_{0}-2\\right), \\ldots,\\left(593, s_{0}-593\\right)\n$$\n\nhave no red-colored components, so Bob can choose these two numbers and immediately achieve the sum of $s_{0}$. And if $s_{0} \\leq 2 \\cdot 593$, then\n$s=\\frac{2023 \\cdot 2024}{4}-\\frac{s_{0}}{2} \\geq(1432+1433+\\ldots+2023)-593=839+(1434+1435+\\ldots+2023)$,\nhence Alice cannot have colored any of the numbers $1,2, \\ldots, 838$. Then Bob can easily choose one or two of these numbers having the sum of $s_{0}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|
|
|
|
| 1 |
+
{"year": "2023", "tier": "T1", "problem_label": "1", "problem_type": null, "exam": "Balkan_MO", "problem": "Find all functions $f: \\mathbb{R} \\rightarrow \\mathbb{R}$ such that for all $x, y \\in \\mathbb{R}$,\n\n$$\nx f(x+f(y))=(y-x) f(f(x))\n$$", "solution": "Answer: For any real $c, f(x)=c-x$ for all $x \\in \\mathbb{R}$ and $f(x)=0$ for all $x \\in \\mathbb{R}$.\n\nLet $P(x, y)$ denote the proposition that $x$ and $y$ satisfy the given equation. $P(0,1)$ gives us $f(f(0))=0$.\n\nFrom $P(x, x)$ we get that $x f(x+f(x))=0$ for all $x \\in \\mathbb{R}$, which together with $f(f(0))=$ 0 gives us $f(x+f(x))=0$ for all $x$.\n\nNow let $t$ be any real number such that $f(t)=0$. If $y$ is any number, we have from $P(t-f(y), y)$ the equality\n\n$$\n(y+f(y)-t) f(f(t-f(y)))=0\n$$\n\nfor all $y$ and all $t$ such that $f(t)=0$. So, by taking $y=f(0)$ we obtain\n\n$$\n(f(0)-t) f(f(t))=0 \\quad \\text { and hence } \\quad(f(0)-t) f(0)=0\n$$\n\nRecall that as $t$ with $f(t)=0$ we can take $x+f(x)$ for any real number $x$. If for all reals $x$ we have $x+f(x)=f(0)$, then $f(x)$ must be of the form $f(x)=c-x$ for some real $c$. It is straightforward that all functions of this form are indeed solutions.\n\nOtherwise we can find some $a \\neq 0$ so that $a+f(a) \\neq f(0)$. If $t=a+f(a)$ in (A1-1), then $f(0)$ must be equal to 0 . Now $P(x, 0)$ gives us $f(f(x))=-f(x)$ for all real $x$. From here $P(x, x+f(x))$ gives us $x f(x)=-f(x)^{2}$ for all real $x$, which means for every $x$ either $f(x)=0$ or $f(x)=-x$.\n\nLet us assume that in this case there is some $b \\neq 0$ so that $f(b)=-b$. For any $y$ we get from $P(b, y)$ and $f(f(b))=-f(b)=b$ the equality $b f(b+f(y))=(y-b) b$, which gives us $f(b+f(y))=y-b$ for all $y$. If $y \\neq b$, then the right hand side in the previous equality is not zero, so we must have $f(b+f(y))=-b-f(y)$, which means that $-b-f(y)=y-b$, or that $f(y)=-y$ for all real $y$. But we already covered this solution (take $c=0$ above). If there is no such $b$, then $f(x)=0$ for all $x$, which gives us the final solution.\n\nThus, all such functions are of the form $c-x$ for real $c$ or the zero function.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 1.", "solution_match": "\nSolution."}}
|
| 2 |
+
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that\n\n$$\n\\angle X B C=\\angle X C B=45^{\\circ} .\n$$\n\nLet $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.", "solution": ". We first state a well-known lemma.\nLemma: In triangle $A B C$, let $D, E, F$ be the points of tangency of the incircle to the sides $B C, C A, A B$ and let $I$ be the incenter. Then the intersection of $E F$ and $B I$ lies on the circle of diameter $B C$.\n\nProof: Let $S$ be the intersection of $E F$ and $B I . \\angle B I C=\\angle E F C$, hence $S$ lies on the circumcircle of $F I C$ in which $I C$ is a diameter. Thus $\\angle I S C=90^{\\circ}$, hence $\\angle B S C=90^{\\circ}$.\n\nReturning to the problem, let $I$ be the incenter. The lemma implies that the two intersection points of $E F$ with the circle of diameter $B C$ are precisely the intersection points of $E F$ with $B I$ and $C I$. We have $\\angle B X C=90^{\\circ}$, therefore either $B X$ or $C X$ is an internal angle bisector, which means either $\\angle B=90^{\\circ}$ or $\\angle C=90^{\\circ}$.\n\nAssume, without loss of generality, that $\\angle B=90^{\\circ}$. Then we have $\\angle A M C=90^{\\circ}$, so $M$ is the second intersection point of $A I$ with the circle of diameter $A C$, thus the lemma implies that $M$ lies on $D F$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "\nSolution 1"}}
|
| 3 |
+
{"year": "2023", "tier": "T1", "problem_label": "2", "problem_type": null, "exam": "Balkan_MO", "problem": "In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that\n\n$$\n\\angle X B C=\\angle X C B=45^{\\circ} .\n$$\n\nLet $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.", "solution": ".\n\nLet $I$ be the incenter of $\\triangle A B C$ and let $K$ be the foot of the perpendicular from $D$ to $E F$. We begin by proving that $B K X C$ is cyclic, which can be done in two ways:\n\nFirst Way. Note that $\\angle K F D=90^{\\circ}-\\frac{\\angle C}{2}$ and $\\angle K E D=90^{\\circ}-\\frac{\\angle B}{2}$, so by using $K D \\perp E F$, we have $\\frac{F K}{E D}=\\frac{\\tan \\frac{\\angle C}{2}}{\\tan \\frac{\\angle B}{2}}$. Similarly, since $\\angle I B D=\\frac{\\angle B}{2}$ and $\\angle I C D=\\frac{\\angle C}{2}$, by using $I D \\perp B C$, we have $\\frac{B F}{E C}=\\frac{B D}{D C}=\\frac{\\tan \\frac{\\angle C}{2}}{\\tan \\frac{\\angle B}{2}}$. Then, since $\\angle B F K=90^{\\circ}+\\frac{\\angle A}{2}=$ $\\angle K E C$, we conclude that $\\triangle B F K$ and $\\triangle C E K$ are similar, so $\\angle F K B=\\angle C K E$ which shows line $E F$ is the external-angle bisector of $\\angle B K C$. Therefore, $X$ lies on both the perpendicular bisector of the segment $B C$ and the external angle bisector of $\\angle B K C$ (and these lines are distinct) thus it lies on the circumcirle of $\\triangle B K C$ (in particular the midpoint of arc $B K C$ ).\n\nSecond Way. Let $T$ be the intersection of $E F$ and $B C$, and $N$ be the midpoint of the segment $B C$. It is well-known that $(T, D ; B, C)$ is harmonic and $T B \\cdot T C=T D \\cdot T N$. On the other hand, since $X B=X C$, we have $\\angle X N D=90^{\\circ}=\\angle X K D$, so $X K D N$ is cyclic and $T D \\cdot T N=T K \\cdot T X$. Therefore, we have $T K \\cdot T X=T B \\cdot T C$, which implies $B K X C$ is cyclic.\n\nNow we will show that either $\\angle B=90^{\\circ}$ or $\\angle C=90^{\\circ}$. Note that $\\angle B K C=\\angle B X C=$ $90^{\\circ}=\\angle F K D=\\angle E K D$ and $\\angle F K B=\\angle E K C$. Then we have\n\n$$\n\\angle F K B=\\angle B K D=\\angle D K C=\\angle C K E=45^{\\circ} .\n$$\n\nHence $B K$ bisects $\\angle F K D$, but $B$ also lies on the perpendicular bisector of $D F$. Therefore, either $F K D B$ is cyclic or $K F=K D$ while the former implies that $\\angle B=180^{\\circ}-\\angle F K D=$ $90^{\\circ}$. In the latter case, we have $K B \\perp F D$, which gives $90^{\\circ}-\\frac{\\angle C}{2}=\\angle K F D=90^{\\circ}-$ $\\angle F K B=45^{\\circ}$ and so $\\angle C=90^{\\circ}$ as desired.\n\nWe consider, without loss of generality, the case where $\\angle B=90^{\\circ}$. Observing that $A, I, M$ are collinear we get:\n\n$$\n\\angle C D I=90^{\\circ}=\\angle C B A=\\angle C M A=\\angle C M I\n$$\n\nHence $M D I C$ is cyclic so:\n\n$$\n\\angle M D C=\\angle M I C=180^{\\circ}-\\angle C I A=180^{\\circ}-\\left(90^{\\circ}+\\frac{\\angle B}{2}\\right)=45^{\\circ}\n$$\n\nWe also have $\\angle F D B=90^{\\circ}-\\frac{\\angle B}{2}=45^{\\circ}$ so $\\angle F D B=\\angle M D C$ and thus $M, D, F$ are collinear as required.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 2.", "solution_match": "# Solution 2"}}
|
| 4 |
+
{"year": "2023", "tier": "T1", "problem_label": "3", "problem_type": null, "exam": "Balkan_MO", "problem": "For each positive integer $n$, denote by $\\omega(n)$ the number of distinct prime divisors of $n$ (for example, $\\omega(1)=0$ and $\\omega(12)=2$ ). Find all polynomials $P(x)$ with integer coefficients, such that whenever $n$ is a positive integer satisfying $\\omega(n)>2023^{2023}$, then $P(n)$ is also a positive integer with\n\n$$\n\\omega(n) \\geq \\omega(P(n)) .\n$$", "solution": "Answer: All polynomials of the form $f(x)=x^{m}$ for some $m \\in \\mathbb{Z}^{+}$and $f(x)=c$ for some $c \\in \\mathbb{Z}^{+}$with $\\omega(c) \\leq 2023^{2023}+1$.\n\nFirst of all we prove the following (well-known) Lemma. Lemma: Let $f(x)$ be a nonconstant polynomial with integer coefficients. Then, the number of primes $p$ such that $p \\mid f(n)$ for some $n$ is infinite.\n\nProof: If $f(0)=0$, then the Lemma is obvious. Otherwise, define the polynomial\n\n$$\ng(x)=\\frac{f(x f(0))}{f(0)}\n$$\n\nwhich has integer coefficients. Observe that $g(0)=1$ and if $g$ satisfies the property of the Lemma, then so does $f$. So, we need to prove that there are infinitely many primes $p$ such that $p \\mid g(n)$ for some $n$. Suppose, for the sake of contradiction that the number of such primes is finite, and let those be $p_{1}, \\ldots, p_{k}$. Then, set $n=N p_{1} \\cdots p_{k}$ for some large $N$, such that $|g(n)|>1$. It is evident that $g(n)$ has a prime divisor, but it is none of the $p_{i}$ 's. This is a contradiction and therefore the result follows.\n\nLet $M=2023{ }^{2023}+1$. Observe that constant polynomials $f(x)=c$ with $c \\in \\mathbb{N}$ such that $\\omega(c) \\leq M$ satisfy the conditions of the problem. On the other hand, if $f(x)=c$ with $\\omega(c)>M$, we can choose some $n$ such that $\\omega(n)=M$ to see that the condition of the problem is not satisfied. Next, we look for non-constant polynomials that satisfy the conditions of the problem. Let $f(x)=x^{m} g(x)$, where $m \\geq 0$ and $g(x)$ is a polynomial with $g(0) \\neq 0$. We claim that $g$ is a constant polynomial. Indeed, if it is not, then (due to the Lemma) there exist pairwise distinct primes $q_{1}, \\ldots, q_{M+1}$ and non-zero integers $n_{1}, \\ldots, n_{M+1}$ such that $q_{i}>|g(0)|$ and $q_{i} \\mid g\\left(n_{i}\\right)$ for $i=1,2, \\ldots, M+1$. Set $n=p_{1} p_{2} \\cdots p_{M}$, where $p_{1}, \\ldots, p_{M}$ are distinct primes such that\n\n$$\np_{1} \\equiv n_{i} \\quad\\left(\\bmod q_{i}\\right), \\forall i=1,2, \\ldots, M+1\n$$\n\nand\n\n$$\np_{j} \\equiv 1 \\quad\\left(\\bmod q_{i}\\right), \\forall i=1,2, \\ldots, M+1, \\forall j=2,3, \\ldots, M\n$$\n\nObserve that since $q_{i}>|g(0)|$, it is impossible to have $q_{i} \\mid n_{i}$, so the existence of such primes is guaranteed by the Chinese Remainder Theorem and the Dirichlet's Theorem. Now, for every $i=1,2, \\ldots, M+1$ we can see that $n=p_{1} \\cdots p_{M} \\equiv n_{i}\\left(\\bmod q_{i}\\right)$, which means that\n\n$$\ng(n) \\equiv g\\left(n_{i}\\right) \\equiv 0 \\quad\\left(\\bmod q_{i}\\right) \\forall i=1,2, \\ldots, M+1\n$$\n\nThus, $\\omega(f(n)) \\geq \\omega(g(n)) \\geq M+1>M=\\omega(n)$, which gives the desired contradiction. Therefore, $f(x)=c x^{m}$, for some $m \\geq 1$ (since $f$ was non-constant). If $c<0$, take some $n$ with $\\omega(n)=M$ to see that $f(n)$ is negative and so, does not satisfy the conditions of the problem. If $c>1$, choose some $n$ with $\\omega(n)=M$ and $\\operatorname{gcd}(n, c)=1$ to observe that $f$ cannot satisfy the conditions of the problem. This means that $f(x)=x^{m}$ (which is for sure a solution to the problem) for some $m \\geq 1$ and $f(x)=c$ for some $c \\in \\mathbb{Z}^{+}$with $\\omega(c) \\leq M$ are the only polynomials that satisfy the conditions of the problem.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 3.", "solution_match": "\nSolution."}}
|
| 5 |
+
{"year": "2023", "tier": "T1", "problem_label": "4", "problem_type": null, "exam": "Balkan_MO", "problem": "Find the greatest integer $k \\leq 2023$ for which the following holds: whenever Alice colours exactly $k$ numbers of the set $\\{1,2, \\ldots, 2023\\}$ in red, Bob can colour some of the remaining uncoloured numbers in blue, such that the sum of the red numbers is the same as the sum of the blue numbers.", "solution": "Answer: 592.\nFor $k \\geq 593$, Alice can color the greatest 593 numbers $1431,1432, \\ldots, 2023$ and any other $(k-593)$ numbers so that their sum $s$ would satisfy\n\n$$\ns \\geq \\frac{2023 \\cdot 2024}{2}-\\frac{1430 \\cdot 1431}{2}>\\frac{1}{2} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right),\n$$\n\nthus anyhow Bob chooses his numbers, the sum of his numbers will be less than Alice's numbers' sum.\n\nWe now show that $k=592$ satisfies the condition. Let $s$ be the sum of Alice's 592 numbers; note that $s<\\frac{1}{2} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)$. Below is a strategy for Bob to find some of the remaining 1431 numbers so that their sum is\n\n$$\ns_{0}=\\min \\left\\{s, \\frac{2023.2024}{2}-2 s\\right\\} \\leqslant \\frac{1}{3} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)\n$$\n\n(Clearly, if Bob finds some numbers whose sum is $\\frac{2023.2024}{2}-2 s$, then the sum of remaining numbers will be $s$ ).\n\nCase 1. $s_{0} \\geq 2024$. Let $s_{0}=2024 a+b$, where $0 \\leqslant b \\leqslant 2023$. Bob finds two of the remaining numbers with sum $b$ or $2024+b$, then he finds $a$ (or $a-1$ ) pairs among the remaining numbers with sum 2024 . Note that $a \\leq 337$ since $s_{0} \\leq \\frac{1}{3} \\cdot\\left(\\frac{2023 \\cdot 2024}{2}\\right)$.\n\nThe $\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor$ pairs\n\n$$\n(1, b-1),(2, b-2), \\ldots,\\left(\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor, b-\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor\\right),\n$$\n\nhave sum of their components equal to $b$ and the $\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor-b$ pairs\n\n$$\n(2023, b+1),(2022, b+2), \\ldots,\\left(2024+b-\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor,\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor\\right)\n$$\n\nhave sum of their components equal to $2024+b$. The total number of these pairs is\n\n$$\n\\left\\lfloor\\frac{2023+b}{2}\\right\\rfloor-b+\\left\\lfloor\\frac{b-1}{2}\\right\\rfloor \\geq \\frac{2022+b}{2}+\\frac{b-2}{2}-b=\\frac{2020}{2}=1010>592\n$$\n\nhence some of these pairs have no red-colored components, so Bob can choose one of these pairs and color those two numbers in blue. Thus 594 numbers are colored so far.\n\nFurther, the 1011 pairs\n\n$$\n(1,2023),(2,2022), \\ldots,(1011,1013)\n$$\n\nhave sum of the components equal to 2024. Among these, at least $1011-594=417>$ $337 \\geq a$ pairs have no components colored, so Bob can choose $a$ (or $a-1$ ) uncolored pairs and color them all blue to achieve a collection of blue numbers with their sum equal to $s_{0}$.\n\nCase 2. $s_{0} \\leq 2023$. Note that $s \\geq 1+2+\\ldots+592>2023$, thus we have $s_{0}=$ $\\frac{2023 \\cdot 2024}{2}-2 s$, i.e. $s=\\frac{2023 \\cdot 2024}{4}-\\frac{s_{0}}{2}$.\n\nIf $s_{0}>2 \\cdot 593$, at least one of the 593 pairs\n\n$$\n\\left(1, s_{0}-1\\right),\\left(2, s_{0}-2\\right), \\ldots,\\left(593, s_{0}-593\\right)\n$$\n\nhave no red-colored components, so Bob can choose these two numbers and immediately achieve the sum of $s_{0}$. And if $s_{0} \\leq 2 \\cdot 593$, then\n$s=\\frac{2023 \\cdot 2024}{4}-\\frac{s_{0}}{2} \\geq(1432+1433+\\ldots+2023)-593=839+(1434+1435+\\ldots+2023)$,\nhence Alice cannot have colored any of the numbers $1,2, \\ldots, 838$. Then Bob can easily choose one or two of these numbers having the sum of $s_{0}$.", "metadata": {"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl", "problem_match": "\nProblem 4.", "solution_match": "\nSolution."}}
|