year
stringdate 1959-01-01 00:00:00
2025-01-01 00:00:00
⌀ | tier
stringclasses 5
values | problem_label
stringclasses 226
values | problem_type
stringclasses 16
values | exam
stringclasses 28
values | problem
stringlengths 0
10.4k
| solution
stringlengths 0
24.1k
⌀ | metadata
dict |
|---|---|---|---|---|---|---|---|
2024
|
T1
|
5
| null |
USAMO
|
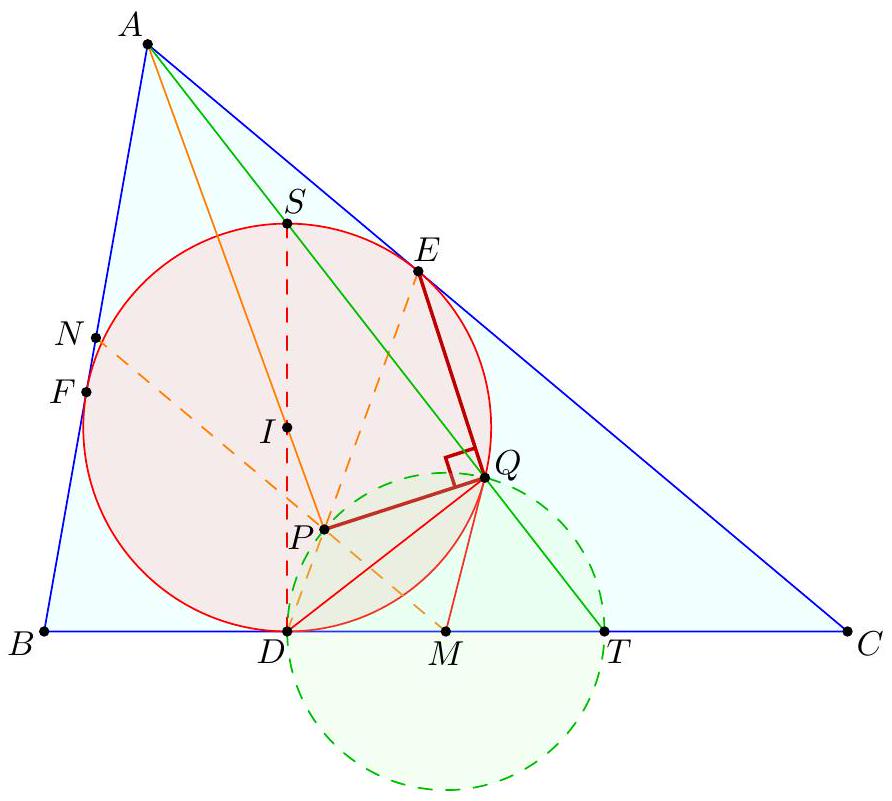
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
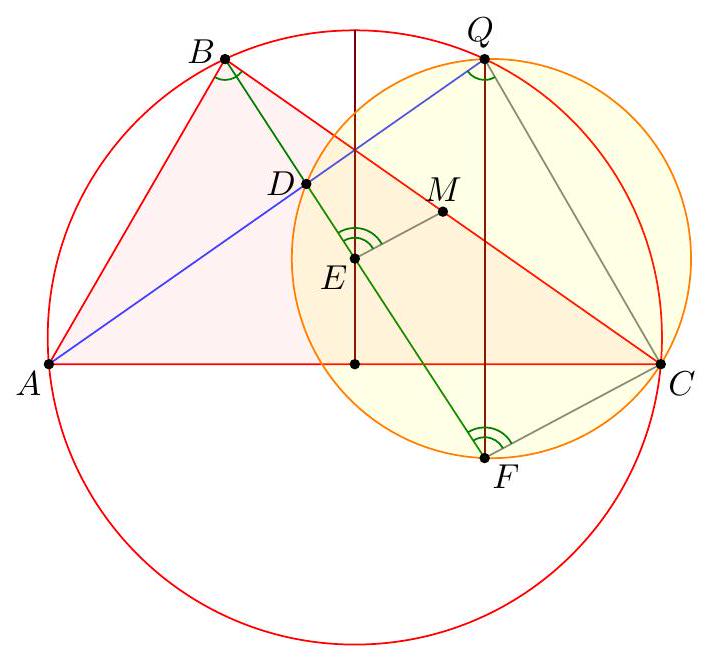 Claim - We have DQCF is cyclic. $$ \begin{aligned} \measuredangle F D C & =-\measuredangle C D B=180^{\circ}-\left(90^{\circ}+\measuredangle C A B\right)=90^{\circ}-\measuredangle C A B \\ & =90^{\circ}-\measuredangle Q C A=\measuredangle F Q C . \end{aligned} $$ To conclude, note that $$ \measuredangle B E M=\measuredangle B F C=\measuredangle D F C=\measuredangle D Q C=\measuredangle A Q C=\measuredangle A B C=\measuredangle A B M . $$ Remark (Motivation). Here is one possible way to come up with the construction of point $F$ (at least this is what led Evan to find it). If one directs all the angles in the obvious way, there are really two points $D$ and $D^{\prime}$ that are possible, although one is outside the triangle; they give corresponding points $E$ and $E^{\prime}$. The circles $B E M$ and $B E^{\prime} M$ must then actually coincide since they are both alleged to be tangent to line $A B$. See the figure below. 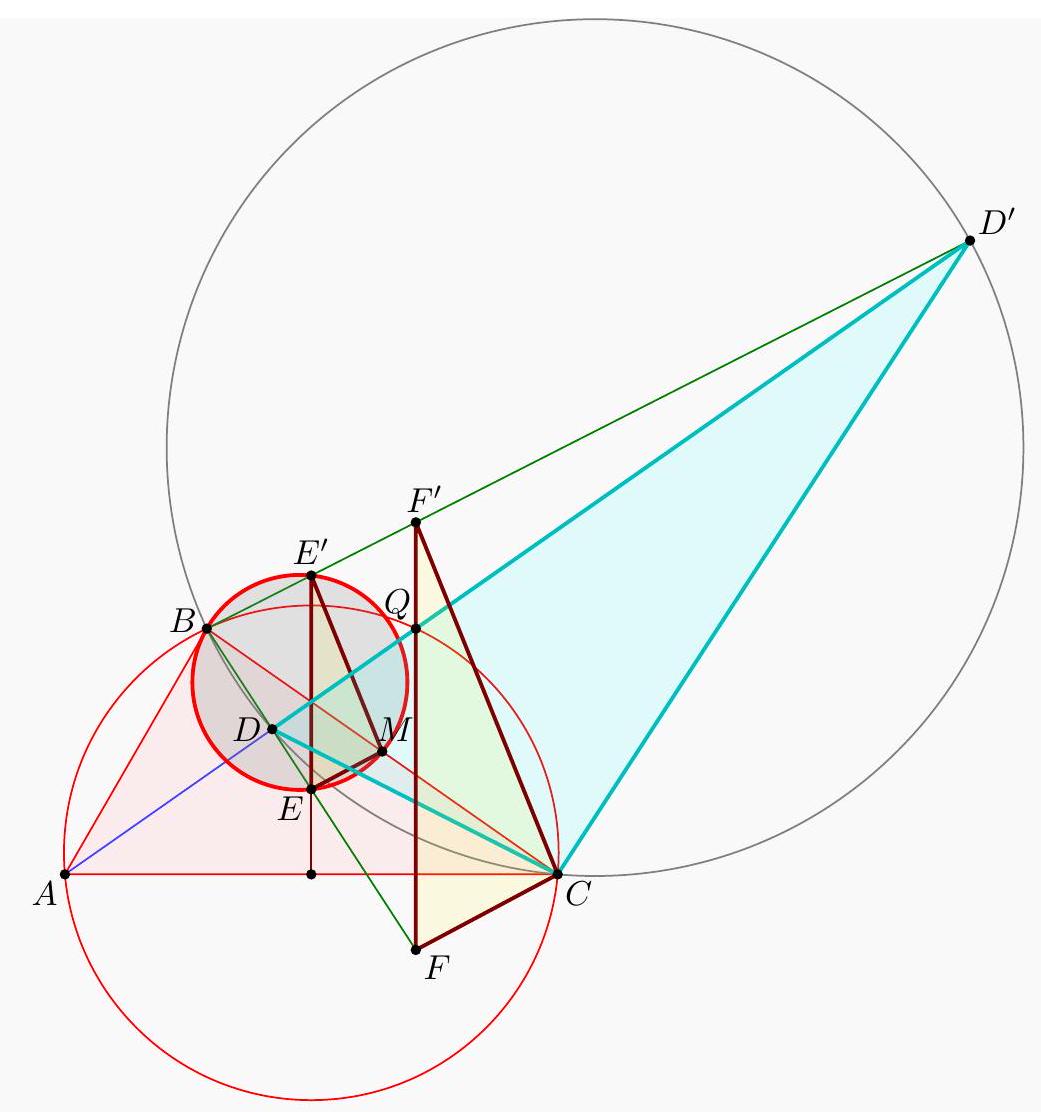 One can already prove using angle chasing that $\overline{A B}$ is tangent to $\left(B E E^{\prime}\right)$. So the point of the problem is to show that $M$ lies on this circle too. However, from looking at the diagram, one may realize that in fact it seems $$ \triangle M E E^{\prime} \stackrel{\triangle}{\sim} \triangle C D D^{\prime} $$ is going to be true from just those marked in the figure (and this would certainly imply the desired concyclic conclusion). Since $M$ is a midpoint, it makes sense to dilate $\triangle E M E^{\prime}$ from $B$ by a factor of 2 to get $\triangle F C F^{\prime}$ so that the desired similarity is actually a spiral similarity at $C$. Then the spiral similarity lemma says that the desired similarity is equivalent to requiring $\overline{D D^{\prime}} \cap \overline{F F^{\prime}}=Q$ to lie on both $(C D F)$ and $\left(C D^{\prime} F^{\prime}\right)$. Hence the key construction and claim from the solution are both discovered naturally, and we find the solution above. (The points $D^{\prime}, E^{\prime}, F^{\prime}$ can then be deleted to hide the motivation.) I A Menelaus-based approach (Kevin Ren). Let $P$ be on $\overline{B C}$ with $A P=P C$. Let $Y$ be the point on line $A B$ such that $\angle A C Y=90^{\circ}$; as $\angle A Y C=90^{\circ}-A$ it follows $B D Y C$ is cyclic. Let $K=\overline{A P} \cap \overline{C Y}$, so $\triangle A C K$ is a right triangle with $P$ the midpoint of its hypotenuse. 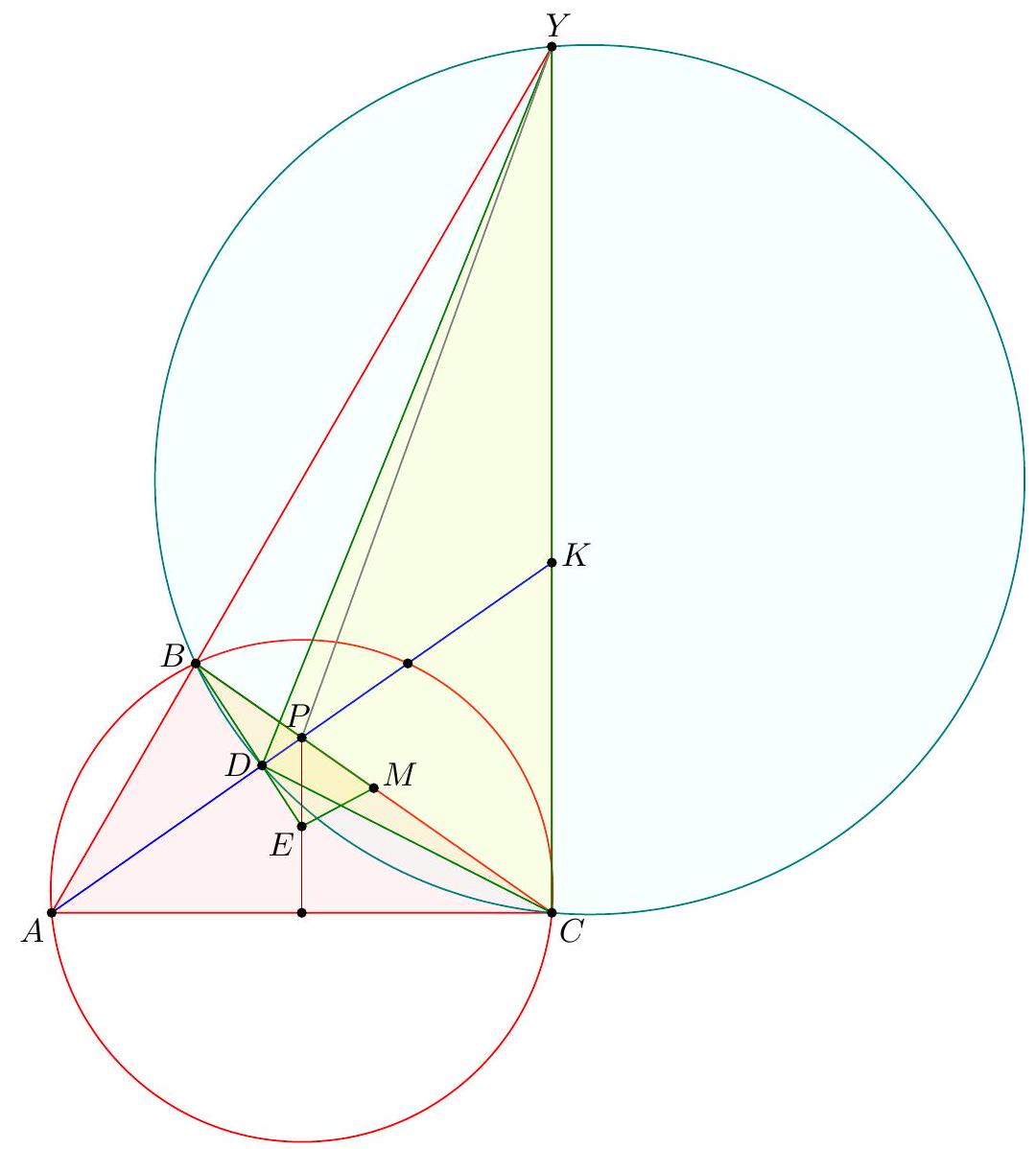 Claim - Triangles $B P E$ and $D Y K$ are similar. Claim - Triangles $B E M$ and $Y D C$ are similar. $$ \frac{B P}{B C} \frac{Y C}{Y K} \frac{A K}{A P}=1 $$ Since $A K / A P=2$ (note that $P$ is the midpoint of the hypotenuse of right triangle $A C K)$ and $B C=2 B M$, this simplifies to $$ \frac{B P}{B M}=\frac{Y K}{Y C} $$ To finish, note that $$ \measuredangle D B A=\measuredangle D B Y=\measuredangle D C Y=\measuredangle B M E $$ implying the desired tangency. 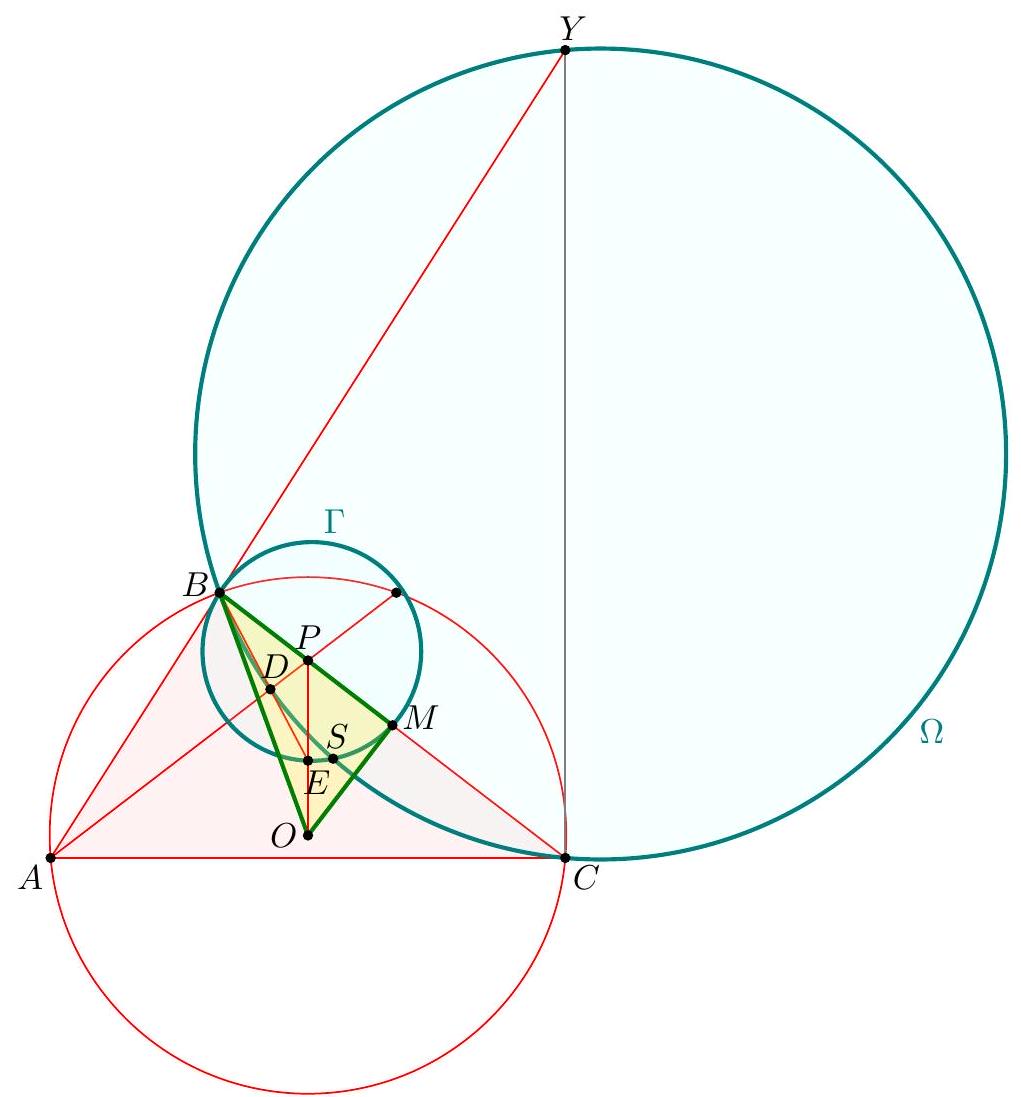 Denote by $S$ the second intersection of $\Gamma$ and $\Omega$. The main idea behind is to consider the spiral similarity $$ \Psi: \Omega \rightarrow \Gamma \quad C \mapsto M \text { and } Y \mapsto B $$ centered at $S$ (due to the spiral similarity lemma), and show that $\Psi(D)=E$. The spiral similarity lemma already promises $\Psi(D)$ lies on line $B D$. Claim - We have $\Psi(A)=O$, the circumcenter of $A B C$. Claim - $\Psi$ maps line $A D$ to line $O P$. $$ \measuredangle(\overline{A D}, \overline{O P})=\measuredangle A P O=\measuredangle O P C=\measuredangle Y C P=\measuredangle(\overline{Y C}, \overline{B M}) $$ As $\Psi$ maps line $Y C$ to line $B M$ and $\Psi(A)=O$, we're done. Hence $\Psi(D)$ should not only lie on $B D$ but also line $O P$. This proves $\Psi(D)=E$, so $E \in \Gamma$ as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2024
|
T1
|
6
| null |
USAMO
|
Let $n>2$ be an integer and let $\ell \in\{1,2, \ldots, n\}$. A collection $A_{1}, \ldots, A_{k}$ of (not necessarily distinct) subsets of $\{1,2, \ldots, n\}$ is called $\ell$-large if $\left|A_{i}\right| \geq \ell$ for all $1 \leq i \leq k$. Find, in terms of $n$ and $\ell$, the largest real number $c$ such that the inequality $$ \sum_{i=1}^{k} \sum_{j=1}^{k} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right| \cdot\left|A_{j}\right|} \geq c\left(\sum_{i=1}^{k} x_{i}\right)^{2} $$ holds for all positive integer $k$, all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{k}$, and all $\ell$-large collections $A_{1}, A_{2}, \ldots, A_{k}$ of subsets of $\{1,2, \ldots, n\}$.
|
The answer turns out to be $$ c=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ 【 Rewriting as a dot product. For $i=1, \ldots, n$ define $\mathbf{v}_{i}$ by $$ \mathbf{v}_{i}[p, q]:=\left\{\begin{array}{ll} \frac{1}{\left|A_{i}\right|} & p \in A_{i} \text { and } q \in A_{i} \\ 0 & \text { otherwise; } \end{array} \quad \mathbf{v}:=\sum_{i} x_{i} \mathbf{v}_{i}\right. $$ Then $$ \begin{aligned} \sum_{i} \sum_{j} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right|\left|A_{j}\right|} & =\sum_{i} \sum_{j} x_{i} x_{j}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle \\ & =\left\langle\sum_{i} x_{i} \mathbf{v}_{i}, \sum_{j} x_{i} \mathbf{v}_{i}\right\rangle=\left\|\sum_{i} x_{i} \mathbf{v}_{i}\right\|^{2}=\|\mathbf{v}\|^{2} . \end{aligned} $$ $$ \begin{aligned} & \langle\mathbf{e}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{e}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i} \\ & \langle\mathbf{1}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{1}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i}\left|A_{i}\right| . \end{aligned} $$ That means for any positive real constants $\alpha$ and $\beta$, by Cauchy-Schwarz for vectors, we should have $$ \begin{aligned} \|\alpha \mathbf{e}+\beta \mathbf{1}\|\|\mathbf{v}\| & \geq\langle\alpha \mathbf{e}+\beta \mathbf{1}, \mathbf{v}\rangle=\alpha\langle\mathbf{e}, \mathbf{v}\rangle+\beta\langle\mathbf{1}, \mathbf{v}\rangle \\ & =\alpha \cdot \sum x_{i}+\beta \cdot \sum x_{i}\left|A_{i}\right| \\ & \geq(\alpha+\ell \beta) \sum x_{i} . \end{aligned} $$ Set $\mathbf{w}:=\alpha \mathbf{e}+\beta \mathbf{1}$ for brevity. Then $$ \mathbf{w}[p, q]= \begin{cases}\alpha+\beta & \text { if } p=q \\ \beta & \text { if } p \neq q\end{cases} $$ SO $$ \|\mathbf{w}\|=\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}} $$ Therefore, we get an lower bound $$ \frac{\|\mathbf{v}\|}{\sum x_{i}} \geq \frac{\alpha+\ell \beta}{\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}}} $$ Letting $\alpha=n-\ell$ and $\beta=\ell-1$ gives a proof that the constant $$ c=\frac{((n-\ell)+\ell(\ell-1))^{2}}{n \cdot(n-1)^{2}+\left(n^{2}-n\right) \cdot(\ell-1)^{2}}=\frac{\left(n+\ell^{2}-2 \ell\right)^{2}}{n(n-1)\left(n+\ell^{2}-2 \ell\right)}=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ makes the original inequality always true. (The choice of $\alpha: \beta$ is suggested by the example below.) 【 Example showing this $c$ is best possible. Let $k=\binom{n}{\ell}$, let $A_{i}$ run over all $\binom{n}{\ell}$ subsets of $\{1, \ldots, n\}$ of size $\ell$, and let $x_{i}=1$ for all $i$. We claim this construction works. To verify this, it would be sufficient to show that $\mathbf{w}$ and $\mathbf{v}$ are scalar multiples, so that the above Cauchy-Schwarz is equality. However, we can compute $$ \mathbf{w}[p, q]=\left\{\begin{array}{ll} n-1 & \text { if } p=q \\ \ell-1 & \text { if } p \neq q \end{array}, \quad \mathbf{v}[p, q]= \begin{cases}\binom{n-1}{\ell-1} \cdot \frac{1}{\ell} & \text { if } p=q \\ \binom{n-2}{\ell-2} \cdot \frac{1}{\ell} & \text { if } p \neq q\end{cases}\right. $$ which are indeed scalar multiples, finishing the proof.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2025
|
T1
|
1
| null |
USAMO
|
Fix positive integers \(k\) and \(d\) . Prove that for all sufficiently large odd positive integers \(n\) , the digits of the base-2 \(n\) representation of \(n^{k}\) are all greater than \(d\) .
|
The problem actually doesn't have much to do with digits: the idea is to pick any length \(\ell \leq k\) , and look at the rightmost \(\ell\) digits of \(n^{k}\) ; that is, the remainder upon division by \((2n)^{\ell}\) . We compute it exactly:
Claim — Let \(n \geq 1\) be an odd integer, and \(k \geq \ell \geq 1\) integers. Then
\[n^{k} \bmod (2n)^{i} = c(k, \ell) \cdot n^{i}\]
for some odd integer \(1 \leq c(k, \ell) \leq 2^{\ell} - 1\) .
Proof. This follows directly by the Chinese remainder theorem, with \(c(k, \ell)\) being the residue class of \(n^{k - i} \pmod{2^{\ell}}\) (which makes sense because \(n\) was odd). \(\square\)
We can now stake the required threshold:
Claim — The problem statement holds once \(n \geq (d + 1) \cdot 2^{k - 1}\) .
Proof. Suppose \(n\) is that large. Then \(n^{k}\) has \(k\) digits in base- \(2n\) . Moreover, for each \(1 \leq \ell \leq k\) we have
\[c(k, \ell) \cdot n^{\ell} \geq (d + 1) \cdot (2n)^{\ell - 1}\]
because \(n\) is large enough; that implies the \(\ell^{\mathrm{th}}\) digit from the right is at least \(d + 1\) . Hence the problem is solved. \(\square\)
Remark. Note it doesn't really matter that \(c(k, i)\) is odd per se; we only need that \(c(k, i) \geq 1\) .
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "1. ",
"solution_match": "## \\(\\S 1.1\\) USAMO 2025/1, proposed by John Berman \n"
}
|
2025
|
T1
|
2
| null |
USAMO
|
Let \(n > k \geq 1\) be integers. Let \(P(x) \in \mathbb{R}[x]\) be a polynomial of degree \(n\) with no repeated roots and \(P(0) \neq 0\) . Suppose that for any real numbers \(a_0, \ldots , a_k\) such that the polynomial \(a_k x^k + \dots + a_1 x + a_0\) divides \(P(x)\) , the product \(a_0 a_1 \ldots a_k\) is zero. Prove that \(P(x)\) has a nonreal root.
|
By considering any \(k + 1\) of the roots of \(P\) , we may as well assume WLOG that \(n = k + 1\) . Suppose that \(P(x) = (x + r_{1})\ldots (x + r_{n})\in \mathbb{R}[x]\) has \(P(0)\neq 0\) . Then the problem hypothesis is that each of the \(n\) polynomials (of degree \(n - 1\) ) given by
\[P_{1}(x) = (x + r_{2})(x + r_{3})(x + r_{4})\ldots (x + r_{n})\] \[P_{2}(x) = (x + r_{1})(x + r_{3})(x + r_{4})\ldots (x + r_{n})\] \[P_{3}(x) = (x + r_{1})(x + r_{2})(x + r_{4})\ldots (x + r_{n})\] \[\vdots\] \[P_{n}(x) = (x + r_{1})(x + r_{2})(x + r_{3})\ldots (x + r_{n - 1})\]
has at least one coefficient equal to zero. (Explicitly, \(P_{i}(x) = \frac{P(x)}{x + r_{i}}\) .) We'll prove that at least one \(r_{i}\) is not real.
Obviously the leading and constant coefficients of each \(P_{i}\) are nonzero, and there are \(n - 2\) other coefficients to choose between. So by pigeonhole principle, we may assume, say, that \(P_{1}\) and \(P_{2}\) share the position of a zero coefficient, say the \(x^{k}\) one, for some \(1\leq k< n - 1\)
Claim — If \(P_{1}\) and \(P_{2}\) both have \(x^{k}\) coefficient equal to zero, then the polynomial
\[Q(x) = (x + r_{3})(x + r_{4})\ldots (x + r_{n})\]
has two consecutive zero coefficients, namely \(b_{k} = b_{k - 1} = 0\)
Proof. Invoking Vieta formulas, suppose that
\[Q(x) = x^{n - 2} + b_{n - 3}x^{n - 3} + \dots +b_{0}.\]
(And let \(b_{n - 2} = 1\) .) Then the fact that the \(x^{k}\) coefficient of \(P_{1}\) and \(P_{2}\) are both zero means
\[r_{1}b_{k} + b_{k - 1} = r_{2}b_{k} + b_{k - 1} = 0\]
and hence that \(b_{k} = b_{k - 1} = 0\) (since the \(r_{i}\) are nonzero).
To solve the problem, we use:
## Lemma
If \(F(x)\in \mathbb{R}[x]\) is a polynomial with two consecutive zero coefficients, it cannot have all distinct real roots.
Here are two possible proofs of the lemma I know (there are more).
First proof using Rolle's theorem. Say \(x^{t}\) and \(x^{t + 1}\) coefficients of \(F\) are both zero.
Assume for contradiction all the roots of \(F\) are real and distinct. Then by Rolle's theorem, every higher- order derivative of \(F\) should have this property too. However, the \(t\) th order derivative of \(F\) has a double root of 0, contradiction. \(\square\)
Second proof using Descartes rule of signs. The number of (nonzero) roots of \(F\) is bounded above by the number of sign changes of \(F(x)\) (for the positive roots) and the number of sign changes of \(F(- x)\) (for the negative roots). Now consider each pair of consecutive nonzero coefficients in \(F\) , say \(x x^{i}\) and \(x x^{j}\) for \(i > j\) .
- If \(i - j = 1\) , then this sign change will only count for one of \(F(x)\) or \(F(-x)\)
- If \(i - j \geq 2\) , then the sign change could count towards both \(F(x)\) or \(F(-x)\) (i.e. counted twice), but also there is at least one zero coefficient between them.
Hence if \(b\) is the number of nonzero coefficients of \(F\) , and \(z\) is the number of consecutive runs of zero coefficients of \(F\) , then the number of real roots is bounded above by
\[1\cdot (b - 1 - z) + 2\cdot z = b - 1 + z\leq \deg F.\]
However, if \(F\) has two consecutive zero coefficients, then the inequality is strict. \(\square\)
Remark. The final claim has appeared before apparently in the HUST Team Selection Test for the Vietnamese Math Society's undergraduate olympiad; see https://aops.com/ community/p33893374 for citation.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "2. ",
"solution_match": "## \\(\\S 1.2\\) USAMO 2025/2, proposed by Carl Schildkraut \n"
}
|
2025
|
T1
|
3
| null |
USAMO
|
Alice the architect and Bob the builder play a game. First, Alice chooses two points \(P\) and \(Q\) in the plane and a subset \(S\) of the plane, which are announced to Bob. Next, Bob marks infinitely many points in the plane, designating each a city. He may not place two cities within distance at most one unit of each other, and no three cities he places may be collinear. Finally, roads are constructed between the cities as follows: each pair \(A\) , \(B\) of cities is connected with a road along the line segment \(AB\) if and only if the following condition holds:
For every city \(C\) distinct from \(A\) and \(B\) , there exists \(R \in S\) such that
\(\triangle PQR\) is directly similar to either \(\triangle ABC\) or \(\triangle BAC\) .
Alice wins the game if (i) the resulting roads allow for travel between any pair of cities via a finite sequence of roads and (ii) no two roads cross. Otherwise, Bob wins. Determine, with proof, which player has a winning strategy.
|
The answer is that Alice wins. Let's define a Bob- set \(V\) to be a set of points in the plane with no three collinear and with all distances at least 1. The point of the problem is to prove the following fact.
Claim — Given a Bob- set \(V\subseteq \mathbb{R}^{2}\) , consider the Bob- graph with vertex set \(V\) defined as follows: draw edge \(ab\) if and only if the disk with diameter \(\overline{ab}\) contains no other points of \(V\) on or inside it. Then the Bob- graph is (i) connected, and (ii) planar.
Proving this claim shows that Alice wins since Alice can specify \(S\) to be the set of points outside the disk of diameter \(PQ\) .
Proof that every Bob- graph is connected. Assume for contradiction the graph is disconnected. Let \(p\) and \(q\) be two points in different connected components. Since \(pq\) is not an edge, there exists a third point \(r\) inside the disk with diameter \(\overline{pq}\) .
Hence, \(r\) is in a different connected component from at least one of \(p\) or \(q\) — let's say point \(p\) . Then we repeat the same argument on the disk with diameter \(\overline{pr}\) to find a new point \(s\) , non- adjacent to either \(p\) or \(r\) . See the figure below, where the \(X\) 'ed out dashed edges indicate points which are not only non- adjacent but in different connected components.

In this way we generate an infinite sequence of distances \(\delta_{1}\) , \(\delta_{2}\) , \(\delta_{3}\) , ... among the non- edges in the picture above. By the "Pythagorean theorem" (or really the inequality for it), we have
\[\delta_{i}^{2}\leq \delta_{i - 1}^{2} - 1\]
and this eventually generates a contradiction for large \(i\) , since we get \(0 \leq \delta_{i}^{2} \leq \delta_{1}^{2} - (i - 1)\) . \(\square\)
Proof that every Bob- graph is planar. Assume for contradiction edges \(ac\) and \(bd\) meet, meaning \(abcd\) is a convex quadrilateral. WLOG assume \(\angle bad \geq 90^{\circ}\) (each quadrilateral has an angle at least \(90^{\circ}\) ). Then the disk with diameter \(\overline{bd}\) contains \(a\) , contradiction. \(\square\)
Remark. In real life, the Bob- graph is actually called the Gabriel graph. Note that we never require the Bob- set to be infinite; the solution works unchanged for finite Bob- sets.
However, there are approaches that work for finite Bob- sets that don't work for infinite sets, such as the relative neighbor graph, in which one joins \(a\) and \(b\) iff there is no \(c\) such that \(d(a,b) \leq \max \{d(a,c),d(b,c)\}\) . In other words, edges are blocked by triangles where \(ab\) is the longest edge (rather than by triangles where \(ab\) is the longest edge of a right or obtuse triangle as in the Gabriel graph).
The relative neighbor graph has fewer edges than the Gabriel graph, so it is planar too. When the Bob- set is finite, the relative distance graph is still connected. The same argument above works where the distances now satisfy
\[\delta_{1} > \delta_{2} > \ldots\]
instead, and since there are finitely many distances one arrives at a contradiction.
However for infinite Bob- sets the descending condition is insufficient, and connectedness actually fails altogether. A counterexample (communicated to me by Carl Schildkraut) is to start by taking \(A_{n} \approx (2n,0)\) and \(B_{n} \approx (2n + 1,\sqrt{3})\) for all \(n \geq 1\) , then perturb all the points slightly so that
\[B_{1}A_{1} > A_{1}A_{2} > A_{2}B_{1} > B_{1}B_{2} > B_{2}A_{2\] \[> A_{2}A_{3} > A_{3}B_{2} > B_{2}B_{3} > B_{3}A_{3\] \[> \dots\]
A cartoon of the graph is shown below.

In that case, \(\{A_{n}\}\) and \(\{B_{n}\}\) will be disconnected from each other: none of the edges \(A_{n}B_{n}\) or \(B_{n}A_{n + 1}\) are formed. In this case the relative neighbor graph consists of the edges \(A_{1}A_{2}A_{3}A_{4}\dots\) and \(B_{1}B_{2}B_{3}B_{4}\dots\) . That's why for the present problem, the inequality
\[\delta_{i}^{2}\leq \delta_{i - 1}^{2} - 1\]
plays such an important role, because it causes the (squared) distances to decrease appreciably enough to give the final contradiction.
## \(\S 2\) Solutions to Day 2
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "3. ",
"solution_match": "## \\(\\S 1.3\\) USAMO 2025/3, proposed by Carl Schildkraut \n"
}
|
2025
|
T1
|
4
| null |
USAMO
|
Let \(H\) be the orthocenter of an acute triangle \(ABC\) , let \(F\) be the foot of the altitude from \(C\) to \(AB\) , and let \(P\) be the reflection of \(H\) across \(BC\) . Suppose that the circumcircle of triangle \(AFP\) intersects line \(BC\) at two distinct points \(X\) and \(Y\) . Prove that \(CX = CY\) .
|
Let \(Q\) be the antipode of \(B\) .
Claim — \(AHQC\) is a parallelogram, and \(APCQ\) is an isosceles trapezoid.
Proof. As \(\overline{AH} \perp \overline{BC} \perp \overline{CQ}\) and \(\overline{CF} \perp \overline{AB} \perp \overline{AQ}\) .

Let \(M\) be the midpoint of \(\overline{QC}\) .
Claim — Point \(M\) is the circumcenter of \(\triangle AFP\) .
Proof. It's clear that \(MA = MP\) from the isosceles trapezoid. As for \(MA = MF\) , let \(N\) denote the midpoint of \(\overline{AF}\) ; then \(\overline{MN}\) is a midline of the parallelogram, so \(\overline{MN} \perp \overline{AF}\) . \(\square\)
Since \(\overline{CM} \perp \overline{BC}\) and \(M\) is the center of \((AFP)\) , it follows \(CX = CY\) .
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "4. ",
"solution_match": "## \\(\\S 2.1\\) USAMO 2025/4, proposed by Carl Schildkraut \n"
}
|
2025
|
T1
|
5
| null |
USAMO
|
Find all positive integers \(k\) such that: for every positive integer \(n\) , the sum
\[\binom{n}{0}^{k} + \binom{n}{1}^{k} + \dots +\binom{n}{n}^{k}\]
is divisible by \(n + 1\) .
|
The answer is all even \(k\) .
Let's abbreviate \(S(n) := \binom{n}{0}^{k} + \dots + \binom{n}{n}^{k}\) for the sum in the problem.
\(\P\) Proof that even \(k\) is necessary. Choose \(n = 2\) . We need \(3 \mid S(2) = 2 + 2^{k}\) , which requires \(k\) to be even.
Remark. It's actually not much more difficult to just use \(n = p - 1\) for prime \(p\) , since \(\binom{p- 1}{i} \equiv (- 1)^{i} \pmod{p}\) . Hence \(S(p- 1) \equiv 1 + (- 1)^{k} + 1 + (- 1)^{k} + \dots + 1 \pmod{p}\) , and this also requires \(k\) to be even. This special case is instructive in figuring out the proof to follow.
\(\P\) Proof that \(k\) is sufficient. From now on we treat \(k\) as fixed, and we let \(p^{e}\) be a prime fully dividing \(n + 1\) . The basic idea is to reduce from \(n + 1\) to \((n + 1) / p\) by an induction.
Remark. Here is a concrete illustration that makes it clear what's going on. Let \(p = 5\) . When \(n = p - 1 = 4\) , we have
\[S(4) = 1^{k} + 4^{k} + 6^{k} + 4^{k} + 1^{k} \equiv 1 + 1 + 1 + 1 + 1 \equiv 0 \pmod{5}.\]
When \(n = p^{2} - 1 = 24\) , the 25 terms of \(S(24)\) in order are, modulo 25,
\[S(24)\equiv 1^{k}+1^{k}+1^{k}+1^{k}+1^{k}\] \[\qquad+4^{k}+4^{k}+4^{k}+4^{k}+4^{k}\] \[\qquad+6^{k}+6^{k}+6^{k}+6^{k}+6^{k}\] \[\qquad+4^{k}+4^{k}+4^{k}+4^{k}+4^{k}\] \[\qquad+1^{k}+1^{k}+1^{k}+1^{k}+1^{k}\] \[\qquad=5(1^{k}+4^{k}+6^{k}+4^{k}+1^{k}).\]
The point is that \(S(24)\) has five copies of \(S(4)\) , modulo 25.
To make the pattern in the remark explicit, we prove the following lemma on each individual binomial coefficient.
## Lemma 2.1
Suppose \(p^{e}\) is a prime power which fully divides \(n + 1\) . Then
\[\binom{n}{i}\equiv\pm\binom{\frac{n+1}{p}-1}{\lfloor i/p\rfloor}\pmod{p^{e}}.\]
Proof of lemma. It's easiest to understand the proof by looking at the cases \(\lfloor i / p\rfloor \in\) \(\{0,1,2\}\) first.
For \(0\leq i< p\) , since \(n\equiv - 1\) mod \(p^{e}\) , we have
\[\binom{n}{i}=\frac{n(n-1)\ldots(n-i+1)}{1\cdot2\cdot\cdots\cdot i}\equiv\frac{(-1)(-2)\ldots(-i)}{1\cdot2\cdot\cdots\cdot i}\equiv\pm 1\pmod{p^{e}}.\]
For \(p\leq i< 2p\) we have
\[\binom{n}{i}\equiv\pm 1\cdot\frac{n-p+1}{p}\cdot\frac{(n-p)(n-p-1)\ldots(n-i+1)}{(p+1)(p+2)\ldots i}\] \[\qquad\equiv\pm 1\cdot\frac{\frac{n-p+1}{p}\cdot\pm 1}{1}\] \[\qquad\equiv\pm\binom{\frac{n+1}{p}-1}{1}\pmod{p^{e}}.\]
For \(2p\leq i< 3p\) the analogous reasoning gives
\[\binom{n}{i}\equiv\pm 1\cdot\frac{n-p+1}{p}\cdot\pm 1\cdot\frac{n-2p+1}{2p}\cdot\pm 1\] \[\qquad\equiv\pm\frac{\binom{n+1}{p}-1}{1\cdot2}\binom{\frac{n+1}{p}-2}{2}\] \[\qquad\equiv\pm\binom{\frac{n+1}{p}-1}{2}\pmod{p^{e}}.\]
And so on. The point is that in general, if we write
\[\binom{n}{i}=\prod_{1\leq j\leq i}\frac{n-(j-1)}{j}\]
then the fractions for \(p\nmid j\) are all \(\pm 1\) (mod \(p^{e}\) ). So only considers those \(j\) with \(p\mid j\) ; in that case one obtains the claimed \(\binom{\frac{n+1}{p}-1}{\lfloor i/p\rfloor}\) exactly (even without having to take modulo \(p^{e}\) ). \(\square\)
From the lemma, it follows if \(p^{e}\) is a prime power which fully divides \(n + 1\) , then
\[S(n)\equiv p\cdot S\left(\frac{n + 1}{p} -1\right)\pmod{p^{e}}\]
by grouping the \(n + 1\) terms (for \(0\leq i\leq n\) ) into consecutive ranges of length \(p\) (by the value of \(\lfloor i / p\rfloor\) ).
Remark. Actually, with the exact same proof (with better \(\pm\) bookkeeping) one may show that
\[n + 1\mid \sum_{i = 0}^{n}\left((-1)^{i}\binom{n}{i}\right)^{k}\]
holds for all nonnegative integers \(k\) , not just \(k\) even. So in some sense this result is more natural than the one in the problem statement.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "5. ",
"solution_match": "## \\(\\S 2.2\\) USAMO 2025/5, proposed by John Berman \n"
}
|
2025
|
T1
|
6
| null |
USAMO
|
Let \(m\) and \(n\) be positive integers with \(m \geq n\) . There are \(m\) cupcakes of different flavors arranged around a circle and \(n\) people who like cupcakes. Each person assigns a nonnegative real number score to each cupcake, depending on how much they like the cupcake. Suppose that for each person \(P\) , it is possible to partition the circle of \(m\) cupcakes into \(n\) groups of consecutive cupcakes so that the sum of \(P\) 's scores of the cupcakes in each group is at least 1. Prove that it is possible to distribute the \(m\) cupcakes to the \(n\) people so that each person \(P\) receives cupcakes of total score at least 1 with respect to \(P\) .
|
Arbitrarily pick any one person — call her Pip — and her \(n\) arcs. The initial idea is to try to apply Hall's marriage lemma to match the \(n\) people with Pip's arcs (such that each such person is happy with their matched arc). To that end, construct the obvious bipartite graph \(\mathfrak{G}\) between the people and the arcs for Pip.
We now consider the following algorithm, which takes several steps.
- If a perfect matching of \(\mathfrak{G}\) exists, we're done!- We're probably not that lucky. Per Hall's condition, this means there is a bad set \(B_{1}\) of people, who are compatible with fewer than \(|B_{1}|\) of the arcs. Then delete \(B_{1}\) and the neighbors of \(B_{1}\) , then try to find a matching on the remaining graph.- If a matching exists now, terminate the algorithm. Otherwise, that means there's another bad set \(B_{2}\) for the remaining graph. We again delete \(B_{2}\) and the fewer than \(B_{2}\) neighbors.- Repeat until some perfect matching \(\mathcal{M}\) is possible in the remaining graph, i.e. there are no more bad sets (and then terminate once that occurs). Since Pip is a universal vertex, it's impossible to delete Pip, so the algorithm does indeed terminate with nonempty \(\mathcal{M}\) .
A cartoon of this picture is shown below.

We commit to assigning each of person in \(\mathcal{M}\) their matched arc (in particular if there are no bad sets at all, the problem is already solved). Now we finish the problem by induction on \(n\) (for the remaining people) by simply deleting the arcs used up by \(\mathcal{M}\) .
To see why this deletion- induction works, consider any particular person Quinn not in \(\mathcal{M}\) . By definition, Quinn is not happy with any of the arcs in \(\mathcal{M}\) . So when an arc \(\mathcal{A}\) of \(\mathcal{M}\) is deleted, it had value less than 1 for Quinn so in particular it couldn't contain entirely any of Quinn's arcs. Hence at most one endpoint among Quinn's arcs was in the deleted arc \(\mathcal{A}\) . When this happens, this causes two arcs of Quinn to merge, and the merged value is
\[(\geq 1) + (\geq 1) - (\leq 1)\qquad \geq \qquad 1\]
meaning the induction is OK. See below for a cartoon of the deletion, where Pip's arcs are drawn in blue while Quinn's arcs and scores are drawn in red (in this example \(n = 3\) ).

Remark. This deletion argument can be thought of in some special cases even before the realization of Hall, in the case where \(\mathcal{M}\) has only one person (Pip). This amounts to saying that if one of Pip's arcs isn't liked by anybody, then that arc can be deleted and the induction carries through.
Remark. Conversely, it should be reasonable to expect Hall's theorem to be helpful even before finding the deletion argument. While working on this problem, one of the first things I said was:
"We should let Hall do the heavy lifting for us: find a way to make \(n\) groups that satisfy Hall's condition, rather than an assignment of \(n\) groups to \(n\) people."
As a general heuristic, for any type of "compatible matching" problem, Hall's condition is usually the go- to tool. (It is much easier to verify Hall's condition than actually find the matching yourself.) Actually in most competition problems, if one realizes one is in a Hall setting, one is usually close to finishing the problem. This is a relatively rare example in which one needs an additional idea to go alongside Hall's theorem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2025-notes.jsonl",
"problem_match": "6. ",
"solution_match": "## \\(\\S 2.3\\) USAMO 2025/6, proposed by Cheng-Yin Chang and Hung-Hsun Yu \n"
}
|
2014
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be an acute triangle, and let $X$ be a variable interior point on the minor $\operatorname{arc} B C$ of its circumcircle. Let $P$ and $Q$ be the feet of the perpendiculars from $X$ to lines $C A$ and $C B$, respectively. Let $R$ be the intersection of line $P Q$ and the perpendicular from $B$ to $A C$. Let $\ell$ be the line through $P$ parallel to $X R$. Prove that as $X$ varies along minor arc $B C$, the line $\ell$ always passes through a fixed point.
|
The fixed point is the orthocenter, since $\ell$ is a Simson line. See Lemma 4.4 of Euclidean Geometry in Math Olympiads.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2014
|
T0
|
2
| null |
USA_TST
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of integers, with the property that every consecutive group of $a_{i}$ 's averages to a perfect square. More precisely, for all positive integers $n$ and $k$, the quantity $$ \frac{a_{n}+a_{n+1}+\cdots+a_{n+k-1}}{k} $$ is always the square of an integer. Prove that the sequence must be constant (all $a_{i}$ are equal to the same perfect square).
|
Let $\nu_{p}(n)$ denote the largest exponent of $p$ dividing $n$. The problem follows from the following proposition. ## Proposition Let $\left(a_{n}\right)$ be a sequence of integers and let $p$ be a prime. Suppose that every consecutive group of $a_{i}$ 's with length at most $p$ averages to a perfect square. Then $\nu_{p}\left(a_{i}\right)$ is independent of $i$. We proceed by induction on the smallest value of $\nu_{p}\left(a_{i}\right)$ as $i$ ranges (which must be even, as each of the $a_{i}$ are themselves a square). First we prove two claims. Claim - If $j \equiv k(\bmod p)$ then $a_{j} \equiv a_{k}(\bmod p)$. Claim - If some $a_{i}$ is divisible by $p$ then all of them are. $$ S_{n}=a_{1}+a_{2}+\cdots+a_{n} \equiv a_{2}+\cdots+a_{n} \quad(\bmod p) $$ Call an integer $k$ with $2 \leq k<p$ a pivot if $1-k^{-1}$ is a quadratic nonresidue modulo $p$. We claim that for any pivot $k, S_{k} \equiv 0(\bmod p)$. If not, then $$ \frac{a_{1}+a_{2}+\cdots+a_{k}}{k} \text { and } \frac{a_{2}+\cdots+a_{k}}{k-1} $$ are both qudaratic residues. Division implies that $\frac{k-1}{k}=1-k^{-1}$ is a quadratic residue, contradiction. Next we claim that there is an integer $m$ with $S_{m} \equiv S_{m+1} \equiv 0(\bmod p)$, which implies $p \mid a_{m+1}$. If 2 is a pivot, then we simply take $m=1$. Otherwise, there are $\frac{1}{2}(p-1)$ pivots, one for each nonresidue (which includes neither 0 nor 1 ), and all pivots lie in [3, $p-1]$, so we can find an $m$ such that $m$ and $m+1$ are both pivots. Repeating this procedure starting with $a_{m+1}$ shows that $a_{2 m+1}, a_{3 m+1}, \ldots$ must all be divisible by $p$. Combined with the first claim and the fact that $m<p$, we find that all the $a_{i}$ are divisible by $p$. The second claim establishes the base case of our induction. Now assume all $a_{i}$ are divisible by $p$ and hence $p^{2}$. Then all the averages in our proposition (with length at $\operatorname{most} p$ ) are divisible by $p$ and hence $p^{2}$. Thus the map $a_{i} \mapsto \frac{1}{p^{2}} a_{i}$ gives a new sequence satisfying the proposition, and our inductive hypothesis completes the proof. Remark. There is a subtle bug that arises if one omits the condition that $k \leq p$ in the proposition. When $k=p^{2}$ the average $\frac{a_{1}+\cdots+a_{p^{2}}}{p^{2}}$ is not necessarily divisible by $p$ even if all the $a_{i}$ are. Hence it is not valid to divide through by $p$. This is why the condition $k \leq p$ was added.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2014
|
T0
|
3
| null |
USA_TST
|
Let $n$ be an even positive integer, and let $G$ be an $n$-vertex (simple) graph with exactly $\frac{n^{2}}{4}$ edges. An unordered pair of distinct vertices $\{x, y\}$ is said to be amicable if they have a common neighbor (there is a vertex $z$ such that $x z$ and $y z$ are both edges). Prove that $G$ has at least $2\binom{n / 2}{2}$ pairs of vertices which are amicable.
|
First, we prove the following lemma. (https://en.wikipedia.org/wiki/Friendship_ paradox). Lemma (On average, your friends are more popular than you) For a vertex $v$, let $a(v)$ denote the average degree of the neighbors of $v$ (setting $a(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} a(v) \geq \sum_{v} \operatorname{deg} v=2 \# E $$ $$ \begin{aligned} \sum_{v} a(v) & =\sum_{v} \frac{\sum_{w \sim v} \operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{v} \sum_{w \sim v} \frac{\operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{\text {edges } v w}\left(\frac{\operatorname{deg} w}{\operatorname{deg} v}+\frac{\operatorname{deg} v}{\operatorname{deg} w}\right) \\ & \stackrel{\text { AM-GM }}{\geq} \sum_{\text {edges } v w} 2=2 \# E=\sum_{v} \operatorname{deg} v \end{aligned} $$ as desired. Corollary (On average, your most popular friend is more popular than you) For a vertex $v$, let $m(v)$ denote the maximum degree of the neighbors of $v$ (setting $m(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} m(v) \geq \sum_{v} \operatorname{deg} v=2 \# E \text {. } $$ We can use this to count amicable pairs by noting that any particular vertex $v$ is in at least $m(v)-1$ amicable pairs. So, the number of amicable pairs is at least $$ \frac{1}{2} \sum_{v}(m(v)-1) \geq \# E-\frac{1}{2} \# V $$ Note that up until now we haven't used any information about $G$. But now if we plug in $\# E=n^{2} / 4, \# V=n$, then we get exactly the desired answer. (Equality holds for $G=K_{n / 2, n / 2}$.)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2014
|
T0
|
4
| null |
USA_TST
|
Let $n$ be a positive even integer, and let $c_{1}, c_{2}, \ldots, c_{n-1}$ be real numbers satisfying $$ \sum_{i=1}^{n-1}\left|c_{i}-1\right|<1 $$ Prove that $$ 2 x^{n}-c_{n-1} x^{n-1}+c_{n-2} x^{n-2}-\cdots-c_{1} x^{1}+2 $$ has no real roots.
|
We will prove the polynomial is positive for all $x \in \mathbb{R}$. As $c_{i}>0$, the result is vacuous for $x \leq 0$, so we restrict attention to $x>0$. Then letting $c_{i}=1-d_{i}$ for each $i$, the inequality we want to prove becomes $$ x^{n}+1+\frac{x^{n+1}+1}{x+1}>\sum_{1}^{n-1} d_{i} x^{i} \quad \text { given } \sum\left|d_{i}\right|<1 $$ But obviously $x^{n}+1>x^{i}$ for any $1 \leq i \leq n-1$ and $x>0$. So in fact $x^{n}+1>\sum_{1}^{n-1}\left|d_{i}\right| x^{i}$ holds for $x>0$, as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2014
|
T0
|
5
| null |
USA_TST
|
Let $A B C D$ be a cyclic quadrilateral, and let $E, F, G$, and $H$ be the midpoints of $A B, B C, C D$, and $D A$ respectively. Let $W, X, Y$ and $Z$ be the orthocenters of triangles $A H E, B E F, C F G$ and $D G H$, respectively. Prove that the quadrilaterals $A B C D$ and $W X Y Z$ have the same area.
|
We begin with: Claim - Point $W$ has coordinates $\frac{1}{2}(2 a+b+d)$. By symmetry, we have $$ \begin{aligned} w & =\frac{1}{2}(2 a+b+d) \\ x & =\frac{1}{2}(2 b+c+a) \\ y & =\frac{1}{2}(2 c+d+b) \\ z & =\frac{1}{2}(2 d+a+c) . \end{aligned} $$ We see that $w-y=a-c, x-z=b-d$. So the diagonals of $W X Y Z$ have the same length as those of $A B C D$ as well as the same directed angle between them. This implies the areas are equal, too.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2014
|
T0
|
6
| null |
USA_TST
|
For a prime $p$, a subset $S$ of residues modulo $p$ is called a sum-free multiplicative subgroup of $\mathbb{F}_{p}$ if - there is a nonzero residue $\alpha$ modulo $p$ such that $S=\left\{1, \alpha^{1}, \alpha^{2}, \ldots\right\}$ (all considered $\bmod p$ ), and - there are no $a, b, c \in S$ (not necessarily distinct) such that $a+b \equiv c(\bmod p)$. Prove that for every integer $N$, there is a prime $p$ and a sum-free multiplicative subgroup $S$ of $\mathbb{F}_{p}$ such that $|S| \geq N$.
|
We first prove the following general lemma. ## Lemma If $f, g \in \mathbb{Z}[X]$ are relatively prime nonconstant polynomials, then for sufficiently large primes $p$, they have no common root modulo $p$. $$ a(X) f(X)+b(X) g(X) \equiv c $$ So, plugging in $X=r$ we get $p \mid c$, so the set of permissible primes $p$ is finite. With this we can give the construction. ## Claim - Suppose that - $n$ is a positive integer with $n \not \equiv 0(\bmod 3)$; - $p$ is a prime which is $1 \bmod n$; and - $\alpha$ is a primitive $n^{\prime}$ th root of unity modulo $p$. Then $|S|=n$ and, if $p$ is sufficiently large in $n$, is also sum-free. $$ 1+\alpha^{k} \equiv \alpha^{m} \quad(\bmod p) $$ for some integers $k, m \in \mathbb{Z}$. This means $(X+1)^{n}-1$ and $X^{n}-1$ have common root $X=\alpha^{k}$. But $$ \underset{\mathbb{Z}[x]}{\operatorname{gcd}}\left((X+1)^{n}-1, X^{n}-1\right)=1 \quad \forall n \not \equiv 0 \quad(\bmod 3) $$ because when $3 \nmid n$ the two polynomials have no common complex roots. (Indeed, if $|\omega|=|1+\omega|=1$ then $\omega=-\frac{1}{2} \pm \frac{\sqrt{3}}{2} i$.) Thus $p$ is bounded by the lemma, as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be a scalene triangle with incenter $I$ whose incircle is tangent to $\overline{B C}$, $\overline{C A}, \overline{A B}$ at $D, E, F$, respectively. Denote by $M$ the midpoint of $\overline{B C}$ and let $P$ be a point in the interior of $\triangle A B C$ so that $M D=M P$ and $\angle P A B=\angle P A C$. Let $Q$ be a point on the incircle such that $\angle A Q D=90^{\circ}$. Prove that either $\angle P Q E=90^{\circ}$ or $\angle P Q F=90^{\circ}$.
|
 First, we claim that $D, P, E$ are collinear. Let $N$ be the midpoint of $\overline{A B}$. It is well-known that the three lines $M N, D E, A I$ are concurrent at a point (see for example problem 6 of USAJMO 2014). Let $P^{\prime}$ be this intersection point, noting that $P^{\prime}$ actually lies on segment $D E$. Then $P^{\prime}$ lies inside $\triangle A B C$ and moreover $$ \triangle D P^{\prime} M \sim \triangle D E C $$ so $M P^{\prime}=M D$. Hence $P^{\prime}=P$, proving the claim. Let $S$ be the point diametrically opposite $D$ on the incircle, which is also the second intersection of $\overline{A Q}$ with the incircle. Let $T=\overline{A Q} \cap \overline{B C}$. Then $T$ is the contact point of the $A$-excircle; consequently, $$ M D=M P=M T $$ and we obtain a circle with diameter $\overline{D T}$. Since $\angle D Q T=\angle D Q S=90^{\circ}$ we have $Q$ on this circle as well. As $\overline{S D}$ is tangent to the circle with diameter $\overline{D T}$, we obtain $$ \angle P Q D=\angle S D P=\angle S D E=\angle S Q E . $$ Since $\angle D Q S=90^{\circ}, \angle P Q E=90^{\circ}$ too. 【 Solution using spiral similarity. We will ignore for now the point $P$. As before define $S, T$ and note $\overline{A Q S T}$ collinear, as well as $D P Q T$ cyclic on circle $\omega$ with diameter $\overline{D T}$. Let $\tau$ be the spiral similarity at $Q$ sending $\omega$ to the incircle. We have $\tau(T)=D$, $\tau(D)=S, \tau(Q)=Q$. Now $$ I=\overline{D D} \cap \overline{Q Q} \Longrightarrow \tau(I)=\overline{S S} \cap \overline{Q Q} $$ and hence we conclude $\tau(I)$ is the pole of $\overline{A S Q T}$ with respect to the incircle, which lies on line $E F$. Then since $\overline{A I} \perp \overline{E F}$ too, we deduce $\tau$ sends line $A I$ to line $E F$, hence $\tau(P)$ must be either $E$ or $F$ as desired. 【 Authorship comments. Written April 2014. I found this problem while playing with GeoGebra. Specifically, I started by drawing in the points $A, B, C, I, D, M, T$, common points. I decided to add in the circle with diameter $D T$, because of the synergy it had with the rest of the picture. After a while of playing around, I intersected ray $A I$ with the circle to get $P$, and was surprised to find that $D, P, E$ were collinear, which I thought was impossible since the setup should have been symmetric. On further reflection, I realized it was because $A I$ intersected the circle twice, and set about trying to prove this. I noticed the relation $\angle P Q E=90^{\circ}$ in my attempts to prove the result, even though this ended up being a corollary rather than a useful lemma.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
2
| null |
USA_TST
|
Prove that for every positive integer $n$, there exists a set $S$ of $n$ positive integers such that for any two distinct $a, b \in S, a-b$ divides $a$ and $b$ but none of the other elements of $S$.
|
The idea is to look for a sequence $d_{1}, \ldots, d_{n-1}$ of "differences" such that the following two conditions hold. Let $s_{i}=d_{1}+\cdots+d_{i-1}$, and $t_{i, j}=d_{i}+\cdots+d_{j-1}$ for $i \leq j$. (i) No two of the $t_{i, j}$ divide each other. (ii) There exists an integer $a$ satisfying the CRT equivalences $$ a \equiv-s_{i} \quad\left(\bmod t_{i, j}\right) \quad \forall i \leq j $$ Then the sequence $a+s_{1}, a+s_{2}, \ldots, a+s_{n}$ will work. For example, when $n=3$ we can take $\left(d_{1}, d_{2}\right)=(2,3)$ giving 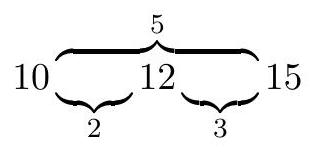 because the only conditions we need satisfy are $$ \begin{aligned} a & \equiv 0 \quad(\bmod 2) \\ a & \equiv 0 \quad(\bmod 5) \\ a & \equiv-2 \quad(\bmod 3) . \end{aligned} $$ But with this setup we can just construct the $d_{i}$ inductively. To go from $n$ to $n+1$, take a $d_{1}, \ldots, d_{n-1}$ and let $p$ be a prime not dividing any of the $d_{i}$. Moreover, let $M$ be a multiple of $\prod_{i \leq j} t_{i, j}$ coprime to $p$. Then we claim that $d_{1} M, d_{2} M, \ldots, d_{n-1} M, p$ is such a difference sequence. For example, the previous example extends as follows with $M=300$ and $p=7$. 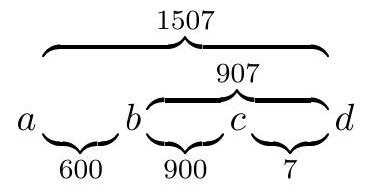 The new numbers $p, p+M t_{n-1, n}, p+M t_{n-2, n}, \ldots$ are all relatively prime to everything else. Hence (i) still holds. To see that (ii) still holds, just note that we can still get a family of solutions for the first $n$ terms, and then the last $(n+1)$ st term can be made to work by Chinese Remainder Theorem since all the new $p+M t_{n-2, n}$ are coprime to everything.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
3
| null |
USA_TST
|
A physicist encounters 2015 atoms called usamons. Each usamon either has one electron or zero electrons, and the physicist can't tell the difference. The physicist's only tool is a diode. The physicist may connect the diode from any usamon $A$ to any other usamon $B$. (This connection is directed.) When she does so, if usamon $A$ has an electron and usamon $B$ does not, then the electron jumps from $A$ to $B$. In any other case, nothing happens. In addition, the physicist cannot tell whether an electron jumps during any given step. The physicist's goal is to isolate two usamons that she is $100 \%$ sure are currently in the same state. Is there any series of diode usage that makes this possible?
|
The answer is no. Call the usamons $U_{1}, \ldots, U_{m}$ (here $m=2015$ ). Consider models $M_{k}$ of the following form: $U_{1}, \ldots, U_{k}$ are all charged for some $0 \leq k \leq m$ and the other usamons are not charged. Note that for any pair there's a model where they are different states, by construction. We can consider the physicist as acting on these $m+1$ models simultaneously, and trying to reach a state where there's a pair in all models which are all the same charge. (This is a necessary condition for a winning strategy to exist.) But we claim that any diode operation $U_{i} \rightarrow U_{j}$ results in the $m+1$ models being an isomorphic copy of the previous set. If $i<j$ then the diode operation can be interpreted as just swapping $U_{i}$ with $U_{j}$, which doesn't change anything. Moreover if $i>j$ the operation never does anything. The conclusion follows from this. Remark. This problem is not a "standard" olympiad problem, so I can't say it's trivial. But the idea is pretty natural I think. You can motivate it as follows: there's a sequence of diode operations you can do which forces the situation to be one of the $M_{k}$ above: first, use the diode into $U_{1}$ for all other $U_{i}$ 's, so that either no electrons exist at all or $U_{1}$ has an electron. Repeat with the other $U_{i}$. This leaves us at the situation described at the start of the problem. Then you could guess the answer was "no" just based on the fact that it's impossible for $n=2,3$ and that there doesn't seem to be a reasonable strategy. In this way it's possible to give a pretty good description of what it's possible to do. One possible phrasing: "the physicist can arrange the usamons in a line such that all the charged usamons are to the left of the un-charged usamons, but can't determine the number of charged usamons".
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
4
| null |
USA_TST
|
Let $f: \mathbb{Q} \rightarrow \mathbb{Q}$ be a function such that for any $x, y \in \mathbb{Q}$, the number $f(x+y)-$ $f(x)-f(y)$ is an integer. Decide whether there must exist a constant $c$ such that $f(x)-c x$ is an integer for every rational number $x$.
|
No, such a constant need not exist. $$ \begin{aligned} & 2 x_{1}=x_{0} \\ & 2 x_{2}=x_{1}+1 \\ & 2 x_{3}=x_{2} \\ & 2 x_{4}=x_{3}+1 \\ & 2 x_{5}=x_{4} \\ & 2 x_{6}=x_{5}+1 \end{aligned} $$ Set $f\left(2^{-k}\right)=x_{k}$ and $f\left(2^{k}\right)=2^{k}$ for $k=0,1, \ldots$ Then, let $$ f\left(a \cdot 2^{k}+\frac{b}{c}\right)=a f\left(2^{k}\right)+\frac{b}{c} $$ for odd integers $a, b, c$. One can verify this works. $$ f\left(\frac{p}{q}\right)=\frac{p}{q}(1!+2!+\cdots+q!) . $$ Remark. Silly note: despite appearances, $f(x)=\lfloor x\rfloor$ is not a counterexample since one can take $c=0$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
5
| null |
USA_TST
|
Fix a positive integer $n$. A tournament on $n$ vertices has all its edges colored by $\chi$ colors, so that any two directed edges $u \rightarrow v$ and $v \rightarrow w$ have different colors. Over all possible tournaments on $n$ vertices, determine the minimum possible value of $\chi$.
|
The answer is $$ \chi=\left\lceil\log _{2} n\right\rceil $$ First, we prove by induction on $n$ that $\chi \geq \log _{2} n$ for any coloring and any tournament. The base case $n=1$ is obvious. Now given any tournament, consider any used color $c$. Then it should be possible to divide the tournament into two subsets $A$ and $B$ such that all $c$-colored edges point from $A$ to $B$ (for example by letting $A$ be all vertices which are the starting point of a $c$-edge). 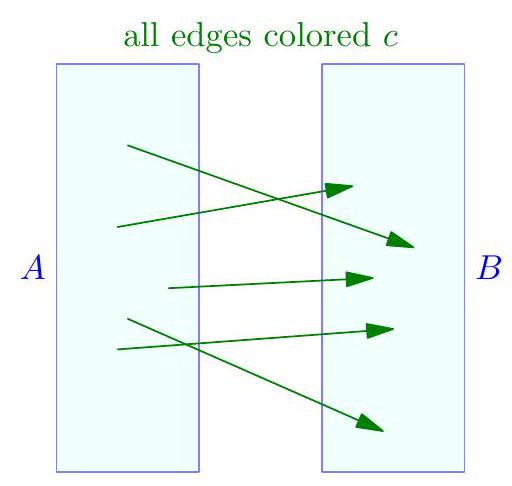 One of $A$ and $B$ has size at least $n / 2$, say $A$. Since $A$ has no $c$ edges, and uses at least $\log _{2}|A|$ colors other than $c$, we get $$ \chi \geq 1+\log _{2}(n / 2)=\log _{2} n $$ completing the induction. One can read the construction off from the argument above, but here is a concrete description. For each integer $n$, consider the tournament whose vertices are the binary representations of $S=\{0, \ldots, n-1\}$. Instantiate colors $c_{1}, c_{2}, \ldots$. Then for $v, w \in S$, we look at the smallest order bit for which they differ; say the $k$ th one. If $v$ has a zero in the $k$ th bit, and $w$ has a one in the $k$ th bit, we draw $v \rightarrow w$. Moreover we color the edge with color $c_{k}$. This works and uses at most $\left\lceil\log _{2} n\right\rceil$ colors. Remark (Motivation). The philosophy "combinatorial optimization" applies here. The idea is given any color $c$, we can find sets $A$ and $B$ such that all $c$-edges point $A$ to $B$. Once you realize this, the next insight is to realize that you may as well color all the edges from $A$ to $B$ by $c$; after all, this doesn't hurt the condition and makes your life easier. Hence, if $f$ is the answer, we have already a proof that $f(n)=1+\max (f(|A|), f(|B|))$ and we choose $|A| \approx|B|$. This optimization also gives the inductive construction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 First solution by barycentric coordinates (Evan Chen). Let $A X$ meet $M_{b} M_{c}$ at $D$, and let $X$ reflected over $M_{b} M_{c}^{\prime}$ 's midpoint be $X^{\prime}$. Let $Y^{\prime}, Z^{\prime}, E, F$ be similarly defined. 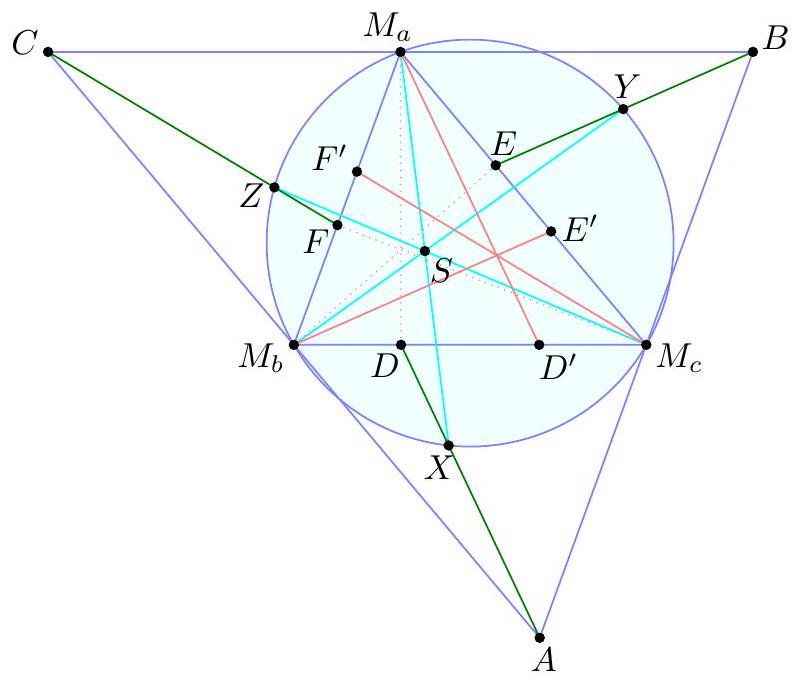 By Cevian Nest Theorem it suffices to prove that $M_{a} D, M_{b} E, M_{c} F$ are concurrent. Taking the isotomic conjugate and recalling that $M_{a} M_{b} A M_{c}$ is a parallelogram, we see that it suffices to prove $M_{a} X^{\prime}, M_{b} Y^{\prime}, M_{c} Z^{\prime}$ are concurrent. We now use barycentric coordinates on $\triangle M_{a} M_{b} M_{c}$. Let $$ S=\left(a^{2} S_{A}+t: b^{2} S_{B}+t: c^{2} S_{C}+t\right) $$ (possibly $t=\infty$ if $S$ is the centroid). Let $v=b^{2} S_{B}+t, w=c^{2} S_{C}+t$. Hence $$ X=\left(-a^{2} v w:\left(b^{2} w+c^{2} v\right) v:\left(b^{2} w+c^{2} v\right) w\right) $$ Consequently, $$ X^{\prime}=\left(a^{2} v w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) v\right) $$ We can compute $$ b^{2} w+c^{2} v=(b c)^{2}\left(S_{B}+S_{C}\right)+\left(b^{2}+c^{2}\right) t=(a b c)^{2}+\left(b^{2}+c^{2}\right) t $$ Thus $$ -a^{2} v+b^{2} w+c^{2} v=\left(b^{2}+c^{2}\right) t+(a b c)^{2}-(a b)^{2} S_{B}-a^{2} t=S_{A}\left((a b)^{2}+t\right) $$ Finally $$ X^{\prime}=\left(a^{2} v w: S_{A}\left(c^{2} S_{C}+t\right)\left((a b)^{2}+2 t\right): S_{A}\left(b^{2} S_{B}+t\right)\left((a c)^{2}+2 t\right)\right) $$ and from this it's evident that $A X^{\prime}, B Y^{\prime}, C Z^{\prime}$ are concurrent.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. \ Second solution by moving points (Anant Mudgal). Let $H_{a}, H_{b}, H_{c}$ be feet of altitudes, and let $\gamma$ denote the nine-point circle. The main claim is that: Claim - Lines $X H_{a}, Y H_{b}, Z H_{c}$ are concurrent, $$ \begin{aligned} & \ell \rightarrow \gamma \rightarrow \ell \\ & S \mapsto X \mapsto S_{a}:=\ell \cap \overline{H_{a} X} \end{aligned} $$ is projective, because it consists of two perspectivities. So we want the analogous maps $S \mapsto S_{b}, S \mapsto S_{c}$ to coincide. For this it suffices to check three positions of $S$; since you're such a good customer here are four. - If $S$ is the orthocenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the circumcenter of $\triangle A B C$ ) then $S_{a}$ coincides with the circumcenter of $M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $S_{a}$ coincides with the de Longchamps point of $\triangle M_{a} M_{b} M_{c}$ (equivalently orthocenter of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=S_{a}=S_{b}=S_{c}$ (as $S=X=Y=Z$ ). 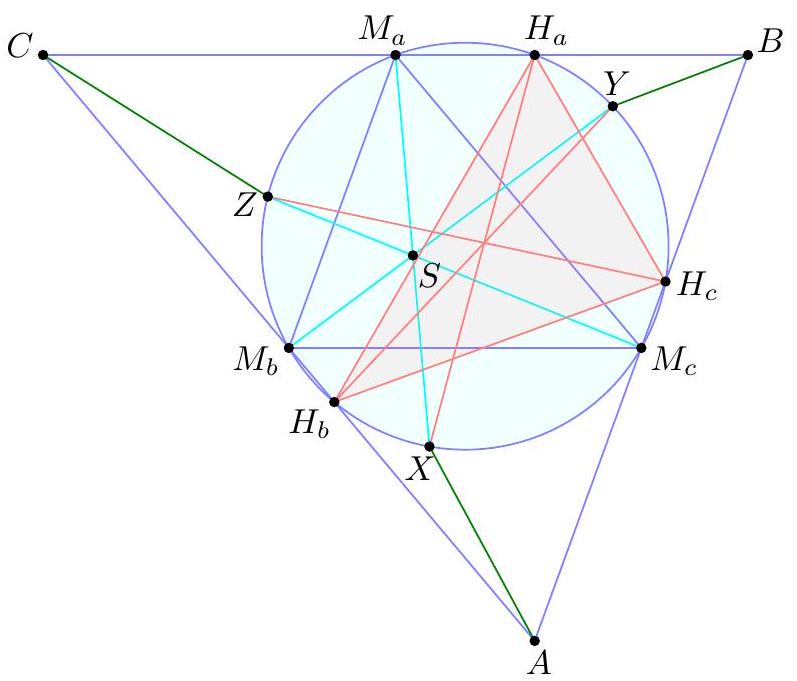 We now use Trig Ceva to carry over the concurrence. By sine law, $$ \frac{\sin \angle M_{c} A X}{\sin \angle A M_{c} X}=\frac{M_{c} X}{A X} $$ and a similar relation for $M_{b}$ gives that $$ \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{M_{c} X}{M_{b} X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ Thus multiplying cyclically gives $$ \prod_{\text {cyc }} \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\prod_{\text {cyc }} \frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \prod_{\text {cyc }} \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ The latter product on the right-hand side equals 1 by Trig Ceva on $\triangle M_{a} M_{b} M_{c}$ with cevians $\overline{M_{a} X}, \overline{M_{b} Y}, \overline{M_{c} Z}$. The former product also equals 1 by Trig Ceva for the concurrence in the previous claim (and the fact that $\angle A M_{c} X=\angle H_{c} H_{a} X$ ). Hence the left-hand side equals 1 , implying the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 『 Third solution by moving points (Gopal Goel). In this solution, we will instead use barycentric coordinates with resect to $\triangle A B C$ to bound the degrees suitably, and then verify for seven distinct choices of $S$. We let $R$ denote the radius of $\triangle A B C$, and $N$ the nine-point center. First, imagine solving for $X$ in the following way. Suppose $\vec{X}=\left(1-t_{a}\right) \vec{M}_{a}+t_{a} \vec{S}$. Then, using the dot product (with $|\vec{v}|^{2}=\vec{v} \cdot \vec{v}$ in general) $$ \begin{aligned} \frac{1}{4} R^{2} & =|\vec{X}-\vec{N}|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)+\vec{M}_{a}-\vec{N}\right|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\left|\vec{M}_{a}-\vec{N}\right|^{2} \\ & =t_{a}^{2}\left|\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\frac{1}{4} R^{2} \end{aligned} $$ Since $t_{a} \neq 0$ we may solve to obtain $$ t_{a}=-\frac{2\left(\vec{M}_{a}-\vec{N}\right) \cdot\left(\vec{S}-\vec{M}_{a}\right)}{\left|\vec{S}-\vec{M}_{a}\right|^{2}} $$ Now imagine $S$ varies along the Euler line, meaning there should exist linear functions $\alpha, \beta, \gamma: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ S=(\alpha(s), \beta(s), \gamma(s)) \quad s \in \mathbb{R} $$ with $\alpha(s)+\beta(s)+\gamma(s)=1$. Thus $t_{a}=\frac{f_{a}}{g_{a}}=\frac{f_{a}(s)}{g_{a}(s)}$ is the quotient of a linear function $f_{a}(s)$ and a quadratic function $g_{a}(s)$. So we may write: $$ \begin{aligned} X & =\left(1-t_{a}\right)\left(0, \frac{1}{2}, \frac{1}{2}\right)+t_{a}(\alpha, \beta, \gamma) \\ & =\left(t_{a} \alpha, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \beta, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \gamma\right) \end{aligned} $$ $$ =\left(2 f_{a} \alpha: g_{a}-f_{a}+2 f_{a} \beta: g_{a}-f_{a}+2 f_{a} \gamma\right) . $$ Thus the coordinates of $X$ are quadratic polynomials in $s$ when written in this way. In a similar way, the coordinates of $Y$ and $Z$ should be quadratic polynomials in $s$. The Ceva concurrence condition $$ \prod_{\text {cyc }} \frac{g_{a}-f_{a}+2 f_{a} \beta}{g_{a}-f_{a}+2 f_{a} \gamma}=1 $$ is thus a polynomial in $s$ of degree at most six. Our goal is to verify it is identically zero, thus it suffices to check seven positions of $S$. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $\overline{A X}, \overline{B Y}, \overline{C Z}$ are altitudes of $\triangle A B C$. - If $S$ is the centroid of $\triangle M_{a} M_{b} M_{c}$ (equivalently the centroid of $\triangle A B C$ ), then $\overline{A X}$, $\overline{B Y}, \overline{C Z}$ are medians of $\triangle A B C$. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=X=Y=Z$ and all cevians concur at $S$. - If $S$ lies on the $\overline{M_{a} M_{b}}$, then $Y=M_{a}, X=M_{c}$, and thus $\overline{A X} \cap \overline{B Y}=C$, which is of course concurrent with $\overline{C Z}$ (regardless of $Z$ ). Similarly if $S$ lies on the other sides of $\triangle M_{a} M_{b} M_{c}$. Thus we are also done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2015
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 Fourth solution using Pascal (official one). We give a different proof of the claim that $\overline{X H_{a}}, \overline{Y H_{b}}, \overline{Z H_{c}}$ are concurrent (and then proceed as in the end of the second solution). Let $H$ denote the orthocenter, $N$ the nine-point center, and moreover let $N_{a}, N_{b}, N_{c}$ denote the midpoints of $\overline{A H}, \overline{B H}, \overline{C H}$, which also lie on the nine-point circle (and are the antipodes of $M_{a}, M_{b}, M_{c}$ ). - By Pascal's theorem on $M_{b} N_{b} H_{b} M_{c} N_{c} H_{c}$, the point $P=\overline{M_{c} H_{b}} \cap \overline{M_{b} H_{c}}$ is collinear with $N=\overline{M_{b} N_{b}} \cap \overline{M_{c} N_{c}}$, and $H=\overline{N_{b} H_{b}} \cap \overline{N_{c} H_{c}}$. So $P$ lies on the Euler line. - By Pascal's theorem on $M_{b} Y H_{b} M_{c} Z H_{c}$, the point $\overline{Y H_{b}} \cap \overline{Z H_{c}}$ is collinear with $S=\overline{M_{b} Y} \cap \overline{M_{c} Z}$ and $P=\overline{M_{b} H_{c}} \cap \overline{M_{c} H_{b}}$. Hence $Y H_{b}$ and $Z H_{c}$ meet on the Euler line, as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
1
| null |
USA_TST
|
Let $S=\{1, \ldots, n\}$. Given a bijection $f: S \rightarrow S$ an orbit of $f$ is a set of the form $\{x, f(x), f(f(x)), \ldots\}$ for some $x \in S$. We denote by $c(f)$ the number of distinct orbits of $f$. For example, if $n=3$ and $f(1)=2, f(2)=1, f(3)=3$, the two orbits are $\{1,2\}$ and $\{3\}$, hence $c(f)=2$. Given $k$ bijections $f_{1}, \ldots, f_{k}$ from $S$ to itself, prove that $$ c\left(f_{1}\right)+\cdots+c\left(f_{k}\right) \leq n(k-1)+c(f) $$ where $f: S \rightarrow S$ is the composed function $f_{1} \circ \cdots \circ f_{k}$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
|
2016
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
【 First solution (angle chasing). Assume for simplicity $A B<A C$. Let $E$ be the contact point of the $A$-excircle on $B C$; also let ray $T D$ meet $\Omega$ again at $L$. From the fact that $\angle M T L=\angle M T D=180^{\circ}-\angle M K D$, we can deduce that $\angle M T L=\angle A C M$, meaning that $L$ is the reflection of $A$ across the perpendicular bisector $\ell$ of $B C$. If we reflect $T, D$, $L$ over $\ell$, we deduce $A, E$ and the reflection of $T$ across $\ell$ are collinear, which implies that $\angle B A T=\angle C A E$. Now, consider the reflection point $E$ across line $A I$, say $S$. Since ray $A I$ passes through the $A$-excenter, $S$ lies on the $A$-excircle. Since $\angle B A T=\angle C A E, S$ also lies on ray $A T$. But the circumcircles of triangles $D K M$ and $K M E$ are congruent (from $D M=E M$ ), so $S$ lies on the circumcircle of $\triangle D K M$ too. Hence $S$ is the desired intersection point. 
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
Second solution (advanced). It's known that $T$ is the touch-point of the $A$-mixtilinear incircle. Let $E$ be contact point of $A$-excircle on $B C$. Now the circumcircles of $\triangle D K M$ and $\triangle K M E$ are congruent, since $D M=M E$ and the angles at $K$ are supplementary. Let $S$ be the reflection of $E$ across line $K M$, which by the above the above comment lies on the circumcircle of $\triangle D K M$. Since $K M$ passes through the $A$-excenter, $S$ also lies on the $A$-excircle. But $S$ also lies on line $A T$, since lines $A T$ and $A E$ are isogonal (the mixtilinear cevian is isogonal to the Nagel line). Thus $S$ is the desired intersection point. 【 Authorship comments. This problem comes from an observation of mine: let $A B C$ be a triangle, let the $\angle A$ bisector meet $\overline{B C}$ and $(A B C)$ at $E$ and $M$. Let $W$ be the tangency point of the $A$-mixtilinear excircle with the circumcircle of $A B C$. Then $A$ Nagel line passed through a common intersection of the circumcircle of $\triangle M E W$ and the $A$-mixtilinear incircle. This problem is the inverted version of this observation.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
3
| null |
USA_TST
|
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 『 First solution (Ankan Bhattacharya). We start with: Claim - If $P \mid Q$ then $\Psi(P) \mid \Psi(Q)$. $$ \Psi(Q)=\Psi\left(P \sum_{i=0}^{k} r_{i} x^{i}\right)=\sum_{i=0}^{k} \Psi\left(P \cdot r_{i} x^{i}\right)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}} $$ which is divisible by $\Psi(P)$. This already implies $$ \Psi(\operatorname{gcd}(F, G)) \mid \operatorname{gcd}(\Psi(F), \Psi(G)) $$ For the converse, by Bezout there exists $A, B \in \mathbb{F}_{p}[x]$ such that $A F+B G=\operatorname{gcd}(F, G)$, so taking $\Psi$ of both sides gives $$ \Psi(A F)+\Psi(B G)=\Psi(\operatorname{gcd}(F, G)) $$ The left-hand side is divisible by $\operatorname{gcd}(\Psi(F), \Psi(G))$ since the first term is divisible by $\Psi(F)$ and the second term is divisible by $\Psi(G)$. So $\operatorname{gcd}(\Psi(F), \Psi(G)) \mid \Psi(\operatorname{gcd}(F, G))$ and noting both sides are monic we are done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
3
| null |
USA_TST
|
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 【 Second solution. Here is an alternative (longer but more conceptual) way to finish without Bezout lemma. Let $\beth \subseteq \mathbb{F}_{p}[x]$ denote the set of polynomials in the image of $\Psi$, thus $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a bijection on the level of sets. Claim - If $A, B \in \beth$ then $\operatorname{gcd}(A, B) \in \beth$. $$ \begin{aligned} x^{p^{k}} & \equiv\left(c_{2} x^{p^{k-2}}+c_{3} x^{p^{k-3}}+\cdots+c_{k}\right)^{p} \quad(\bmod B) \\ & \equiv c_{2} x^{p^{k-1}}+c_{3} x^{p^{k-2}} \cdots+c_{k} \quad(\bmod B) \end{aligned} $$ since exponentiation by $p$ commutes with addition in $\mathbb{F}_{p}$. This is enough to imply the conclusion. The proof if $\operatorname{deg} B$ is smaller less than $p^{k-1}$ is similar. Thus, if we view $\mathbb{F}_{p}[x]$ and $\beth$ as partially ordered sets under polynomial division, then gcd is the "greatest lower bound" or "meet" in both partially ordered sets. We will now prove that $\Psi$ is an isomorphism of the posets. We have already seen that $P|Q \Longrightarrow \Psi(P)| \Psi(Q)$ from the first solution. For the converse: Claim - If $\Psi(P) \mid \Psi(Q)$ then $P \mid Q$. Remark. In fact $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a ring isomorphism if we equip $\beth$ with function composition as the ring multiplication. Indeed in the proof of the first claim (that $P|Q \Longrightarrow \Psi(P)|$ $\Psi(Q)$ ) we saw that $$ \Psi(R P)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}}=\Psi(R) \circ \Psi(P) $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
4
| null |
USA_TST
|
Let $\sqrt{3}=1 . b_{1} b_{2} b_{3} \cdots(2)$ be the binary representation of $\sqrt{3}$. Prove that for any positive integer $n$, at least one of the digits $b_{n}, b_{n+1}, \ldots, b_{2 n}$ equals 1 .
|
Assume the contrary, so that for some integer $k$ we have $$ k<2^{n-1} \sqrt{3}<k+\frac{1}{2^{n+1}} . $$ Squaring gives $$ \begin{aligned} k^{2}<3 \cdot 2^{2 n-2} & <k^{2}+\frac{k}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{2^{n-1} \sqrt{3}}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & =k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{16} \\ & <k^{2}+1 \end{aligned} $$ and this is a contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
5
| null |
USA_TST
|
Let $n \geq 4$ be an integer. Find all functions $W:\{1, \ldots, n\}^{2} \rightarrow \mathbb{R}$ such that for every partition $[n]=A \cup B \cup C$ into disjoint sets, $$ \sum_{a \in A} \sum_{b \in B} \sum_{c \in C} W(a, b) W(b, c)=|A||B||C| . $$
|
$ Of course, $W(k, k)$ is arbitrary for $k \in[n]$. We claim that $W(a, b)= \pm 1$ for any $a \neq b$, with the sign fixed. (These evidently work.) First, let $X_{a b c}=W(a, b) W(b, c)$ for all distinct $a, b, c$, so the given condition is $$ \sum_{a, b, c \in A \times B \times C} X_{a b c}=|A||B||C| . $$ Consider the given equation with the particular choices - $A=\{1\}, B=\{2\}, C=\{3,4, \ldots, n\}$. - $A=\{1\}, B=\{3\}, C=\{2,4, \ldots, n\}$. - $A=\{1\}, B=\{2,3\}, C=\{4, \ldots, n\}$. This gives $$ \begin{aligned} X_{123}+X_{124}+\cdots+X_{12 n} & =n-2 \\ X_{132}+X_{134}+\cdots+X_{13 n} & =n-2 \\ \left(X_{124}+\cdots+X_{12 n}\right)+\left(X_{134}+\cdots+X_{13 n}\right) & =2(n-3) . \end{aligned} $$ Adding the first two and subtracting the last one gives $X_{123}+X_{132}=2$. Similarly, $X_{123}+X_{321}=2$, and in this way we have $X_{321}=X_{132}$. Thus $W(3,2) W(2,1)=$ $W(1,3) W(3,2)$, and since $W(3,2) \neq 0$ (clearly) we get $W(2,1)=W(3,2)$. Analogously, for any distinct $a, b, c$ we have $W(a, b)=W(b, c)$. For $n \geq 4$ this is enough to imply $W(a, b)= \pm 1$ for $a \neq b$ where the choice of sign is the same for all $a$ and $b$. Remark. Surprisingly, the $n=3$ case has "extra" solutions for $W(1,2)=W(2,3)=$ $W(3,1)= \pm 1, W(2,1)=W(3,2)=W(1,3)=\mp 1$. Remark (Intuition). It should still be possible to solve the problem with $X_{a b c}$ in place of $W(a, b) W(b, c)$, because we have about far more equations than variables $X_{a, b, c}$ so linear algebra assures us we almost certainly have a unique solution.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2016
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be an acute scalene triangle and let $P$ be a point in its interior. Let $A_{1}$, $B_{1}, C_{1}$ be projections of $P$ onto triangle sides $B C, C A, A B$, respectively. Find the locus of points $P$ such that $A A_{1}, B B_{1}, C C_{1}$ are concurrent and $\angle P A B+\angle P B C+$ $\angle P C A=90^{\circ}$.
|
In complex numbers with $A B C$ the unit circle, it is equivalent to solving the following two cubic equations in $p$ and $q=\bar{p}$ : $$ \begin{aligned} (p-a)(p-b)(p-c) & =(a b c)^{2}(q-1 / a)(q-1 / b)(q-1 / c) \\ 0 & =\prod_{\text {cyc }}(p+c-b-b c q)+\prod_{\text {сус }}(p+b-c-b c q) \end{aligned} $$ Viewing this as two cubic curves in $(p, q) \in \mathbb{C}^{2}$, by Bézout's Theorem it follows there are at most nine solutions (unless both curves are not irreducible, but it's easy to check the first one cannot be factored). Moreover it is easy to name nine solutions (for $A B C$ scalene): the three vertices, the three excenters, and $I, O, H$. Hence the answer is just those three triangle centers $I, O$ and $H$. Remark. On the other hand it is not easy to solve the cubics by hand; I tried for an hour without success. So I think this solution is only feasible with knowledge of algebraic geometry. Remark. These two cubics have names: - The locus of $\angle P A B+\angle P B C+\angle P C A=90^{\circ}$ is the McCay cubic, which is the locus of points $P$ for which $P, P^{*}, O$ are collinear. - The locus of the pedal condition is the Darboux cubic, which is the locus of points $P$ for which $P, P^{*}, L$ are collinear, $L$ denoting the de Longchamps point. Assuming $P \neq P^{*}$, this implies $P$ and $P^{*}$ both lie on the Euler line of $\triangle A B C$, which is possible only if $P=O$ or $P=H$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
1
| null |
USA_TST
|
In a sports league, each team uses a set of at most $t$ signature colors. A set $S$ of teams is color-identifiable if one can assign each team in $S$ one of their signature colors, such that no team in $S$ is assigned any signature color of a different team in $S$. For all positive integers $n$ and $t$, determine the maximum integer $g(n, t)$ such that: In any sports league with exactly $n$ distinct colors present over all teams, one can always find a color-identifiable set of size at least $g(n, t)$.
|
Answer: $\lceil n / t\rceil$. To see this is an upper bound, note that one can easily construct a sports league with that many teams anyways. A quick warning: Remark (Misreading the problem). It is common to misread the problem by ignoring the word "any". Here is an illustration. Suppose we have two teams, MIT and Harvard; the colors of MIT are red/grey/black, and the colors of Harvard are red/white. (Thus $n=4$ and $t=3$.) The assignment of MIT to grey and Harvard to red is not acceptable because red is a signature color of MIT, even though not the one assigned. 【 Approach by deleting teams (Gopal Goel). Initially, place all teams in a set $S$. Then we repeat the following algorithm: If there is a team all of whose signature colors are shared by some other team in $S$ already, then we delete that team. (If there is more than one such team, we pick arbitrarily.) At the end of the process, all $n$ colors are still present at least once, so at least $\lceil n / t\rceil$ teams remain. Moreover, since the algorithm is no longer possible, the remaining set $S$ is already color-identifiable. Remark (Gopal Goel). It might seem counter-intuitive that we are deleting teams from the full set when the original problem is trying to get a large set $S$. This is less strange when one thinks of it instead as "safely deleting useless teams". Basically, if one deletes such a team, the problem statement implies that the task must still be possible, since $g(n, t)$ does not depend on the number of teams: $n$ is the number of colors present, and deleting a useless team does not change this. It turns out that this optimization is already enough to solve the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
1
| null |
USA_TST
|
In a sports league, each team uses a set of at most $t$ signature colors. A set $S$ of teams is color-identifiable if one can assign each team in $S$ one of their signature colors, such that no team in $S$ is assigned any signature color of a different team in $S$. For all positive integers $n$ and $t$, determine the maximum integer $g(n, t)$ such that: In any sports league with exactly $n$ distinct colors present over all teams, one can always find a color-identifiable set of size at least $g(n, t)$.
|
Answer: $\lceil n / t\rceil$. To see this is an upper bound, note that one can easily construct a sports league with that many teams anyways. A quick warning: Remark (Misreading the problem). It is common to misread the problem by ignoring the word "any". Here is an illustration. Suppose we have two teams, MIT and Harvard; the colors of MIT are red/grey/black, and the colors of Harvard are red/white. (Thus $n=4$ and $t=3$.) The assignment of MIT to grey and Harvard to red is not acceptable because red is a signature color of MIT, even though not the one assigned. 【 Approach by adding colors. For a constructive algorithmic approach, the idea is to greedy pick by color (rather than by team), taking at each step the least used color. Select the color $C_{1}$ with the fewest teams using it, and a team $T_{1}$ using it. Then delete all colors $T_{1}$ uses, and all teams which use $C_{1}$. Note that - By problem condition, this deletes at most $t$ teams total. - Any remaining color $C$ still has at least one user. Indeed, if not, then $C$ had the same set of teams as $C_{1}$ did (by minimality of $C$ ), but then it should have deleted as a color of $T_{1}$. Now repeat this algorithm with $C_{2}$ and $T_{2}$, and so on. This operations uses at most $t$ colors each time, so we select at least $\lceil n / t\rceil$ colors. As before, assume our league has teams, MIT and Harvard; the colors of MIT are red/grey/black, and the colors of Harvard are red/white. (Thus $n=4$ and $t=3$.) If we start by selecting MIT and red, then it is impossible to select any more teams; but $g(n, t)=2$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$, and let $T$ be on line $B C$ such that $\angle T A O=90^{\circ}$. The circle with diameter $\overline{A T}$ intersects the circumcircle of $\triangle B O C$ at two points $A_{1}$ and $A_{2}$, where $O A_{1}<O A_{2}$. Points $B_{1}, B_{2}, C_{1}, C_{2}$ are defined analogously. (a) Prove that $\overline{A A_{1}}, \overline{B B_{1}}, \overline{C C_{1}}$ are concurrent. (b) Prove that $\overline{A A_{2}}, \overline{B B_{2}}, \overline{C C_{2}}$ are concurrent on the Euler line of triangle $A B C$.
|
Let triangle $A B C$ have circumcircle $\Gamma$. Let $\triangle X Y Z$ be the tangential triangle of $\triangle A B C$ (hence $\Gamma$ is the incircle of $\triangle X Y Z$ ), and denote by $\Omega$ its circumcircle. Suppose the symmedian $\overline{A X}$ meets $\Gamma$ again at $D$, and let $M$ be the midpoint of $\overline{A D}$. Finally, let $K$ be the Miquel point of quadrilateral $Z B C Y$, meaning it is the intersection of $\Omega$ and the circumcircle of $\triangle B O C$ (other than $X$ ).  We first claim that $M$ and $K$ are $A_{1}$ and $A_{2}$. In that case $O M<O A<O K$, so $M=A_{1}, K=A_{2}$. To see that $M=A_{1}$, note that $\angle O M X=90^{\circ}$, and moreover that $\overline{T A}, \overline{T D}$ are tangents to $\Gamma$, whence we also have $M=\overline{T O} \cap \overline{A D}$. Thus $M$ lies on both $(B O C)$ and $(A T)$. This solves part (a) of the problem: the concurrency point is the symmedian point of $\triangle A B C$. Now, note that since $K$ is the Miquel point, $$ \frac{Z K}{Y K}=\frac{Z B}{Y C}=\frac{Z A}{Y A} $$ and hence $\overline{K A}$ is an angle bisector of $\angle Z K Y$. Thus from $(T A ; Y Z)=-1$ we obtain $\angle T K A=90^{\circ}$. It remains to show $\overline{A K}$ passes through a fixed point on the Euler line. We claim it is the exsimilicenter of $\Gamma$ and $\Omega$. Let $L$ be the midpoint of the $\operatorname{arc} Y Z$ of $\triangle X Y Z$ not containing $X$. Then we know that $K, A, L$ are collinear. Now the positive homothety sending $\Gamma$ to $\Omega$ maps $A$ to $L$; this proves the claim. Finally, it is well-known that the line through $O$ and the circumcenter of $\triangle X Y Z$ coincides with the Euler line of $\triangle A B C$; hence done. I Authorship comments. This problem was inspired by the fact that $K, A, L$ are collinear in the figure, which was produced by one of my students (Ryan Kim) in a solution to a homework problem. I realized for example that this implied that line $A K$ passed through the $X_{56}$ point of $\triangle X Y Z$ (which lies on the Euler line of $\triangle A B C$ ). This problem was the result of playing around with the resulting very nice picture: all the power comes from the "magic" point $K$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
3
| null |
USA_TST
|
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 First solution using transformations. We will prove the claim in the following form: Claim - Assume $P, Q \in \mathbb{C}[x]$ are relatively prime. If $\alpha P+\beta Q$ is a square for four different choices of the ratio $[\alpha: \beta]$ then $P$ and $Q$ must be constant. Call pairs $(P, Q)$ as in the claim bad; so we wish to show the only bad pairs are pairs of constant polynomials. Assume not, and take a bad pair with $\operatorname{deg} P+\operatorname{deg} Q$ minimal. By a suitable Möbius transformation, we may transform $(P, Q)$ so that the four ratios are $[1: 0],[0: 1],[1:-1]$ and $[1:-k]$, so we find there are polynomials $A$ and $B$ such that $$ \begin{aligned} A^{2}-B^{2} & =C^{2} \\ A^{2}-k B^{2} & =D^{2} \end{aligned} $$ where $A^{2}=P+\lambda_{1} Q, B^{2}=P+\lambda_{2} Q$, say. Of course $\operatorname{gcd}(A, B)=1$. Consequently, we have $C^{2}=(A+B)(A-B)$ and $D^{2}=(A+\mu B)(A-\mu B)$ where $\mu^{2}=k$. Now $\operatorname{gcd}(A, B)=1$, so $A+B, A-B, A+\mu B$ and $A-\mu B$ are squares; id est $(A, B)$ is bad. This is a contradiction, since $\operatorname{deg} A+\operatorname{deg} B<\operatorname{deg} P+\operatorname{deg} Q$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
3
| null |
USA_TST
|
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 Second solution using derivatives (by Zack Chroman). We will assume without loss of generality that $\operatorname{deg} P \neq \operatorname{deg} Q$; if not, then one can replace $(P, Q)$ with $(P+c Q, Q)$ for a suitable constant $c$. Then, there exist $\lambda_{i} \in \mathbb{C}$ and polynomials $R_{i}$ for $i=1,2,3,4$ such that $$ \begin{aligned} & P+\lambda_{i} Q=R_{i}^{2} \\ \Longrightarrow & P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime} \\ & \Longrightarrow R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=Q^{\prime} P-Q P^{\prime} \end{aligned} $$ On the other hand by Euclidean algorithm it follows that $R_{i}$ are relatively prime to each other. Therefore $$ R_{1} R_{2} R_{3} R_{4} \mid Q^{\prime} P-Q P^{\prime} $$ However, we have $$ \begin{aligned} \sum_{1}^{4} \operatorname{deg} R_{i} & \geq \frac{3 \max (\operatorname{deg} P, \operatorname{deg} Q)+\min (\operatorname{deg} P, \operatorname{deg} Q)}{2} \\ & \geq \operatorname{deg} P+\operatorname{deg} Q>\operatorname{deg}\left(Q^{\prime} P-Q P^{\prime}\right) \end{aligned} $$ This can only occur if $Q^{\prime} P-Q P^{\prime}=0$ or $(P / Q)^{\prime}=0$ by the quotient rule! But $P / Q$ can't be constant, the end. Remark. The result is previously known; see e.g. Lemma 1.6 of http://math.mit.edu/ ebelmont/ec-notes.pdf or Exercise 6.5.L(a) of Vakil's notes.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
4
| null |
USA_TST
|
You are cheating at a trivia contest. For each question, you can peek at each of the $n>1$ other contestant's guesses before writing your own. For each question, after all guesses are submitted, the emcee announces the correct answer. A correct guess is worth 0 points. An incorrect guess is worth -2 points for other contestants, but only -1 point for you, because you hacked the scoring system. After announcing the correct answer, the emcee proceeds to read out the next question. Show that if you are leading by $2^{n-1}$ points at any time, then you can surely win first place.
|
We will prove the result with $2^{n-1}$ replaced even by $2^{n-2}+1$. We first make the following reductions. First, change the weights to be $+1,-1,0$ respectively (rather than $0,-2,-1$ ); this clearly has no effect. Also, WLOG that all contestants except you initially have score zero (and that your score exceeds $2^{n-2}$ ). WLOG ignore rounds in which all answers are the same. Finally, ignore rounds in which you get the correct answer, since that leaves you at least as well off as before - in other words, we'll assume your score is always fixed, but you can pick any group of people with the same answers and ensure they lose 1 point, while some other group gains 1 point. The key observation is the following. Consider two rounds $R_{1}$ and $R_{2}$ such that: - In round $R_{1}$, some set $S$ of contestants gains a point. - In round $R_{2}$, the set $S$ of contestants all have the same answer. Then, if we copy the answers of contestants in $S$ during $R_{2}$, then the sum of the scorings in $R_{1}$ and $R_{2}$ cancel each other out. In other words we can then ignore $R_{1}$ and $R_{2}$ forever. We thus consider the following strategy. We keep a list $\mathcal{L}$ of subsets of $\{1, \ldots, n\}$, initially empty. Now do the following strategy: - On a round, suppose there exists a set $S$ of people with the same answer such that $S \in \mathcal{L}$. (If multiple exist, choose one arbitrarily.) Then, copy the answer of $S$, causing them to lose a point. Delete $S$ from $\mathcal{L}$. (Importantly, we do not add any new sets to $\mathcal{L}$.) - Otherwise, copy any set $T$ of contestants, selecting $|T| \geq n / 2$ if possible. Let $S$ be the set of contestants who answer correctly (if any), and add $S$ to the list $\mathcal{L}$. Note that $|S| \leq n / 2$, since $S$ is disjoint from $T$. By construction, $\mathcal{L}$ has no duplicate sets. So the score of any contestant $c$ is bounded above by the number of times that $c$ appears among sets in $\mathcal{L}$. The number of such sets is clearly at most $\frac{1}{2} \cdot 2^{n-1}$. So, if you lead by $2^{n-2}+1$ then you ensure victory. This completes the proof! Remark. Several remarks are in order. First, we comment on the bound $2^{n-2}+1$ itself. The most natural solution using only the list idea gives an upper bound of $\left(2^{n}-2\right)+1$, which is the number of nonempty proper subsets of $\{1, \ldots, n\}$. Then, there are two optimizations one can observe: - In fact we can improve to the number of times any particular contestant $c$ appears in some set, rather than the total number of sets. - When adding new sets $S$ to $\mathcal{L}$, one can ensure $|S| \leq n / 2$. Either observation alone improves the bound from $2^{n}-1$ to $2^{n-1}$, but both together give the bound $2^{n-2}+1$. Additionally, when $n$ is odd the calculation of subsets actually gives $2^{n-2}-\frac{1}{2}\binom{n-1}{\frac{n-1}{2}}+1$. This gives the best possible value at both $n=2$ and $n=3$. It seems likely some further improvements are possible, and the true bound is suspected to be polynomial in $n$. 1. The exponential bound $2^{n}$ suggests looking at subsets. 2. The $n=2$ case suggests the idea of "repeated rounds". (I think this $n=2$ case is actually really good.) 3. The "two distinct answers" case suggests looking at rounds as partitions (even though the WLOG does not work, at least not without further thought). 4. There's something weird about this problem: it's a finite bound over unbounded time. This is a hint to not worry excessively about the actual scores, which turn out to be almost irrelevant.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
5
| null |
USA_TST
|
Let $A B C$ be a triangle with altitude $\overline{A E}$. The $A$-excircle touches $\overline{B C}$ at $D$, and intersects the circumcircle at two points $F$ and $G$. Prove that one can select points $V$ and $N$ on lines $D G$ and $D F$ such that quadrilateral $E V A N$ is a rhombus.
|
Let $I$ denote the incenter, $J$ the $A$-excenter, and $L$ the midpoint of $\overline{A E}$. Denote by $\overline{I Y}$, $\overline{I Z}$ the tangents from $I$ to the $A$-excircle. Note that lines $\overline{B C}, \overline{G F}, \overline{Y Z}$ then concur at $H$ (unless $A B=A C$, but this case is obvious), as it's the radical center of cyclic hexagon $B I C Y J Z$, the circumcircle and the $A$-excircle. 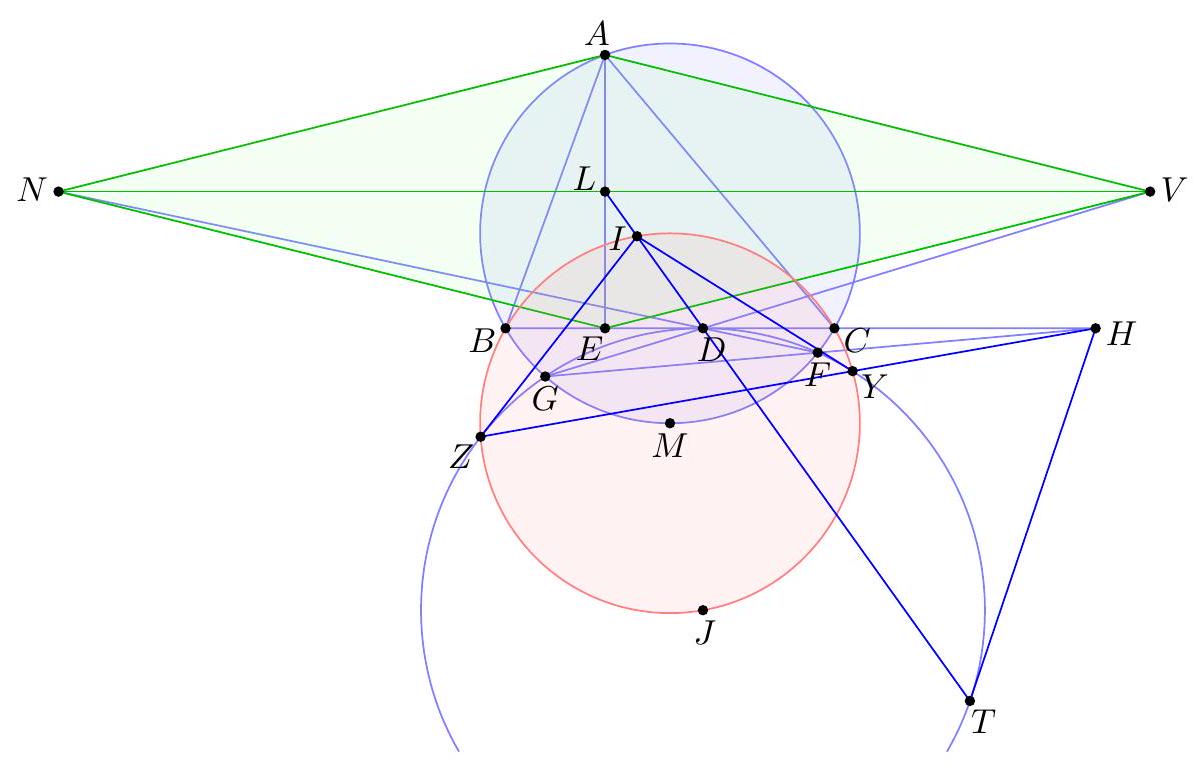 Now let $\overline{H D}$ and $\overline{H T}$ be the tangents from $H$ to the $A$-excircle. It follows that $\overline{D T}$ is the symmedian of $\triangle D Z Y$, hence passes through $I=\overline{Y Y} \cap \overline{Z Z}$. Moreover, it's well known that $\overline{D I}$ passes through $L$, the midpoint of the $A$-altitude (for example by homothety). Finally, $(D T ; F G)=-1$, hence project through $D$ onto the line through $L$ parallel to $\overline{B C}$ to obtain $(\infty L ; V N)=-1$ as desired. 【 Authorship comments. This is a joint proposal with Danielle Wang (mostly by her). The formulation given was that the tangents to the $A$-excircle at $F$ and $G$ was on line $\overline{D I}$; I solved this formulation using the radical axis argument above. I then got the idea to involve the point $L$, already knowing it was on $\overline{D I}$. Observing the harmonic quadrilateral, I took perspectivity through $M$ onto the line through $L$ parallel to $\overline{B C}$ (before this I had tried to use the $A$-altitude with little luck). This yields the rhombus in the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2017
|
T0
|
6
| null |
USA_TST
|
Prove that there are infinitely many triples $(a, b, p)$ of integers, with $p$ prime and $0<a \leq b<p$, for which $p^{5}$ divides $(a+b)^{p}-a^{p}-b^{p}$.
|
The key claim is that if $p \equiv 1(\bmod 3)$, then $$ p\left(x^{2}+x y+y^{2}\right)^{2} \text { divides }(x+y)^{p}-x^{p}-y^{p} $$ as polynomials in $x$ and $y$. Since it's known that one can select $a$ and $b$ such that $p^{2} \mid a^{2}+a b+b^{2}$, the conclusion follows. (The theory of quadratic forms tells us we can do it with $p^{2}=a^{2}+a b+b^{2}$; Thue's lemma lets us do it by solving $x^{2}+x+1 \equiv 0\left(\bmod p^{2}\right)$.) To prove this, it is the same to show that $$ \left(x^{2}+x+1\right)^{2} \text { divides } F(x):=(x+1)^{p}-x^{p}-1 $$ since the binomial coefficients $\binom{p}{k}$ are clearly divisible by $p$. Let $\zeta$ be a third root of unity. Then $F(\zeta)=(1+\zeta)^{p}-\zeta^{p}-1=-\zeta^{2}-\zeta-1=0$. Moreover, $F^{\prime}(x)=p(x+1)^{p-1}-p x^{p-1}$, so $F^{\prime}(\zeta)=p-p=0$. Hence $\zeta$ is a double root of $F$ as needed. (Incidentally, $p=2017$ works!) $$ (x+1)^{7}-x^{7}-1=7 x(x+1)\left(x^{4}+2 x^{3}+3 x^{2}+2 x+1\right) $$ The key is now to notice that the last factor is $\left(x^{2}+x+1\right)^{2}$, which suggests the entire solution. In fact, even if $p \equiv 2(\bmod 3)$, the polynomial $x^{2}+x+1$ still divides $(x+1)^{p}-x^{p}-1$. So even the $p=5$ case can motivate the main idea.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
1
| null |
USA_TST
|
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. 【 First solution. In what follows, by $[a, b]$ we mean $\{a, a+1, \ldots, b\}$. First, we make the following easy observation. Claim - If $a$ and $d$ are positive integers, then precisely $\varphi(d)$ elements of $[a, a+d-1]$ are relatively prime to $d$. Let $d_{1}, d_{2}, \ldots, d_{k}$ denote denote the divisors of $n$ in some order. Consider the intervals $$ \begin{aligned} I_{1} & =\left[1, d_{1}\right] \\ I_{2} & =\left[d_{1}+1, d_{1}+d_{2}\right] \\ & \vdots \\ I_{k} & =\left[d_{1}+\cdots+d_{k-1}+1, d_{1}+\cdots+d_{k}\right] . \end{aligned} $$ of length $d_{1}, \ldots, d_{k}$ respectively. The $j$ th interval will have exactly $\varphi\left(d_{j}\right)$ elements which are relatively prime $d_{j}$, hence at most $\varphi\left(d_{j}\right)$ which are relatively prime to $n$. Consequently, in $I=\bigcup_{j=1}^{k} I_{k}$ there are at most $$ \sum_{j=1}^{k} \varphi\left(d_{j}\right)=\sum_{d \mid n} \varphi(d)=n $$ integers relatively prime to $n$. On the other hand $I=[1, \sigma(n)]$ so this implies the inequality. We see that the equality holds for $n=p^{e}$. Assume now $p<q$ are distinct primes dividing $n$. Reorder the divisors $d_{i}$ so that $d_{1}=q$. Then $p, q \in I_{1}$, and so $I_{1}$ should contain strictly fewer than $\varphi\left(d_{1}\right)=q-1$ elements relatively prime to $n$, hence the inequality is strict.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
1
| null |
USA_TST
|
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. I Second solution (Ivan Borsenco and Evan Chen). Let $n=p_{1}^{e_{1}} \ldots p_{k}^{e_{k}}$, where $p_{1}<p_{2}<\ldots$. We are going to assume $k \geq 2$, since the $k=1$ case was resolved in the very beginning, and prove the strict inequality. For a general $N$, the number of relatively prime integers in $[1, N]$ is given exactly by $$ f(N)=N-\sum_{i}\left\lfloor\frac{N}{p_{i}}\right\rfloor+\sum_{i<j}\left\lfloor\frac{N}{p_{i} p_{j}}\right\rfloor-\ldots $$ according to the inclusion-exclusion principle. So, we wish to show that $f(\sigma(n))<n$ (as $k \geq 2$ ). Discarding the error terms from the floors (noting that we get at most 1 from the negative floors) gives $$ \begin{aligned} f(N) & <2^{k-1}+N-\sum_{i} \frac{N}{p_{i}}+\sum_{i<j} \frac{N}{p_{i} p_{j}}-\ldots \\ & =2^{k-1}+N \prod_{i}\left(1-p_{i}^{-1}\right) \\ & =2^{k-1}+\prod_{i}\left(1-p_{i}^{-1}\right)\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{e_{i}}\right) \\ & =2^{k-1}+\prod_{i}\left(p_{i}^{e_{i}}-p_{i}^{-1}\right) . \end{aligned} $$ $$ \begin{aligned} f(N) & <2+\left(p_{1}^{e_{1}}-p_{1}^{-1}\right)\left(p_{2}^{e_{2}}-p_{2}^{-1}\right) \\ & =2+n-\frac{p_{2}^{e_{2}}}{p_{1}}-\frac{p_{1}^{e_{1}}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & \leq 2+n-\frac{p_{2}}{p_{1}}-\frac{p_{1}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & =n+\frac{1-\left(p_{1}-p_{2}\right)^{2}}{p_{1} p_{2}} \leq n \end{aligned} $$ On the other hand if $k \geq 3$ we may now write $$ \begin{aligned} f(N) & <2^{k-1}+\left[\prod_{i=2}^{k-1}\left(p_{i}^{e_{i}}\right)\right]\left(p_{1}^{e_{1}}-p_{1}^{-1}\right) \\ & =2^{k-1}+n-\frac{p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}}{p_{1}} \\ & \leq 2^{k-1}+n-\frac{p_{2} p_{3} \ldots p_{k}}{p_{1}} . \end{aligned} $$ If $p_{1}=2$, then one can show by induction that $p_{2} p_{3} \ldots p_{k} \geq 2^{k+1}-1$, which implies the result. If $p_{1}>2$, then one can again show by induction $p_{3} \ldots p_{k} \geq 2^{k}-1$ (since $p_{3} \geq 7$ ), which also implies the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
2
| null |
USA_TST
|
Find all functions $f: \mathbb{Z}^{2} \rightarrow[0,1]$ such that for any integers $x$ and $y$, $$ f(x, y)=\frac{f(x-1, y)+f(x, y-1)}{2} $$
|
We claim that the only functions $f$ are constant functions. (It is easy to see that they work.) TI First solution (hands-on). First, iterating the functional equation relation to the $n$th level shows that $$ f(x, y)=\frac{1}{2^{n}} \sum_{i=0}^{n}\binom{n}{i} f(x-i, y-(n-i)) $$ In particular, $$ \begin{aligned} |f(x, y)-f(x-1, y+1)| & =\frac{1}{2^{n}}\left|\sum_{i=0}^{n+1} f(x-i, y-(n-i)) \cdot\left(\binom{n}{i}-\binom{n}{i-1}\right)\right| \\ & \leq \frac{1}{2^{n}} \sum_{i=0}^{n+1}\left|\binom{n}{i}-\binom{n}{i-1}\right| \\ & =\frac{1}{2^{n}} \cdot 2\binom{n}{\lfloor n / 2\rfloor} \end{aligned} $$ where we define $\binom{n}{n+1}=\binom{n}{-1}=0$ for convenience. Since $$ \binom{n}{\lfloor n / 2\rfloor}=o\left(2^{n}\right) $$ it follows that $f$ must be constant.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
2
| null |
USA_TST
|
Find all functions $f: \mathbb{Z}^{2} \rightarrow[0,1]$ such that for any integers $x$ and $y$, $$ f(x, y)=\frac{f(x-1, y)+f(x, y-1)}{2} $$
|
We claim that the only functions $f$ are constant functions. (It is easy to see that they work.) I Second solution (random walks, Mark Sellke). We show that if $x+y=x^{\prime}+y^{\prime}$ then $f(x, y)=f\left(x^{\prime}, y^{\prime}\right)$. Let $Z_{n}, Z_{n}^{\prime}$ be random walks starting at $(x, y)$ and $\left(x^{\prime}, y^{\prime}\right)$ and moving down/left. Then $f\left(Z_{n}\right)$ is a martingale so we have $$ \mathbb{E}\left[f\left(Z_{n}\right)\right]=f(x, y), \quad \mathbb{E}\left[f\left(Z_{n}^{\prime}\right)\right]=f\left(x^{\prime}, y^{\prime}\right) $$ We'll take $Z_{n}, Z_{n}^{\prime}$ to be independent until they hit each other, after which they will stay together. Then $$ \left|\mathbb{E}\left[f\left(Z_{n}\right)-f\left(Z_{n}^{\prime}\right)\right]\right| \leq \mathbb{E}\left[\left|f\left(Z_{n}\right)-f\left(Z_{n}^{\prime}\right)\right|\right] \leq p_{n} $$ where $p_{n}$ is the probability that $Z_{n}, Z_{n}^{\prime}$ never collide. But the distance between $Z_{n}, Z_{n}^{\prime}$ is essentially a 1 -dimensional random walk, so they will collide with probability 1 , meaning $\lim _{n \rightarrow \infty} p_{n}=0$. Hence $$ \left|f(x, y)-f\left(x^{\prime}, y^{\prime}\right)\right|=\left|\mathbb{E}\left[f\left(Z_{n}\right)-f\left(Z_{n}^{\prime}\right)\right]\right|=o(1) $$ as desired. Remark. If the problem were in $\mathbb{Z}^{d}$ for large $d$, this solution wouldn't work as written because the independent random walks wouldn't hit each other. However, this isn't a serious problem because $Z_{n}, Z_{n}^{\prime}$ don't have to be independent before hitting each other. Indeed, if every time $Z_{n}, Z_{n}^{\prime}$ agree on a new coordinate we force them to agree on that coordinate forever, we can make the two walks individually have the distribution of a coordinate-decreasing random walk but make them intersect eventually with probability 1. The difference in each coordinate will be a 1-dimensional random walk which gets stuck at 0 .
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
2
| null |
USA_TST
|
Find all functions $f: \mathbb{Z}^{2} \rightarrow[0,1]$ such that for any integers $x$ and $y$, $$ f(x, y)=\frac{f(x-1, y)+f(x, y-1)}{2} $$
|
We claim that the only functions $f$ are constant functions. (It is easy to see that they work.) I Third solution (martingales). Imagine starting at $(x, y)$ and taking a random walk down and to the left. This is a martingale. As $f$ is bounded, this martingale converges with probability 1 . Let $X_{1}, X_{2}, \ldots$ each be random variables that represent either down moves or left moves with equal probability. Note that by the Hewitt-Savage 0-1 law, we have that for any real numbers $a<b$, $$ \operatorname{Pr}\left[\lim _{n \rightarrow \infty} f\left((x, y)+X_{1}+X_{2}+\cdots+X_{n}\right) \in[a, b]\right] \in\{0,1\} $$ Hence, there exists a single value $v$ such that with probability 1 , $$ \operatorname{Pr}\left[\lim _{n \rightarrow \infty} f\left((x, y)+X_{1}+X_{2}+\cdots+X_{n}\right)=v\right]=1 $$ Obviously, this value $v$ must equal $f(x, y)$. Now, we show this value $v$ is the same for all $(x, y)$. Note that any two starting points have a positive chance of meeting. Therefore, we are done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
3
| null |
USA_TST
|
At a university dinner, there are 2017 mathematicians who each order two distinct entrées, with no two mathematicians ordering the same pair of entrées. The cost of each entrée is equal to the number of mathematicians who ordered it, and the university pays for each mathematician's less expensive entrée (ties broken arbitrarily). Over all possible sets of orders, what is the maximum total amount the university could have paid?
|
In graph theoretic terms: we wish to determine the maximum possible value of $$ S(G):=\sum_{e=v w} \min (\operatorname{deg} v, \operatorname{deg} w) $$ across all graphs $G$ with 2017 edges. We claim the answer is $63 \cdot\binom{64}{2}+1=127009$. 【 First solution (combinatorial, Evan Chen). First define $L_{k}$ to consist of a clique on $k$ vertices, plus a single vertex connected to exactly one vertex of the clique. Hence $L_{k}$ has $k+1$ vertices, $\binom{k}{2}+1$ edges, and $S\left(L_{k}\right)=(k-1)\binom{k}{2}+1$. In particular, $L_{64}$ achieves the claimed maximum, so it suffices to prove the upper bound. ## Lemma Let $G$ be a graph such that either - $G$ has $\binom{k}{2}$ edges for some $k \geq 3$ or - $G$ has $\binom{k}{2}+1$ edges for some $k \geq 4$. Then there exists a graph $G^{*}$ with the same number of edges such that $S\left(G^{*}\right) \geq S(G)$, and moreover $G^{*}$ has a universal vertex (i.e. a vertex adjacent to every other vertex). 1. Suppose $n=k$ and $m=\binom{k}{2}$. Then $G$ must be a clique so pick $G^{*}=G$. 2. Suppose $n=k+1$ and $m=\binom{k}{2}+1$. If $G$ has no universal vertex, we claim we may take $G^{*}=L_{k}$. Indeed each vertex of $G$ has degree at most $k-1$, and the average degree is $$ \frac{2 m}{n}=\frac{k^{2}-k+2}{k+1}<k-1 $$ using here $k \geq 4$. Thus there exists a vertex $w$ of degree $1 \leq d \leq k-2$. The edges touching $w$ will have label at most $d$ and hence $$ \begin{aligned} S(G) & \leq(k-1)(m-d)+d^{2}=(k-1) m-d(k-1-d) \\ & \leq(k-1) m-(k-2)=(k-1)\binom{k}{2}+1=S\left(G^{*}\right) \end{aligned} $$ Now we settle the inductive step. Let $w$ be a vertex with minimal degree $0 \leq d<k-1$, with neighbors $w_{1}, \ldots, w_{d}$. By our assumption, for each $w_{i}$ there exists a vertex $v_{i}$ for which $v_{i} w_{i} \notin E$. Now, we may delete all edges $w w_{i}$ and in their place put $v_{i} w_{i}$, and then delete the vertex $w$. This gives a graph $G^{\prime}$, possibly with multiple edges (if $v_{i}=w_{j}$ and $w_{j}=v_{i}$ ), and with one fewer vertex.  We then construct a graph $G^{\prime \prime}$ by taking any pair of double edges, deleting one of them, and adding any missing edge of $G^{\prime \prime}$ in its place. (This is always possible, since when $m=\binom{k}{2}$ we have $n-1 \geq k$ and when $m=\binom{k}{2}+1$ we have $n-1 \geq k+1$.) Thus we have arrived at a simple graph $G^{\prime \prime}$ with one fewer vertex. We also observe that we have $S\left(G^{\prime \prime}\right) \geq S(G)$; after all every vertex in $G^{\prime \prime}$ has degree at least as large as it did in $G$, and the $d$ edges we deleted have been replaced with new edges which will have labels at least $d$. Hence we may apply the inductive hypothesis to the graph $G^{\prime \prime}$ to obtain $G^{*}$ with $S\left(G^{*}\right) \geq S\left(G^{\prime \prime}\right) \geq S(G)$. The problem then is completed once we prove the following: Claim - For any graph $G$, - If $G$ has $\binom{k}{2}$ edges for $k \geq 3$, then $S(G) \leq\binom{ k}{2} \cdot(k-1)$. - If $G$ has $\binom{k}{2}+1$ edges for $k \geq 4$, then $S(G) \leq\binom{ k}{2} \cdot(k-1)+1$. Let $H$ be the subgraph obtained when $v$ is deleted. Then $m=\binom{k}{2}+\varepsilon-p$ is the number of edges in $H$; from $p \geq k-1+\varepsilon$ we have $m \leq\binom{ k-1}{2}$ and so we may apply the inductive hypothesis to $H$ to deduce $S(H) \leq\binom{ k-1}{2} \cdot(k-2)$.  Now the labels of edges $v w_{i}$ have sum $$ \sum_{i=1}^{p} \min \left(\operatorname{deg}_{G} v, \operatorname{deg}_{G} w_{i}\right)=\sum_{i=1}^{p} \operatorname{deg}_{G} w_{i}=\sum_{i=1}^{p}\left(\operatorname{deg}_{H} w_{i}+1\right)=2 m+p $$ For each of the edges contained in $H$, the label on that edge has increased by exactly 1, so those edges contribute $S(H)+m$. In total, $$ \begin{aligned} S(G) & =2 m+p+(S(H)+m)=(m+p)+2 m+S(H) \\ & \leq\binom{ k}{2}+\varepsilon+2\binom{k-1}{2}+\binom{k-1}{2}(k-2)=\binom{k}{2}(k-1)+\varepsilon \end{aligned} $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
3
| null |
USA_TST
|
At a university dinner, there are 2017 mathematicians who each order two distinct entrées, with no two mathematicians ordering the same pair of entrées. The cost of each entrée is equal to the number of mathematicians who ordered it, and the university pays for each mathematician's less expensive entrée (ties broken arbitrarily). Over all possible sets of orders, what is the maximum total amount the university could have paid?
|
In graph theoretic terms: we wish to determine the maximum possible value of $$ S(G):=\sum_{e=v w} \min (\operatorname{deg} v, \operatorname{deg} w) $$ across all graphs $G$ with 2017 edges. We claim the answer is $63 \cdot\binom{64}{2}+1=127009$. 【I Second solution (algebraic, submitted by contestant James Lin). We give a different proof of $S(G) \leq 127009$. The proof proceeds using the following two claims, which will show that $S(G) \leq 127010$ for all graphs $G$. Then a careful analysis of the equality cases will show that this bound is not achieved for any graph $G$. Since the example $L_{64}$ earlier has $S\left(L_{64}\right)=127009$, this will solve the problem. ## Lemma (Combinatorial bound) Let $G$ be a graph with 2017 edges and let $d_{1} \geq d_{2} \geq \cdots \geq d_{n}$ be the degree sequence of the graph (thus $n \geq 65$ ). Then $$ S(G) \leq d_{2}+2 d_{3}+3 d_{4}+\cdots+63 d_{64}+d_{65} $$ $$ S(G)=\sum_{i=1}^{n} a_{i} d_{i} $$ The inequality $\sum a_{i} d_{i} \leq d_{2}+2 d_{3}+3 d_{4}+\cdots+63 d_{64}+d_{65}$ then follows for smoothing reasons (by "smoothing" the $a_{i}$ ), since the $d_{i}$ are monotone. This proves the given inequality. Once we have this property, we handle the bounding completely algebraically. ## Lemma (Algebraic bound) Let $x_{1} \geq x_{2} \geq \cdots \geq x_{65}$ be any nonnegative integers such that $\sum_{i=1}^{65} x_{i} \leq 4034$. Then $$ x_{2}+2 x_{3}+\cdots+63 x_{64}+x_{65} \leq 127010 $$ Moreover, equality occurs if and only if $x_{1}=x_{2}=x_{3}=\cdots=x_{64}=63$ and $x_{65}=2$. - Suppose there are indices $1 \leq i<j \leq 64$ such that $x_{i}>x_{i+1} \geq x_{j-1}>x_{j}$. Then replacing $\left(x_{i}, x_{j}\right)$ by $\left(x_{i}-1, x_{j}+1\right)$ strictly increases $A$ preserving all conditions. Thus we may assume all numbers in $\left\{x_{1}, \ldots, x_{64}\right\}$ differ by at most 1 . - Suppose $x_{65} \geq 4$. Then we can replace $\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{65}\right)$ by $\left(x_{1}+1, x_{2}+1, x_{3}+\right.$ $\left.1, x_{4}+1, x_{65}-4\right)$ and strictly increase $A$. Hence we may assume $x_{65} \leq 3$. We will also tacitly assume $\sum x_{i}=4034$, since otherwise we can increase $x_{1}$. These two properties leave only four sequences to examine: - $x_{1}=x_{2}=x_{3}=\cdots=x_{63}=63, x_{64}=62$, and $x_{65}=3$, which gives $A=126948$. - $x_{1}=x_{2}=x_{3}=\cdots=x_{63}=x_{64}=63$ and $x_{65}=2$, which gives $A=127010$. - $x_{1}=64, x_{2}=x_{3}=\cdots=x_{63}=x_{64}=63$ and $x_{65}=1$, which gives $A=127009$. - $x_{1}=x_{2}=64, x_{3}=\cdots=x_{63}=x_{64}=63$ and $x_{65}=0$, which gives $A=127009$. This proves that $A \leq 127010$. To see that equality occurs only in the second case above, note that all the smoothing operations other than incrementing $x_{1}$ were strict, and that $x_{1}$ could not have been incremented in this way as $x_{1}=x_{2}=63$. This shows that $S(G) \leq 127010$ for all graphs $G$, so it remains to show equality never occurs. Retain the notation $d_{i}$ and $a_{i}$ of the combinatorial bound now; we would need to have $d_{1}=\cdots=d_{64}=63$ and $d_{65}=2$ (in particular, deleting isolated vertices from $G$, we may assume $n=65$ ). In that case, we have $a_{i} \leq i-1$ but also $a_{65}=2$ by definition (the last vertex gets all edges associated to it). Finally, $$ \begin{aligned} S(G) & =\sum_{i=1}^{n} a_{i} d_{i}=63\left(a_{1}+\cdots+a_{64}\right)+a_{65} \\ & =63\left(2017-a_{65}\right)+a_{65} \leq 63 \cdot 2015+2=126947 \end{aligned} $$ Remark. Another way to finish once $S(G) \leq 127010$ is note there is a unique graph (up to isomorphism and deletion of universal vertices) with degree sequence $\left(d_{1}, \ldots, d_{65}\right)=$ $(63, \ldots, 63,2)$. Indeed, the complement of the graph has degree sequence $(1, \ldots, 1,63)$, and so it must be a 63 -star plus a single edge. One can then compute $S(G)$ explicitly for this graph. ## 【 Some further remarks. Remark. Interestingly, the graph $C_{4}$ has $\binom{3}{2}+1=4$ edges and $S\left(C_{4}\right)=8$, while $S\left(L_{3}\right)=7$. This boundary case is visible in the combinatorial solution in the base case of the first claim. It also explains why we end up with the bound $S(G) \leq 127010$ in the second algebraic solution, and why it is necessary to analyze the equality cases so carefully; observe in $k=3$ the situation $d_{1}=d_{2}=d_{3}=d_{4}=2$. Remark. Some comments about further context for this problem: - The obvious generalization of 2017 to any constant was resolved in September 2018 by Mehtaab Sawhney and Ashwin Sah. The relevant paper is On the discrepancy between two Zagreb indices, published in Discrete Mathematics, Volume 341, Issue 9, pages 2575-2589. The arXiv link is https://arxiv.org/pdf/1801.02532.pdf. - The quantity $$ S(G)=\sum_{e=v w} \min (\operatorname{deg} v, \operatorname{deg} w) $$ in the problem has an interpretation: it can be used to provide a bound on the number of triangles in a graph $G$. To be precise, $\# E(G) \leq \frac{1}{3} S(G)$, since an edge $e=v w$ is part of at most $\min (\operatorname{deg} v, \operatorname{deg} w)$ triangles. - For planar graphs it is known $S(G) \leq 18 n-36$ and it is conjectured that for $n$ large enough, $S(G) \leq 18 n-72$. See https://mathoverflow.net/a/273694/70654. I Authorship comments. I came up with the quantity $S(G)$ in a failed attempt to provide a bound on the number of triangles in a graph, since this is natural to consider when you do a standard double-counting via the edges of the triangle. I think the problem was actually APMO 1989, and I ended up not solving the problem (the solution is much simpler), but the quantity $S(G)$ stuck in my head for a while after that. Later on that month I was keeping Danielle company while she was working on art project (flower necklace), and with not much to do except doodle on tables I began thinking about $S(G)$ again. I did have the sense that $S(G)$ should be maximized at a graph close to a complete graph. But to my frustration I could not prove it for a long time. Finally after many hours of trying various approaches I was able to at least show that $S(G)$ was maximized for complete graphs if the number of edges was a triangular number. I had come up with this in March 2016, which would have been perfect since 2016 is a triangular number, but it was too late to submit it to any contest (the USAMO and IMO deadlines were long past). So on December 31, 2016 I finally sat down and solved it for the case 2017, which took another few hours of thought, then submitted it to that year's IMO. To my dismay it was rejected, but I passed it along to the USA TST after that, thus making it just in time for the close of the calendar year.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
4
| null |
USA_TST
|
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 First solution (induction). We prove all $P_{k}$ are equivalent by induction on $n \geq 2$, with the base case $n=2$ being easy to check by hand. (The case $n=1$ is also vacuous; however, the inductive step is not able to go from $n=1$ to $n=2$.) For the inductive step, we proceed by contradiction; assume $S$ satisfies $P_{\ell}$, but not $P_{k}$, so there exist $x_{1}, \ldots, x_{2 k+1} \in S$ whose majority $y=M\left(x_{1}, \ldots, x_{k}\right)$ is not in $S$. We contend that: Claim - Let $y_{i}$ be the string which differs from $y$ only in the $i^{\text {th }}$ bit. Then $y_{i} \in S$. $$ T=\{\hat{s} \mid s \in S\} $$ Since $S$ satisfies $P_{\ell}$, so does $T$; thus by the induction hypothesis on $n, T$ satisfies $P_{k}$. Consequently, $T \ni M\left(\hat{x}_{1}, \ldots, \hat{x}_{2 k+1}\right)=\hat{y}$. Thus there exists $s \in S$ such that $\hat{s}=\hat{y}$. This implies $s=y$ or $s=y_{i}$. But since we assumed $y \notin S$ it follows $y_{i} \in S$ instead. Now take any $2 \ell+1$ copies of the $y_{i}$, about equally often (i.e. the number of times any two $y_{i}$ are taken differs by at most 1 ). We see the majority of these is $y$ itself, contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
4
| null |
USA_TST
|
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 Second solution (circuit construction). Note that $P_{k} \Longrightarrow P_{1}$ for any $k$, since $$ M(\underbrace{a, \ldots, a}_{k}, \underbrace{b, \ldots, b}_{k}, c)=M(a, b, c) $$ for any $a, b, c$. We will now prove $P_{1}+P_{k} \Longrightarrow P_{k+1}$ for any $k$, which will prove the result. Actually, we will show that the majority of any $2 k+3$ strings $x_{1}, \ldots, x_{2 k+3}$ can be expressed by 3 and $(2 k+1)$-majorities. WLOG assume that $M\left(x_{1}, \ldots, x_{2 k+3}\right)=0 \ldots 0$, and let $\odot$ denote binary AND. Claim - We have $M\left(x_{1}, x_{2}, M\left(x_{3}, \ldots, x_{2 k+3}\right)\right)=x_{1} \odot x_{2}$. By analogy we can construct any $x_{i} \odot x_{j}$. Finally, note that $$ M\left(x_{1} \odot x_{2}, x_{2} \odot x_{3}, \ldots, x_{2 k+1} \odot x_{2 k+2}\right)=0 \ldots 0 $$ as desired. (Indeed, if we look at any index, there were at most $k+1$ 's in the $x_{i}$ strings, and hence there will be at most $k$ 's among $x_{i} \odot x_{i+1}$ for $i=1, \ldots, 2 k+1$.)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
5
| null |
USA_TST
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$. 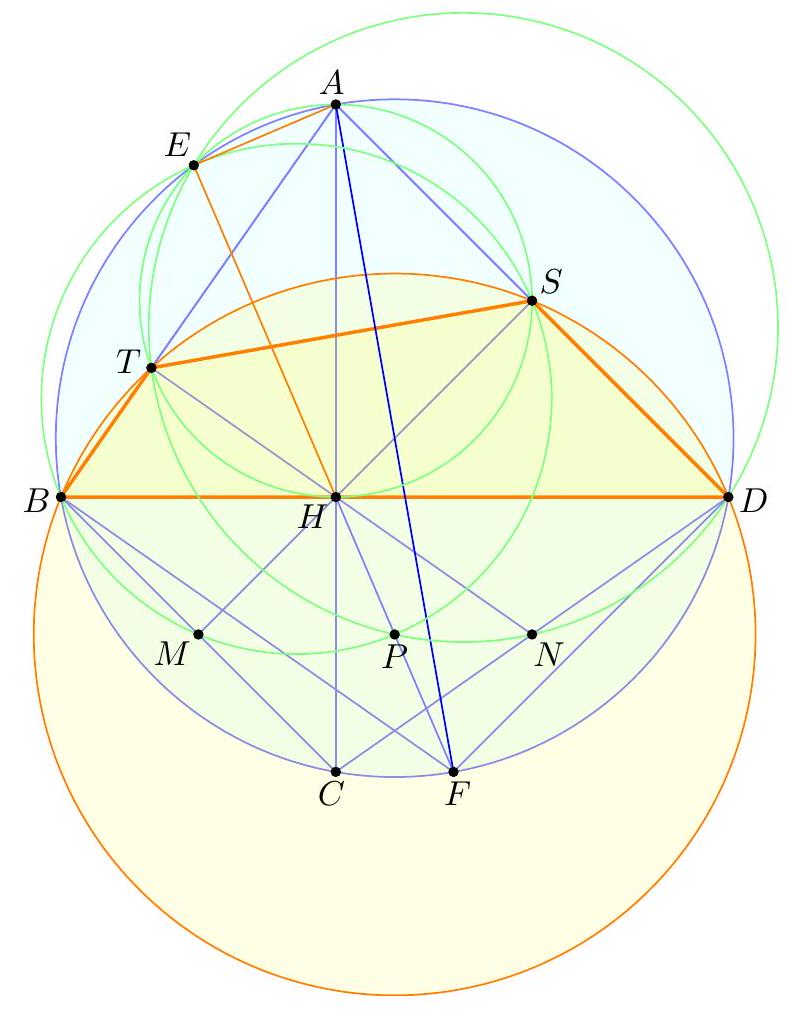 The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I First proof (original solution). Let $P$ be the circumcenter of $B T S D$. The properties of the Miquel point imply $P$ lies on the common bisector $\overline{E H}$ already, and it also lies on the perpendicular bisector of $\overline{B D}$, hence it must be the midpoint of $\overline{H F}$. We now contend quadrilaterals $B M P S$ and $D N P T$ are cyclic. Obviously $\overline{M P}$ is the external angle bisector of $\angle B M S$, and $P B=P S$, so $P$ is the arc midpoint of $(B M S)$. The proof for $D N P T$ is analogous. It remains to show $\angle B E N=\angle M E D$, or equivalently $\angle B E M=\angle N E D$. By properties of Miquel point we have $E \in(B M P S) \cap(T P N D)$, so $$ \measuredangle B E M=\measuredangle B P M=\measuredangle P B D=\measuredangle B D P=\measuredangle N P D=\measuredangle N E D $$ as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
5
| null |
USA_TST
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. 【 Second proof (2011 G4). By 2011 G 4 , the circumcircle of $\triangle E M N$ is tangent to the circumcircle of $A B C D$. Hence if we extend $\overline{E M}$ and $\overline{E N}$ to meet $(A B C D)$ again at $X$ and $Y$, we get $\overline{X Y}\|\overline{M N}\| \overline{B D}$. Thus $\measuredangle B E M=\measuredangle B E X=\measuredangle Y E D=\measuredangle N E D$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
5
| null |
USA_TST
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I Third proof (involutions, submitted by Daniel Liu). Let $G=\overline{B N} \cap \overline{M D}$ denote the centroid of $\triangle B C D$, and note that it lies on $\overline{E H F}$. Now consider the dual of Desargues involution theorem on complete quadrilateral $B M D N C G$ at point $E$. We get $$ (E B, E D), \quad(E M, E N), \quad(E C, E G) $$ form an involutive pairing. However, the bisector of $\angle B E D$, say $\ell$, is also the angle bisector of $\angle C E F$ (since $\overline{C F} \| \overline{B D})$. So the involution we found must coincide with reflection across $\ell$. This means $\angle M E N$ is bisected by $\ell$ as well, as desired. 【 Authorship comments. This diagram actually comes from the inverted picture in IMO 2014/3 (which I attended). I had heard for many years that one could solve this problem quickly by inversion at $H$ afterwards. But when I actually tried to do it during an OTIS class years later, I ended up with the picture in the TST problem, and couldn't see why it was true! In the process of trying to reconstruct this rumored solution, I ended up finding most of the properties that ended up in the January TST problem (but were overkill for the original IMO problem). Let us make the equivalence explicit by deducing the IMO problem from our work. Let rays $E M$ and $E N$ meet the circumcircles of $\triangle B H C$ and $\triangle B N C$ again at $X$ and $Y$, with $E M<E X$ and $E N<E Y$. As above we concluded $E M / E X=E N / E Y$ and so $\overline{M N} \| \overline{X Y} \Longrightarrow \overline{X Y} \perp \overline{A H C}$. Now consider an inversion at $H$ which swaps $B \leftrightarrow D$ and $A \leftrightarrow C$. The point $E$ goes to $E^{*}$ diametrically opposite $A$. Points $X$ and $Y$ go to points on $X^{*} \in \overline{A D}$ and $Y^{*} \in \overline{A B}$. Since the reflection of $E$ across $\overline{P X}$ is supposed to lie on $(B A E)$, it follows that the circumcenter of $\triangle H X^{*} E^{*}$ lies on $\overline{A D}$. Consequently $X^{*}$ plays the role of point " $T$ " in the IMO problem. Then $Y^{*}$ plays the role of point " $S$ " in the IMO problem. Now the fact that $\left(H X^{*} Y^{*}\right)$ is tangent to $\overline{B D}$ is equivalent to $\overline{X Y} \perp \overline{A H C}$ which we already knew.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2018
|
T0
|
6
| null |
USA_TST
|
Alice and Bob play a game. First, Alice secretly picks a finite set $S$ of lattice points in the Cartesian plane. Then, for every line $\ell$ in the plane which is horizontal, vertical, or has slope +1 or -1 , she tells Bob the number of points of $S$ that lie on $\ell$. Bob wins if he can then determine the set $S$. Prove that if Alice picks $S$ to be of the form $$ S=\left\{(x, y) \in \mathbb{Z}^{2} \mid m \leq x^{2}+y^{2} \leq n\right\} $$ for some positive integers $m$ and $n$, then Bob can win. (Bob does not know in advance that $S$ is of this form.)
|
Clearly Bob can compute the number $N$ of points. The main claim is that: Claim - Fix $m$ and $n$ as in the problem statement. Among all sets $T \subseteq \mathbb{Z}^{2}$ with $N$ points, the set $S$ is the unique one which maximizes the value of $$ F(T):=\sum_{(x, y) \in T}\left(x^{2}+y^{2}\right)\left(m+n-\left(x^{2}+y^{2}\right)\right) . $$ As a result of this observation, it suffices to show that Bob has enough information to compute $F(S)$ from the data given. (There is no issue with fixing $m$ and $n$, since Bob can find an upper bound on the magnitude of the points and then check all pairs ( $m, n$ ) smaller than that.) The idea is that he knows the full distribution of each of $X, Y$, $X+Y, X-Y$ and hence can compute sums over $T$ of any power of a single one of those linear functions. By taking linear combinations we can hence compute $F(S)$. Let us make the relations explicit. For ease of exposition we take $Z=(X, Y)$ to be a uniformly random point from the set $S$. The information is precisely the individual distributions of $X, Y, X+Y$, and $X-Y$. Now compute $$ \begin{aligned} \frac{F(S)}{N} & =\mathbb{E}\left[(m+n)\left(X^{2}+Y^{2}\right)-\left(X^{2}+Y^{2}\right)^{2}\right] \\ & =(m+n)\left(\mathbb{E}\left[X^{2}\right]+\mathbb{E}\left[Y^{2}\right]\right)-\mathbb{E}\left[X^{4}\right]-\mathbb{E}\left[Y^{4}\right]-2 \mathbb{E}\left[X^{2} Y^{2}\right] \end{aligned} $$ On the other hand, $$ \mathbb{E}\left[X^{2} Y^{2}\right]=\frac{\mathbb{E}\left[(X+Y)^{4}\right]+\mathbb{E}\left[(X-Y)^{4}\right]-2 \mathbb{E}\left[X^{4}\right]-2 \mathbb{E}\left[Y^{4}\right]}{12} $$ Thus we have written $F(S)$ in terms of the distributions of $X, Y, X-Y, X+Y$ which completes the proof. - An obstruction to purely combinatorial arguments is that if you take an octagon with points $( \pm a, \pm b)$ and $( \pm b, \pm a)$ then the two ways to pick every other point (going around clockwise) are indistinguishable by Bob. This at least shows that Bob's task is far from possible in general, and hints at proving an inequality. - A related and more standard fact (among a certain type of person) is that given a probability distribution $\mu$ on $\mathbb{R}^{n}$, if I tell you the distribution of all 1-dimensional projections of $\mu$, that determines $\mu$ uniquely. This works because this information gives me the Fourier transform $\hat{\mu}$, and Fourier transforms are injective. For the continuum version of this problem, this connection gives a much larger family of counterexamples to any proposed extension to arbitrary non-annular shapes. Indeed, take a fast-decaying smooth function $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ which vanishes on the four lines $$ x=0, y=0, x+y=0, x-y=0 . $$ Then the Fourier transform $\hat{f}$ will have mean 0 on each line $\ell$ as in the problem statement. Hence the positive and negative parts of $\hat{f}$ will not be distinguishable by Bob.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
『 First solution using symmedians (Merlijn Staps). Let $\overline{X Y}$ be the other tangent from $X$ to $(A M N)$. Claim - Line $\overline{X M}$ is tangent to $(B M Y)$; hence $Y$ lies on $\omega_{B}$. 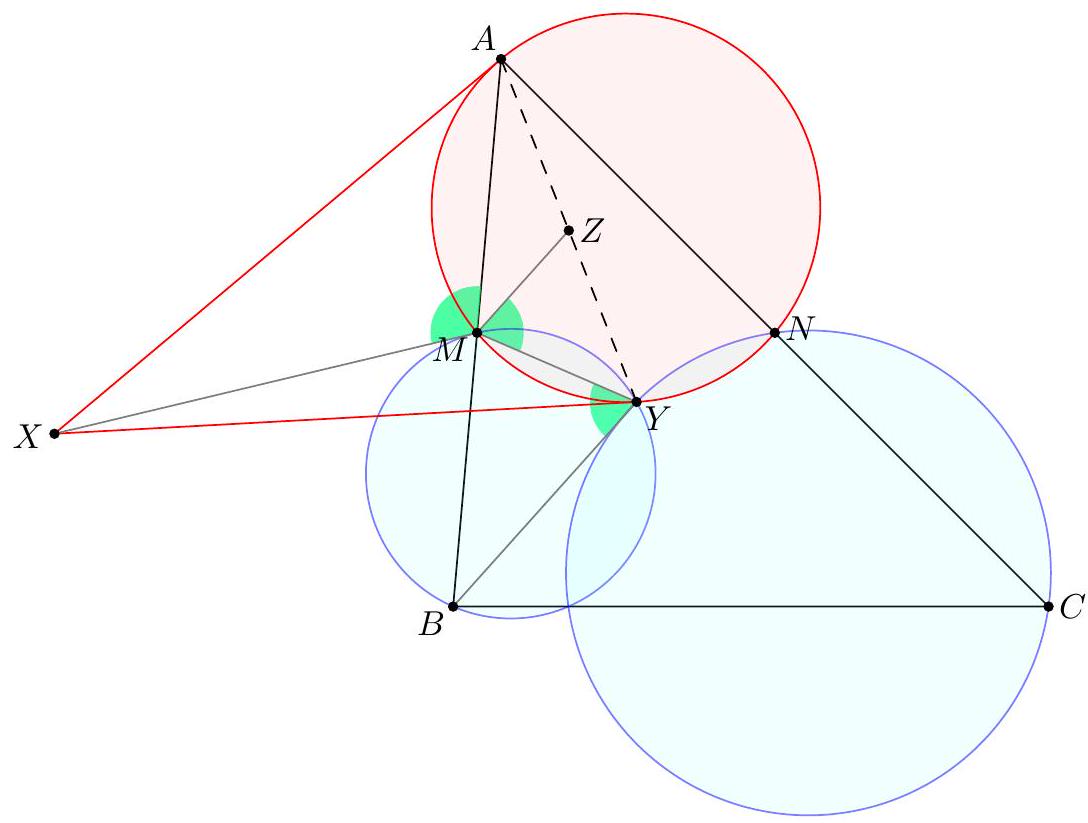 Similarly, $\omega_{C}$ is the circumcircle of triangle $C N Y$. As $A M Y N$ is cyclic too, it follows that $\omega_{B}$ and $\omega_{C}$ intersect on $\overline{B C}$, by Miquel's theorem. Remark. The converse of Miquel's theorem is true, which means the problem is equivalent to showing that the second intersection of the $\omega_{B}$ and $\omega_{C}$ moves along $(A M N)$. Thus the construction of $Y$ above is not so unnatural.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Second solution (Jetze Zoethout). Let $\omega_{B}$ intersect $\overline{B C}$ again at $S$ and let $\overline{M S}$ intersect $\overline{A C}$ again at $Y$. Angle chasing gives $\measuredangle X M Y=\measuredangle X M S=\measuredangle M B S=\measuredangle A B C=$ $\measuredangle X A C=\measuredangle X A Y$, so $Y$ is on the circumcircle of triangle $A M X$. Furthermore, from $\measuredangle X M Y=\measuredangle A B C$ and $\measuredangle A C B=\measuredangle X A B=\measuredangle X Y M$ it follows that $\triangle A B C \sim \triangle X M Y$ and from $\measuredangle X A Y=\measuredangle M B S$ and $\measuredangle Y X A=\measuredangle Y M A=\measuredangle B M S$ it follows that $\triangle A X Y \sim$ $\triangle B M S$. 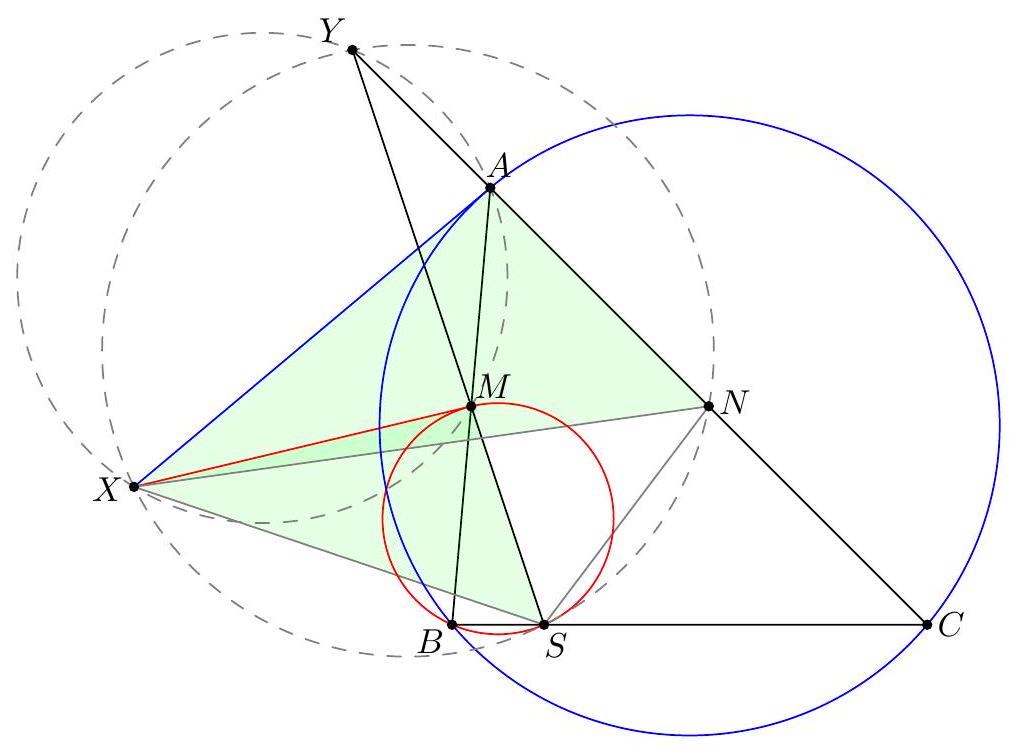 We now find $$ \frac{A N}{A X}=\frac{A N / B M}{A X / B M}=\frac{A C / A B}{M S / X Y}=\frac{A B / A B}{M S / X M}=\frac{X M}{M S} $$ which together with $\angle X M S=\angle X A N$ yields $\triangle X M S \sim \triangle X A N$. From $\measuredangle X S Y=$ $\measuredangle X S M=\measuredangle X N A=\measuredangle X N Y$ we now have that $S$ is on the circumcircle of triangle $X N Y$. Finally, we have $\measuredangle X N S=\measuredangle X Y S=\measuredangle X Y M=\measuredangle A C B=\measuredangle N C S$ so $\overline{X N}$ is tangent to the circle through $C, N$, and $S$, as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Third solution by moving points method. Fix triangle $A B C$ and animate $X$ along the tangent at $A$. We let $D$ denote the second intersection point of $\omega_{C}$ with line $\overline{B C}$. Claim - The composed map $X \mapsto D$ is a fractional linear transformation (i.e. a projective map) in terms of a real coordinate on line $\overline{A A}, \overline{B C}$. We claim that the composed map $$ \begin{aligned} & \overline{A A} \rightarrow \ell \rightarrow \ell \rightarrow \overline{B C} \rightarrow \overline{B C} \\ & \text { by } \quad X \mapsto P \mapsto S \mapsto T \mapsto D \end{aligned} $$ is projective, by showing each individual map is projective. 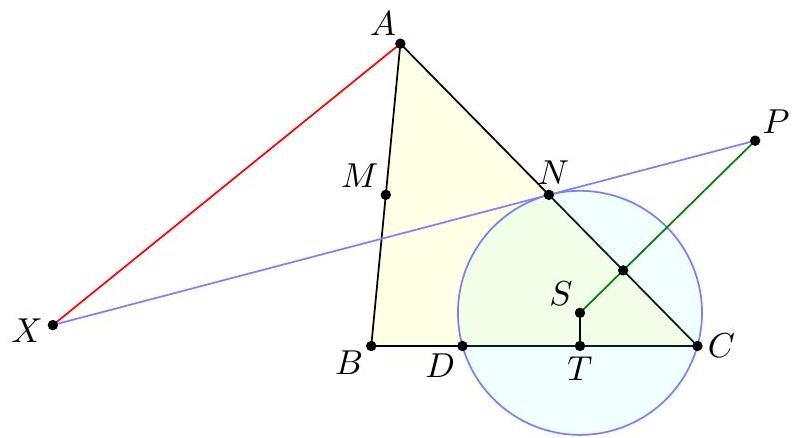 - The map $X \mapsto P$ is projective since it is a perspectivity through $N$ from $\overline{A A}$ to $\ell$. - The map $P \mapsto S$ is projective since it is equivalent to a negative inversion on $\ell$ at the midpoint of $\overline{N C}$ with radius $\frac{1}{2} N C$. (Note $\angle P N S=90^{\circ}$ is fixed.) - The map $S \mapsto T$ is projective since it is a perspectivity $\ell \rightarrow \overline{B C}$ through the point at infinity perpendicular to $\overline{B C}$ (in fact, it is linear). - The map $T \mapsto D$ is projective (in fact, linear) since it is a homothety through $C$ with fixed ratio 2 . Thus the composed map is projective as well. Similarly, if we define $D^{\prime}$ so that $\overline{X M}$ is tangent to $\left(B M D^{\prime}\right)$, the map $X \mapsto D^{\prime}$ is projective as well. We aim to show $D=D^{\prime}$, and since the maps correspond to fractional linear transformations in projective coordinates, it suffices to verify it for three distinct choices of $X$. We do so: - If $X=\overline{A A} \cap \overline{M N}$, then $D$ and $D^{\prime}$ satisfy $M B=M D^{\prime}, N C=N D$. This means they are the feet of the $A$-altitude on $\overline{B C}$. - If $X$ is a point at infinity along $\overline{A A}$, then $D$ and $D^{\prime}$ coincide with the midpoint of $\overline{B C}$. Remark (Anant Mudgal). An alternative (shorter) way to show $X \mapsto D$ is projective is to notice $\measuredangle X N D$ is a constant angle. I left the longer "original" proof for instructional reasons.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
1
| null |
USA_TST
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
ब Fourth solution by isogonal conjugates (Anant Mudgal). Let $Y$ be the isogonal conjugate of $X$ in $\triangle A M N$ and $Z$ be the reflection of $Y$ in $\overline{M N}$. As $\overline{A X}$ is tangent to the circumcircle of $\triangle A M N$, it follows that $\overline{A Y} \| \overline{M N}$. Thus $Z$ lies on $\overline{B C}$ since $\overline{M N}$ bisects the strip made by $\overline{A Y}$ and $\overline{B C}$. 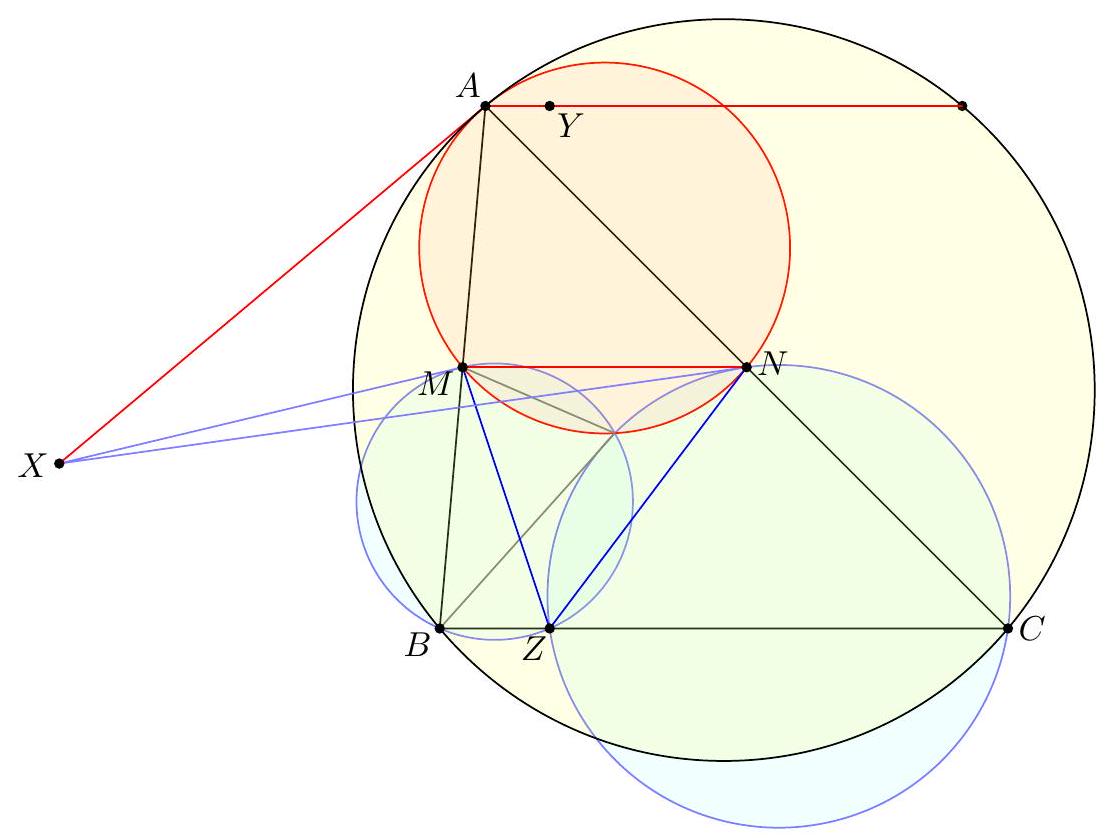 Finally, $$ \measuredangle Z M X=\measuredangle Z M N+\measuredangle N M X=\measuredangle N M Y+\measuredangle Y M A=\measuredangle N M A=\measuredangle Z B M $$ so $\overline{X M}$ is tangent to the circumcircle of $\triangle Z M B$, hence $Z$ lies on $\omega_{B}$. Similarly, $Z$ lies on $\omega_{C}$ and we're done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
2
| null |
USA_TST
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. TI First solution (original one). The proof is split into two essentially orthogonal claims, which we state as lemmas. Lemma (Lemma I: elimination of $g$ ) Assume valiant $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ exists. Then $$ k!\sum_{x \in \mathbb{Z} / n \mathbb{Z}} x^{k} \equiv 0 \quad(\bmod n) $$ for $k=0,1, \ldots, 100$. $$ k!x^{k}=\binom{k}{0} g_{x}(k)^{k}-\binom{k}{1} g_{x}(k-1)^{k}+\binom{k}{2} g_{x}(k-2)^{k}-\cdots+(-1)^{k}\binom{k}{k} g_{x}(0)^{k} $$ On the other hand, for any $1 \leq k \leq 100$ we should have $$ \begin{aligned} \sum_{x} g_{x}(0)^{k} \equiv \sum_{x} g_{x}(1)^{k} & \equiv \cdots \equiv \sum_{x} g_{x}(k)^{k} \\ & \equiv S_{k}:=0^{k}+\cdots+(n-1)^{k} \quad(\bmod n) \end{aligned} $$ by the hypothesis. Thus we find $$ k!\sum_{x} x^{k} \equiv\left[\binom{k}{0}-\binom{k}{1}+\binom{k}{2}-\cdots\right] S_{k} \equiv 0 \quad(\bmod n) $$ for any $1 \leq k \leq 100$, but also obviously for $k=0$. We now prove the following self-contained lemma. ## Lemma (Lemma II: power sum calculation) Let $p$ be a prime, and let $n, M$ be positive integers such that $$ M \quad \text { divides } \quad 1^{k}+2^{k}+\cdots+n^{k} $$ for $k=0,1, \ldots, p-1$. If $p \mid n$ then $\nu_{p}(M)<\nu_{p}(n)$. $$ \begin{aligned} 0 & \equiv \sum_{x=1}^{n}(x-1)(x-2) \cdots(x-(p-1)) \\ & =(p-1)!\sum_{x=1}^{n}\binom{x-1}{p-1}=(p-1)!\binom{n}{p} \quad(\bmod M) . \end{aligned} $$ But now $\nu_{p}(M) \leq \nu_{p}\left(\binom{n}{p}\right)=\nu_{p}(n)-1$. Now assume for contradiction that valiant $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ exists, and $p \leq 101$ is the smallest prime dividing $n$. Lemma I implies that $k!\sum_{x} x^{k} \equiv 0(\bmod n)$ for $k=1, \ldots, p-1$ and hence $\sum_{x} x^{k} \equiv 0(\bmod n)$ too. Thus $M=n$ holds in the previous lemma, impossible.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
2
| null |
USA_TST
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. \ A second solution. Both lemmas above admit variations where we focus on working modulo $p^{e}$ rather than working modulo $n$. ## Lemma (Lemma I') Assume valiant $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ exists. Let $p \leq 101$ be a prime, and $e=\nu_{p}(n)$. Then $$ \sum_{x \in \mathbb{Z} / n \mathbb{Z}} x^{k} \equiv 0 \quad\left(\bmod p^{e}\right) $$ for $k=0,1, \ldots, p-1$. $$ \sum_{x}(g(x)+T x)^{k} \equiv \sum_{x} x^{k} \quad\left(\bmod p^{e}\right) . $$ Both sides are integer polynomials in $T$, which vanish at $T=0,1, \ldots, p-1$ by hypothesis (since $p-1 \leq 100$ ). We now prove the following more general fact: if $f(T) \in \mathbb{Z}[T]$ is an integer polynomial with $\operatorname{deg} f \leq p-1$, such that $f(0) \equiv \cdots \equiv f(p-1) \equiv 0\left(\bmod p^{e}\right)$, then all coefficients of $f$ are divisible by $p^{e}$. The proof is by induction on $e \geq 1$. When $e=1$, this is just the assertion that the polynomial has at most $\operatorname{deg} f$ roots modulo $p$. When $e \geq 2$, we note that the previous result implies all coefficients are divisible by $p$, and then we divide all coefficients by $p$. Applied here, we have that all coefficients of $$ f(T):=\sum_{x}(g(x)+T x)^{k}-\sum_{x} x^{k} $$ are divisible by $p^{e}$. The leading $T^{k}$ coefficient is $\sum_{k} x^{k}$ as desired. ## Lemma (Lemma II') If $e \geq 1$ is an integer, and $p$ is a prime, then $$ \nu_{p}\left(1^{p-1}+2^{p-1}+\cdots+\left(p^{e}-1\right)^{p-1}\right)=e-1 $$ Let $g$ be an integer which is a primitive root modulo $p^{e}$. Then, we can sum the terms which are relatively prime to $p$ as $$ S_{0}:=\sum_{\operatorname{gcd}(x, p)=1} x^{p-1} \equiv \sum_{i=1}^{\varphi\left(p^{e}\right)} g^{(p-1) \cdot i} \equiv \frac{g^{p^{e-1}(p-1)^{2}}-1}{g^{p-1}-1} \quad\left(\bmod p^{e}\right) $$ which implies $\nu_{p}\left(S_{0}\right)=e-1$, by lifting the exponent. More generally, for $r \geq 1$ we may set $$ S_{r}:=\sum_{\nu_{p}(x)=r} x^{p-1} \equiv\left(p^{r}\right)^{p-1} \sum_{i=1}^{\varphi\left(p^{e-r}\right)} g_{r}^{(p-1) \cdot i} \quad\left(\bmod p^{e}\right) $$ where $g_{r}$ is a primitive root modulo $p^{e-r}$. Repeating the exponent-lifting calculation shows that $\nu_{p}\left(S_{r}\right)=r(p-1)+((e-r)-1)>e$, as needed. Assume to the contrary that $p \leq 101$ is a prime dividing $n$, and a valiant $g: \mathbb{Z} / n \mathbb{Z} \rightarrow$ $\mathbb{Z} / n \mathbb{Z}$ exists. Take $k=p-1$ in Lemma I' to contradict Lemma II'
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
2
| null |
USA_TST
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. 【 A third remixed solution. We use Lemma I and Lemma II' from before. As before, assume $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ is valiant, and $n$ has a prime divisor $p \leq 101$. Also, let $e=\nu_{p}(n)$. Then $(p-1)!\sum_{x} x^{p-1} \equiv 0(\bmod n)$ by Lemma I, and now $$ \begin{aligned} 0 & \equiv \sum_{x} x^{p-1} \quad\left(\bmod p^{e}\right) \\ & \equiv \frac{n}{p^{e}} \sum_{x=1}^{p^{e}-1} x^{p-1} \not \equiv 0 \quad\left(\bmod p^{e}\right) \end{aligned} $$ by Lemma II', contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
2
| null |
USA_TST
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. 【I A fourth remixed solution. We also can combine Lemma I' and Lemma II. As before, assume $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ is valiant, and let $p$ be the smallest prime divisor of $n$. Assume for contradiction $p \leq 101$. By Lemma I' we have $$ \sum_{x} x^{k} \equiv 0 \quad\left(\bmod p^{e}\right) $$ for $k=0, \ldots, p-1$. This directly contradicts Lemma II with $M=p^{e}$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
3
| null |
USA_TST
|
A snake of length $k$ is an animal which occupies an ordered $k$-tuple $\left(s_{1}, \ldots, s_{k}\right)$ of cells in an $n \times n$ grid of square unit cells. These cells must be pairwise distinct, and $s_{i}$ and $s_{i+1}$ must share a side for $i=1, \ldots, k-1$. If the snake is currently occupying $\left(s_{1}, \ldots, s_{k}\right)$ and $s$ is an unoccupied cell sharing a side with $s_{1}$, the snake can move to occupy ( $s, s_{1}, \ldots, s_{k-1}$ ) instead. The snake has turned around if it occupied $\left(s_{1}, s_{2}, \ldots, s_{k}\right)$ at the beginning, but after a finite number of moves occupies $\left(s_{k}, s_{k-1}, \ldots, s_{1}\right)$ instead. Determine whether there exists an integer $n>1$ such that one can place some snake of length at least $0.9 n^{2}$ in an $n \times n$ grid which can turn around.
| null |
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
4
| null |
USA_TST
|
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
【 First solution (Nikolai Beluhov). Let $k=a_{0}=b_{0}=c_{0}=d_{0}$. We let $f, g, h$ be great functions for $(A, B),(B, C),(C, D)$ and write the following infinite array: $$ \left[\begin{array}{ccccccc} & \vdots & \vdots & b_{3} & \vdots & \vdots & \\ \cdots & g(2,2) & g(2,1) & b_{2} & f(1,2) & f(2,2) & \cdots \\ \cdots & g(1,2) & g(1,1) & b_{1} & f(1,1) & f(2,1) & \cdots \\ c_{3} & c_{2} & c_{1} & k & a_{1} & a_{2} & a_{3} \\ \cdots & h(2,1) & h(1,1) & d_{1} & & & \\ \cdots & h(2,2) & h(1,2) & d_{2} & & & \\ & \vdots & \vdots & d_{3} & & & \ddots \end{array}\right] $$ The greatness condition is then equivalent to saying that any $2 \times 2$ sub-grid has determinant $\pm 1$ (the sign is +1 in two quadrants and -1 in the other two), and we wish to fill in the lower-right quadrant. To this end, it suffices to prove the following. ## Lemma Suppose we have a $3 \times 3$ sub-grid $$ \left[\begin{array}{lll} a & b & c \\ x & y & z \\ p & q & \end{array}\right] $$ satisfying the determinant conditions. Then we can fill in the ninth entry in the lower right with an integer while retaining greatness. If $y=0$ we have $-1=b z=b x=x q$, hence $q z=-1$, and we can fill in the entry arbitrarily. Otherwise, we have $b x \equiv x q \equiv b z \equiv-1(\bmod y)$. This is enough to imply $q z \equiv-1$ $(\bmod y)$, and so we can fill in the integer $\frac{q z+1}{y}$. Remark. In this case (of all +1 determinants), I think it turns out the bottom entry is exactly equal to $q z a-c y p-c-p$, which is obviously an integer.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
4
| null |
USA_TST
|
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
Second solution (Ankan Bhattacharya). We will give an explicit classification of great sequences: ## Lemma The pair $(A, B)$ is great if and only if $a_{0}=b_{0}, a_{0} \mid a_{1} b_{1}+1$, and $a_{n} \mid a_{n-1}+a_{n+1}$ and $b_{n} \mid b_{n-1}+b_{n+1}$ for all $n$. Now, focus on six entries $f(x, y)$ with $x \in\{n-1, n, n+1\}$ and $y \in\{0,1\}$. Let $f(n-1,1)=u, f(n, 1)=v$, and $f(n+1,1)=w$, so $$ \begin{aligned} v a_{n-1}-u a_{n} & =1 \\ w a_{n}-v a_{n+1} & =1 \end{aligned} $$ Then $$ u+w=\frac{v\left(a_{n-1}+a_{n+1}\right)}{a_{n}} $$ and from above $\operatorname{gcd}\left(v, a_{n}\right)=1$, so $a_{n} \mid a_{n-1}+a_{n+1}$; similarly for $b_{n}$. (If $a_{n}=0$, we have $v a_{n-1}=1$ and $v a_{n+1}=-1$, so this is OK.) First we set $f(1,1)$ so that $a_{0} f(1,1)=a_{1} b_{1}+1$, which is possible. Consider an uninitialized $f(s, t)$; without loss of generality suppose $s \geq 2$. Then we know five values of $f$ and wish to set a sixth one $z$, as in the matrix below: $$ \begin{array}{cc} u & x \\ v & y \\ w & z \end{array} $$ (We imagine $a$-indices to increase southwards and $b$-indices to increase eastwards.) If $v \neq 0$, then the choice $y \cdot \frac{u+w}{v}-x$ works as $u y-v x=1$. If $v=0$, it easily follows that $\{u, w\}=\{1,-1\}$ and $y=w$ as $y w=1$. Then we set the uninitialized entry to anything. Now we verify that this is compatible with the inductive hypothesis. From the determinant 1 condition, it easily follows that $\operatorname{gcd}(w, z)=\operatorname{gcd}(v, z)=1$. The proof that $y \mid x+z$ is almost identical to a step performed in the "necessary" part of the lemma and we do not repeat it here. By induction, a desired great function $f$ exists. Remark. To simplify the problem, we may restrict the codomain of great functions and elements in great pairs of sequences to $\mathbb{Z}_{>0}$. This allows the parts of the solution dealing with zero entries to be ignored. $$ f(x+1, y+1) f(x, y)-f(x+1, y) f(x, y+1)=-1 $$ A quick counterexample to transitivity of $\sim$ as is without the condition $f(0,0)=1$, for concreteness: let $a_{n}=c_{n}=3+n$ and $b_{n}=3+2 n$ for $n \geq 0$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
5
| null |
USA_TST
|
Let $n$ be a positive integer. Tasty and Stacy are given a circular necklace with $3 n$ sapphire beads and $3 n$ turquoise beads, such that no three consecutive beads have the same color. They play a cooperative game where they alternate turns removing three consecutive beads, subject to the following conditions: - Tasty must remove three consecutive beads which are turquoise, sapphire, and turquoise, in that order, on each of his turns. - Stacy must remove three consecutive beads which are sapphire, turquoise, and sapphire, in that order, on each of her turns. They win if all the beads are removed in $2 n$ turns. Prove that if they can win with Tasty going first, they can also win with Stacy going first.
|
In the necklace, we draw a divider between any two beads of the same color. Unless there are no dividers, this divides the necklace into several zigzags in which the beads in each zigzag alternate. Each zigzag has two endpoints (adjacent to dividers). Observe that the condition about not having three consecutive matching beads is equivalent to saying there are no zigzags of lengths 1.  The main claim is that the game is winnable (for either player going first) if and only if there are at most $2 n$ dividers. We prove this in two parts, the first part not using the hypothesis about three consecutive letters. Claim - The game cannot be won with Tasty going first if there are more than $2 n$ dividers. Consider removing a TST in some zigzag (necessarily of length at least 3). We illustrate the three possibilities in the following table, with Tasty's move shown in red. | Before | After | Change | | :---: | :---: | :---: | | . ST \| TST | TS . | ST \| TS . | One less divider; two zigzags merge | | . . ST \| TSTST . | STST | One less divider; two zigzags merge | | .STSTS . . | ..S\|S... | One more divider; a zigzag splits in t | The analysis for Stacy's move is identical. Claim - If there are at most $2 n$ dividers and there are no zigzags of length 1 then the game can be won (with either player going first). At any point if there are no dividers at all, then the necklace alternates $T S T S T \ldots$ and the game can be won. So we will prove that on each of Tasty's turns, if there exists at least one divider, then Tasty and Stacy can each make a move at an endpoint of some zigzag (i.e. the first two cases above). As we saw in the previous proof, such moves will (a) decrease the number of dividers by exactly one, (b) not introduce any singleton zigzags (because the old zigzags merge, rather than split). Since there are fewer than $2 n$ dividers, our duo can eliminate all dividers and then win. Note that as the number of $S$ and $T$ 's are equal, there must be an equal number of - zigzags of odd length ( $\geq 3$ ) with $T$ at the endpoints (i.e. one more $T$ than $S$ ), and - zigzags of odd length $(\geq 3)$ with $S$ at the endpoints (i.e. one more $S$ than $T$ ). Now iff there is at least one of each, then Tasty removes a TST from the end of such a zigzag while Stacy removes an $S T S$ from the end of such a zigzag. Otherwise suppose all zigzags have even size. Then Tasty finds any zigzag of length $\geq 4$ (which must exist since the average zigzag length is 3 ) and removes TST from the end containing $T$. The resulting merged zigzag is odd and hence $S$ endpoints, hence Stacy can move as well. Remark. There are many equivalent ways to phrase the solution. For example, the number of dividers is equal to the number of pairs of two consecutive letters (rather than singleton letters). So the win condition can also be phrased in terms of the number of adjacent pairs of letters being at least $2 n$, or equivalently the number of differing pairs being at least $4 n$. If one thinks about the game as a process, this is a natural "monovariant" to consider anyways, so the solution is not so unmotivated. Remark. The constraint of no three consecutive identical beads is actually needed: a counterexample without this constraint is TTSTSTSTTSSS. (They win if Tasty goes first and lose if Stacy goes first.) Remark (Why induction is unlikely to work). Many contestants attempted induction. However, in doing so they often implicitly proved a different problem: "prove that if they can win with Tasty going first without ever creating a triplet, they can also win in such a way with Stacy going first". This essentially means nearly all induction attempts fail. Amusingly, even the modified problem (which is much more amenable to induction) sill seems difficult without some sort of global argument. Consider a position in which Tasty wins going first, with the sequence of winning moves being Tasty's first move in red below and Stacy's second move in blue below:  There is no "nearby" STS that Stacy can remove instead on her first turn, without introducing a triple- $T$ and also preventing Tasty from taking a TST. So it does not seem possible to easily change a Tasty-first winning sequence to a Stacy-first one, even in the modified version.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 First solution using spiral similarity (Ankan Bhattacharya). First, we prove the part of the problem which does not depend on the condition $A B_{1} A_{1} C_{1}$ is cyclic. ## Lemma Let $A B C$ be a triangle and define $I, D, B_{1}, C_{1}$ as in the problem. Moreover, let $M$ denote the midpoint of $\overline{A D}$. Then $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$, and moreover $\overline{B_{1} C_{1}} \| \overline{I M}$. Note that $A, Z, D$ are collinear, by radical axis on $(A B C),(A F I E),(B I C)$. 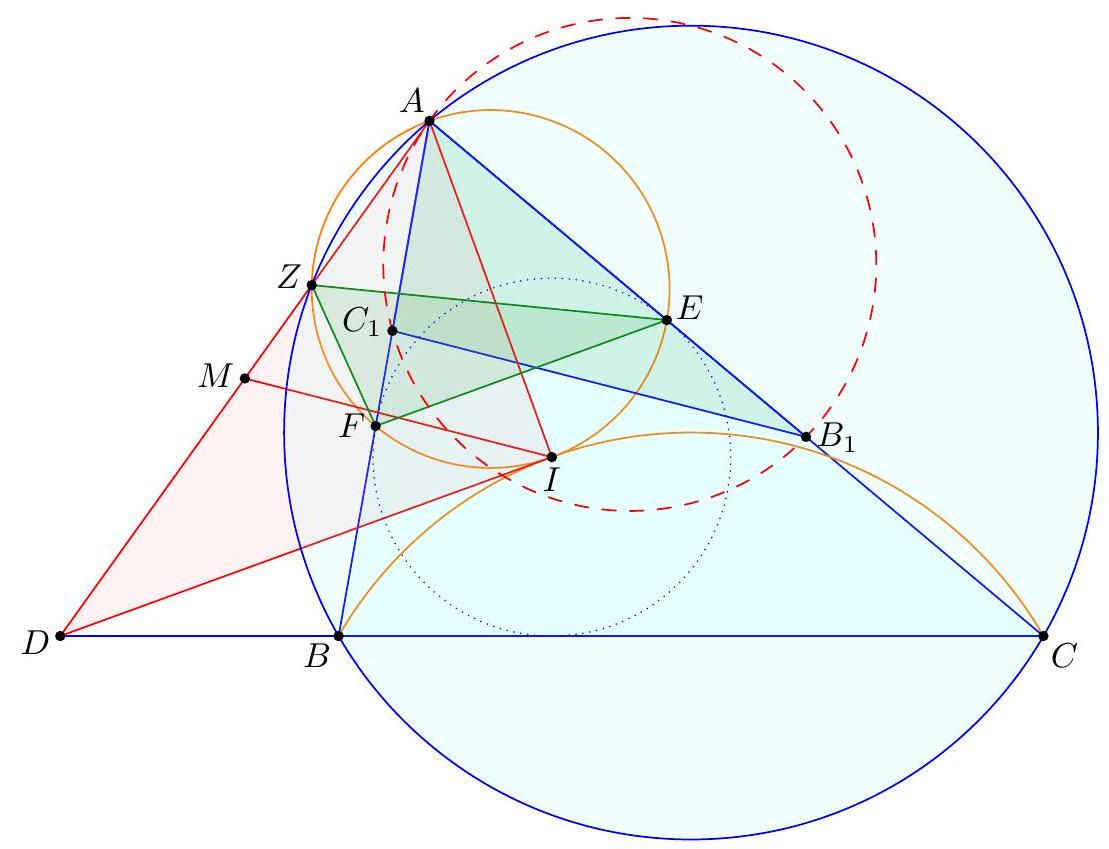 Then the spiral similarity gives us $$ \frac{Z F}{Z E}=\frac{B F}{C E}=\frac{A C_{1}}{A B_{1}} $$ which together with $\measuredangle F Z E=\measuredangle F A E=\measuredangle B A C$ implies that $\triangle Z F E$ and $\triangle A C_{1} B_{1}$ are (directly) similar. (See IMO Shortlist 2006 G9 for a similar application of spiral similarity.) $$ \measuredangle D A C_{1}=\measuredangle Z A F=\measuredangle Z E F=\measuredangle A B_{1} C_{1} $$ we have $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$. Moreover, to see that $\overline{I M} \| \overline{B_{1} C_{1}}$, write $$ \begin{aligned} \measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right) & =\measuredangle I A C+\measuredangle A B_{1} C_{1}=\measuredangle B A I+\measuredangle Z E F=\measuredangle F A I+\measuredangle Z A F \\ & =\measuredangle Z A I=\measuredangle M A I=\measuredangle A I M \end{aligned} $$ the last step since $\triangle A I D$ is right with hypotenuse $\overline{A D}$, and median $\overline{I M}$. Now we return to the present problem with the additional condition. 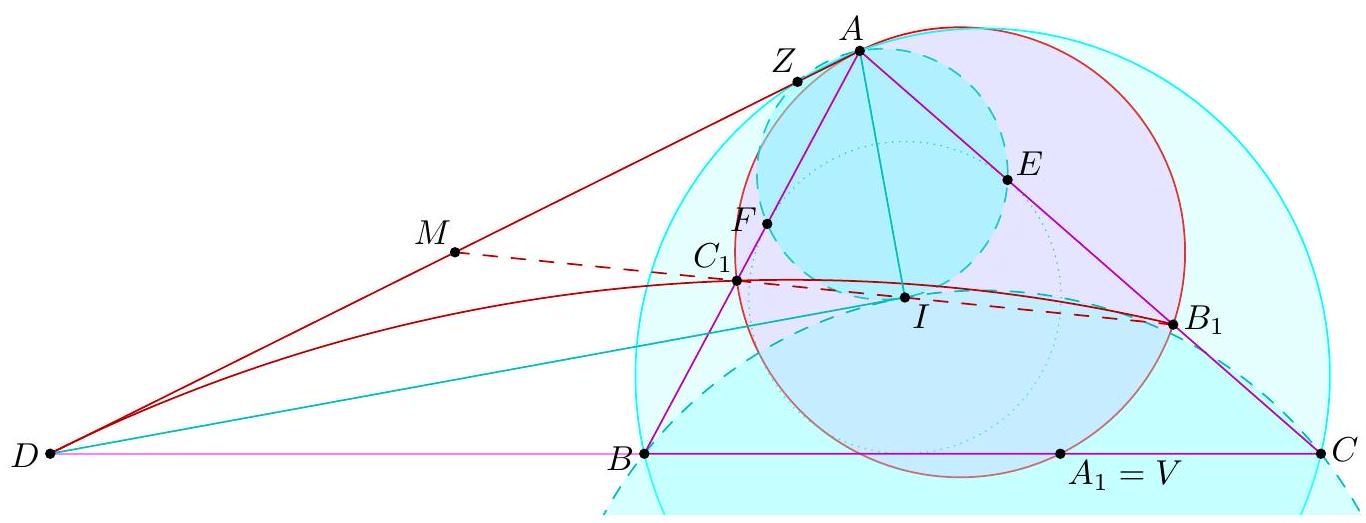 Claim - Given the condition, we actually have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$. Now $\triangle A B_{1} C_{1}$ has circumdiameter $\overline{A V}$. We are given $A_{1}$ lies on this circle, so if $V \neq A_{1}$ then $\overline{A A_{1}} \perp \overline{A_{1} V}$. But $\overline{A_{1} V} \perp \overline{B C}$ by definition, which would imply $\overline{A A_{1}} \| \overline{B C}$, which is absurd. Claim - Given the condition the points $B_{1}, I, C_{1}$ are collinear (hence with $M$ ). To finish, since $\overline{D M A}$ was tangent to the circumcircle of $\triangle A B_{1} C_{1}$, we have $M D^{2}=$ $M A^{2}=M C_{1} \cdot M B_{1}$, implying the required tangency. Remark. The triangles satisfying the problem hypothesis are exactly the ones satisfying $r_{A}=2 R$, where $R$ and $r_{A}$ denote the circumradius and $A$-exradius. Remark. If $P$ is the foot of the $A$-altitude then this should also imply $A B_{1} P C_{1}$ is harmonic.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2019
|
T0
|
6
| null |
USA_TST
|
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 Second solution by inversion and mixtilinears (Anant Mudgal). As in the end of the preceding solution, we have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$ and $I \in \overline{B_{1} C_{1}}$. Let $M$ be the midpoint of minor arc $B C$ and $N$ be the midpoint of $\operatorname{arc} \widehat{B A C}$. Let $L$ be the intouch point on $\overline{B C}$. Let $O$ be the circumcenter of $\triangle A B C$. Let $K=\overline{A I} \cap \overline{B C}$. 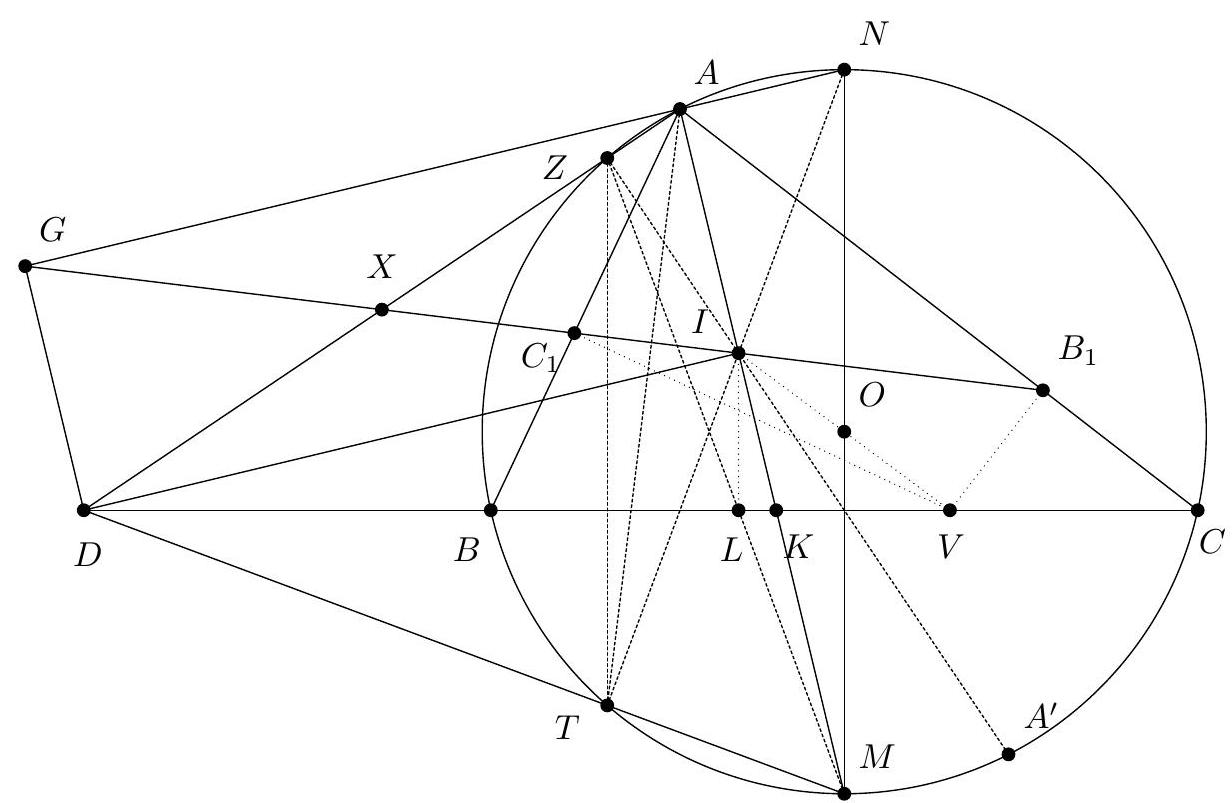 Claim — We have $\angle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)=\angle I A D$. Inversion in $(B I C)$ maps $\overline{A I}$ to $\overline{K I}$ and $(A B C)$ to $\overline{B C}$. Thus, $Z$ maps to $L$, so $Z, L, M$ are collinear. Since $B L=C V$ and $O I=O V$, we see that MLIN is a trapezoid with $\overline{I L} \| \overline{M N}$. Thus, $\overline{Z T} \| \overline{M N}$. It is known that $\overline{A T}$ and $\overline{A A_{1}}$ are isogonal in angle $B A C$. Since $\overline{A V}$ is a circumdiameter in $\left(A B_{1} C_{1}\right)$, so $\overline{A T} \perp \overline{B_{1} C_{1}}$. So $\measuredangle Z A I=\measuredangle N M T=90^{\circ}-\measuredangle T A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$. Let $X$ be the midpoint of $\overline{A D}$ and $G$ be the reflection of $I$ in $X$. Since $A I D G$ is a rectangle, we have $\measuredangle A I G=\measuredangle Z A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$, by the previous claim. So $\overline{I G}$ coincides with $\overline{B_{1} C_{1}}$. Now $\overline{A I}$ bisects $\angle B_{1} A C_{1}$ and $\angle I A G=90^{\circ}$, so $\left(\overline{I G} ; \overline{B_{1} C_{1}}\right)=-1$. Since $\angle I D G=90^{\circ}$, we see that $\overline{D I}$ and $\overline{D G}$ are bisectors of angle $B_{1} D C_{1}$. Now $\angle X D I=\angle X I D \Longrightarrow \angle X D C_{1}=\angle X I D-\angle I D B_{1}=\angle D B_{1} C_{1}$, so $\overline{X D}$ is tangent to $\left(D B_{1} C_{1}\right)$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
1
| null |
USA_TST
|
Choose positive integers $b_{1}, b_{2}, \ldots$ satisfying $$ 1=\frac{b_{1}}{1^{2}}>\frac{b_{2}}{2^{2}}>\frac{b_{3}}{3^{2}}>\frac{b_{4}}{4^{2}}>\cdots $$ and let $r$ denote the largest real number satisfying $\frac{b_{n}}{n^{2}} \geq r$ for all positive integers $n$. What are the possible values of $r$ across all possible choices of the sequence $\left(b_{n}\right)$ ?
|
The answer is $0 \leq r \leq 1 / 2$. Obviously $r \geq 0$. In one direction, we show that Claim (Greedy bound) - For all integers $n$, we have $$ \frac{b_{n}}{n^{2}} \leq \frac{1}{2}+\frac{1}{2 n} $$ $$ \begin{aligned} b_{n} & <n^{2} \frac{b_{n-1}}{(n-1)^{2}} \leq n^{2}\left(\frac{1}{2}+\frac{1}{2(n-1)}\right)=\frac{n^{3}}{2(n-1)} \\ & =\frac{1}{2}\left[n^{2}+n+1+\frac{1}{n-1}\right] \\ & =\frac{n(n+1)}{2}+\frac{1}{2}\left[1+\frac{1}{n-1}\right] \\ & \leq \frac{n(n+1)}{2}+1 \end{aligned} $$ So $b_{n}<\frac{n(n+1)}{2}+1$ and since $b_{n}$ is an integer, $b_{n} \leq \frac{n(n+1)}{2}$. This implies the result. We now give a construction. For $r=1 / 2$ we take $b_{n}=\frac{1}{2} n(n+1)$ for $r=0$ we take $b_{n}=1$. Claim (Explicit construction, given by Nikolai Beluhov) - Fix $0<r<1 / 2$. Let $N$ be large enough that $\left\lceil r n^{2}+n\right\rceil<\frac{1}{2} n(n+1)$ for all $n \geq N$. Then the following sequence works: $$ b_{n}= \begin{cases}\left\lceil r n^{2}+n\right\rceil & n \geq N \\ \frac{n^{2}+n}{2} & n<N\end{cases} $$ $$ \frac{b_{n}}{n^{2}}=\frac{r n^{2}+n+O(1)}{n^{2}} \xrightarrow{n \rightarrow \infty} r $$ Mainly, we contend $b_{n} n^{-2}$ is strictly decreasing. We need only check this for $n \geq N$; in fact $$ \frac{b_{n}}{n^{2}} \geq \frac{r n^{2}+n}{n^{2}}>\frac{\left[r(n+1)^{2}+(n+1)\right]+1}{(n+1)^{2}}>\frac{b_{n+1}}{(n+1)^{2}} $$ where the middle inequality is true since it rearranges to $\frac{1}{n}>\frac{n+2}{(n+1)^{2}}$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
2
| null |
USA_TST
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
ब First solution, elementary (original). We have $\triangle Y A C \sim \triangle Y B D$, from which it follows $$ \frac{d(Y, A C)}{d(Y, B D)}=\frac{A C}{B D} $$ Moreover, if we denote by $r_{1}$ and $r_{2}$ the radii of $\Gamma_{1}$ and $\Gamma_{2}$, then $$ \frac{d(T, A C)}{d(T, B D)}=\frac{T A \sin \angle\left(A C, \ell_{1}\right)}{T B \sin \angle\left(B D, \ell_{2}\right)}=\frac{2 r_{1} \sin \angle\left(A C, \ell_{1}\right)}{2 r_{2} \sin \angle\left(B D, \ell_{2}\right)}=\frac{A C}{B D} $$ the last step by the law of sines. 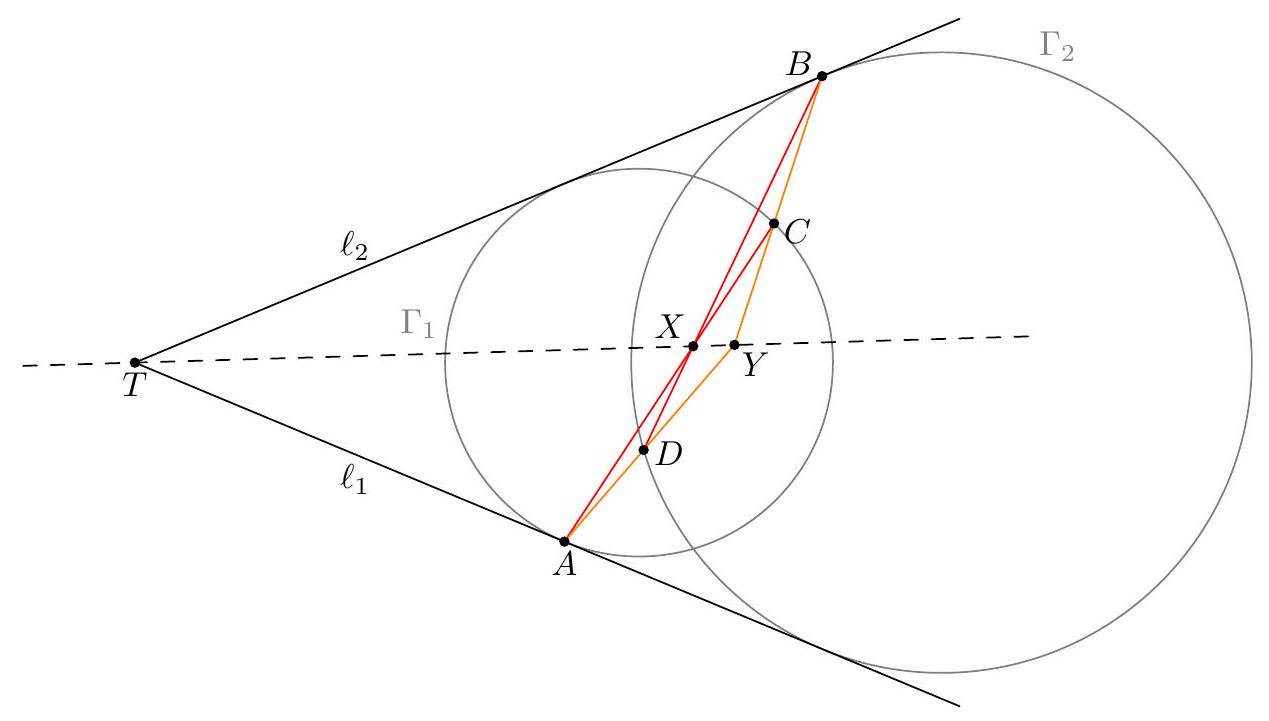 This solves the problem up to configuration issues: we claim that $Y$ and $T$ both lie inside $\angle A X B \equiv \angle C X D$. WLOG $T A<T B$. - The former is since $Y$ lies outside segments $B C$ and $A D$, since we assumed $A B C D$ was convex. - For the latter, we note that $X$ lies inside both $\Gamma_{1}$ and $\Gamma_{2}$ in fact on the radical axis of the two circles (since $X$ was an interior point of both chords $A C$ and $B D$ ). In particular, $X$ is contained inside $\angle A T B$, and moreover $\angle A T B<90^{\circ}$, and this is enough to imply the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
2
| null |
USA_TST
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
『 Second solution, inversive. This is based on the solution posted by kapilpavase on AoPS. Consider the inversion at $T$ swapping $\Gamma_{1}$ and $\Gamma_{2}$; we let it send $A$ to $E, B$ to $F$, $C$ to $V, D$ to $W$, as shown. Draw circles $A D W E$ and $B C V F$.  Claim - Points $T$ and $Y$ lie on the radical axis of $(A D E)$ and $(B C F)$. Claim - Point $X$ has equal power to $(A D E)$ and $(B C F)$. But since $A E=B F$ and moreover $$ \begin{aligned} \measuredangle B C F+\measuredangle A D E & =(\measuredangle B C A+\measuredangle A C F)+(\measuredangle A D B+\measuredangle B D E) \\ & =(\measuredangle B C A+\measuredangle A D B)+(\measuredangle A C F+\measuredangle B D E)=0+0=0 \end{aligned} $$ we conclude that $(A D E)$ and $(B C F)$ are congruent. As $X$ was the center of negative inversion between them, we're done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
2
| null |
USA_TST
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Third solution, projective (Nikolai Beluhov). We start with some definitions. Let $\ell_{1}$ touch $\Gamma_{2}$ at $E, \ell_{2}$ touch $\Gamma_{1}$ at $F, K=\ell_{1} \cap \overline{B D}, L=\ell_{2} \cap \overline{A C}$, line $F X$ meet $\Gamma_{1}$ again at $M$, line $E X$ meet $\Gamma_{2}$ again at $N$, and lines $A B, A D$, and $B C$ meet line $T X$ at $Z, Y_{1}$, and $Y_{2}$. Thus the desired statement is equivalent to $Y_{1}=Y_{2}$. $$ \text { Claim - }(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} $$ Consider the inversion with center $T$ which swaps $\Gamma_{1}$ and $\Gamma_{2} ;$ it also swaps the pairs $\{A, E\}$ and $\{B, F\}$. Since $A E C N$ is cyclic, $C$ is on $\Gamma_{1}$, and $N$ is on $\Gamma_{2}$, it also swaps $\{C, N\}$; similarly it swaps $\{D, M\}$. Thus $(E B ; N D)_{\Gamma_{2}}=(A F ; C M)_{\Gamma_{1}}=(F A ; M C)_{\Gamma_{1}}$ as desired. $\left(T Z ; X Y_{1}\right) \stackrel{A}{=}(K B ; X D) \stackrel{E}{=}(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} \stackrel{F}{=}(L A ; X C) \stackrel{B}{=}\left(T Z ; X Y_{2}\right)$ implies $Y_{1}=Y_{2}$ as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
2
| null |
USA_TST
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Fourth solution by untethered moving points. Fix $\ell_{1}, \ell_{2}, T, \Gamma_{1}$ and $\Gamma_{2}$, and let $\Gamma_{1}$ and $\Gamma_{2}$ meet at $U$ and $V$. By the radical axis theorem, $X$ lies on $U V$. Thus we instead treat $X$ as a variable point on line $U V$ and let $C=A X \cap \Gamma_{1}$, $D=B X \cap \Gamma_{2}$. By definition, $X$ has degree 1 and $T$ has degree 0 . We apply Zack's lemma to untethered point $Y$. Note that $C$ and $D$ move projectively on conics, and therefore have degree 2 . Then, lines $A D$ and $B C$ each have degree at most $\operatorname{deg}(A)+\operatorname{deg}(D)=0+2=2$, and so their intersection $Y$ has degree at most $2+2=4$. But when $X \in A B$, the lines $A D$ and $B C$ are the same, so Zack's lemma implies that $$ \operatorname{deg} Y \leq 4-1=3 . $$ Thus the assertion that $T, X, Y$ are collinear (which for example can be seen as a certain vanishing determinant) is a statement of degree at most $0+1+3=4$. Thus it suffices to find 5 values of $X$ (other than $X \in \overline{A B}$, which we used already). This is remarkably easy: 1. When $X=U$ or $X=V$, then $X=C=D=Y$ and the statement is obvious. 2. When $X \in \ell_{1}$, say, then $A=C$ and so $Y$ lies on $A C=\ell_{1}$ as well. The case $X \in \ell_{2}$ is symmetric. 3. Finally, take $X$ at infinity along $U V$. Then $C$ and $D$ are the other tangency points of the circles with $\ell_{1}, \ell_{2}$, and so $A C=\ell_{1}, B D=\ell_{2}$, so $Y=T$. This finishes the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
3
| null |
USA_TST
|
Let $\alpha \geq 1$ be a real number. Hephaestus and Poseidon play a turn-based game on an infinite grid of unit squares. Before the game starts, Poseidon chooses a finite number of cells to be flooded. Hephaestus is building a levee, which is a subset of unit edges of the grid, called walls, forming a connected, non-self-intersecting path or loop. The game then begins with Hephaestus moving first. On each of Hephaestus's turns, he adds one or more walls to the levee, as long as the total length of the levee is at most $\alpha n$ after his $n$th turn. On each of Poseidon's turns, every cell which is adjacent to an already flooded cell and with no wall between them becomes flooded as well. Hephaestus wins if the levee forms a closed loop such that all flooded cells are contained in the interior of the loop - hence stopping the flood and saving the world. For which $\alpha$ can Hephaestus guarantee victory in a finite number of turns no matter how Poseidon chooses the initial cells to flood?
|
We show that if $\alpha>2$ then Hephaestus wins, but when $\alpha=2$ (and hence $\alpha \leq 2$ ) Hephaestus cannot contain even a single-cell flood initially. Strategy for $\alpha>2$ : Impose $\mathbb{Z}^{2}$ coordinates on the cells. Adding more flooded cells does not make our task easier, so let us assume that initially the cells $(x, y)$ with $|x|+|y| \leq d$ are flooded for some $d \geq 2$; thus on Hephaestus's $k$ th turn, the water is contained in $|x|+|y| \leq d+k-1$. Our goal is to contain the flood with a large rectangle. We pick large integers $N_{1}$ and $N_{2}$ such that $$ \begin{gathered} \alpha N_{1}>2 N_{1}+(2 d+3) \\ \alpha\left(N_{1}+N_{2}\right)>2 N_{2}+\left(6 N_{1}+8 d+4\right) \end{gathered} $$ Mark the points $X_{i}, Y_{i}$ as shown in the figure for $1 \leq i \leq 6$. The red figures indicate the distance between the marked points on the rectangle.  We follow the following plan. - Turn 1: place wall $X_{1} Y_{1}$. This cuts off the flood to the north. - Turns 2 through $N_{1}+1$ : extend the levee to segment $X_{2} Y_{2}$. This prevents further flooding to the north. - Turn $N_{1}+2$ : add in broken lines $X_{4} X_{3} X_{2}$ and $Y_{4} Y_{3} Y_{2}$ all at once. This cuts off the flood west and east. - Turns $N_{1}+2$ to $N_{1}+N_{2}+1$ : extend the levee along segments $X_{4} X_{5}$ and $Y_{4} Y_{5}$. This prevents further flooding west and east. - Turn $N_{1}+N_{2}+2$ : add in the broken line $X_{5} X_{6} Y_{6} Y_{5}$ all at once and win. Let $c_{0}, c_{1}, \ldots, c_{n}$ be a path of cells such that $c_{0}$ is the initial cell flooded, and in general $c_{i}$ is flooded on Poseidon's $i$ th turn from $c_{i-1}$. The levee now forms a closed loop enclosing all $c_{i}$. Claim - If $c_{i}$ and $c_{j}$ are adjacent then $|i-j|=1$. Thus the $c_{i}$ actually form a path. We color green any edge of the unit grid (wall or not) which is an edge of exactly one $c_{i}$ (i.e. the boundary of the polyomino). It is easy to see there are exactly $2 n+4$ green edges. Now, from the center of each cell $c_{i}$, shine a laser towards each green edge of $c_{i}$ (hence a total of $2 n+4$ lasers are emitted). An example below is shown for $n=6$, with the levee marked in brown.  Claim - No wall is hit by more than one laser. We consider two cases on the position of $w$. - If $w$ is between $c_{i}$ and $c_{j}$, then we have found a segment intersecting the levee exactly once. But the endpoints of the segment lie inside the levee. This contradicts the assumption that the levee is a closed loop. - Suppose $w$ lies above both $c_{i}$ and $c_{j}$ and assume WLOG $i<j$. Then we have found that there is no levee at all between $c_{i}$ and $c_{j}$. Let $\rho \geq 1$ be the distance between the centers of $c_{i}$ and $c_{j}$. Then $c_{j}$ is flooded in a straight line from $c_{i}$ within $\rho$ turns, and this is the unique shortest possible path. So this situation can only occur if $j=i+\rho$ and $c_{i}, \ldots, c_{j}$ form a column. But then no vertical lasers from $c_{i}$ and $c_{j}$ may point in the same direction, contradiction. This implies the levee has at least $2 n+4$ walls (the number of lasers) on Hephaestus's $(n+1)$ st turn. So $\alpha \geq \frac{2 n+4}{n+1}>2$. Remark (Author comments). The author provides the following remarks. - Even though the flood can be stopped when $\alpha=2+\varepsilon$, it takes a very long time to do that. Starting from a single flooded cell, the strategy I have outlined requires $\Theta\left(1 / \varepsilon^{2}\right)$ days. Starting from several flooded cells contained within an area of diameter $D$, it takes $\Theta\left(D / \varepsilon^{2}\right)$ days. I do not know any strategies that require fewer days than that. - There is a gaping chasm between $\alpha \leq 2$ and $\alpha>2$. Since $\alpha \leq 2$ does not suffice even when only one cell is flooded in the beginning, there are in fact no initial configurations at all for which it is sufficient. On the other hand, $\alpha>2$ works for all initial configurations. It appears that this has not been done before, or at least I was unable to find any reference for it. I did find tons of references where the perimeter of a polyomino is estimated in terms of its area, but nothing concerning the diameter. My argument is a formalisation of the intuition that if $P$ is any shortest path within some weirdly-shaped polyomino, then the boundary of that polyomino must hug $P$ rather closely so that $P$ cannot be shortened.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
4
| null |
USA_TST
|
For a finite simple graph $G$, we define $G^{\prime}$ to be the graph on the same vertex set as $G$, where for any two vertices $u \neq v$, the pair $\{u, v\}$ is an edge of $G^{\prime}$ if and only if $u$ and $v$ have a common neighbor in $G$. Prove that if $G$ is a finite simple graph which is isomorphic to $\left(G^{\prime}\right)^{\prime}$, then $G$ is also isomorphic to $G^{\prime}$.
|
We say a vertex of a graph is fatal if it has degree at least 3, and some two of its neighbors are not adjacent. Claim - The graph $G^{\prime}$ has at least as many triangles as $G$, and has strictly more if $G$ has any fatal vertices. Thus we only need to consider graphs $G$ with no fatal vertices. Looking at the connected components, the only possibilities are cliques (including single vertices), cycles, and paths. So in what follows we restrict our attention to graphs $G$ only consisting of such components. Remark (Warning). Beware: assuming $G$ is connected loses generality. For example, it could be that $G=G_{1} \sqcup G_{2}$, where $G_{1}^{\prime} \cong G_{2}$ and $G_{2}^{\prime} \cong G_{1}$. First, note that the following are stable under the operation: - an isolated vertex, - a cycle of odd length, or - a clique with at least three vertices. In particular, $G \cong G^{\prime \prime}$ holds for such graphs. On the other hand, cycles of even length or paths of nonzero length will break into more connected components. For this reason, a graph $G$ with any of these components will not satisfy $G \cong G^{\prime \prime}$ because $G^{\prime}$ will have strictly more connected components than $G$, and $G^{\prime \prime}$ will have at least as many as $G^{\prime}$. Therefore $G \cong G^{\prime \prime}$ if and only if $G$ is a disjoint union of the three types of connected components named earlier. Since $G \cong G^{\prime}$ holds for such graphs as well, the problem statement follows right away. Remark. The proposers included a variant of the problem where given any graph $G$, the operation stabilized after at most $O(\log n)$ operations, where $n$ was the number of vertices of $G$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
5
| null |
USA_TST
|
Find all integers $n \geq 2$ for which there exists an integer $m$ and a polynomial $P(x)$ with integer coefficients satisfying the following three conditions: - $m>1$ and $\operatorname{gcd}(m, n)=1$; - the numbers $P(0), P^{2}(0), \ldots, P^{m-1}(0)$ are not divisible by $n$; and - $P^{m}(0)$ is divisible by $n$. Here $P^{k}$ means $P$ applied $k$ times, so $P^{1}(0)=P(0), P^{2}(0)=P(P(0))$, etc.
|
The answer is that this is possible if and only if there exists primes $p^{\prime}<p$ such that $p \mid n$ and $p^{\prime} \nmid n$. (Equivalently, the radical $\operatorname{rad}(n)$ must not be the product of the first several primes.) For a polynomial $P$, and an integer $N$, we introduce the notation $$ \operatorname{zord}(P \bmod N):=\min \left\{e>0 \mid P^{e}(0) \equiv 0 \bmod N\right\} $$ where we set $\min \varnothing=0$ by convention. Note that in general we have $$ \operatorname{zord}(P \bmod N)=\operatorname{lcm}_{q \mid N}(\operatorname{zord}(P \bmod q)) $$ where the index runs over all prime powers $q \mid N$ (by Chinese remainder theorem). This will be used in both directions. Construction: First, we begin by giving a construction. The idea is to first use the following prime power case. Claim - Let $p^{e}$ be a prime power, and $1 \leq k<p$. Then $$ f(X)=X+1-k \cdot \frac{X(X-1)(X-2) \ldots(X-(k-2))}{(k-1)!} $$ viewed as a polynomial in $\left(\mathbb{Z} / p^{e}\right)[X]$ satisfies $\operatorname{zord}\left(f \bmod p^{e}\right)=k$. This gives us a way to do the construction now. For the prime power $p^{e} \mid n$, we choose $1 \leq p^{\prime}<p$ and require $\operatorname{zord}\left(P \bmod p^{e}\right)=p^{\prime}$ and $\operatorname{zord}(P \bmod q)=1$ for every other prime power $q$ dividing $n$. Then by $(\dagger)$ we are done. Remark. The claim can be viewed as a special case of Lagrange interpolation adapted to work over $\mathbb{Z} / p^{e}$ rather than $\mathbb{Z} / p$. Thus the construction of the polynomial $f$ above is quite natural. Necessity: by ( $\dagger$ ) again, it will be sufficient to prove the following claim. Claim - For any prime power $q=p^{e}$, and any polynomial $f(x) \in \mathbb{Z}[x]$, if the quantity $\operatorname{zord}(f \bmod q)$ is nonzero then it has all prime factors at most $p$. Now assume $e \geq 2$. Let us define $$ k:=\operatorname{zord}\left(P \bmod p^{e-1}\right), \quad Q:=P^{k} $$ Since being periodic modulo $p^{e}$ requires periodic modulo $p^{e-1}$, it follows that $$ \operatorname{zord}\left(P \bmod p^{e}\right)=k \cdot \operatorname{zord}\left(Q \bmod p^{e}\right) $$ However since $Q(0) \equiv 0 \bmod p^{e-1}$, it follows $\left\{Q(0), Q^{2}(0), \ldots\right\}$ are actually all multiples of $p^{e-1}$. There are only $p$ residues modulo $p^{e}$ which are also multiples of $p^{e-1}$, so $\operatorname{zord}\left(Q \bmod p^{e}\right) \leq p$, as needed. Remark. One reviewer submitted the following test-solving comments: This is one of these problems where you can make many useful natural observations, and if you make enough of them eventually they cohere into a solution. For example, here are some things I noticed while solving: - The polynomial $1-x$ shows that $m=2$ works for any odd $n$. - In general, if $\zeta$ is a primitive $m$ th root of unity modulo $n$, then $\zeta(x+1)-1$ has the desired property (assuming $\operatorname{gcd}(m, n)=1$ ). We can extend this using the Chinese remainder theorem to find that if $p|n, m| p-1$, and $\operatorname{gcd}(m, n)=1$, then $n$ works. So by this point I already have something about the prime factors of $n$ being sort-of closed downwards. - By iterating $P$ we see it is enough to consider $m$ prime. - In the case where $n=2^{k}$, it is not too difficult to show that no odd prime $m$ works.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2020
|
T0
|
6
| null |
USA_TST
|
Let $P_{1} P_{2} \ldots P_{100}$ be a cyclic 100-gon, and let $P_{i}=P_{i+100}$ for all $i$. Define $Q_{i}$ as the intersection of diagonals $\overline{P_{i-2} P_{i+1}}$ and $\overline{P_{i-1} P_{i+2}}$ for all integers $i$. Suppose there exists a point $P$ satisfying $\overline{P P_{i}} \perp \overline{P_{i-1} P_{i+1}}$ for all integers $i$. Prove that the points $Q_{1}, Q_{2}, \ldots, Q_{100}$ are concyclic.
|
 Claim - The points $K_{\bullet}$ are concyclic say with circumcircle $\gamma$. Let $E_{i}$ be the second intersection of line $\overline{P_{i-1} K_{i} P_{i+1}}$ with $\gamma$; then it follows that the perpendiculars to $\overline{P_{i-1} P_{i+1}}$ at $E_{i}$ all concur at a point $E$, which is the reflection of $P$ across the center of $\gamma$. We let $H_{2}=\overline{P_{1} P_{3}} \cap \overline{P_{2} P_{4}}$ denote the orthocenter of $\triangle P P_{2} P_{3}$ and define $H_{\bullet}$ cyclically. Claim - We have $$ \overline{E H_{2}} \perp \overline{P_{1} P_{4}} \| \overline{K_{2} K_{3}} \quad \text { and } \overline{P H_{2}} \perp \overline{E_{2} E_{3}} \| \overline{P_{2} P_{3}} . $$ Note that $\overline{H_{2} P}$ and $\overline{H_{2} E}$ are respectively circum-diameters of $\triangle H_{2} K_{2} K_{3}$ and $\triangle H_{2} E_{2} E_{3}$. As $\overline{K_{2} K_{3}}$ and $\overline{E_{2} E_{3}}$ are anti-parallel, it follows $\overline{H_{2} P}$ and $\overline{H_{2} E}$ are isogonal and we derive both perpendicularities. Claim - The points $E, Q_{3}, E_{3}$ are collinear. $$ \frac{E_{3} H_{2}}{E_{3} P_{2}}=\frac{E_{2} H_{2}}{E_{2} P_{3}}=\frac{E_{4} H_{3}}{E_{4} P_{3}}=\frac{E_{3} H_{3}}{E_{3} P_{4}} $$ Now consider a homothety centered at $E_{3}$ sending $H_{2}$ to $P_{2}$ and $H_{3}$ to $P_{4}$. Then it should send the orthocenter of $\triangle E H_{2} H_{3}$ to $Q_{3}$, proving the result. From all this it follows that $\triangle E Q_{2} Q_{3} \sim \triangle P K_{2} K_{3}$ as the opposite sides are all parallel. Repeating this we actually find a homothety of 100 -gons $$ Q_{1} Q_{2} Q_{3} \cdots \sim K_{1} K_{2} K_{3} \ldots $$ Remark. The proposer remarks that in fact, if one lets $s$ be an integer and instead defines $R_{i}=P_{i} P_{i+s} \cap P_{i+1} P_{i+s+1}$, then the $R_{\bullet}$ are concyclic. The present problem is the case $s=3$. We comment on a few special cases: - There is nothing to prove for $s=1$. - If $s=0$, this amounts to proving that poles of $\overline{P_{i} P_{i+1}}$ are concyclic; by inversion this is equivalent to showing the midpoints of the sides are concyclic. This is an interesting problem but not as difficult. - The problem for $s=2$ is to show that our $H_{\bullet}$ are concyclic, which uses the $s=0$ case as a lemma. 【 Solution to generalization (Nikolai Beluhov). We are going to need some well-known lemmas. ## Lemma Suppose that $A B C D$ is inscribed in a circle $\Gamma$. Let the tangents to $\Gamma$ at $A$ and $B$ meet at $E$, let the tangents to $\Gamma$ at $C$ and $D$ meet at $F$, and let diagonals $A C$ and $B D$ meet at $P$. Then points $E, F$, and $P$ are collinear. ## Lemma Suppose that points $X$ and $Y$ are isogonal conjugates in polygon $\mathcal{A}=A_{1} A_{2} \ldots A_{n}$. (This means that lines $A_{i} X$ and $A_{i} Y$ are symmetric with respect to the interior angle bisector of $\angle A_{i-1} A_{i} A_{i+1}$ for all $i$, where $A_{n+j} \equiv A_{j}$ for all $j$.) Then the $2 n$ projections of $X$ and $Y$ on the sides of $\mathcal{A}$ are concyclic. ## Lemma Let $\Gamma^{\prime}$ and $\Gamma^{\prime \prime}$ be two circles and let $r$ be some fixed real number. Then the locus of points $X$ satisfying $\operatorname{Pow}\left(X, \Gamma^{\prime}\right): \operatorname{Pow}\left(X, \Gamma^{\prime \prime}\right)=r$ is a circle. We are ready to solve the problem. Let $\mathcal{P}$ be our polygon, let $O$ be its the circumcenter, and let $\Gamma$ be its circumcircle. Fix any index $i$. In triangle $P_{i-1} P_{i} P_{i+1}$, we have that line $P_{i} P$ contains the altitude through $P_{i}$ and line $P_{i} O$ contains the circumradius through $P_{i}$. Therefore, these two lines are symmetric with respect to the interior angle bisector of $\angle P_{i-1} P_{i} P_{i+1}$. Thus points $P$ and $O$ are isogonal conjugates in $\mathcal{P}$. By Lemma 2, it follows that the projections of $O$ onto the sides of $\mathcal{P}$ are concyclic. In other words, the midpoints of the sides of $\mathcal{P}$ lie on some circle $\omega$. Let $M_{i}$ be the midpoint of segment $P_{i} P_{i+1}$ and let the tangents to $\Gamma$ at points $P_{i}$ and $P_{i+1}$ meet at $T_{i}$. Since inversion with respect to $\Gamma$ swaps $M_{i}$ and $T_{i}$ for all $i$, and also since all of the $M_{i}$ lie on the same circle $\omega$, we obtain that all of the $T_{i}$ lie on the same circle $\Omega$.  Again, fix any index $i$. By Lemma 1 applied to cyclic quadrilateral $P_{i-2} P_{i-1} P_{i+1} P_{i+2}$, we have that point $Q_{i}$ lies on line $T_{i-2} T_{i+1}$. Similarly, point $Q_{i+1}$ lies on line $T_{i-1} T_{i+2}$. Define $$ f_{i}=\frac{\operatorname{Pow}\left(Q_{i}, \Gamma\right)}{\operatorname{Pow}\left(Q_{i}, \Omega\right)} . $$ Claim - We have $f_{i}=f_{i+1}$ for all $i$. $$ \begin{aligned} \operatorname{Pow}\left(Q_{i}, \Gamma\right) & =Q_{i} P_{i-1} \cdot Q_{i} P_{i+2} \\ \operatorname{Pow}\left(Q_{i+1}, \Gamma\right) & =Q_{i+1} P_{i-1} \cdot Q_{i+1} P_{i+2} . \\ \operatorname{Pow}\left(Q_{i}, \Omega\right) & =Q_{i} T_{i-2} \cdot Q_{i} T_{i+1} \\ \operatorname{Pow}\left(Q_{i+1}, \Omega\right) & =Q_{i+1} T_{i-1} \cdot Q_{i+1} T_{i+2} . \end{aligned} $$ Consider cyclic quadrilateral $T_{i-2} T_{i-1} T_{i+1} T_{i+2}$. Since $\Gamma$ touches its opposite sides $T_{i-2} T_{i-1}$ and $T_{i+1} T_{i+2}$ at points $P_{i-1}$ and $P_{i+2}$, we have that line $P_{i-1} P_{i+2}$ makes equal angles with these opposite sides. From here, a simple angle chase shows that triangles $P_{i-1} Q_{i} T_{i-2}$ and $P_{i+2} Q_{i+1} T_{i+2}$ are similar. Thus $$ \frac{Q_{i} P_{i-1}}{Q_{i} T_{i-2}}=\frac{Q_{i+1} P_{i+2}}{Q_{i+1} T_{i+2}} . $$ Similarly, $$ \frac{Q_{i} P_{i+2}}{Q_{i} T_{i+1}}=\frac{Q_{i+1} P_{i-1}}{Q_{i+1} T_{i-1}} . $$ From these, the desired identity $f_{i}=f_{i+1}$ follows. Therefore, the power ratio $f_{i}$ is the same for all $i$. By Lemma 3 for circles $\Gamma$ and $\Omega$, the solution is complete. Remark. Polygon $T_{1} T_{2} \ldots T_{100}$ is both circumscribed about a circle and inscribed inside a circle. Polygons like that are known as Poncelet polygons. See, for example, https: //en.wikipedia.org/wiki/Poncelet's_closure_theorem. This solution borrows a lot from the discussion of Poncelet's closure theorem in Advanced Euclidean Geometry, referenced above for Lemma 3.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
2021
|
T0
|
1
| null |
USA_TST
|
Determine all integers $s \geq 4$ for which there exist positive integers $a, b, c, d$ such that $s=a+b+c+d$ and $s$ divides $a b c+a b d+a c d+b c d$.
|
The answer is $s$ composite. Composite construction. Write $s=(w+x)(y+z)$, where $w, x, y, z$ are positive integers. Let $a=w y, b=w z, c=x y, d=x z$. Then $$ a b c+a b d+a c d+b c d=w x y z(w+x)(y+z) $$ so this works. $$ (a+b)(a+c)(a+d)=(a b c+a b d+a c d+b c d)+a^{2}(a+b+c+d) \equiv 0 \quad(\bmod s) $$ Hence $s$ divides a product of positive integers less than $s$, so $s$ is composite. Suppose that $s$ is prime. Then the polynomial $(x-a)(x-b)(x-c)(x-d) \in \mathbb{F}_{s}[x]$ is even, so the roots come in two opposite pairs in $\mathbb{F}_{s}$. Thus the sum of each pair is at least $s$, so the sum of all four is at least $2 s>s$, contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
2021
|
T0
|
2
| null |
USA_TST
|
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 First approach by Vincent Huang. We need the following claim: Claim - Suppose distinct lines $A C$ and $B D$ meet at $X$. Then for any point $K$ $$ \operatorname{pow}(K, X A B)+\operatorname{pow}(K, X C D)=\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C) $$ Construct the points $P=\ell_{1} \cap \overline{B E}$ and $Q=\ell_{2} \cap \overline{A F}$, which do not depend on $X$. Claim - Quadrilaterals $B P C X$ and $A Q D X$ are cyclic. 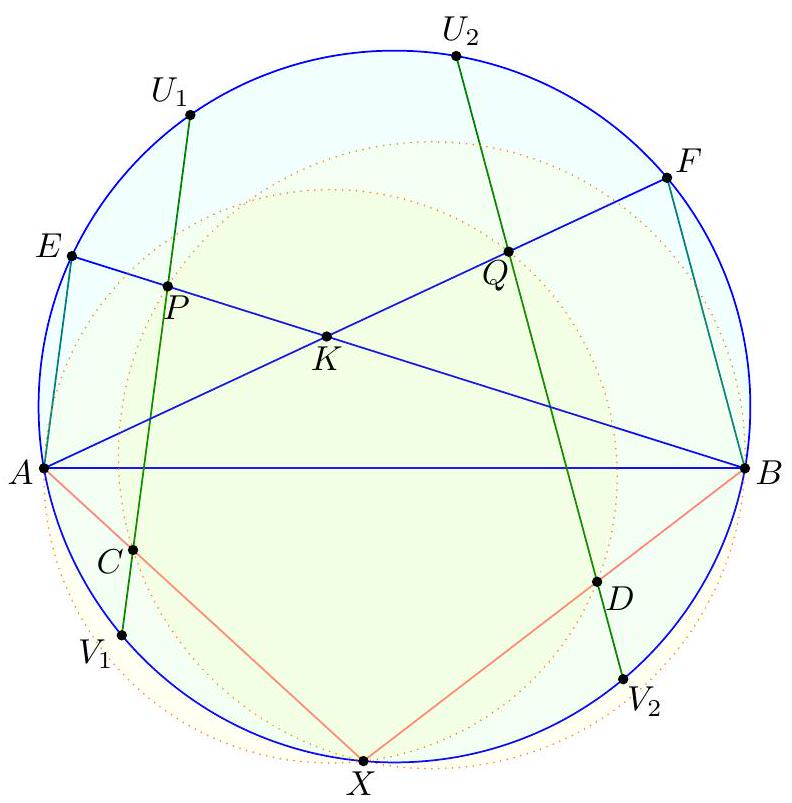 Now, for the particular $K$ we choose, we have $$ \begin{aligned} \operatorname{pow}(K, X C D) & =\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C)-\operatorname{pow}(K, X A B) \\ & =K A \cdot K Q+K B \cdot K P-\operatorname{pow}(K, \Gamma) . \end{aligned} $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
2021
|
T0
|
2
| null |
USA_TST
|
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 Second approach by authors. Let $Y$ be the second intersection of $(X C D)$ with $\Gamma$. Let $S=\overline{E Y} \cap \ell_{1}$ and $T=\overline{F Y} \cap \ell_{2}$. Claim - Points $S$ and $T$ lies on ( $X C D)$ as well. Now let $X^{\prime}$ be any other choice of $X$, and define $C^{\prime}$ and $D^{\prime}$ in the obvious way. We are going to show that $K$ lies on the radical axis of $(X C D)$ and $\left(X^{\prime} C^{\prime} D^{\prime}\right)$. 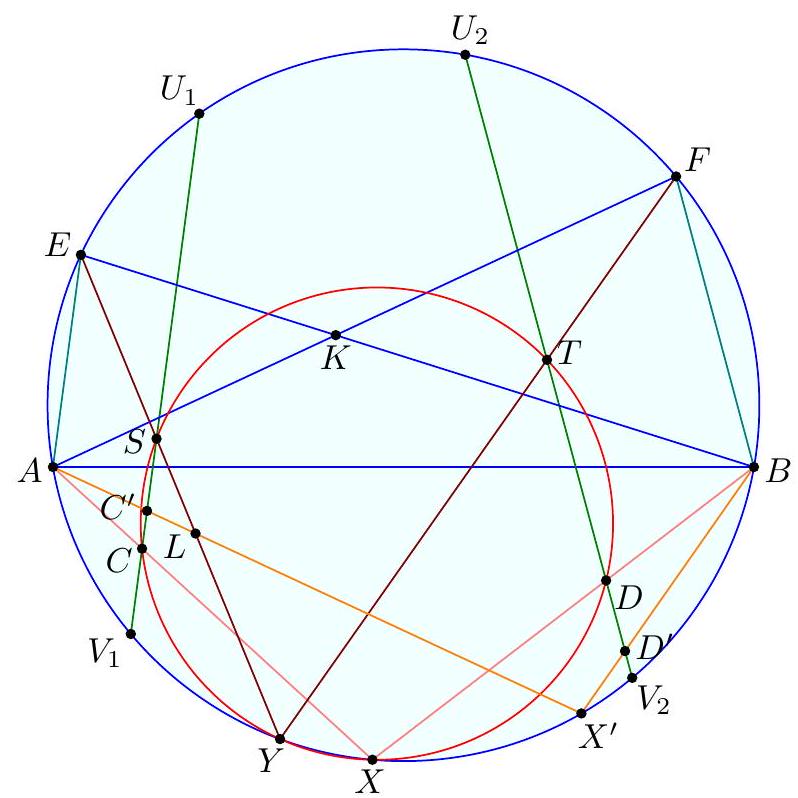 The main idea is as follows: Claim - The point $L=\overline{E Y} \cap \overline{A X^{\prime}}$ lies on the radical axis. By symmetry, so does the point $M=\overline{F Y} \cap \overline{B X^{\prime}}$ (not pictured). $$ \operatorname{pow}\left(L, X^{\prime} C^{\prime} D^{\prime}\right)=L C^{\prime} \cdot L X^{\prime}=L S \cdot L Y=\operatorname{pow}(L, X C D) $$ To conclude, note that by Pascal theorem on $$ E Y F A X^{\prime} B $$ it follows $K, L, M$ are collinear, as needed. Remark. All the conditions about $U_{1}, V_{1}, U_{2}, V_{2}$ at the beginning are there to eliminate configuration issues, making the problem less obnoxious to the contestant. In particular, without the various assumptions, there exist configurations in which the point $K$ is at infinity. In these cases, the center of $X C D$ moves along a fixed line.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
2021
|
T0
|
3
| null |
USA_TST
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy the inequality $$ f(y)-\left(\frac{z-y}{z-x} f(x)+\frac{y-x}{z-x} f(z)\right) \leq f\left(\frac{x+z}{2}\right)-\frac{f(x)+f(z)}{2} $$ for all real numbers $x<y<z$.
|
Answer: all functions of the form $f(y)=a y^{2}+b y+c$, where $a, b, c$ are constants with $a \leq 0$. If $I=(x, z)$ is an interval, we say that a real number $\alpha$ is a supergradient of $f$ at $y \in I$ if we always have $$ f(t) \leq f(y)+\alpha(t-y) $$ for every $t \in I$. (This inequality may be familiar as the so-called "tangent line trick". A cartoon of this situation is drawn below for intuition.) We will also say $\alpha$ is a supergradient of $f$ at $y$, without reference to the interval, if $\alpha$ is a supergradient of some open interval containing $y$.  Claim - The problem condition is equivalent to asserting that $\frac{f(z)-f(x)}{z-x}$ is a supergradient of $f$ at $\frac{x+z}{2}$ for the interval $(x, z)$, for every $x<z$. At this point, we may readily verify that all claimed quadratic functions $f(x)=$ $a x^{2}+b x+c$ work - these functions are concave, so the graphs lie below the tangent line at any point. Given $x<z$, the tangent at $\frac{x+z}{2}$ has slope given by the derivative $f^{\prime}(x)=2 a x+b$, that is $$ f^{\prime}\left(\frac{x+z}{2}\right)=2 a \cdot \frac{x+z}{2}+b=\frac{f(z)-f(x)}{z-x} $$ as claimed. (Of course, it is also easy to verify the condition directly by elementary means, since it is just a polynomial inequality.) Now suppose $f$ satisfies the required condition; we prove that it has the above form. Claim - The function $f$ is concave. $$ \begin{aligned} \frac{z-y}{z-x} f(x)+\frac{y-x}{z-x} f(z) & \leq \frac{z-y}{z-x}(f(y)+\alpha(x-y))+\frac{y-x}{z-x}(f(y)+\alpha(z-y)) \\ & =f(y) \end{aligned} $$ That is, $f$ is a concave function. Continuity follows from the fact that any concave function on $\mathbb{R}$ is automatically continuous. Lemma (see e.g. https://math.stackexchange.com/a/615161 for picture) Any concave function $f$ on $\mathbb{R}$ is continuous. $$ f(p)+\frac{f(b)-f(p)}{b-p} \varepsilon \leq f(p+\varepsilon) \leq f(p)+\frac{f(p)-f(a)}{p-a} \varepsilon $$ Claim - The function $f$ cannot have more than one supergradient at any given point. $$ g(t)=\frac{f(y)-f(y-t)}{t}-\frac{f(y+t)-f(y)}{t} . $$ We contend that $g(\varepsilon) \leq \frac{3}{5} g(3 \varepsilon)$ for any $\varepsilon>0$. Indeed by the problem condition, $$ \begin{aligned} & f(y) \leq f(y-\varepsilon)+\frac{f(y+\varepsilon)-f(y-3 \varepsilon)}{4} \\ & f(y) \leq f(y+\varepsilon)-\frac{f(y+3 \varepsilon)-f(y-\varepsilon)}{4} . \end{aligned} $$  Summing gives the desired conclusion. Now suppose that $f$ has two supergradients $\alpha<\alpha^{\prime}$ at point $y$. For small enough $\varepsilon$, we should have we have $f(y-\varepsilon) \leq f(y)-\alpha^{\prime} \varepsilon$ and $f(y+\varepsilon) \leq f(y)+\alpha \varepsilon$, hence $$ g(\varepsilon)=\frac{f(y)-f(y-\varepsilon)}{\varepsilon}-\frac{f(y+\varepsilon)-f(y)}{\varepsilon} \geq \alpha^{\prime}-\alpha . $$ This is impossible since $g(\varepsilon)$ may be arbitrarily small. Claim - The function $f$ is quadratic on the rational numbers. $$ f(x+3 d)-3 f(x+2 d)+3 f(x+d)-f(x)=0 . $$ If we fix $d=1 / n$, it follows inductively that $f$ agrees with a quadratic function $\widetilde{f}_{n}$ on the set $\frac{1}{n} \mathbb{Z}$. On the other hand, for any $m \neq n$, we apparently have $\widetilde{f}_{n}=\widetilde{f}_{m n}=\widetilde{f}_{m}$, so the quadratic functions on each "layer" are all equal. Since $f$ is continuous, it follows $f$ is quadratic, as needed. Remark (Alternate finish using differentiability due to Michael Ren). In the proof of the main claim (about uniqueness of supergradients), we can actually notice the two terms $\frac{f(y)-f(y-t)}{t}$ and $\frac{f(y+t)-f(y)}{t}$ in the definition of $g(t)$ are both monotonic (by concavity). Since we supplied a proof that $\lim _{t \rightarrow 0} g(t)=0$, we find $f$ is differentiable. Now, if the derivative at some point exists, it must coincide with all the supergradients; (informally, this is why "tangent line trick" always has the slope as the derivative, and formally, we use the mean value theorem). In other words, we must have $$ f(x+y)-f(x-y)=2 f^{\prime}(x) \cdot y $$ holds for all real numbers $x$ and $y$. By choosing $y=1$ we obtain that $f^{\prime}(x)=f(x+1)-f(x-1)$ which means $f^{\prime}$ is also continuous. Finally differentiating both sides with respect to $y$ gives $$ f^{\prime}(x+y)-f^{\prime}(x-y)=2 f^{\prime}(x) $$ which means $f^{\prime}$ obeys Jensen's functional equation. Since $f^{\prime}$ is continuous, this means $f^{\prime}$ is linear. Thus $f$ is quadratic, as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
1
| null |
USA_TST
|
There are 2022 equally spaced points on a circular track $\gamma$ of circumference 2022. The points are labeled $A_{1}, A_{2}, \ldots, A_{2022}$ in some order, each label used once. Initially, Bunbun the Bunny begins at $A_{1}$. She hops along $\gamma$ from $A_{1}$ to $A_{2}$, then from $A_{2}$ to $A_{3}$, until she reaches $A_{2022}$, after which she hops back to $A_{1}$. When hopping from $P$ to $Q$, she always hops along the shorter of the two $\operatorname{arcs} \overparen{P Q}$ of $\gamma$; if $\overline{P Q}$ is a diameter of $\gamma$, she moves along either semicircle. Determine the maximal possible sum of the lengths of the 2022 arcs which Bunbun traveled, over all possible labellings of the 2022 points.
|
Replacing 2022 with $2 n$, the answer is $2 n^{2}-2 n+2$. (When $n=1011$, the number is 2042222.)  【 Construction. The construction for $n=5$ shown on the left half of the figure easily generalizes for all $n$. Remark. The validity of this construction can also be seen from the below proof. ब First proof of bound. Let $d_{i}$ be the shorter distance from $A_{2 i-1}$ to $A_{2 i+1}$. Claim - The distance of the leg of the journey $A_{2 i-1} \rightarrow A_{2 i} \rightarrow A_{2 i+1}$ is at most $2 n-d_{i}$. That means the total distance is at most $$ \sum_{i=1}^{n}\left(2 n-d_{i}\right)=2 n^{2}-\left(d_{1}+d_{2}+\cdots+d_{n}\right) $$ Claim - We have $$ d_{1}+d_{2}+\cdots+d_{n} \geq 2 n-2 $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
1
| null |
USA_TST
|
There are 2022 equally spaced points on a circular track $\gamma$ of circumference 2022. The points are labeled $A_{1}, A_{2}, \ldots, A_{2022}$ in some order, each label used once. Initially, Bunbun the Bunny begins at $A_{1}$. She hops along $\gamma$ from $A_{1}$ to $A_{2}$, then from $A_{2}$ to $A_{3}$, until she reaches $A_{2022}$, after which she hops back to $A_{1}$. When hopping from $P$ to $Q$, she always hops along the shorter of the two $\operatorname{arcs} \overparen{P Q}$ of $\gamma$; if $\overline{P Q}$ is a diameter of $\gamma$, she moves along either semicircle. Determine the maximal possible sum of the lengths of the 2022 arcs which Bunbun traveled, over all possible labellings of the 2022 points.
|
Replacing 2022 with $2 n$, the answer is $2 n^{2}-2 n+2$. (When $n=1011$, the number is 2042222.)  【 Construction. The construction for $n=5$ shown on the left half of the figure easily generalizes for all $n$. Remark. The validity of this construction can also be seen from the below proof. Second proof of bound. Draw the $n$ diameters through the $2 n$ arc midpoints, as shown on the right half of the figure for $n=5$ in red. Claim (Interpretation of distances) - The distance between any two points equals the number of diameters crossed to travel between the points. With this in mind, call a diameter critical if it is crossed by all $2 n$ arcs. Claim - At most one diameter is critical. Claim - Every diameter is crossed an even number of times. This immediately implies that the maximum possible total distance is achieved when one diameter is crossed all $2 n$ times, and every other diameter is crossed $2 n-2$ times, for a total distance of at most $$ n \cdot(2 n-2)+2=2 n^{2}-2 n+2 $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
\I Inversion solution submitted by Ankan Bhattacharya and Nikolai Beluhov. Let $H$ be the orthocenter of $\triangle A B C$. We use inversion in the circle with diameter $\overline{B C}$. We identify a few images: - The circumcircles of $\triangle B M E$ and $\triangle C M F$ are mapped to lines $B E$ and $C F$. - The common external tangents are mapped to the two circles through $M$ which are tangent to lines $B E$ and $C F$. - The image of $K$, denoted $K^{*}$, is the second intersection of these circles. - The assertion that $K$ lies on $(A B C)$ is equivalent to $K^{*}$ lying on $(B H C)$. However, now $K^{*}$ is simple to identify directly: it's just the reflection of $M$ in the bisector of $\angle B H C$.  In particular, $\overline{H K^{*}}$ is a symmedian of $\triangle B H C$. However, since $K^{*}$ lies on $(B H C)$, this means $\left(H K^{*} ; B C\right)=-1$. Then, we obtain that $\overline{B C}$ bisects $\angle H M K^{*} \equiv \angle H M K$. However, $K$ also lies on $(A B C)$, which forces $K$ to be the reflection of $H$ in $\overline{B C}$. Thus $\overline{A K} \perp \overline{B C}$, as wanted.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
ๆ Solution with coaxial circles (Pitchayut Saengrungkongka). Let $H$ be the orthocenter of $\triangle A B C$. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We first prove the following well-known properties of $Q$. Claim - $Q$ is the Miquel point of $B C E F$. In particular, $Q$ lies on both $\odot(A E F)$ and $\odot(A B C)$. Claim - $A(Q, H ; B, C)=-1$. Claim - $Q T$ is tangent to $\odot(B Q C)$. $$ \begin{aligned} \frac{B T}{T C} & =\frac{T B \cdot T M}{T C \cdot T M} \\ & =\frac{\operatorname{pow}(T, \odot(B M E))}{\operatorname{pow}(T, \odot(C M F))} \\ & =\frac{\operatorname{pow}(K, \odot(B M E))}{\operatorname{pow}(K, \odot(C M F))} \\ & =\left(\frac{r_{\odot(B M E)}}{r_{\odot(C M F)}}\right)^{2} \\ & =\left(\frac{B Q / \sin \angle Q M B}{C Q / \sin \angle Q M C}\right)^{2} \\ & =\frac{B Q^{2}}{C Q^{2}} \end{aligned} $$ implying the result. To finish, let $O$ be the center of $\odot(A B C)$. Then, from the claim, $\angle O Q T=90^{\circ}=$ $\angle O M T$, so $O$ also lies on $\odot(Q M T K)$. Thus, $\angle O K T=90^{\circ}$, so $K T$ is also tangent to $\odot(A B C)$ as well. This implies that $Q B K C$ is harmonic quadrilateral, and the result follows from the second claim.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Solution by Luke Robitaille. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We use the first two claims of the previous solution. In particular, $Q \in$ $\odot(A B C)$. We have the following claim. Claim (Also appeared in ISL 2017 G7) - We have $\measuredangle Q K M=\measuredangle Q B M+\measuredangle Q C M$. $$ \begin{aligned} \measuredangle Q K M & =\measuredangle Q^{\prime} Q M^{\prime}+\measuredangle Q M^{\prime} M \\ & =\measuredangle Q C M+\measuredangle Q B M, \end{aligned} $$ as desired. Now, we extend $K M$ to meet $\odot(A B C)$ again at $Q_{1}$. We have $$ \begin{aligned} \measuredangle Q_{1} Q B=\measuredangle Q_{1} K B & =\measuredangle Q_{1} K Q+\measuredangle Q C B \\ & =\measuredangle M K Q+\measuredangle Q K B \\ & =(\measuredangle M B Q+\measuredangle M C Q)+\measuredangle Q C B \\ & =\measuredangle C B Q, \end{aligned} $$ implying that $Q Q_{1} \| B C$. This implies that $Q B K C$ is harmonic quadrilateral, so we are done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
I Synthetic solution due to Andrew Gu (Harvard 2026). Define $O_{1}$ and $O_{2}$ as the circumcenters of $(B M E)$ and $(C M F)$. Let $T$ be the point on $(A B C)$ such that $\overline{A T} \perp \overline{B C}$. Denote by $L$ the midpoint of minor arc $\overparen{B C}$. We are going to ignore the condition that $K$ lies on the circumcircle of $A B C$, and prove the following unconditional result: ## Proposition The points $T, L, K$ are collinear. This will solve the problem because if $K$ is on the circumcircle of $A B C$, it follows $K=T$ or $K=L$; but $K=L$ can never occur since $O_{1}$ and $O_{2}$ are obviously on different sides of line $L M$ so line $L M$ must meet $O_{1} O_{2}$ inside segment $O_{1} O_{2}$, and $K$ lies outside this segment.  Claim - Lines $A C$ and $L M$ meet at the antipode $Q_{1}$ of $B$ on $(B M E)$, so that $B P_{1} Q_{1} M$ is a rectangle. Similarly, lines $A B$ and $L M$ meet at the antipode $Q_{2}$ of $C$ on $(C M F)$, so that $C P_{2} Q_{2} M$ is a rectangle. From this, it follows that $P_{1} Q_{1}=B M=\frac{1}{2} B C=M C=P_{2} Q_{2}$. Letting $r_{1}$ denote the radius of $\omega_{1}$ (and similarly for $\omega_{2}$ ), we deduce that $C Q_{1}=B Q_{1}=2 r_{1}$. Claim - $K M=K L$. $$ \measuredangle Q_{1} C L=\measuredangle A C L=\measuredangle A B L=\measuredangle Q_{2} B L=\measuredangle Q_{2} C L $$ The external angle bisector theorem then gives an equality of directed ratios $$ \frac{L Q_{1}}{L Q_{2}}=\frac{\left|C Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{\left|B Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{2 r_{1}}{2 r_{2}}=\frac{r_{1}}{r_{2}} $$ Let the reflection of $M$ over $K$ be $P$; then $P$ lies on $\overline{P_{1} P_{2}}$ and $$ \frac{P P_{1}}{P P_{2}}=\frac{2 K O_{1}}{2 K O_{2}}=\frac{K O_{1}}{K O_{2}}=\frac{r_{1}}{r_{2}}=\frac{L Q_{1}}{L Q_{2}} $$ where again the ratios are directed. Projecting everything onto line $L M$, so that $P_{1}$ lands at $Q_{1}$ and $P_{2}$ lands at $Q_{2}$, we find that the projection of $P$ must land exactly at $L$. Claim - Line $K M$ is an external angle bisector of $\angle O_{1} M O_{2}$. To finish, note that we know that $\overline{M P_{1}} \| \overline{C Q_{1}} \equiv \overline{A C}$ and $\overline{M P_{2}} \| \overline{B Q_{2}} \equiv \overline{A B}$, meaning the angles $\angle O_{1} M O_{2}$ and $\angle C A B$ have parallel legs. Hence, if $N$ is the antipode of $L$, it follows that $\overline{M K} \| \overline{A N}$. Now from $M K=K L$ and the fact that $A N L T$ is an isosceles trapezoid, we deduce that $\overline{L T}$ and $\overline{L K}$ are lines in the same direction (namely, the reflection of $M K \| A N$ across $\overline{B C}$ ), as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
2
| null |
USA_TST
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Complex numbers approach with Apollonian circles, by Carl Schildkraut. We use complex numbers. As in the first approach, we will ignore the hypothesis that $K$ lies on ( $A B C$ ). Let $Q:=(A H) \cap(A B C) \cap(A E F) \neq A$ be the Miquel point of $B F E C$ again. Construct the point $T$ on $(A B C)$ for which $A T \perp B C$; note that $T=-\frac{b c}{a}$. This time the unconditional result is: ## Proposition We have $Q, M, T, K$ are concyclic (or collinear) on an Apollonian circle of $\overline{O_{1} O_{2}}$. This will solve the original problem since once $K$ lies on $(A B C)$ it must be either $Q$ or $T$. But since $K$ is not on $(B M E), K \neq Q$, it will have to be $T$. We now prove the proposition. Suppose $(A B C)$ is the unit circle and let $A=a, B=b$, $C=c$. Let $H=a+b+c$ be the orthocenter of $\triangle A B C$. By the usual formulas, $$ E:=\frac{1}{2}\left(a+b+c-\frac{b c}{a}\right) . $$ Let $O_{1}$ be the center of $(B M E)$ and $O_{2}$ be the center of $(C M F)$. Claim (Calculation of the Miquel point) - We have $Q=\frac{2 a+b+c}{a\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+1}$. $$ 0=\frac{q-h}{q-a}+\frac{1 / q-\bar{h}}{1 / q-1 / a}=\frac{q-h}{q-a}-\frac{a(1-q \bar{h})}{q-a} $$ This solves to $q=\frac{h+a}{a \bar{h}+1}=\frac{2 a+b+c}{a \bar{h}+1}$. Claim (Calculation of $O_{1}$ and $\left.O_{2}\right)-$ We have $O_{1}=\frac{b(2 a+b+c)}{2(a+b)}$ and $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. $$ \begin{aligned} O_{1} & =\operatorname{Circum}(B, M, E) \\ & =b+\frac{1}{2} \operatorname{Circum}\left(0, c-b, \frac{(a-b)(b-c)}{b}\right) \\ & =b-\frac{b-c}{2 b} \operatorname{Circum}(0, b, b-a) \\ & =b-\frac{b-c}{2 b}(b-\operatorname{Circum}(0, b, a)) \\ & =b-\frac{b-c}{2 b}\left(b-\frac{a b}{a+b}\right)=b-\frac{b(b-c)}{2(a+b)}=\frac{b(2 a+b+c)}{2(a+b)} \end{aligned} $$ Similarly, $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. We are now going to prove the following: Claim - We have $$ \frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}} $$ $$ M O_{1}=B O_{1}=\left|b-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|\frac{b(b-c)}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right| $$ and $Q O_{1}=\left|r-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|1-\frac{b(a+h)}{2(a+b) r}\right|=\left|1-\frac{b(a \bar{h}+1)}{2(a+b)}\right|=\left|\frac{a-\frac{a b}{c}}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right|$. This implies both (by symmetry) that $\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}=\left|\frac{a+c}{a+b}\right|$ and that $Q$ is on (BME) and $(C M F)$. Also, $$ \frac{T O_{1}}{T O_{2}}=\frac{\left|\frac{b(2 a+b+c)}{2(a+b)}+\frac{b c}{a}\right|}{\left|\frac{c(2 a+b+c)}{2(a+c)}+\frac{b c}{a}\right|}=\left|\frac{\frac{b\left(2 a^{2}+a b+a c+2 a c+2 b c\right)}{2 a(a+b)}}{\frac{c\left(2 a^{2}+a b+a c+2 a b+2 b c\right)}{2 a(a+c)}}\right|=\left|\frac{a+c}{a+b}\right| \cdot\left|\frac{2 a^{2}+2 b c+a b+3 a c}{2 a^{2}+2 b c+3 a b+a c}\right| $$ if $z=2 a^{2}+2 b c+a b+3 a c$, then $a^{2} b c \bar{z}=2 a^{2}+2 b c+3 a b+a c$, so the second term has magnitude 1. This means $\frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}$, as desired. To finish, note that this common ratio is the ratio between the radii of these two circles, so it is also $\frac{K O_{1}}{K O_{2}}$. By Apollonian circles the points $\{Q, M, T, K\}$ lie on a circle or a line.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
3
| null |
USA_TST
|
Consider pairs $(f, g)$ of functions from the set of nonnegative integers to itself such that - $f(0) \geq f(1) \geq f(2) \geq \cdots \geq f(300) \geq 0 ;$ - $f(0)+f(1)+f(2)+\cdots+f(300) \leq 300$; - for any 20 nonnegative integers $n_{1}, n_{2}, \ldots, n_{20}$, not necessarily distinct, we have $$ g\left(n_{1}+n_{2}+\cdots+n_{20}\right) \leq f\left(n_{1}\right)+f\left(n_{2}\right)+\cdots+f\left(n_{20}\right) . $$ Determine the maximum possible value of $g(0)+g(1)+\cdots+g(6000)$ over all such pairs of functions.
|
Replace $300=\frac{24 \cdot 25}{2}$ with $\frac{s(s+1)}{2}$ where $s=24$, and 20 with $k$. The answer is $115440=$ $\frac{k s(k s+1)}{2}$. Equality is achieved at $f(n)=\max (s-n, 0)$ and $g(n)=\max (k s-n, 0)$. To prove $$ g\left(n_{1}+\cdots+n_{k}\right) \leq f\left(n_{1}\right)+\cdots+f\left(n_{k}\right) $$ write it as $$ \max \left(x_{1}+\cdots+x_{k}, 0\right) \leq \max \left(x_{1}, 0\right)+\cdots+\max \left(x_{k}, 0\right) $$ with $x_{i}=s-n_{i}$. This can be proven from the $k=2$ case and induction. It remains to show the upper bound. For this problem, define a partition to be a nonincreasing function $p: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}_{\geq 0}$ such that $p(n)=0$ for some $n$. The sum of $p$ is defined to be $\sum_{n=0}^{\infty} p(n)$, which is finite under the previous assumption. Let $L=\mathbb{Z}_{\geq 0}^{2}$. The Young diagram of the partition is the set of points $$ \mathcal{P}:=\{(x, y) \in L: y<p(x)\} . $$ The number of points in $\mathcal{P}$ is equal to the sum of $p$. The conjugate of a partition defined as $$ p_{*}(n)=\text { the number of } i \text { for which } p(i)>n \text {. } $$ This is a partition with the same sum as $p$. Geometrically, the Young diagrams of $p$ and $p_{*}$ are reflections about $x=y$. Since each $g(n)$ is independent, we may maximize each one separately for all $n$ and assume that $$ g(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f\left(n_{1}\right)+\cdots+f\left(n_{k}\right)\right) . $$ The conditions of the problem statement imply that $f\left(\frac{s(s+1)}{2}\right)=0$. Then, for any $n \leq k \frac{s(s+1)}{2}$, there exists an optimal combination $\left(n_{1}, \ldots, n_{k}\right)$ in $\left(^{*}\right)$ where all $n_{i}$ are at most $\frac{s(s+1)}{2}$, by replacing any term in an optimum greater than $\frac{s(s+1)}{2}$ by $\frac{s(s+1)}{2}$ and shifting the excess to smaller terms (because $f$ is nonincreasing). Therefore we may extend $f$ to a partition by letting $f(n)=0$ for $n>\frac{s(s+1)}{2}$ without affecting the relevant values of $g$. Then $\left(^{*}\right)$ implies that $g$ is a partition as well. The problem can be restated as follows: $f$ is a partition with sum $\frac{s(s+1)}{2}$, and $g$ is a partition defined by $\left(^{*}\right)$. Find the maximum possible sum of $g$. The key claim is that the problem is the same under conjugation. Claim - Under these conditions, we have $$ g_{*}(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f_{*}\left(n_{1}\right)+\cdots+f_{*}\left(n_{k}\right)\right) . $$ $$ \overline{\mathcal{G}}=\underbrace{\overline{\mathcal{F}}+\cdots+\overline{\mathcal{F}}}_{k \overline{\mathcal{F}}^{\prime} \mathrm{s}} $$ where + denotes set addition. This definition remains invariant under reflection about $x=y$, which swaps $f$ and $g$ with their conjugates. Let $A$ be the sum of $g$. We now derive different bounds on $A$. First, by Hermite's identity $$ n=\sum_{i=0}^{k-1}\left\lfloor\frac{n+i}{k}\right\rfloor $$ we have $$ \begin{aligned} A & =\sum_{n=0}^{\infty} g(n) \\ & \leq \sum_{n=0}^{\infty} \sum_{i=0}^{k-1} f\left(\left\lfloor\frac{n+i}{k}\right\rfloor\right) \\ & =k^{2} \sum_{n=0}^{\infty} f(n)-\frac{k(k-1)}{2} f(0) \\ & =k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) . \end{aligned} $$ By the claim, we also get the second bound $A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0)$. For the third bound, note that $f\left(f_{*}(0)\right)=0$ and thus $g\left(k f_{*}(0)\right)=0$. Moreover, $$ g\left(q f_{*}(0)+r\right) \leq q \cdot f\left(f_{*}(0)\right)+(k-q-1) f(0)+f(r)=(k-q-1) f(0)+f(r), $$ so we have $$ \begin{aligned} A & =\sum_{\substack{0 \leq q<k \\ 0 \leq r<f_{*}(0)}} g\left(q f_{*}(0)+r\right) \\ & \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \sum_{0 \leq r<f_{*}(0)} f(r) \\ & =\frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} . \end{aligned} $$ Now we have three cases: - If $f(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) \leq \frac{k s(k s+1)}{2} $$ - If $f_{*}(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0) \leq \frac{k s(k s+1)}{2} $$ - Otherwise, $f(0) f_{*}(0) \leq s^{2}$ and $$ A \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} \leq \frac{k s(k s+1)}{2} $$ In all cases, $A \leq \frac{k s(k s+1)}{2}$, as desired. Remark. One can estimate the answer to be around $k^{2} \frac{s(s+1)}{2}$ by observing the set addition operation "dilates" $\mathcal{F}$ by a factor of $k$, but significant care is needed to sharpen the bound.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
4
| null |
USA_TST
|
For nonnegative integers $a$ and $b$, denote their bitwise xor by $a \oplus b$. (For example, $9 \oplus 10=1001_{2} \oplus 1010_{2}=0011_{2}=3$.) Find all positive integers $a$ such that for any integers $x>y \geq 0$, we have $$ x \oplus a x \neq y \oplus a y . $$
|
Answer: the function $x \mapsto x \oplus a x$ is injective if and only if $a$ is an even integer. đ Even case. First, assume $\nu_{2}(a)=k>0$. We wish to recover $x$ from $c:=x \oplus a x$. Notice that: - The last $k$ bits of $c$ coincide with the last $k$ bits of $x$. - Now the last $k$ bits of $x$ give us also the last $2 k$ bits of $a x$, so we may recover the last $2 k$ bits of $x$ as well. - Then the last $2 k$ bits of $x$ give us also the last $3 k$ bits of $a x$, so we may recover the last $3 k$ bits of $x$ as well. - ...and so on. đ Odd case. Conversely, suppose $a$ is odd. To produce the desired collision: Claim - Let $n$ be any integer such that $2^{n}>a$, and define $$ x=\underbrace{1 \ldots 1}_{n}=2^{n}-1, \quad y=1 \underbrace{0 \ldots 0}_{n} 1=2^{n}+1 . $$ Then $x \oplus a x=y \oplus a y$. $$ \begin{aligned} & a x=\overline{Q R} \Longrightarrow x \oplus a x=\overline{Q Q} \\ & a y=\overline{P P} \Longrightarrow y \oplus a y=\overline{Q Q} . \end{aligned} $$ We're done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
5
| null |
USA_TST
|
Let $m$ and $n$ be fixed positive integers. Tsvety and Freyja play a game on an infinite grid of unit square cells. Tsvety has secretly written a real number inside of each cell so that the sum of the numbers within every rectangle of size either $m \times n$ or $n \times m$ is zero. Freyja wants to learn all of these numbers. One by one, Freyja asks Tsvety about some cell in the grid, and Tsvety truthfully reveals what number is written in it. Freyja wins if, at any point, Freyja can simultaneously deduce the number written in every cell of the entire infinite grid. (If this never occurs, Freyja has lost the game and Tsvety wins.) In terms of $m$ and $n$, find the smallest number of questions that Freyja must ask to win, or show that no finite number of questions can suffice.
|
The answer is the following: - If $\operatorname{gcd}(m, n)>1$, then Freyja cannot win. - If $\operatorname{gcd}(m, n)=1$, then Freyja can win in a minimum of $(m-1)^{2}+(n-1)^{2}$ questions. First, we dispose of the case where $\operatorname{gcd}(m, n)>1$. Write $d=\operatorname{gcd}(m, n)$. The idea is that any labeling where each $1 \times d$ rectangle has sum zero is valid. Thus, to learn the labeling, Freyja must ask at least one question in every row, which is clearly not possible in a finite number of questions. Now suppose $\operatorname{gcd}(m, n)=1$. We split the proof into two halves. 【 Lower bound. Clearly, any labeling where each $m \times 1$ and $1 \times m$ rectangle has sum zero is valid. These labelings form a vector space with dimension $(m-1)^{2}$, by inspection. (Set the values in an $(m-1) \times(m-1)$ square arbitrarily and every other value is uniquely determined.) Similarly, labelings where each $n \times 1$ and $1 \times n$ rectangle have sum zero are also valid, and have dimension $(n-1)^{2}$. It is also easy to see that no labeling other than the all-zero labeling belongs to both categories; labelings in the first space are periodic in both directions with period $m$, while labelings in the second space are periodic in both directions with period $n$; and hence any labeling in both categories must be constant, ergo all-zero. Taking sums of these labelings gives a space of valid labelings of dimension $(m-1)^{2}+$ $(n-1)^{2}$. Thus, Freyja needs at least $(m-1)^{2}+(n-1)^{2}$ questions to win. Claim (Periodicity) - Any valid labeling is doubly periodic with period $m n$. Then both $m n \times N$ and $m n \times(N+1)$ rectangles have zero sum, so $m n \times 1$ rectangles have zero sum. This implies that any two cells with a vertical displacement of $m n$ are equal; similarly for horizontal displacements. With that in mind, consider a valid labeling. It naturally corresponds to a generating function $$ f(x, y)=\sum_{a=0}^{m n-1} \sum_{b=0}^{m n-1} c_{a, b} x^{a} y^{b} $$ where $c_{a, b}$ is the number in $(a, b)$. The generating function corresponding to sums over $n \times m$ rectangles is $$ f(x, y)\left(1+x+\cdots+x^{m-1}\right)\left(1+y+\cdots+y^{n-1}\right)=f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} . $$ Similarly, the one for $m \times n$ rectangles is $$ f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} . $$ Thus, the constraints for $f$ to be valid are equivalent to $$ f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} \quad \text { and } \quad f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} $$ being zero when reduced modulo $x^{m n}-1$ and $y^{m n}-1$, or, letting $\omega=\exp (2 \pi i / m n)$, both terms being zero when powers of $\omega$ are plugged in. To restate the constraints one final time, we need $$ f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 $$ for all $a, b \in\{0, \ldots, m n-1\}$. Claim - This implies that $f\left(\omega^{a}, \omega^{b}\right)=0$ for all but at most $(m-1)^{2}+(n-1)^{2}$ values of $(a, b) \in\{0, \ldots, m n-1\}^{2}$. $$ \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=\frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 . $$ This happens when (at least) one fraction in either product is zero. - If the first fraction is zero, then either $n \mid a$ and $a>0$, or $m \mid b$ and $b>0$. - If the second fraction is zero, then either $m \mid a$ and $a>0$, or $n \mid b$ and $b>0$. If the first condition holds in both cases, then $m n \mid a$, but $0<a<m n$, a contradiction. Thus if $n \mid a$, then we must have $n \mid b$, and similarly if $m \mid a$ then $m \mid b$. The former case happens $(m-1)^{2}$ times, and the latter case happens $(n-1)^{2}$ times. Thus, at most $(m-1)^{2}+(n-1)^{2}$ values of $f\left(\omega^{a}, \omega^{b}\right)$ are nonzero. Claim - The $(m n)^{2}$ equations $f\left(\omega^{a}, \omega^{b}\right)=0$ are linearly independent when viewed as linear equations in $(m n)^{2}$ variables $c_{a, b}$. Hence, any subset of these equations is also linearly independent. It follows that the dimension of the space of valid labelings is at most $(m-1)^{2}+(n-1)^{2}$, as desired. T Explicit version of winning algorithm by Freyja, from author. Suppose that $\operatorname{gcd}(m, n)=1$ and $m \leq n$. Let $[a, b]$ denote the set of integers between $a$ and $b$ inclusive. Let Freyja ask about all cells $(x, y)$ in the two squares $$ \begin{aligned} & S_{1}=[1, m-1] \times[1, m-1] \\ & S_{2}=[m, m+n-2] \times[1, n-1] . \end{aligned} $$ In the beginning, one by one, Freyja determines all values inside of the rectangle $Q:=$ $[1, m-1] \times[m, n-1]$. To that end, on each step she considers some rectangle with $m$ rows and $n$ columns such that its top left corner is in $Q$ and all of the other values in it have been determined already. In this way, Freyja uncovers all of $Q$, starting with its lower right corner and then proceeding upwards and to the left. Thus Freyja can learn all numbers inside of the rectangle $$ R:=[1, m+n-2] \times[1, n-1]=Q \cup S_{1} \cup S_{2} . $$ See the figure below for an illustration for $(m, n)=(5,8)$. The first cell of $Q$ is uncovered using the dotted green rectangle.  We need one lemma: ## Lemma Let $m$ and $n$ be positive integers with $\operatorname{gcd}(m, n)=1$. Consider an unknown sequence of real numbers $z_{1}, z_{2}, \ldots, z_{s}$ with $s \geq m+n-2$. Suppose that we know the sums of all contiguous blocks of size either $m$ or $n$ in this sequence. Then we can determine all individual entries in the sequence as well. Let $T$ be the rectangle $[1, m+n-2] \times\{n\}$. By looking at appropriate rectangles of sizes $m \times n$ and $n \times m$ such that their top row is contained within $T$ and all of their other rows are contained within $R$, Freyja can learn the sums of all contiguous blocks of values of sizes $m$ and $n$ within $T$. By the Lemma, it follows that Freyja can uncover all of $T$. In this way, with the help of the Lemma, Freyja can extend her rectangular area of knowledge both upwards and downwards. Once its height reaches $m+n-2$, by the same method she will be able to extend it to the left and right as well. This allows Freyja to determine all values in the grid. Therefore, $(m-1)^{2}+(n-1)^{2}$ questions are indeed sufficient. Let $m$ and $n$ be relatively prime positive integers. Consider an infinite grid of unit square cells coloured in such a way that every rectangle of size either $m \times n$ or $n \times m$ contains the same multiset of colours. Then the colouring is either doubly periodic with period length $m$ or doubly periodic with period length $n$. (Here, "doubly periodic with period length $s$ " means "both horizontally and vertically periodic with period length $s$ ".) $$ f_{i j}(x, y):=\left\{\begin{array}{rll} +1 & \text { when }(x, y) \equiv(0,0) \text { or }(i, j) & (\bmod m) ; \\ -1 & \text { when }(x, y) \equiv(0, j) \text { or }(i, 0) & (\bmod m) ; \text { and } \\ 0 & \text { otherwise. } \end{array}\right. $$ Define $g_{i, j}$ similarly, but with $1 \leq i, j \leq n-1$ and " $\bmod m$ " everywhere replaced by " $\bmod$ $n$ ". First we show that if a linear combination $h:=\sum \alpha_{i, j} f_{i, j}+\sum \beta_{i, j} g_{i, j}$ of the $f_{i, j}$ and $g_{i, j}$ contains only two distinct values, then either all of the $\alpha_{i, j}$ vanish or all of the $\beta_{i, j}$ do. It follows that each colour, considered in isolation, is either doubly periodic with period length $m$ or doubly periodic with period length $n$. Finally, we check that different period lengths cannot mix. On the other hand, if $m$ and $n$ are not relatively prime, then there exist infinitely many non-isomorphic valid colourings. Furthermore, when $\operatorname{gcd}(m, n)=2$, there exist valid colourings which are not horizontally periodic; and, when $\operatorname{gcd}(m, n) \geq 3$, there exist valid colourings which are neither horizontally nor vertically periodic.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2023
|
T0
|
6
| null |
USA_TST
|
Fix a function $f: \mathbb{N} \rightarrow \mathbb{N}$ and for any $m, n \in \mathbb{N}$ define $$ \Delta(m, n)=\underbrace{f(f(\ldots f}_{f(n) \text { times }}(m) \ldots))-\underbrace{f(f(\ldots f}_{f(m) \text { times }}(n) \ldots)) . $$ Suppose $\Delta(m, n) \neq 0$ for any distinct $m, n \in \mathbb{N}$. Show that $\Delta$ is unbounded, meaning that for any constant $C$ there exist $m, n \in \mathbb{N}$ with $|\Delta(m, n)|>C$.
|
Suppose for the sake of contradiction that $|\Delta(m, n)| \leq N$ for all $m, n$. Note that $f$ is injective, as $$ f(m)=f(n) \Longrightarrow \Delta(m, n)=0 \Longrightarrow m=n $$ as desired. Let $G$ be the "arrow graph" of $f$, which is the directed graph with vertex set $\mathbb{N}$ and edges $n \rightarrow f(n)$. The first step in the solution is to classify the structure of $G$. Injectivity implies that $G$ is a disjoint collection of chains (infinite and half-infinite) and cycles. We have the following sequence of claims that further refine the structure. Claim - The graph $G$ has no cycles. $$ f^{f(n)}\left(m_{1}\right)=f^{f(n)}\left(m_{2}\right) $$ for some $m_{1} \neq m_{2}$, which contradicts injectivity. Claim - The graph $G$ has at most $2 N+1$ chains. $$ \left|\Delta\left(m_{i}, f^{B-f\left(m_{i}\right)}(1)\right)\right| \leq N \Longrightarrow\left|f^{B}(1)-f^{f B-f\left(m_{i}\right)+1}(1)\left(m_{i}\right)\right| \leq N . $$ Since the $m_{i} \mathrm{~S}$ are in different chains, we have that $f^{f\left(-f\left(m_{i}\right)+1\right.}(1)\left(m_{i}\right)$ are distinct for each $i$, which implies that $k \leq 2 N+1$, as desired. Claim - The graph $G$ consists of exactly one half-infinite chain. Since there are only finitely many chains, $f^{f(c)}(n)$ achieves all sufficiently large positive integers, say all positive integers at least $M$. Fix $A$ and $B$ such that $B>A \geq M$. If $f^{f(c)}(n) \in[A, B]$, then $f^{f(n)}(c) \in[A-N, B+N]$, and distinct $n$ generate distinct $f^{f(n)}(c)$ due to the structure of $G$. Therefore, we have at least $B-A+1$ good numbers in $[A-N, B+N]$, so there are at most $2 N$ bad numbers in $[A-N, B+N]$. Varying $B$, this shows there are at most $2 N$ bad numbers at least $A-N$. Let $c$ be the starting point of the chain, so every integer is of the form $f^{k}(c)$, where $k \geq 0$. Define a function $g: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{N}$ by $$ g(k):=f^{k}(c) $$ Due to the structure of $G, g$ is a bijection. Define $$ \delta(a, b):=\Delta\left(f^{a}(c), f^{b}(c)\right)=g(g(b+1)+a)-g(g(a+1)+b) $$ so the conditions are equivalent to $|\delta(a, b)| \leq N$ for all $a, b \in \mathbb{Z}_{\geq 0}$ and $\delta(a, b) \neq 0$ for $a \neq b$, which is equivalent to $g(a+1)-a \neq g(b+1)-b$ for $a \neq b$. This tells us that $g(x)-x$ is injective for $x \geq 1$. ## Lemma For all $M$, there exists a nonnegative integer $x$ with $g(x) \leq x-M$. Now pick $B$ such that $g(B)+N \leq B$ and $g(B)>N$. Note that infinitely many such $B$ exist, since we can take $M$ to be arbitrarily small in the above lemma. Let $$ t=\max \left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ Note that $g(t) \leq g(B)+N \leq B$, so we have $$ |\delta(t-1, B-g(t))|=|g(B)-g(t-1+g(B+1-g(t)))| \leq N $$ so $$ t-1+g(B+1-g(t)) \in\left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ so by the maximality of $t$, we must have $g(B+1-g(t))=1$, so $B+1-g(t)=g^{-1}(1)$. We have $|g(t)-g(B)| \leq N$, so $$ \left|(B-g(B))+1-g^{-1}(1)\right| \leq N . $$ This is true for infinitely many values of $B$, so infinitely many values of $B-g(B)$ (by injectivity of $g(x)-x)$, which is a contradiction. This completes the proof.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2024
|
T0
|
1
| null |
USA_TST
|
Find the smallest constant \(C > 1\) such that the following statement holds: for every integer \(n\geq 2\) and sequence of non-integer positive real numbers \(a_{1}\) , \(a_{2}\) , ..., \(a_{n}\) satisfying
\[\frac{1}{a_{1}} +\frac{1}{a_{2}} +\dots +\frac{1}{a_{n}} = 1,\]
it's possible to choose positive integers \(b_{i}\) such that
(i) for each \(i = 1,2,\ldots ,n\) , either \(b_{i} = \lfloor a_{i}\rfloor\) or \(b_{i} = \lfloor a_{i}\rfloor +1\) ; and
(ii) we have
\[1< \frac{1}{b_{1}} +\frac{1}{b_{2}} +\dots +\frac{1}{b_{n}}\leq C.\]
|
Answer. The answer is \(C = \frac{3}{2}\) .
Lower bound. Note that if \(a_{1} = \frac{4n - 3}{2n - 1}\) and \(a_{i} = \frac{4n - 3}{2n - 1}\) for \(i > 1\) , then we must have \(b_{1} \in \{1,2\}\) and \(b_{i} \in \{2n - 2,2n - 1\}\) for \(i > 1\) . If we take \(b_{1} = 2\) then we obtain
\[\frac{1}{b_{1}} +\frac{1}{b_{2}} +\dots +\frac{1}{b_{n}}\leq \frac{1}{2} +(n - 1)\cdot \frac{1}{2n - 2} = 1,\]
whereas if we take \(b_{1} = 1\) then we obtain
\[\frac{1}{b_{1}} +\frac{1}{b_{2}} +\dots +\frac{1}{b_{n}}\geq 1 + (n - 1)\cdot \frac{1}{2n - 1} = \frac{3n - 2}{2n - 1}.\]
This shows that \(C \geq \frac{3n - 2}{2n - 1}\) , and as \(n \to \infty\) this shows that \(C \geq \frac{3}{2}\) .
Upper bound. For \(0 \leq k \leq n\) , define
\[c_{i} = \sum_{i = 1}^{k}\frac{1}{\lfloor a_{i}\rfloor} +\sum_{i = k + 1}^{n}\frac{1}{\lfloor a_{i}\rfloor + 1}.\]
Note that \(c_{0} < c_{1} < \dots < c_{n}\) and
\[c_{0} < \frac{1}{a_{1}} +\frac{1}{a_{2}} +\dots +\frac{1}{a_{n}} = 1 < c_{n}.\]
This means there exists a unique value of \(k\) for which \(c_{k - 1} < 1 < c_{k}\) . For this \(k\) we have
\[1< c_{k} = c_{k - 1} + \frac{1}{(\lfloor a_{k}\rfloor)(\lfloor a_{k}\rfloor + 1)} < 1 + \frac{1}{1\cdot 2} = \frac{3}{2}.\]
Therefore we may choose \(b_{i} = \lfloor a_{i}\rfloor\) for \(i \leq k\) and \(b_{i} = \lfloor a_{i}\rfloor +1\) for \(i > k\) .
Remark. The solution can be phrased in the following “motion- based” way. Imagine starting with all floors (corresponding to \(c_{0}\) ), then changing each floor to a ceiling one by one until after \(n\) steps every floor is a ceiling (arriving at \(c_{n}\) ). As we saw, \(c_{0} < 1 < c_{n}\) , but \(c_{0} < \dots < c_{n}\) . Moreover, each discrete step increases the sum by at most
\[\frac{1}{\lfloor a_{i}\rfloor} -\frac{1}{\lfloor a_{i}\rfloor + 1}\leq \frac{1}{2}\]
and so the changing sum must be in the interval \([1,3 / 2]\) at some point.
\(\P\) Upper bound (alternate). First suppose \(a_{i}< 2\) for some \(i\) . Assume without loss of generality \(i = 1\) here. Let \(b_{1} = 1\) and \(b_{i} = \lfloor a_{i}\rfloor +1\) for all other \(i\) . Then
\[1< \frac{1}{b_{1}} +\dots +\frac{1}{b_{n}} = 1 + \frac{1}{\lfloor a_{2}\rfloor +1} +\dots +\frac{1}{\lfloor a_{n}\rfloor +1}\] \[< \left(\frac{1}{2} +\frac{1}{a_{1}}\right) + \frac{1}{a_{2}} +\dots +\frac{1}{a_{n}} = \frac{3}{2}.\]
Now suppose \(a_{i} > 2\) always. Then \(\frac{a_{i}}{\lfloor a_{i}\rfloor} < \frac{3}{2}\) , so
\[1 = \frac{1}{a_{1}} +\dots +\frac{1}{a_{n}} < \frac{1}{\lfloor a_{1}\rfloor} +\dots +\frac{1}{\lfloor a_{n}\rfloor} < \frac{3}{2}\left(\frac{1}{a_{1}} +\dots +\frac{1}{a_{n}}\right) = \frac{3}{2}.\]
Therefore we may let \(b_{i} = \lfloor a_{i}\rfloor\) for all \(i\) .
Remark. The original proposal asked to find the optimal \(C\) for a fixed \(n\) . The answer is \(\frac{3n - 2}{2n - 1}\) , i.e. the lower bound construction in the solution is optimal.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "1. ",
"solution_match": "## \\(\\S 1.1\\) USA TST 2024/1, proposed by Merlijn Staps \n"
}
|
2024
|
T0
|
2
| null |
USA_TST
|
Let \(A B C\) be a triangle with incenter \(I\) . Let segment \(A I\) intersect the incircle of triangle \(A B C\) at point \(D\) . Suppose that line \(B D\) is perpendicular to line \(A C\) . Let \(P\) be a point such that \(\angle B P A = \angle P A I = 90^{\circ}\) . Point \(Q\) lies on segment \(B D\) such that the circumcircle of triangle \(A B Q\) is tangent to line \(B I\) . Point \(X\) lies on line \(P Q\) such that \(\angle I A X = \angle X A C\) . Prove that \(\angle A X P = 45^{\circ}\) .
|
We show several approaches.
First solution, by author.

Claim — We have \(B P = B Q\) .
Proof. For readability, we split the proof into three unconditional parts.
- We translate the condition \(\overline{B D} \perp \overline{A C}\) . It gives \(\angle D B A = 90^{\circ} - A\) , so that
\[\angle D B I = \left|\frac{B}{2} -(90^{\circ} - A)\right| = \frac{|A - C|}{2}\] \[\angle B D I = \angle D B A + \angle B A D = (90^{\circ} - A) + \frac{A}{2} = 90^{\circ} - \frac{A}{2}.\]
Hence, letting \(r\) denote the inradius, we can translate \(\overline{BD} \perp \overline{AC}\) into the following trig condition:
\[\sin \frac{B}{2} = \frac{r}{BI} = \frac{DI}{BI} = \frac{\sin \angle DBI}{\sin \angle BDI} = \frac{\sin \frac{|A - C|}{2}}{\sin \left(90^{\circ} - \frac{A}{2}\right)}.\]
- The length of \(BP\) is given from right triangle \(APB\) as
\[BP = BA \cdot \sin \angle PAB = BA \cdot \sin \left(90^{\circ} - \frac{A}{2}\right).\]
- The length of \(BQ\) is given from the law of sines on triangle \(ABQ\) . The tangency gives \(\angle BAQ = \angle DBI\) and \(\angle BQA = 180^{\circ} - \angle ABI = 180^{\circ} - \angle IBE\) and thus
\[BQ = BA \cdot \frac{\sin \angle BAQ}{\sin \angle AQB} = BA \cdot \frac{\sin \angle DBI}{\sin \angle ABI} = BA \cdot \frac{\sin \frac{|A - C|}{2}}{\sin \frac{B}{2}}.\]
The first bullet implies the expressions in the second and third bullet for \(BP\) and \(BQ\) are equal, as needed. \(\square\)
Remark. In the above proof, one dos not actually need to compute \(\angle DBI = \frac{|A - C|}{2}\) . The proof works equally leaving that expression intact as \(\sin \angle DBI\) in place of \(\sin \frac{|A - C|}{2}\) .
Now we can finish by angle chasing. We have
\[\angle PBQ = \angle PBA + \angle ABD = \frac{A}{2} +90^{\circ} - A = 90^{\circ} - \frac{A}{2}.\]
Then
\[\angle BPQ = \frac{180^{\circ} - \angle PBQ}{2} = 45^{\circ} + \frac{A}{4},\]
so \(\angle APQ = 90^{\circ} - \angle BPQ = 45^{\circ} - \frac{A}{4}\) . Also, if we let \(J\) be the incenter of \(IAC\) , then \(\angle PAJ = 90^{\circ} + \frac{A}{4}\) , and clearly \(X\) lies on line \(AJ\) . Then \(\angle APQ + \angle PAJ = 135^{\circ} < 180^{\circ}\) , so \(X\) lies on the same side of \(AP\) as \(Q\) and \(J\) (by the parallel postulate). Therefore \(\angle AXP = 180^{\circ} - 135^{\circ} = 45^{\circ}\) , as desired.
Remark. The problem was basically written backwards by starting from the \(BD \perp AC\) condition, turning that into trig, and then contriving \(P\) and \(Q\) so that the \(BD \perp AC\) condition implied \(BP = BQ\) .
Second solution, by Jeffrey Kwan. We prove the following restatement:
Consider isosceles triangle \(AEF\) with \(AE = AF\) and incenter \(D\) . Let \(B\) be the point on ray \(AE\) such that \(BD \perp AF\) , and let \(P\) be the projection of \(B\) onto the line through \(A\) parallel to \(EF\) . Let \(I\) be the point diametrically opposite \(A\) in the circumcircle of \(AEF\) , and let \(Q\) be the point on line \(BD\) such that \(BI\) is tangent to the circumcircle of \(AQB\) . Then \(\angle APQ = 45^{\circ} - \angle A / 4\) .
First note that \(\angle DFE = 45^{\circ} - \angle A / 4\) , so it suffices to show that \(\overline{PQ} \parallel \overline{DF}\) . Let \(U = \overline{BD} \cap \overline{EF}\) , and let \(V = BI \cap (AEF)\) . Observe that:
- \(P\) and \(V\) both lie on the circle with diameter \(AB\) , so \(\angle BVP = \angle PAB = 90^{\circ} - \angle A / 2\) .
- We have \(\angle EVB = \angle EVI = \angle A / 2 = \angle DUF = \angle BUE\) . Hence \(BEUV\) is cyclic.
Now \(\angle BUV = \angle AEU = 90^{\circ} - \angle A / 2 = \angle BVP\) , so \(\overline{PUV}\) are collinear.

From the tangency condition, we have that \(\angle AQB = 180^{\circ} - \angle ABI\) , which implies that
\[\angle AQU + \angle APU = \angle AQB + \angle APV = (180^{\circ} - \angle ABI) + \angle ABI = 180^{\circ},\]
and so \(APUQ\) is cyclic. Finally, note that \(D\) is the orthocenter of \(\triangle AUVF\) , which implies that
\[\angle APQ = \angle AUQ = \angle AUD = \angle AFD = \angle DFE.\]
This forces \(\overline{PQ} \parallel \overline{DF}\) , as desired.
\(\P\) Third solution by Pitchayut Saengrungkongka and Maxim Li. We provide yet another proof that \(BP = BQ\) .

Let the incircle be \(\omega\) and touch \(BC\) and \(AB\) at point \(U\) and \(W\) . Let the tangent to \(\omega\) at \(D\) meet \(UW\) at \(T\) . Notice that \(T\) is the pole of \(BD\) with respect to \(\omega\) , so \(IT \perp BD\) . Now, we make the following critical claim, which in particular implies \(BP = BQ\) .
Claim — Quadrilaterals \(DIWT\) and \(PBQA\) are inversely similar.
Proof. This follows from four angle relations.
\(\angle IDT = \angle BPA = 90^{\circ}\) . \(\angle TIW = \angle ABQ\) . \(\angle DIT = \angle IAC = \angle BAI = \angle ABP\) . \(\angle ITW = \angle QBI = \angle QAB\) .
With \(BP = BQ\) obtained, one finishes with the same angle chasing as in the first solution.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "2. ",
"solution_match": "## \\(\\S 1.2\\) USA TST 2024/2, proposed by Luke Robitaille \n"
}
|
2024
|
T0
|
3
| null |
USA_TST
|
Let \(n > k\geq 1\) be integers and let \(p\) be a prime dividing \(\textstyle{\binom{n}{k}}\) . Prove that the \(k\) -element subsets of \(\{1,\ldots ,n\}\) can be split into \(p\) classes of equal size, such that any two subsets with the same sum of elements belong to the same class.
|
## Problem statem
Let \(\sigma (S)\) denote the sum of the elements of \(S\) , so that
\[P(x):= \sum_{S\subseteq \{1,\ldots ,n\}}x^{\sigma (S)}\]
is the generating function for the sums of \(k\) - element subsets of \(\{1, \ldots , n\}\) .
By Legendre's formula,
\[\nu_{p}\left(\binom{n}{k}\right) = \sum_{r = 1}^{\infty}\left(\left\lfloor \frac{n}{p^{r}}\right\rfloor -\left\lfloor \frac{k}{p^{r}}\right\rfloor -\left\lfloor \frac{n - k}{p^{r}}\right\rfloor\right)\]
so there exists a positive integer \(r\) with
\[\left\lfloor \frac{n}{p^{r}}\right\rfloor -\left\lfloor \frac{k}{p^{r}}\right\rfloor -\left\lfloor \frac{n - k}{p^{r}}\right\rfloor >0.\]
The main claim is the following:
Claim — \(P(x)\) is divisible by
\[\Phi_{p^{r}}(x) = x^{(p - 1)p^{r - 1}} + \dots +x^{p^{r - 1}} + 1.\]
Before proving this claim, we will show how it solves the problem. It implies that there exists a polynomial \(Q\) with integer coefficients satisfying
\[P(x) = \Phi_{p^{r}}(x)Q(x)\] \[\qquad = (x^{(p - 1)p^{r - 1}} + \dots +x^{p^{r - 1}} + 1)Q(x).\]
Let \(c_{0}\) , \(c_{1}\) , ... denote the coefficients of \(P\) , and define
\[s_{i} = \sum_{j\equiv i\pmod{p^{r}}}c_{j}.\]
Then it's easy to see that
\[s_{0} = s_{p^{r - 1}} = \dots = s_{(p - 1)p^{r - 1}}\] \[s_{1} = s_{p^{r - 1} + 1} = \dots = s_{(p - 1)p^{r - 1} + 1}\] \[\qquad \vdots\] \[s_{p^{r - 1} - 1} = s_{2p^{r - 1} - 1} = \dots = s_{p^{r} - 1}.\]
This means we can construct the \(p\) classes by placing a set with sum \(z\) in class \(\left\lfloor \frac{z \mod p^{r}}{p^{r - 1}}\right\rfloor\) . Now we present two ways to prove the claim.
First proof of claim. There's a natural bijection between \(k\) - element subsets of \(\{1,\ldots ,n\}\) and binary strings consisting of \(k\) zeroes and \(\ell\) ones: the set \(\{a_{1},\ldots ,a_{k}\}\) corresponds to the string which has zeroes at positions \(a_{1}\) , ..., \(a_{k}\) . Moreover, the inversion count of this string is simply \((a_{1} + \dots +a_{k}) - \frac{1}{2} k(k + 1)\) , so we only deal with these inversion counts (equivalently, we are factoring \(x^{\frac{k(k + 1)}{2}}\) out of \(P\) ).
Recall that the generating function for these inversion counts is given by the \(q\) - binomial coefficient
\[P(x) = \frac{(x - 1)\cdot\cdot\cdot(x^{k + \ell} - 1)}{[(x - 1)\cdot\cdot\cdot(x^{k} - 1)]\times[(x - 1)\cdot\cdot\cdot(x^{\ell} - 1)]}.\]
By choice of \(r\) , the numerator of \(P(x)\) has more factors of \(\Phi_{p^{r}}(x)\) than the denominator, so \(\Phi_{p^{r}}(x)\) divides \(P(x)\) .
Remark. Here is a proof that \(P(x)\) is divisible by \(\Phi_{p^{r}}(x)\) for some \(r\) using the \(q\) - binomial formula, without explicitly identifying \(r\) . We know that \(P(x)\) is the product of several cyclotomic polynomials, and that \(P(1)\) is a multiple of \(p\) . Thus there is a factor \(\Phi_{q}(x)\) for which \(\Phi_{q}(1)\) is a multiple of \(p\) , which is equivalent to \(q\) being a power of \(p\) .
Second proof of claim. Note that \(P(x)\) is the coefficient of \(y^{k}\) in the polynomial
\[Q(x,y):= (1 + xy)(1 + x^{2}y)\cdot \cdot \cdot (1 + x^{n}y).\]
Let \(a\) be the remainder when \(n\) is divided by \(p^{r}\) , and let \(b\) be the remainder when \(k\) is divided by \(p^{r}\) ; then we have \(a< b\) by the choice of \(r\) . Let \(q = \lfloor n / p^{r}\rfloor\) so \(n = p^{r}q + a\) . Consider taking \(x\) to be a primitive \(p^{r}\) th root of unity, say \(\omega\) . Then
\[Q(\omega ,y) = \left[(1 + \omega y)(1 + \omega^{2}y)\cdot \cdot \cdot (1 + \omega^{p^{r}}y)\right]^{q}(1 + \omega y)(1 + \omega^{2}y)\cdot \cdot \cdot (1 + \omega^{a}y).\]
Now \(\omega\) , \(\omega^{2}\) , ..., \(\omega^{p^{r}}\) are all the \(p^{r}\) th roots of unity, each exactly once; then we can see that
\[(1 + \omega y)(1 + \omega^{2}y)\cdot \cdot \cdot (1 + \omega^{p^{r}}y)\] \[= (1 - \omega (-y))(1 - \omega^{2}(-y))\cdot \cdot \cdot (1 - \omega^{p^{r}}(-y))\] \[= 1 - (-y)^{p^{r}},\]
so
\[Q(\omega ,y) = (1 - (-y)^{p^{r}})^{q}(1 + \omega y)(1 + \omega^{2}y)\cdot \cdot \cdot (1 + \omega^{a}y).\]
In particular, for any \(m\) , if the coefficient of \(y^{m}\) in \(Q(w,x)\) is nonzero, then \(m\) must be congruent to one of \(0,1,\ldots ,a\) (mod \(p^{r}\) ). Therefore the coefficient of \(y^{k}\) in \(Q(\omega ,y)\) is zero. This means that \(P(\omega) = 0\) whenever \(\omega\) is a primitive \(p^{r}\) th root of unity, which proves the claim.
## \(\S 2\) Solutions to Day 2
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "3. ",
"solution_match": "## \\(\\S 1.3\\) USA TST 2024/3, proposed by Ankan Bhattacharya \n"
}
|
2024
|
T0
|
4
| null |
USA_TST
|
Find all integers \(n\geq 2\) for which there exists a sequence of \(2n\) pairwise distinct points \((P_{1},\ldots ,P_{n},Q_{1},\ldots ,Q_{n})\) in the plane satisfying the following four conditions:
(i) no three of the \(2n\) points are collinear;
(ii) \(P_{i}P_{i + 1}\geq 1\) for all \(i = 1,2,\ldots ,n\) , where \(P_{n + 1} = P_{1}\)
(iii) \(Q_{i}Q_{i + 1}\geq 1\) for all \(i = 1,2,\ldots ,n\) , where \(Q_{n + 1} = Q_{1}\) ; and
(iv) \(P_{i}Q_{j}\leq 1\) for all \(i = 1,2,\ldots ,n\) and \(j = 1,2,\ldots ,n\)
|
Find alln\) .
Answer. Even integers only.
Proof that even \(n\) work. If we ignore the conditions that the points are pairwise distinct and form no collinear triples, we may take
\[P_{2i + 1} = (0.51,0), \quad P_{2i} = (-0.51,0), \quad Q_{2i + 1} = (0,0.51), \quad Q_{2i} = (0, -0.51).\]
The distances \(P_{i}P_{i + 1}\) and \(Q_{i}Q_{i + 1}\) are \(1.02 > 1\) , while the distances \(P_{i}Q_{j}\) are \(0.51\sqrt{2} < 1\) . We may then perturb each point by a small amount to ensure that the distance inequalities still hold and have the points in general position.
Proof that odd \(n\) do not work. The main claim is the following.
Claim — For \(1 \leq i \leq n\) , points \(Q_{i}\) and \(Q_{i + 1}\) must lie on opposite sides of line \(P_{1}P_{2}\) .
To isolate the geometry component of the problem, we rewrite the claim in the following contrapositive form, without referencing the points \(Q_{i}\) and \(Q_{i + 1}\) :
## Lemma
Suppose \(A\) and \(B\) are two points such that \(\max (P_{1}A, P_{1}B, P_{2}A, P_{2}B) \leq 1\) , and moreover \(A\) and \(B\) lie on the same side of line \(P_{1}P_{2}\) . Further assume no three of \(\{P_{1}, P_{2}, A, B\}\) are collinear. Then \(AB < 1\) .

Proof of lemma. Suppose for the sake of contradiction that \(A\) and \(B\) lie on the same side of \(P_{1}P_{2}\) . The convex hull of these four points is either a quadrilateral or a triangle.
- If the convex hull is a quadrilateral, assume WLOG that the vertices are \(P_{1}P_{2}AB\) in order. Let \(X\) denote the intersection of segments \(P_{1}A\) and \(P_{2}B\) . Then
\[1 + AB = P_{1}P_{2} + AB< P_{1}X + XP_{2} + AX + XB = P_{1}A + P_{2}B\leq 2.\]
- Otherwise, assume WLOG that \(B\) is in the interior of triangle \(P_{1}P_{2}A\) . Since \(\angle P_{1}BA + \angle P_{2}BA = 360^{\circ} - \angle P_{1}BP_{2} > 180^{\circ}\) , at least one of \(\angle P_{1}BA\) and \(\angle P_{2}BA\) is obtuse. Assume WLOG the former angle is obtuse; then \(AB< P_{1}A\leq 1\) . \(\square\)
Remark. Another proof of the lemma can be found by replacing segment \(AB\) with the intersection of this line on the boundary of the blue region above, which does not decrease the distance. In other words, one can assume WLOG that \(A\) and \(B\) lie on either segment \(AB\) or one of the two circular arcs. One then proves that \(AB\leq 1\) , and that for equality to occur, one of \(A\) and \(B\) must lie on segment \(P_{1}P_{2}\) However, this approach seems to involve a fair bit more calculation.
Yet another clever approach uses the trivia- fact that a Reuleaux triangle happens to have constant width.
In any case, it's important to realize that this claim is not trivial; while it looks like it is easy to prove, it is not, owing to the two near- equality cases.
It follows from the claim that \(Q_{i}\) is on the same side of line \(P_{1}P_{2}\) as \(Q_{1}\) if \(i\) is odd, and on the opposite side if \(i\) is even. Since \(Q_{1} = Q_{n + 1}\) , this means the construction is not possible when \(n\) is odd.
Remark. The fact that \(n\) cannot be odd follows from Theorem 3 of EPTAS for Max Clique on Disks and Unit Balls. In the language of that paper, if \(G\) is a unit ball graph, then the induced odd cycle parking number of \(\bar{G}\) is at most 1.
In earlier versions of the proposed problem, the points were not necessarily distinct to make the even \(n\) case nicer, but this resulted in annoying boundary conditions for the odd \(n\) case.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "4. ",
"solution_match": "## \\(\\S 2.1\\) USA TST 2024/4, proposed by Ray Li \n"
}
|
2024
|
T0
|
5
| null |
USA_TST
|
Suppose \(a_{1}< a_{2}< \dots < a_{2024}\) is an arithmetic sequence of positive integers, and \(b_{1}< b_{2}< \dots < b_{2024}\) is a geometric sequence of positive integers. Find the maximum possible number of integers that could appear in both sequences, over all possible choices of the two sequences.
|
Answer. 11 terms.
Construction. Let \(a_{i} = i\) and \(b_{i} = 2^{i - 1}\)
Bound. We show a \(\nu_{p}\) - based approach communicated by Derek Liu, which seems to be the shortest one. At first, we completely ignore the geometric sequence \(b_{i}\) and focus only on the arithmetic sequence.
Claim — Let \(p\) be any prime, and consider the sequence
\[\nu_{p}(a_{1}), \nu_{p}(a_{2}), \ldots , \nu_{p}(a_{2024}).\]
Set \(C := \lfloor \log_{p}(2023) \rfloor\) . Then there are at most \(C + 2\) different values in this sequence.
Proof. By scaling, assume the \(a_{i}\) do not have a common factor, so that \(a_{i} = a + d i\) where \(\gcd (a,d) = 1\) .
- If \(p \mid d\) , then \(p \nmid a\) and \(\nu_{p}(a_{i})\) is constant.
- Otherwise, assume \(p \nmid d\) . We will in fact prove that every term in the sequence is contained in \(\{0,1,\ldots ,C\}\) with at most one exception.
Define \(M := \max_{i} \nu_{p}(a_{i})\) . If \(M \leq C\) , there is nothing to prove. Otherwise, fix some index \(m\) such that \(\nu_{p}(a_{m}) = M\) . We know \(\nu_{p}(i - m) \leq C\) since \(|i - m| \leq 2023\) . But now for any other index \(i \neq m\) ;
\[\nu_{p}(d(i - m)) = \nu_{p}(i - m)\leq C< M = \nu_{p}(a_{m})\] \[\implies \nu_{p}(a_{i}) = \nu_{p}(a_{m} + d(i - m)) = \nu_{p}(i - m)\leq C.\]
so \(\nu_{p}(a_{m})\) is the unique exceptional term of the sequence exceeding \(C\) .
Remark. The bound in the claim is best possible by taking \(a_{i} = p^{M} + (i - 1)\) for any \(M > C\) . Then indeed, the sequence \(\nu_{p}(a_{i})\) takes on values in \(\{0,1,\ldots ,C\}\) for \(i > 1\) while \(\nu_{p}(a_{1}) = M\) .
Back to the original problem with \((b_{i})\) . Consider the common ratio \(r \in \mathbb{Q}\) of the geometric sequence \((b_{i})\) . If \(p\) is any prime with \(\nu_{p}(r) \neq 0\) , then every term of \((b_{i})\) has a different \(\nu_{p}\) . So there are two cases to think about.
Suppose any \(p \geq 3\) has \(\nu_{p}(r) \neq 0\) . Then there are at most
\[2 + \log_{p}(2023) = 2 + \log_{3}(2023) \approx 8.929 < 11\]
overlapping terms, as needed.
Otherwise, suppose \(r\) is a power of 2 (in particular, \(r \geq 2\) is an integer). We already have an upper bound of 12; we need to improve it to 11.
As in the proof before, we may assume WLOG by scaling down by a power of 2 that the common difference of \(a_{i}\) is odd. (This may cause some \(b_{i}\) to become rational non- integers, but that's OK. However, unless \(\nu_{2}(a_{i})\) is constant, the \(a_{i}\) will still be integers.)
Then in order for the bound of 12 to be achieved, the sequence \(\nu_{2}(a_{i})\) must be contained in \(\{0,1,\ldots ,10,M\}\) for some \(M \geq 11\) . In particular, we only need to work with \(r = 2\) .
Denote by \(b\) the unique odd- integer term in the geometric sequence, which must appear among \((a_{i})\) . Then \(2b\) appears too, so the common difference of \(a_{i}\) is at most \(b\) .
But if \((a_{i})\) is an arithmetic progression of integers that contains \(b\) and has common difference at most \(b\) , then no term of the sequence can ever exceed \(b + 2023 \cdot b = 2024b\) . Hence \(2^{M}b\) cannot appear for any \(M \geq 11\) . This completes the proof.
Remark. There are several other approaches to the problem, but most take some time to execute. The primary issue is that the common difference of the \(a_{i}\) 's could share prime factors with the common ratio in the \(b_{i}\) 's, which means that merely trying to write out a lot of modular arithmetic equations leads to a lot of potential technical traps that are not pleasant to defuse.
One unusual thing is that many solutions end up proving a bound of 12 (in the case the common ratio is 2) and then having to adjust it to 11 later.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "5. ",
"solution_match": "## \\(\\S 2.2\\) USA TST 2024/5, proposed by Ray Li \n"
}
|
2024
|
T0
|
6
| null |
USA_TST
|
Solve over \(\mathbb{R}\) the functional equation
\[f(x f(y)) + f(y) = f(x + y) + f(x y).\]
|
In addition to all constant functions, \(f(x)\equiv x + 1\) clearly works too. We prove these are the only solutions. The solution that follows is by the original proposer.
Let \(P(x,y)\) denote the given assertion.
Claim 2.1 — If \(f\) is periodic, then \(f\) is constant.
Proof. Let \(f\) have period \(d\neq 0\) . From \(P(x,y + d)\) , we have
\[f(x(y + d)) = f(x + y + d) - f(y + d) - f(x f(y + d)) = f(x + y) - f(y) - f(x f(y)).\]
Applying \(P(x,y)\) gives
\[f(x(y + d)) = f(x y).\]
In particular, taking \(y = 0\) yields that \(f(d x) = f(0)\) . Thus \(f\) is constant, as \(d\neq 0\) .
Claim 2.2 — For all real numbers \(x\) and \(y\) , we have \(f(f(x) + y) = f(f(y) + x)\) .
Proof. Applying \(P(f(x),y)\) and then \(P(y,x)\) gives us
\[f(f(x)f(y)) = f(f(x) + y) + f(f(x)y) - f(y)\] \[\qquad = f(f(x) + y) + f(x + y) + f(xy) - f(x) - f(y).\]
Now swapping \(x\) and \(y\) gives us \(f(f(x) + y) = f(f(y) + x)\) .
Claim 2.3 — If \(f\) is nonconstant, then \(f(f(x) + y) = f(x) + f(y)\) for all reals \(x,y\) .
Proof. Let \(x,y\in \mathbb{R}\) and let \(d:= f(f(x) + y) - f(x) - f(y)\) . Let \(z\) be an arbitrary real number. By repeatedly applying Claim 2.2, we have
\[f(z + f(f(x) + y)) = f(f(z) + f(x) + y)\] \[\qquad = f(f(x) + f(z) + y)\] \[\qquad = f(x + f(f(z) + y))\] \[\qquad = f(x + f(f(y) + z))\] \[\qquad = f(f(x) + f(y) + z)\] \[\qquad = f(z + f(x) + f(y)).\]
If \(d\neq 0\) , then \(f\) is periodic with period \(d\) , contradicting Claim 2.1.
Claim 2.4 — If \(f\) is nonconstant, then \(f(0) = 1\) and \(f(x + 1) = f(x) + 1\) .
Proof. From \(P(z,0)\) we have \(f(zf(0)) = f(z)\) for all real \(z\) . Then \(P(xf(0),y)\) and \(P(x,y)\) give us
\[f(xf(0) + y) = f(y) + f(xf(0)f(y)) - f(xf(0)y)\] \[\qquad = f(y) + f(xf(y)) - f(xy) = f(x + y).\]
If \(f(0)\neq 1\) , then \(x f(0) - x\) is a period of \(f\) for all \(x\) , violating Claim 2.1. So we must have \(f(0) = 1\) .
Now putting \(x = 0\) in Claim 2.3 gives \(f(x + 1) = f(x) + 1\) .
Claim 2.5 — If \(f\) is nonconstant, then \(f(x) + f(y) = f(x + y) + 1\) .
Proof. From \(P(x + 1,y)\) and Claim 2.4, we have
\[f((x + 1)f(y)) = f(x + y + 1) + f(xy + y) - f(y) = f(x + y) + f(xy + y) - f(y) + 1.\]
Also, from Claim 2.3 and \(P(x,y)\) , we have
\[f((x + 1)f(y)) = f(xf(y)) + f(y) = f(x + y) + f(xy).\]
Thus \(f(xy) = f(xy + y) - f(y) + 1\) . Replacing \(x\) with \(\frac{x}{y}\) gives the claim for all \(y\neq 0\) (whereas \(y = 0\) follows from Claim 2.4). \(\square\)
Claim 2.6 — If \(f\) is nonconstant, then \(f(x)\equiv x + 1\) .
Proof. We apply Claim 2.3, Claim 2.5, and Claim 2.4:
\[f(f(x) + y) = f(x) + f(y) = f(x + y) + 1 = f(x + y + 1).\]
If \(f(x)\neq x + 1\) for some \(x\) , then Claim 2.1 again gives a contradiction. \(\square\)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2024.jsonl",
"problem_match": "6. ",
"solution_match": "## \\(\\S 2.3\\) USA TST 2024/6, proposed by Milan Haiman \n"
}
|
2025
|
T0
|
1
| null |
IMO
|
Let \(n\) be a positive integer. Ana and Banana play a game. Banana thinks of a function \(f\colon \mathbb{Z}\to \mathbb{Z}\) and a prime number \(p\) . He tells Ana that \(f\) is nonconstant, \(p< 100\) and \(f(x + p) = f(x)\) for all integers \(x\) . Ana's goal is to determine the value of \(p\) . She writes down \(n\) integers \(x_{1},\ldots ,x_{n}\) . After seeing this list, Banana writes down \(f(x_{1}),\ldots ,f(x_{n})\) in order. Ana wins if she can determine the value of \(p\) from this information. Find the smallest value of \(n\) for which Ana has a winning strategy.
|
The answer is \(n = 83 + 89 - 1 = 171\)
In general, if Ana has to decide between periods from the set \(\mathcal{P}:= \{p_{1} > p_{2} > \dots >p_{r}\}\) of pairwise distinct relatively prime positive integers for \(r\geq 3\) , the answer is \(p_{2} + p_{3} - 1\)
## Bound
Suppose for the sake of contradiction that Ana has a winning sequence of integers \(x_{1},\ldots ,x_{n}\) with \(n\leq p_{2} + p_{3} - 2\) . We will generate contradictions by providing two primes \(p,q\in \mathcal{P}\) and associated nonconstant functions \(f_{p},f_{q}:\mathbb{Z}\to \mathbb{Z}\) with periods \(p\) and \(q\) respectively such that \(f_{p}(x_{i}) = f_{q}(x_{i})\) for all \(i\)
Claim — There exists a prime \(r\in \mathcal{P}\) such that for all primes \(p\in \mathcal{P}\setminus \{r\}\) , the set of integers \(\{x_{1},\ldots ,x_{n}\}\) forms a complete residue class modulo \(p\) (i.e. for all \(t\) , there exists \(i\) such that \(x_{i}\equiv t\) (mod \(p\) )).
Claim — Suppose for the sake of contradiction that such \(r\) didn't exist, and there were in fact two primes \(p,q\in \mathcal{P}\) such that \(\{x_{1}\ldots ,x_{n}\}\) did not form a complete residue class modulo either \(p\) or \(q\) . Concretely, consider \(t,s\) such that there is no \(i\) with \(x_{i}\equiv t\) (mod \(p\) ) and not \(j\) with \(x_{j}\equiv s\) (mod \(q\) ).
Construct the functions \(f_{p},f_{q}:\mathbb{Z}\to \mathbb{Z}\) as
and
We have \(f_{p}(x_{i}) = f_{q}(x_{i}) = 0\) for all \(i\) , which is the desired contradiction.
Let \(r\) be the prime from the above claim. Let \(p,q\) be the largest two primes in \(\mathcal{P}\setminus \{r\}\) , so \(n\leq p + q - 2\) . Construct the graph \(G_{pq}\) with vertex set \(\{x_{1},\ldots ,x_{n}\}\) and edge \(x_{i}\sim x_{j}\) if \(p\mid x_{i} - x_{j}\) or \(q\mid x_{i} - x_{j}\) . The following claim allows us to construct a pair of bad functions \(f_{p},f_{q}\) .
Claim — The graph \(G_{pq}\) is disconnected.
Proof. Let \(G_{p}\) be the graph on vertex set \(\{x_{1},\ldots ,x_{n}\}\) with edge \(x_{i}\sim x_{j}\) if \(p\mid x_{i} - x_{j}\) . Note that \(G_{p}\) is a collection of \(p\) disjoint cliques, one for each residue class modulo \(p\) .
Prune the graph into \(G_{p}^{\prime}\) , where each clique \(K_{r}\) is replaced by a path of edge- length \(r - 1\) . Define \(G_{q}^{\prime}\) similarly, and let \(G_{p q}^{\prime}\) be the union of \(G_{p}^{\prime}\) and \(G_{q}^{\prime}\) .
Note that \(G_{p q}\) and \(G_{p q}^{\prime}\) have the exact same connectivity properties. We have
\[|E(G_{p q}^{\prime})|\leq |E(G_{p}^{\prime})| + |E(G_{q}^{\prime})| = (n - p) + (n - q)\leq n - 2,\]
so \(G_{p q}^{\prime}\) is disconnected, as desired.
Suppose \(A\sqcup B = \{x_{1},\ldots ,x_{n}\}\) are sets of disjoint vertices in \(G_{p q}\) . Construct the functions \(f_{p},f_{q}:\mathbb{Z}\to \mathbb{Z}\) as
and
These are well defined due to the fact that \(p,q\nmid a - b\) for \(a\in A\) and \(b\in B\) , and the fact that \(A\sqcup B\) forms a complete residue class modulo \(p\) . Again, we have \(f_{p}(x_{i}) = f_{q}(x_{i})\) for all \(i\) , which is the desired contradiction.
## Construction
Let \(n = p_{2} + p_{3} - 1\) . We claim that Ana has a winning strategy with the selection \(x_{i} = p_{1}(i - 1)\) . Indeed, suppose that Banana writes down the values \(y_{1},\ldots ,y_{n}\) in order. We will show that Ana can always reconstruct \(p\) .
Claim — If \(y_{1} = \dots = y_{n}\) , then Ana can correctly guess \(p = p_{1}\) .
Proof. Suppose for the sake of contradiction that \(p< p_{1}\) . Then, since \(x_{1},\ldots ,x_{n}\) forms a complete residue class modulo \(p\) , \(f\) must be a constant function, which is the desired contradiction.
We can now assume that \(y_{1},\ldots ,y_{n}\) are not all equal, which means \(p\neq p_{1}\) . Suppose for the sake of contradiction that there are two primes \(q,r< p_{1}\) with associated nonconstant functions \(f_{p},f_{q}:\mathbb{Z}\to \mathbb{Z}\) with periods \(q\) and \(r\) respectively, such that \(f_{q}(x_{i}) = f_{r}(x_{i}) = y_{i}\) for all \(i\) .
The following claim shows that \(y_{1},\ldots ,y_{n}\) must all be equal, which is the desired contradiction.
Claim — Let \(G\) be the graph on vertex set \(\{0,\ldots ,q + r - 2\}\) with edge \(i\sim j\) if \(|i - j|\in \{q,r\}\) . The graph \(G\) is connected.
Proof. Note that \(G\) has \(q + r - 2\) edges, so it suffices to show that it has no cycles. Suppose for the sake of contradiction it had a cycle \(c_{1},\ldots ,c_{k}\) with \(k\geq 3\) and indices taken mod \(k\) .
Suppose first that \(c_{i + 1} - c_{i} = q\) . Then, \(c_{i + 2} - c_{i + 1}\) cannot be \(- q\) (else \(c_{i} = c_{i + 2}\) ), it cannot be \(r\) (else \(c_{i + 2} > q + r - 2\) ), so \(c_{i + 2} - c_{i + 1}\in \{q, - r\}\) .
The same logic shows the following collated results:
\[c_{i + 1} - c_{i} = q\Longrightarrow c_{i + 2} - c_{i + 1}\in \{q, - r\}\]
\[c_{i + 1} - c_{i} = -q \Rightarrow c_{i + 2} - c_{i + 1} \in \{-q, r\}\] \[c_{i + 1} - c_{i} = r \Rightarrow c_{i + 2} - c_{i + 1} \in \{-q, r\}\] \[c_{i + 1} - c_{i} = -r \Rightarrow c_{i + 2} - c_{i + 1} \in \{q, -r\}.\]
Thus, either all consecutive differences of vertices in the cycle are in \(\{q, - r\}\) , or all in \(\{- q, r\}\) . Assume the first case, proof is similar for second case.
Let \(a\) be the number of consecutive differences that are \(q\) , and \(b\) be the number that are \(- r\) . We see that \(a + b = k\) and \(qa - rb = 0\) . The second condition implies that \(a \geq r\) and \(b \geq q\) , so we have \(k \geq q + r\) , which is the desired contradiction since \(G\) has only \(q + r - 1\) vertices. \(\square\)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2025.jsonl",
"problem_match": "Problem 1. ",
"solution_match": "## \\(\\S 1.1\\) Solution to TST 1, by Anthony Wang \n"
}
|
2025
|
T0
|
2
| null |
IMO
|
Let \(a_{1},a_{2},\ldots\) and \(b_{1},b_{2},\ldots\) be sequences of real numbers for which \(a_{1} > b_{1}\) and
\[a_{n + 1} = a_{n}^{2} - 2b_{n\] \[b_{n + 1} = b_{n}^{2} - 2a_{n\]
for all positive integers \(n\) . Prove that \(a_{1},a_{2},\ldots\) is eventually increasing (that is, there exists a positive integer \(N\) for which \(a_{k}< a_{k + 1}\) for all \(k > N\) ).
|
Let \(r\) , \(s\) , and \(t\) be the complex roots of the polynomial \(p(\lambda) = \lambda^{3} - a_{1}\lambda^{2} + b_{1}\lambda - 1\) . By Vieta's formulas,
\[a_{1} = r + s + t\] \[b_{1} = 1 / r + 1 / s + 1 / t\] \[1 = rst.\]
Claim — For every positive integer \(n\) ,
\[a_{n} = r^{2^{n - 1}} + s^{2^{n - 1}} + t^{2^{n - 1}}\]
and
\[b_{n} = (1 / r)^{2^{n - 1}} + (1 / s)^{2^{n - 1}} + (1 / t)^{2^{n - 1}}.\]
Proof. The base case follows from Vieta's formulas above. For the inductive step, observe that \(rst = 1\) , so
\[a_{n + 1} = a_{n}^{2} - 2b_{n\] \[\qquad = \left(r^{2^{n - 1}} + s^{2^{n - 1}} + t^{2^{n - 1}}\right)^{2} - 2\left((1 / r)^{2^{n - 1}} + (1 / s)^{2^{n - 1}} + (1 / t)^{2^{n - 1}}\right)\] \[\qquad = \left(r^{2^{n - 1}} + s^{2^{n - 1}} + t^{2^{n - 1}}\right)^{2} - 2\left((st)^{2^{n - 1}} + (tr)^{2^{n - 1}} + (rs)^{2^{n - 1}}\right)\] \[\qquad = r^{2^{n}} + s^{2^{n}} + t^{2^{n}}\]
and similarly for \(b_{n + 1}\) .
Since \(p(1) = b_{1} - a_{1}< 0\) , \(p\) has a real root greater than 1; let \(r\) be the largest such root.
- If \(s\) and \(t\) are real, let \(m = \max (|r|,|s|,|t|) > 1\) be the largest magnitude of the roots and \(k\in \{1,2,3\}\) be the number of roots with that magnitude. Then asymptotically
\[a_{n} = r^{2^{n - 1}} + s^{2^{n - 1}} + t^{2^{n - 1}}\approx k m^{2^{n - 1}}\]
which implies that \(\{a_{n}\}\) is eventually increasing.
- If \(s\) and \(t\) are not real, they must be complex conjugates of each other, each with magnitude \(\frac{1}{\sqrt{r}} < 1\) . Therefore
\[r^{2^{n - 1}} - 2< a_{n}< r^{2^{n - 1}} + 2,\]
so \(\{a_{n}\}\) is eventually increasing.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2025.jsonl",
"problem_match": "Problem 2. ",
"solution_match": "## \\(\\S 1.2\\) Solution to TST 2, by Holden Mui \n"
}
|
2025
|
T0
|
3
| null |
IMO
|
Let \(A_{1}A_{2}\dots A_{2025}\) be a convex 2025- gon, and let \(A_{i} = A_{i + 2025}\) for all integers \(i\) . Distinct points \(P\) and \(Q\) lie in its interior such that \(\angle A_{i - 1}A_{i}P = \angle QA_{i}A_{i + 1}\) for all \(i\) . Define points \(P_{i}^{j}\) and \(Q_{i}^{j}\) for integers \(i\) and positive integers \(j\) as follows:
For all \(i\) \(P_{i}^{1} = Q_{i}^{1} = A_{i}\) For all \(i\) and \(j\) \(P_{i}^{j + 1}\) and \(Q_{i}^{j + 1}\) are the circumcenters of \(P P_{i}^{j}P_{i + 1}^{j}\) and \(Q Q_{i}^{j}Q_{i + 1}^{j}\) respectively.
Let \(\mathcal{P}\) and \(\mathcal{Q}\) be the polygons \(P_{1}^{2025}P_{2}^{2025}\ldots P_{2025}^{2025}\) and \(Q_{1}^{2025}Q_{2}^{2025}\ldots Q_{2025}^{2025}\) , respectively.
(a) Prove that \(\mathcal{P}\) and \(\mathcal{Q}\) are cyclic.
(b) Let \(O_{P}\) and \(O_{Q}\) be the circumcenters of \(\mathcal{P}\) and \(\mathcal{Q}\) , respectively. Assuming that \(O_{P}\neq O_{Q}\) , show that \(O_{P}O_{Q}\) is parallel to \(P Q\) .
|
Let \(n = 2025\) . Let \(\mathcal{P}_{i}\) and \(\mathcal{Q}_{i}\) denote the polygons \(P_{1}^{i}\cdot \cdot \cdot P_{n}^{i}\) and \(Q_{1}^{i}\cdot \cdot \cdot Q_{n}^{i}\) . In this notation, \(\mathcal{P} = \mathcal{P}_{n}\) , \(\mathcal{Q} = \mathcal{Q}_{n}\) , and \(\mathcal{P}_{1} = \mathcal{Q}_{1} = A_{1}\cdot \cdot \cdot A_{n}\) .
The angle condition for \(P\) and \(Q\) just says that they are isogonal conjugates in \(\mathcal{P}_{1}\) . We will first find some properties that do not depend on \(P\) having an isogonal conjugate.
Note that \(P_{i - 1}^{j + 1}P_{i}^{j + 1}\) is the perpendicular bisector of \(P P_{i + 1}^{j}\) , so we can go backwards from \(\mathcal{P}_{j}\) to \(\mathcal{P}_{j - 1}\) by reflecting over the sides. Use this to extend the points backwards to \(\mathcal{P}_{0}\) , i.e. define \(P_{i}^{0}\) to be the reflection of \(P\) over \(P_{i - 1}^{1}P_{i}^{1}\) .
## Lemma 1.1
For integers \(j \geq 0\) and \(i\) ,
\[\angle P P_{i}^{j}P_{i + 1}^{j} = \angle P P_{i}^{j + 1}P_{i + 1}^{j + 1}\quad \mathrm{and}\] \[\angle P P_{i + 1}^{j}P_{i}^{j} = \angle P P_{i}^{j + 1}P_{i - 1}^{j + 1}.\]
Proof. This is a standard circumcenter fact in disguise but we will prove it here for completeness. If \(X\) is the antipode of \(P\) on \((P P_{i}^{j}P_{i + 1}^{j})\) (equivalently, the reflection of \(P\) over \(P P_{i}^{j + 1}\) ) and \(M\) is the midpoint of \(P P_{i + 1}^{j}\) then
\[\angle P P_{i}^{j}P_{i + 1}^{j} = \angle P X P_{i + 1}^{j} = \angle P P_{i}^{j + 1}M = \angle P P_{i}^{j + 1}P_{i + 1}^{j + 1}.\]
The second equality is analogous.

## Lemma
The following similarity holds: \(\mathcal{P}_{n} \cup P \stackrel{\perp}{\sim} \mathcal{P}_{0} \cup P\) .
Proof. By Lemma 1.1,
\[\begin{aligned} \angle P P_{i}^{0} P_{i + 1}^{0} & = \angle P P_{i}^{1} P_{i + 1}^{1} = \dots = \angle P_{i}^{n} P_{i + 1}^{n} \quad \text{and} \\ \angle P P_{i + 1}^{0} P_{i}^{0} & = \angle P P_{i}^{1} P_{i - 1}^{1} = \dots = \angle P_{i - n + 1}^{n} P_{i - n}^{n} = \angle P_{i + 1}^{n} P_{i}^{n}. \end{aligned}\]
Therefore \(P P_{i}^{n} P_{i + 1}^{n} \stackrel{\perp}{\sim} P P_{i}^{0} P_{i + 1}^{0}\) . Combining these similarities for all \(i\) shows that \(\mathcal{P}_{n} \cup P \stackrel{\perp}{\sim} \mathcal{P}_{0} \cup P\) . \(\square\)
To solve part (a), we just need to show that \(\mathcal{P}_{0}\) and \(\mathcal{Q}_{0}\) are cyclic. This is where we need the isogonal conjugate property, and we can generalize from analogous facts for the \(n = 3\) case.

We have
\[\angle P P_{i + 1}^{0}P_{i}^{0} = \angle P A_{i}A_{i - 1} = \angle A_{i + 1}A_{i}Q\]
so
\[90^{\circ} = \angle (P P_{i + 1}^{0},A_{i}A_{i + 1}) = \angle (P_{i + 1}^{0}P_{i}^{0},A Q).\]
Since \(A_{i}P_{i}^{0} = A_{i}P_{i + 1}^{0}\) , it follows that \(A_{i}Q\) is the perpendicular bisector of \(P_{i}^{0}P_{i + 1}^{0}\) and \(Q P_{i}^{0} = Q P_{i + 1}^{0}\) . By applying this equality for all \(i\) , it follows that \(\mathcal{P}_{0}\) is cyclic with circumcenter \(Q\) . This completes the solution for part (a).
For part (b), we will analyze the angle of rotation and scale factor for the similarity \(\mathcal{P}_{n}\cup P\stackrel {\star}{\sim}\mathcal{P}_{0}\cup P\) . Assume without loss of generality that \(A_{1}A_{2}\dots A_{n}\) is labeled in clockwise order as in the earlier diagrams.
Claim — The spiral similarity at \(P\) sending \(\mathcal{P}_{0}\cup Q\) to \(\mathcal{P}_{n}\cup O_{P}\) is the composition of a clockwise rotation by \(\theta_{P}\) and a dilation with factor \(r_{P}\) , where
\[\theta_{P} = \frac{n\pi}{2} -\sum_{i = 1}^{n}\angle P A_{i}A_{i - 1}\quad \mathrm{and}\quad r_{P} = \prod_{i = 1}^{n}\frac{1}{2\sin\angle P A_{i}A_{i - 1}}.\]
Analogously, the spiral similarity at \(Q\) sending \(\mathcal{Q}_{0}\cup P\) to \(\mathcal{Q}_{n}\cup O_{Q}\) is the composition of a clockwise rotation by \(\theta_{Q}\) and a dilation with factor \(r_{Q}\) , where
\[\theta_{Q} = \frac{n\pi}{2} -\sum_{i = 1}^{n}\angle Q A_{i}A_{i - 1}\quad \mathrm{and}\quad r_{Q} = \prod_{i = 1}^{n}\frac{1}{2\sin\angle Q A_{i}A_{i + 1}}.\]
Proof. Note that
\[\angle P P_{0}^{i}P P_{0}^{i + 1} = \frac{\pi}{2} -\angle P P_{1}^{i}P_{0}^{i} = \frac{\pi}{2} -\angle P P_{1}^{i}P_{i - 1}^{1} = \frac{\pi}{2} -\angle P A_{i}A_{i - 1}\]
by circumcenter properties and Lemma 1.1. Summing over \(0\leq i< n\) yields the claimed formula for \(\theta_{P}\) , since the left hand side adds up to the rotation angle from \(P P_{0}^{0}\) to \(P P_{0}^{n}\) .
By the law of sines,
\[\prod_{i = 1}^{n}\frac{P P_{i}^{j + 1}}{P_{i}^{j}} = \prod_{i = 1}^{n}\frac{1}{2\sin\angle P P_{i + 1}^{j}P_{i}^{j}} = \prod_{i = 1}^{n}\frac{1}{2\sin\angle P A_{i}A_{i - 1}}\]
where in the last equality we use Lemma 1.1 again. Multiply over \(0\leq j< n\) and raise to the power \(\frac{1}{n}\) to obtain
\[\left(\prod_{i = 1}^{n}\frac{P P_{i}^{n}}{P_{i}^{0}}\right)^{\frac{1}{n}} = \prod_{i = 1}^{n}\frac{1}{2\sin\angle P A_{i}A_{i - 1}}.\]
This proves the formula for \(r_{P}\) because the left hand side gives the scale factor. The argument for \(Q\) is similar. Note that we reversed the angle in the formula for \(r_{Q}\) but not \(\theta_{Q}\) because \(\theta_{Q}\) depends on orientation.
By the given angle conditions on \(P\) and \(Q\) we have \(r_{P} = r_{Q}\) . Meanwhile,
\[\theta_{P} + \theta_{Q} = n\pi -\sum_{i = 1}^{n}(\angle P A_{i}A_{i - 1} + \angle Q A_{i}A_{i - 1}) = n\pi -\sum_{i = 1}^{n}\angle A_{i - 1}A_{i}A_{i + 1} = 2\pi .\]
This means that clockwise rotation by \(\theta_{Q}\) is just counterclockwise rotation by \(\theta_{P}\) . The combination of these two implies that \(P Q O_{Q}O_{P}\) is an isosceles trapezoid with \(O_{P}O_{Q}\) parallel to \(P Q\) , which proves part (b).
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2025.jsonl",
"problem_match": "Problem 3. ",
"solution_match": "## \\(\\S 1.3\\) Solution to TST 3, by Ruben Carpenter \n"
}
|
2025
|
T0
|
4
| null |
IMO
|
Let \(ABC\) be a triangle, and let \(X\) , \(Y\) , and \(Z\) be collinear points such that \(AY = AZ\) , \(BZ = BX\) , and \(CX = CY\) . Points \(X'\) , \(Y'\) , and \(Z'\) are the reflections of \(X\) , \(Y\) , and \(Z\) over \(BC\) , \(CA\) , and \(AB\) , respectively. Prove that if \(XY'Z'\) is a nondegenerate triangle, then its circumcenter lies on the circumcircle of \(ABC\) .
|
## \(\P\) Solution 1 (Pitchayut Saengrungkonga)

Let \(S\) denote the circumcenter of \(\triangle X^{\prime}Y^{\prime}Z^{\prime}\) . Observe that \(A Y = A Z = A Y^{\prime} = A Z^{\prime}\) , so \(Y Z Y^{\prime}Z^{\prime}\) is cyclic and \(A S\perp Y^{\prime}Z^{\prime}\) . Similarly, \(B S\perp Z^{\prime}X^{\prime}\) and \(C S\perp X^{\prime}Y^{\prime}\) .
The rest is angle chasing. Let \(\angle \ell\) denote the angle between line \(\ell\) and a fixed line. Then, we have
\[\angle A S = 90^{\circ} + \angle Y^{\prime}Z^{\prime} = 90^{\circ} + \angle Y Y^{\prime} + \angle Z Z^{\prime} - \angle Y Z\] \[\qquad = 90^{\circ} + \angle C A + \angle A B - \angle Y Z.\]
Analogously, we get
\[\angle B S = 90^{\circ} + \angle A B + \angle B C - \angle X Z,\]
so subtracting these gives \(\angle A S B = \angle A C B\) , as desired.
Remark. There are some other angle chasing solutions that use the fact that \(X X^{\prime}\) , \(Y Y^{\prime}\) , and \(Z Z^{\prime}\) meet at a point on \((X^{\prime}Y^{\prime}Z^{\prime})\) . This one is featured as it does not require any additional points.
\(\P\) Solution 2 (author) Let \(A^{\prime}B^{\prime}C^{\prime}\) be the anticomplimentary triangle of \(A B C\) . Note that \(X\) , \(Y\) , and \(Z\) are the projections of \(A^{\prime}\) , \(B^{\prime}\) , and \(C^{\prime}\) onto line \(X Y Z\) . Let \(A_{0}\) , \(B_{0}\) , and \(C_{0}\) be the reflections of \(A^{\prime}\) , \(B^{\prime}\) , and \(C^{\prime}\) over \(B C\) , \(C A\) , and \(A B\) , respectively. If we take \(A^{\prime}B^{\prime}C^{\prime}\) as our reference triangle, we see that \(A_{0}B_{0}C_{0}\) is the orthic triangle so \((A B C A_{0}B_{0}C_{0})\) is the nine- point circle of \(A^{\prime}B^{\prime}C^{\prime}\) .
Let \(A_{0}X^{\prime}\) meet \((A B C)\) again at \(P\) . Then
\[{\angle B B_{0}P=\angle A A_{0}P+\angle B C A}\] \[{\quad=\angle A A_{0}X+\angle B C A}\] \[{\quad=\angle(A^{\prime}X,B C)+\angle B C A}\] \[{\quad=\angle(B^{\prime}Y,C A)}\] \[{\quad=\angle B B_{0}Y^{\prime}.}\]
Therefore \(P\) lies on \(B_{0}Y^{\prime}\) , and likewise \(C_{0}Z^{\prime}\) by symmetry.

Let \(X_{0}\) , \(Y_{0}\) , and \(Z_{0}\) be the reflections of \(P\) across \(B C\) , \(C A\) , and \(A B\) respectively. By reflection, \(X_{0}\) lies on \(A^{\prime}X\) and \(P X^{\prime} = X_{0}X\) . We also know that if \(H\) is the orthocenter of \(A B C\) , then \(X_{0}Y_{0}Z_{0}H\) is the Steiner line of \(P\) . Let \(D\) be the reflection of \(H\) across \(B C\) , which is also the antipode of \(A_{0}\) on \((A B C)\) . Then \(\angle A^{\prime}X_{0}H = \angle A_{0}P D = 90^{\circ}\) , so \(X_{0}Y_{0}Z_{0}H\) is perpendicular to \(A^{\prime}X_{0}X\) and parallel to \(X Y Z\) .
This means that \(X X_{0} = Y Y_{0} = Z Z_{0}\) . Combined with \(P X^{\prime} = X X_{0}\) and analogous statements, we have \(P X^{\prime} = P Y^{\prime} = P Z^{\prime}\) so \(P\) is the circumcenter of \(X^{\prime}Y^{\prime}Z^{\prime}\) . This solves the problem.
Remark. If the condition that \(X\) , \(Y\) , and \(Z\) are collinear is removed, then in general the circumcenters of \(X Y Z\) and \(X^{\prime}Y^{\prime}Z^{\prime}\) are isogonal conjugates with respect to \(A B C\) .
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2025.jsonl",
"problem_match": "Problem 4. ",
"solution_match": "## \\(\\S 2.1\\) Solution to TST 4, by Michael Ren \n"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.